第六章固体中的光吸收和光发射
光的吸收、色散和散射

棱镜P1和P2的棱边相互垂直,从S发出的白光经透镜L1变为平行光束,通过P1后 沿水平方向偏折,如果在光路中不放置棱镜P2,光束由P1经透镜L2后将在幕上 形成水平的彩色光带ab,插入棱镜P2时,各色光束还要向下偏折,但偏折程度 随波长而异,于是幕上显现倾斜的光带 a ′b′ ,如果制做棱镜P1和P2材料的色散规 律(即n与 λ 的依赖关系)不同,倾斜光带 a ′b′ 将是弯曲的,它的形状直观地反 映了两种材料色散性能的差异。 色散曲线——折射率n与波长 λ 的之间依赖关系曲线,称色散曲线。 凡在可见光范围内无色透明的物质,它们的色散曲线形式上很相似, 其间有许多的特点,如n随 λ 的增加而单调下降,且下降率在短波一端更大等 等。这种色散称为正常色散。 正常色散 1836年科希(A、L、Cauchy)给出一个正常色散的经验公式: n=A+B/ λ2 +C/ λ4 式中A、B、C是与物质无关的常数,其数值由实验数据确定。当 λ 变化范围不大
/software/net/wangke/jiaoan/chapter8.htm
5/10/2011
w
页码,2/14(W)
− dI =I dx
式中 α 是个与光强无关的比例系数,称为该物质的吸收系数。 为了求出光束穿过厚度为l的媒质后光强度的改变,将上式改写为
dI = −α dx I dI ∫ I =∫ I0 0 — α dx
∴ I= I 0
I l
两边取积分
e
−αl
式中 I 0 和I分别为X=0和X=L处的光强,L是媒质的厚度, α 的量纲是长度的倒 数。
α −1 的物理意义是光强因吸收而减到原来的 e − 1 ≈36%时所穿过媒质的厚度。
式I= I 0 e −αL 称为布格尔定律(P、Bouguer,1729年)此定律后来经朗伯作了详细 说明,故也称朗伯定律。 布格尔定律是光吸收的线性规律 适用范围:线性光学领域,光强I不能太强。 如果光强太强,如用激光,则光与物质的非线性相互作用过程显示出来了,在 非线性光学领域内,吸收系数 α 将和其它许多系数(如折射率)一样,依赖于 电、磁场或光的强度,布格尔定律不再成立。 实验证明: 当光被透明溶剂中溶解的物质所吸收时,吸收系数 α 与溶液的浓度C成正比
固体发光课件

根据激发方式的不同,固体发光 可分为光致发光、电致发光、阴 极射线发光、化学发光和生物发 光等。
固体发光物质结构
晶体结构
固体发光物质多为晶体,其内部原子 或分子按一定规律排列,形成周期性 结构。
能级结构
固体发光物质的能级结构包括基态和 激发态,激发态的能量高于基态,当 物质吸收能量后,电子从基态跃迁到 激发态。
生物医学领域应用前景展望
生物成像
01
利用固体发光材料的荧光特性,进行生物标记和成像,可用于
研究细胞、组织等生物样本的结构和功能。
生物传感
02
将固体发光材料与生物分子相结合,构建生物传感器件,用于
检测生物分子、离子等物质的含量和变化。
光动力治疗
03
利用固体发光材料产生的光能,激活光敏剂并产生毒性作用,
材料性能参数及影响因素
发光效率
发光效率是衡量固体发光材料性能的重要指标, 包括量子效率和流明效率。量子效率表示发光的 量子数与吸收的量子数之比,流明效率则表示发 光的亮度与输入的电功率之比。
余辉时间
余辉时间是指发光材料在停止激发后,发光强度 衰减到初始强度的1/e所需的时间。长余辉材料在 夜间或暗环境下具有良好的指示和装饰效果。
发光颜色
发光颜色由材料的能级结构和发光机制决定,可 以通过改变材料的组成、结构或掺杂元素等方式 实现发光颜色的调控。
热稳定性
热稳定性是指固体发光材料在高温环境下的发光 性能保持能力。良好的热稳定性有助于提高材料 的可靠性和使用寿命。
新型固体发光材料研究进展
钙钛矿发光材料
钙钛矿是一类具有优异光电性能的材料,近年来在固体发光领域取得了重要进展。通过调 控钙钛矿的组成和结构,可以实现高效、稳定的固体发光。
固体中光的吸收和发射
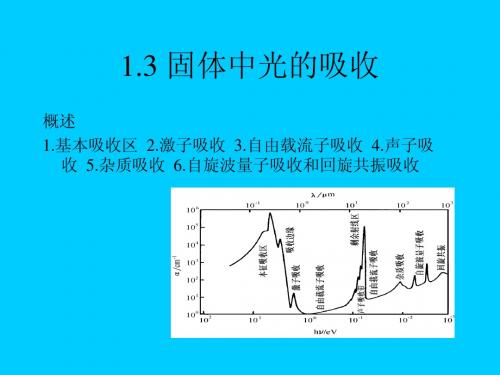
1.3 固体中光的吸收
概述 1.基本吸收区 2.激子吸收 3.自由载流子吸收 4.声子吸 收 5.杂质吸收 6.自旋波量子吸收和回旋共振吸收
h ax E g Eexc E p h ex E g Eexc E p
• 激子吸收谱是一个具有确定下限的带光 谱。单声子过程,还有多声子过程。 • 间接激子的吸收系数 (h Eg Eexc E p )1/ 2
1.3.3 杂质吸收
• 三个方面 1)从杂质中心的基态到激发 态的激发,可引起线状吸收 谱。 2)电子从施主能级到导带或 从价带到受主能级的吸收跃 迁 红外区
3)施主受主对的 辐射跃迁 分立谱线,远间 距的合并为连续 谱线 辐射跃迁几率与 空间间距的关系
W (r ) W0e
2 r / a*
外量子效率高
1.4.3 本征发光
• 导带电子和价带空穴复合发光 • 分为直接跃迁和间接跃迁 • 在较高温度下可以观察到,低温下很弱
1.直接跃迁
• 表现为谱带。自吸收 • 光谱分布 I (h ) 2 (h Eg )1/ 2 e[ ( h E ) / kT ]
g
2.间接跃迁
• 间接带隙半导体,带间复合发光需要声 子参加。发射声子时,光谱分布
1.3.1本征吸收
• 半导体吸收一个能量大于禁带宽度的光 子,电子由价带跃迁到导带,称本征吸 收 • 两种跃迁 直接跃迁:仅涉及一个(或多 个)光子的吸收。 间接跃迁:还包含声子的吸收 • 两种半导体:直接带隙半导体 间接带隙 半导体
固体激光器原理固体激光器

固体激光器原理-固体激光器固体激光器发展历程固体激光器发展历程固体激光器用固体激光材料作为工作物质的激光器。
1960年,梅曼发明的红宝石激光器就是固体激光器,也是世界上第一台激光器。
固体激光器一般由激光工作物质、激励源、聚光腔、谐振腔反射镜和电源等部分构成。
这类激光器所采用的固体工作物质,是把具有能产生受激发射作用的金属离子掺入晶体而制成的。
在固体中能产生受激发射作用的金属离子主要有三类:(1)过渡金属离子;(2)大多数镧系金属离子;(3)锕系金属离子。
这些掺杂到固体基质中的金属离子的主要特点是:具有比较宽的有效吸收光谱带,深圳市星鸿艺激光科技有限公司专业生产激光打标机,激光焊接机,深圳激光打标机,东莞激光打标机比较高的荧光效率,比较长的荧光寿命和比较窄的荧光谱线,因而易于产生粒子数反转和受激发射。
用作晶体类基质的人工晶体主要有:刚玉、钇铝石榴石、钨酸钙、氟化钙等,以及铝酸钇、铍酸镧等。
用作玻璃类基质的主要是优质硅酸盐光学玻璃,例如常用的钡冕玻璃和钙冕玻璃。
与晶体基质相比,玻璃基质的主要特点是制备方便和易于获得大尺寸优质材料。
对于晶体和玻璃基质的主要要求是:易于掺入起激活作用的发光金属离子;;具有适于长期激光运转的物理和化学特性。
晶体激光器以红宝石和掺钕钇铝石榴石为典型代表。
玻璃激光器则是以钕玻璃激光器为典型代表。
工作物质固体激光器的工作物质,由光学透明的晶体或玻璃作为基质材料,掺以激活离子或其他激活物质构成。
这种工作物质一般应具有良好的物理-化学性质、窄的荧光谱线、强而宽的吸收带和高的荧光量子效率。
玻璃激光工作物质容易制成均匀的大尺寸材料,可用于高能量或高峰值功率激光器。
但其荧光谱线较宽,热性能较差,不适于高平均功率下工作。
常见的钕玻璃有硅酸盐、磷酸盐和氟磷酸盐玻璃。
80年代初期,研制成功折射率温度系数为负值的钕玻璃,可用于高重复频率的中、小能量激光器。
晶体激光工作物质一般具有良好的热性能和机械性能,窄的荧光谱线,但获得优质大尺寸材料的晶体生长技术复杂。
固体激光器

固体激光器简介固体激光器是一种基于固体材料的激光发射器件。
与其他类型的激光器相比,固体激光器具有较高的效率、较高的输出功率和较低的噪声。
它们在多个领域中得到广泛应用,包括医学、材料加工、通信和科学研究等。
在固体激光器中,激光通过在固体材料中激发原子或离子引起的电子跃迁来产生。
这些材料通常是晶体或玻璃,并且它们的结构和组成决定了激光器的性能和特性。
原理固体激光器的工作原理基于三个基本过程:吸收、放大和辐射。
首先,固体材料吸收外部激发源(例如光或电能)的能量。
这种能量转移导致材料的原子或离子中的电子被激发到更高的能级。
当电子处于这种高能级时,它们有望通过受激辐射产生辐射能量。
然后,在经历一系列非辐射过程后,高能级的电子通过自发辐射受激发射出激光光子。
这种发射过程又被称为光放大。
这些激光光子在光学谐振腔中来回反射,同时经历光放大过程,最终形成高功率、高能量的激光束。
固体材料固体激光器中常用的材料包括晶体和玻璃。
不同的材料具有不同的性质和应用。
1.晶体材料:晶体激光器最早使用的材料是人工合成的天然晶体,如红宝石 (ruby) 和人工蓝宝石 (sapphire)。
这些材料具有较高的光学透明性和较高的激光输出功率。
晶体激光器通常在固体材料中掺入外来的色心(如Cr3+)来调节激光输出的波长。
其他常见的晶体材料还包括掺铱的钛蓝宝石和掺钬的氧化铽。
2.玻璃材料:相比晶体材料,玻璃激光器具有更大的放大带宽和更高的辐射受激发射截面。
这意味着玻璃激光器可以实现更宽波长范围内的激光输出。
常见的玻璃材料包括钕玻璃、铽玻璃和铒玻璃。
无论是晶体材料还是玻璃材料,固体激光器的性能和特性都取决于材料的结构和化学成分。
应用领域固体激光器在多个领域中应用广泛。
1.医学:固体激光器被广泛用于医学领域,用于激光手术、皮肤美容、眼科手术和牙科治疗等。
例如,钕玻璃激光器被用于激光眼部手术,以纠正近视、远视和散光等眼部问题。
2.材料加工:固体激光器可以用于材料切割、焊接和打孔等加工过程。
固体材料发光的过程

固体材料发光的过程固体材料发光是指一种特殊的物理过程,通过该过程使一些物质在受到外界激发后,从基态的低能级跃迁到激发态的高能级,随后再退回到基态而释放出能量。
这种能量释放就被称为发光。
在科学研究中,固体材料发光的过程又被称为发光效应。
发光效应除了在物理学中有着广泛应用外,也在许多现代高科技领域中发挥着重要作用,例如发光二极管(LED)、激光、荧光探测等。
因此,我们有必要更加深入地了解这种特殊的物理现象。
1. 固体材料发光的原理在固体材料中,原子与原子之间会相互作用,这种相互作用被称为晶格振动。
当固体材料受到能量激发时,晶格振动也会加强。
在这种情况下,一部分电子会从基态跃迁到激发态,形成一个高能电子空穴对。
在跃迁过程中,能量被吸收,电子将占据更高的能级。
接着,高能电子会以自旋转移过程或释放光子的形式退回到基态能级,此时它会释放出能量,使光子被激发并发出光线。
发出的光的颜色和物质交互的能量有关。
2. 固体材料发光的分类固体材料发光根据其发光机理的不同,可以分为热光发射、荧光发射、磷光发射三类。
(1)热光发射热光发射是指当物质被激发时,由于物质自身迁移、俩常相互碰撞、杂质等因素导致激发态电子从一个能级到达另一个能级,从而产生较为连续的光谱。
热发射通常重点考虑于固体,例如,金属的金属氧化物复合物(MOSFET)器件中,金属掺杂杂质随热上升转移时会发射光谱。
(2)荧光发射荧光发射是指物质在光子激发下产生荧光现象。
当物质受到较短的光辐射时,它的电子会从基态跃迁到激发态,它们会留在高级位置,直至它们的能量低于最初吸收的激发光子的能量。
此时,电子就会返回到基态位置,发散一个与吸收的激发光子的波长不相同、色散谱具有特定势能和外激发电子几何形状的新光子。
荧光相机、光发光材料、光伏器件都是荧光效应的应用物。
(3)磷光发射磷光发射是指物质激发到亚稳态和稳态后,再向低能级跃迁发射光谱。
它又被分为自激发发光、导致发光、化学发光三个部分。
固体物理中的光学性质

固体物理中的光学性质在固体物理领域中,光学性质是一个重要且引人瞩目的研究方向。
光学性质涉及到光的传播、吸收、散射、折射等现象,对于理解固体材料的结构和行为具有重要意义。
本文将简要介绍固体物理中的光学性质及其应用。
一、光的传播速度固体物理中的光学性质首先涉及到光的传播速度。
在真空中,光的传播速度为常数,即299,792,458米/秒。
然而,当光线进入介质中时,由于介质折射率的不同,其传播速度会发生改变。
根据斯涅尔定律,光线在两种介质之间传播时,入射角和折射角之间遵循一定的关系。
这个现象在固体物理中得到了广泛研究和应用。
二、吸收与发射固体物理中的光学性质还涉及到固体材料对光的吸收和发射现象。
在特定波长下,固体材料可以吸收光的能量,导致电子从基态跃迁到激发态。
不同材料对光的吸收和发射的特性不同,这一特性对于光电子器件和光催化反应等应用具有重要意义。
三、光的散射固体物理中的光学性质还包括光的散射现象。
当光线通过固体材料时,会与固体中的原子、离子或杂质发生相互作用,导致光的散射。
根据散射的形式,可以将其分为弹性散射和非弹性散射。
弹性散射不改变光的能量,而非弹性散射会导致光的能量发生改变。
这一现象在材料表征和光学传感器等方面具有广泛的应用。
四、材料的折射率固体物理中的光学性质还涉及到材料的折射率。
折射率是一个描述光在介质中传播行为的重要参数,定义为光在线速度和介质中的传播速度之比。
折射率越大,光在介质中传播的速度越慢。
折射率对于材料的光学性能和光学器件的设计具有重要意义。
五、光学材料的应用固体物理中的光学性质在许多领域中得到了广泛的应用。
例如,在光通信领域,光纤作为一种光学传输介质,其光学性质对于数据的传输速率和传输距离具有重要影响。
在光电子学领域,光学性质的研究和应用推动了光电子器件的发展,例如激光器、光电二极管和太阳能电池等。
此外,光学性质还在材料科学、能源领域、环境监测和医学诊断等方面有着重要应用。
例如,可见光谱技术被广泛应用于材料表征和质量检测领域,红外光谱技术在环境监测和生物医学领域具有重要应用。
光谱分析-光吸收

1/ v2 0 0 i0 /
则这解满足方程式。
(4.3)
这里v=c/N,c是真空中的光速,N是媒质的复折 射率,且N2=εc= εr- iεi, εc是媒质的复价电函数, εr和 εi分别是其实部和虚部。
考虑到自由空间中N=1, ε=1,μ=1,σ=0,
则媒质中:
c i / 0
3. 实验方法
3.1 吸收光谱测量
晶体的吸收光谱是通过光谱透射率测量而得到的, 按照(4.9)式和(4.10)式
T (1 R)2 (1 k 2 / n2 ) /[exp( d ) R2 exp( d )]
(4.9)
T (1 R)2 exp( d )
(4.10)
由实验得到的光谱反射率R和光谱透射率T以及实验 厚度d,可计算出吸收系数α的值,作α与光谱长λ(或
化为:
T (1 R)2 exp( d )
(4.13)
在上述类型实验中,只能在一些吸收微弱的 材料,即试样的厚度只是1/α的几倍时,才能分 别确定n和k。对于一些吸收性强,光学性质近似
于金属的材料而言,就必须测量偏振光的反射或
测量相当宽波段的光谱反射率来求出n和k。
光垂直入射时,反射波和入射波的振幅比是
膜干涉),由此可较准确地求得折射率。 如果薄膜中存在吸收,条纹的衬度就会降低或消 失,此时的光谱透射率表示为
T (1 R)2 (1 k 2 / n2 ) /[exp( d ) R2 exp( d )]
d:薄板厚度;R:光谱反射率
(4.12)
在半导体和介质的透射率测量中,一般
k2<<n2,而且exp(2αd)>>R2,因此上式简
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章固体中的光吸收和光发射光通过固体后,其强度或多或少地会减弱,实际上就是一部分光能量被固体吸收。
而固体施加外界作用,如加电磁场等激发,固体有时会产生发光现象。
这里涉及两个相反的过程:光吸收和光发射。
光吸收:光通过固体时,与固体中存在的电子、激子、晶格振动及杂质和缺陷等相互作用而产生光的吸收。
光发射:固体吸收外界能量,其中一部分能量以可见光或近于可见光的形式发射出来。
研究目的:研究固体中的光吸收和光发射,可直接地获得有关固体中的电子状态,即电子的能带结构及其它各种激发态的信息。
本章首先引出描述固体光学性质的若干参数及相互间的关系,主要用到电动力学知识;然后将陆续介绍几种主要的光吸收过程;最后还有固体发光的一些基本知识,其中用到固体物理和半导体物理一些知识。
1. 固体光学常数间的基本关系 (1) 吸收系数我们知道,当光透射(射向)固体时,光的强度或多或少地被削弱,这一衰减现象为光的吸收。
从宏观上讲,固体的光学性质可由折射率n 和消光系数κ来描述。
实际上,它们分别是复数折射率n c 的实部和虚部。
κi n n c +=.(1)当角频率为ω的平面电磁波射入一固体并沿固体中某一方向(x 轴)传播时,电场强度E :E =)](exp[0t vxi E -ω. (2)其中,v 为波在固体中的波速,而v 与复数折射率有如下关系:c n c v /=,c 为光速.(3)结合(1)、(2)和(3)式可得到,)exp()exp()exp(0cx cni t i E E κωκωω--=. (4)上式最后为衰减因子。
光强:I *2EE E =∝,于是,)exp()0()(x I x I α-=.(5)其中42λπκωκα==c . (6)为吸收系数。
而20)0(E I =(注:自由空间中022λππωcf ==。
)(2) 介电常数与电导率当电磁波在一种磁导率系数为μ,介电系数为ε和电导率σ为的各向同性介质中传播时,Maxwelll 方程组可写为:t H E ∂∂-=⨯∇ρρ0μμtE E H ∂∂+=⨯∇ρρρ0εεσ0=⋅∇H ρ0=⋅∇E ρ.求解波动方程,其中用到矢量运算法则,F F F ρρρ2)(∇-⋅∇∇=⨯∇⨯∇。
因为0=⋅∇E ρ,从tH E ∂⨯∇∂-=⨯∇⨯∇)(0ρρμμ,于是沿x 方向有2200022dtEd dt dE dx E d εεμμσμμ+=(7)取)](exp[0t vx i E E -=ω,于是得002022εεμμωσωμμω--=-i v(8a ) ωσμμεεμμ00021i v +=(8b )对光学中所讨论的大多数固体材料一般都是非磁性材料,因此它们的磁导率系数接近于真空的情形,1=μ。
因此,)(11222ωεσεc i c v +=. (9)其中用到001εμ=c 。
又因为c n c v /=,)2(12)(12222222κκκin n c c i n c n v c +-=+==,与(9)式比较得εκ=-22n (10a ) 02ωεσκ=n(10b )解上式可得,}1])(1{[212/1202++=ωεεσεn (11a ) }1])(1{[212/1202-+=ωεεσεκ(11b )对于电介质材料,一般导电能力很差,即σ → 0,于是其折射率n →ε,而消光系数κ → 0,材料是透明的。
对于金属材料,σ 很大,即202)(ωεσε<<,1)(2>>ωεεσ。
取极限0042πνεσωεσκ===n ,ν为电磁波频率。
前面已经提到,)exp()0()(x I x I α-=,04λπκα=,当透入距离x =d 1= α1 =πκλ40时,光的强度衰减到原来的1/e ,通常称1-α为穿透深度。
对金属材料:πσλεπνεπλπκλα4444000001cc ===- (12a )对于不良导体,σ较小,当202)(ωεσε>>时,则有(引入Taylor展开,1)(2<<ωεεσ), εωεεσε≅++=...])(212[21202n ; (13a ) 2040202)2(1...])(81)(21[21ωεσεωεεσωεεσεκ≅+-=.(13b )因此这种材料具有较小的消光系数κ,其穿透深度εσεεσωεπλα0001124c d ===-. (14)举例说明,对半导体材料Ge 而言,电导率σ=0.11Ω-1⋅cm -1,ε= 16,满足条件1)(2<<ωεεσ,因此折射率ε=n ,与电介质材料类似。
(3) 一个有用的关系式——Kramers-Kronig 关系式 可以参考C. Kittel 书中有关这一关系式的推导过程。
这里只给出结果。
定义复介电常数2c cn =ε,c ε为电磁波角频率ω的函数,)()(21ωεωεεi c +=,)(1ωε和)(2ωε分别为c ε的实部和虚部。
而二者满足以下关系式,'')('21)(022'21ωωωωεωπωεd ⎰∞-P += (15a ) ]'')(1[2)(022'12ωωωωεπωωεd ⎰∞-P --=(15b )其中P 代表Cathy 积分主值,)(0lim ⎰⎰⎰∞+-→∞+≡P αωαωα。
如果实验上测得吸收系数)()(ωααη=E ,ωη=E 为光子能量,吸收能谱关系,就可以将折射率的色散关系)(E n 用)(E α来加以表示。
前面我们定义,类比有'022''')(21)(dE EE E E P E n ⎰∞-=-κπ. (16)利用hcE E hc E h c E E )(4)(4)(44)(0κπνκππνκλπκα====,最后有 '022''2)(21)(dE EE E P hc E n ⎰∞-=-απ. (17)原则上讲,如果吸收光谱)('E α已知,就可以从上式求出折射率的色散关系。
(4) 反射率光从自由空间射入固体表面时,反射光与入射光强度之比为反射率R ,考虑简单的正入射情形时,])1/[(])1[(2222κκ+++-=n n R 。
对透明材料,κ = 0,22)1()1(+-=n n R . (18)对金属材料,前文已指出140>>==πνεσκn ,那么 σπνεκκ0222222421122122)1()1(-≈+++-=+++-=n n n n n n R . (19)2.固体中的光吸收过程以半导体为代表,吸收区主要可以划分为六个区。
光吸收的微观机制。
a.基本吸收区谱范围:紫外-可见光-近红外光机制:电子从价带跃迁到导带引起光的强吸收,吸收系数很高,常伴随可以迁移的电子和空穴,出现光电导。
b.吸收边缘界限机制:电子跃迁跨越的最小能量间隙,其中对于非金属材料,还常伴随激子的吸收而产生精细光谱线。
c.自由载流子吸收机制:导带中电子或价带中空穴在同一带中吸收光子能量所引起的扩展到整个红外甚至扩展到微波波段,显然吸收系数是电子(空穴)的浓度的函数,金属材料载流子浓度较高,因而这一区吸收谱线强度很大,甚至掩盖其它吸收区光谱。
d.晶体振动引起的吸收机制:入射光子和晶格振动(声子)相互作用引起的,波长在20~50 m。
e. 杂质吸收机制:杂质在本征能带结构中引入浅能级,电离能在0.01 eV 左右,只有在低温下易被观察到。
(为什么?)f. 自旋波或回旋共振吸收机制:自旋波量子、回旋共振与入射光产生作用,能量更低,波长更长,达到mm 量级。
接着我们将根据这几种吸收区分别加以介绍,首先是基本吸收。
可参见李名復著《半导体物理》第三章,科学出版社。
3. 基本吸收 机制与条件:电子吸收光子后由价带跃迁到导带的过程,显然只有当光子能量νh 大于禁带宽度g E 时,即g E h ≥ν,才有可能产生基本吸收现象。
因此存在一个长波极限,gE ch≤λ。
波长大于此值,不能引起基本吸收。
除能量要求外,电子从价带跃迁到导带还要满足一定的动量选择定则-动量守恒律,光子动量=-k k ηη';而光子的能量一般比电子的动量小许多,因此上述公式可以写为k k ≈'。
假定:半导体是纯净半导体材料,0 K 时其价带满导带空。
基本吸收分为两类,一是直接跃迁;另一是间接跃迁。
a. 直接跃迁电子吸收光子能量产生跃迁,保持波数(准动量)不变,称为直接吸收,这一过程无需声子的辅助,如图1所示。
如果所有跃迁都是许可的,跃迁几率P if 是一个常数。
能量守恒:if E h E +=ν. (20) 对于抛物线型简单能带结构:eg f m k E E 222η=-,hi m k E 222η-=。
其中m e 和m h 分别为导带电子和价带空穴的有效质量。
因此,rh e g m k m m k E h 2)11(22222ηη=+=-ν. (21)其中,he r m m m 111+=,m r 为约化有效质量。
单位能量间隔内,在k 空间从k 到k +d k 范围内的状态数,为)()(2)2()2(8)()(2/1322/332ννπππννh d E h m dk k h d h N g r -==η.(22)吸收系数)(ναh 当然与)(νh N 成正比:2/1)()()(g f i E h B h N AP h -==νννα. (23a )理论上可以求得,EE f 终态能量 E i 初态能量E g 0e he h e m nch m m m m e B 22/32/])2([+≈. (23b )B 与ν无关,上式中n 为纯净半导体材料的折射率。
以上讨论是在假定电子的跃迁对于任何k 值跃迁都是许可得出的。
而在某些材料中,在k =0处,电子的直接跃迁是禁止的,因为它不满足量子力学的选择定则;而对k ≠ 0,直接跃迁是许可的,而且跃迁几率P if 不再是一个常数,它正比于k 2,即正比于(h ν-E g ),此时有2/3'')()()(g f i E h B h N P A h -==νννα,(24a )νh m m B B h r 1)(32'≈. (B ’与ν有关)(24b )b. 间接跃迁由于某些半导体材料其导带底k 值和价带顶k 值不同,如图2所示(间接带隙材料)。
电子从价带到导带的跃迁为间接跃迁。
显然在满足能量守恒律时,动量也必须守恒,因此必须有声子的参与。
光子动量=±-q k k ρηρηρη'.(25)因为光子动量很小,上式简化为 图2 电子吸收光子能量从价带到导带的间接跃迁kE g +E pE g -E pq k k ρμηρηρη=-'.(26)其中q 为声子波矢,μ表示电子在跃迁时 发射(-)或吸收(+)一个声子;假定 声子具有能量E p ,能量守恒律表示为νh E E E p i f =±-. (27)对具有抛物线型简单能带结构的材料而言,能量处于E i 的初态态密度为2/12/332)2(21)(ih i E m E N ηπ=. (28)m h 为价带空穴有效质量。
