六年级数学《百分数的应用》错题案例及分析
六年级百分数应用中计算错题案例分析

六年级百分数应用中计算错题案例分析第二小学张海霞错题案例:百分数应用中学生都能根据利息=本金×利率×时间准确的列出式子,但对于计算方面出错率仍然很高。
主要表现在以下几方面:1、带入利率时忘记加百分号,个别学生数学解题习惯太差,总是出现遗漏现象。
2、学生将百分数转化成小数时出现错误;3、小数乘法计算时出现小数位数多或者少的现象;计算错误的现象。
错因分析:这些错误归结起来都反映了学生基础知识不扎实,数学学习习惯较差。
对于百分数与小数的互相转化思路不清,小数与整百,整千,整万数字相乘时步骤不清,小数乘法运算法则掌握不扎实导致的。
这也是此类习题必须解决的问题所在,如果不能解决此类习题很难做到100%全对。
改进措施︰1、旧知复习巩固(1)解决百分数与小数的互划问题。
在解题的过程中让学生明白百分数划小数:去掉百分号小数点向前移两位并在讲解的过程中理清思路,明确算理。
如给0.6添上百分号那么就变为60%了,也就是缩小了六十倍要想使大小不变就应利用积不变的规律给前面的数字扩大100倍,就变成了60%。
学生在理解算理的基础上会对这部分知识有了更深的认识,记忆更加牢固。
(2)解决小数与整百,整千,整万数字相乘时竖式列式技巧。
让学生总结概括出竖式列式时应将除零外的数字数位多的写上面,除零外的数字与数字对齐,并将零写在数字末尾。
(3)解决小数乘法计算。
明确步骤先依照整数乘法的方法进行计算,在将零移下来,最后数小数的位数并移动小数点。
以上三类为以前学习知识的复习与巩固,只要学生掌握了计算方法就可以准确的计算出得数。
但计算复杂且效率低2、渗透简算的方法学生理解积不变的定律:明确一个乘数扩大或缩小几倍,另一个乘数缩小或扩大几倍(0除外)积不变将此类题分为以下几种:(1)本金是整百数的。
本金缩小100倍,利率扩大100倍(去掉百分号)积不变,将给出的式子变形。
(2)本金是整千数的。
本金缩小1000倍,利率扩大1000倍(去掉百分号)积不变,将给出的式子变形。
百分数常见错例分析及剖析解答

百分数应用题常见错例分析及剖析解答学生在学习了“百分数的应用”后,做题时往往容易出错,这种情况很令老师们头痛。
以下3道题就是百分数应用题中常见的错例分析及剖析解答:1.一件毛衣现价150元,比原价贵25%,原价多少元?学生错解:生1: 150÷(1-25%)=150÷0.75=200(元)生2: 150×(1+25%)=150×1.25=187.5(元)生3:150×(1-25%)=150×0.75=112.5(元)错因分析: 学生在做这道题时,出现很多错解。
主要原因是没有去很好的理解题意,同时缺乏认真动脑思考问题的意识,还有就是对百分数应用题的解题方法没有学透彻。
因而造成列式出错。
题意剖析:本题关键要认真分析已知条件,看清现价是比原价“贵” 25%,因此首先要让学生明白单位“1”原价是未知的,而现价正好是原价的1+25%=125% 。
正确解答:150÷(1+125%)=150÷1.25=120(元)2.某校今年有学生3200人,比去年减少了310人,今年比去年减少了百分之几?(百分号前保留一位小数)学生错解:3200-310=2890(人) 310÷2890≈0.107=10.7% 错因分析: 学生在本题中出错是由于没有认真分析题意,对“今年比去年减少了310人”这一重要数学信息没有理解,才会造成列式出错。
题意剖析:此题中关键要让学生明白“今年比去年减少了310人”是指去年要比今年多310人。
因此应该先算出去年的人数,再去计算才行。
正确解答:3200+310=3510(人) 310÷3510≈0.088=8.8%3.某商场搞促销活动,所有商品一律打七五折,一件毛衣的现价是60元,比原价便宜了多少元?学生错解:60×75%=60×0.75=45(元) 60-45=15(元)错因分析:学生在本题中出错关键是没有弄清题意,盲目列式造成的。
人教数学六年级上《百分数》易错题解析(错题本),提高正确率!

人教数学六年级上《百分数》易错题解析(错题本),提高正确率!人教版数学六年级上册《百分数》易错点解析(错题本及答案),家长收藏吧一、填空1、六(1)班今天到校40人,请病假的5人,该班的出勤率是(88.9%)。
【解析:用到校人数就是出勤人数。
出勤人数÷全班人数×100%=出勤率。
40÷(40+5)×100%≈88.9%】2、(12.6)米比9米多40%【9×(1+40%)=12.6】 , 9米比(20)少55%【9÷(1-55%)=20】,200千克比160千克多(25)%【(200-160)÷160=25%】;160千克比200千克少(20)%【(200-160)÷200=20%】;16米比(6.4)米多它的60%【16×(1-60%)=6.4 注意:“它”是指16。
】;( )比32少30%【32×(1-30%)=22.4】。
【解析:本题主要是考查单位“1”(总量)、对应量、对应分率之间的关系。
单位“1”(总量)× 对应分率=对应量】3、某种皮衣价格为1650元,打八折出售可盈利10%。
那么若以1650元出售,可盈利(450)元。
【解析:本题关键是要先算出进价,原题中的“10%”是针对进价的。
设皮衣的进价为x元。
(1+10%)x=1650*80% 解得:x=1200。
以1650元出售,可盈利:1650-1200=450(元)】二、判断1、某商品先提价5%,后又降阶5%,这件商品的现价与原价相等。
(×)【解析:错。
两个5%的单位“1”不一样。
1×(1+5%)×(1-5%)=0.9975 值小于1表示现价比原价少,值大于1表示多。
】【解析:错。
用假设法来验证:假设盐是20克,水是80克,则含盐就是20%。
如果分别同时加入10克盐和水,那么这时含盐率就是:(20+10)÷(20+10+80+10)×100%=25%,含盐率变大了。
六年级上册数学 百分数单位1易错应用题解析
六年级上册数学
百分数单位1易错应用题解析
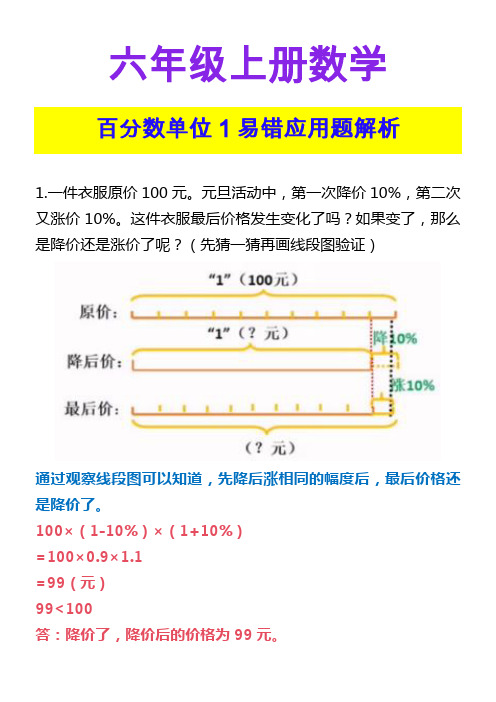
1.一件衣服原价100元。
元旦活动中,第一次降价10%,第二次又涨价10%。
这件衣服最后价格发生变化了吗?如果变了,那么是降价还是涨价了呢?(先猜一猜再画线段图验证)
通过观察线段图可以知道,先降后涨相同的幅度后,最后价格还是降价了。
100×(1-10%)×(1+10%)
=100×0.9×1.1
=99(元)
99<100
答:降价了,降价后的价格为99元。
六年级上册数学
百分数单位1易错应用题解析
2.一条围巾原价30元。
元旦活动中,先涨价10%,后又降价10%。
这围巾最后价格发生变化了吗?如果变了,那么是降价还是涨价了呢?(先猜一猜再画线段图验证)
通过观察线段图可以知道,先涨后降相同的幅度后,最后价格还是降价了。
30×(1+10%)×(1-10%)
=30×1.1×0.9
=29.7(元)
29.7<30
答:降价了,降价后的价格为29.7元。
六年级上册数学
百分数单位1易错应用题解析
3.一种电脑销售中第一次比原价3600元降低了10%,第二次又降低了10%。
这种电脑现价多少元?(先猜一猜再画线段图且计算出结果)
3600×(1-10%)×(1-10%)
=3600×0.9×0.9
=2916(元)
答:这种电脑现价是2916元。
百分数应用题解答典型错例剖析

220
=
:
n 0
( 千克 )
“
-
t
、
·
对策
:
向学生 说 明原 题 的 1 0 肠是 以现 在制
“
剖析 学 生 对单位
’
1
”
的 量 混 淆不 清
。
-
造零 件数 为单 位
l
”
的 , 这样反 过来 理 解的
1 0 拍 是 以 原 来 制 造 零件数 为单
1 0 帕 这 个分 率 虽 未变 ,
位
“
互
”
,
显然
单位
“
1
”
:
的 过程
路
,
对策
〔例 2 〕 一 根 铅 丝 长 2 米 ,
帮 助学 生 明确本 题 需 在 统 一 单位
。
’l t
”
的 前 提 下求 运来水 果 总 数
“
教给学 生 统
x
2“ ”
,
扎` 箩 口 用 去
2
’
米 奋
(
,
还 剩 多少 米 :
25 呱
一
一单 位
l
”
的方 法
,
将 第 二 天 卖出第 ~ 天 的
,
使学 生严 格 加 以
学生 解 答百 分 数 应用题 常 发生
进 而 根据 数 量 之 间
〔 例 3 〕 发电 厂
,
、
错误
,
本 文将 搜集 的 典 型 错例
,
加以 剖 析
分率 之 间 的 关 系 进行 解答
。
分率 之 ’ & I
一
数 最与
’
`
六年级数学百分数的应用试题答案及解析
六年级数学百分数的应用试题答案及解析1.工程队计划20天挖一条800米的水渠,实际16天就完成了任务.工程队的实际工作效率比计划提高了百分之几?【答案】25%【解析】先求出计划的工作效率,再求出实际的工作效率,再看实际提高的效率占原计划的百分之几。
解:计划每天的效率:800÷20=40(米)实际每天的效率:800÷16=50(米)提高的效率:(50-40)÷40=25%答:工程队的实际工作效率比计划提高了25%。
【考点】百分数的实际应用。
点评:此题关键是找准单位“1”。
然后用已知一个数的百分之几是多少求这个数,用除法计算。
2.科技小组进行玉米种子发芽实验,结果有500粒种子发芽了,25粒种子未发芽,求这批种子的发芽率。
【答案】95.2%【解析】首先理解发芽率,发芽率是指发芽的种子粒数占种子总粒数的百分之几,先求出种子的总粒数,进而用:×100%=发芽率,由此列式解答即可。
解:实验种子的总粒数:500+25=525(粒)发芽率:×100%≈0.952=95.2%。
答:这批种子的发芽率是95.2%。
【考点】百分率应用题。
3.甲、乙两个书架共有本书,从甲书架借出,从乙书架借出以后,甲书架是乙书架的倍还多本,问乙书架原有多少本书?【答案】500【解析】这个题目的难点就在于甲乙的数目同时发生了变化,变化之后的关系是两倍还多本,也就是说:甲的比乙的的两倍还多本,如果能够正确地理解和转化这个条件,这道题也就迎刃而解了,从上图中不难看出,“甲的比乙的的两倍还多本”其实也就是“甲的比乙的多本”,如果同时扩大两倍,他们之间的关系就变成了“甲的比乙多本”,结合“甲乙的和为本”这个条件,这个问题就变成了一个简单的和倍问题了。
,,(本),,(本)甲的书本数目(本)乙的书本数目方法二:设甲原有x本书,,解得,则乙为500本。
4.一副羽毛球拍现价35元,比原价降低了5元。
现价是原价的百分之几?降低了百分之几?【答案】(1)35÷(35+5)=35÷40=87.5%(2)5÷(35+5)=5÷40=12.5%答:现价是原价的87.5%,降低了12.5%。
分数百分数应用题常见错误原因分析及解题策略

分数百分数应用题常见错误原因分析及解题策略学生在解答分数百分数应用题时,经常会出现这样或那样的错误。
通过分析造成这些错误的原因,提出相应的对策,有利于帮助学生防错、纠错,提高解答分数应用题的能力。
一、把抽象的分率当成具体数量。
例1:一根绳子长10米,剪去4/5又4/5米,还剩多少米?错解:10-4/5-4/5=8.4(米)产生以上错误的原因是:把抽象的分率"4/5"当成具体数量"4/5米"。
"4/5"与"4/5米"表示的实际意义并不相同。
"4/5"是指"10米的4/5",它表示10×4/5=8(米);"3/5米"是指实际数量。
正确解法为:10-10×4/5-4/5=1.2(米)或10-(10×4/5+4/5)=1.2(米)。
为了防止学生出现这样的错误,教师应帮助他们弄清一个分数不带单位时,表示相对意义,它是由单位"1"的大小决定的;一个分数带上单位后,就表示一个具体数量,具有绝对意义,它的大小是不能改变的。
二、把具体数量当成抽象的分率。
例2:一件工作,单独做,甲要1/5小时,乙要1/4小时。
今甲、乙二人同时合做,多少小时可以做完?错解:1÷(1/5+1/4)=2 2/9(小时)出现这种错误解法,是学生被常见的分数工作效率所干扰,因而误认为分数表示的工作时间是工作效率。
甲的工作效率应为(1÷1/5),乙的工作效率应为(1÷1/4)。
正确解法为:1÷(1÷1/5﹢1÷1/4)=1/9(小时)。
为了避免解题错误,教师要帮助学生认真审题,弄清工程问题的数量关系,预防工作时间与工作效率混淆。
三、对某些数量关系一知半解。
例3:车站有45吨货物,用甲汽车10小时可以运完,用乙汽车15小时可以运完。
六年级下册数学试卷错题

一、错题回顾1. 错题一:分数乘法应用题题目:一个长方形的长是3/4米,宽是1/2米,求这个长方形的面积。
解答:3/4 × 1/2 = 3/8(平方米)正确答案:3/8(平方米)错因分析:在计算过程中,没有注意到乘法交换律,导致计算错误。
2. 错题二:百分数应用题题目:一件衣服原价是200元,打八折后,求现价。
解答:200 × 80% = 160(元)正确答案:160(元)错因分析:在计算过程中,没有正确理解“打八折”的含义,导致计算错误。
3. 错题三:比例应用题题目:一辆汽车从A地到B地,每小时行驶60千米,用了3小时。
求A地到B地的距离。
解答:60 × 3 = 180(千米)正确答案:180(千米)错因分析:在计算过程中,没有正确理解比例的概念,导致计算错误。
4. 错题四:方程应用题题目:小明有x个苹果,比小华多5个。
如果小明给小华5个苹果,那么小明的苹果数是小华的2倍。
求小明和小华原来各有多少个苹果。
解答:x + 5 = 2(x - 5)x + 5 = 2x - 10x = 15正确答案:小明有15个苹果,小华有10个苹果。
错因分析:在解方程的过程中,没有正确运用等式的性质,导致计算错误。
二、总结与反思通过分析以上错题,我发现自己在以下几个方面存在不足:1. 对基本概念和性质理解不透彻,导致计算错误。
2. 在解决应用题时,没有正确理解题意,导致计算错误。
3. 解方程时,没有正确运用等式的性质,导致计算错误。
针对以上不足,我将在今后的学习中加强以下方面:1. 重视基础知识的学习,加强对基本概念和性质的理解。
2. 在解决应用题时,提高自己的阅读理解能力,准确把握题意。
3. 在解方程时,熟练掌握等式的性质,提高解题速度和准确性。
通过不断努力,我相信自己能够克服这些不足,提高数学成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学《百分数的应用》错题案例及分析
1、错因分析
在五年级下学期,学生已经学习了百分数的意义和读写,百分数和分数、小数的互化,百分数的简单应用,运用方程解决简单的百分数问题,在此基础上,本单元进一步学习百分数的应用。
但百分数应用题仍是小学数学较难学好的内容之一,小学生解题时容易把解法混淆,该用乘法解答的却用除法解答,该用除法解答的却用乘法解答。
其次是在解答稍复杂的百分数应用题时,难以找到题目中数量的对应关系。
正确辨认应用题中的单位“1”,这是解答分数、百分数应用题的关键。
在确定单位“1”时,要特别注意分析应用题中含有“分率”或“百分率”的词句(即关键句)。
当正确地确定题中的单位“1”以后,再看题中的已知条件是什么,要求的是什么,从而正确地选择解法。
例如:人民机床厂计划生产400台机床,结果多生产了50台。
实际完成了计划的百分之几
[解](400+50)÷400=450÷400
==%。
答:实际完成了计划的%。
[常见错误]
400÷(400+50)
=400÷450
≈=%。
答:实际完成了计划的%。
错误原因:关键是要明确谁与谁比,被比的为单位“1”,然后用单位“1”作除数,求出商以后用百分数表示出来。
而本题是“完成了计划的百分之几”,这句问话的意思是:完成数是计划数的百分之几。
而错解中则恰恰弄反,求出了“计划是实际完成的百分之几”。
例如:育林小学三月份支出电费400元,四月份支出电费320元,四月份支出的电费比三月份节省了百分之几
[解](400-320)÷400
=80÷400
=
=20%。
答:四月份比三月份节省了20%。
[常见错误]
(400-320)÷320
=80÷320
=
=25%。
答:四月份比三月份节省了25%。
错误原因:所问“四月份支出的电费比三月份节省了百分之几”,正确理解是“四月份比三月份节省的电费是三月份的百分之几”。
而错解求的是“四月比三月节省的电费是四月份的百分之几”。
要避免出现这种错误,要对问题中的单位“1”加以正确的理解。
解答这类问题常见的错误是不能正确地确定谁是单位“1”,尤其有些题中,单位“1”并不明显,因此,常常发生错误。
2、改进措施:以上2个例题,都是属于“求一个数是另一个数的几(百)分之几”的应用题,解答这类题一般都用除法,除以谁关键是找单位“1”。
而单位“1”是在比较中得来的,如求甲数是乙数的几(百)分之几,则以乙数为单位“1”,若求乙数是甲数的几(百)分之几,则以甲数为单位“1”。
为了防止学生出现这样的错误,我会帮助他们弄清题中被比较的量(单位"1"的量)。
单位"1"的量,有时在题目中是明显的,有时要从题意去理解。
经过一系列的诱导训练,学生对负数的意义就理解得比较透切了,错误越来越小了。
