中考数学复习课教案 课时3 整式及其运算
中考复习第一轮课件3整式及其运算

课前热身
5、若|x+y-5|+(xy-6)2=0,则x2+y2的值为( A ) 、 |x+y-5|+(xy- =0,则 的值为( A.13 B.26 C.28 D.37 6、( 、(2007福建泉州课改)先化简下面的代数式, 福建泉州课改) 、( 福建泉州课改 先化简下面的代数式, 再求值: 再求值:a+2)(a−2)+a(4−a),其中 a = 2 + 1 ( 解:原式 = a 2 − 4 + 4 a − a 2 = 4a − 4 当 a = 2 +1 时,原式 =4( 2 +1) −4 =4 2+4−4 =4 2
中考数学复习整式教案

中考数学复习整式教案教案标题:中考数学复习整式教案教案目标:1.复习整式的基本概念和运算法则。
2.提升学生对整式的理解和应用能力。
3.培养学生解决数学问题的思维能力。
教学重点:1.整式的概念及其特点。
2.整式的加减乘除法运算法则。
3.整式在实际问题中的应用能力。
教学难点:1.整式的长乘法和除法运算。
2.整式的因式分解和合并同类项。
教学准备:1.教师准备:教学课件、教学素材。
2.学生准备:教科书、作业本、计算器。
教学过程:一、导入(5分钟)向学生介绍整式的定义,并回顾整式的基本概念。
例如:多项式中的项、次数、系数等。
二、整式的加减运算(10分钟)1.复习整式的加法运算法则,并通过例题进行巩固练习。
2.介绍整式的减法运算法则,并通过例题进行讲解和练习。
三、整式的乘法运算(15分钟)1.复习整式的乘法运算法则,并通过例题进行巩固练习。
2.讲解整式的长乘法运算方法,并通过例题进行引导和练习。
四、整式的除法运算(15分钟)1.复习整式的除法运算法则,并通过例题进行巩固练习。
2.讲解整式的除法运算方法,并通过例题进行引导和练习。
五、整式的因式分解(15分钟)1.复习整式的因式分解概念,并通过例题进行巩固练习。
2.讲解整式的因式分解方法,并通过例题进行引导和练习。
六、整式的合并同类项(10分钟)1.复习整式的合并同类项概念,并通过例题进行巩固练习。
2.讲解整式的合并同类项方法,并通过例题进行引导和练习。
七、实际问题的应用(10分钟)通过一些实际问题的例题,引导学生将所学的整式知识应用到解决实际问题中,并进行讨论和解答。
八、总结与作业布置(5分钟)总结整节课的重点内容,并布置相应的作业,以巩固学生对整式的理解和应用能力。
教学反思:1.整式是中考数学中的重要内容,需要学生在理解上下功夫。
因此在教学过程中要注重引导学生思考,加强练习巩固。
2.教学中可以准备一些实际生活中的问题,以引发学生的兴趣和思考,提高他们解决问题的能力。
九年级数学总复习第3课代数式整式运算教案新人教版
第3课 代数式 整式运算复习教学目标:1. 了解字母表示数的意义,了解单项式、多项式、整式以及单项式的系数与次数、多项式的项与次数、同类项的概念,并能说出单项式的系数和次数、多项式的项和次数。
知道正整数幂的运算性质,能说出去括号、添括号法则,了解两个乘法公式的几何背景。
2. 会用代数式表示简单问题中的数量关系,会求代数式的值,会把一个多项式按某个字母升(降)幂排列,会判断同类项,并能熟练地合并同类项,会准确地进行去括号与添括号,会推导乘法公式,能运用整式的运算性质、公式以及混合运算顺序进行简单的整式的加、减、乘、除运算。
3. 通过运用幂的运算性质、整式的运算法则和公式进一步发展观察、归纳、类比、概括等能力,会运用类比思想,一般到特殊、再由特殊到一般的数学思想和数形结合思想解决问题。
复习教学过程设计: Ⅰ.【唤醒】知识结构(阅读):一、填空:1.___ __ 和 _____ __ 统称为整式。
2. _____(_____(()_____(()_____(nnn ma a m n a a m n a m n ab m ⋅=÷===mmm 、都是正整数) 、都是正整数,且m>n )、都是正整数) 是正整数)____(0)a a =≠,____(0,paa p -=≠是正整数)()______m a b c ++=,()()__________m n a b ++=()_________am bm cm m ++÷= ()()__________a b a b +-=2()_________a b += 2()_________a b -=3.整式的混合运算顺序:先________、后________、再________、有括号先____________. 二、判断:1.22134a b ab -和是同类项。
( ) 2.244,333x y --单项式的系数是次数是。
( )3.3523x xy -+多项式的次数是五次三项式。
九年级数学复习教案整式新课标人教版【教案】.doc

课题基本内容练习石牌中学集体备课教案整式课的类型复习复备记录1、代数式的有关概念.(1)代数式是由运算符号把数或表示数的字母连结而成的式子.(2)求代数式的值的方法:①化简求值,②整体代人2、整式的有关概念(1)单项式:只含有数与字母的积的代数式叫做单项式.(2)多项式:几个单项式的和,叫做多项式(3)多项式的降幂排列与升幂排列(4)同类项:所含字母相同,并且相同字母的指数也分别相同的项,叫做同类顷.3、整式的运算(1)整式的加减:几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接.整式加减的一般步骤是:(2)如果遇到括号.按去括号法则先去括号:括号前是“十”号,把括号和它前面的“ +”号去掉。
括号里各项都不变符号,括号前是“一”号,把括号和它前面的“一”号去掉.括号里各项都改变符号.(3)合并同类项:同类项的系数相加,所得的结果作为系数.字母和字母的指数不变.4、乘法公式(1). 平方差公式 : a b a b a 2 b 2(2). 完全平方公式 : (a b)2 a 2 2ab b2 ,5、因式分解(1). 多项式的因式分解,就是把一个多项式化为几个整式的积.分解因式要进行到每一个因式都不能再分解为止.(2). 分解因式的常用方法有:提公因式法和运用公式法2 31、-л a b,是次单项式;12 的系数是2、多项式3x2-1-6x5-4x3是次项式,其中最高次项是,常数项是,三次项系数是,按 x 的降幂排列;3、如果 3m7x n y+7和 -4m2-4y n2x是同类项,则 x= ,y= ;这两个单项式的积是__。
4、下列运算结果正确的是()①2x3-x 2=x ② x3 ?(x 5 ) 2=x13 ③(-x) 6÷(-x) 3 =x3 ④(0.1) -2 ?10-1 =10(A)①②(B)②④( C)②③(D)②③④5、若 x2+ 2( m-3)x+ 16 是一个完全平方式,则 m的值是()21 1 xy2 x+y6、代数式 a - 1, 0, 3a ,x+ y ,- 4 , m,2 , 2 – 3b 中单项式是,多项式是,分式是。
初中数学整式及其运算教案

初中数学整式及其运算教案教学目标:1. 理解整式的概念,掌握整式的加减运算法则。
2. 能够正确进行整式的加减运算,解决实际问题。
3. 培养学生的逻辑思维能力,提高学生的数学运算技能。
教学内容:1. 整式的概念及分类2. 整式的加减运算法则3. 整式的加减实际应用教学过程:一、导入(5分钟)1. 引导学生回顾代数式的概念,让学生思考:代数式可以表示哪些数学关系?2. 学生分享代数式的应用场景,如方程、不等式等。
3. 教师总结:代数式是数学中用来表示数量关系的一种表达形式,而整式是代数式的一种特殊形式。
二、新课讲解(15分钟)1. 介绍整式的概念:整式是由数字、变量和运算符号组成的代数式,其中变量和数字的乘积称为单项式,多个单项式的和称为多项式。
2. 讲解整式的分类:单项式、多项式。
3. 介绍整式的加减运算法则:(1)同类项的加减法:同类项是指字母相同且相同字母的指数也相同的项。
同类项相加(减)时,只需将它们的系数相加(减)。
(2)合并同类项:将表达式中的同类项进行合并,合并时注意系数的正负号。
三、实例讲解(15分钟)1. 举例讲解整式的加减运算:例1:计算整式2x + 3 - 4x + 5的值。
解:2x + 3 - 4x + 5 = (2x - 4x) + (3 + 5) = -2x + 8。
例2:计算整式4x^2 - 2x + 1 - 3x^2 + 2x的值。
解:4x^2 - 2x + 1 - 3x^2 + 2x = (4x^2 - 3x^2) + (-2x + 2x) + 1 = x^2 + 1。
2. 让学生尝试解决实际问题:如一元二次方程的解法、线性方程组的求解等。
四、课堂练习(10分钟)1. 完成课本练习题,巩固整式的加减运算。
2. 教师挑选部分学生的作业进行讲解,解答学生的疑问。
五、总结(5分钟)1. 回顾本节课所学内容,让学生总结整式的概念、分类和加减运算法则。
2. 强调整式在实际问题中的应用,提醒学生注意整式运算的规则。
初中数学整式复习教案

初中数学整式复习教案教学目标:1. 理解整式的概念,掌握整式的基本性质。
2. 熟练掌握整式的加减法、乘除法运算规则。
3. 能够解决实际问题,运用整式进行表达和计算。
教学内容:1. 整式的概念及其基本性质。
2. 整式的加减法运算。
3. 整式的乘除法运算。
4. 实际问题中的整式应用。
教学过程:一、复习导入(5分钟)1. 回顾整式的概念:整式是由数字、变量和运算符组成的代数表达式。
2. 复习整式的基本性质:整式的系数、次数、项等概念。
二、整式的加减法运算(15分钟)1. 讲解整式加减法的运算规则:同类项相加减,系数相加减,变量及其指数不变。
2. 举例演示整式加减法的运算过程,让学生跟随老师一起完成。
3. 学生自主练习一些整式加减法的题目,老师进行个别辅导。
三、整式的乘除法运算(15分钟)1. 讲解整式乘除法的运算规则:整式乘法按照分配律进行,整式除法按照除法规则进行。
2. 举例演示整式乘除法的运算过程,让学生跟随老师一起完成。
3. 学生自主练习一些整式乘除法的题目,老师进行个别辅导。
四、实际问题中的整式应用(15分钟)1. 讲解如何将实际问题转化为整式问题,如何运用整式进行表达和计算。
2. 举例演示几个实际问题,让学生跟随老师一起解决。
3. 学生自主解决一些实际问题,老师进行个别辅导。
五、总结与反思(5分钟)1. 让学生回顾本节课所学的整式知识,总结整式的加减乘除运算规则。
2. 强调整式在实际问题中的应用,让学生认识到整式的重要性。
教学评价:1. 课后布置一些整式的练习题目,检验学生对本节课知识的掌握程度。
2. 在下一节课开始时,进行一个小测验,检验学生对整式的理解和运用能力。
以上是一份初中数学整式复习的教案,根据学生的实际情况,老师可以适当调整教学内容和教学过程。
初中整式的复习教案

初中整式的复习教案教学目标:1. 理解整式的概念,掌握整式的基本性质和运算规律。
2. 能够准确地识别和应用整式,解决实际问题。
3. 培养学生的逻辑思维能力和解决问题的能力。
教学内容:1. 整式的概念和基本性质2. 整式的运算规律3. 整式在实际问题中的应用教学过程:一、导入(5分钟)1. 引导学生回顾整数的定义和性质,为新课的学习打下基础。
2. 提问学生:整数在数学中有什么重要作用?你们能想到哪些实际问题需要用到整数?二、整式的概念和基本性质(15分钟)1. 介绍整式的定义:整式是由数字、变量和运算符组成的表达式,其中变量是有字母表示的数,运算符包括加、减、乘、除等。
2. 讲解整式的基本性质:整式的值是确定的,不随变量的取值而改变;整式可以进行加、减、乘、除等运算,遵循相应的运算规律。
3. 举例说明整式的应用:如解方程、求解实际问题等。
三、整式的运算规律(15分钟)1. 讲解整式的加减法运算规律:同类项可以相加减,不同类项不能直接相加减;整式的加减法遵循交换律、结合律等运算律。
2. 讲解整式的乘法运算规律:整式的乘法可以看作是多项式与多项式的乘法,遵循分配律、结合律等运算律。
3. 举例说明整式的运算规律的应用:如解代数式、求解实际问题等。
四、整式在实际问题中的应用(15分钟)1. 举例讲解整式在实际问题中的应用:如求解几何问题、经济问题等。
2. 让学生分组讨论,尝试解决给定的实际问题,并分享解题过程和结果。
五、课堂小结(5分钟)1. 回顾本节课所学的内容,让学生总结整式的概念、性质和运算规律。
2. 强调整式在实际问题中的应用,鼓励学生在日常生活中多观察、多思考、多应用。
六、作业布置(5分钟)1. 布置一些有关整式的练习题,让学生巩固所学知识。
2. 鼓励学生自主探究,发现整式在实际问题中的更多应用。
教学反思:本节课通过讲解整式的概念、性质和运算规律,让学生掌握了整式的基础知识,并能应用于实际问题中。
《整式及其加减的复习课》优秀教案
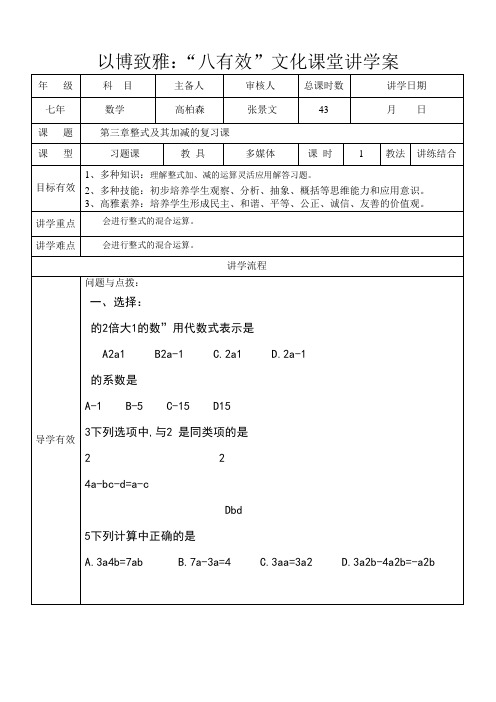
-5a-10a是( )次( ) 项式,其中最高次项的系数是
=10,=9时,代数式2-2的值是( )
8体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元,则代数式500-3a-2b表示的数为( )
4a2a4-5b5按字母b的升幂排列是;按字母a的升幂排列()
10某书每本定价8元,若购书不超过10本,按原价付款;若一次购书10本以上,>10本,付款金额为 ( ) 元。
三、解答:
111-2a24a2-2a-1-3a2-a1;
2-2ab-3a2-2a2-[5aba2-2ab]
12先化简,再求值:2222-2-32-222其中=-3,=2
展评有效
课堂分组学习——口头展示——教师点评——学生纠错
总结有效
师生同台
测试有效
中考链接(结合本节知识点)
板书设计
第三章整式及其运算的复习课
讲学重点
会进行整式的混合运算。
讲学难点
会进行整式的混合运算。
讲学流程
导学有效
问题与点拨:
一、选择:
的2倍大1的数”用代数式表示是
A2a1B2a-1C.2a1D.2a-1
的系数是
A-1B-5C-15D15
3下列选项中,与2是同类项的是
22
4a-bc-d=a-c
Dbd
5下列计算中正确的是
A.3a4b=7abB.7a-3a=4C.3aa=3a2D.3a2b-4a2b=-a2b
一选择:二填空: 三解答:
教学反思
以博致雅:“八有效”文化课堂讲学案
年级
科目
主备人
审核人
总课时数
讲学日期
七年
数学
高柏森
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 代数式
课时3.整式及其运算
【课前热身】 1. 3
1-
x 2
y 的系数是_________,次数是_________. 2.计算:2
(2)a a -÷=_________. 3.下列计算正确的是( )
A .5510x x x +=
B .5510·x x x =
C .55
10
()x x = D .20210x x x ÷= 4.计算2
3
()x x -所得的结果是( ) A .5x
B .5x -
C .6x
D .6x -
5. a ,b 两数的平方和用代数式表示为( )
A.22a b +
B.2
()a b + C.2a b + D.2a b +
6.某工厂一月份产值为a 万元,二月份比一月份增长5%,则二月份产值为( ) A.)1(+a ·5%万元 B.5%a 万元 C.(1+5%)a 万元 D.(1+5%)2a
【知识整理】
1. 代数式:用运算符号(加、减、乘、除、乘方、开方)把______________________连接而成的式子叫做代数式. 单独一个数或一个字母也是代数式.
2. 整式 (1)单项式:由数与字母的_______组成的代数式叫做单项式(单独一个数或字母也是单项式).
单项式中的________________叫做这个单项式的系数;单项式中的所有字母因数的 _________叫做这个单项式的次数.
(2)多项式:几个单项式的________叫做多项式.在多项式中,每个单项式叫 做多项式的_______,其中次数最高的项的_______叫做这个多项式的次数.不含字母的项叫做__________.
(3)整式:____________与____________统称整式.
3. 同类项:在一个多项式中,所含_________相同并且相同字母的_________也分别相等的项叫做同类项. 合并同类项的法则是______________________________________________.
4. 幂的运算性质: a m ·a n =_______; (a m )n =_______; a m ÷a n =_______; (ab )n =_______.
5. 乘法公式:
(1) (a +b )(c +d )= ____________________; (2)(a +b )(a -b )= _____________________; (3) (a +b )2=_____________________; (4) (a -b )2=_____________________. 6. 整式的除法
⑴ 单项式除以单项式的法则:把___________、___________________分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
⑵ 多项式除以单项式的法则:先把这个多项式的每一项分别除以______________,再把所得的商_________.
【例题讲解】
例1 若0a >且2x a =,3y a =,则x y a -的值为( ) A .1-
B .1
C .
23
D .
32
例2 按下列程序计算,把答案写在表格内:
⑴ 填写表格:
输入n 3 2
1 -
2 -
3 … 输出答案
1
1
…
⑵ 请将题中计算程序用代数式表达出来,并给予化简.
例3 化简
(1)2x 2+(-x 2+3xy +2y 2)-(x 2-xy +2y 2); (2)(
25x 3y 2-7xy 2+23y 3)÷(23
y 2)
例4 先化简,再求值: (1) x (x +2)-(x +1)(x -1),其中x =-2
1;
(2)2
2
(3)(2)(2)2x x x x +++--,其中13
x =-.
n 平方 +n n -n 答案
例5 观察下面的点阵图和相应的等式,探究其中的规律: (1)在④和⑤后面的横线上分别写出相应的等式;
① 1=12 ② 1+3=22 ③ 1+3+5=32 ④________________ ⑤______________________… (2)通过猜想写出与第n 个点阵相对应的等式为_____________________________________. 例6 已知:a =
120x +20,b =120x +19,c =120
x +21,求代数式a 2+b 2+c 2-ab -bc -ac 的值.
【中考演练】
1. 计算(-3a 3)2÷a 2的结果是( )
A. -9a 4
B. 6a 4
C. 9a 2
D. 9a 4
2. 下列运算中,结果正确的是( )
A.633·x x x =
B.422523x x x =+
C.23
5
()x x = D .2
2
2
()x y x y +=+ 3. 下列各对式子是同类项的是( ) A.4x 2y 与4y 2x B.2abc 与2ab C.3a -
与-3a D.-x 3y 2与1
2
y 2x 3 4. 小马虎在下面的计算中只做对了一道题,他答对的题目是( ) A.(a -b )2=a 2-b 2 B.(-2a 3)2=4a 6 C.a 3+a 2=2a 5 D.-(a -1)=-a -1
5. 如图所示,在边长为a 的正方形中挖去一个边长为b 的小正方形(a >b ),再把剩余的部分剪拼成一个平行四边形,通过计算图形(阴影部分)的面积,验证了一个等式是( )
A.a 2-b 2=(a +b )(a -b )
B.(a +b )2=a 2+2ab +b 2
C.(a -b )2=a 2-2ab +b 2
D.(a +2b )(a -b )=a 2+ab -2b 2
6. 已知代数式2346x x -+的值为9,则24
63
x x -
+的值为( ) A .18 B .12 C .9 D .7 7. -102x 2y 的系数是________,次数是______. 8.若a +b =2,ab =-1,则a 2+b 2=________.
9. 若3
2
23m
n
x y x y -与 是同类项,则m +n =____________.
10.观察下面的单项式:x ,-2x 2,4x 3,-8x 4,…根据你发现的规律,写出第7个式子____. 11.化简:[(-y )2·(-2x )]2-(-2xy )3÷xy 2·(-12
y 3)
12. 先化简,再求值:
⑴ 3
(2)(2)()a b a b ab ab -++÷-
,其中a =1b =-;
⑵ ,其中1x =
,y =
.
13.大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)
根据前面各式规律,则5
()a b +=_____________________________________________.
)(2)(2
y x y y x -+- 1
1 1 1
2 1 1
3 3 1 1
4 6 4 1 .......................................
Ⅰ
Ⅱ
1222332234432234
()()2()33()464a b a b
a b a ab b a b a a b ab b a b a a b a b ab b +=++=+++=++++=++++
14.先阅读下列材料,再解答后面的问题:
材料:一般地,n个相同的因数a相乘:记为a n.如23=8,此时,3叫做以2为底,8的对数,记为log28(即l og28=3).一般地,若a n=b(a>0且a≠1,b>0),则n叫做以a为底,b的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:
(1)计算以下各对数的值:log24=______;log216=______;log264=______.
(2)观察(1)中三数4、16、64之间满足怎样的关系式?log24,log216,log264之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
log a M+log a N=___________.(a>0且a≠1,M>0,N>0)
根据幂的运算法则:a m·a n= a m+n以及对数的含义证明上述结论.。
