第七章统计指数作业试题及答案
概率论与数理统计习题及答案第七章

习题7-11.选择题(1)设总体X 的均值口与方差 /都存在但未知,而X 1,X 2,L ,X n 为来自X 的样本,则均值 口与方差 (T 2的矩估计量分别是 ().(A) X 和(B)1 nX 和—(Xn i 1i )2.(C)口和 2(T・1 (D) X 和一 nn(X ii 1 x)2.解 选(D).(2) 设X : U[0,],其中 e >0为未知参数,又X ,,X 2,L ,X n 为来自总体X 的样本 ,则e 的矩估计量是().(A) X . (B)2X . (C)max{X i }.(D)mi^X i}.解选(B).2.设总体X 其中0v B v 为未知参数,X1, X 2,…,X.为来自总体X 的样本,试求e 的矩 估计量.解 因为 E (X )=(- 2)x3 e +1x (1 -4 e )+5x e =1-5 e ,令 1 5 X 得到的矩估计量为3.设总体X 的概率密度为f(x ;)(1)x ,0 x 1,0,其它•其中 0> -1是未知参数,X ,冷… ,X n 是来自 X 的容量为n 的简单随机样本求:(1) 的矩估计量;⑵ 0的极大似然估计量•解 总体X 的数学期望为-19 2X 1令E(X) X ,即一1 X,得参数B 的矩估计量为?•21 X设X 1, X 2,…,x n 是相应于样本X 1, X 2,…,X n 的一组观测值,则似然函 数为n(1)n X i , 0x i 1,i 10,其它.In xi 1In X ii 14.设总体X 服从参数为的指数分布,即X 的概率密度为E(X)1xf(x)dx o (1)x dx当 0<X i <1(i =1,2,3,…,n )时,L >0 且 In L nln(1)In X i ,i 1dln LnIn x =0,得0的极大似然估计值为而0的极大似然估计量为f(X,xe , x 0,其中0为未知参数,X, X2,)0, x< 0,…,X n为来自总体X的样本,试求未知参数的矩估计量与极大似然估计量解因为E(X)= 1= X , 所以的矩估计量为设X1, X2,…,x n是相应于样本X i, X2,…,X 的一组观测值,则似然函数取对数Xii 1然估计量为In L 0,得5.设总体X的概率密度为f (x,) 其中(0< <1)是未知参数.X, N为样本值x1, X2,L ,x n中小于极大似然估计量•解⑴ X E(X) xnInnXn e 11X).的极大似然估计值为1,的极大似X0,X2,0x1,, 1< x< 2,其它,…,X n为来自总体的简单随机样本,记1的个数.dx 2x(1求:(1)e的矩估计量;(2)e的3 3 —)dx ,所以矩一X .2 21⑵ 设样本X ,X 2 ,L X n 按照从小到大为序(即顺序统计量的观测值)有如下关系:X (1) w X (2)X ( Ni <1 W X ( N +1) W X (N+2)X (n ).似然函数为N n NL()(1 ),X (1) w X (2) w L w X ( N ) 1W X (N1) W X (N2) w L w X n ,0,其它.考虑似然函数非零部分,得到In L ( 0 ) = N ln 0 + ( n -N ) ln(1 - 0 ),令d |nL ( )」o ,解得0的极大似然估计值为? N .d1n习题7-2的无偏估计量•1.选择题:设总体X 的均值与方差 2都存在但未知,X i ,X 2,L ,X n 为X 的样本,则无论总体 X 服从什么分布,()1X i和丄 (XiX)2.(B)n i 1 n i1 n(C)X i 和n 1 i 1解 选(D).2.若X 1 ,X 2lx1 1X 2kX 334解 要求E( 7X 1-X j 和丄 1 i 1 n 1n(X ii 1X)2.(X i1)2 • (D)X i 和丄(X i)2.X 3为来 自总体X : N(,2)的样本,且的无偏估计量,问k 等于多少1 11 「2 kX 3)3 4k解之,k=g(A)13.设总体X的均值为0,方差2存在但未知,又X「X2为来自总体X1 2 2的样本,试证:—(X i X2)为的无偏估计21 2 1 2 2证因为E[—(X i X2) ] —E[(X i 2X^2 X2 )]2 2-[E(X i2) 2E(X i X2)E(X22)]-2 2所以-(X i X2)2为2的无偏估计•2习题7-31.选择题(1)总体未知参数的置信水平为的置信区间的意义是指()(A)区间平均含总体95%的值.(B)区间平均含样本95%的值.(C) 未知参数有95%的可靠程度落入此区间.(D) 区间有95%的可靠程度含参数的真值•解选(D).(2)对于置信水平1- a (0< a <1),关于置信区间的可靠程度与精确程度F列说法不正确的是().(A)若可靠程度越咼,则置信区间包含未知参数真值的可能性越大(B)如果a越小,则可靠程度越高,精确程度越低•(C)如杲1 - a越小,则可靠程度越高,精确程度越低•(D)若精确程度越高,则可靠程度越低,而1- a越小.解选(C)习题7-41. 某灯泡厂从当天生产的灯泡中随机抽取9只进行寿命测试,取得数据如下(单位:小时): 1050, 1100, 1080 , 1120, 1250, 1040, 1130, 1300, 1200设灯泡寿命服从正态分布 N 口 , 902),取置信度为,试求当天生产的全部灯泡的平均寿命的置信区间所求置信区间为(x - z /2 , X - z /2 ) \l n J n 90 90 (1141.11 = 1.96,1141.11 r 1.96)V 9V 9(1082.31,1199.91).2.为调查某地旅游者的平均消费水平,随机访问了40名旅游者,算得平均消费额为 X 105元,样本标准差s 28元•设消费额服从正态分布 取置信水平为,求该地旅游者的平均消费额的置信区间解计算可得X 105, s 2 =282.对于a =,查表可得t_(n 1) t o.025(39)2.0227.2所求口的置信区间为3. 假设某种香烟的尼古丁含量服从正态分布 .现随机抽取此种香烟 8支解计算得到X1141.11, CT 2 =902.对于a =,查表可得Z /2Z).Q25匸96*(Xt (n 1), x ■■- n 2s —t (n ■■- n 21)) (1052.0227, 1052.0227)2828为一组样本,测得其尼古丁平均含量为毫克,样本标准差s=毫克.试求此种香烟尼古丁含量的总体方差的置信水平为的置信区间.a =,查表可得 2(n 1) 爲5(7) 20.278,并说明该置信区间的实际意义1 2的置信水平为的置信区间是,”的实际意义是:在两总体第一个正态总体的均值1比第二个正态总体均值 2大〜,此结 论的可靠性达到95%.5.某商场为了了解居民对某种商品的需求 ,调查了 100户,得出每户月2解已知n =8, s2 2 (n 1)0.995(7) 1 - 20.989,所以方差d 2的置信区间为((n 1)S 2(2_ (n 1)22 22(8 1) 2.4 (8 1) 2.4 _2 —)(, )=,.2(n 廿丿 20.2780.9891 -(n 1)S 4.某厂利用两条自动化流水线灌装番茄酱 ,分别从两条流水线上抽取样本:X ,X 2,…,X 12 及 Y ,Y 2,…,丫17,算出 x 10.6g, y2 29.5g, s 1 2.4, s 2 4.7 .假设这两条流水线上装的番茄酱的重量都服从正态分布 ,且相互独立,其均值分别为2又设两总体方差1:.求2置信水平为的置信区间解由题设2 2x 10.6,y 9.5,s 12.4, s 2 4.7,n12,n 2 17,m 1)s 2 仏 1)s :(12 1) 2.4(171) 471.94212 17 2t_gn 22q n 2 22) t °.°25(27)2.05181,所求置信区间为((X y)11) ((10.6 9.5) 2.05181 1.94结论“方差相等时, [(a n 22)s w2)平均需求量为10公斤,方差为9 .如果这种商品供应10000户,取置信水平为•(1) 取置信度为,试对居民对此种商品的平均月需求量进行区间估计(2) 问最少要准备多少这种商品才能以99%的概率满足需要解(1) 每户居民的需求量的置信区间为_ s(xt(n* n_ s1), xt (nV n1)) (xs卅,%s川)(10,9J492.575,10 2.575)(9.2275,10.7725). 100J10010000户居民对此种商品月需求量的置信度为的置信区间为(92275,107725);(2)最少要准备92275公斤商品才能以99%的概率满足需要。
统计指数习题及答案

统计指数习题及答案统计学是一门研究数据收集、分析和解释的学科,具有广泛的应用领域。
在统计学学习过程中,习题是非常重要的一部分,通过解答习题可以帮助我们巩固知识,提高应用能力。
本文将介绍一些常见的统计指数习题,并给出相应的答案。
1. 平均数习题a) 某班级有10名学生,他们的身高分别为160、165、170、155、175、180、170、165、160、175(单位:厘米),求班级学生的平均身高。
答案:将所有身高相加得到:160+165+170+155+175+180+170+165+160+175=1695,然后除以学生人数10,得到平均身高为169.5厘米。
b) 一家电商公司在过去一周的每天销售额分别为5000、6000、7000、8000、9000、10000、11000元,求这一周的平均销售额。
答案:将每天销售额相加得到:5000+6000+7000+8000+9000+10000+11000=57000,然后除以7天,得到平均销售额为8142.86元。
2. 中位数习题a) 某班级有30名学生,他们的考试成绩从低到高排列如下:60、65、70、75、80、85、90、95、100、105、110、115、120、125、130、135、140、145、150、155、160、165、170、175、180、185、190、195、200、205。
求班级学生的中位数。
答案:由于学生人数为偶数,中位数为第15和第16个成绩的平均值,即(135+140)/2=137.5。
b) 一家公司的员工薪资从低到高排列如下:3000、3500、4000、4500、5000、5500、6000、6500、7000、7500、8000、8500、9000、9500、10000元。
求公司员工的中位数。
答案:由于员工人数为奇数,中位数为第8个薪资,即6000元。
3. 众数习题a) 某班级有40名学生,他们的考试成绩如下:60、70、80、80、90、90、90、100、100、100、100、110、110、110、110、120、120、120、120、120、130、130、130、130、130、130、140、140、140、150、150、150、150、150、150、150、150、150、160、160。
《概率论与数理统计》第7章作业题

第七章
(2)
1 x x 0
1
1
dx
2
1
0
1 由此得 1 , 在上式中以 X 1
x dx , 1
代替1 ,
得到 的矩估计量和矩估计值分别为:
X x ˆ ˆ . 1 X , 1 x
解 由题设可得 1-2 的一个置信水平为1- 的置信区间为
第七章
1 1 ( X Y ) t 2 ( n1 n2 2) S w n1 n2
由题设1- = 0.95, /2 = 0.025, n1 = 4, n2 = 5, n1+ n2-2 = 7,查表和计算得
x1 0.14125,
3s12 0.00002475,
x2 0.1392,
2 2 3 s 4 s 2 2 1 2 4s2 0.0000208, s 2 ( 0 . 00255 ) w 7 t 2 (n1 n2 2) t 0.025 (7) 2.3646, x1 x2 0.00205,
1 0.95,n A n B 10 F (n A - 1, n B - 1) F0.025(9,9) 4.03,
2
1 F (n A - 1, n B - 1) F0.975(9,9) 14.03 2
第七章
2 2 / 故方差比 A B
得 1-2 的一个置信水平为0.95的置信区间为
1 1 ( x1 x2 ) t 2 ( n1 n2 2) s w n1 n2 1 1 0 . 00205 2 . 3646 0 . 00255 4 5 (0.002 0.004) (0.002,0.006).
统计学第七章课后题及答案解析

第七章一、单项选择题1.按指数所包括的范围不同, 可以把它分为( )A .个体指数和总指数B .数量指标指数和质量指标指数C .综合指数和平均指数D .定基指数和环比指数2.某集团公司为了反映所属各企业劳动生产率水平的提高情况,需要编制( ) A.质量指标综合指数 B.数量指标综合指数 C.可变构成指数 D.固定构成指数3.在一般情况下,商品销售量指数和工资水平指数的同度量因素分别为( ) A .商品销售量、平均工资水平 B .商品销售量、职工人数C .单位商品销售价格、职工人数D .单位商品销售价格、平均工资水平 4.下列指数中属于数量指标指数的是( )A .产品价格指数B .单位成本指数C .产量指数D .劳动生产率指数 5.下面属于价格指数的是( ) A .1101PQ P Q ∑∑ B .1100PQ P Q ∑∑ C .0100P Q P Q ∑∑ D .1000PQ P Q ∑∑ 6.某商品价格发生变化,现在的100元只值原来的90元,则价格指数为( ) A .10% B .90% C .110% D .111% 7.固定构成指数的公式是( )A .001110X F X F F F ∑∑÷∑∑ B .010010X F X F F F ∑∑÷∑∑ C .011111X F X F F F ∑∑÷∑∑ D .011010X F X F F F ∑∑÷∑∑ 二、多项选择题1.下列属于数量指标指数的有( )A .产量指数B .销售量指数C .价格指数D .单位产品成本指数E .职工人数指数 2.下列表述正确的是( )A .综合指数是先综合后对比B .平均数指数是先对比后综合C .平均数指数必须使用全面资料D .平均数指数可以使用固定权数E .固定构成指数受总体结构影响 3.同度量因素的作用有( )A .同度量作用B .联系作用C .权数作用D .比较作用E .平衡作用4.对某商店某时期商品销售额的变动情况进行分析,其指数体系包括( ) A .销售量指数 B .销售价格指数C .总平均价格指数D .销售额指数E .个体指数5.若用某企业职工人数和劳动生产率的分组资料来进行分析时,该企业总的劳动生产率的变动主要受到( )A.企业全部职工人数变动的影响 B.企业劳动生产率变动的影响C.企业各类职工人数在全部职工人数中所占比重的变动影响D.企业各类工人劳动生产率的变动影响E.受各组职工人数和相应劳动生产率两因素的影响6.下列指数中,属于拉氏指数的有()A.∑∑1QpQpB.∑∑11QpQPC.∑∑1pQpQD.∑∑111QpQpE.∑∑111pQpQ7.某企业产品总成本报告期为183150元,比基期增长10%,单位成本综合指数为104%,则()A.总成本指数110% B.产量增长了5.77% C.基期总成本为166500元D.单位成本上升使总成本增加了7044元 E.产量增产使总成本增加了9606元三、判断题1.综合指数的编制方法是先综合后对比。
应用统计学第七章课后练习题
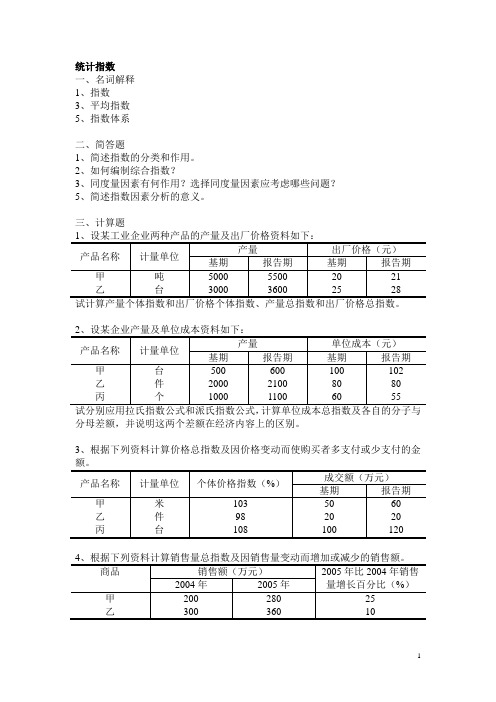
统计指数
一、名词解释
1、指数
3、平均指数
5、指数体系
二、简答题
1、简述指数的分类和作用。
2、如何编制综合指数?
3、同度量因素有何作用?选择同度量因素应考虑哪些问题?
5、简述指数因素分析的意义。
三、计算题
分母差额,并说明这两个差额在经济内容上的区别。
3、根据下列资料计算价格总指数及因价格变动而使购买者多支付或少支付的金
成本和产量变动对产品总成本的影响。
水平和总厂产量结构变动的影响。
7、已知某企业某种产品产量增长10%,消耗某种原材料总量增长6%,试计算单位产品耗用该种原材料数量的变动程度。
8、已知某商店销售额增长20%,销售价格总的上涨8%,试求销售量增长的百分数。
9、在价格降低后同样多的人民币可多购商品15%,求物价指数。
10、某厂2005年的产量比2004年增长13.6%,生产费用增长12.9%,问该厂2005年产品成本的变动情况如何?
11、据调查,某地甲、乙、丙、丁四种代表商品的个体价格指数分别为110%、95%、100%、150%,各类代表商品的固定权数分别为10%、30%、40%、20%,试求这四种商品的价格总指数。
统计业务知识(初中级)_第七章 统计指数_2010年版

1、下列指数中属于狭义指数的是:()A:原油产量指数B:石油价格指数C:石油化工行业销售量指数D:石油化工行业销售额指数E:答案:C解析:狭义指数是指不能直接相加的复杂现象总体综合变动的相对数。
C项是不同产品构成的总体,其销售量不能直接加总,故属于狭义指数。
2、A: 112.5%B:116.7%C:117.9%D:122.2%E:答案:B解析:3、派氏价格指数是()A:B:C:D:E:答案:B解析:见教材338页4、在编制综合指数时,同度量因素的作用有:()A:同度量作用B:比较作用C:权数作用D:稳定作用E:平衡作用答案:A,C解析:同度量因素在综合指数中的作用主要有同度量作用,即将不可直接综合对比的指标过渡成可以综合对比的指标,即同度量作用,同时还有权数作用。
5、某地区2007年比2006年社会商品零售价格总指数为108.5%,这一结果说明()。
A:商品零售价格平均上涨了8.5%B:商品零售额上涨了8.5%C:由于物价上涨使商品零售额下降了8.5%D:商品零售量平均上涨了8.5%E:在商品零售量保持不变条件下,由于物价上涨使零售额提高了8.5% 答案:A,E6、我国居民消费价格指数采用的是()。
A:个体指数B:综合指数C:总指数D:平均指数E:答案:C,D解析:见教材339页7、已知A、B、C三种商品的有关资料,如表:名称计量单位产品销售额(万元)产品销售量个体指数基期报告期ABC台吨套1000420090096046206801.201.101.13合计—61006260—根据上述资料回答:三种商品的销售量总指数计算公式:()A:B:C:D:E:答案:A解析:销售量总指数一般采用拉式物量指数8、已知A、B、C三种商品的有关资料,如表:名称计量单位产品销售额(万元)产品销售量个体指数基期报告期ABC台吨套1000420090096046206801.201.101.13合计—61006260—根据上述资料回答:三种商品的销售价格指数为:()A:90.69%B:91.56%C:102.62%D:102.78%E:答案:B解析:9、已知A、B、C三种商品的有关资料,如表:名称计量单位产品销售额(万元)产品销售量个体指数基期报告期ABC台吨套1000 4200 900960 4620 6801.20 1.10 1.13合计—61006260—根据上述资料回答:三种商品销售量指数和绝对额为:()A:112.08%B:1.11.96%C:737万元D:658万元E:答案:A,C解析:10、已知A、B、C三种商品的有关资料,如表:名称计量单位产品销售额(万元)产品销售量个体指数基期报告期ABC台吨套1000 4200 900960 4620 6801.20 1.10 1.13合计—6100 6260 —根据上述资料回答:三种商品的价格指数和绝对额为:()A:91.56%B:-577万元C:91.81%D:-498万元E:答案:A,B解析:11、已知A、B、C三种商品的有关资料,如表:名称计量单位产品销售额(万元)产品销售量个体指数报告期ABC台吨套1000 4200 900960 4620 6801.20 1.10合计—61006260—根据上述资料回答:下列说法正确的是:()A:三种商品的销售量增长了12.08%B:三种商品的价格降低了8.44%C:销售额增长2.62%是由于销售量增长了12.08%和价格降低了8.44%共同影响的结果D:销售额报告期比基期增加169万元是由于销售量增长了12.08%使销售额增加737万元,价格降低8.44%使销售额减少了577万元的结果E:答案:C,D解析:12、如果零售物价上升2%,商品销售量增长5%,则商品销售额增长10%。
概率论与数理统计习题及答案第七章

习题7-11. 选择题(1) 设总体X 的均值μ与方差σ2都存在但未知, 而12,,,n X X X L 为来自X 的样本, 则均值μ与方差σ2的矩估计量分别是( ) .(A) X 和S 2. (B) X 和211()nii X nμ=-∑. (C) μ和σ2. (D) X 和211()nii X X n=-∑.解 选(D).(2) 设[0,]X U θ:, 其中θ>0为未知参数, 又12,,,n X X X L 为来自总体X 的样本, 则θ的矩估计量是( ) .(A) X . (B) 2X . (C) 1max{}i i nX ≤≤. (D) 1min{}i i nX ≤≤.解 选(B).2. 设总体X 的分布律为其中0<θ<12n , 试求θ的矩估计量.解 因为E (X )=(-2)×3θ+1×(1-4θ)+5×θ=1-5θ, 令15X θ-=得到θ的矩估计量为ˆ15X θ-=. 3. 设总体X 的概率密度为(1),01,(;)0, x x f x θθθ+<<=⎧⎨⎩其它.其中θ>-1是未知参数, X 1,X 2,…,X n 是来自X 的容量为n 的简单随机样本, 求: (1) θ的矩估计量;(2) θ的极大似然估计量. 解 总体 X 的数学期望为1101()()d (1)d 2E X xf x x x x θθθθ+∞+-∞+==+=+⎰⎰. 令()E X X =, 即12X θθ+=+, 得参数θ的矩估计量为21ˆ1X X θ-=-. 设x 1, x 2,…, x n 是相应于样本X 1, X 2,… , X n 的一组观测值, 则似然函数为1(1),01,0,n n i i i x x L θθ=⎧⎛⎫+<<⎪ ⎪=⎨⎝⎭⎪⎩∏其它. 当0<x i <1(i =1,2,3,…,n )时, L >0且 ∑=++=ni ixn L 1ln )1ln(ln θθ,令1d ln ln d 1ni i L nx θθ==++∑=0, 得θ的极大似然估计值为 1ˆ1ln nii nxθ==--∑,而θ的极大似然估计量为 1ˆ1ln nii nXθ==--∑.4. 设总体X 服从参数为λ的指数分布, 即X 的概率密度为e ,0,(,)0,0,x x f x x λλλ->=⎧⎨⎩≤ 其中0λ>为未知参数, X 1, X 2, …, X n 为来自总体X 的样本, 试求未知参数λ的矩估计量与极大似然估计量.解 因为E (X )=1λ =X , 所以λ的矩估计量为1ˆXλ=. 设x 1, x 2,…, x n 是相应于样本X 1, X 2,… ,X n 的一组观测值, 则似然函数11nii inxx nni L eeλλλλ=--=∑==∏,取对数 1ln ln ()ni i L n x λλ==-∑.令1d ln 0,d ni i L n x λλ==-=∑ 得λ的极大似然估计值为1ˆxλ=,λ的极大似然估计量为1ˆXλ=. 5. 设总体X 的概率密度为,01(,)1,120,x f x x θθθ<<=-⎧⎪⎨⎪⎩,≤≤,其它,其中θ(0<θ<1)是未知参数. X 1, X 2, …, X n 为来自总体的简单随机样本, 记N 为样本值12,,,n x x x L 中小于1的个数. 求: (1) θ的矩估计量; (2) θ的极大似然估计量.解 (1) 1213()d (1)d 2X E X x x x x θθθ==+-=-⎰⎰, 所以32X θ=-矩.(2) 设样本12,,n x x x L 按照从小到大为序(即顺序统计量的观测值)有如下关系:x (1) ≤ x (2) ≤…≤ x (N ) <1≤ x (N +1)≤ x (N +2)≤…≤x (n ) .似然函数为(1)(2)()(1)(2)(1),1()0,,N n N N N N n x x x x x x L θθθ-++-<=⎧⎨⎩L L ≤≤≤≤≤≤≤其它.考虑似然函数非零部分, 得到ln L (θ ) = N ln θ + (n − N ) ln(1−θ ),令d ln ()0d 1L N n N θθθθ-=-=-, 解得θ的极大似然估计值为ˆN nθ=. 习题7-21. 选择题: 设总体X 的均值μ与方差2σ都存在但未知, 而12,,,n X X X L 为X 的样本, 则无论总体X 服从什么分布, ( )是μ和2σ的无偏估计量.(A) 11nii X n=∑和211()nii X X n=-∑. (B)111nii X n =-∑和211()1nii X X n =--∑.(C)111nii X n =-∑和211()1nii X n μ=--∑. (D)11nii X n=∑和211()nii X nμ=-∑.解 选(D).2. 若1X ,2X ,3X 为来自总体2(,)X N μσ:的样本, 且Y 1231134X X kX =++为μ的无偏估计量, 问k 等于多少?解 要求1231111()3434E X X kX k μμμμ++=++=, 解之, k =512.3. 设总体X 的均值为0, 方差2σ存在但未知, 又12,X X 为来自总体X的样本, 试证:2121()2X X -为2σ的无偏估计.证 因为22212112211[()][(2)]22E X X E X X X X -=-+2222112212[()2()()]22E X E X X E X σσ=-+==,所以2121()2X X -为2σ的无偏估计.习题7-31. 选择题(1) 总体未知参数θ的置信水平为0.95的置信区间的意义是指( ). (A) 区间平均含总体95%的值. (B) 区间平均含样本95%的值.(C) 未知参数θ有95%的可靠程度落入此区间. (D) 区间有95%的可靠程度含参数θ的真值. 解 选(D).(2) 对于置信水平1-α(0<α<1), 关于置信区间的可靠程度与精确程度, 下列说法不正确的是( ).(A) 若可靠程度越高, 则置信区间包含未知参数真值的可能性越大. (B) 如果α越小, 则可靠程度越高, 精确程度越低. (C) 如果1-α越小, 则可靠程度越高, 精确程度越低. (D) 若精确程度越高, 则可靠程度越低, 而1-α越小. 解 选(C )习题7-41. 某灯泡厂从当天生产的灯泡中随机抽取9只进行寿命测试, 取得数据如下(单位:小时):1050, 1100, 1080, 1120, 1250, 1040, 1130, 1300, 1200. 设灯泡寿命服从正态分布N (μ, 902), 取置信度为0.95, 试求当天生产的全部灯泡的平均寿命的置信区间.解 计算得到1141.11,x = σ2 =902. 对于α = 0.05, 查表可得/20.025 1.96z z ==α.所求置信区间为/2/2(,)(1141.11 1.96,1141.11 1.96)(1082.31,1199.91).x x z +=-=αα2. 为调查某地旅游者的平均消费水平, 随机访问了40名旅游者, 算得平均消费额为105=x 元, 样本标准差28=s 元. 设消费额服从正态分布. 取置信水平为0.95, 求该地旅游者的平均消费额的置信区间.解 计算可得105,x = s 2 =282.对于α = 0.05, 查表可得0.0252(1)(39) 2.0227t n t α-==.所求μ的置信区间为22((1),(1))(105 2.0227,105 2.0227)x n x n αα--+-=+=(96.045, 113.955).3. 假设某种香烟的尼古丁含量服从正态分布. 现随机抽取此种香烟8支为一组样本, 测得其尼古丁平均含量为18.6毫克, 样本标准差s =2.4毫克. 试求此种香烟尼古丁含量的总体方差的置信水平为0.99的置信区间.解 已知n =8, s 2 =2.42, α = 0.01, 查表可得220.0052(1)(7)20.278n αχχ-==, 220.99512(1)(7)0.989n αχχ--==, 所以方差σ 2的置信区间为2222122(1)(1)(,)(1)(1)n S n S n n ααχχ---=--22(81) 2.4(81) 2.4(,)20.2780.989-⨯-⨯=(1.988, 40.768). 4. 某厂利用两条自动化流水线灌装番茄酱, 分别从两条流水线上抽取样本:X 1,X 2,…,X 12及Y 1,Y 2,…,Y 17, 算出221210.6g,9.5g, 2.4, 4.7x y s s ====.假设这两条流水线上装的番茄酱的重量都服从正态分布, 且相互独立, 其均值分别为12,μμ. 又设两总体方差2212σσ=. 求12μμ-置信水平为0.95的置信区间, 并说明该置信区间的实际意义.解 由题设22121210.6,9.5, 2.4, 4.7,12,17,x y s s n n ======2222112212(1)(1)(121) 2.4(171) 4.71.94212172wn s n s s n n -+--⨯+-⨯===+-+-120.0252(2)(27) 2.05181,t n n t α+-==所求置信区间为122(()(2)((10.69.5) 2.05181 1.94x y t n n s α-±+-=-±⨯ =(-0.40,2.60).结论“21μμ-的置信水平为0.95 的置信区间是(-0.40,2.60)”的实际意义是:在两总体方差相等时, 第一个正态总体的均值1μ比第二个正态总体均值2μ大-0.40~2.60,此结论的可靠性达到95%.5. 某商场为了了解居民对某种商品的需求, 调查了100户, 得出每户月平均需求量为10公斤, 方差为9 . 如果这种商品供应10000户, 取置信水平为0.99.(1) 取置信度为0.99,试对居民对此种商品的平均月需求量进行区间估计; (2) 问最少要准备多少这种商品才能以99%的概率满足需要? 解 (1) 每户居民的需求量的置信区间为2222((1),(1))()(10 2.575,10 2.575)(9.2275,10.7725).,x n x n x z x αααα-+-≈+=-=10000户居民对此种商品月需求量的置信度为0.99的置信区间为(92275,107725);(2)最少要准备92275公斤商品才能以99%的概率满足需要.。
(完整版)统计指数习题及答案

指数分析一、填空题1.统计指数按其反映现象范围的不同可分为和,按其反映指标性质的不同可分为和。
2.总指数的编制方法有和两种。
3.编制综合指数的原则是:编制数量指标指数是以 为同度量因素,编制质量指标指数是以 为同度量因素。
4.在指数体系中,总量指标指数等于各因素指数的。
5.平均指标指数等于标志水平指数乘以指数。
二、单选题1.甲产品报告期产量与基期产量的比值是110%,这是()。
A.综合指数B.总指数 C.个体指数 D.平均数指数2.下列指数中属于数量指标指数的是()。
A.物价指数B.平均工资指数C.销售量指数D.销售额指数3.某企业总成本报告期比基期增长30%,产量增长20%,则单位成本增长()。
A.10%B.8.33%C.50%D.80%4.某企业产品物价上涨,销售额持平,则销售量指数()A.增长B.下降C.不变D.不能确定5.我国股票价格指数采用的计算方法是()。
A.平均指数B.综合指数 C.固定权数平均指数 D.实际权数平均指数三、多选题1.综合指数是()。
A.总指数的一种形式B.由两个总量指标对比形成的指数C.可变形为平均指数D.由两个平均指标对比形成的指数E.一切现象的动态相对数 2.某市商品物价指数为108%,其分子与分母之差为100万元,这表明()。
A.该市所有商品的价格平均上涨8%B.该市由于物价上涨使销售额增加100万元C.该市商品物价上涨108%D.该市由于物价上涨使商业多收入100万元E.该市由于物价水平的上涨使居民多支出100万元3.零售物价总指数是()。
A.综合指数B.平均指数C.固定权数物价指数D.实际权数物价指数E.质量指标指数4.指数体系的作用有()。
A.对现象进行综合评价B.进行指数之间的相互推算C.对现象的总变动进行因素分析D.可以测定复杂现象的综合变动E.分析总体数量特征的长期变动趋势5.我国证券交易所股价指数包括()。
A.上证综合指数B.深圳综合指数C.上证30指数D.深圳成分指数E.股价平均指数四、判断题1.总指数使反映复杂现象综合变动的相对数,具有平均的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章统计指数一、判断题1.分析复杂现象总体的数量变动,只能采用综合指数的方法。
< )2.在特定的权数条件下,综合指数与平均指数有变形关系。
< )3.算术平均数指数是通过数量指标个体指数,以基期的价值量指标为权数,进行加权平均得到的。
< )4.在简单现象总量指标的因素分析中,相对量分析一定要用同度量因素,绝对量分析可以不用同度量因素。
< )设p表示单位成本,q表示产量,则∑p1q1 -∑p0q1 表示由于产品单位成本的变动对总产量的影响。
< )b5E2RGbCAP设p表示价格,q表示销售量,则∑p0q1 -∑p0q0 表示由于商品价格的变动对商品总销售额的影响。
< )p1EanqFDPw7.从指数化指标的性质来看,单位成本指数是数量指标指数。
< )8.如果各种商品价格平均上涨5%,销售量平均下降5%,则销售额指数不变。
< )1、×2、√3、√4、×5、×6、×7、×8、×。
单项选择题1.广义上的指数是指< )。
A.价格变动的相对数B.物量变动的相对数C.社会经济现象数量变动的相对数D.简单现象总体数量变动的相对数2.编制总指数的两种形式是 < )。
A.数量指标指数和质量指标指数B.综合指数和平均数指数C.算术平均数指数和调和平均数指数D.定基指数和环比指数3.综合指数是< )。
A.用非全面资料编制的指数B.平均数指数的变形应用C.总指数的基本形式D.编制总指数的唯一方法4.当数量指标的加权算术平均数指数采用特定权数时,计算结果与综合指数相同,其特定权数是< )。
A.q1p1B.q0p1C.q1p0D.q0p05.当质量指标的加权调和平均数指数采用特定权数时,计算结果与综合指数相同,其特定权数是< )。
A.q1p1B.q0p1C.q1p0D.q0p06.在由三个指数所组成的指数体系中,两个因素指数的同度量因素通常 < )。
A.都固定在基期B.都固定在报告期C.一个固定在基期,一个固定在报告期D.采用基期和报告期交叉7.某市1995年社会商业零售额为12000万元,1999年增至15600万元,这四年物价上涨了4%,则商业零售量指数为< )。
A.130%B.104%C.80%D.125%8.某造纸厂1999年的产量比98年增长了13.6%,总成本增长了12.9%,则该厂1999年产品单位成本< )。
A.减少0.62%B.减少5.15%C.增加12.9%D.增加1.75%9.已知某工厂生产三种产品,在掌握其基期、报告期生产费用和个体产量指数时,编制三种产品的产量总指数应采用< )。
A、加权调和平均数指数B、加权算术平均数指数C、数量指标综合指数D、固定加权算术平均数指数DXDiTa9E3d1、C2、B3、C4、D5、A6、C7、D8、A9、B。
多项选择题1.下列属于质量指标指数的有 ( >A、商品零售量指数B、商品零售额指数C、商品零售价格指数D、职工劳动生产率指数E、产品单位成本指数2.下列属于数量指标指数的有 ( >A、工业生产指数B、劳动生产率指数C、职工人数指数D、产品产量指数E、产品单位成本指数3.编制综合指数的原则是 ( >A、质量指标指数以报告期的数量指标作为同度量因素B、质量指标指数以基期的数量指标作为同度量因素C、数量指标指数以基期的数量指标作为同度量D、数量指标指数以基期质量指标作为同度因素E、数量指标指数以固定时期质量指标作为同度因素4.下面哪些指数式是综合指数 ( >RTCrpUDGiT5.对某商店某时期商品销售额变动情况分析,其指数体系包括( >A、销售量指数B、销售价格指数C、总平均价格指数D、销售额指数E、个体指数5PCzVD7HxA1、CDE2、ACD3、AD4、AC5、ABD填空题1.综合反映商品销售量变动程度的指数称< ),综合反映产品单位成本变动程度的指标称< )。
2一般来说,算术平均数指数是以< )为权数计算的;调和平均数指数是以< )为权数计算的。
3.平均指数有独立应用的意义,它的计算形式有( >和( >两种。
4.影响商品销售额总指数变动的数量指标指数是< ),质量指标指数是< )。
5.影响产品产量总指数变动的数量指标指数是< ),质量指标指数是< )。
6.利用统计指数体系进行因素分析主要有< )和< )两个方面。
jLBHrnAILg1、数量指标指数质量指标指数2、基期总值指标报告期总值指标3、算术平均数指数调和平均数指数4、商品销售量指数销售价格指数5、职工人数指数劳动生产率指数6、总量指标平均指标。
xHAQX74J0X五、简答题1:在现象总体变动分析中,统计指数的作用主要表现在哪些方面?2:统计指数的分类主要有哪些方面?3:平均指数和综合指数计算结论相同的条件是什么?1、答:统计指数的作用主要:1.综合反映复杂现象总体数量上的变动状态;2.分析现象总体变动中受各个因素变动的影响程度;3.利用连续编制的指数数列,对复杂现象总体长时间发展变化趋势进行分析。
2、答:统计指数的分类主要有:1.统计指数按其所反映的对象范围不同,分为个体指数和总指数。
2.统计指数按其所表明的指标性质的不同,分为数量指标指数和质量指标指数。
3.统计指数按所采用基期的不同,分为定基指数和环比指数3、答:当数量指标的算术平均数指数,在采用基期总值为权数的特定情况下,与一般综合指数的计算结论相同;当质量指标的调和平均数指数,在采用报告期总值为权数的特定情况下,与一般综合指数的计算结论相同。
LDAYtRyKfE六、计算题1、某商场对两类商品的收购价格和收购额资料如下:试求价格总指数和价格变动引起的收购额变动的绝对数。
2、某公司销售的三种商品的资料如下:试求价格总指数和销售额总指数。
<要计算其变动的绝对额)3、某企业产品总成本和产量资料如下:试计算总成本指数、产量指数及产品单位成本总指数<要计算其变动过的绝对额)4、某企业生产三种产品的有关资料如下:试计算两种产品的总成本指数、产量总指数和单位成本总指数。
<要计算其变动的绝对额)5、某企业四个车间2005年和2006年的工人数和年收入总额资料如下:车间职工人数<人)年收入<千元)2005年2006年2005年2006年甲乙丙丁3237559533359613573711322147472233339要求:<1)计算该企业工人的年平均收入指数;<2)计算固定基期年收入水平的结构影响指数;<3)计算固定报告期工人结构的固定构成指数;<4)用上述结果验证指数体系公式。
1、解:商品种类价格(元>报告期收购额(元>基期报告期A101210000120.008333.33 B151********.6717307.69 C222525000113.6422000.00合计——50000—47641.03价格总指数由于价格变动引起的收购额变动的绝对额=2、解:商品种类单位商品销售额<万元)价格提高<%)基期报告期甲条1011210210.78乙件1513510512.38丙块2022010022.00合计—4546——45.173、解:产品名称总成本<万元)产量增加<+)或减少<-)%基期报告期A5060┼1011055.0 B3045┼2012036.0 C1012-1999.9合计90117——100.94、解:产品名称产量单位成本<元)基期报告期基期报告期甲2003001012200360300乙150020002021300004200040000合计————3200045600430005、解:车间职工人数<人)(f>年收入<千元)(xf> 1995年1996年1995年1996年甲乙丙丁3237559533359613573711322147472233339<1)<2)<3)<4)申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
