《大学物理实验》准稳态法测量不良导体的导热系数和比热
准稳态法测不良导体的导热系数和比热预习报告
准稳态法测不良导体的导热系数和比热预习报告实验目的1. 了解准稳态法测量不良导体的导热系数和比热的原理,并通过快速测量学习掌握该方法;2. 掌握使用温差电偶测量温度的方法。
一. 实验原理1. 热传导物体相邻部分间存在温度差,在各部分之间不发生相对位移的前提下,仅依靠分子、原子及自由电子等微观粒子的热运动而产生的热量传递成为热传导。
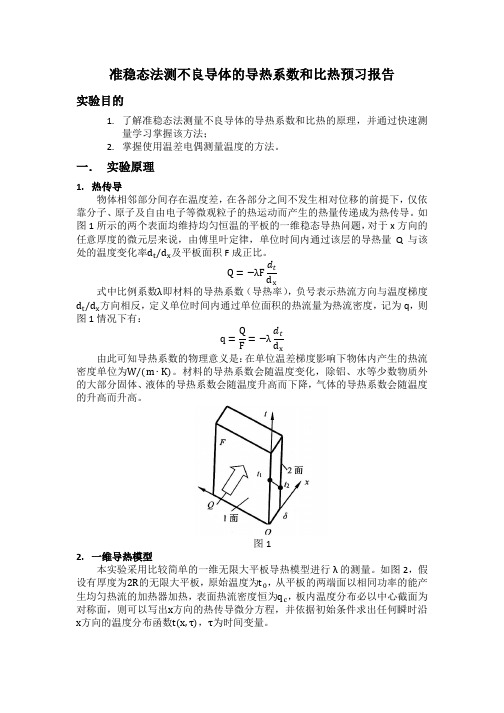
如图1所示的两个表面均维持均匀恒温的平板的一维稳态导热问题,对于x 方向的任意厚度的微元层来说,由傅里叶定律,单位时间内通过该层的导热量Q 与该处的温度变化率d t /d x 及平板面积F 成正比。
Q =−λF d tx式中比例系数λ即材料的导热系数(导热率),负号表示热流方向与温度梯度d t /d x 方向相反,定义单位时间内通过单位面积的热流量为热流密度,记为q ,则图1情况下有:q =Q =−λd t x由此可知导热系数的物理意义是:在单位温差梯度影响下物体内产生的热流密度单位为W/(m ∙K)。
材料的导热系数会随温度变化,除铝、水等少数物质外的大部分固体、液体的导热系数会随温度升高而下降,气体的导热系数会随温度的升高而升高。
图12. 一维导热模型本实验采用比较简单的一维无限大平板导热模型进行λ的测量。
如图2,假设有厚度为2R 的无限大平板,原始温度为t 0,从平板的两端面以相同功率的能产生均匀热流的加热器加热,表面热流密度恒为q c ,板内温度分布必以中心截面为对称面,则可以写出x 方向的热传导微分方程,并依据初始条件求出任何瞬时沿x 方向的温度分布函数t(x,τ),τ为时间变量。
3.热传导方程及求解∂t(x,τ)∂τ=a∂2t(x,τ)∂x(0<x<R,τ>0) (式4)初始条件t(x,τ)τ=0=t0(式5)边界条件q c=λ∂t(x,τ)∂x x=R(式6)λ∂t(x,τ)∂x x=0=0(式7)式中a=λ/cρ为热扩散率(或称热扩散系数),单位为m2/s,c为比热容,单位为J/(kg∙K),ρ为密度,单位为kg/m3。
准稳态法测不良导体的导热系数和比热

1实验目的1.了解准稳态法测量不良导体的导热系数和比热的原理,并通过快速测量学习掌握该方法。
2.掌握使用温差电偶测量温度的方法。
2实验数据记录与处理2.1数字万用表的练习使用实验中的交流信号是正弦波,有效值设为1V,频率设为1000Hz。
测量对象测量值量程精度不确定度完整测量结果交流电压有效值0.98058V2V0.2+0.050.00296V(0.98058±0.00296)F 交流信号频率999.96Hz20Hz-2kHz0.01+0.0030.16Hz(999.96±0.16)Hz电阻10.9289kΩ20kΩ0.020+0.0040.0023kΩ(10.9289±0.0023)kΩ电容1.046µF2µF1+0.50.020µF(1.046±0.020)µF二极管正向导通电压0.5826V0-2V0.06+0.0200.0007V(0.5829±0.0007)V表1:数字万用表的练习使用数据记录以电阻测量值为例计算,读数为10.9289kΩ,量程为20kΩ,精度为0.020+0.004,则∆R=0.020%×10.9289+0.004%×20.0000=0.0023kΩ最终得到R=(10.9289±0.0023)kΩ,其他测量值的不确定度计算过程类似。
3测导热系数和比热容3.1实验前的准备实验样品为有机玻璃,长宽L=W=90mm,厚度R=10mm,密度ρ=1196kgm3。
室温t0=19.9◦C。
中心面热电偶电阻为3.296Ω,加热面热电偶电阻为3.124Ω,冷端热电偶电阻为4.136Ω,并联而成的加热薄膜电阻r/2=55.071Ω。
加热前,测得加热面和中心面的温差U1(t2,t1)=4µV<10µV,故不必进行零位修正。
加热前,加热薄膜电压U前=17.9928V,∆U前=0.015%×17.9928+0.004%×20.0000=0.0035V;加热后,加热薄膜电压U后=17.9932V,∆U后=0.015%×17.9932+0.004%×20.0000=0.0035V。
准稳态法测量比热和导热系数

准稳态法测量比热和导热系数
比热和导热系数是材料物理性质中的两个重要参数。
比热是指单位质量物质在温度变
化下吸收或释放的热量,而导热系数是指在温度梯度下单位面积材料所传导的热量。
准稳
态法是一种常用的测量比热和导热系数的方法。
准稳态法的原理是将材料置于热源和冷源之间,使其温度从热源端到冷源端逐渐降低。
在稳态时,材料的温度分布和热流分布达到了平衡状态,此时材料的导热系数和比热可通
过测量温度和热流来计算得到。
具体实验步骤如下:
1.在实验装置的热源端和冷源端分别接上热源和冷却器,并在中间加装被测材料。
2.启动热源和冷却器,使其保持恒定的温度。
3.通过热电偶等温度计测量被测材料的温度分布。
通常可以在材料表面粘贴一定数量
的热电偶,并通过微型电脑采集数据。
4.通过热流计测量热源和冷源之间传导的热流。
热流计是一种基于热电效应的电子仪器,可以测量电导率和温度梯度来计算热流。
5.通过实验数据计算被测材料的比热和导热系数。
根据热传导定律,可以将热流和导
热系数表示为以下关系:Q=λ×A×(T1-T2)/L,其中Q为热流,λ为导热系数,A为横截
面积,T1和T2分别为热源和冷源的温度,L为材料长度。
由于准稳态法测量过程中需要维持恒定的温度和热流,因此实验装置的设计和操作都
需要具备一定的技术水平。
此外,不同材料的比热和导热系数可能有很大的差异,因此在
实验计算中需要注意各项参数的精确度和精度。
用准稳态法测介质的导热系数和比热的实验报告

用准稳态法测介质的导热系数和比热的实验报告实验目的本实验旨在通过准稳态法来测量介质的导热系数和比热。
实验原理介质热传导定律可以表示为:$\frac{dQ}{dt}=-kA\frac{dT}{dx}$其中$dQ$表示通过横截面$A$传导的热量、$dT/dx$表示温度梯度,$k$表示介质的导热系数。
考虑一根长为$L$、半径为$r$的柱形介质,将其放置在恒定温度$T_1$的热源上,使其与热源建立稳定热流,由于介质与外界的热交换可能会影响温度场的分布,但如果用温度计沿柱形介质的径向测量,可以保证温度场分布近似于径向对称的形态。
当恒定稳态建立后,热传导方程的解析解可以表示为:$T(r)=T_1+\frac{dQ}{2\pi kL}ln{\frac{r}{r_0}}$其中$r_0$表示温度计的距离。
同时根据恒定稳态条件,热流向是恒定的,可以通过测量温度差得到热流,即:$q=-k\frac{A}{\Delta x}(T_2-T_1)$其中$A$表示圆柱体的横截面积,$\Delta x$表示$\Delta T$的距离。
结合以上两式,可以得到介质的导热系数$k$为:$k=\frac{qd}{2\pi T_1 L ln{\frac{r_2}{r_1}}}$其中$d$为材料的直径,$T_1$为热源的温度,$r_1$和$r_2$为温度计的测量位置。
而比热则是通过热平衡条件给出的:$q_1t_1=q_2t_2$其中$q$为热流,$t$为温度,1和2表示两个状态。
在本实验中,温度上升了$\Delta T$,热流在某一时间间隔$t$内对介质的热量为$q=mC_p\Delta T$,其中$m$为穿过某一截面的质量,$C_p$为比热容。
因此可以得到比热:$C_p=\frac{q}{m\Delta T}$实验步骤1.准备材料:圆柱形样品和两台K型热电偶。
2.组装实验装置:将圆柱形样品嵌入加热炉中,将热电偶分别穿过样品并与数据采集仪相连。
B2不良导体热传导率的测量准稳态法实验报告 2

在实际操作中要实现这样的条件比较困难,因而会导致测量的重复性、稳定性、一致性较差,误差也较大。
为了克服稳态法测量的这些弊端,本实验使用了一种新的测量方法——准稳态法,使用准稳态法只要求温差恒定和温升速率恒定,而不必通过长时间的加热达到稳态,就可以通过简单的计算得到导热系数和比热。
1.准稳态法测量原理考虑如图1 所示的一维无限大导热模型:一无限大不良导体平板厚度为2R,初始温度为t0,现在平板两侧同时施加均匀的指向中心面的热流密度q c,则平板各处的温度t(x, τ )将随加热时间τ 而变化。
以试样中心为坐标原点,上述模型的数学描述可表达如下:式中a = λ/ρc,λ为材料的导热系数,ρ为材料的密度,c 为材料的比热。
可以给出此方程的解为:考察t(x,τ )的解析式(2)可以看到,随加热时间的增加,样品各处的温度将发生变化,而且我们注意到式中的级数求和项由于指数衰减的原因,会随加热时间的增加而逐渐变小,直至所占份额可以忽略不计。
定量分析表明,当以后,上述级数求和项可以忽略。
这时式(2)可简写成:这时,在试件中心处有x = 0,因而有:在试件加热面处有x = R,因而有:由式(4)和(5)可见,当加热时间满足条件时,在试件中心面和加热面处温度和加热时间成线性关系,温升速率都为此值是一个和材料导热性能和实验条件有关的常数,此时加热面和中心面间的温度差为:由式(6)可以看出,此时加热面和中心面间的温度差↵t和加热时间⎜没有直接关系,保持恒定。
系统各处的温度和时间呈线性关系,温升速率也相同,我们称此种状态为准稳态。
当系统达到准稳态时,由式(6)得到根据式(7),只要测量进入准稳态后加热面和中心面间的温度差⊿t,并由实验条件确定相关参量q c和R ,则可以得到待测材料的导热系数λ。
另外在进入准稳态后,由比热的定义和能量守恒关系,可以得到下列关系式:比热为:式中为准稳态条件下试件中心面的温升速率(进入准稳态后各点的温升速率是相同的)。
用准稳态法测介质的导热系数和比热的实验报告

用准稳态法测介质的导热系数和比热的实验报告实验报告:
本实验组进行了一系列实验,目的是测量介质的导热系数和比热。
为此,我们采用了准稳态法(Steady-State Method),通过测量系统的热流,温度和物理量来评估介质的热特性。
实验装置由两个金属块构成,它们之间以一定宽度填充介质。
两个金属块用热电偶连接,控制机械温度。
一个块由常温水浴恒温,使另一块保持稳定的温度,以产生恒定的热流。
然后,通过特殊测量仪器读取温度差。
通过改变被测物质的厚度,实验运行三次,同时测量温度。
在改变热流情况下,记录温度差随热导率的变化情况。
根据所得温度与热导率的关系,用分析技术计算出介质的导热系数和比热。
实验运行时,实验装置保持在常温水浴中,当热偶发出热量时,两个金属块之间的温差增大,测量装置会自动调整两个金属块的温度,以保持恒定的热流输出。
本实验的结果显示,随着介质的厚度的增加,介质的导热系数和比热值也随之增加。
未来,我们可以改进实验装置,看看它们是否可以产生更精确的结果。
《大学物理实验》教案实验1测定不良导体的导热系数

实验1 测定不良导体的导热系数一 引语 (Introduction )热量的传输方式有多种,如辐射、对流、传导等。
对于固体材料而言,热传导是热量传输的方式之一,它是物体直接接触温度不均匀时而产生的。
导热系数是反映材料的导热性能的重要参数之一;在工程技术方面是不可缺少的。
如熔炼炉、传热管道、散热器、加热器,以及日常生活中水瓶、冰箱等都要考虑它们的导热程度大小。
所以,对导热系数的研究和测量就显得很有必要。
我们把导热系数大、导热性能较好的材料称为良导体;而把导热系数小,导热性能较差的材料称为不良导体。
一般说来,金属的导热系数比非金属的要大;固体的导热系数比液体的要大;气体的导热系数最小。
本实验仅介绍一种比较简单的利用稳态法测不良导体的导热系数的实验方法。
稳态法是通过热源在样品内部形成一稳定的温度分布后,用热电偶测出其温度的方法。
二 实验目的 (Purpose)1.掌握稳态法测不良导体的导热系数的方法。
2.了解物体散热速率和传热速率的关系。
3.理解温差热电偶特性。
三 实验仪器 (Instruments)红外灯、传热筒、杜瓦瓶、温差电偶、待测橡胶样品、调压器、数字电压表、硅油、停表。
图 1 导热系数测定仪装置图杜瓦瓶样品数字电压表热电偶四 实验原理 (principle)1. 热传导方程当物体内部各处的温度不均匀时,就会有热量从温度较高处传递到温度较低处,这种现象叫热传导现象。
测定导热系数的原理是法国数学、物理学家约瑟夫·傅立叶给出的导热方程式。
该方程式指出,在物体内部,垂直于导热方向上,二个相距为h ,面积为A ,温度分别为1θ、2θ的平行平面,在t ∆秒内,从一个平面传到另一平面的热量Q ∆,满足下述表达式:ht QA 21θθ∆∆λ-= (2-6-1)式中tQ ∆∆为传热速率,A 为样品面积,h 为样品厚度,1θ、2θ分别为样品上下表面温度,λ为该物体的导热系数,其值等于相距单位长度的两平面的温度相差一个单位时,在单位时间内,垂直通过单位面积所传递的热量。
B2用准稳态法测介质的导热系数和比热OK

补2 用准稳态法测介质的导热系数和比热热传导是热传递三种基本方式之一。
导热系数定义为单位温度梯度下每单位时间内由单位面积传递的热量,单位为W / (m · K)。
它表征物体导热能力的大小。
比热是单位质量物质的热容量。
单位质量的某种物质,在温度升高(或降低)1度时所吸收(或放出)的热量,叫做这种物质的比热,单位为J/(kg ·K )。
测量导热系数和比热通常都用稳态法,使用稳态法要求温度和热流量均要稳定,但在实际操作中要实现这样的条件比较困难,因而会导致测量的重复性、稳定性、一致性较差,误差也较大。
为了克服稳态法测量的这些弊端,本实验使用了一种新的测量方法——准稳态法,使用准稳态法只要求温差恒定和温升速率恒定,而不必通过长时间的加热达到稳态,就可以通过简单的计算得到导热系数和比热。
【实验目的】1. 了解准稳态法测量导热系数和比热的原理;2. 学习热电偶测量温度的原理和使用方法;3. 用准稳态法测量不良导体的导热系数和比热。
【实验仪器】1. ZKY-BRDR 型准稳态法比热、导热系数测定仪2. 实验装置一个,实验样品两套(橡胶和有机玻璃,每套四块),加热板两块,热电偶两只,导线若干,保温杯一个【实验原理】1. 准稳态法测量原理考虑如图B2-1所示的一维无限大导热模型:一无限大不良导体平板厚度为R 2,初始温度为0t ,现在平板两侧同时施加均匀的指向中心面的热流密度c q ,则平板各处的温度),(τx t 将随加热时间τ而变化。
以试样中心为坐标原点,上述模型的数学描述可表达如下:⎪⎪⎪⎩⎪⎪⎪⎨⎧==∂∂=∂∂∂∂=∂∂022)0,(0),0(),(),(),(t x t x t q x R t x x t a x t c τλττττ式中c a ρλ/=,λ为材料的导热系数,ρ为材料的密度,c 为材料的比热。
可以给出此方程的解为(参见附录):)cos)1(2621(),(222121220τπππτλτR an n n c e x Rn n R R x R R a q t x t -∞=+⋅∑-+-++=(B2-1)考察),(τx t 的解析式(B2-1)可以看到,随加热时间的增加,样品各处的温度将发生变化,而且我们注意到式中的级数求和项由于指数衰减的原因,会随加热时间的增加而逐渐变小,直至所图B2-1理想的无限大不良导体平板占份额可以忽略不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自由电子出来进去 动态平衡
一层电子气, 一个电偶层(约10 -10m厚)
电子要逸出金属,必须克服金属表面层内正离子晶体 点阵势井和表面电偶层电场作功,称为逸出功。 10
逸出功与表层电势差的关系为 A=eU*
不同金属的逸出功A不同,逸出 电势U*不同。
2、自由电子数密度不同
“电子气”扩散,金属2中的电子将 多于金属1中的电子。
接触电势差为 U12 (T, n1 ,n2 )
接触面上有一种把正负电荷拉开的非静电力,相当 于一个电源,其电动势
= U12(T, n1 , n2)
11
温差电现象:把两种金属接成闭合回路,若两个接
点A、B处的温度相同,则回路中无电动势;若两 个接点A,B处的温度不同,则回路中有电动势,也 有电流。
3)四块样品组合有利于 在加热面、中心面中 心安装测温元件
① ②③④
O
x
样 样样 样
品 品品 品
加热面热偶 中心面热偶
9
热电偶测温原理
介绍概念:接触电势差 温差电现象 接触电势差:两种不同的金属接触时会出现电势差
产生的原因:逸出功不同,自由电子数密度不同. 1、逸出功 金属表面层内存在着一种阻止电子逸出 表面的作用力 正离子晶体点阵势井
t t( R, ) t( 0, ) qc R 2
qc R 2t
准稳态时利用中心面(x=0)的温升速率可以 计算材料比热c
qc F
cRF
dt
d
c qc
R t x0
8
实验装置及特色
1)实验样品长宽均为厚 度R的9倍可忽略长宽 非无限大
绝热泡沫
加热器 绝热泡沫
2)采取四块样品紧密组 合由两个阻值一致的 薄膜加热器并联供热, 以保证两加热面向中 心的加热热流恒定并 对称相等
热对流:由于流体的宏观运动,从而流体各部分之 间发生相对位移、冷热流体相互掺混所引起的热 量传递过程。
热辐射:物体因为自身温度的原因而发出电磁波传 递能量,此称为热辐射。
3
热传导的三种状的导热过程 称为稳态导热。 非稳态:相对稳态而言,物体内温度分布随时间 改变。 准稳态:物体内任意两点间温度差恒定,各点温 度变化速率相同。 (测量时间短,重复性好,稳定性好,结果较准确)
热
TA
接 头
这一对金属接成回路,
接头温度不同。称为
Fe
冷
“热电偶”。
I
接
头TB 回路中温差电动势
I
与(TA-TB)有关。
Cu
12
热电偶测温原理
A
T
B
T0 T
U(TT0) T0
U (TT0 ) a(T T0 ) b(T T0 )2
✓测量温度范围较小时,可以忽略二次项, 近似认为热电偶输出与温差成正比
± (2.0%+5) 1×10-3=0.024
15
2.热导实验
检查4个热电偶(测其电阻,记录) 材料 ;室温t0= ;加热器r/2= ; 加热电压U加热初始= ;加热电压U加热结束= ; 加热电压U加热平均= ;
τ(min) 0 1 2
…
25
中心面温度
…
U(t1tc)
温差U(t2t1)
…
16
注意事项
δ
O
平板的一维稳态导热
5
一维导热模型及热传导方程
t( x , ) 2t( x , ) a x2
式中
a c
初始条件 t( x ,0 ) t0
qc qc
O
x
qc qc
边界条件
t( x, ) qc x xR
RR 无限大平板导热模型
t( x, )
0 x x0
6
方程的解为:
t(
x ,
)
t0
热电偶冷端温度对实验的影响是怎样的?
18
要求:实验报告1周之内交到J13报告柜内。
预祝同学们 实验顺利!
Thank you!
19
19
13
实验仪器
热导测量仪 直流稳压电源 交流电源 数字万用表 双刀双掷开关(换向开关) 秒表
14
实验任务及参考数据表格
1、数字万用表使用
测量任务 测量值 量程/分辨率 /误差极限
测交流电 压有效值
测交流信 号的频率
二端法 测电阻
电容
二极管 正向导通电压=
不确定度
完整测量结果
例:电容 0.937uF 6uF/1nF/ 0.937×2.0%+5× (0.937±0.024)uF
热偶丝较细,注意保护,加热面热偶横梁任何情 况下都禁止取下。
直流恒压源严谨短路。 实验结束后,松开仪器,以免泡沫挤压变形。
17
问题探讨
实际上,我们只需测量一块样品的热流密度及端 面温升速率,进而求出导热系数和比热。那么本 实验为何使用四块样品,能否只用两块或一块?
本实验中准稳态会无限保持下去吗?为什么不是 时间越长实验数据越好?
大学物理实验——
准稳态法测量不良导体的导热系数和比热
实验目的
1、了解准稳态法测量不良导体的导热系数和比热 2、掌握热电偶测量温度的方法 3、学习使用数字万用表
2
实验原理
热量传递三种方式:热传导,热对流,热辐射
热传导:物体相邻部分有温差,在各部分之间不发 生相对位移,仅依靠原子、分子及自由电子等粒 子的热运动而产生的热量传递。
物体导热性能:良导体、不良导体 热良导体:导热系数100——1000 不良导体:导热系数1以内
4
一维热传导
傅里叶定律
t
热量
Q = -λF dt dx
热流密度
q Q = -λ dt F dx
导热系数λ意义:单位时间 内在单位温度梯度作用下的 热流密度,单位:W/(m·K)
F
t1
2面 t2 x
Q
1面
qc
a
R
R2 3x2 6R
R ( 1 )n1
n1
2
n2
cos( n
x R
)exp( n2F0
)
式中:
n n , n 1,2,3...
a
F0 R2
a
F0 R2 0.5
当
t(
x ,
)
t0
qc R
a
R2
x2 2R2
1 6
时进入准稳态
7
准稳态时利用同一时刻加热面(x=R)与中心 面(x=0)的温度之差可以计算导热系数λ
