材料热力学(第3版)
合集下载
材料热力学课件-第三章-1
9
△rGm = △rGm (T) + RTlnΠ (pB/p) νΒ
平衡时， △rGm = 0, 所以有
△rGm (T) = - RTlnΠ (pB/p) νΒ
定义：K
(T
)
def
exp
r Gm RT
或
K
(T
)
def
exp
B
B
T
B
RT
10
所以有： K(T ) pB / p B
33
TiO2(s)+2C(石墨)+2Cl2(g) = TiCl4(g)+2CO(g) 解: rGm(1000K) = ∑fGm(B,1000K)
=( - 637.6 -2×200.2+764.4) kJmol-1 = -273.6 kJmol-1
34
K(1000K) =exp[- rGm(1000K) /RT] =exp[273600Jmol-1/(8.3145×1000 Jmol-1)] = 1.96×1014
(3)虽然等温方程是由理想气体反应推导出来的， 但是，它可以用于任意化学反应，如纯凝聚系 统的反应。在用于纯凝聚系统的反应时，J不 是用分压，而是用浓度或活度表示。
29
/ K
K
p
pB
p
B
平衡态
r
Gm
RT
ln
K
p
RT
ln
J
p
实际应用此方程解决有关平衡问题
J p
pB,g
B,g
p
任意态
K
(T
)
def
exp[
(a
A
b
B
y
Y
材料热力学1-7
PbO2 NiOOH
H2SO4 KOH
NiOOH
KOH
Li(I-X)CoO2 有机溶剂
电解质 NH4Cl/ZnCl2 KOH
KOH
KOH
KOH PC/DME +LiClO4
E0/V 1.5 1.5 1.3 1.646 1.72
3.5
W′/Wh·kg-1 10-50 30-100 30-100 100-250 60-160
课程名称:
材料热力学
授课人: 徐洪辉 (教授) Tel: 13077377087, 88877108(o) E-mail: hhxu@
参考教材
2009年4月
（适用于研究生）
1. 材料热力学
(索书号:TB301/XZY=3)
徐祖耀、李麟箸
科学出版社 2005年, 第三版
2. 材料热力学
L. Kelvin (W. Thomson,1824-1907年) 1848年建立了热力学温标，并在其 著作中首次使用Thermodynamic一 词。
热力学历史名家
热力学发展简史 (续)
W.H. Nernst (1864-1941年)，1920年获诺贝尔化学奖
能斯特方程： E
E
0
(RT
/
nF
)
ln
随着热力学第一、二定律的不断发展，演绎出 严密的经典热力学
吉布斯(J.W. Gibbs, 1839-1903): 美国物理学 家，在热力学领域作出了划时代的贡献。
他提出了描述多相体系平衡条件的相律及吉布斯自 由能及化学势。为纪念Gibbs的卓越贡献，人们把等 温等压自由能称为Gibbs自由能。
热力学发展简史 (续)
- Baker and Cahn
材料热力学(三大定律)要点
说明任意可逆过程的热 温商的值决定于始终状态，
而与可逆途径无关，这个热
温商具有状态函数的性质。 任意可逆过程
Clausius根据可逆过程的热温商值决定于始终态而与可逆 过程无关这一事实定义了“熵”（entropy）这个函数，用符 号“S”表示，单位为： J K 1
设始、终态A，B的熵分别为 SA 和 SB，则：
1.0 mol R ln 2 5.76 J K 1
非等温过程中熵的变化值
1、 物质的量一定的可逆等容、变温过程
S
T2
nCV ,m dT T
T1
2、 物质的量一定的可逆等压、变温过程
S
T2
nC p ,m dT T
T1
热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
则有
Q Q <0 T T i I, AB i R, B A
Q S A SB T i R, B A
Q SB SA T i I, AB
或
B Q SAB 0 A T I
解法1
22.4 V2 S (O 2 ) nR ln 0.5R ln V1 12.2
0.5 mol 0.5 mol O 2 (g) N 2 (g)
22.4 S (N 2 ) 0.5 R ln 12.2
22.4 nR ln 2 > 0 mix S S (O2 ) S (N2 ) nR ln 12.2
SAB
B Q T A I
如AB为可逆过程
Q S A B T i R,A B
S是状态函数，在确定的始、终态间，ΔS为定值，与过程是否 可逆无关。但过程的热温商之和与过程是否可逆有关。若可逆则过程 的热温商之和等于ΔS；若过程不可逆则过程的热温商之和小于ΔS。
材料热力学_热力学基本原理
用溶解热法测得该反应在 978K 时的转变热为-22.18KJ/mol。 试分别 H =-26.78KJ/mol， 计算两种测量值所得 r Al 2 O 3 的标准生成焓。并比较两者是否一致。 3. 与 CuO、 Cu 2 O 平衡的氧气分压，在 900℃时为 0.028atm，在 1000℃时为 0.1303atm， 试计算反应 2Cu 2 O O 2 4CuO 在 298K，1173K，1273K 时的 H 。
• • 恒容热容：在不发生相变与化学变化、恒容、不做非 体积功的情况下体系每升高1度体系所需吸收的热量:
dQ U Cv dT V T V
•
• •
在不发生相变与化学变化的情况下，温度由T1升高至 T2所引起的内能变化为：
U Cv dT
T1
• •
•
与内能和焓一样，Gibbs自由能与Helmholtz自由能也没有绝对值 Gibbs自由能与Helmholtz自由能的变化可以由焓变、熵变、内能的 变化求出来 对于等温反应： G H TS
F U TS G H S T T F U S T T
材料热力学什么是材料热力学材料热力学是热力学基本原理在材料设计制备与使用过程中的应用包括相平衡相图热力学相变热力学等相图反映的是物质的存在状态而热力学反映的是物质所包含的能量而能量是物质状态变化的起因与因此相图与热力学有非常密切的关系目前材料热力学主要内容是相图或相平衡热力学本课程包括热力学基本原理回顾热力学在冶金材料过程中的应用相平衡热力学与相图计算相图与合金设计热力学基本原理回顾平衡状态
热力学第二定律及其相关基本概念
• 化学反应过程中生成物的熵的总和减去反应物 熵的总和即化学反应的熵变。 • 在不做非体积功的情况下，对于可逆过程有：
• • 恒容热容：在不发生相变与化学变化、恒容、不做非 体积功的情况下体系每升高1度体系所需吸收的热量:
dQ U Cv dT V T V
•
• •
在不发生相变与化学变化的情况下，温度由T1升高至 T2所引起的内能变化为：
U Cv dT
T1
• •
•
与内能和焓一样，Gibbs自由能与Helmholtz自由能也没有绝对值 Gibbs自由能与Helmholtz自由能的变化可以由焓变、熵变、内能的 变化求出来 对于等温反应： G H TS
F U TS G H S T T F U S T T
材料热力学什么是材料热力学材料热力学是热力学基本原理在材料设计制备与使用过程中的应用包括相平衡相图热力学相变热力学等相图反映的是物质的存在状态而热力学反映的是物质所包含的能量而能量是物质状态变化的起因与因此相图与热力学有非常密切的关系目前材料热力学主要内容是相图或相平衡热力学本课程包括热力学基本原理回顾热力学在冶金材料过程中的应用相平衡热力学与相图计算相图与合金设计热力学基本原理回顾平衡状态
热力学第二定律及其相关基本概念
• 化学反应过程中生成物的熵的总和减去反应物 熵的总和即化学反应的熵变。 • 在不做非体积功的情况下，对于可逆过程有：
材料热力学3-1第二 第三定律
T2 S1 nC p , m H 2 O, l ln T1
T2 S 3 nC p , m H 2 O, s ln T1
ΔS环境？？？？？
恒压条件下：
S 环境
H m 263 . 15 H 1 H m 273 . 15 H 3 1 75 . 3 10 6020 37 . 6 10 5463 J H m 263 .15 K S 环境 21 .44 J K 1 263 .15 K
解：由于是正常相变：
QR S T
n fu s H m 1 5995 . 8 273 .15 T 1 1 22 . 01( J K m ol )
2. 不可逆相变：定温定压下两相不平衡时的相变。 不是发生在两相平衡共存的T，P下的相变——不可逆相变
亚（介）稳态：过冷、过热的液体；过 饱和溶液等。 不可逆相变的ΔS 计算：
不可逆过程： H2O （l）263K p0
需 计 逆 程 计 ΔS
设 可 过 来 算
ΔS=?
H2O （s）263K p0
等压可 逆降温
ΔS1
等压可 逆升温
ΔS3
H2O （l）273K p0
ΔS2
可逆相变
H2O （s） 273K p0
H2O （l）263K
p0
ΔS=?
H2O （s）263K p0
等压可 逆降温
pdV = nRT
∫
V1 +V 2 V1
dV V 1+V 2 = nRT ln V V1
Q V 1+V 2 S = S 2 _S 1 = = nR ln T V1
1mol理想气体在298K时等温膨胀，体积增大10倍，求系统的熵
T2 S 3 nC p , m H 2 O, s ln T1
ΔS环境？？？？？
恒压条件下：
S 环境
H m 263 . 15 H 1 H m 273 . 15 H 3 1 75 . 3 10 6020 37 . 6 10 5463 J H m 263 .15 K S 环境 21 .44 J K 1 263 .15 K
解：由于是正常相变：
QR S T
n fu s H m 1 5995 . 8 273 .15 T 1 1 22 . 01( J K m ol )
2. 不可逆相变：定温定压下两相不平衡时的相变。 不是发生在两相平衡共存的T，P下的相变——不可逆相变
亚（介）稳态：过冷、过热的液体；过 饱和溶液等。 不可逆相变的ΔS 计算：
不可逆过程： H2O （l）263K p0
需 计 逆 程 计 ΔS
设 可 过 来 算
ΔS=?
H2O （s）263K p0
等压可 逆降温
ΔS1
等压可 逆升温
ΔS3
H2O （l）273K p0
ΔS2
可逆相变
H2O （s） 273K p0
H2O （l）263K
p0
ΔS=?
H2O （s）263K p0
等压可 逆降温
pdV = nRT
∫
V1 +V 2 V1
dV V 1+V 2 = nRT ln V V1
Q V 1+V 2 S = S 2 _S 1 = = nR ln T V1
1mol理想气体在298K时等温膨胀，体积增大10倍，求系统的熵
材料热力学(三大定律)要点
Q Qc Qc 则： I h 1 Qh Qh
根据Carnot定理： 则
Th Tc Tc R 1 Th Th
I R
Qc Q h 0 Tc Th
n Qi 0 < 0 i Ti I
将不可逆热机的结论推广到任意的不可逆循环，则：
二、不可逆过程的热温商
热力学第二定律的数学表达
Clausius不等式
SAB
对于微小变化：
Q ( ) A B T i
Q dS T
Q 是实际过程的热效应，T是环境温度。若是不可逆过 程，用“>”号，可逆过程用“=”号，这时环境与系统温度相同。
熵增加原理
2、 等温、等压可逆相变（若是不可逆相变，应设计始终 态相同的可逆过程）
解法1
22.4 V2 S (O 2 ) nR ln 0.5R ln V1 12.2
0.5 mol 0.5 mol O 2 (g) N 2 (g)
22.4 S (N 2 ) 0.5 R ln 12.2
22.4 nR ln 2 > 0 mix S S (O2 ) S (N2 ) nR ln 12.2
SAB
B Q T A I
如AB为可逆过程
Q S A B T i R,A B
S是状态函数，在确定的始、终态间，ΔS为定值，与过程是否 可逆无关。但过程的热温商之和与过程是否可逆有关。若可逆则过程 的热温商之和等于ΔS；若过程不可逆则过程的热温商之和小于ΔS。
H (相变） S (相变） T (相变）
3、 理想气体（或理想溶液）的等温混合过程，并符合分 体积定律，即 x V
B B
V
mix S R nB ln xB
材料热力学 第三章 单组元材料热力学
Cp
H T
p
Cv
U T
v
H CpdT H (0K) U CvdT U(0K)
H(0K)和U(0K)是绝对零度的焓和内能， 目前其绝对值尚无法得知。
dS Q CdT
TT
S p
T 0
Cp T
dT
S(0K)
Sv
T 0
Cv T
dT
S (0K )
S(0K)为绝对零度下的熵，根据热力学第三定律(Third Law)，认为单组元在绝对零度下的熵为0。
第三章 单组元材料热力学
3.2 晶体中的热空位
理想晶体中不存在空位，但实际金属晶体中存在空位。 随着温度升高，晶体中的空位浓度增加，大多数常用金 属（Cu、Al、Pb、W、Ag…）在接近熔点时，其空位 平衡浓度约为10-4，即晶格内每10000个结点中有一 个空位。
把高温时金属中存在的平衡空位通过淬火固定下来，形 成过饱和空位，这种过饱和空位状态对金属中的许多物 理过程（例如扩散、时效、回复、位错攀移等）产生重 要影响。
G
T
C pdT
0
T
T
0
Cp T
dT
H (0K)
F
T 0
Cv dT
T
T
0
Cv T
dT
U (0K)
能量均分定理在解释热容问题所遇到的巨大困 难迫使人们至新审查能量均分定理。能量均分 定理是由经典统计力学导出的，在经典物理包 括经典统计力学中有一个根本的假设就是能量 是连续改变的，能量均分定理在解释热容以及 热辐射问题上所遇到的不可克服的困难使得普 朗克提出量子论假设。
例题：
由实验求得Cp值： C p a bT cT 2 状态改变时：
材料热力学课件-第三章-2
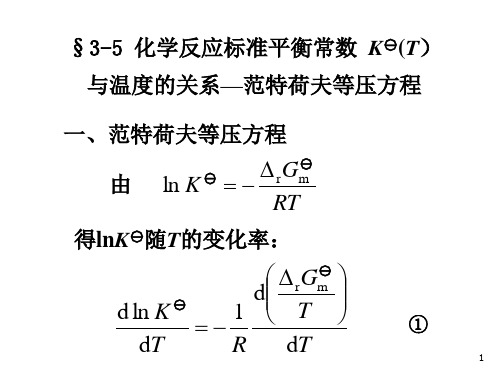
以△Hm =18.86kJmol-1代入
lnK
(T
)
r
H
m
B
RT
得 B = 0.045+(18860/2.303×8.3145×873)
= 1.17 lgK = - 18860 Jmol-1/(2.303RT) + 1.17
= -985/(T/K) + 1.17
13
(3)根据上式求1373 K 时的 lgK(1373 K)= - 983/1373 + 1.17
+1/2∑bBT 2 +1/3∑cBT 3
其中 △H0 =△rHm (298K)-298K×∑aB – 1/2×(298K)2 ∑bB -1/3(298K)3∑cB
22
△rHm(T)=△H0+∑aBT
+1/2∑bBT 2 +1/3∑cBT 3
代入dlnK(T) =[△rHm/RT2 ]dT，得
ln
△rGm –T 的近似直线关系是在BCp,m
很小或0时。因为
△rSm （T） = △rSm （298K） +
C T
B dT
298K
B p,m
B
T
19
dlnK dT
T
r
H
m
(T
RT 2
)
ln
K (T2 ) K (T1)
r
H
m
R
1 T2
1 T1
lnK
(T
)
r
H
m
B
RT
20
2、△rHm随温度变化
说明计算中做了哪些假设。
G 已知
f
m
Ag
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
材料热力学(第3版)
材料热力学是材料科学中重要的一门基础学科，它研究了材料体系在不同温度、压力和组分条件下的热平衡和相变规律。
本文将从基本概念、热力学定律、热力学函数以及应用等方面介绍材料热力学的主要内容。
第一部分：基本概念
材料热力学研究的对象是物质的热平衡和相变规律。
热平衡是指系统内部各部分之间没有温度、压力和组分的变化，达到了热力学平衡的状态。
相变是指物质由一种相态转变为另一种相态的过程，如固态到液态的熔化、液态到气态的汽化等。
第二部分：热力学定律
材料热力学的研究基于一些基本的热力学定律，包括能量守恒定律、熵增定律、Gibbs-Helmholtz方程等。
能量守恒定律是指能量在封闭系统中不会产生或消失，只会转化为其他形式的定律。
熵增定律是指系统的总熵在不可逆过程中只会增加，不会减小的定律。
Gibbs-Helmholtz方程是描述物质体系在不同温度下的自由能变化与热力学函数之间的关系。
第三部分：热力学函数
热力学函数是描述材料体系热平衡和相变规律的重要工具。
常见的热力学函数包括熵、内能、焓和自由能等。
熵是描述系统无序程度
的物理量，内能是系统的总能量，焓是系统的内能加上对外界做的功，自由能是系统的内能减去对外界做的功以及系统的熵与温度的乘积。
通过热力学函数的计算和分析，可以得到材料体系在不同条件下的稳定相态和相变规律。
第四部分：应用
材料热力学在材料科学和工程中有着广泛的应用。
例如，材料的相图就是利用热力学原理和实验数据绘制出的描述材料体系相态和相变规律的图表。
相图可以帮助研究人员预测材料的相变温度、相平衡条件等，为材料设计和制备提供指导。
此外，材料热力学还在材料合金设计、材料的热处理和相变控制等方面起着重要的作用。
材料热力学是研究材料体系热平衡和相变规律的学科。
通过基本概念的介绍，热力学定律的阐述，热力学函数的解释以及应用的讨论，我们可以更深入地理解材料热力学的重要性和应用价值。
在实际应用中，材料热力学为材料科学和工程领域的研究和发展提供了有力的支持。
通过不断深入研究和应用，我们可以更好地理解材料的热平衡和相变规律，为材料设计和制备提供更准确的指导和优化方案。