勾股定理与面积计算
勾股定理解析三角形面积和边长之间的关系

勾股定理解析三角形面积和边长之间的关系勾股定理是初中数学中最基础的知识点之一,它指出:在一个直角三角形中,直角边的长度的平方等于另外两条边的长度平方之和。
用数学符号来表示就是:a² + b² = c²,其中c为斜边的长度,a、b为直角边的长度。
该定理的证明方法有很多种,其中最著名的莫过于毕达哥拉斯的证明。
面积和长度的关系三角形是初中数学中的另一个基础知识点,它有许多性质和公式,例如,三角形的面积可以用底边和高来表示,即面积等于底边长度乘以高的长度再除以2,公式可以表示为:S = 1/2 * a * h。
而在勾股定理中,三角形的斜边可以用另外两条直角边的长度表示,此时三角形的面积可以表示为:S = 1/2 * a * b。
三角形的面积公式中的“底边”和“高”都是用长度表示的,而勾股定理中的“直角边”和“斜边”也是用长度表示的。
这就说明,三角形的面积和边长之间存在着某种关系。
为了探究这种关系,我们可以结合勾股定理和三角形的面积公式来进行推导。
在勾股定理中,有c² = a² + b²,两边同时乘以2再除以c²,可以得到:2S/c² = 2ab/c²这里,S表示三角形的面积,c为斜边的长度,a、b为直角边的长度。
式子左边表示三角形的面积与斜边的平方之间的比值,式子右边表示直角边之积与斜边的平方之间的比值。
进一步移项得到:S = ab/c这就是三角形面积和边长之间的关系式。
结论:在任意一个三角形中,其面积等于底边长度和高的乘积再除以2,也等于任意两边长度之积再除以第三边的长度。
这两个公式是等价的。
结语通过对勾股定理和三角形面积公式的推导过程,我们可以发现它们之间存在着紧密的关系。
这不仅可以加深我们对数学知识的理解,还有助于我们更加灵活地运用它们,更好地解决实际问题。
勾股定理面积问题
1 S1 S2
2 S2
若变为作其它任意正 多边形,情形会怎样? S3
B
C
S2
a c
B
b
A
S3 A S2
S1
C
S1
四变: 如图,分别以直角△ABC三边 为直径向外作三个半圆,其面积分别用S1、 S2、S3表示,则S1、S2、S3有什么关系? 不难证明S3=S1+S2 .
C S1 a B
S2
b c
A
S3
观察下列图形,正方形1的边长为7,则 正方形2、3、4、5的面积之和为多少? 规律:
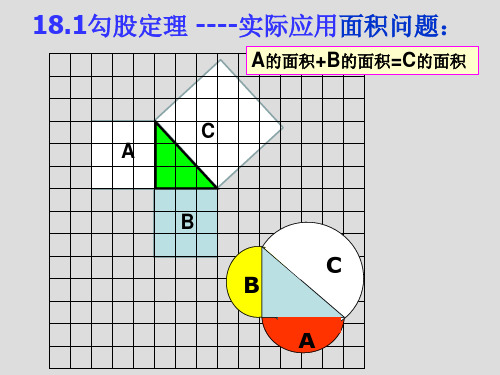
18.1勾股定理 ----实际应用面积问题:
A的面积+B的面积=C的面积
C
A
B
B A
C
D
二变:如图,分别以Rt △ABC三边为 斜边向外作三个等腰直角三角形,其面 积分别用S1、S2、S3表示,则S1、S2、S3 之间的关系是 S1 S2 S3,请说理。
C
S3
A
b
a c
S2
B
S1
三变:如图,分别以Rt △ABC三边为 边向外作三个正三角形,其面积分别用 S1、S2、S3表示,则S1、S2、S3之间的关 系是 S1 S2 S3 ,请说理。
2 3 4 5
S2+S3+S4+S5= S1
1
二.y=0 复习面积法证明勾股定理
已知S1=1,S2=3,S3=2,S4=4,求 S5、S6、S7的值
S3
S4
S2
结论:
S1+S2+S3+S4 =S5+S6 =S7
S1
S5
S6
勾股定理--与图形面积

17.1(3.2)勾股定理--与图形面积一.【知识要点】1.如图,以直角三角形的边为边,向外作等边三角形,半圆,等腰直角三角形和正方形,都满足123S S S +=.二.【经典例题】1. 在△ABC 中,AB=13cm ,AC=20cm ,BC 边上的高为12cm ,则△ABC 的面积为 cm2.2.(绵阳2020年期末8题)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图,分别以Rt △ABC 的三条边为边向外作正方形,面积分别记为S 1,S 2,S 3.若S 1+S 2=36,则S 3=( )A .25B .36C .40D .493.如图所示,直线l 上有三个正方形a ,b ,c ,若a ,c 的面积分别为5和11,则b 的面积为( ).A .4B .6C .16D .55三.【题库】【A 】1.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD 、正方形EFGH 、正方形MNPQ 的面积分别为S 1、S 2、S 3.若S 1+S 2+S 3=60,则S 2的值是 .2.如图,在Rt △ABC 中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙,当AC=4,BC=2时,则阴影部分的面积为__________.【B 】1.已知:如图,以Rt △ABC 的三边为斜边分别向外作等腰直角三角形,若斜边AB =3,则图中阴影部分的面积为( )A. 9B. 3C.49 D. 292.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm ,则正方形A 、B 、C 、D 的面积之和为 cm 2.3.如图,分别以直角△ABC 的三边AB ,BC ,CA 为直径向外作半圆.设直线AB 左边阴影部分的面积为S 1,右边阴影部分的面积和为S 2,则( )A.S 1=S 2B.S 1<S 2C.S 1>S 2D.无法确定4.如图所示,AB =BC =CD =DE =1,AB ⊥BC ,AC ⊥CD ,AD ⊥DE ,则AE 等于( )A.1B. 2C. 3D.25.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D 的面积分别为2,5,1,2,则最大的正方形E 的面积是__________.6.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A ,B ,C ,D 的边长分别为12,16,9,12,则最大正方形E 的面积为( )A .625B .675C .725D .765ABC BC A ED图3【C】1.在直线l上依次摆放着七个正方形(如图).已知斜放置的三个正方形的面积分别是l,2,3,正放置的四个正方形的面积依次是S l,S2,S3,S4,求S1+S2+S3+S4= .2、以OA为斜边作等腰直角三角形OAB,再以OB为斜边在△OAB外侧作等腰直角三角形OBC,如此继续,得到8个等腰直角三角形(如图),则图中△OAB与△OHJ的面积比值是()A.32 B.64 C.128 D.2563、如图所示是一种“羊头”形图案,其作法是:从正方形1开始,以它的一条边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,…,以此类推,若正方形7的边长为1cm,则正方形1的边长为 cm.ABCDE4.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2007次后形成的图形中所有的正方形的面积和是()A.2006 B.2007 C.2008 D.15.如图,Rt△ABC 的面积为20cm2,在AB的同侧,分别以AB,BC,AC为直径作三个半圆,则阴影部分的面积为6.已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3.则图中阴影部分的面积为______.7.有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是()A.2022 B.2021 C.2020 D.1第19题图CBA1【D 】1.如图,Rt △ABC 中,∠ACB=90°,∠BAC=30°,AB=4,分别以AB 、BC 、AC 为边作正方形ABED 、BCFK 、ACGH ,再作Rt △PQR ,使∠R=90°,点H 在边QR 上,点D 、E 在边PR 上,点G 、F 在边PQ 上,则PQ的长为( ) A.327+ B.3214+C.347+D.3414+【JS 】1.如图,在△ABC 中,∠ACB =90°,以△ABC 的各边为边作三个正方形,点G 落在HI 上,若AC +BC =6,空白部分面积为10.5,则AB 的长为 .2.勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内.若图中阴影部分图形的面积为3,则较小两个正方形重叠部分图形的面积为( )A.2 B.3 C.5 D.63.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为()A.S1+S2+S3=S4 B.S1+S2=S3+S4C.S1+S3=S2+S4D.不能确定。
正方形面积法证明勾股定理

正方形面积法证明勾股定理正方形面积法证明勾股定理引言:勾股定理是数学中著名的定理之一,它是指在直角三角形中,斜边的平方等于直角两边的平方和。
这个定理被广泛地应用于各个领域,如物理、工程等。
本文将通过正方形面积法来证明勾股定理。
一、正方形面积法的原理二、证明勾股定理1. 画出直角三角形ABC2. 构造正方形ABDE和ACFG3. 求解正方形ABDE和ACFG的面积4. 推导出勾股定理三、结论一、正方形面积法的原理正方形面积法是指在一个平面直角坐标系中,通过构造两个相同的正方形来证明一个几何问题。
这种方法可以利用平面几何中图形的对称性和相似性来得到结论。
二、证明勾股定理1. 画出直角三角形ABC首先,在平面直角坐标系中画出一个直角三角形ABC。
假设AB为斜边,AC为邻边,BC为对边。
2. 构造正方形ABDE和ACFG其次,在BC上构造正方形ABDE,使D点在BC的延长线上。
在AC 上构造正方形ACFG,使F点在AC的延长线上。
3. 求解正方形ABDE和ACFG的面积由于正方形ABDE和ACFG是相同的,所以它们的面积也相等。
因此,我们只需要求出其中一个正方形的面积即可。
设AB=c, AC=b, BC=a,则BD=a-c,CF=a-b。
根据勾股定理可知:BD²+AD²=AB²CF²+AF²=AC²将BD和CF带入上式得:(a-c)²+AD²=c²(a-b)²+AF²=b²化简得:a²-2ac+c²+AD²=c²a²-2ab+b²+AF²=b²移项得:AD²=2ac-a^2AF^2=2ab-b^24. 推导出勾股定理因为ABDE和ACFG都是正方形,所以它们的面积分别为:S1 = AD×AD = (2ac-a^2)/4S2 = AF×AF = (2ab-b^2)/4同时,由于直角三角形ABC中斜边AB与直角边AC垂直,所以S1+S2=S(ABC),即:(2ac-a^2)/4 + (2ab-b^2)/4 = ab/2移项得:a^2+b^2=c^2这就是勾股定理。
勾股定理常用个公式

勾股定理常用个公式勾股定理是数学中一个非常重要的定理,它是平面几何中的基础定理,常用来求解直角三角形的边长和角度。
根据勾股定理,我们可以推导出多个相关的公式来解决各种问题。
在本篇文章中,我将介绍11个常用的勾股定理公式,每个公式都会附带一个解析和一个示例。
1.三角形斜边的长度(已知两边长度):c=√(a²+b²),其中a和b分别是直角三角形的两条直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的两条直角边的长度分别为3和4,求斜边的长度。
解析:根据公式,c=√(3²+4²)=√(9+16)=√25=5、因此,斜边的长度为52.直角三角形的直角边长度(已知斜边长度和另一直角边长度):a=√(c²-b²),其中b是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为4,求第二个直角边的长度。
解析:根据公式,a=√(5²-4²)=√(25-16)=√9=3、因此,第二个直角边的长度为33.直角三角形的直角边长度(已知斜边长度和另一直角边长度):b=√(c²-a²),其中a是已知直角边的长度,c是斜边的长度。
示例:已知一个直角三角形的斜边长度为5,另一直角边的长度为3,求第二个直角边的长度。
解析:根据公式,b=√(5²-3²)=√(25-9)=√16=4、因此,第二个直角边的长度为44.直角三角形的面积(已知两个直角边的长度):A=1/2*a*b,其中a和b为直角三角形的两个直角边的长度。
示例:已知一个直角三角形的两个直角边的长度分别为3和4,求其面积。
解析:根据公式,A=1/2*3*4=6、因此,直角三角形的面积为65.直角三角形的周长(已知两个直角边的长度):P=a+b+c,其中a和b分别为直角三角形的两个直角边的长度,c为斜边的长度。
勾股定理求圆环面积

勾股定理求圆环面积
《利用勾股定理求圆环面积》
圆环是一种特殊的几何图形,由两个不同大小的圆相结合形成。
两个圆半径分别记作r1和r2,r1>r2,学生在学习几何图形时经常使用勾股定理来求圆环的面积。
勾股定理是以古希腊数学家勾股提出的。
它告诉我们,任何一个三角形的三边都遵循a<sup>2</sup>+b<sup>2</sup>=c<sup>2</sup>。
圆环的半径记作 r,则 r=r1-r2,根据勾股定理可以由已知r1和r2求出圆环的半径r。
圆环的面积S可以由公式S=π (r1<sup>2</sup>-
r2<sup>2</sup>) 来计算。
π是圆周率,圆环的面积等于将内圆和外圆的面积相减得到。
其中r1<sup>2</sup>代表外半圆的面积,而
r2<sup>2</sup>代表内半圆的面积。
因此,我们可以利用勾股定理来求出圆环的半径,再利用圆环的面积公式来计算出圆环的面积。
勾股定理是一个简单而实用的数学原理,它极大简化了计算几何图形的过程,使得科学家和学生更容易理解几何图形的本质。
利用勾股定理求面积

S2
π 8
a2,S3
π 8
b 2 ,S1
π 8
c2
S2 S3 S1
总结:与直角三角形三边相连的正方 形、等腰直角三角形、等边三角形以 及半圆甚至正多边形都有相同的结论: 即两直角边上图形面积的和等于斜边 上的图形的面积。
பைடு நூலகம்
1、如图,所有的四边形都是正方形,所有的三 角形都是直角三角形,其中最大的正方形的边 和长为7cm,则正方形A,B,C,D的面积之和为
a2 b2 c2
3 2
c2
S2
S3
S1
探究二:向外拓展半圆
1、如图,已知在△ABC中,∠ACB=90°,
AC=b,BC=a,AB=c,分别以Rt △ABC三边为 边向外作三个半圆,其面积分别用S1,S2, S3表示,求证:S1 S2 S3
ACB 90
a2 b2 c2
由以上探究知:SDCA SCBF SABE
即:S1 S4 S3 S5 S2 S4 S5 S6
S1
S3
S2
S6
68 2
24
勾股定理在求图形面积中的应用
如图,已知在△ABC中,∠ACB=90°,
AC=b,BC=a,AB=c,分别以Rt △ABC三边为边向 外作三个正方形,其面积分别用S1,S2,S3表 示,容易得出S1,S2,S3之间的关系
为 S1 S2 S3 .
探究一:向外拓展三角形
1、如图,已知在△ABC中,∠ACB=90°,
AC=b,BC=a,AB=c,分别以Rt △ABC三边为
边向外作三个等腰直角三角形,其面积分
半圆的面积关系勾股定理

半圆的面积关系勾股定理
半圆的面积与勾股定理之间存在着一定的关系。
首先,让我们来看一下半圆的面积计算公式。
假设半圆的半径为r,则半圆的面积S可以通过以下公式计算,S = (1/2)πr^2,其中π是圆周率,约为3.14159。
这是基本的半圆面积的计算方法。
现在让我们来谈谈勾股定理。
勾股定理是指直角三角形中,直角边的平方等于另外两条边的平方和。
具体而言,如果一个直角三角形的两条直角边长分别为a和b,斜边长为c,那么勾股定理可以表示为,a^2 + b^2 = c^2。
将这两个概念结合起来,我们可以得出一个有趣的结论。
考虑一个半径为r的半圆,我们可以将其看作一个直角三角形的斜边,而半圆的直径就是这个直角三角形的斜边。
根据勾股定理,直角三角形的两条直角边的平方和等于斜边的平方,即(r/2)^2 + r^2 = c^2,化简得到,r^2/4 + r^2 = c^2,进一步化简得到,5r^2/4 = c^2。
因此,半圆的直径的平方等于5/4倍半圆的面积。
综上所述,半圆的面积与勾股定理之间的关系可以通过半圆的直径和半圆的面积之间的关系来体现。
这种关系为我们提供了一种
有趣的方式来理解几何形状之间的数学关系,并展示了数学在不同领域之间的重要应用。
希望这个回答能够帮助你更好地理解半圆的面积和勾股定理之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理与面积计算
1.(1)如图①,S 1、S 2和S 3分别是以直角三角形的两直角边和斜边长为直径的半圆的面积,你能找出S 1、S 2和S 3之间的关系吗?请说明理由
(2)如图②,如果直角三角形的两直角边分别为6cm ,8cm ,你能根据(1)的结论求出阴影部分的面积吗?你能得出什么结论吗?
2.如图(2)R t ⊿ABC 中,∠ACB=900,AC=6,BC=8,S 1、S 2和S 3分
别是以直角三角形的两直角边和斜边长为边长的等边三角形。
你能找出S 1、S 2和S 3之间的关系吗?请说明理由
3. 如图(3)R t ⊿ABC 中,∠ACB=900,AB=3,S 1、S 2和S 3分别是以直角三角形的三边为斜边的等腰直角三角形,则图中阴影部分的面积为 。
4. 如图(4) 以R t ⊿ABC 的三边为边长向形外画正方形,以AB 为边的正方形的 面积为100cm 2,则这三个正方形的面积共为 cm 2。
5、如图14.1.3,所有的四边形都是正方形,所有的三角形都是直角三角形, 其中最大的正方形E 的面积为81cm 2,则正方形A 、B 、C 、D 的面积之和为 。
6、如图14.1.4,是一个“羊头型”的图案,其作法是:从正方形1开始以它的一边为斜边向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,依次类推。
若正方
形1的面积为64cm 2,则正形7的边长为 。
7.如图所示的弦图中,大正方形的面积为13,小正方形的面积为1,直角三角形的短直角边
为a ,较长直角边为b ,求(a+b )=。
8. 有一块土地的形状如图,
∠B=∠D=90°,AB=20m ,BC=15m ,CD=7m ,请计算这块土地面积。
(2) (3)
(4) 1242334图14.1.4B 8题图。
