平行线相关题目
题目:《平行线》单元测试题(含答案)

题目:《平行线》单元测试题(含答案)平行线单元测试题(含答案)第一部分:选择题(每小题2分,共20分)1. 下列选项中,哪个是平行线的性质?- A. 两条平行线之间的距离恒定- B. 两条平行线不会相交- C. 两条平行线的斜率相等- D. 两条平行线的夹角为90度2. 已知两条直线L和M是平行线,且L与M之间的距离为5cm。
如果将直线L向上平移2cm,那么L和M之间的距离将变为多少?- A. 3cm- B. 5cm- C. 7cm- D. 10cm3. 在平面直角坐标系中,过点(2,3)和(5,7)的直线与x轴的交点为:- A. (2,0)- B. (3,0)- C. (5,0)- D. (7,0)4. 两条平行线的斜率分别为2和-3,那么这两条直线的夹角为:- A. 30度- B. 45度- C. 60度- D. 90度5. 在平面直角坐标系中,过点(-3,4)和(5,-2)的直线的斜率为:- A. -2- B. -1/2- C. -1- D. 26. 在某个平面上,直线L的斜率为3,直线M的斜率为1/3。
如果L与M相互垂直,那么L和M的斜率乘积为多少?- A. -1- B. 0- C. 1- D. 37. 已知直线L的斜率为2,且它在平面上与y轴相交于点(0,4),那么直线L的方程式为:- A. y = 2x + 4- B. y = 2x - 4- C. y = 4x + 2- D. y = -4x + 28. 两条平行线L和M的斜率分别为1/2和2/3,它们之间的夹角为:- A. 20度- B. 30度- C. 40度- D. 50度9. 已知直线L和M是平行线,且直线L的斜率为2。
如果直线L过点(3,5),那么直线M的方程式为:- A. y = 2x - 7- B. y = 2x + 7- C. y = -2x - 1- D. y = -2x + 110. 若两条平行线的斜率分别为a和2a,且a不等于0,那么这两条直线的夹角为:- A. 30度- B. 45度- C. 60度- D. 90度第二部分:简答题(每小题5分,共20分)1. 简述平行线的性质。
三年级数学平行线练习题

三年级数学平行线练习题题目一:平行线的基本概念和判断1. 请判断下列线段是否平行:AB || CD,EF || GH,IJ || KL。
2. 在下列选项中选出并圈出一组平行线:(1)AB、BC、CD、DE;(2)EF、FG、GH、HI。
3. 通过观察四边形的内部线段,判断下列四边形中的哪些线段是平行的:(1)ABCD;(2)EFGH;(3)IJKL。
题目二:平行线的性质及推理1. 已知直线l和直线m是平行线,若以一个点P为顶点,作与直线l和直线m分别交于点A和点B的两个直线,是否可以确定直线PA和直线PB的关系?为什么?2. 已知直线l和直线m是平行线,若一段线段与直线l平行,并且与直线m有一交点,则这段线段与直线m是否平行?请说明理由。
3. 图中的线段有AB // CD,EF ⊥ CD,DE ⊥ BC,请判断下列说法是否正确,并解释原因:(1)角A和角B是对顶角;(2)AB ⊥EF;(3)角BCD和角DEF互为对应角。
题目三:平行线的应用1. 请根据图中已知条件,判断下列说法是否正确,并解释原因:(1)ABCD是一个平行四边形;(2)AC ⊥ BD;(3)BC // DE。
2. 请根据图中已知条件完成下列推理:如图为一个平行四边形ABCD,已知AB = 2 cm,BD = 3 cm,AC ⊥ BD,求AC的长度。
3. 图中的线段有AB // CD,EF ⊥ CD,若EF的长度为5 cm,BC 的长度为8 cm,请问DE的长度是多少?题目四:平行线的综合练习1. 请根据图中平行线的已知条件,推导出下列等式,并说明推导过程:(1)BD = ?;(2)DE = ?。
2. 图中的线段有AB // CD,EF ⊥ CD,若BC的长度为6 cm,DE 的长度为3 cm,请问AB的长度是多少?3. 已知四边形ABCD中,AB // CD,AE ⊥ BC,BF ⊥ AD,若AB 的长度为5 cm,BC的长度为8 cm,请问AE的长度是多少?注意:以上题目仅供参考,可以根据需要自行修改和调整。
(完整版)小学四年级数学平行线的认识练习题

(完整版)小学四年级数学平行线的认识练习题一、判断题1. 平行线是指在同一个平面内永远不相交的两条直线。
()2. 如果两条直线相交成一个角,那么这两条直线一定不平行。
()3. 只有平行线才能构成平行四边形。
()4. 平行线之间的夹角是180度。
()5. 两条平行线之间的距离在任何地方都是相同的。
()二、选择题1. 下列图形中,能构成平行线的是()A. B. C. D.2. 下列直线中,与直线L平行的是()A. B. C. D.3. 以下哪个是平行四边形?()A. B. C. D.4. 平行线之间的夹角是()A. 90度B. 120度C. 180度D. 360度三、填空题1. 两条直线在平面上不相交,我们可以说这两条直线是()。
2. 在平行四边形中,对角线之间的夹角度数是()。
3. 在下图中,直线a与直线b是()。
四、解答题1. 请你举出一个例子,说明两条直线相交成一个角,那么这两条直线一定不平行。
2. 如果两条直线平行,那么它们之间的夹角应该是多少度?3. 画出一个平行四边形,并标明其对角线。
答案:判断题:1. √2. ×3. √4. √5. √选择题:1. C2. B3. A4. C填空题:1. 平行线2. 180度3. 平行解答题:1. 举例:直线AB与直线CD相交成角ACD,但直线AB与直线CD不平行。
2. 180度。
3. (示意图,标注对角线的线段)。
平行线的判定和性质经典题
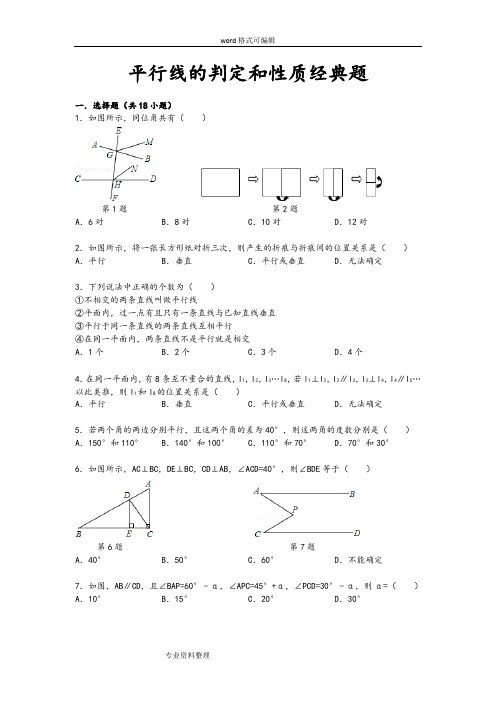
平行线的判定和性质经典题一.选择题(共18小题)1.如图所示,同位角共有()3.下列说法中正确的个数为()①不相交的两条直线叫做平行线②平面内,过一点有且只有一条直线与已知直线垂直③平行于同一条直线的两条直线互相平行4.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠BDE等于()8.下列所示的四个图形中,∠1和∠2是同位角的是()11.如图所示,BE∥DF,DE∥BC,图中相等的角共有()13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有()14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有()15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角16.把直线a 沿水平方向平移4cm ,平移后的像为直线b ,则直线a 与直线b 之间的距离为17.(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是18.(2004•烟台)4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成的象形文字是( )二.填空题(共12小题)19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β= _________ .20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 _________ 个;若∠1=50°,则∠AHG= _________ 度.第20题 第21题 第22题21.(2009•永州)如图,直线a 、b 分别被直线c 、b 所截,如果∠1=∠2,那么∠3+∠4= _________ 度.直线a 、b 分别被直线c 、b 所截.22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3= _________ 度.23.如图,已知BO 平分∠CBA,CO 平分∠ACB,MN∥BC,且过点O ,若AB=12,AC=14,则△AMN 的周长是 _________ .第23题第24题24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为_________ cm;(2)如图2,若∠_________ =∠_________ ,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=_________ 度;25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为_________ .26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有_________ 个.第26题第27题27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有_________ 个.28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为_________ .第28题第29题第30题29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动_________ 格.30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是_________ cm2.平行线的判定和性质经典题参考答案与试题解析一.选择题(共18小题)1.如图所示,同位角共有()2.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是()3.下列说法中正确的个数为()①不相交的两条直线叫做平行线②平面内,过一点有且只有一条直线与已知直线垂直③平行于同一条直线的两条直线互相平行4.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠BDE等于()7.如图,AB∥CD,且∠BAP=60°﹣α,∠APC=45°+α,∠PCD=30°﹣α,则α=()8.下列所示的四个图形中,∠1和∠2是同位角的是()10.如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有()11.如图所示,BE∥DF,D E∥BC,图中相等的角共有()13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有()14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有()15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角16.把直线a沿水平方向平移4cm,平移后的像为直线b,则直线a与直线b之间的距离为17.(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是18.(2004•烟台)4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成的象形文字是( )二.填空题(共12小题)19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β= 60°或120° .20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 5 个;若∠1=50°,则∠AHG=130 度.21.(2009•永州)如图,直线a、b分别被直线c、b所截,如果∠1=∠2,那么∠3+∠4= 180 度.直线a、b分别被直线c、b所截.22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3=53 度.23.如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN 的周长是26 .24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为 2 cm;(2)如图2,若∠ 1 =∠ 2 ,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=25 度;25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为2cm或8cm .26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有 5 个.27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有 5 个.28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为30 .29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动9 格.30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是36 cm2.。
数的平行线与垂直线练习题

数的平行线与垂直线练习题题目一:平行线1. 请判断以下直线是否平行:a) AB与CDb) EF与GHc) IJ与KL2. 已知折线ABCDEF,其中AB∥CD,EF∥GH,请判断以下直线是否平行:a) AD与GHb) EF与KJc) BC与DE3. 在平面直角坐标系中,已知直线y=2x+3和y=-3x+5,请判断它们是否平行。
4. 已知线段AB和线段CD,其中AB∥CD。
若线段EF∥AB且EF 与CD相交于点G,请问线段EF与CD是否平行。
题目二:垂直线1. 请判断以下直线是否垂直:a) AB与CDb) EF与GHc) IJ与KL2. 已知线段AC和线段BD,其中AC⊥BD。
若线段EF⊥AC且EF与AB相交于点G,请问线段EF与AB是否垂直。
3. 在平面直角坐标系中,已知直线y=2x+3和y=-1/2x+2,请判断它们是否垂直。
4. 已知线段AB和线段CD,其中AB⊥CD。
若线段EF⊥AB且EF与CD相交于点G,请问线段EF与CD是否垂直。
题目三:平行线和垂直线的综合运用1. 在直角坐标系中,已知点A(-1, 2),B(3, 5),C(6, 7),D(3, 1),请判断线段AB和线段CD是否平行,线段AB是否垂直于线段CD。
2. 在平面直角坐标系中,已知直线y=-2x+3,点E(-4, -5)和点F(1, 1),请判断直线EF与直线y=-2x+3是否平行,直线EF是否垂直于直线y=-2x+3。
3. 在平面直角坐标系中,已知点A(2, 4),B(5, 6),C(7, 8),D(4, 2),请判断线段AB和线段CD是否平行,线段AB是否垂直于线段CD。
4. 在直角坐标系中,已知直线y=x+1与直线y=-x+1,请判断这两条直线是否平行,是否垂直。
注意:题目中的直线均指直线段,平行线指两条直线段在同一平面内没有交点,垂直线指两条直线段的斜率乘积为-1。
几何平行练习题

几何平行练习题练习一:平行线与平面1. 在平面P上,画一条直线AB,并以点C为中心、画一条与AB 平行的直线CD。
a) 证明直线CD和直线AB平行。
b) 若直线AB与另一条直线EF相交于点G,证明直线CD与直线EF平行。
2. 平面P上有一条直线AB和另一条直线CD,且这两条直线不在同一平面内。
a) 证明直线AB与直线CD平行。
b) 若直线CD与另一条直线EF相交于点G,证明直线AB与直线EF平行。
练习二:判断平行线1. 已知直线AB和直线CD平面上不重合且不相交,且它们的方向相同。
a) 证明直线AB与直线CD平行。
b) 若直线AB与另一条直线EF相交于点G,证明直线CD与直线EF平行。
2. 已知直线AB和直线CD平面上不重合且不相交,且它们的方向相反。
a) 证明直线AB与直线CD平行。
b) 若直线AB与另一条直线EF相交于点G,证明直线CD与直线EF平行。
练习三:平行线之间的性质1. 在△ABC中,直线DE与直线AB和直线AC平行,分别交边AB于点D、边AC于点E。
a) 证明直线DE与边BC平行。
b) 若直线FG与直线BC平行,交边AB于点F、边AC于点G,证明直线FG与直线DE平行。
2. 在△ABC中,直线DE和直线FG分别平行于边BC,分别交边AB于点D和F、边AC于点E和G。
a) 证明直线DE和直线FG平行。
b) 若直线HI与直线BC平行,交边AB于点H、边AC于点I,证明直线HI与直线DE、直线FG都平行。
练习四:平行线的证明1. 在平面P上,已知三条平行线l1,l2,l3。
a) 若直线m与l1平行且交直线l2于点A,证明直线m与直线l3平行。
b) 若直线n与直线l1平行且交直线l3于点B,证明直线n与直线l2平行。
2. 已知四条平行线l1,l2,l3,l4。
a) 若直线m通过直线l1,l2之间的交点且与直线l3平行,证明直线m与直线l4平行。
b) 若直线n通过直线l1,l2之间的交点且与直线l4平行,证明直线n与直线l3平行。
平行线判定练习题

平行线判定练习题题目一:判断下列直线是否平行。
1. 直线AB:y = 2x + 3直线CD:y = 2x - 12. 直线EF:2x + 3y = 6直线GH:6x + 9y = 183. 直线IJ:3x - 4y = 12直线KL:6x - 8y = 24题目二:判断下列线段是否平行。
1. 线段AB:A(1, 2), B(3, 4)线段CD:C(-1, 0), D(1, 2)2. 线段EF:E(-3, 4), F(-1, 2)线段GH:G(2, 3), H(4, 1)3. 线段IJ:I(0, 0), J(3, 0)线段KL:K(1, 1), L(4, 1)解答:题目一:1. 直线AB:y = 2x + 3直线CD:y = 2x - 1两条直线的斜率都是2,且斜率相等,因此直线AB与直线CD平行。
2. 直线EF:2x + 3y = 6直线GH:6x + 9y = 18将两条直线转化为斜截式形式:直线EF:y = (-2/3)x + 2直线GH:y = (-2/3)x + 2两条直线具有相同的斜率 (-2/3),且截距也相同,因此直线EF与直线GH平行。
3. 直线IJ:3x - 4y = 12直线KL:6x - 8y = 24将两条直线转化为斜截式形式:直线IJ:y = (3/4)x - 3直线KL:y = (3/4)x - 3两条直线具有相同的斜率 (3/4),且截距也相同,因此直线IJ与直线KL平行。
题目二:1. 线段AB:A(1, 2), B(3, 4)线段CD:C(-1, 0), D(1, 2)计算线段AB的斜率:斜率m = (y2 - y1) / (x2 - x1)= (4 - 2) / (3 - 1)= 2 / 2= 1计算线段CD的斜率:斜率m = (y2 - y1) / (x2 - x1)= (2 - 0) / (1 - (-1))= 2 / 2= 1两条线段的斜率相等,并且不共线,因此线段AB与线段CD平行。
平行线知识点归纳及典型题目练习(含答案)

平行线知识点归纳及典型题目练习(含答案) -第一篇:平行线知识点归纳及典型题目练习(含答案)第五章相交线与平行线1. 两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2. 两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.3. 两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4. 直线外一点到这条直线的垂线段的长度,叫做________________________.5. 两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.6. 在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7. 平行公理:经过直线外一点,有且只有一条直线与这条直线______. 推论:如果两条直线都与第三条直线平行,那么_____________________. 8. 平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________. 9. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .- 115. 如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.16. 如图,AOC与BOC是邻补角,OD、OE分别是AOC与BOC的平分线,试判断OD与OE的位置关系,并说明理由.17. 如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE 过点C作CF∥AB,则B____()又∵AB∥DE,AB∥CF,∴____________()∴∠E=∠____()∴∠B+∠E=∠1+∠2 即∠B+∠E=∠BCE.- 321.如图,已知ABC,AD BC于D,E为AB上一点,EF BC于F,DG//BA交CA于G.求证1 2.22.已知:如图∠1=∠2,∠C=∠D,问∠A与∠F相等吗?试说明理由.- 5第二篇:第五章相交线与平行线全章知识点归纳及典型题目练习(含答案)第五章相交线与平行线1. 两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2. 两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.3. 两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4. 直线外一点到这条直线的垂线段的长度,叫做________________________.5. 两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________. 6. 在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种. 7. 平行公理:经过直线外一点,有且只有一条直线与这条直线______. 推论:如果两条直线都与第三条直线平行,那么_____________________. 8. 平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________. 9. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .- 115. 如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.16. 如图,AOC与BOC是邻补角,OD、OE分别是AOC与BOC的平分线,试判断OD与OE的位置关系,并说明理由.17. 如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE 过点C作CF∥AB,则B____()又∵AB∥DE,AB∥CF,∴____________()∴∠E=∠____()∴∠B+∠E=∠1+∠2 即∠B+∠E=∠BCE.- 321. 如图,已知ABC,AD BC于D,E为AB上一点,EF BC于F,DG//BA交CA于G.求证1 2.22. 已知:如图∠1=∠2,∠C=∠D,问∠A与∠F相等吗?试说明理由.- 5第三篇:相交线与平行线知识点归纳相交线与平行线知识点小结一、相交线1.相交线:两条直线相交,有且只有一个交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
创作编号:
GB8878185555334563BT9125XW
创作者:凤呜大王*
一、三角板放平行线中问题
1、如图,将三角板的直角顶点放在两条平行线a、b中的直线b上,如果
∠1=40°,则∠2的度数是。
2、小明同学把一个含有45°角的直角三角板放在如图的两条平行线m,n 上,测得∠α=120°,则∠β的度数是______.
3、如图,把一块直角三角板放在直尺的一边上,如果∠2=65°,那么∠
1= .
4、如图,将透明的三角板(其中∠A=90°)置于平行线l1、l2上,则∠α的
度数为.
5、如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,
若∠1=25°,则∠2的度数是
6、已知一副三角板如图(1)放置,其中两条斜边互相平行,则图(2)中
∠1为
二、平行线带拐点的问题
1、如图,已知直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α
等于()
第2题图
第1题图第3题图第4题图第6题图
第5题图
第2题图
第3题图第4题图
2、如图所示,AB∥CD,∠D=26°,∠E=35°,则∠ABE的度数是
3、如图,直线l1∥
l
2
∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=
4、如图:AB∥CD,∠B=115°,∠C=45°,则∠BEC的度数为.
5、如图,已知AB∥CD,∠BAF=∠FED=21°,∠CDE=17°,则∠AFC= .
创作编号:
GB8878185555334563BT9125XW
创作者:凤呜大王*
6、如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,则∠AEF的度数是.
7、如图所示,a∥b,∠1=158°,∠2=42°,∠4=50°.那么∠3=
8、仔细观察,寻找规律:在图中的各图的MA1与NA n平行.
(1)图①中的∠A1+∠A2= 度;
图②中的∠A1+∠A2+∠A3= 度;
图③中的∠A1+∠A2+∠A3+∠A4= 度;
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度;
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= 度;
(2)按上图规律,第n个图中的∠A1+∠A2+∠A3+…+∠A n+1= 度.第5题图第6题图第7题图
9、小明在参加数学兴趣活动小组时,探究如图甲这一基本图形.
【问题】:如图甲,AB∥CD,试探究∠B、∠E、∠D三者之间的数量关系,并说明理由;
【拓展】:将图甲变为图乙、图丙(其中AB∥CD不变),请你直接写出相应的结论:图乙:;图丙:.
【应用】:如图丁,运用上面的结论解决问题:AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED的度数.
三、平行线证明题
1、如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,试判断∠AGF
与∠ABC的大小关系,并说明理由.
2、如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4
3、探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB 的中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结BC、BE.若∠MAN=150°,则∠CBE的大小为
创作编号:
GB8878185555334563BT9125XW
创作者:凤呜大王*。
