长度和距离的概念
长度和距离的概念
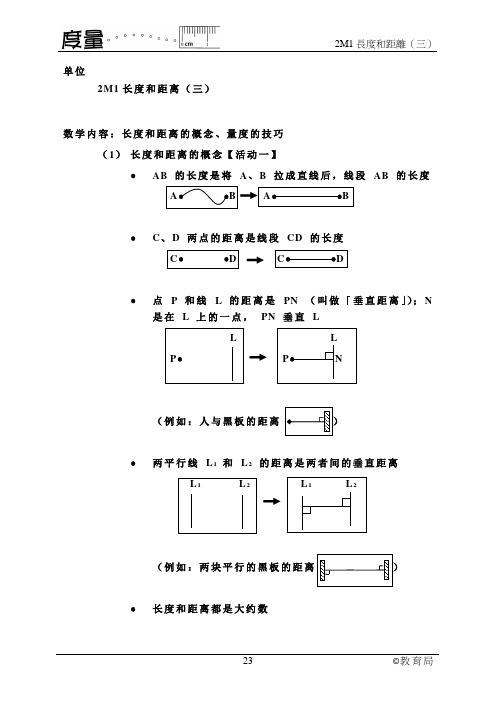
单位 2M1长度和距离(三)数学内容:长度和距离的概念、量度的技巧 (1) 长度和距离的概念【活动一】∙AB 的长度是将 A 、B 拉成直线后,线段 AB 的长度A ∙ ∙B∙C 、D 两点的距离是线段 CD 的长度C ∙ ∙D C ∙ ∙D∙点 P 和线 L 的距离是 PN (叫做「垂直距离」);N 是在 L 上的一点, PN 垂直 L L P ∙(例如:人与黑板的距离∙ 两平行线 L 1 和 L 2 的距离是两者间的垂直距离L 1 L 2(例如:两块平行的黑板的距离∙ 长度和距离都是大约数(2)利用「永备尺」或脑海中1厘米或1米的影象估计长度和距离的技巧【活动一】(3)量度物件的长度或物件间距离的技巧【活动一】∙用尺子上有cm∕m 刻度的一边进行量度∙将尺子置于要量度的长度或距离上,首尾两端点显示的刻度之差,便是要量度的长度或距离(4)以单名数「厘米」记录物件的长度或物件间距离的技巧【活动二】∙名数由两个项目组成:数和单位(例如:「3 厘米」是名数;「3」是数;「厘米」是单位)(5)化复名数为单名数【活动二】∙复名数由两个或多个同度量但不同单位的名数组成(例如:2米 3 厘米)∙在现阶段只能将「米、厘米」化作「厘米」;或只用大约的述语如「比… 米多些」、「比… 米少些」∙有了小数概念之后才可将「米、厘米」化作「米」∙先把米的部分转为厘米,然后再加上厘米的部分∙将x 米y 厘米写成(100 x + y)厘米(6)比较长度和距离的技巧【活动二】∙只用一个单位「米」或「厘米」表达长度和距离较大的数字表示较长的长度和距离,较小的数字表示较短的长度和距离,而两数字相同时则表示长度和距离相等∙用只有两个单位「米」或「厘米」的复名数表达长度和距离先比较以「米」为单位名数中的数字数字不同时,较大的数字表示较长的长度和距离,较小的数字表示较短的长度和距离,而两数字相同时则表示长度和距离相等数字相同时,比较以「厘米」为单位名数中的数字。
长度的基本概念和计算

长度的基本概念和计算长度是物体在某一方向上的延伸距离,是物体的尺寸之一。
在日常生活中,我们常常需要计算和比较物体的长度,因此了解长度的基本概念和计算方法具有重要的意义。
一、长度的基本概念长度是物体的延伸距离,我们可以用长度来描述和比较物体的大小。
长度通常用米(m)作为单位,是国际单位制中的基本单位之一。
除了使用米作为单位之外,我们还常用到厘米(cm)、分米(dm)、千米(km)等单位来表示不同大小的长度。
在物理学中,常用符号"L"表示长度。
例如,如果我们要计算一块木板的长度,可以用L来表示。
长度也可以用数量来表示,比如一个物体的长度是3米,可以用L=3m来表示。
二、长度的计算方法1. 直尺测量法直尺是一种常用的测量工具,可以用来测量物体的长度。
在直尺的一边有一条刻度线,我们可以将物体放在刻度线上,然后读取物体两端所在的刻度线位置,两个刻度线之间的差值就是物体的长度。
使用直尺测量法时,需要注意直尺与物体的接触面要平行,以确保测量结果的准确性。
此外,还要注意读数的精确性,尽量将目光垂直于刻度线,避免产生视觉上的偏差。
2. 卷尺测量法卷尺是另一种常用的测量工具,它比直尺更加灵活。
卷尺通常是带有可伸缩的卷尺表面,可以方便地测量较大尺寸的物体。
卷尺上有刻度线和数字标记,我们可以将卷尺放在物体上,然后读取卷尺上与物体两端对齐的刻度或数字来得到长度。
使用卷尺测量法时,同样要注意与物体的接触面要平行,确保测量的准确性。
同时,在读取测量结果时要仔细观察,防止误读。
3. 仪器测量法对于一些需要更高精度的长度测量,我们可以借助专用的仪器来完成。
例如,经纬仪可以精确测量地球上两个地点之间的距离;激光测距仪可以通过激光束来测量较远距离物体的长度。
使用仪器测量法时,需要根据具体的仪器使用说明进行操作,以确保测量结果的准确性和精确性。
三、长度的单位换算在实际应用中,我们常常需要进行长度的单位换算。
以下是常见长度单位之间的换算关系:1米(m)= 100厘米(cm)1米(m)= 10分米(dm)1米(m)= 0.001千米(km)1千米(km)= 1000米(m)当我们需要在不同单位之间进行换算时,可以利用上述换算关系进行计算。
初中数学距离的概念

初中数学距离的概念数学中,距离是一个非常重要的概念。
它不仅仅出现在数学中,还在其他学科中被广泛使用。
作为一个基本概念,它帮助我们确定物体之间的间隔、两个点之间的长度、测量线和曲线的长度等等。
首先,我们来讨论一下距离的概念。
距离是指两个物体或点之间的间隔,通常用d来表示。
距离有很多种类型,我们常见的有直线距离、曲线距离、欧氏距离、曼哈顿距离等等。
直线距离是最常见的距离类型。
它是指两点之间的最短路径的长度。
比如我们从A点走到B点,我们可以选择直线路径,这条路径的长度就是A点到B点的直线距离。
直线距离可以通过勾股定理来计算得到。
如果两点的坐标分别为(Ax, Ay)和(Bx, By),那么直线距离可以表示为:d = √((Bx - Ax)²+ (By - Ay)²)曲线距离是指两点之间的路径长度,这条路径可以是直线或曲线,不存在直线路径的限制。
比如我们从A点走到B点,我们可以选择一条弯曲的路径,这条路径的长度就是A点到B点的曲线距离。
曲线距离通常比直线距离要大,因为曲线会增加路径的长度。
曲线距离可以通过积分计算得到。
欧氏距离是二维平面上两点之间的直线距离。
欧氏距离是直线距离的一种特殊形式。
如果两点的坐标分别为(Ax, Ay)和(Bx, By),那么欧氏距离可以表示为:d = √((Bx - Ax)²+ (By - Ay)²)曼哈顿距离是二维平面上两点之间的路径长度,与欧氏距离不同,曼哈顿距离是沿着坐标轴走的路径。
它的名字来源于曼哈顿城市的格子街道。
如果两点的坐标分别为(Ax, Ay)和(Bx, By),那么曼哈顿距离可以表示为:d = Bx - Ax + By - Ay除了二维平面上的距离,我们还可以讨论三维空间中的距离。
在三维空间中,直线距离、欧氏距离和曼哈顿距离的定义方法和二维平面上的情况类似。
距离的概念在几何学、物理学、计算机科学等领域应用广泛。
在几何学中,距离可以用来计算图形的周长、表面积和体积等。
数学上册第七单元:长度的比较

数学上册第七单元:长度的比较
引言
在数学中,我们经常需要比较不同事物的长度。
本单元将介绍如何进行长度的比较以及相关概念和技巧。
1. 长度的定义
长度是指物体的长短或延伸的距离。
通常使用一定的单位来表示长度,如米(m)、厘米(cm)等。
2. 长度的比较方法
比较长度时,常用的方法有以下几种:
2.1 比较长度的数值
通过比较长度的数值来确定哪个长度更长或更短。
较大的数值表示较长的长度,较小的数值表示较短的长度。
2.2 使用工具进行比较
使用适当的工具可以更直观地比较长度。
例如,使用尺子或标尺可以直接测量物体的长度,并进行比较。
2.3 利用已知的长度关系进行比较
有时,我们可以利用已知的长度关系来进行比较。
例如,如果知道物体A的长度是物体B的两倍,那么可以推断物体A的长度比物体B的长度更长。
3. 长度的应用
长度的比较在日常生活和实际问题中有着广泛的应用。
以下是一些例子:
3.1 比较尺寸
在购物时,我们可能需要比较不同商品的尺寸,以确定哪个更适合我们的需求。
3.2 比较行程长度
在旅行规划中,我们可能需要比较不同行程的长度,以选择最适合的旅行路线。
3.3 比较运动员速度
在体育竞赛中,我们常常比较不同运动员的速度和跑道的长度,以确定最快的运动员。
结论
长度的比较是数学中常见的基本概念之一。
通过了解不同的比
较方法和应用场景,我们可以更好地理解和运用长度的比较知识。
在实际生活中,我们可以通过比较长度来做出更好的决策和选择。
长度单位换算与运用

长度单位换算与运用长度单位是指用于量度物体长短、距离的单位。
在生活和工作中,我们经常需要进行长度单位的换算和运用。
本文将介绍长度单位的常见换算和运用方式,帮助读者更好地理解和应用长度单位。
一、长度单位的基本概念长度是一个物体的长短或者两个物体之间的距离。
在国际单位制(SI)中,长度的基本单位是米(m)。
除了米,常见的长度单位还有厘米(cm)、毫米(mm)、千米(km)、英寸(inch)、英尺(foot)、码(yard)等。
二、长度单位的换算1. 米与千米的换算1米(m)= 0.001千米(km)1千米(km)= 1000米(m)2. 米与厘米的换算1米(m)= 100厘米(cm)1厘米(cm)= 0.01米(m)3. 米与毫米的换算1米(m)= 1000毫米(mm)1毫米(mm)= 0.001米(m)4. 千米与英里的换算1千米(km)= 0.62137119英里(mile)1英里(mile)= 1.609344千米(km)5. 英寸与厘米的换算1英寸(inch)= 2.54厘米(cm)1厘米(cm)= 0.39370079英寸(inch)6. 英尺与米的换算1英尺(foot)= 0.3048米(m)1米(m)= 3.2808399英尺(foot)三、长度单位的运用1. 学习和工作中的长度单位换算在学习和工作中,我们常常需要进行长度单位的换算,例如计算物体的周长、面积、体积等。
通过灵活运用长度单位的换算,我们可以更精确地计算和衡量。
2. 生活中的长度单位运用长度单位换算不仅在学习和工作中有用,也在日常生活中能够帮助我们更好地理解和应用。
例如,在购买家具时,我们需要测量家具的长度和宽度,以确保其适合我们的家居空间。
在旅行中,我们可以根据里程表上的距离单位,了解旅行的时间和距离。
3. 地理和导航中的长度单位运用在地理和导航中,长度单位的运用尤为重要。
例如,在谷歌地图或导航软件中,我们可以通过输入起点和终点的坐标来计算两地之间的距离,并根据不同的长度单位进行显示。
物理学中常见的计量单位介绍

物理学中常见的计量单位介绍物理学作为一门研究自然现象的科学,广泛使用各种计量单位来描述和衡量物理量。
这些计量单位在物理学的学习和研究中起着至关重要的作用。
本文将介绍物理学中常见的计量单位,帮助读者更好地理解和应用物理学知识。
一、长度和距离单位1. 米(m):米是国际单位制中基本长度单位,用来表示长度、距离等概念。
例如,光的速度约为每秒30万公里,也就是每秒300,000,000米。
2. 厘米(cm):厘米是长度单位,1厘米等于0.01米。
在实验室中常常用厘米作为长度的单位。
3. 千米(km):千米是长度单位,1千米等于1000米,通常用来表示较长的距离,比如两个城市之间的距离。
4. 英尺(ft):英尺是英制长度单位,1英尺等于0.3048米,常用于英语国家。
二、时间单位1. 秒(s):秒是国际单位制中基本时间单位,用来表示时间的短暂。
例如,1分钟等于60秒。
2. 小时(h):小时是时间单位,1小时等于60分钟,通常用来表示较长的时间段。
3. 天(d):天是时间单位,1天等于24小时。
三、质量单位1. 千克(kg):千克是国际单位制中基本质量单位,用来表示物体的质量。
例如,一个标准的西瓜约重2千克。
2. 克(g):克是质量单位,1克等于千克的一千分之一。
通常用来表示较小的质量,比如物体的重量。
四、功、能和功率单位1. 焦耳(J):焦耳是国际单位制中能量单位,用来表示物体的能量。
例如,1焦耳等于1牛顿的力作用下物体移动1米。
2. 瓦特(W):瓦特是功率单位,1瓦特等于每秒1焦耳的能量转化速率。
常用来表示电力的大小。
五、温度单位1. 摄氏度(℃):摄氏度是常用的温度单位,通常用来表示室内气温等。
例如,水的沸点为100℃,冰的融点为0℃。
2. 开尔文(K):开尔文是国际单位制中温度单位,也是热力学温度的单位。
0开尔文表示绝对零度,通常用来进行科学计算。
六、电磁学单位1. 安培(A):安培是电流单位,用来表示电子的流动情况。
数学中距离的概念

数学中距离的概念
距离是数学中一个重要的概念,它可以用来衡量两个点之间的远近程度。
在这里,我们将探讨距离的含义、性质以及应用。
一、距离的含义
距离可以定义为两个点之间的长度。
例如,在数轴上,点A和点B之间的距离等于它们之间的线段AB的长度。
而在平面上,两个点之间的距离则可由它们在坐标系上的坐标计算得出。
二、距离的性质
1. 非负性质:距离必须是非负数,也就是说,两点之间的距离要么是零,要么是一个正实数。
2. 对称性质:点A到点B的距离等于点B到点A的距离,即
d(A,B)=d(B,A)。
3. 三角不等式:对于三个点A、B和C,d(A,B)+d(B,C)≥d(A,C)。
这个不等式告诉我们,在任何情况下,最短的路径总是直线。
三、距离的应用
距离在数学中有许多应用,下面列举几个例子:
1. 应用于几何中,比如可以用来计算平面上的任意两点之间的距离;在三维空间中,距离也可以用来计算点与点之间的距离。
2. 应用于机器学习中,比如可以用来计算两个向量之间的相似度,从而衡量它们之间的距离。
3. 应用于运输及订单配送中,比如在物流中,两个物件之间的距离可决定它们到达目的地的时间,以及运输成本等。
总之,距离是数学中一个十分重要的概念,不同领域都有着广泛的应用。
在实际应用中,我们需要根据不同的情境选择合适的距离定义和计算方法,以达到最佳的效果。
小学数学点知识归纳认识长度和距离

小学数学点知识归纳认识长度和距离小学数学点知识归纳:认识长度和距离在小学数学学习中,学生需要对一些基本的数学概念进行认识和归纳。
其中,长度和距离是数学中重要的概念之一。
本文将对小学数学中关于长度和距离的知识进行归纳和总结。
一、长度和距离的概念及其关系长度是表示物体部分的长短的概念,常用单位有米、厘米和毫米等。
而距离是表示两个物体之间的远近程度的概念。
长度和距离之间存在紧密的关系,它们都与物体的大小和位置有关。
二、长度和距离的测量方法对于长度和距离的测量,我们可以使用尺子、卷尺等工具进行准确测量。
在小学数学教学中,老师通常会引导学生掌握使用尺子等测量工具的方法,并进行实际操作训练。
三、长度和距离的加减运算在数学中,我们可以将长度和距离进行加减运算。
例如,我们可以根据题目给定的条件,计算两段长度的总和或者计算两个点之间的距离。
在小学阶段,这类题目主要以实际生活中的情境为背景,让学生通过实际问题的解决,培养他们的数学思维能力。
四、长度和距离的比较在数学中,我们经常需要比较不同的长度和距离。
学生可以通过观察、估算和测量,判断出哪个长度或者距离更长或更短。
这样的练习可以培养学生的观察力和思维能力,提高他们的数学推理能力。
五、长度和距离的换算长度和距离可以通过改变单位来进行换算。
在小学数学中,学生需要学会使用不同的长度单位进行换算,例如将厘米换算成米,或者将米换算成厘米。
这样的训练可以提高学生的数学计算和转化能力。
六、长度和距离与日常生活的联系长度和距离是我们日常生活中经常遇到的概念,与我们的日常生活密切相关。
例如,测量房屋面积、购买商品时的计算和比较、安排行程中的距离估算等等。
学生在学习长度和距离的同时,也能够将所学内容应用到实际生活中,增强他们对数学的兴趣和实用性。
综上所述,通过对小学数学中长度和距离的知识进行归纳和认识,可以帮助学生建立起对长度和距离的基本概念和运用能力。
在实际教学中,教师应该注重培养学生的观察力、思维能力和应用能力,提供多样化的问题,让学生通过实际操作、思考和解决问题的过程来深入理解和掌握相关知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
單位 2M1長度和距離(三)
數學內容:長度和距離的概念、量度的技巧 (1) 長度和距離的概念【活動一】
∙
AB 的長度是將 A 、B 拉成直線後,線段 AB 的長度
A ∙ ∙B
∙
C 、
D 兩點的距離是線段 CD 的
長
度
C ∙ ∙
D C ∙ ∙D
∙
點 P 和線 L 的距離是 PN (叫做「垂直距離」);N 是在 L 上的一點, PN 垂直 L L P ∙
(例如:人與黑板的距離
∙ 兩平行線 L 1 和 L 2 的距離是兩者間的垂直距離
L 1 L 2
(例如:兩塊平行的黑板的距離
∙ 長度和距離都是大約數
(2)利用「永備尺」或腦海中1厘米或1米的影象估計長度和距離的技巧【活動一】
(3)量度物件的長度或物件間距離的技巧【活動一】
∙用尺子上有cm∕m 刻度的一邊進行量度
∙將尺子置於要量度的長度或距離上,首尾兩端點顯示的刻度之差,便是要量度的長度或距離
(4)以單名數「厘米」記錄物件的長度或物件間距離的技巧【活動二】
∙名數由兩個項目組成:數和單位(例如:「3 厘米」是名數;「3」是數;「厘米」是單位)
(5)化複名數為單名數【活動二】
∙複名數由兩個或多個同度量但不同單位的名數組成(例如:2米 3 厘米)
∙在現階段只能將「米、厘米」化作「厘米」;或只用大約的述語如「比…米多些」、「比…米少些」∙有了小數概念之後才可將「米、厘米」化作「米」
∙先把米的部分轉為厘米,然後再加上厘米的部分
∙將x 米y 厘米寫成(100 x + y)厘米
(6)比較長度和距離的技巧【活動二】
∙只用一個單位「米」或「厘米」表達長度和距離
較大的數字表示較長的長度和距離,較小的數字表示較
短的長度和距離,而兩數字相同時則表示長度和距離相
等
∙用只有兩個單位「米」或「厘米」的複名數表達長度和距離
先比較以「米」為單位名數中的數字
數字不同時,較大的數字表示較長的長度和距離,較小
的數字表示較短的長度和距離,而兩數字相同時則表示
長度和距離相等
數字相同時,比較以「厘米」為單位名數中的數字。
較
大的數字表示較長的長度和距離,較小的數字表示較短
的長度和距離,而兩數字相同時則表示長度和距離相等
先備知識
(1)直線、線段的概念
(2)直角的概念
(3)長度和距離的概念
(4)長度單位「厘米」和「米」的概念
(5)選擇及使用合適的工具量度不同的長度和距離的技巧
(6)使用合適的單位量度長度和距離及記錄結果的技巧(可用兩個長度單位「米」和「厘米」)
(7)以單名數「厘米」記錄長度和距離的技巧
教學資源
(1)量度工具:厘米尺、米尺、捲尺
(2)供量度的物件:一般課室內的物品
(3)工作紙(一)、(二)
(4)電腦簡報
活動內容解說
1. 學生分組進行估計及量度活動,完成工作紙
一。
學生運用已有知識,思
考量度的物件長度和物
件之間的距離與量度單
位的關係,創作估計、
量度及記錄結果的方
法。
2. 學生匯報活動結果。
學生運用批判性思考能
力判斷結果的正誤,比
較不同方法的優劣,改
善自己的方法。
學生說出估計、量度及記錄結果的方法和須
注意的事項,其他同學判斷它們的合理性和
可行性。
3. 教師提出問題,總結學習內容。
學生重看自己已有的長
度和距離概念,估計長
度方法和量度技巧,建
構和改進這些知識。
∙如何估計及量度物件的長度和物件之間
的距離?
∙過程中要注意什麼?
∙可用什麼單位記錄量度結果?為什麼?
活動內容解說
1. 教師提出問題,讓個別學生思考:學生運用已有知識,創
造不同的比較方法。
∙若教師桌長125厘米,壁報板長1米30
厘米,教師桌比較長,還是壁報板比較
長呢?為什麼會有這樣的猜想?
2. 讓學生回答解決問題的方法,全班討論。
學生運用批判性思考能
力,創意表達所思所
想。
∙可以利用「米」、「厘米」(兩個單位)記
錄長度和距離
∙
在作比較時,可選擇先將長度或距離化作「厘米」來比較,或是採用其他方法
3. 學生將複名數化為單名數,從中找出轉換單位的規律。
個別完成工作紙二。
學生運用批判性思考能
力和創造力找出轉換的
規律,進行學習。
4. 教師利用電腦簡報(見附頁)與學生分享將複名數化為單名數的技巧。
5. 學生將工作紙一的結果分別用複名數和只用「厘米」作記錄。
比較各物件的長度和距離。
學生運用剛學習得的知
識,創造記錄和比較長
度距離的方法。
6. 教師提出比較只用「厘米」記錄長度和用複名數記錄方法的異同及如何比較長度和距離。
學生運用批判性思考能
力,分析只用「厘米」記錄長度會否在進行比較時較方便。
7. 教師引導學生討論及作總結。
學生運用批判性思考和創造能力進行交流,互相觀摩仿傚,完善及鞏固新建構的知識。
∙ 估計長度和距離的方法 ∙ 記錄長度和距離的方法
∙ 將複名數化為單名數的方法 ∙ 比較長度和距離的方法。
