云南省三校生高考复习——集合
云南省三校生高考《数学》集合与充要条件测试题

“集合”单元测试题班级: 姓名: 得分:一、选择题(每小题4分,共80分)1、①“全体著名文学家”构成一个集合;②集合{0}中不含元素;③{1,2},{2,1}是不同的集合;上面三个叙述中,正确的个数是( )A 、0B 、1C 、2D 、32、已知集合{|21}M x x =-<<,则下列关系式正确的是()M A 、∈5B.0M ∉C.1M ∈D.2M π-∈3、在下列式子中,①}210{1,,∈ ②}210{}1{,,∈ ③}210{}210{,,,,⊆ ④{0,1,2}⊂∅≠⑤{0,1,2}={2,1,0},其中错误的个数是( ) A 、1个B 、2个C 、3个D 、4个4、}3,2,1,0{}1,0{⊆⊆A ,则集合A 的个数有( )A 、2个B 、3个C 、4个D 、5个5、下列各式中,不正确的是( )A 、A A =B 、A A ⊆C 、A A ⊂≠D 、A A ⊇6、已知集合*{|2}A x x x N =≥∈且,*{|6}B x x x N =≤∈且,则B A ⋂等于( )A 、{1,2,3,4,5,6}B 、{2,3,4,5,6}C 、{2,6}D 、{|26}x x ≤≤7、集合A={0,1,2,3,4,5},B={2,3,4},A B ⋃=( )A 、{0,1,2,3,4,5}B 、{2,3,4}C 、{0,1,2,2,3,3,4,4,5}D 、{1,2,3,4}8、设{|A x x a =≤=( )A 、{}a A ∉B 、{}a A ∈C 、a A ∉D 、a A ∈9、设{}()M 1{1,2},{1,2,3},S P M S P ===⋃⋂,则等于( )A 、{1,2,3}B 、{1,2}C 、{1}D 、{3}10、满足条件{}M 1{1,2,3}⋃=的集合M 的个数是( )A 、4B 、3C 、2D 、111、设全集{0,123456}U =,,,,,,集合{3456}A =,,,,则U C A =( ) A 、{0,3,4,5,6}B 、{3,4,5,6}C 、∅D 、{0,1,2}12、225x =的充分必要条件是( ) A 、55x x ==-且B 、55x x ==-或C 、5x =D 、5x =-13、设3{|23},{|},2A x xB x x =-≤<=≥则A B ⋃=( )A 、{|2}x x <-B 、{|23}x x x <-≤或C 、{|23}x x x <->或D 、}2|{-≥x x14、下列集合是无限集的是( ) A 、{|01}x x ≤≤B 、2{|10}x x +=C 、2{|60}x x x --=D 、{|(1),}n x x n N =-∈15、下列四个推理:①()a A B a A ∈⋃⇒∈ ; ② ()()a A B a A B ∈⋂⇒∈⋃; ③A B A B B ⊆⇒⋃=; ④A B A A B B ⋃=⇒⋂=。
高考关于集合的知识点总结

高考关于集合的知识点总结在高考数学考试中,集合是一个重要的数学概念,也是考试中常常出现的题型。
本文将从一些基本概念和运算法则入手,总结高考中关于集合的知识点。
一、基本概念集合是由一些确定的对象组成的整体。
在集合中,对象称为元素,记作x∈A,表示x是集合A的一个元素。
如果集合A中的某个元素x没有特定的性质,只要它属于集合A,都可以被接受。
集合的表示方法有两种:列举法和描述法。
列举法是把集合中的元素一一列出来,用大括号括起来表示,如A={1, 2, 3}。
描述法是通过一定的条件描述集合中的元素,用大括号括起来表示,如A={x|x>0},表示集合A中的元素x满足x大于0。
二、集合的关系1. 相等关系:当两个集合A和B中的元素完全相同,记作A=B。
2. 包含关系:当集合A中的所有元素都是集合B的元素时,称集合A是集合B的子集,记作A⊆B。
3. 真包含关系:当集合A是集合B的子集,并且集合B中还有集合A没有的元素时,称集合A是集合B的真子集,记作A⊂B。
4. 并集:将两个集合A和B中所有的元素都放在一起构成的集合,记作A∪B。
5. 交集:集合A和集合B中都有的公共元素构成的集合,记作A∩B。
6. 差集:集合A中去掉与集合B相同的元素所剩下的元素构成的集合,记作A-B。
三、集合的运算法则1. 交换律:A∪B=B∪A,A∩B=B∩A2. 结合律:(A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C)3. 分配律:A∪(B∩C)=(A∪B)∩(A∪C),A∩(B∪C)=(A∩B)∪(A∩C)4. 吸收律:A∪(A∩B)=A,A∩(A∪B)=A5. 互补律:A∪A' = U(全集),A∩A' = φ(空集)6. De Morgan定律:(A∪B)'=A'∩B',(A∩B)'=A'∪B'四、应用题解析在高考中,常常出现一些应用题考查集合的知识点。
集合知识点高三复习笔记

集合知识点高三复习笔记一、集合的定义和表示方法在数学中,集合是由一些确定的对象组成的特定的整体。
集合通常用大写字母表示,元素用小写字母表示,并且用花括号 {} 表示。
例如,集合 A 可以表示为 A = {a, b, c},其中 a、b、c 是集合A 的元素。
二、集合的基本运算1. 并集:两个集合的并集是包含这两个集合所有元素的集合。
表示为 A ∪ B。
例如,如果 A = {1, 2, 3},B = {3, 4},则 A ∪ B = {1, 2, 3, 4}。
2. 交集:两个集合的交集是同时包含在这两个集合中的元素的集合。
表示为A ∩ B。
例如,如果 A = {1, 2, 3},B = {3, 4},则 A ∩ B = {3}。
3. 差集:两个集合的差集是除去两个集合共有元素之外的元素所构成的集合。
表示为 A - B。
例如,如果 A = {1, 2, 3},B = {3, 4},则 A - B = {1, 2}。
4. 互斥:如果两个集合没有共同的元素,则称它们为互斥的。
例如,如果 A = {1, 2},B = {3, 4},则 A 和 B 是互斥的。
三、集合的特性和性质1. 空集:不包含任何元素的集合称为空集,用符号∅表示。
2. 子集:如果一个集合的所有元素都属于另一个集合,则称该集合为另一个集合的子集。
表示为 A ⊆ B。
例如,如果 A = {1, 2},B = {1, 2, 3},则 A ⊆ B。
3. 互为子集:如果集合 A 是集合 B 的子集,同时集合 B 也是集合 A 的子集,则称集合 A 和集合 B 为互为子集。
4. 幂集:一个集合的所有子集所构成的集合称为该集合的幂集。
例如,如果 A = {1, 2},则 A 的幂集为 P(A) = {{}, {1}, {2}, {1, 2}}。
5. 交换律:并集和交集的运算满足交换律,即 A ∪ B = B ∪ A,A ∩B = B ∩ A。
6. 结合律:并集和交集的运算满足结合律,即 (A ∪ B) ∪ C =A ∪ (B ∪ C),(A ∩ B) ∩C = A ∩ (B ∩ C)。
云南省三校生高考数学知识点及难易分布表
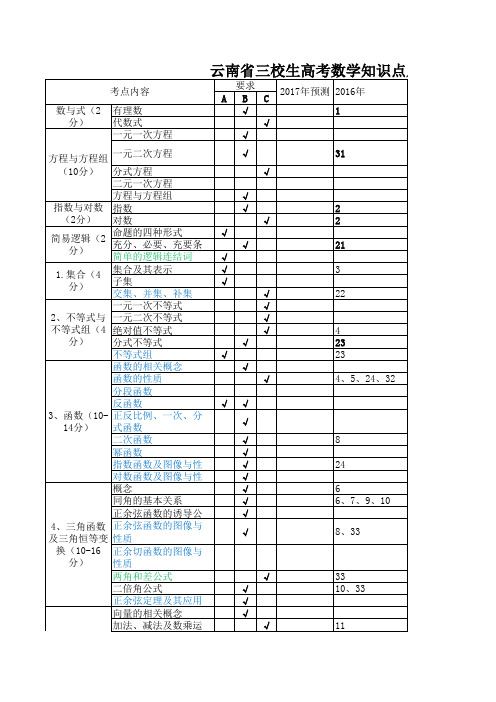
7
7
15、23
16
24
19
29
5
2
25
17
必考 必考 必考 必考 必考
必考
1.集合(4 分)
集合及其表示 子集 交集、并集、补集
一元一次不等式
2、不等式与 一元二次不等式
不等式组(4 绝对值不等式
分) 分式不等式
不等式组
函数的相关概念
函数的性质
分段函数
反函数
3、函数(10- 正反比例、一次、分
14分) 式函数
二次函数
幂函数
指数函数及图像与性
对数函数及图像与性
概念
同角的基本关系
考点内容
数与式(2 有理数 分) 代数式 一元一次方程
云南省三校生高考数学知识点及难易分布表
要求 ABC
2017年预测 2016年
√
1
√
√
方程与方程组 一元二次方程
(10分) 分式方程
二元一次方程
方程与方程组
指数与对数 指数
(2分) 对数
简易逻辑(2 分)
命题的四种形式 充分、必要、充要条 简单的逻辑连结词
面积和表面积
圆柱、圆锥、球的体
8、数列(8 分)
数列的概念通项公式 等差数列 等比数列
复数的相关概念
9、复数(1012分)
复数的向量表示 复数的辐角及主值 复数的四则运算
复数的三种形式互化
√ √
√ √
√ √
√ √
√
√
√
√ √ √ √ √ √ √ √
√ √ √
√ √ √
√ √
25 12、26 13 14
考点1集合—高考数学(理科旧高考)二轮专题复习课件

={x|x≤-1 或 x≥2},B={x|x-1>0}={x|x>1},∴A∩B={x|x≥2}.故选
A.
解析 答案
12.(2020·全国卷Ⅱ)已知集合 U={-2,-1,0,1,2,3},A={-1,0,1},
B={1,2},则∁U(A∪B)=( )
A.{-2,3}
B.{-2,2,3}
C.{-2,-1,0,3}
解析 答案
3.(2020·辽宁沈阳东北育才学校高三第八次模拟考试)已知集合 A={x|y
=x2-2},集合 B={y|y=x2-2},则有( )
A.A=B
B.A∩B=∅
C.A∪B=A
D.A∩B=A
解析 A={x|y=x2-2}=R,B={y|y=x2-2}=[-2,+∞),所以 B⊆
A,故 A∪B=A,故选 C.
解析 答案
2.(2020·山西大同高三模拟)已知集合 A={x|(x-2)(x+2)≤0},B={y|x2
+y2,3]
B.[-2,2]
C.[-4,4]
D.∅
解析 由题意,得 A={x|-2≤x≤2},B={y|-4≤y≤4},所以 A∩B
={x|-2≤x≤2}.故选 B.
解析 答案
21.(2020·福建福州 6 月模拟)已知集合 A={x|x<a},B={x|1<x<2},且 A∪(∁RB)=R,则实数 a 的取值范围是________.
答案 a≥2 解析 ∁RB={x|x≤1 或 x≥2},由 A∪(∁RB)={x|x<a}∪{x|x≤1 或 x≥2} =R,得 a≥2.
10.(2020·陕西咸阳市高三第一次模拟)已知集合 A={(x,y)|y=2x},B
高考总复习:高三数学总复习—集合

高考复习科目:数学高中数学总复习(一)I. 基础知识要点1. 集合中元素具有确定性、无序性、互异性.2. 集合的性质:①任何一个集合是它本身的子集,记为;②空集是任何集合的子集,记为;③空集是任何非空集合的真子集;如果,同时,那么A = B.如果.[注]:①Z= {整数}(√)Z ={全体整数} (×)②已知集合S中A的补集是一个有限集,则集合A也是有限集.(×)(例:S=N; A=,则C sA= {0})③空集的补集是全集.④若集合A=集合B,则C B A = ,C A B = C S(C A B)= D(注:C A B = ).3. ①{(x,y)|xy =0,x∈R,y∈R}坐标轴上的点集.②{(x,y)|xy<0,x∈R,y∈R二、四象限的点集.③{(x,y)|xy>0,x∈R,y∈R} 一、三象限的点集.[注]:①对方程组解的集合应是点集.例:解的集合{(2,1)}.②点集与数集的交集是. (例:A ={(x,y)| y =x+1} B={y|y =x2+1} 则A∩B =)4. ①n个元素的子集有2n个. ②n个元素的真子集有2n-1个. ③n个元素的非空真子集有2n-2个.5. ⑴①一个命题的否命题为真,它的逆命题一定为真. 否命题逆命题.②一个命题为真,则它的逆否命题一定为真. 原命题逆否命题.例:①若应是真命题.解:逆否:a = 2且b = 3,则a+b = 5,成立,所以此命题为真.②.解:逆否:x + y =3x = 1或y = 2.,故是的既不是充分,又不是必要条件. ⑵小范围推出大范围;大范围推不出小范围.例:若.II. 竞赛知识要点1. 集合的运算.De Morgan公式C u A∩C u B= C u(A∪B)C u A∪C u B = C u(A∩B)2. 容斥原理:对任意集合AB有..。
高三数学高考基础知识复习:集合

高考数学基础知识复习:集合一、知识清单:1.元素与集合的关系:用∈或∉表示;2.集合中元素具有确定性、无序性、互异性.3.集合的分类:①按元素个数分:有限集,无限集;②按元素特征分;数集,点集。
如数集{y |y =x 2},表示非负实数集,点集{(x ,y )|y =x 2}表示开口向上,以y 轴为对称轴的抛物线; 4.集合的表示法:①列举法:用来表示有限集或具有显著规律的无限集,如N +={0,1,2,3,…}; ②描述法③字母表示法:常用数集的符号:自然数集N ;正整数集*N N +或;整数集Z ;有理数集Q 、实数集R;5.集合与集合的关系:用⊆,≠⊂,=表示;A 是B 的子集记为A ⊆B ;A 是B 的真子集记为A ≠⊂B 。
①任何一个集合是它本身的子集,记为A A ⊆;②空集是任何集合的子集,记为A ⊆φ;空集是任何非空集合的真子集;③如果B A ⊆,同时A B ⊆,那么A = B ;如果A B ⊆,B C ⊆,A C ⊆那么.④n 个元素的子集有2n 个;n 个元素的真子集有2n -1个;n 个元素的非空真子集有2n -2个.6.交集A∩B={x |x ∈A 且x ∈B};并集A ∪B={x |x ∈A ,或x ∈B};补集C U A={x |x ∈U ,且x ∉A },集合U 表示全集. 7.集合运算中常用结论: ①;A B AB A ⊆⇔=A B A B B ⊆⇔=②()()();U U U A B A B =()()()UU U A B A B =③()()card A B card A =+()()card B card A B - 二、课前预习1.下列关系式中正确的是( )(A){}Φ⊆Φ (B){}0∈Φ (C)0{}Φ= (D)0{}⊆Φ 2. 3231x y x y +=⎧⎨-=⎩解集为______.3.设{}{}24,21,,9,5,1A a a B a a =--=--,已知{}9AB =,求实数a 的值.4.设{}220,M x x x x R =++=∈,a =lg(lg10),则{a }与M 的关系是( ) (A){a }=M (B)M{a } (C){a }M (D)M ⊇{a }5.集合A={x |x =3k -2,k ∈Z},B={y |y=3n +1,n ∈Z},S={y |y =6m +1,m ∈Z}之间的关系是( ) (A)SBA (B)S=BA (C)SB=A (D)SB=A6.用适当的符号()∈∉、、=、、填空: ①π___Q ; ②{3.14}____Q ;③-R ∪R +_____R; ④{x |x =2k +1, k ∈Z}___{x |x =2k -1, k ∈Z}。
(完整版)高考集合专题复习
高中集合专题复习一、集合有关概念1.集合的含义2.集合的中元素的三个特性:确定性、互异性、无序性。
(1)元素的确定性如:世界上最高的山(2)元素的互异性如:由HAPPY 的字母组成的集合{H,A,P,Y}(3)元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集合3.集合的表示:{ … } 如:{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}(1)用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}(2)集合的表示方法:列举法与描述法。
注意:常用数集及其记法:非负整数集(即自然数集) 记作:N正整数集:N*或 N+ 整数集Z 有理数集Q 实数集R1)列举法:{a,b,c ……}2)描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{x ∈R|x-3>2} ,{x|x-3>2}3)语言描述法:例:{不是直角三角形的三角形}4)Venn 图:4、集合的分类:(1)有限集:含有有限个元素的集合(2)无限集:含有无限个元素的集合(3)空集:不含任何元素的集合 例:{x|x2=-5}二、集合间的基本关系1.“包含”关系—子集注意:B A ⊆有两种可能(1)A 是B 的一部分;(2)A 与B 是同一集合。
反之: 集合A 不包含于集合B,或集合B 不包含集合A,记作B A ⊄或A B ⊄2.“相等”关系:A=B (5≥5,且5≤5,则5=5)实例:设A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”即:① 任何一个集合是它本身的子集。
A A ⊆②真子集:如果A 属于B,且A ≠B 那就说集合A 是集合B 的真子集,记作B A ⊆(或A B ⊆) ③如果 B A ⊂,C B ⊂ ,那么 C A ⊂④ 如果B A ⊂ 同时A B ⊂,那么A=B3. 不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列举 把集合中的元素一一列举出 法 来,并用花括号“{}”括起
来表示集合的方法叫做列举 法.常用于表示有限集。
描述 法
用语言,符号,式子等来描 数集:{x/x怎么样} 述元素的特征、性质的方法 点集:{(x,y)/x、y怎么样 常用于表示无限极集。 文字描述:{中国人}
注: (1)实数、有理数、无理数等无法列举:
{0,1,2,3,4} N={0,1,2,3,…}
{x
x
2
1 0}
Ø, {Ø},{0}的区别:
三个都是集合,元素不同, Ø无元素, {Ø}元素是Ø符号,{0}元素是0. 若集合中只含有一个元素,则称这个集合为单元素集,如{1}。
练习:P42页例1(2)
4.常用的数集:
数集
自然数集 整数集 正整数集 有理数集 实数集
(3).无序性: 集合中的元素没有先后顺序。{a,b,c}={b,a,c}={c,b,a}
练习:P42页例1(1)、P47页4
3.集合的分类:
分类
有限集 无限集 空集Ø
定义
由有限个元素组成 的集合 由无限多个元素组 成的集合 没有元素的集合
举例
小于5的自然数集
注意
无省略号 有省略号 Ø 是集合 Ø={ }
(2)x属于R一般省略不写。 练习:P43例2—2 ;P47页5、P48页8、 练习:P48页32、31
列举法优先原则:
(1)能列举尽量用列举法,无法列举再描述;
(2)描述法表示的集合尽量化为列举法,元素一目了然;
{x x 2 x 3 0} {1,3}.
(3)元素多但有规律的集合和也可用列举法表示; 小于100的正整数组成的集合={1,2,3,…,100} (4)元素有规律的无限集也可用列举表示;
ð U A{x U 且x A}= A
相减是补:“房子里面 端点要变。 (1)列举法求交集、并集时相同元素只写一次(互异性); (2)数轴法求交、并、补时要特别注意端点处的准确性; (3)补集的概念必须要有全集的限制。
交、并、补集的性质: (1)交集性质:
A
A∩B
B
A B B A A A B A A B
3.相等关系:
,则A=B A ⊆ B,B ⊆ A
练习:P42页例1(4)
二、集合的运算
运算
交集 并集 补集
定义
列举法
公共元素 全部元素 剩余元素
数轴法
公共是交:公共部分 “两层房子”。 相加是并:房子里面 “单双通吃”。
A B {x A且x B} A B {x A或x B}
2
N {1, 2,3, 4,...}
奇、偶数集的表示:
{0, 2, 4,...} {x x 2n, n Z}.
{1, 2, 3,...} {x x 2n 1, n Z} {x x 2n 1, n Z}.
二、两种关系
1.元素与集合的从属关系:只能用 或 关系 定义
符号
N Z N*或N+ Q R C
集合表示
{0,1,2,3,…} {….-3,-2,-1,0,1,2,3,…}
{1,2,3…}
{理数和无理数} {分数和整数}
复数集
(正实数集:R+,负实数集:R-) (正有理数集:Q+,负有理数集:Q-)
二、集合的表示方法
表示 定义 方法 书写格式
{a,b,c}
{a,b,c,…}
练习: P45页例8、P46页例11, P,48页36,P49页41、42; P45页例9、P46页例10,例12; P49页40.
高考链接
1.(2015 4)设集合M ={ x (x-1)(x-2)(x-3)=0}, 则下列各式中正确的是 A.{0, 1, 2, 3} M B.{1, 2} M C.{0, 1, 2, 3} 苘M B {3, 5} ,则A B 3.(2013 1)设集合M ={ (x,y) x+y=1}, N ={ (x,y) 2x-y=5},则M N = 4.(2012 1)集合{1,2,3}的真子集有( 则集合A B的子集的个数为 6.(2010 1)设集合M ={ x x 2 -x-6<0}, N ={ x x >1},则M N =( ) )个 5.(2011 1)设集合A={0, 1, 2, 3}, B { 1, 2, 3, 4}, D.{1, 2} M 2.(2015 23)设全集I ={ 1, 2, 3, 4, 5, 6}, A { 1, 2},
表示方法:列举法、描述法、图示法
集合与元素的关系
关系:
a A 元素a不是集合A的元素 a A A B或B A 集合与集合的关系 集合A是集合B的子集 集合A是集合B的真子集 A B或B A 集合相等 集合A与集合B元素完全相同A B且 B A
元素a是集合A的元素 运算关系 A B, A B, ð A. U
A叫做B的子集. 不相等的子集
A B
B A
A真包含于B (B真包含A)
A、B不可以相等
A B BA
A B
{ A = B.
A是B的一部分;
A
B
判断子集、真子集关系:开口向多多包涵。
注意:
(1)空集是一切集合的子集
A
;
) (2)空集是一非空集合的真子集 A( A ; (3) 任何一个集合都是它自己的子集,即: A A
元素a是集合A中的元素 元素a不是集合A中的元素
符号
读法
a属于A
属于关系
不属于关系
练习:P43页例3
a A a A
a不属于A
2.集合与集合的包含关系
定义 符号
A B B A
读法
A包含于B (B包含A)
区别
A、B可以相等
子集 若集合A是集合B的
一部分或A=B,则 A叫做B的子集.
真子 若集合A是集合B的 一部分且A≠B,则 集
1.集 合:某些确定的对象集中在一起叫做集合(简称集);
组成集合的对象叫做这个集合的元素. 集合为一堆“东西”,每个“东西”为元素。
大写英文字母表示集合:如集合A,B,C… 小写英文字母表示集合的元素:如元素a,b,c…
2.集合元素的性质:
(1).确定性: 给定的集合,它的元素必须是确定的; 不确定的对象不能构成集合。 高个子;矮个子。 (2).互异性: 集合中的元素不能相同;{1,1}
概念:
没有元素的集合叫空集,最小的集合
集合
空集:
空集是一切集合的子集; A
性质:
A 空集是一切非空集合的真子集。
实数集:R 整数集:Z 有理数集:Q 自然数集:N 正整数集:N 或N
*
特殊集合的表示: 集 合 元素:
概念: 构成集合的每个对象叫做集合的元素,用a,b,c,…表示 性质: 确定性、互异性、无序性
(2)并集性质: A B
B A
A
U
A
A B A B A
(3)补集性质:
A
A A
A A U
A A
A B
A
A B
A B
A B
练习:P42页例2—1(9)、(10)、(11);P43页3 P45页例7,P48页34、35、37、38、39
概念: 一些确定的对象组成的整体叫做集合(集)用A,B,C…表示。 分类: 有限集、无限集。
(4) 子集可分为相等子集和不相等子集两类。
A
B
子集个数问题:若集合A中有n个元素,则集合A的
子集个数为: 真子集个数为:
2n 个;
2n -1 个; 2n -2 个;
非空真子集个数为:
书写子集的方法: 从空集开始,元素从少到多。
练习:P42页例1(4);例2—1、P44页例4,P47页2,3,6,10,11—29
