受弯构件挠度计算
受弯构件的挠度验算(混凝土结构设计原理)

Bs
1 2 bh0 Ec h0 As Es
h0
E 1.15
Es A h
2 s 0
开裂截面的内力臂系数 试验和理论分析表明,在短期弯矩Msk=(0.5~0.7)Mu范围, 裂缝截面的相对受压区高度 变化很小,内力臂的变化也不大。 对常用的混凝土强度和配筋情况, 值在0.83~0.93之间波动。 《规范》为简化计算,取=0.87。
⑶长期荷载作用下的抗弯刚度
在长期荷载作用下,由于混凝土的徐变,会使梁的挠度随时 间增长。此外,钢筋与混凝土间粘结滑移徐变、混凝土收缩等 也会导致梁的挠度增大。根据长期试验观测结果,长期抗弯刚 度B可按下式计算, Bs B
θ ––– 考虑荷载长期作用对挠度增大的影响系数。;
' 0时, =2.0; ' =时, =1.6; ' 为中间数值时, 按线性内插法取用。
1.1 0.65
sk te
在短期弯矩Msk=(0.5~0.7)Mu范围,三个参数、 和 中, 和 为常数,而 随弯矩增长而增大。 该参数反映了裂缝间混凝土参与受拉工作的情况,随着弯矩增 加,由于裂缝间粘结力的逐渐破坏,混凝土参与受拉的程度减 小,平均应变增大, 逐渐趋于1.0,抗弯刚度逐渐降低。
a
a
b
b
h0 由三角形oab和o’a’b’相似,得:
c s
lcr
求解εcmεsm
1、几何关系: 2、物理关系:
1
e cm e sm
h0
es
s
Es
,
c
c ec Ec
c e cm e c ' Ec c
e sm e s
受弯构件的挠度容许值

受弯构件的挠度容许值
在建筑设计中,受弯构件的挠度容许值是一个十分关键的参数。
本篇文档将详细介绍受弯构件的挠度容许值的定义、计算方法以及影响因素。
定义
受弯构件的挠度容许值是指在设计荷载或实际荷载作用下,构件产生的挠度不能超出规定的极限值;超出极限值将导致构件变形过大、出现裂缝、关键部位的破坏等安全隐患。
挠度容许值的计算需要考虑结构的受力性能、荷载的作用情况、结构的材料和尺寸等多种因素,并且需要符合相关的规范和标准。
计算方法
受弯构件的挠度容许值计算一般采用“平衡法”确定,具体计算方法如下:
1.根据极限荷载计算构件的截面抗弯强度。
2.确定荷载作用点处的曲率半径。
3.根据构件的几何尺寸和材料弹性模量计算构件的惯性矩和截面模量。
4.根据计算公式计算出挠度容许值。
在实际应用中,计算方法需要根据具体情况进行适当调整,包括采用不同的计算公式,考虑不同的荷载作用情况等。
影响因素
受弯构件的挠度容许值受到多种因素的影响,如下:
1. 结构的受力性能
挠度容许值的计算需要考虑受力性能,包括结构的受力状态、截面尺寸和形状等。
2. 荷载的作用情况
荷载的作用情况对挠度容许值也有很大的影响。
如荷载的大小、类型、分布等都会影响到构件产生的挠度。
3. 结构的材料和尺寸
结构的材料和尺寸也是影响挠度容许值的因素。
不同的材料和尺寸对挠度容许值有着不同的限制。
受弯构件的挠度容许值是建筑设计中一个十分重要的参数。
在设计过程中,需要充分考虑受力性能、荷载作用情况、结构材料和尺寸等各种因素,以确保构件的挠度在安全范围内。
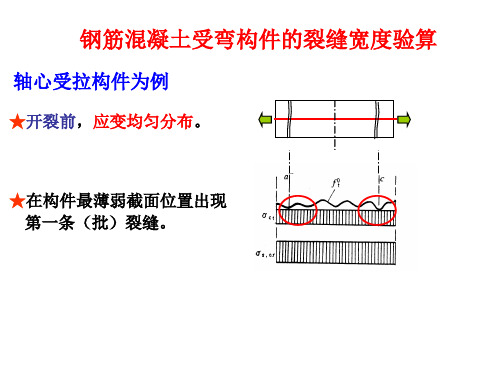
钢筋混凝土受弯构件的裂缝宽度和挠度验算
受压翼缘加强系数
3、钢筋应变不均匀系数
sm sk s sm s sk
钢筋应力不均匀系数 是反映裂缝间混凝土参加受拉工作 程度的影响系数。 越小,裂缝之间的混凝土协助钢筋抗拉的
作用越强。
1.1 0.65 ftk s sk te
sk分布图
1.1 0.65 ftk s sk te
sm sk
Sm cm cck
sm
cm
c
(
' f
Mk
0 )bh02Ec
cm
Mk
bh02 Ec
sm
Mk
Ash0 Es
ቤተ መጻሕፍቲ ባይዱ
Bs
Mk
M k h0
sm cm
cm
Mk
bh02 Ec
Bs
1
Ash02 Es
1
bh03 Ec
Bs
Es Ash02
E
E 0.2 6 E
1 3.5 f
Bs
1.15
Es Ash02 0.2
6E
1 3.5 f
1.1 0.65 ftk s sk te
在短期弯矩Mk=(0.5~0.7)Mu范围,三个参数、 和 中, 和 为常数,而 随弯矩增长而增大。
wm smlm cmlm
εsm、εcm——分别为裂缝间钢筋及砼的平均应变; lm——裂缝间距。
平均裂缝宽度wm
wm smlm cmlm
sm
(1
cm sm
受弯构件挠度验算计算示例

构与抗震系列微课
受弯构件挠度验算计算示例
授课人 四川建筑职业技术学院
杨晓红
2015.11
目录
受弯构件挠度计算的步骤
例题
思考题
Page
2
1 、受弯构件变形验算的步骤
1 )已知条件:构件的截面尺寸、跨度、荷载、材料强度以及
钢筋配置情况
2)计算荷载效应准永久组合下的弯矩Mq 3)计算短期刚度Bs, 受弯构件采用规范公式(7.2.3-1)计算 4)计算长期刚度B ; 受弯构件采用规范公式(7.2.2-2)计算
纵向受拉钢筋为 3 25 ,混凝土强度等级为 C25 ,挠度限
值为l0/200,试验算挠度。
Page
5
【 解 】 A s = 1 4 7 3 m m 2 , h 0 = 405 m m ( 纵 筋 排 一 排 ) ,
ftk=1.78N/mm2,Ec=2.8×104N/ mm2,Es=2×105N/ mm2,活
故该梁满足刚度要求。
Page 9
请思考如下问题:
(1)增加梁刚度的措施有哪些?
(2)受弯构件挠度验算的步骤是什么?
Page
10
谢 谢
2015.11
荷载准永久值系数ψq=0.4,γ0=1.0
(1)计算荷载效应
Mgk= Mqk =
Mq= Mgk +ψqMqk= 74.48+0.4×12.15=79.335kN·m
(2)计算短期刚度Bs
1 gk l0 2 = 8 1 g l 2= k 0 8
1 ×16.55×62=74.48kN·m 8 1 ×2.7×62=12.15kN·m 8
f 1.78 ψ 1.1 0.65 t k 1.1 0.65 0.871 ρ 0.033 152.86 tσ e sq ( 混 凝 土 规 范 公 式 7. 1.2 - 2)
挠度计算方法

乘以 [1 + φ(t, t0 )]求得。此处φ(t,t0 ) 为混凝土徐变系数,按m桥规{(+5(%)规定方法计
算。 公路桥梁规范中规定,对于钢筋混凝土梁桥,当由荷载短期效应组合并考虑荷载长期效
应影响产生的长期挠度不超过跨径的 1 时,可不设预拱度;当不符合上述规定时应设预 1600
(即预拱度)来加以抵消,使竣工后的桥梁达到理想的设计线形。
可变作用产生的挠度,使梁产生反复变形,变形的幅度愈大,可能发生的冲击和振动作
用也愈强烈,对行车的影响也愈大。因此,在桥梁设计中需要通过验算可变作用产生的挠度
以体现结构的刚度特性。
公路桥梁规范中规定,对于钢筋混凝土及预应力混凝土梁式桥,在使用阶段的长期挠度
2
拉 边 缘 的 距 离 y0 =613.8mm , , 换 算 截 面 重 心 以 上 部 分 面 积 对 重 心 轴 的 面 积 矩 为
S0 =78179812.8mm2,求梁跨中截面挠度。
解:荷载短期效应作用下,跨中截面挠度可按下式计算:
fs
=
5× 48
M s L2 B
其中:
B=
B0
⎜⎜⎝⎛
B=
B0
⎜⎜⎝⎛
M cr Ms
⎟⎟⎠⎞ 2
+
⎢⎢⎣⎡⎜⎜⎝⎛1 −
M cr Ms
⎟⎟⎠⎞ 2
⎤ ⎥ ⎥⎦
B0 Bcr
(4.78)
M cr = γftkW0
(4.79)
式中: B ——开裂构件等效截面的抗弯刚度;
B0 ——全截面的抗弯刚度, B0 = 0.95Ec I 0 ;
Ec ——混凝土弹性模量;
本科毕业设计-钢桥验算(受弯构件-抗倾覆验算-挠度及预拱度验算)

第五章 整体分析验算5.1 一般规定5.1.1 局部受压稳定折减系数钢桥在验算受压稳定性时,一般结构在屈曲前后仍在小变形假设范围内处于弹性状态,即弹性屈曲。
对于局部受压的板件,由于构件的弹性屈曲,对构件材料的标准值有所影响。
在计算时,需要考虑弹性屈曲引起的局部稳定折减,局部稳定折减系数ρ应按下列规定计算[3]:()020.4=1110.4=112p λρλρελ⎧≤⎪⎪⎧⎨⎪>++⎨⎪⎪⎪⎩⎩时:时: (5-1)()00.80.4p ελ=- (5-2)1.05p p b t λ⎛== ⎝ (5-3) 式中:p λ——相对宽厚比; t ——加劲板的母板厚度;y f ——屈服强度; E——弹性模量;cr σ——加劲板弹性屈曲欧拉应力;p b ——加劲板局部稳定计算宽度,对开口刚性加劲肋,按加劲肋的间距 b i计算;对闭口刚性加劲肋,按加劲肋腹板间的间距计算;对柔性加劲肋,按腹板间距或腹板至悬臂端的宽度i b 计算;k ——加劲板的弹性屈曲系数,可参考规范《公路钢结构桥梁设计规范》附录B 计算,计算如下。
参考规范《公路钢结构桥梁设计规范》附录B 规定,加劲肋和加劲板对弹性屈曲系数k 有很大的影响。
对纵向加劲肋等间距布置且无横向加劲肋布置的顶板和底板,其弹性屈曲系数k 可由式5-4、5-5计算:*4l l k γγ≥=时: (5-4)()()(()2202*011211l l l l l n a k n b a k n b αγαααδγγααδ⎧++⎛⎫⎪==≤ ⎪⎪+⎝⎭⎪<⎨⎪⎛⎫==>⎪ ⎪+⎝⎭⎪⎩时: (5-5)式中:n ——受压板被纵向加劲肋分割的板元数,1l n n =+; l n ——等间距布置纵向加劲肋根数;a ——加劲板的计算长度(横隔板或刚性横向加劲肋的间距);b——加劲板的计算宽度(腹板或刚性纵向加劲肋的间距);α——加劲板的长宽比,按时5-6计算:abα=(5-6) l δ——单根纵向加劲肋的截面面积与母板的面积之比, 按式5-7计算:l l Abtδ= (5-7)t ——加劲板的厚度;l A ——单根纵向加劲肋的截面面积;l γ——纵向加劲肋相对刚度,按式5-8计算:l l EIbDγ= (5-8)l I ——单根纵向加劲肋对加劲板的抗弯惯性矩;D——单宽板刚度,按式5-9计算:()32121Et D ν=- (5-9) ν——泊松比; t ——加劲板的厚度;E——弹性模量。
受弯构件的挠度计算的基本概念及原则

受弯构件的挠度计算的基本概念及原则下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一、绪论受弯构件在工程建设中广泛应用,其挠度计算是结构分析和设计的重要内容。
第五章 钢筋混凝土受弯构件的裂缝宽度和挠度验算

5.3.5 电机层楼面的支承梁应按作用的长期效应的准永久 组合进行变形计算,其允许挠度应符合下式要求:
wv
l0 750
式中wv ——支承梁的计算挠度(mm);10
第正五常章 使钢用筋混极凝限土受状弯态构件下的,裂缝作宽用度和短挠期度验效算应的标准组合Ss 作用长期效应的准永久组合Sd
轴心受拉构件
sk
Nk As
式中 N k ——按荷载效应标准组合计算的轴向拉力
A s ——受拉钢筋总截面面积
41
第五章 钢筋混凝土受弯构件的裂缝宽度和挠度验算
3 平均裂缝宽度
裂缝截面处的钢筋应力 s k
受弯构件
sk
Mk
As h0
受弯构件裂缝截面处的应力
式中 M k ——按荷载效应标准组合计算的截面弯矩 h 0 ——截面有效高度
应变均匀分布; MMcr 时,在薄弱处,出现第一批裂缝;
MM crM时,出现第二批裂缝,裂缝之间混凝土应力
达到 f t k ,裂缝间距在l~2l之间,“裂缝出现阶 段”; 继续增加,裂缝开展。
32
第五章 钢筋混凝土受弯构件的裂缝宽度和挠度验算
33
第五章 钢筋混凝土受弯构件的裂缝宽度和挠度验算
34
(d) 剪力墙在地震作用下的裂缝
第五章 钢筋混凝土受弯构件的裂缝宽度和挠度验算
(二)非荷载因素引起的裂缝
1.温度变化引起的裂缝
❖ 温度变化产生变形即热胀冷缩。
变形受到约束,就产生裂缝。
❖对策:设伸缩缝,减小约束,允许
自由变形。
❖大体积砼,内部温度大,外周温度
低,内外温差大,引起温度裂缝。
❖减小温度差:分层分块浇筑,采用
5.3.3 对钢筋混凝土贮水或水质净化处理等构筑物,当在组合 作用下,构件截面处于受弯或大偏心受压、受拉状态时, 应按限制裂缝宽度控制;并应取作用长期效应的准永久组 合进行验算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④纵向受拉钢筋的应力取等于钢筋应变与其弹性模量的乘积, 但其绝对值不应大于其相应的强度设计值
等效矩形应力图
等效矩形应力图
fc C
1 fc
M
xc
yc
z
M
x=b1 xc
C yc
z
Ts
M = C· z
x β1 xc
C f bx
Ts 1 c
基本计算公式
基本计算公式
1 ffcc
M
x =b xn
3.1.1概述 3.1.2单筋矩形截面受弯构件承载力计算 3.1.3双筋矩形截面受弯构件承载力计算 3.1.4T形截面受弯构件承载力计算 3.1.5构造要求
3.1.1概述 受弯构件是钢筋混凝土结构中应用最广泛的一种构件。梁和 板是典型的受弯构件。梁和板的区别在于:梁的截面高度一 般大于其宽度,而板的截面高度则远小于其宽度。
梁的截面形式一般有矩形、T形和I形;板的截面形式有矩形、多 孔形和槽形等仅在受弯构件受拉区配置纵向受力钢筋的构件称为 单筋受弯构件,同时也在受压区配置纵向受力钢筋的构件称为双 筋受弯构件 。
对于单筋梁,梁中通常配有纵向受力钢筋、架立筋和箍 筋,有时还配有弯起钢筋对于板,通常配有受力钢筋和 分布钢筋。受力钢筋沿板的受力方向配置,分布钢筋则 与受力钢筋相垂直,放置在受力钢筋的内侧。
受弯构件正截面的破坏形式
(1)适筋破坏 这种破坏的特点是受拉区纵向受力钢筋首先屈服,然后受压区混凝 土被压碎。梁完成破坏之前,受拉区纵向受力钢筋要经历较大的塑 性变形,沿梁跨产生较多的垂直裂缝,裂缝不断开展和延伸,挠度 也不断增大,所以能给人以明显的破坏预兆。 (2)超筋破坏 其特点是破坏时受压区混凝土被压碎而受拉区纵向受力钢筋没有达 到屈服。梁破坏时由于纵向受拉钢筋尚处于弹性阶段,所以梁受拉 区裂缝宽度小,形不成裂缝,破坏没有明显预兆,呈脆性性质。 (3)少筋破坏 其特点是一裂即坏。梁受拉区混凝土一开裂,裂缝截面原来由混凝 土承担的拉力转由钢筋承担.破坏时钢筋和混凝土的强度虽然得到了 充分利用,但破坏前无明显预兆,呈脆性性质。
x
f c bx C= fc1bx
N 0 M 0
x h0
1 fc bx f y As
x M u 1 f c bx( h0 ) 2
Ts=sfsA s s yA
基本公式的适用条件
1. 为了防止将构件设计成少筋构件,要求构件的配 筋面积As不得小于按最小配筋率所确定的钢筋面 积As,min,即 As≥As,min 《规范》规定:对受弯构件,ρmin取0.2%和 0.45ft/fy中的较大值。 最小配筋率ρmin的数值是根据钢筋混凝土受弯构件的 破坏弯矩等于同样截面的素混凝土受弯构件的破 坏弯矩确定的
h0
分布筋
h0 = h -20
C≥15, d
≤200 ≥ 70
适筋受弯构件正截面工作 试验
b
ec
f
As
h0
h
xc
es
as
适筋受弯构件正截面工作试验
M/Mu
1.0 0.8 0.6 0.4
M/Mu
Mu My
ò ¢ ò ¢ a ó ¢ ó ¢ a
1.0 0.8 0.6 0.4
Mu My
Mcr
0
Hale Waihona Puke ñ ¢ñ ¢ a第Ⅱ阶段——从截面开裂到受拉区纵筋开始屈服的 阶段
随着荷载继续增大,裂缝进一步开展,钢筋和混 凝土的应力和应变不断增大,挠度增大逐渐加快。 当荷载增大到某一数值时,受拉区纵向受力钢筋 开始屈服,钢筋应力达到其屈服强度fy,这种特定 的工作阶段称为Ⅱa阶段第Ⅱ阶段为一般梁的正常 使用工作阶段,其应力状态可作为使用阶段的变 形和裂缝宽度验算时的依据。
的主要因素;
一 学习目的
5 掌握有腹筋梁斜截面受剪承载力计算公式及其 适用条件以及防止斜压破坏和斜拉破坏的措施;
6 熟悉纵筋伸入支座的锚固要求和箍筋构造要求;
7 了解钢筋混凝土荷载裂缝宽度(以下简称裂缝宽
度)和变形验算的目的和条件;
8 了解钢筋混凝土裂缝宽度和受弯构件挠度的验算 方法。
3.1 正截面承载力计算
第Ⅲ阶段——破坏阶段
当受压区边缘混凝土达到极限压应变εcu时,梁受 压区两侧及顶面出现纵向裂缝,混凝土被完全压 碎,截面发生破坏。这一特定工作阶段称为第Ⅲa 阶段第Ⅲa阶段为梁的承载能力极限状态,其状态 可作为受弯承载力计算的依据。
受弯构件正截面的破坏形式
梁正截面的破坏形式还与混凝土强度等级、钢筋 级别面形式等许多因素有关。当材料品种及截面 形式选定以后,梁正截面的破坏形式主要取决于 配筋量的多少。矩形截面梁配筋量的多少是用配 筋率ρ来衡量的。配筋率是指纵向受力钢筋截面面 积与截面有效面积的百分比
普通高等教育“十一五”国家级规划教材——工 程 结 构(第三版)
第3章 钢筋混凝土受弯构件
一 学习目的
1 了解配筋率对受弯构件破坏特征的影响以及适
筋受弯构件在各个工作阶段的受力特点;
2 掌握单筋矩形截面、双筋矩形截面和T形截面承
载力的计算方法;
3 熟悉受弯构件正截面的构造要求;
4 了解斜截面破坏的主要形态和影响斜截面承载力
Mcr
M-f
0
f
fcr
fy
M-f
fu
f
第Ⅰ阶段——截面开裂前阶段
当开始加载不久,截面内产生的弯矩很小,这时梁的弯矩 挠度关系、截面应力应变关系、弯矩钢筋应力关系均成直 线变化。由于应变很小,混凝土基本上处于弹性工作阶段, 应力与应变成正比,受压区和受拉区混凝土应力分布图形 为三角形由于混凝土应力应变曲线受拉时的弹性范围比受 压时的小得多,因此随着荷载的增大,受拉区混凝土首先 出现塑性变形,受拉区应力图形呈曲线分布,而受压区应 力图形仍为直线。当荷载增大到某一数值时,受拉边缘的 混凝土达到其实际的抗拉强度ft和抗拉极限应变εtu,截面 处于将裂未裂的临界状态这种工作阶段称为第Ⅰa阶段, 相应的截面弯矩称为抗裂弯矩Mcr . Ⅰa阶段所表示的截面 应力状态,可作为受弯构件抗裂验算的依据。
3.1.2单筋矩形截面受弯构件承载力计算
1. 2. 3. 4. 5.
基本假定 计算简图 基本计算公式 基本公式的适用条件 基本公式的应用
基本假定
根据《规范》规定,采用下述4个基本假定: ①截面应变保持平面。 ②不考虑混凝土的抗拉强度。 ③混凝土受压的应力与应变曲线采用曲线加直线段。 当εc≤ ε0时, 当ε0 < εc ≤ εcu时,σc=fc
