《材料力学》交变应力和冲击应力
材料力学 第十四章动荷载及交变应力

2.5m
FNd
2.5m
σ d m ax
M d m ax = = 13 5.4 M P a < [σ ] Wz
梁的强度足够. 梁的强度足够.
二,构件作匀速转动时的应力
轮缘
ω
D
δ
轮幅
y
ω
qd d
D
O
O
m m FNd
O n n FNd x
an=ω2D/2
FNd Aρω 2 D 2 = 4
D Aρω 2 D qd = 1. A.ρω 2 = 2 2 FNd ρω 2 D 2 σd = = = ρ v 2 ≤ [σ ] A 4
di = kd sti Fd = kd P
σ d = kdσ st
动荷因数kd中的st计算:是将冲击物的重量P 动荷因数 中的 计算:是将冲击物的重量 作为静荷载沿冲击方向作用在被冲击构件的冲 击点,引起该点沿冲击方向的位移. 击点,引起该点沿冲击方向的位移.
P
st
l
EA
P h P l
Pd
Δd
如:轮船靠泊时的冲击力 起吊重物时的惯性力
t
构件由动荷载引起的应力和变形称为动应力和动变形. 构件由动荷载引起的应力和变形称为动应力和动变形. 构件在动荷载作用下,同样有强度,刚度和稳定性问题. 构件在动荷载作用下,同样有强度,刚度和稳定性问题. 构件内的应力随时间作交替变化,则称为交变应力. 构件内的应力随时间作交替变化,则称为交变应力.
动荷载作用下构件的材料仍服从虎克定律. 动荷载作用下构件的材料仍服从虎克定律. 构件的材料仍服从虎克定律
§14-2 构件作匀加速直线运动 14和匀速转动时的应力
构件作匀加速直线运动时,内部各质点具有相同的 构件作匀加速直线运动时, 加速度;构件作匀速转动时, 加速度;构件作匀速转动时,内部各质点均具有向 心加速度. 心加速度.
材料力学第九章动荷载和交变应力_new

运动的物体称为冲击物。 静止的物体称为被冲击物。
工程中大都采用简化计算方法,它以如下假设为前提:
假设1:冲击物为刚体,不变形(不吸收能量),从开始 冲击到冲击产生最大位移时,冲击物与被冲击构件一起 运动,而不发生回弹; 假设2:冲击时,不考虑被冲击构件的质量,被冲击构 件的材料仍处在弹性范围内,服从胡克定律; 假设3:冲击过程中没有其它形式的能量转换,机械 能守恒定律仍成立。
第九章 动荷载和交变应力
§9-1 概 述
动荷载(dynamic load)是指随时间显著变化的荷载,或 是作加速运动或高速转动构件的惯性力。
例如:冲击荷载、惯性力等 构件由动荷载所引起的应力和变形分别称为动应力和动变形。
若构件内的应力随时间周期性变化,称为交变应力 (alternating stress)。
强度条件: dmax kd stmax [ ]
例 已知W1=20 kN,W2=40 kN ,a =2.5 m/s2 。梁由2 根22b的工字钢组成,钢索d =20 mm,梁与钢索材料相同, [σ]=160 MPa ,试校核钢索与梁的强度(不计钢索与梁 的自重)。
W1 解:1.钢索的强度校核。
kd 1 a g 1 2.5 9.8 1.26
st FNst / A W2 / A 127.3MPa d kd st 160.4MPa 1.05[ ]
∴ 钢索满足强度要求。
2.5m
FNd W2
W2 g
a
2.5m a
W2
2.梁的强度校核
W1
kd 1 a g 1 2.5 9.8 1.26
量W当作静荷载作用于被冲击构件上冲击点处,在构件冲 击点处沿冲击方向所产生的与静荷载类型相对应的静变形。
冲击应力和变形的计算

解:飞轮的惯性力矩为
M d I 0
d
A
n
(1)
在掣动时,若为匀减速旋转,则,
2n n t 60t 30t 代入式(1),得
(a)Байду номын сангаас
n a
πn M d I0 ( ) (2) 30t 沿与 相反的转向,将 Md
作用于轴上 (图b),得到一个 假想的平衡力偶系。可得轴横截 面上的扭矩 Td 为
材料力学
§12-2 构件作匀加速直线运动或 匀速转动时的应力计算
一、起重机匀加速吊杆问题(或:杆件匀加速运动问题)
a L m X n
材料力学
原始数据:杆件的长度:L 横截面面积:A 材料的比重: 加 速 度 :a
解:采用动静法(理论力学中的达朗伯原理) 1.受力分析:如图所示,在距下端为x的 横截面mn处将杆件分成两部分,并研究截 面以下的部分。 作用其上的重力集度为:
材料力学
二、圆环在匀角速旋转时的动应力计算问题(动静法)
w
t
D
qd
d
Nd
Nd
原始数据:环的平均直径D ;环的匀角速度w ;环的比重 环的厚度t ;环的横截面积A
材料力学
1.受力分析:沿圆环直径将它分成两部分,研究其上 半部分;由已知条件可知, 环内各点的向心加速度 :
2 D an r 2 2
材料力学
略去负值,得:
2h d j 1 1 j
(g)
令:
d 2h Kd 1 1 j j
——冲击动荷系数
d Kd j
代入(f)、(g)式得
讨论:
Pd K d Q
材料力学C11_交变应力

对称循环,r=-1 ②查图表求各影响系数,计算构件持久限。 求K:
D r 1.4 ; 0.15 ; b 600MPa 查图 d d 求 :查图得 0.79
r=7.5
K 1.4
求 :表面精车, =0.94 0 1 0.79 0.94 1 250 69.8MPa 1 1
第11章 交变应力
11.1 交变应力与疲劳失效 11.2 交变应力的循环特征、应力幅和平均应力 11.3 持久极限 11.4 影响持久极限的因素 11.5* 对称循环下构件的疲劳强度计算 11.6* 持久极限曲线 11.7* 不对称循环下构件的疲劳强度计算 11.8* 弯扭组合交变应力的强度计算 11.9* 变幅交变应力 11.10 提高构件疲劳强度的措施 11.* 习题**
2 max min 应力幅(~ Amplitude): a 2 min 循环特征、 r max /应力比(~ ratio):
5特征量仅2个独立,如m+a 或max+r
不稳定
max m min max m min a
t t
a
对称循环(symmetric reversed
加工方法 磨 削 车 削 粗 车 未加工的表面 轴表面粗糙度 Ra/m 0.4~0.2 3.2~0.8 1.25~6.3
b/MPa
400 1 0.95 0.85 0.75 800 1 0.90 0.80 0.65 1200 1 0.80 0.65 0.45
下降明显
b高者
表面越差,下降越多 b越高,影响越显著
m, ra
K
1
a rm m
a rm
材料力学第九章交变应力1

由表查尺寸系数 0.77
2.扭转时的有效应力集中系数和尺寸系数
由图表查有效应力集中系数
当 :b 10 M 0时 P 0 ,K a 1 .28
当 :b 9M 00时 PK a , 1 .25
当 :b92M 0 P时 a,应用直线插值法
K 1.2 5 1 1 .20 1 9 8.2 00 (9 502 900 ) 1.0 26
形速率疲劳条件下,是类似于蠕变变形的位错攀移机制。当循 环次数增加时,发现有循环软化现象,即:外加载荷非对称, 应变响应近似对称。
2、变幅与过载影响裂纹扩展速率 通过对带有环状V型切口的45#--钢圆棒料在恒幅过载
和变幅过载下的低周次疲劳试验,表明变幅递增过载的裂纹 扩展速率比恒幅过载裂纹扩展速率显著增大。基于试验事实 和断口分析,说明过载时裂纹扩展速率瞬时显著增大是裂纹 钝化的结果 。
谢谢大家!
材料力学第九章交变应力1
§11-1 交变应力与疲劳失效
交变应力:随时间周期性变化的应力。
P
P PP(t)P(tT)
(t)(tT)
a a2 a
a
a
1
•
1
31
4a
M y(t)
I
2
• •
3
y(t)Rsi nt
1
•
t
•
4
齿轮传动:齿轮啮合点处的应力随时间作周期性变化,这 种应力就是交变应力。
强度。
f70 f50
M
M 解:① 确定危险点应力及循环
特征
r=7.5
r min 1 max
maxW Mmin
8003265.2MPa
0.053
为对称循环
② 查图表求各影响系数,计算构件持久限。
(完整版)材料力学知识点总结
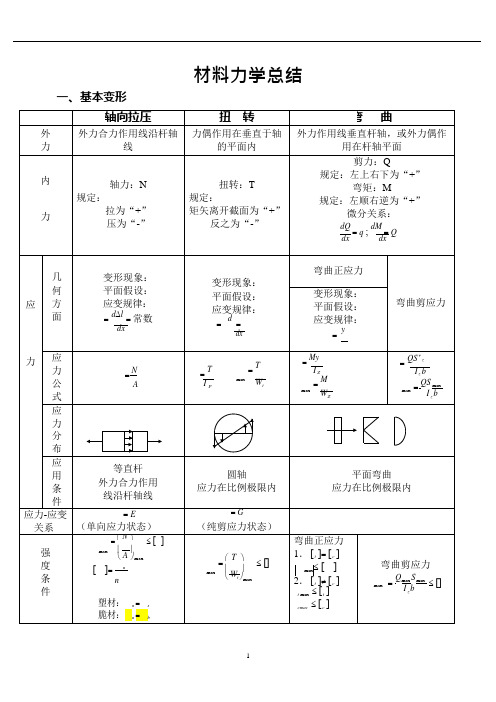
一、基本变形材料力学总结变形现象: 平面假设: 应变规律: = d ∆l = 常数dx变形现象:平面假设: 应变规律:=d = dx变形现象:平面假设: 应变规律:= y= N =T= T = MyI Z = M max WZ= QS * z I z b = QS max max I bz max W= E (单向应力状态) = G(纯剪应力状态)=⎛ N ⎫≤ []maxA ⎪ ⎝ ⎭max[]=un塑材:u=s 脆材:u =bmax= ⎛ T ⎫ ≤ [] ⎪ ⎝ W t ⎭max弯曲正应力 1. [t ]= [c ]max≤ []2. [t ]≠ [c ] t max ≤ [t ] cmac ≤ [c ]弯曲剪应力=Q max S max ≤ [] max I bz轴向拉压扭转弯曲刚度条=T ⋅180 ≤[]max GIP注意:单位统一ymax≤[y]max≤[]件变形d∆l=N ; ∆L =NLdx EA EAEA—抗拉压刚度=d=Tdx GIZ=TLGIPGI p—抗扭刚度1=M (x)(x) EIy '' =M (x)EIEI—抗弯刚度应用条件应力在比例极限圆截面杆,应力在比例极限小变形,应力在比例极限矩形A=bhbh 3bh 2IZ=12;WZ=6实心圆A= d 24d4d3IP=32;Wt=16d4d3IZ=64;WZ=32空心圆D 2A =(1-2)4d44IP=32(1 -)d 3W =(1 -4)t16d 4I =(1-4)Z64d34WZ=32(1-)其(1)'剪切(1)强度条件:=Q≤[]A—剪切面积A(2)挤压条件:=P bs ≤[]bs A bsJA j—挤压面积矩形:=3Qmax 2 A圆形:=4Qmax 3A环形:= 2Qmax Amax均发生在中性轴上它公(2)GE式2(1 )二、还有:(1)外力偶矩:m = 9549 N (N •m)n(2)薄壁圆管扭转剪应力:=TN—千瓦;n—转/分2r 2t(3)矩形截面杆扭转剪应力:max =Tb2h;=TG b3hDB c AD 'Z ZC c cn n三、截面几何性质(1)平行移轴公式:I =I +a 2A;(2)组合截面:IYZ=IZ Y+abA1.形心:y c∑A i y ci=i =1 ;∑A ii =1∑A i z ciz =i =1∑A ii =12.静矩:S Z =∑A i y ci ;S y =∑A i z ci3.惯性矩:I Z =∑(I Z ) i ;I y =∑(I y ) i四、应力分析:(1)二向应力状态(解析法、图解法)a.解析法: b.应力圆:n σ:拉为“+”,压为“-”xτ:使单元体顺时针转动为“+”x yx y cos 2sin 2α:从x 轴逆时针转到截面的法线为“+”2 2 xx y sin 2cos 22 xtg22xmaxminxx yy2c:适用条件:平衡状态(2)三向应力圆:;; 1 3max 1 min 3 max 2nn2x y22xyxc121223311(3) 广义虎克定律:1(1 (1E 123xE xyz1 ( 1(2E 231yE yzx1(1(3E3 1 2zExy*适用条件:各向同性材料;材料服从虎克定律(4) 常用的二向应力状态 31. 纯剪切应力状态:1,20 ,3x2. 一种常见的二向应力状态:132r 3r 4五、强度理论破坏形式脆性断裂塑性断裂强度理论 第一强度理论(最大拉应力理论)莫尔强度理论 第三强度理论 (最大剪应力理论) 第四强度理论(形状改变比能理论) 破坏主要因素 单元体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件 1 = bmax =su f = u fs强度条件 1 ≤ [] 1-3≤ []适用条件 脆性材料 脆性材料 塑性材料 塑性材料*相当应力:r,,]r 11r 313r 4222242232r=2+42≤[]=2+32≤[]4r22(M +N ) + 4≤ []r3 =r=(M+N)2+32≤[]WM 2 +T 2r3 =圆截面WM 2 + 0.75T 2r4=(M+N)2 + 4(T)2W Z A W t(M+N)2 + 4(T)2W Z A W t α 中性轴ZMpr3 =≤ []r 4 =≤ []i 2I Z*y =-=-ZAe y e ytg=y=-I ZtgZ I y中性轴Z≤ []Z≤ []A W≤ []P Mmax =±max ±max≤ []sincos( +)W Z W y=max maxM强度条件43=±P ±MA W)I yI Z=M (y c os+z s in公式简图弯扭拉(压)弯扭拉(压)弯斜弯曲类型六、材料的力学性质脆性材料<5%塑性材料≥5%低碳钢四阶段:(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部收缩阶段b强度指标s ,b e sα塑性指标,tg E七.组合变形只有σs,无σbb剪断断口垂直轴线拉断断口与轴夹角45ºb45º拉断铸铁断口垂直轴线剪断s b 滑移线与轴线45︒,剪45低碳钢扭压拉八、压杆稳定欧拉公式: P=2EI min,=2E,应用范围:线弹性范围,σ<σ ,λ>λcr(l ) 2cr2crpp柔度:=ul;=E;0 =a -s, σib柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:cr =2E2临界应力λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σsλoλPλ稳定校核:安全系数法: n P c rP I n w ,折减系数法:P []A提高杆件稳定性的措施有: 1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
《材料力学》第十章 动载荷

基本要求: 基本要求: 了解构件作变速运动时和冲击时应力与变形的计 算。 重点: 重点: 1.构件有加速度时应力计算; 2.冲击时的应力计算。 难点: 难点: 动荷因数的计算。 学时: 学时: 4学时
第十章
§lO.1 概述
动 载 荷
§10.2 动静法的应用 §10.4 杆件受冲击时的应力和变形 §10.5 冲击韧性
( 2 )突然荷载 h = 0 : K
d
=2
△st--冲击物落点的静位移
五、不计重力的轴向冲击问题
冲击前∶
动能T1 = Pv 2 / 2 g 势能V1 = 0 变形能V1εd = 0
冲击后:
动能T2 = 0 势能V 2 = 0 变形能V 2εd = Pd ∆ d / 2
ห้องสมุดไป่ตู้
v P
冲击前后能量守恒,且
Pd = K d P
补例10-1 起重机钢丝绳的有效横截面面积为A , 已知[σ], 补例 物体单位体积重为γ , 以加速度a上升,试建立钢丝绳(不计自 重)的强度条件。 外力分析。 解:1.外力分析。包括惯性力 外力分析
惯性力:q a
x a L x m m a Nd qg +qa
=
γA
g
a
2.内力分析。 内力分析。 内力分析 3.求动应力。 求动应力。 求动应力
任何冲击系统都 可简化弹簧系统
能量法(机械能守恒) 三、能量法(机械能守恒)
冲击过程中机械能守恒。即动能 ,势能V,变形能V 冲击过程中机械能守恒。即动能T,势能 ,变形能 εd守恒 冲击前:系统动能为T, 势能为V=Q∆d, 变形能Vεd=0 冲击后:系统动能为0, 势能为V=0, 变形能Vεd
材料力学之交变应力

§3-1 §3-2 §3-3 §3-4 §3-5
动载荷
概述 构件作 冲击时应力和变形的计算 冲击韧度 提高构件抗冲击能力的措施
§4-1
概述
一、交变应力的概念 交变应力:随时间作周期性变化的应力,金属 在交变应力作用下发生的破坏称为疲劳破坏。 如:机车车轴
§4-1
概述
My Pa d sin t I I 2
min
m
o
max :最大应力
m :应力幅度
t
min :最小应力
a :平均应力
§4-2 交变应力的循环特征
a
a
max
min m
min 循环特征:r max
t
o
1 1 m max min max (1 r ) 2 2 1 1 a max min max (1 r ) 2 2 min m a max m a
n
1
k
a m
§4-6
对于塑性材料制成的构件,除应满足疲劳强度 外,危险点的应力不应超过屈服极限.
a
非对称循环下构件的 疲劳强度计算
L
* 1
K
1
A1
s
P1
K
C1
* 1
P2
m
O
s
C
J
B
§4-6
疲劳强度计算
非对称循环下构件的 疲劳强度计算
N
r
O
r 1
E
D
C
A
N0
材料的疲劳极限与强度极限的近似关系:
弯曲: 拉压: 扭转:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
max 或 min 其中之一为0.
a ( max min ) max
(2) 静应力
1 2
m ( max min ) max
1 2
1 2
r 1 st C max min m st a 0
st
构件的许用应力
1
或
0 1
n
其中:
n--为规定的安全系数
构件的疲劳强度条件为:
max 1
由 max n
0 1
max
得
0 1
n
0 1 n max
0 若构件工作安全系数 n 1 max
用安全系数表示的构件的疲劳强度条件为:
v2 d st g st
Kd
v2 g st
四 冲击载荷下的强度条件 试验结果表明,材料在冲击载荷下的强度比在静载荷下的强 度要略高一些,但对光滑的受冲击载荷作用的构件进行强度 计算时,通常任以静载荷下的基本许用应力来建立强度条件. 冲击载荷下的强度条件为:
d max K d st max [ ]
0
t
§12.3材料的持久极限及其测定 1 材料的持久极限 持久极限:在某一循环特征下, 材料具有经历无限次应力循环 而不破坏的应力临界值. 用 r 或者 r 表示. 2 材料的持久极限的测定 纯弯曲,对称循环下材料的持久 max M Pa 极限的测定. max
W W
a P
Pa
P a
第12章 交变应力和冲击应力
第12章
交变应力和冲击应力
§12.1交变应力和疲劳破坏 1 交变应力的概念 交变应力:随时间作周期性变化的应力. (1)两个齿轮的啮合传动,齿根上的应力随时间 作有规律周期性变化.
σ
t
(2) 传动轴工作时,横截面上任意一点的应力随时间作有规律 周期性变化. y
4
A
t
3 2
1
x
y r sin t
σ σ2 σ3
My Mr sin t I I
0
σ1
σ4
σ1
t
(3) 作强迫振动的梁,其应力随时间作有规律周期性变化.
H
pt
Q
Ql lH sin pt 4W 4W
最小位移衡位置 静平衡位置 最大位移衡位置
σ σmax
σst σmin
0 t
2 疲劳破坏的特点及过程 (1) 疲劳破坏的特点 低应力破坏. 破坏有一个过程. 突然的脆性断裂. (2) 疲劳断口的特点 •裂纹源 •光滑区 •粗糙区 3 疲劳破坏 材料在多次重复载荷作用下的破坏称为所谓疲劳破坏或 疲劳失效. 在交变应力下,构件的疲劳破坏实质上是指裂纹的发生, 发展和构件最后断裂的全过程.
st max
M max 6Ql 2 W bh 6 1103 2 2.5MPa 2 9 120 200 10
Ql 12Ql 3EI 3Ebh3 12 1103 23 10 mm 9 3 12 3 10 10 120 200 10 3 yst max
3
y d max K d y st max
10 6 20mm 3
200
作业
12.8
12.12
光滑小试件条件:
(1) 有足够大的圆角过渡; (2) 中间直径7-10mm; (3) 磨削加工; (4) 同一炉钢10根为一组; 钢 N0=107 有色金属 N0=108
max 1 max 2
0
水平渐近线
N1 N 2
S N曲线
N0 t
§12.2影响构件持久极限的主要因素 一 构件外形(应力集中)的影响 构件外形的突然变化,如:轴肩,槽,孔,缺口,螺纹等.会引起应力集 中,使材料持久极限降低,其影响因素用有效应力集中系数表示.
2 st
Q Pd h
d
动位移总是大于静位移. 2h 1 1 故去掉负号. st
2h d st [1 1 ] st
Q
st
动荷系数
动位移 动应力 冲击力
Kd 1 1
2h st
d K d st d K d st Pd K d Qst
3 校核疲劳强度
n
1
K
max
400 106 2.78 n 2 1.55 71.6 106 0.77 1
§12.6 冲击应力 一 冲击的概念 1冲击 当物体以一定的运动速度作用于构件上时,构件在瞬间(10-3105s内, 使物体速度发生很大变化,从而使物体产生很大的加速度,而构件则 受到很大的压力,这种现象称为冲击 2 用能量法计算冲击问题时的简化假设: • 被冲击物(或缓冲系)为无质量的线弹性体 • 把冲击物视为刚体(无变形). • 冲击过程中没有能量转换的其他损失 3 计算过程 计算动能T和势能V. 计算变形能Ud . 根据机械能守恒定律建立方程 T + V = Ud 求解动载荷,动应力或动变形.
M M 71.6 MPa 3 W d 32
0.2
M D
r
d
0.2
M
2 确定影响系数
应力集中系数 K 尺寸系数
d 40mm 0.77
D r 1.25, 0.125, b 900MPa K 1.55 d d
表面质量系数 由表面粗糙度0.2 1
其他加工情况的试件的持久极限 表面磨光的标准试件的持久极限
构件表面质量低于表面磨光试件 构件表面质量高于表面磨光试件
1 1
四 构件的持久极限 考虑以上因素的影响,构件的持久极限为: 弯曲或拉压 扭转
0 1
K
1
0 1
K
1
§12.5 对称循环下构件的疲劳强度计算
在线弹性范围
Pd d d Q st st
Q d Pd st
Q( h d ) Q d d st 2
2d 2 st d 2h st 0
2h d st 2h st st [1 1 ] st
或者
st max
[ ] Kd
图示悬臂梁,A端固定,自由端B上方有一重物自由落下,撞 击到梁上.已知:梁材料为木材,弹性模量E=10GPa;梁长 l=2m,截面为矩形,面积120mm×200mm;重物高度为400mm, 重量Q=1kN. 求:(1) 梁所受到的冲击载荷; (2) 梁横截面上的最大冲击正应力与最大冲击挠度. 解: 1 梁的最大静应力和最大静挠度
§12.2交变应力的循环特征、应力幅和平均应力
一 循环特征,应力幅和平均应力
1 循环特征 min r min max max max r max min min
σ σmax σst σmin 0
一个应力循环
循环特征取值
1 r 1
t
一个周期
2 应力幅和平均应力 1 a ( max min ) 应力幅 2 1 ( max min ) 平均应力 m 2
冲击物(物体)
被冲击物构件)
二 自由落体冲击 当重量为Q的物体自高度为h处以速度v=0自由下落, 冲击到弹性体(如梁)上,称为自由落体冲击.
1计算动能T和势能V
Q Pd
T 0
h
d
V Q( h d )
2 计算变形能Ud
1 U d Pd d 2
3 建立方程
T V Ud
1 Q(h d ) Pd d 2
3 3
Q
400
120
A
l
B
200
2 确定动荷系数
Kd 1 1 1 1
400
2h st
Q
120
2 40 3 6 10
A
B
3 计算冲击载荷 最大冲击应力和最大冲击挠度
Pd K d Q 6 1 10 6kN d max K d st max 6 2.5 15MPa
n
1
K
max
n
或
n
1
K
max
n
例题:合金钢阶梯轴如图示,D=50mm,d=40mm,r=5mm.材料的 σb=900MPa,σ-1=400MPa,M=±450N· m,n=2.试校核该轴的疲 劳强度. 解: 1 计算最大弯曲应力
max
为动应力部分
为静应力部分
max m a
min m a
二 交变应力的几种特殊情况 1 对称循环
max min
r 1
符号相反
1 m ( max min ) 2
2 非对称循环 (1) 脉动循环
r 0 1 2
1 a ( max min ) 2
2
2hg v2 Kd 1 1 1 1 st g g st
3 突加载荷
h0
20 Kd 1 1 2 st
4 水平冲击 势能 动能 V=0
1Q 2 T v 2 g
v
2 1 1 d 变形能 U P Q d d d 2 2 st
1 Q 2 1 2d v Q 2g 2 st
无应力集中的光滑小试件的持久极限 K (或K ) 1 同尺寸而有应力集中的试件的持久极限 ( 1 ) d 1 例如纯弯曲对称循环: K ( 1 ) k 二 构件尺寸的影响 试验证明:试件尺寸越大,存在的缺陷越多,更容易形成疲 劳裂纹.使材料持久极限降低.其影响因素用尺寸系数表示.
