2018届中考数学复习专题题型(七)--圆的有关计算与证明
2018届中考数学复习专题三圆的证明与计算试题(含答案)
专题三 圆的证明与计算类型一 切线的判定判定某直线是圆的切线.首先看是否有圆的半径过直线与圆的交点.有半径则证垂直；没有半径.则连接圆心与切点.构造半径证垂直．(2016·黄石)如图.⊙O 的直径为AB.点C 在圆周上(异于A.B).AD⊥CD . (1)若BC ＝3.AB ＝5.求AC 的值；(2)若AC 是∠DAB 的平分线.求证：直线CD 是⊙O 的切线．【分析】 (1)根据直径所对的圆周角为直角.利用勾股定理求AC 的长；(2)连接OC.利用AC 是∠DAB 的平分线.证得∠OAC＝∠CAD .再结合半径相等.可得OC∥AD .进而结论得证．1．(2016·六盘水)如图.在⊙O 中.AB 为直径.D.E 为圆上两点.C 为圆外一点.且∠E＋∠C＝90°. (1)求证：BC 为⊙O 的切线；(2)若sin A ＝35.BC ＝6.求⊙O 的半径．2．(2017·济宁)如图.已知⊙O 的直径AB ＝12.弦AC ＝10.D 是BC ︵的中点.过点D 作DE⊥AC .交AC 的延长线于点E.(1)求证：DE 是⊙O 的切线； (2)求AE 的长．类型二 切线的性质已知某条直线是圆的切线.当圆心与切点有线段连接时.直接利用切线的性质：圆的切线垂直于过切点的半径；当圆心与切点没有线段相连时.则作辅助线连接圆心与切点.再利用切线的性质解题．(2016·资阳)如图.在⊙O 中.点C 是直径AB 延长线上一点.过点C 作⊙O 的切线.切点为D.连接BD.(1)求证：∠A＝∠BDC；(2)若CM 平分∠ACD .且分别交AD.BD 于点M.N.当DM ＝1时.求MN 的长．【分析】 (1)连接OD.由切线的性质可得∠CDB＋∠ODB＝90°.由AB 是直径.可得∠ADB＝90°.进而可得∠A ＋∠ABD＝90°.进而求得∠A＝∠BDC；(2)由角平分线及三角形外角性质可得∠A＋∠ACM＝∠BDC＋∠DCM .即∠DMN＝∠DNM .再根据勾股定理求得MN 的长．3．(2016·南平)如图.PA.PB 是⊙O 切线.A.B 为切点.点C 在PB 上.OC∥AP .CD⊥AP 于点D. (1)求证：OC ＝AD ；(2)若∠P＝50°.⊙O 的半径为 4.求四边形AOCD 的周长(精确到0.1.参考数据sin 50°≈0.77.cos 50°≈0.64.t an 50°≈1.19)．4．(2017·长沙)如图.AB 与⊙O 相切于点C.OA.OB 分别交⊙O 于点D.E.CD ︵＝CE ︵. (1)求证：OA ＝OB ；(2)已知AB ＝4 3.OA ＝4.求阴影部分的面积．类型三 圆与相似的综合圆与相似的综合主要体现在圆与相似三角形的综合.一般结合切线的判定及性质综合考查.求线段长或半径．一般的解题思路是利用切线的性质构造角相等.进而构造相似三角形.利用相似三角形对应边成比例求出所求线段或半径．(2016·荆门)如图.AB 是⊙O 的直径.AD 是⊙O 的弦.点F 是DA 延长线的一点.AC 平分∠FAB 交⊙O 于点C.过点C 作CE⊥DF .垂足为点E.(1)求证：CE是⊙O的切线；(2)若AE＝1.CE＝2.求⊙O的半径．【分析】 (1)连接CO.证得∠OCA＝∠CAE.由平行线的判定得到OC∥FD.再证得OC⊥CE即可；(2)连接BC.由圆周角定理得到∠BCA＝90°.再证得△ABC∽△ACE.根据相似三角形的性质即可求得半径．5．(2017·德州)如图.已知Rt△ABC.∠C＝90°.D为BC的中点．以AC为直径的⊙O交AB于点E.(1)求证：DE是⊙O的切线；(2)若AE∶EB＝1∶2.BC＝6.求AE的长．6．(2017·黄冈)如图.已知MN为⊙O的直径.ME是⊙O的弦.MD垂直于过点E的直线DE.垂足为点D.且ME 平分∠DMN.求证：(1)DE是⊙O的切线；(2)ME2＝MD·MN.7．(2016·丹东)如图.AB是⊙O的直径.点C在AB的延长线上.CD与⊙O相切于点D.CE⊥AD.交AD的延长线于点E.(1)求证：∠BDC＝∠A；(2)若CE＝4.DE＝2.求AD的长．参考答案【例1】 (1)∵AB 是⊙O 的直径.点C 在⊙O 上. ∴∠ACB＝90°. ∴AC＝AB 2－BC 2＝4. (2)如图.连接OC.∵AC 平分∠DAB . ∴∠OAC＝∠CAD.∵OA＝OC.∴∠OAC＝∠OCA . ∴∠OCA＝∠CAD . ∴OC∥AD.∵AD⊥CD .∴OC⊥CD.∵OC 是⊙O 的半径.∴直线CD 是⊙O 的切线． 【变式训练】1．(1)证明：∵∠A 与∠E 所对的弧都是BD ︵. ∴∠A＝∠E.∵∠E＋∠C＝90°.∴∠A＋∠C＝90°.∴∠ABC＝180°－∠A－∠C＝90°.即AB⊥BC. ∵AB 是直径.∴BC 为⊙O 的切线． (2)解：∵sin A ＝BC AC ＝35.BC ＝6.∴AC＝10.在Rt △ABC 中.AB ＝AC 2－BC 2＝8.∴AO＝12AB ＝4.即⊙O 的半径是4.2．(1)证明：如图.连接OD.∵D 是BC ︵的中点.∴BD ︵＝DC ︵. ∴∠BOD＝∠BAE .∴OD∥AE.∵DE⊥AC .∴∠AED＝90°.∴∠ODE＝90°. ∴OD⊥DE .∴DE 是⊙O 的切线．(2)解：如图.过点O 作OF⊥AC 于点F.∵AC＝10.∴AF＝CF ＝12AC ＝12×10＝5.∵∠OFE＝∠DEF＝∠ODE＝90°.∴四边形OFED 是矩形. ∴FE＝OD ＝12AB ＝6.∴AE＝AF ＋FE ＝5＋6＝11. 【例2】 (1)如图.连接OD.∵CD 是⊙O 的切线. ∴∠ODC＝90°.∴∠BDC＋∠ODB＝90°. ∵AB 是⊙O 的直径. ∴∠ADB＝90°.∴∠A＋∠ABD＝90°. ∵OB＝OD.∴∠OBD＝∠ODB .∴∠A＋∠ODB＝90°.∴∠A＝∠BDC. (2)∵CM 平分∠ACD .∴∠DCM＝∠ACM. ∵∠A＝∠BDC .∴∠A＋∠ACM＝∠BDC＋∠DCM. 即∠DMN＝∠DNM.∵∠ADB＝90°.DM ＝1.∴DN＝DM ＝1.∴MN＝DM 2＋DN 2＝ 2. 【变式训练】3．(1)证明：∵PA 是⊙O 的切线.A 为切点. ∴OA⊥PA .即∠OAD＝90°. ∵OC∥AP .∴∠COA＝180°－∠OAD＝180°－90°＝90°. ∵CD⊥PA .∴∠CDA＝∠OAD＝∠COA＝90°. ∴四边形AOCD 是矩形.∴OC＝AD.(2)解：∵PB 切⊙O 于点B.∴∠OBP＝90°. ∵OC∥AP .∴∠BCO＝∠P＝50°. 在Rt △OBC 中.sin ∠BCO＝OBOC .OB ＝4.∴OC＝4sin 50°≈5.22.∴矩形OADC 的周长为2(OA ＋OC)＝2×(4＋5.22)≈18.4. 4．(1)证明：如图.连接OC.∵AB 与⊙O 相切于点C. ∴∠ACO ＝90°. ∵CD ︵＝CE ︵.∴∠AOC＝∠BOC . ∴∠A＝∠B . ∴OA＝OB.(2)解：由(1)可知△OAB 是等腰三角形. ∴BC＝12AB ＝2 3.∴sin ∠COB＝BC OB ＝32.∴∠COB＝60°.∴∠B＝30°.∴OC＝12OB ＝2.∴S 扇形OCE ＝60π×4360＝2π3.S △OCB ＝12×23×2＝2 3.∴S 阴影＝S △OCB －S 扇形OCE ＝23－2π3. 【例3】 (1)如图.连接CO. ∵OA＝OC.∴∠OCA＝∠OAC.∵AC 平分∠FAB .∴∠OAC＝∠FAC . ∴∠OCA＝∠FAC .∴OC∥FD.∵CE⊥FD .∴CE⊥OC.∵OC 是⊙O 的半径.∴CE 是⊙O 的切线． (2)如图.连接BC.在Rt △ACE 中.AC ＝AE 2＋EC 2＝ 5. ∵AB 是⊙O 的直径.∴∠BCA＝90°. ∴∠BCA＝∠CEA.∵∠CAE＝∠BAC .∴△ACE∽△ABC . ∴CA AB ＝AE AC .即5AB ＝15.∴AB＝5. ∴AO＝12AB ＝2.5即⊙O 的半径是2.5.【变式训练】5．(1)证明：如图.连接OE.CE.∵AC 是⊙O 的直径.∴∠AEC＝∠BEC＝90°.∴ED＝12BC ＝DC.∴∠1＝∠2.∵OE＝OC.∴∠3＝∠4.∴∠1＋∠3＝∠2＋∠4.即∠OED＝∠ACD. ∵∠ACD＝90°.∴∠OED＝90°.即OE⊥DE. 又∵E 是⊙O 上一点. ∴DE 是⊙O 的切线．(2)解：由(1)知∠BEC＝90°.在Rt △BEC 与Rt △BCA 中.∠B 为公共角. ∴△BEC∽△BCA . ∴BE BC ＝BC BA. 即BC 2＝BE·BA.∵AE∶EB＝1∶2.设AE ＝x.则BE ＝2x.BA ＝3x. 又∵BC＝6.∴62＝2x·3x.∴x＝ 6.即AE ＝ 6. 6．证明：(1)∵ME 平分∠DMN .∴∠OME＝∠DME. ∵OM＝OE.∴∠OME＝∠OEM . ∴∠DME＝∠OEM .∴OE∥DM. ∵DM⊥DE .∴OE⊥DE.∵OE 是⊙O 的半径.∴DE 是⊙O 的切线． (2)如图.连接EN.∵DM⊥DE .MN 为⊙O 的直径. ∴∠MDE＝∠MEN＝90°. ∵∠NME＝∠DME . ∴△MDE∽△MEN . ∴ME MD ＝MN ME. ∴ME 2＝MD·MN.7．(1)证明：如图.连接OD.∴∠ODC＝90°.即∠ODB＋∠BDC＝90°.∵AB为⊙O的直径.∴∠ADB＝90°.即∠ODB＋∠ADO＝90°.∴∠BDC＝∠ADO.∵OA＝OD.∴∠ADO＝∠A.∴∠BDC＝∠A.(2)解：∵CE⊥AE.∴∠E＝90°.∴DB∥EC.∴∠DCE＝∠BDC.∵∠BDC＝∠A.∴∠A＝∠DCE.又∵∠E＝∠E.∴△AEC∽△CED.∴CEDE＝AECE.∴CE2＝DE·AE.即16＝2(2＋AD)．∴AD＝6.。
2018中考数学压轴题专题复习_圆的综合
2017中考专题复习——圆题型一、勾股定理在圆中的应用1、（2012成都）如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．（1）求证：KE=GE；（2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；（3）在（2）的条件下，若sinE=，AK=FG的长．2、（2014•孝感）如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE．（1）求证：AC平分∠DAB；（2）求证：△PCF是等腰三角形；（3）若tan∠ABC=，BE=7，求线段PC的长．2KG353、（2015•黄陂区校级模拟）如图，点P在y轴的正半轴上，⊙P交x轴于B、C两点，以AC 为直角边作等腰Rt△ACD，BD分别交y轴和⊙P于E、F两点，交连接AC、FC．（1）求证：∠ACF=∠ADB；（2）若点A到BD的距离为m，BF+CF=n，求线段CD的长；（3）当⊙P的大小发生变化而其他条件不变时，的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．4、（2013•成都模拟）已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连接DE，DE=．（1）求证：AM•MB=EM•MC；（2）求sin∠EOB的值；（3）若P是直径AB延长线上的点，且BP=12，求证：直线PE是⊙O的切线．5、（2012•杭州）如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT 于点B，已知∠EAT=30°，AE=3，MN=2．（1）求∠COB的度数；（2）求⊙O的半径R；（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．6、（2011•潍坊）如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM 上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN 相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q．（1）求证：△ABC∽△OFB；（2）当△ABD与△BFO的面枳相等时，求BQ的长；（3）求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点．专题二、三角函数在圆中的应用1、（2014成都）如图，在⊙O 的内接△ABC 中，∠ACB=90°，AC=2BC ，过C 作AB 的垂线l 交⊙O 于另一点D ，垂足为E.设P 是⌒AC 上异于A,C 的一个动点，射线AP 交l 于点F ，连接PC 与PD ，PD 交AB 于点G.（1）求证：△PAC ∽△PDF ；（2）若AB=5，⌒AP =⌒BP ，求PD 的长；（3）在点P 运动过程中，设x BGAG =，y AFD =∠tan ，求y 与x 之间的函数关系式.（不要求写出x 的取值范围） tan AE AFD FE∠=，2、（2012•襄阳）如图，PB 为⊙O 的切线，B 为切点，直线PO 交⊙于点E 、F ，过点B 作PO 的垂线BA ，垂足为点D ，交⊙O 于点A ，延长AO 与⊙O 交于点C ，连接BC ，AF ．（1）求证：直线PA 为⊙O 的切线；（2）试探究线段EF 、OD 、OP 之间的等量关系，并加以证明；（3）若BC=6，tan∠F=，求cos∠ACB 的值和线段PE 的长．3、（2014•武侯区校级自主招生）如图，⊙O与直线PC相切于点C，直径AB∥PC，PA交⊙O于D，BP交⊙O于E，DE交PC于F．（1）求证：PF2=EF•FD；（2）当tan∠APB=，tan∠ABE=，AP=时，求PF的长；（3）在（2）条件下，连接BD，判断△ADB是什么三角形？并证明你的结论．4、（2014•盘锦）如图，△ABC中，∠C=90°，点G是线段AC上的一动点（点G不与A、C重合），以AG为直径的⊙O交AB于点D，直线EF垂直平分BD，垂足为F，EF交BC于点E，连结DE．（1）求证：DE是⊙O的切线；（2）若cosA=，AB=8，AG=2，求BE的长；（3）若cosA=，AB=8，直接写出线段BE的取值范围．专题三、相似三角形与圆的综合应用1、（2010）已知：如图，ABC ∆内接于O ，AB 为直径，弦CE AB ⊥于F ，C 是AD 的中点，连结BD 并延长交EC 的延长线于点G ，连结AD ，分别交CE 、BC 于点P 、Q ．（1）求证：P 是ACQ ∆的外心；（2）若3tan ,84ABC CF ∠==,求CQ 的长； （3）求证：2()FP PQ FP FG +=．2、（2014•镇江）如图，⊙O 的直径AC 与弦BD 相交于点F ，点E 是DB 延长线上的一点，∠EAB=∠ADB．（1）求证：EA 是⊙O 的切线；（2）已知点B 是EF 的中点，求证：以A 、B 、C 为顶点的三角形与△AEF 相似；（3）已知AF=4，CF=2．在（2）条件下，求AE 的长．3、（2013•桂林）如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于D，过点D作DE⊥AD 交AB于E，以AE为直径作⊙O．（1）求证：点D在⊙O上；（2）求证：BC是⊙O的切线；（3）若AC=6，BC=8，求△BDE的面积．4、（2012•泰州）如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5．OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．（1）试判断线段AB与AC的数量关系，并说明理由；（2）若PC=2，求⊙O的半径和线段PB的长；（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．5、（2012•德阳）如图，已知点C 是以AB 为直径的⊙O 上一点，CH⊥AB 于点H ，过点B 作⊙O 的切线交直线AC 于点D ，点E 为CH 的中点，连接AE 并延长交BD 于点F ，直线CF 交AB 的延长线于G ．（1）求证：AE •FD=AF •EC ；（2）求证：FC=FB ；（3）若FB=FE=2，求⊙O 的半径r 的长．6、如图，在Rt △ABC 中，∠B=90°，它的内切圆分别与三角形的三边切于点D,E,F ，连接AD 与内切圆相交于点P ，连接PC,PE,PF,FD,ED ，且PC ⊥PF 。
2018圆证明---(-含答案)
圆证明1.如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．(1)求证：EF是⊙O的切线；(2)当DF：DE＝2：1时，∠BAC的度数为多少？说明理由；2如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．（Ⅰ）求证：直线BF是⊙O的切线；（Ⅱ）若AB=5，sin∠CBF=，求BC和BF的长．3.四边形ABCD是 O的内接四边形，∠ABC=2∠D，连接OA、OB、OC、AC，OB与求则图中阴影部分面积（结果保留π和根号）4.如图，点A、B在⊙O上，直线AC是⊙O的切线，OD⊥OB，连接AB交OC于点D。
（1）求证：AC=CD；（2）若AC=2，AO=，求OD的长度。
CD（1）求证：AD=CD ；（2）若AB=10，cos ∠ABC=53，求tan ∠DBC 的值.． 6如图，OC 平分∠MON ，点A 在射线OC 上，以点A 为圆心，半径为2的⊙A 与OM相切与点B ，连接BA 并延长交⊙A 于点D ，交ON 于点E ．（1）求证：ON 是⊙A 的切线；（2）若∠MON=60°，求图中阴影部分的面积．（结果保留π）如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD．（1）求证：BD平分∠ABC；（2）当∠ODB=30°时，求证：BC=OD．8如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D,点E在⊙O上．（1）若∠AOD=52°，求∠DEB的度数；（2）若OC=3，OA=5，求AB的长．已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧上取一点E使∠EBC=∠DEC，延长BE 依次交AC于G，交⊙O于H。
（1）求证：AC⊥BH；（2）若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长。
广东省深圳市2018年中考数学专题专练圆的证明与计算专题
圆的证明与计算专题1.如图，A ，P ，B ，C 是圆上的四个点，∠APC ＝∠CPB＝60°，AP ，CB 的延长线相交于点D.(1)求证：△ABC 是等边三角形；(2)若∠PAC＝90°，AB ＝23，求PD 的长．2.如图，OA ，OD 是⊙O 半径，过A 作⊙O 的切线，交∠AOD 的平分线于点C ，连接CD ，延长AO 交⊙O 于点E ，交CD 的延长线于点B.(1)求证：直线CD 是⊙O 的切线；(2)如果D 点是BC 的中点，⊙O 的半径为3 cm ，求DE ︵的长度．(结果保留π)3.如图，点D 是等边三角形ABC 的外接圆上一点，M 是BD 上一点，且满足DM ＝DC ，点E 是AC 与BD 的交点．(1)求证：CM∥AD；(2)如果AD ＝1，CM ＝2.求线段BD 的长及△BCE 的面积．4.如图，△ABC 内接于⊙O，BD 为⊙O 的直径，BD 与AC 相交于点H ，AC 的延长线与过点B 的直线交于点E ，且∠A ＝∠EBC.(1)求证：BE 是⊙O 的切线；(2)已知CG∥EB，且CG 与BD 、BA 分别相交于点F 、G ，若BG·BA＝48，FG ＝2，DF ＝2BF ；求AH 的值．5.如图，AB 为△ABC 外接圆⊙O 的直径，点P 是线段CA 延长线上一点，点E 在圆上且满足PE 2＝PA·PC，连接CE ，AE ，OE ，OE 交CA 于点D.(1)求证：△PAE∽△PEC； (2)求证：PE 为⊙O 的切线；(3)若∠B＝30°，AP ＝12AC ，求证：DO ＝DP.6.如图，在矩形ABCD 中，点O 在对角线AC 上，以OA 的长为半径的⊙O 与AD,AC 分别交于点E,F ，且∠ACB＝∠DCE.(1)判断直线CE 与⊙O 的位置关系，并证明你的结论； (2)若tan ∠ACB ＝22，BC ＝2，求⊙O 的半径．7.如图①，以△ABC 的边AB 为直径的⊙O 交边BC 于点E ，过点E 作⊙O 的切线交AC 于点D ，且ED⊥AC.(1)试判断△ABC 的形状 ，并说明理由；(2)如图②，若线段AB 、DE 的延长线交于点F ，∠C ＝75°，CD ＝2－3，求⊙O 的半径和BF 的长．8.如图，四边形ABCD 内接于⊙O，对角线AC 为⊙O 的直径，过点C 作AC 的垂线交AD 的延长线于点E ，点F 为CE 的中点，连接DB ，DC ，DF.(1)求∠CDE 的度数； (2)求证：DF 是⊙O 的切线；(3)若AC ＝25DE ，求tan ∠ABD 的值．9.如图，在Rt △ABC 与Rt △OCD 中，∠ACB ＝∠DCO＝90°，O 为AB 的中点．(1)求证：∠B＝∠ACD；(2)已知点E 在AB 上，且BC 2＝AB·BE. (i)若tan ∠ACD ＝34，BC ＝10，求CE 的长；(ii)试判定CD 与以A 为圆心，AE 为半径的⊙A 的位置关系，并说明理由．参考答案1. (1)证明：由题意可得：∠BPC＝∠BAC，∠APC ＝∠ABC，∵∠APC ＝∠CPB＝60°，∴∠ABC ＝∠BAC＝60°，∴△ABC 是等边三角形．(2)解：∵∠PAC＝90°，∴PC 是圆的直径，∴∠PBC ＝90°，∴∠PBD ＝90°，∵△ABC 是等边三角形，∴AB ＝BC ＝23，∵∠CPB ＝60°，∴PB ＝23tan 60°＝2，∵∠APC ＝60°，∴∠DPB ＝180°－60°－60°＝60°，∴PD ＝2PB ＝4.2. (1)证明：∵CA 切⊙O 于点A ，∴∠CAO ＝90°.∵OC 平分∠AOD ，∴∠AOC ＝∠DOC ，在△AOC 和△DOC 中，，∴△AOC ≌△DOC(SAS)，∴∠CDO＝∠CAO＝90°，∵OD 是⊙O 的半径，∴CD 是⊙O 的切线．(2)解：由(1)知：OD⊥BC，又∵D 是BC 的中点，∴OD 是BC 的垂直平分线，∴OC ＝OB ，∴∠BOD ＝∠DOC＝∠COA＝13×180°＝60°，∴∠DOE ＝60°，∴DE ︵的长度为60180π×3＝π.3. (1)证明：∵△ABC 是等边三角形，∴∠BAC ＝∠ACB＝60°，∴∠BDC ＝∠BAC＝60°，∠ADB ＝∠ACB＝60°，∴∠ADC ＝120°，∵DM ＝DC ，∴△DMC 是等边三角形，∴∠MCD ＝60°，∴∠MCD ＋∠ADC＝180°，∴CM ∥AD. (2)解：∵BC＝AC ，∠ADC ＝∠BMC＝120°，∠CBM ＝∠CAD，∴△ADC ≌△BMC ，∴AD ＝MB ＝1，∴BD ＝BM ＋MD ＝AD ＋CM ＝1＋2＝3，∵CM ∥AD ，∴∠CAD ＝∠ACM，∠ADE ＝∠EMC，∴△ADE ∽△CME ，∴AD CM ＝AE EC ＝DE EM ＝12，∴S △ADE ＝14S △EMC ，∵S △CMD ＝12×3×2＝3，∴S △EMC ＝23S △CMD ＝233，S △EDC ＝13S △CDM ＝33，∴S △ADE ＝14S △EMC ＝36，∴S △ADC ＝S △ADE ＋S △DCE ＝36＋33＝32，∴S △BCE ＝S △BMC ＋S △MCE ＝S △ADC ＋S △CME ＝32＋233＝763. 4. 解：(1)连接DC ，∵DB 是⊙O 的直径，∴∠DCB ＝90°，∴∠D ＋∠DBC＝90°，∵∠D ＝∠A，∠EBC ＝∠A.∴∠D ＝∠EBC，∴∠EBC ＋∠DBC＝90°，即∠DBE＝90°，∴BE 是⊙O 的切线．(2)∵CG∥EB，∴∠BCG ＝∠EBC，∴∠A ＝∠BCG，又∵∠CBG＝∠ABC，∴△ABC ∽△CBG ，∴BC BG ＝AB BC ，即BC 2＝BG·AB＝48，∴BC ＝43，∵CG ∥EB ，∴CF ⊥BD，∴∠CFB ＝∠DCB＝90°，又∵∠CBF＝∠DBC，∴Rt △BFC ∽Rt △BCD ，∴BF BC ＝BC BD ，∴BC 2＝BF·BD＝48，又∵DF＝2BF ，BD ＝DF ＋BF ＝3BF ，∴BF ＝4，在Rt △BCF 中，CF ＝BC 2－BF 2＝42，∴CG ＝CF ＋FG ＝52，在Rt △BFG 中，BG ＝BF 2＋FG2＝32，∵BA ＝48BG ＝82，∴AG ＝52，∴CG ＝AG ，∴∠A ＝∠ACG＝∠BCG，∠CFH ＝∠CFB＝90°，∴∠CHF ＝∠CBF，∴CH ＝CB ＝43，∵∠ABC ＝∠CBG，∠BCG ＝∠A，∴△ABC ∽△CBG ，∴AC CG ＝BC BG ，∴AC ＝BC ·CG BG ＝43×5232＝2033，∴AH ＝AC －CH ＝2033－43＝833.5. (1)解：∵PE 2＝PA·PC，∴PA PE ＝PE PC ，∵∠P ＝∠P，∴△PAE ∽△PEC. (2)证明：∵△PAE∽△PEC，∴∠PEA ＝∠PCE，∵OA ＝OE ，∴∠OEA ＝∠OAE，∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴∠OAE ＋∠ECA＝90°，∴∠PEO ＝∠PEA＋∠OEA ＝∠PCE＋∠OAE＝90°，∵OE 为⊙O 半径，∴PE 是⊙O 的切线．(3)证明：过点O 作OH⊥CP 于点H ，∵AB 是⊙O 的直径，∠B ＝30°，∴BC ＝AC tan 30°＝AC 33＝3AC ，∵O 是AB 的中点，∴OH ＝12BC ＝32AC ，∵PE 2＝PA·PC，AP ＝12AC ，∴PE 2＝12AC ·(12AC ＋AC)＝12AC ·32AC ＝34AC 2，∴PE ＝32AC ，∴OH ＝PE ，∵∠OHA ＝∠PED＝90°，∠HDO ＝∠EDP，∴△HDO ≌△EDP ，∴DO ＝DP. 6. 解：(1)直线CE 与⊙O 相切．证明如下：连接OE ，∴∠OAE ＝∠AEO，∵四边形ABCD 是矩形，∴BC ∥AD ，∠ACB ＝∠DAC, 又∵∠ACB＝∠DCE，∴∠DAC ＝∠AEO＝∠DCE，∵∠DCE ＋∠DEC＝90°，∴∠AEO ＋∠DEC＝90°，∴∠OEC ＝90°，∵OE 是⊙O 的半径，∴直线CE 与⊙O 相切．(2)∵tan ∠ACB ＝AB BC ＝22，BC ＝2，∴AB ＝BC·tan ∠ACB ＝2，∴AC ＝AB 2＋BC 2＝6，又∵∠ACB＝∠DCE，∴tan ∠DCE ＝22，∴DE ＝DC·tan ∠DCE ＝AB·tan ∠DCE ＝2×22＝1，在Rt △CDE 中，CE ＝CD 2＋DE 2＝3，设⊙O 的半径为r ，在Rt △COE 中，CO 2＝OE 2＋CE 2，即(6－r)2＝r 2＋3，解得r ＝64.∴⊙O 的半径为64. 7. 解：(1)△ABC 为等腰三角形，理由如下：如解图①，连接OE ，在⊙O 中，∵OE ＝OB ，∴∠OEB ＝∠B，图①∵DE 是⊙O 的切线，∴∠OED ＝90°，∵ED ⊥AC ，∴∠ADE ＝90°＝∠OED，∴OE ∥AC 且BE ＝CE ＝12BC ，∴∠OEB ＝∠C，∴∠B ＝∠C，∴AC ＝AB ，∴△ABC 为等腰三角形．(2)如图②，过点B 作BH⊥DF，∵AC ⊥DF ，∴BH ∥AC ，∠EBH＝∠C，由(1)知∠CDE＝∠BHE＝90°，BE ＝CE ，∴△CDE ≌△BHE(AAS)，∴CD ＝BH ＝2－3，∵∠HBF ＝180°－∠OBE－∠EBH ＝180°－75°－75°＝30°，图②∴∠F ＝90°－30°＝60°，在Rt △BFH 中，∴BF ＝BH sin 60°＝43－63，设OE ＝x ，在Rt △OEF 中，sin60°＝OE OF ＝xx ＋BF，解得x ＝2，故⊙O 的半径为2，BF 的长为43－63.8. (1)解：∵对角线AC 为⊙O 直径，∴∠ADC ＝90°，∴∠CDE ＝90°.(2)证明：连接OD ，∵AC 为⊙O 的直径，CE ⊥AC ，∴∠ADC ＝∠CDE＝90°，∠ACF ＝90°，又∵在Rt △CDE 中，点F 为斜边CE 的中点，∴DF ＝FC ，∠CDF ＝∠DCF，又∵OD＝OC，∴∠ODC ＝∠OCD，∴∠ODF ＝∠ODC＋∠CDF＝∠OCD＋∠DCF＝∠ACE＝90°，∵OD 为⊙O 半径，∴DF是⊙O 的切线．(3)解：由圆周角定理可得，∠ABD ＝∠ACD，由题意知，∠ADC ＝∠CDE＝90°，∠CAD ＝∠ECD，∴△ADC ∽△CDE ，∴AD CD ＝CD DE ，∴CD 2＝AD·DE，∵AC ＝25DE ，设DE ＝a ，AD ＝b ，∴AC ＝25a ，CD ＝ab ，在Rt △ACD中，由勾股定理可得：AD 2＋CD 2＝AC 2，即b 2＋(ab)2＝(25a)2，上式两边同时除以a 2，整理后得到：(b a )2＋b a －20＝0，解得b a ＝4或b a ＝－5(舍去)．∴tan ∠ABD ＝tan ∠ACD ＝AD CD ＝bab＝ba＝2. 9. (1)证明：∵点O 为直角三角形斜边AB 上的中点，∴OC ＝OB ，∴∠B ＝∠BCO，∵∠ACB ＝∠DCO＝90°，即∠ACO ＋∠BCO＝∠ACO＋∠ACD＝90°，∴∠BCO ＝∠ACD∴∠B ＝∠ACD.(2)解：(i)∵BC 2＝AB·BE，即BC BA ＝BE BC ，又∵∠B＝∠B，∴△BCA ∽△BEC ，∴∠BEC ＝∠BCA＝90°，∵tan ∠ACD ＝34，又由(1)知∠B＝∠ACD，∴tan ∠B ＝34，即CE EB ＝34，设CE ＝3x ，EB ＝4x ，∵在Rt △BCE 中，CE 2＋EB 2＝BC 2，∴(3x)2＋(4x)2＝102，∴x ＝2，∴CE ＝3x ＝6.(ii)CD 与⊙A 相切，理由如下：过A 作AF⊥DC，∵∠ACB ＝90°，∴∠ACE ＋∠BCE＝90°，∵∠BEC ＝90°，∴∠B ＋∠BCE＝90°，∴∠B ＝∠ACE，又∵∠B＝∠ACD，∴∠ACE ＝∠ACD.又∵AF⊥DC，AE ⊥EC ，∴AE ＝AF ，又∵AE 为⊙O 半径，F 为CD 上一点，∴CD 与⊙A 相切．。
(完整版)天津市南开区2018届中考《圆证明题》专项复习试卷(含答案),推荐文档
2018 年九年级数学中考复习圆证明题专项复习卷1、如图，点 A，B 在⊙O 上，直线 AC 是⊙O 的切线，OC⊥OB，连接 AB 交 OC 于点 D．求证：AC=CD．2、如图，AD 是⊙O的切线，切点为 A，AB 是⊙O的弦．过点 B 作BC∥AD，交⊙O于点C，连接 AC，过点 C 作CD∥AB，交AD 于点D．连接 AO 并延长交 BC 于点M，交过点 C 的直线于点 P，且∠BCP=∠ACD． (1)判断直线 PC 与⊙O的位置关系，并说明理由；(2)若 AB=9，BC=6．求 PC 的长．3、如图，在△ABC 中，∠ACB=90°，点 D 是 AB 上一点，以 BD 为直径的⊙O 和 AB 相切于点 P．（1）求证：BP 平分∠ABC；（2）若PC=1，AP=3，求BC 的长．4、已知：如图，AC 是⊙O 的直径，BC 是⊙O 的弦，点 P 是⊙O 外一点，∠PBA=∠C．（1）求证：PB 是⊙O的切线．（2）若OP∥BC，且OP=8，∠C=60°，求⊙O的半径．5、如图，在△ABC中，AB=AC，以AB 为直径的⊙O交BC 于点M，MN⊥AC于点N．求证：MN 是⊙O的切线．6、如图，AB 是⊙O 的直径，点 C 在 AB 的延长线上，CD 与⊙O 相切于点 D，CE⊥AD，交 AD 的延长线于点E．（1）求证：∠BDC=∠A；（2）若CE=4，DE=2，求⊙O的直径．7、已知：AB 是⊙O的直径，BD 是⊙O的弦，延长 BD 到点C，使AB=AC，连结 AC，过点 D 作DE⊥AC，垂足为E．（1）求证：DC=BD（2）求证：DE 为⊙O的切线．8、如图，AB 是⊙O的直径，C 为⊙O上一点，经过点 C 的直线与 AB 的延长线交于点 D，连接AC，BC，∠BCD=∠CAB．E 是⊙O上一点，弧 CB=弧CE，连接 AE 并延长与 DC 的延长线交于点 F．（1）求证：DC 是⊙O的切线；（2）若⊙O的半径为3，sinD=，求线段AF 的长．9、如图，已知 MN 是⊙O 的直径，直线 PQ 与⊙O 相切于 P 点，NP 平分∠MNQ．（1）求证：NQ⊥PQ；（2）若⊙O的半径R=2，NP=，求NQ 的长．10、已知：AB 是⊙O的直径，BD 是⊙O的弦，延长 BD 到点C，使AB=AC；连结 AC，过点 D 作DE⊥AC，垂足为 E．(1)求证：DC=BD(2)求证：DE 为⊙O的切线11、如图，以Rt△ABC的AC 边为直径作⊙O交斜边 AB 于点E，连接 EO 并延长交 BC 的延长线于点 D，点F 为 BC 的中点，连接 EF 和 AD．（1）求证：EF 是⊙O的切线；（2）若⊙O的半径为 2，∠EAC=60°，求AD 的长．12、如图，AB 是⊙O的直径，点E 是上的一点，∠DBC=∠BED．⑴求证：BC 是⊙O 的切线；⑵已知 AD=3，CD=2，求 BC 的长．13、如图，已知 AB 是⊙O 的直径，点 C、D 在⊙O 上，点 E 在⊙O 外，∠EAC=∠D=60°．（1）求∠ABC的度数；（2）求证：AE 是⊙O的切线；（3）当BC=4 时，求劣弧 AC 的长．14、已知△ABC，以 AB 为直径的⊙O 分别交 AC 于 D，BC 于 E，连接 ED，若 ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD 的长．15、如图，以△ABC的边AB 上一点 O 为圆心的圆经过 B、C 两点，且与边 AB 相交于点 E，D 是弧BE 的中点，CD 交 AB 于F，AC=AF．（1）求证：AC 是⊙O的切线；（2）若EF=5，DF=，求⊙O的半径．参考答案1、∵直线 AC 与⊙O 相切，∴OA⊥AC，∴∠OAC=90°，即∠OAB+∠CAB=90°，∵OC⊥OB，∴∠BOC=90°，∴∠B+∠ODB=90°，而∠ODB=∠ADC，∴∠ADC+∠B=90°，∴OA=OB，∴∠OAB=∠B，∴∠ADC=∠CAB，∴AC=CD．2、（1）解：PC 与圆 O 相切，理由为：过 C 点作直径 CE，连接 EB，如图，∵CE 为直径，∴∠EBC=90°，即∠E+∠BCE=90°，∵AB∥DC，∴∠ACD=∠BAC，∵∠BAC=∠E，∠BCP=∠ACD．∴∠E=∠BCP，∴∠BCP+∠BCE=90°，即∠PCE=90°，∴CE⊥PC，∴PC 与圆 O 相切；（2）解：∵AD 是⊙O 的切线，切点为 A，∴OA⊥AD，∵BC∥AD，∴AM⊥BC，∴BM=CM= BC=3，∴AC=AB=9，在Rt△AMC中，AM= =6 ，设⊙O的半径为r，则OC=r，OM=AM﹣r=6 ﹣r，在Rt△OCM中，OM2+CM2=OC2，即32+（6 ﹣r）2=r2，解得r= ，∴CE=2r=，OM=6 ﹣= ，∴BE=2OM=，∵∠E=∠MCP，∴Rt△PCM∽Rt△CEB，∴= ，即= ，∴PC= 3、（1）证明：连接 OP，∵AC 是⊙O 的切线，∴OP⊥AC，BC⊥AC，∴OP∥BC，∴∠OPB=∠PBC，∵OP=OB，∴∠OPB=∠OBP，∴∠PBC=∠OBP，∴BP 平分∠ABC（2）作PH⊥AB 于 H．∵PB 平分∠ABC，PC⊥BC，PH⊥AB，∴PC=PH=1，在Rt△APH中，AH= =2 ，∵∠A=∠A，∠AHP=∠C=90°，∴△APH∽△ABC，∴= ，∴= ，∴AB=3，∴BH=AB﹣AH= ，在Rt△PBC和Rt△PBH中，，∴Rt△PBC≌Rt△PBH，∴BC=BH=．4、（1）证明：连接 OB，∵AC 是⊙O 直径，∴∠ABC=90°，∵OC=OB，∴∠OBC=∠C，∵∠PBA=∠C，∴∠PBA=∠OBC，即∠PBA+∠OBA=∠OBC+∠ABO=∠ABC=90°，∴OB⊥PB，∵OB 为半径，∴PB 是⊙O 的切线；（2）解：∵OC=OB，∠C=60°，∴△OBC 为等边三角形，∴BC=OB，∵OP∥BC，∴∠CBO=∠POB，∴∠C=∠POB，在△ABC和△PBO中∵，∴△ABC≌△PBO（ASA），∴AC=OP=8，即⊙O的半径为4．5、证明：连接 OM，∵AB=AC，∴∠B=∠C，∵OB=OM，∴∠B=∠OMB，∴∠OMB=∠C，∴OM∥AC，∵MN⊥AC，∴OM⊥MN．∵点 M 在⊙O 上，∴MN 是⊙O 的切线．6、（1）证明：连接 OD，∵CD 是⊙O 切线，∴∠ODC=90°，即∠ODB+∠BDC=90°，∵AB 为⊙O 的直径，∴∠ADB=90°，即∠ODB+∠ADO=90°，∴∠BDC=∠ADO，∵OA=OD，∴∠ADO=∠A，∴∠BDC=∠A；（2）∵CE⊥AE，∴∠E=∠ADB=90°，∴DB∥EC，∴∠DCE=∠BDC，∴∠DCE=∠A，∵CE=4，DE=2∴在Rt△ACE 中，可得AE=8∴AD=6在在Rt△ADB中可得BD=3∴根据勾股定理可得7、证明：（1）连接 AD，∵AB 是⊙O 的直径，∴∠ADB=90°，又∵AB=AC，∴DC=BD；（2）连接半径 OD，∵OA=OB，CD=BD，∴OD∥AC，∴∠ODE=∠CED，又∵DE⊥AC，∴∠CED=90°，∴∠ODE=90°，即OD⊥DE．∴DE 是⊙O 的切线．8、（1）证明：连接 OC，BC，∵AB 是⊙O 的直径，∴∠ACB=90°，即∠1+∠3=90°．∵OA=OC，∴∠1=∠2．∵∠DCB=∠BAC=∠1．∴∠DCB+∠3=90°．∴OC⊥DF．∴DF 是⊙O 的切线；（2）解：在Rt△OCD中，OC=3，sinD=．∴OD=5，AD=8．∵= ，∴∠2=∠4．∴∠1=∠4．∴OC∥AF．∴△DOC∽△DAF．∴．∴AF=．9、（1）证明：连结 OP，如图，∴直线 PQ 与⊙O 相切，∴OP⊥PQ，∵OP=ON，∴∠ONP=∠OPN，∵NP 平分∠MNQ，∴∠ONP=∠QNP，∴∠OPN=∠QNP，∴OP∥NQ，∴NQ⊥PQ；（2）解：连结 PM，如图，∵MN 是⊙O 的直径，∴∠MPN=90°，∵NQ⊥PQ，∴∠PQN=90°，而∠MNP=∠QNP，∴Rt△NMP∽Rt△NPQ，∴=，即=，∴NQ=3．10、（1）证明：（1）连接 AD；∵AB是⊙O的直径，∴∠ADB=90°．又∵AB=AC∴DC=BD（2）连接半径 OD；∵OA=OB，CD=BD，∴OD∥AC．∴∠0DE=∠CED．又∵DE⊥AC，∴∠CED=90°．∴∠ODE=90°，即OD⊥DE．∴DE 是⊙O 的切线．11、（1）证明：连接 CE，如图所示：∵AC为⊙O的直径，∴∠AEC=90°．∴∠BEC=90°．∵点 F 为BC 的中点，∴EF=BF=CF．∴∠FEC=∠FCE．∵OE=OC，∴∠OEC=∠OCE．∵∠FCE+∠OCE=∠ACB=90°，∴∠FEC+∠OEC=∠OEF=90°．∴EF 是⊙O 的切线．（2）解：∵OA=OE，∠EAC=60°，∴△AOE 是等边三角形．∴∠AOE=60°．∴∠COD=∠AOE=60°．∵⊙O 的半径为 2，∴OA=OC=2 在Rt△OCD 中，∵∠OCD=90°，∠COD=60°，∴∠ODC=30°．∴OD=2OC=4，∴CD=．在Rt△ACD中，∵∠ACD=90°，AC=4，CD=．∴AD== ．12、1）AB 是⊙O的直径，得∠ADB=90°，从而得出∠BAD=∠DBC，即∠ABC=90°，即可证明BC 是⊙O的切线；（2）可证明△ABC∽△BDC，则=，即可得出BC= ；13、解：（1）∵∠ABC 与∠D 都是弧 AC 所对的圆周角，∴∠ABC=∠D=60°；（2）∵AB 是⊙O 的直径，∴∠ACB=90°．∴∠BAC=30°，∴∠BAE=∠BAC+∠EAC=30°+60°=90°，即BA⊥AE，∴AE 是⊙O 的切线；（3）如图，连接OC，∵∠ABC=60°，∴∠AOC=120°，∴劣弧AC 的长为．14、（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC= ，∵△CDE∽△CBA，∴，∴CE•CB=CD•CA，AC=AB=4，∴•2=4CD，∴CD=．15、（1）证明：连结 OD、OC，如图，∵D 是弧 BE 的中点，∴OD⊥BE，∴∠D+∠3=90°，∵∠3=∠2，∴∠D+∠2=90°，∵AF=AC，OD=OC，∴∠1=∠2，∠D=∠4，∴∠1+∠4=90°，∴OC⊥AC，∴AC 是⊙O 的切线；（2）解：设⊙O 的半径为 r，则 OF=OE﹣EF=r﹣5，在Rt△ODF中，∵OD2+OF2=DF2，∴r2+（r﹣5）2=（）2，整理得 r2﹣5r﹣6=0，解得 r1=6，r2=﹣1，∴，⊙O 的半径为 6．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
(完整版)天津市南开区2018届中考《圆证明题》专项复习试卷(含答案),推荐文档
2018年九年级数学中考复习圆证明题专项复习卷1、如图，点A，B在⊙O上，直线AC是⊙O的切线，OC⊥OB，连接AB交OC于点D．求证：AC=CD．2、如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过点B作BC∥AD，交⊙O于点C，连接AC，过点C 作CD∥AB，交AD于点D．连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD．(1)判断直线PC与⊙O的位置关系，并说明理由；(2)若AB=9，BC=6．求PC的长．3、如图，在△ABC中，∠ACB=90°，点D是AB上一点，以BD为直径的⊙O和AB相切于点P．（1）求证：BP平分∠ABC；（2）若PC=1，AP=3，求BC的长．4、已知：如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，∠PBA=∠C．（1）求证：PB是⊙O的切线．（2）若OP∥BC，且OP=8，∠C=60°，求⊙O的半径．5、如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点M，MN⊥AC于点N．求证：MN是⊙O的切线．6、如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E．（1）求证：∠BDC=∠A；（2）若CE=4，DE=2，求⊙O的直径．7、已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB=AC，连结AC，过点D作DE⊥AC，垂足为E．（1）求证：DC=BD（2）求证：DE为⊙O的切线．8、如图，AB是⊙O的直径，C为⊙O上一点，经过点C的直线与AB的延长线交于点D，连接AC，BC，∠BCD=∠CAB．E是⊙O上一点，弧CB=弧CE，连接AE并延长与DC的延长线交于点F．（1）求证：DC是⊙O的切线；（2）若⊙O的半径为3，sinD=，求线段AF的长．9、如图，已知MN是⊙O的直径，直线PQ与⊙O相切于P点，NP平分∠MNQ．（1）求证：NQ⊥PQ；（2）若⊙O的半径R=2，NP=，求NQ的长．10、已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB=AC；连结AC，过点D作DE⊥AC，垂足为E．(1)求证：DC=BD(2)求证：DE为⊙O的切线11、如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F 为BC的中点，连接EF和AD．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为2，∠EAC=60°，求AD的长．12、如图，AB是⊙O的直径，点E是上的一点，∠DBC=∠BED．⑴求证：BC是⊙O的切线；⑵已知AD=3，CD=2，求BC的长．13、如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．（1）求∠ABC的度数；（2）求证：AE是⊙O的切线；（3）当BC=4时，求劣弧AC的长．14、已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．15、如图，以△ABC的边AB上一点O为圆心的圆经过B、C两点，且与边AB相交于点E，D是弧BE的中点，CD交AB于F，AC=AF．（1）求证：AC是⊙O的切线；（2）若EF=5，DF=，求⊙O的半径．参考答案1、∵直线AC与⊙O相切，∴OA⊥AC，∴∠OAC=90°，即∠OAB+∠CAB=90°，∵OC⊥OB，∴∠BOC=90°，∴∠B+∠ODB=90°，而∠ODB=∠ADC，∴∠ADC+∠B=90°，∴OA=OB，∴∠OAB=∠B，∴∠ADC=∠CAB，∴AC=CD．2、（1）解：PC与圆O相切，理由为：过C点作直径CE，连接EB，如图，∵CE为直径，∴∠EBC=90°，即∠E+∠BCE=90°，∵AB∥DC，∴∠ACD=∠BAC，∵∠BAC=∠E，∠BCP=∠ACD．∴∠E=∠BCP，∴∠BCP+∠BCE=90°，即∠PCE=90°，∴CE⊥PC，∴PC与圆O相切；（2）解：∵AD是⊙O的切线，切点为A，∴OA⊥AD，∵BC∥AD，∴AM⊥BC，∴BM=CM=BC=3，∴AC=AB=9，在Rt△AMC中，AM= =6，设⊙O的半径为r，则OC=r，OM=AM﹣r=6﹣r，在Rt△OCM中，OM2+CM2=OC2，即32+（6﹣r）2=r2，解得r=，∴CE=2r=，OM=6 ﹣= ，∴BE=2OM=，∵∠E=∠MCP，∴Rt△PCM∽Rt△CEB，∴= ，即= ，∴PC= 3、（1）证明：连接OP，∵AC是⊙O的切线，∴OP⊥AC，BC⊥AC，∴OP∥BC，∴∠OPB=∠PBC，∵OP=OB，∴∠OPB=∠OBP，∴∠PBC=∠OBP，∴BP平分∠ABC（2）作PH⊥AB于H．∵PB平分∠ABC，PC⊥BC，PH⊥AB，∴PC=PH=1，在Rt△APH中，AH= =2 ，∵∠A=∠A，∠AHP=∠C=90°，∴△APH∽△ABC，∴= ，∴= ，∴AB=3，∴BH=AB﹣AH=，在Rt△PBC和Rt△PBH中，，∴Rt△PBC≌Rt△PBH，∴BC=BH=．4、（1）证明：连接OB，∵AC是⊙O直径，∴∠ABC=90°，∵OC=OB，∴∠OBC=∠C，∵∠PBA=∠C，∴∠PBA=∠OBC，即∠PBA+∠OBA=∠OBC+∠ABO=∠ABC=90°，∴OB⊥PB，∵OB为半径，∴PB是⊙O的切线；（2）解：∵OC=OB，∠C=60°，∴△OBC为等边三角形，∴BC=OB，∵OP∥BC，∴∠CBO=∠POB，∴∠C=∠POB，在△ABC和△PBO中∵，∴△ABC≌△PBO（ASA），∴AC=OP=8，即⊙O的半径为4．5、证明：连接OM，∵AB=AC，∴∠B=∠C，∵OB=OM，∴∠B=∠OMB，∴∠OMB=∠C，∴OM∥AC，∵MN⊥AC，∴OM⊥MN．∵点M在⊙O上，∴MN是⊙O的切线．6、（1）证明：连接OD，∵CD是⊙O切线，∴∠ODC=90°，即∠ODB+∠BDC=90°，∵AB为⊙O的直径，∴∠ADB=90°，即∠ODB+∠ADO=90°，∴∠BDC=∠ADO，∵OA=OD，∴∠ADO=∠A，∴∠BDC=∠A；（2）∵CE⊥AE，∴∠E=∠ADB=90°，∴DB∥EC，∴∠DCE=∠BDC，∴∠DCE=∠A，∵CE=4，DE=2∴在Rt△ACE中，可得AE=8∴AD=6在在Rt△ADB中可得BD=3∴根据勾股定理可得7、证明：（1）连接AD，∵AB是⊙O的直径，∴∠ADB=90°，又∵AB=AC，∴DC=BD；（2）连接半径OD，∵OA=OB，CD=BD，∴OD∥AC，∴∠ODE=∠CED，又∵DE⊥AC，∴∠CED=90°，∴∠ODE=90°，即OD⊥DE．∴DE是⊙O的切线．8、（1）证明：连接OC，BC，∵AB是⊙O的直径，∴∠ACB=90°，即∠1+∠3=90°．∵OA=OC，∴∠1=∠2．∵∠DCB=∠BAC=∠1．∴∠DCB+∠3=90°．∴OC⊥DF．∴DF是⊙O的切线；（2）解：在Rt△OCD中，OC=3，sinD=．∴OD=5，AD=8．∵=，∴∠2=∠4．∴∠1=∠4．∴OC∥AF．∴△DOC∽△DAF．∴．∴AF=．9、（1）证明：连结OP，如图，∴直线PQ与⊙O相切，∴OP⊥PQ，∵OP=ON，∴∠ONP=∠OPN，∵NP平分∠MNQ，∴∠ONP=∠QNP，∴∠OPN=∠QNP，∴OP∥NQ，∴NQ⊥PQ；（2）解：连结PM，如图，∵MN是⊙O的直径，∴∠MPN=90°，∵NQ⊥PQ，∴∠PQN=90°，而∠MNP=∠QNP，∴Rt△NMP∽Rt△NPQ，∴=，即=，∴NQ=3．10、（1）证明：（1）连接AD；∵AB是⊙O的直径，∴∠ADB=90°．又∵AB=AC∴DC=BD（2）连接半径OD；∵OA=OB，CD=BD，∴OD∥AC．∴∠0DE=∠CED．又∵DE⊥AC，∴∠CED=90°．∴∠ODE=90°，即OD⊥DE．∴DE是⊙O的切线．11、（1）证明：连接CE，如图所示：∵AC为⊙O的直径，∴∠AEC=90°．∴∠BEC=90°．∵点F为BC的中点，∴EF=BF=CF．∴∠FEC=∠FCE．∵OE=OC，∴∠OEC=∠OCE．∵∠FCE+∠OCE=∠ACB=90°，∴∠FEC+∠OEC=∠OEF=90°．∴EF是⊙O的切线．（2）解：∵OA=OE，∠EAC=60°，∴△AOE是等边三角形．∴∠AOE=60°．∴∠COD=∠AOE=60°．∵⊙O的半径为2，∴OA=OC=2在Rt△OCD中，∵∠OCD=90°，∠COD=60°，∴∠ODC=30°．∴OD=2OC=4，∴CD=．在Rt△ACD中，∵∠ACD=90°，AC=4，CD=．∴AD==．12、1）AB是⊙O的直径，得∠ADB=90°，从而得出∠BAD=∠DBC，即∠ABC=90°，即可证明BC是⊙O的切线；（2）可证明△ABC∽△BDC，则=，即可得出BC=；13、解：（1）∵∠ABC与∠D都是弧AC所对的圆周角，∴∠ABC=∠D=60°；（2）∵AB是⊙O的直径，∴∠ACB=90°．∴∠BAC=30°，∴∠BAE=∠BAC+∠EAC=30°+60°=90°，即BA⊥AE，∴AE是⊙O的切线；（3）如图，连接OC，∵∠ABC=60°，∴∠AOC=120°，∴劣弧AC的长为．14、（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC=，∵△CDE∽△CBA，∴，∴CE•CB=CD•CA，AC=AB=4，∴•2=4CD，∴CD=．15、（1）证明：连结OD、OC，如图，∵D是弧BE的中点，∴OD⊥BE，∴∠D+∠3=90°，∵∠3=∠2，∴∠D+∠2=90°，∵AF=AC，OD=OC，∴∠1=∠2，∠D=∠4，∴∠1+∠4=90°，∴OC⊥AC，∴AC是⊙O的切线；（2）解：设⊙O的半径为r，则OF=OE﹣EF=r﹣5，在Rt△ODF中，∵OD2+OF2=DF2，∴r2+（r﹣5）2=（）2，整理得r2﹣5r﹣6=0，解得r1=6，r2=﹣1，∴，⊙O的半径为6．。
武汉市2018年中考数学21题圆的有关证明和计算2
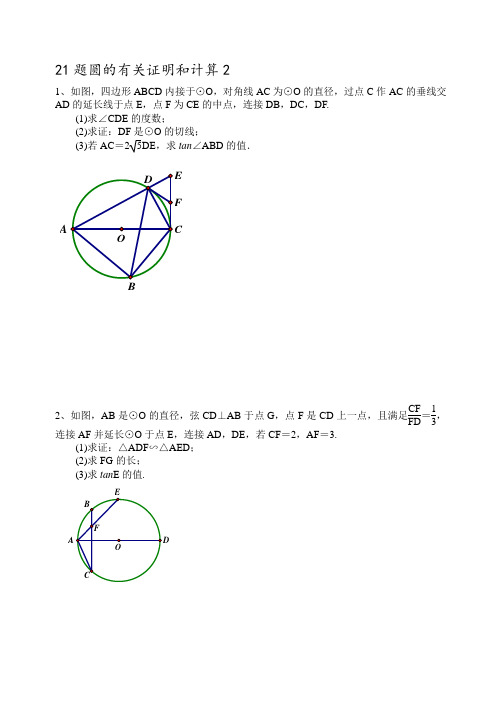
21题圆的有关证明和计算2
1、如图，四边形ABCD 内接于⊙O ，对角线AC 为⊙O 的直径，过点C 作AC 的垂线交AD 的延长线于点E ，点F 为CE 的中点，连接DB ，DC ，DF.
(1)求∠CDE 的度数；
(2)求证：DF 是⊙O 的切线；
(3)若AC ＝25DE ，求tan ∠ABD 的值．
2、如图，AB 是⊙O 的直径，弦CD ⊥AB 于点G ，点F 是CD 上一点，且满足CF FD ＝1
3
，
连接AF 并延长⊙O 于点E ，连接AD ，DE ，若CF ＝2，AF ＝3.
(1)求证：△ADF ∽△AED ； (2)求FG 的长； (3)求tan E 的值.
A
C
E F
3、如图，AB 为⊙O 的直径，点C 为弧AB 上一点，弦CD 交AB ①若点C 为弧AB 的中点，4
5
DE CE =，求tanB 的值.
②在①中，若E 是OB 的中点，连AC ，求tan ∠ACD 的值.
③如图，DC ＝DB ，若5
8
DE CE =，求tan ∠CDB 的值.
4、等腰直角△AOB ，F 是以OA 为半径的⊙O 上一点.
(1) FC ⊥AB 于C ， 若∠BCF =1
2
∠BOF ，求证：CF
为⊙O 的切线；
(2)连BF ，D 在直线BF 上，DC ⊥AB 于C ，交AF 的延长线于E ，若，CE =4，DE =3，求AE 的长.。
2018届中考数学复习专题题型(七) 圆的有关计算与证明
（2017浙江衢州第19题）如图，AB 为半圆O 的直径，C 为BA 延长线上一点，CD 切半圆O 于点D 。
连结OD ，作BE ⊥CD 于点E ，交半圆O 于点F 。
已知CE=12，BE=9[来源:学#科#网Z#X#X#K]（1）求证：△COD ∽△CBE ；（2）求半圆O 的半径r 的长：试题解析： （1）∵CD 切半圆O 于点D ，∴CD ⊥OD ，∴∠CDO=90°，∵BE ⊥CD ，∴∠E=90°=∠CDO ，又∵∠C=∠C ，∴△COD ∽△CBE ．（2）在Rt △BEC 中，CE=12，BE=9，∴22CE BE +=15，∵△COD ∽△CBE ． ∴OD OC BE BC=，即15915r r -=， 解得：r=458． 考点：1. 切线的性质；2.相似三角形的判定与性质.2.（2017山东德州第20题）如图，已知Rt ΔABC,∠C=90°，D 为BC 的中点.以AC 为直径的圆O 交AB 于点E.（1）求证：DE 是圆O 的切线.(2)若AE:EB=1:2,BC=6，求AE 的长.(1)如图所示，连接OE，CE∵AC是圆O的直径∴∠AEC=∠BEC=90°∵D是BC的中点∴ED＝12BC＝DC∴∠1=∠2∵OE=OC∴∠3=∠4∴∠1+∠3=∠2+∠4,即∠OED=∠ACD ∵∠ACD=90°∴∠OED=90°,即OE⊥DE又∵E是圆O上的一点∴DE是圆O的切线.考点：圆切线判定定理及相似三角形3.（2017甘肃庆阳第27题）如图，AN 是⊙M 的直径，NB ∥x 轴，AB 交⊙M 于点C ．（1）若点A （0，6），N （0，2），∠ABN=30°，求点B 的坐标；（2）若D 为线段NB 的中点，求证：直线CD 是⊙M 的切线．（1）∵A 的坐标为（0，6），N （0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=2243ABAN -=，∴B （43，2）．（2）连接MC ，NC∵AN 是⊙M 的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt △NCB 中，D 为NB 的中点，∴CD=12NB=ND ， ∴∠CND=∠NCD ，∵MC=MN ，∴∠MCN=∠MNC ， ∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC ⊥CD ．∴直线CD 是⊙M 的切线．考点：切线的判定；坐标与图形性质．4.（2017广西贵港第24题）如图，在菱形ABCD 中，点P 在对角线AC 上，且PA PD =，O 是PAD ∆的外接圆.（1）求证：AB 是O 的切线；（2）若28,tan 2AC BAC =∠=求O 的半径. 【答案】(1)证明见解析；（236． （1）连结OP 、OA ，OP 交AD 于E ，如图，∵PA=PD ，∴弧AP=弧DP ，∴OP ⊥AD ，AE=DE ，∴∠1+∠OPA=90°，∵OP=OA ，∴∠OAP=∠OPA ，∴∠1+∠OAP=90°，∵四边形ABCD 为菱形，∴∠1=∠2，∴∠2+∠OAP=90°，∴OA ⊥AB ，∴直线AB 与⊙O 相切；（2）连结BD ，交AC 于点F ，如图，∵四边形ABCD 为菱形，∴DB 与AC 互相垂直平分，∵AC=8，tan ∠∴AF=4，tan ∠DAC=DFAF∴∴∴在Rt △PAE 中，tan ∠1=PE AE =2，∴设⊙O 的半径为R ，则OE=R OA=R ，在Rt △OAE 中，∵OA 2=OE 2+AE 2，∴R 2=（R 2+2，∴R=4，即⊙O 的半径为4．考点：切线的判定与性质；菱形的性质；解直角三角形．5.（2017贵州安顺第25题）如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）设OE交⊙O于点F，若DF=1，BC=2 3，求阴影部分的面积．【答案】(1)证明见解析；（2）43﹣43π．（1）证明：连接OC，如图，∵CE为切线，∴OC⊥CE，∴∠OCE=90°，∵OD⊥BC，∴CD=BD，即OD垂中平分BC，∴EC=EB ，在△OCE 和△OBE 中OC OB OE OE EC EB ⎧=⎪=⎨⎪=⎩，∴△OCE ≌△OBE ，∴∠OBE=∠OCE=90°，∴OB ⊥BE ，∴BE 与⊙O 相切；（2）解：设⊙O 的半径为r ，则OD=r ﹣1，在Rt △OBD 中，BD=CD=12BC=3， ∴（r ﹣1）2+（3）2=r 2，解得r=2， ∵tan ∠BOD=BD OD=3， ∴∠BOD=60°，∴∠BOC=2∠BOD=120°，在Rt △OBE 中，BE=3OB=23，∴阴影部分的面积=S 四边形OBEC ﹣S 扇形BOC=2S △OBE ﹣S 扇形BOC=2×12×2×23﹣21202360π⨯⨯343π． 考点：切线的判定与性质；扇形面积的计算．6.（2017湖北武汉第21题）如图，ABC ∆内接于O ，,AB AC CO =的延长线交AB 于点D ．（1）求证AO平分BAC∠；（2）若36,sin5BC BAC=∠=，求AC和CD的长．【答案】（1）证明见解析；（2）310；90 13.（2）过点C作CE⊥AB于E∵sin∠BAC=35,设AC=5m，则CE=3m∴AE=4m，BE=m在RtΔCBE中，m2+(3m)2=36∴m=3105，∴AC=310延长AO交BC于点H，则AH⊥BC，且BH=CH=3，过点O作OF⊥AH交AB于点F，∵∠HOC=∠BAC∴OH=4，OC=5 ∴AH=9∴tan∠BAH=1 3∴OF=13AO=53∵OF∥BC∴OF DOBC DC，即5DC-53=6DC∴DC=90 13.考点：1.全等三角形的判定与性质；2.解直角三角形；3.平行线分线段成比例.7.（2017湖南怀化第23题）如图，已知BC是O⊙的直径，点D为BC延长线上的一点，点A为圆上一点，且AB AD，AC CD.(1)求证：ACD BAD△∽△；(2)求证：AD是O⊙的切线.试题解析：（1）∵AB=AD，∴∠B=∠D，∵AC=CD，∴∠CAD=∠D，∴∠CAD=∠B，∵∠D=∠D，∴△ACD∽△BAD；（2）连接OA，∵OA=OB，∴∠B=∠OAB，∴∠OAB=∠CAD，∵BC是⊙O的直径，∴∠BAC=90°，∴OA⊥AD，∴AD是⊙O的切线．考点：相似三角形的判定与性质；切线的判定．11.（2017江苏盐城第25题）如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE平分∠BAC交边BC于点E，经过点A、D、E的圆的圆心F恰好在y轴上，⊙F与y轴相交于另一点G．（1）求证：BC是⊙F的切线；（2）若点A、D的坐标分别为A（0，-1），D（2，0），求⊙F的半径；（3）试探究线段AG、AD、CD三者之间满足的等量关系，并证明你的结论．【答案】（1）证明见解析；（2）⊙F的半径为52；（3）AG=AD+2CD．证明见解析.试题解析：（1）连接EF ，∵AE 平分∠BAC ，∴∠FAE=∠CAE ，∵FA=FE ，∴∠FAE=∠FEA ，∴∠FEA=∠EAC ，∴FE ∥AC ，∴∠FEB=∠C=90°，即BC 是⊙F 的切线；（2）连接FD ，设⊙F 的半径为r ，则r 2=（r-1）2+22，解得，r=52，即⊙F 的半径为52； （3）AG=AD+2CD ．证明：作FR ⊥AD 于R ，则∠FRC=90°，又∠FEC=∠C=90°，∴四边形RCEF 是矩形，∴EF=RC=RD+CD ，∵FR ⊥AD ，∴AR=RD ，∴EF=RD+CD=12AD+CD ， ∴AG=2FE=AD+2CD ．.考点：圆的综合题．13.（2017甘肃兰州第27题）如图，ABC △内接于O ⊙，BC 是O ⊙的直径，弦AF 交BC 于点E ，延长BC 到点D ，连接OA ，AD ，使得FAC AOD ∠∠，D BAF ∠∠.(1)求证：AD 是O ⊙的切线；(2)若O ⊙的半径为5，2CE ，求EF 的长.（1）由BC 是⊙O 的直径，得到∠BAF+∠FAC=90°，等量代换得到∠D+∠AOD=90°，于是得到结论；（2）连接BF ，根据相似三角形的判定和性质即可得到结论．（2）连接BF ，∴∠FAC=∠AOD ，∴△ACE ∽△DCA ， ∴AC AE CE OC OA AC==， ∴255ACAEAC ==，∴10，∵∠CAE=∠CBF ，∴△ACE ∽△BFE ，∴AE BE CE EF=，∴108EF=，∴EF=810．考点：切线的判定与性质；相似三角形的判定与性质．14.（2017贵州黔东南州第21题）如图，已知直线PT与⊙O相切于点T，直线PO与⊙O相交于A，B两点．（1）求证：PT2=PA•PB；（2）若PT=TB=3，求图中阴影部分的面积．（1）证明：连接OT．∵PT是⊙O的切线，∴PT⊥OT，∴∠PTO=90°，∴∠PTA+∠OTA=90°，∵AB是直径，∴∠ATB=90°，∴∠TAB+∠B=90°，∵OT=OA，∴∠OAT=∠OTA，∴∠PTA=∠B，∵∠P=∠P，∴△PTA∽△PBT，∴PT PA PB PT=，∴PT2=PA•PB．（2）∵TP=TB=3，∴∠P=∠B=∠PTA，∵∠TAB=∠P+∠PTA，∴∠TAB=2∠B，∵∠TAB+∠B=90°，∴∠TAB=60°，∠B=30°，∴tanB=3 ATTB=∴AT=1，∵OA=OT，∠TAO=60°，∴△AOT是等边三角形，∴S阴=S扇形OAT﹣S△AOT=22601331360464ππ⨯-⨯=-.考点：相似三角形的判定与性质；切线的性质；扇形面积的计算．16.（2017四川泸州第24题）如图，⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D，与边BC相交于点F，OA与CD相交于点E，连接FE并延长交AC边于点G．（1）求证：DF∥AO；（2）若AC=6，AB=10，求CG的长．【答案】（1）证明见解析；（2）2.（1）证明：连接OD．∵AB与⊙O相切与点D，又AC与⊙O相切与点，∴AC=AD，∵OC=OD，∴OA⊥CD，∴CD⊥OA，∵CF是直径，∴∠CDF=90°，∴DF⊥CD，∴DF∥AO．（2）过点作EM⊥OC于M，∵AC=6，AB=10，∴，∴AD=AC=6，∴BD=AB-AD=4，∵BD2=BF•BC，∴BF=2，∴CF=BC-BF=6．OC=12CF=3，∴，∵OC2=OE•OA，∴，∵EM∥AC，∴15 EM OM OEAC OC OA===，∴OM=35，EM=65，FM=OF+OM=185，∴3.6365 EM FMCG FC===，∴CG=53EM=2．考点：切线的性质．17.（2017四川宜宾第23题）如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE ⊥CD，垂足为点E．（1）求证：直线CE是⊙O的切线．（2）若BC=3，CD=32，求弦AD的长．（1）证明：连结OC，如图，∵AD平分∠EAC，∴∠1=∠3，∵OA=OD，∴∠1=∠2，∴∠3=∠2，∴OD∥AE，∵AE⊥DC，∴OD⊥CE，∴CE是⊙O的切线；（2）∵∠CDO=∠ADB=90°，∴∠2=∠CDB=∠1，∵∠C=∠C，∴△CDB∽△CAD，∴CD CB BD CA CD AD==，∴CD2=CB•CA，∴（22=3CA，∴CA=6，∴AB=CA﹣BC=3，32262BDAD==,设2，AD=2K，在Rt△ADB中，2k2+4k2=5，∴k=306，∴AD=303．考点：切线的判定与性质．18.（2017新疆建设兵团第22题）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB=30°，延长CB至点D，使得CB=BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：BE是⊙O的切线；（2）当BE=3时，求图中阴影部分的面积．【答案】（1）证明见解析；（2）333-22 ．（1）如图所示，连接BO，∵∠ACB=30°，∴∠OBC=∠OCB=30°，∵DE⊥AC，CB=BD，∴Rt△DCE中，BE=12CD=BC，∴∠BEC=∠BCE=30°，∴△BCE中，∠EBC=180°﹣∠BEC﹣∠BCE=120°，∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°，∴BE是⊙O的切线；（2）当BE=3时，BC=3，∵AC为⊙O的直径，∴∠ABC=90°，又∵∠ACB=30°，∴AB=tan30°×BC=3， ∴AC=2AB=23，AO=3，∴阴影部分的面积=半圆的面积﹣Rt △ABC 的面积=12π×AO 2﹣12AB ×BC=12π×3﹣12×3×3=333-22π． 考点：切线的判定与性质；扇形面积的计算．1. (2017北京第24题)如图，AB 是O 的一条弦，E 是AB 的中点，过点E 作EC OA ⊥于点C ，过点B 作O 的切线交CE 的延长线于点D .（1）求证：DB DE =；（2）若12,5AB BD ==，求O 的半径.（1）证明：∵DC ⊥OA, ∴∠1+∠3=90°, ∵BD 为切线，∴OB ⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2，∵∠3=∠4，∴∠4=∠5，在△DEB 中, ∠4=∠5，∴DE=DB.(2)作DF ⊥AB 于F,连接OE,∵DB=DE, ∴EF=12BE=3，在 RT △DEF 中，EF=3，DE=BD=5，EF=3 , ∴22534-=∴sin ∠DEF=DF DE = 45 , ∵∠AOE=∠DEF, ∴在RT △AOE 中，sin ∠AOE=45AE AO = , ∵AE=6, ∴AO=152. 考点：圆的性质，切线定理，三角形相似，三角函数2. (2017天津第21题)已知AB 是⊙O 的直径，AT 是⊙O 的切线，050=∠ABT ，BT 交⊙O 于点C ，E 是AB 上一点，延长CE 交⊙O 于点D .（1）如图①，求T ∠和CDB ∠的大小；（2）如图②，当BC BE =时，求CDO ∠的大小.：(1)如图，连接AC,21世纪教育网∵AB 是⊙O 的直径，AT 是⊙O 的切线，∴AT ⊥AB,即∠TAB=90°.∵050=∠ABT ，∴∠T=90°-∠ABT=40°由AB 是⊙O 的直径，得∠ACB=90°，∴∠CAB=90°-∠ABC=40°∴∠CDB=∠CAB=40°;（2）如图，连接AD,在△BCE 中，BE=BC ，∠EBC=50°，∴∠BCE=∠BEC=65°,∴∠BAD=∠BCD=65°∵OA=OD∴∠ODA=∠OAD=65°∵∠ADC=∠ABC=50°∴∠CDO=∠ODA-∠ADC=15°.3. (2017福建第21题)如图，四边形ABCD 内接于O ，AB 是O 的直径，点P 在CA 的延长线上，45CAD ∠=．（Ⅰ）若4AB =，求弧CD 的长；（Ⅱ）若弧BC =弧AD ，AD AP =，求证：PD 是O 的切线．（Ⅰ）连接OC ，OD ，∵∠COD=2∠CAD ，∠CAD=45°，∴∠COD=90°，∵AB=4，∴OC=12 AB=2，∴CD 的长=902180π⨯⨯ =π； （Ⅱ）∵BC =AD ，∴∠BOC=∠AOD ，∵∠COD=90°，∴∠AOD=1802COD ︒-∠ =45°，∵OA=OD ，∴∠ODA=∠OAD ，∵∠AOD+∠ODA+∠OAD=180°，∴∠ODA=1802AOD ︒-∠=67.5°，∵AD=AP ，∴∠ADP=∠APD ，∵∠CAD=∠ADP+∠APD ，∠CAD=45°，∴∠ADP=12∠CAD=22.5°，∴∠ODP=∠ODA+∠ADP=90°，又∵OD 是半径，∴PD 是⊙O 的切线.4. (2017河南第18题)如图，在ABC ∆中， AB AC =，以AB 为直径的⊙O 交AC 边于点D ，过点C 作//CF AB ，与过点B 的切线交于点F ，连接BD .（1）求证：BD BF =；（2）若10AB =，4CD =，求BC 的长.(1)∵AB AC =∴∠ABC=∠ACB∵//CF AB∴∠ABC=∠FCB∴∠ACB=∠FCB ，即CB 平分∠DCF∵AB 为⊙O 直径∴∠ADB=90°，即BD AC ⊥∵BF 为⊙O 的切线∴BF AB ⊥∵//CF AB∴BF CF ⊥∴BD=BF考点：圆的综合题.6. （2017湖南长沙第23题）如图，AB 与⊙O 相切于C ，OB OA ,分别交⊙O 于点E D ,，CD CE =．（1）求证：OB OA =；（2）已知34=AB ，4=OA ，求阴影部分的面积．【答案】（1）证明见解析（2）2=233S π-阴影试题解析：（1）连接OC ，则OC ⊥AB∵CD CE =∴∠AOC=∠BOC在△AOC 和△BOC 中，90AOC BOC OC OCOCA OCB ⎧∠=∠⎪=⎨⎪∠=∠=⎩∴△AOC ≌△BOC （ASA ） ∴AO=BO（2）由（1）可得AC=BC=12AB=3∴在Rt △AOC 中，OC=2∴∠AOC=∠BOC=60° ∴11==232=2322BOC S BC OC ⋅⨯△26022==3603S ππ⨯⨯扇形BOC ∴2==233BOC S S S π-△阴影扇形BOC考点：1、切线的性质，2、三角形的面积，3、扇形的面积7. （2017山东临沂第23题）如图，BAC ∠的平分线交ABC 的外接圆于点D ，ABC ∠的平分线交AD 于点E .（1）求证：DE DB =；（2）若90BAC ∠=︒，4BD =，求ABC 外接圆的半径.【试题解析：（1）AD 平分BAC ∠，BE 平分ABC ∠，,BAD CAD ABE CBE ∴∠=∠∠=∠，又BED ABE BAD ∠=∠+∠，DBE DBC CBE ∠=∠+∠，DBC DAC ∠=∠,BED DBE ∴∠=∠.DE DB ∴=.（2）解：连接CD ，90BAC ∠=，BC ∴是圆的直径.90BDC ∴∠=，90BDC ∴∠=.BAD CAD ∠=∠，BD CD ∴=，BD CD ∴=，BCD ∴∆是等腰直角三角形.4BD =，42BC ∴=.ABC ∴∆的外接圆的半径为22.考点：1、三角形的外接圆的性质，2、圆周角定理，3、三角形的外角性质，4、勾股定理8. (2017四川泸州第24题)如图，⊙O 与ABC Rt ∆的直角边AC 和斜边AB 分别相切于点;,D C 与边BC 相交于点F ,OA 与CD 相交于点E ，连接FE 并延长交AC 边于点G .（1）求证：DF //AO（2）若,10,6==AB AC 求CG 的长.（1）证明：AB 与⊙O 相切与点DBDF BCD ∠=∠∴ （弦切角定理）又AC 与⊙O 相切与点C由切线长定理得：;,DAO CAO AD AC ∠=∠=AO CD ⊥∴,;BDF DAO DAO CAO BCD ∠=∠∴∠=∠=∠∴ 即：DF//AO（2）：过点E 作OC EM ⊥与M88,622=-=∴==AC AB BC AB AC4,6=-=∴==AD AB BD AC AD∴由切割线定理得：BC BF BD ⋅=2,解得：;2=BF;321,6===-=∴FC OC BF BC FC 21世纪教育网 5322=+=∴OC AC OA 由射影定理得：553,2=⋅=OE OA OE OC 解之得： 235;5366.3;518;56,53;51==∴===∴=+===∴===∴EM CG FC FM CG EM OM OF FM EM OM OA OE OC OM AC EM 9. (2017山东滨州第23题)（本小题满分10分）如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D；连接BD，过点D作直线DM，使∠BDM＝∠DAC．（1）求证：直线DM是⊙O的切线；（2）求证：DE2＝DF·DA．【答案】详见解析.试题解析：证明：（1）如图1，连接DO，并延长交⊙O于点G，连接BG；∵点E是△ABC的内心，∴AD平分∠BAC，∴∠BAD＝∠DAC．21世纪教育网∵∠G＝∠BAD，∴∠MDB＝∠G，21世纪教育网∵DG为⊙O的直径，∴∠GBD＝90°，∴∠G＋∠BDG＝90°．∴∠MDB＋∠BDG＝90°．∴直线DM是⊙O的切线；（2）如图2，连接BE．∵点E是△ABC的内心，∴∠ABE＝∠CBE，∠BAD＝∠CAD．∵∠EBD＝∠CBE＋∠CBD，∠BED＝∠ABE＋∠BAD，∠CBD＝∠CAD．∴∠EBD＝∠BED，∴DB＝DE．∵∠CBD＝∠BAD，∠ADB＝∠ADB，∴△DBF∽△DAB，∴BD2＝DF·DA．∴DE2＝DF·DA．10. (2017辽宁沈阳第22题)如图，在ABC∆中，以BC为直径的O交AC于点E，过点E做EF AB⊥于点F，延长EF交CB的延长线于点G，且2ABG C∠=∠.（1）求证：EF是O的切线；（2）若3sin5EGC∠=，O的半径是3，求AF的长.【答案】（1）详见解析；（2）245.试题解析：(1)连接OE，则2EOG C∠=∠,∵2ABG C∠=∠∴ABG EOG∠=∠∴//AB OE∵EF AB⊥∴090AFE∠=∴090 GEO AFE∠=∠=∴OE EG⊥又∵OE是O的半径∴EF是O的切线；（2）∵2ABG C ∠=∠，∵ABG C A ∠=∠+∠∴C A ∠=∠∴BA=BC又O 的半径为3，∴OE=OB=OC∴BA=BC=2×3=6在Rt △OEG 中，sin ∠EGC=OE OG ，即335OG = ∴OG=5在Rt △FGB 中，sin ∠EGC=BF GB ，即352FB = ∴BF=65∴AF=AB-BF=6-65=245. 考点：圆的综合题.13. (2017山东菏泽第22题)如图，AB 是⊙O 的直径，PB 与⊙O 相切于点B ，连接PA 交⊙O 于点C .连接BC .（1）求证：CBP BAC ∠=∠；（2）求证：PA PC PB ⋅=2；（3）当3,6==CP AC 时，求PAB ∠sin 的值.【答案】(1)详见解析；（2）详见解析；（3）3.【解析】试题分析：（1）根据直径所对的圆周角为直角、切线的性质定理、同角的余角相等，即可证得CBP BAC ∠=∠；（2）先证△PB ∽C △ABP ，根据相似三角形的性质即可得结论； （3）利用PA PC PB ⋅=2，得33=PB ，从而求PAB ∠sin =3试题解析：【解】（1）∵AB 是⊙O 的直径∴∠ACB=90°∴∠A+∠ABC=90°∵PB 与⊙O 相切于点B∴∠CBP+∠ABC=90°∴CBP BAC ∠=∠(2)∵CBP BAC ∠=∠，∠P=∠P∴△PB ∽C △ABP∴BPPC AP PB = ∴PA PC PB ⋅=2（3）∵3,6==CP AC∴AP=9∵PA PC PB ⋅=2∴33=PB∴PAB ∠sin =3339==AP PB 14. (2017浙江金华第22题)如图，已知：AB 是O 的直径，点C 在O 上，CD 是O 的切线，AD CD ⊥于点,D E 是AB 延长线上的一点，CE 交O 于点F ，连接,OC AC ．(1)求证：AC 平分DAO ∠．(2)若105DAO ∠=，30E ∠=．①求OCE ∠的度数．②若O 的半径为22，求线段EF 的长．【答案】(1)详见解析；（2）①∠OCE=45°；②23-2.（1）解：∵直线与⊙O 相切，∴OC ⊥CD ；又∵AD ⊥CD,∴AD//OC,∴∠DAC=∠OCA;又∵OC=OA,∴∠OAC=∠OCA,∴∠DAC=∠OAC;∴AC 平分∠DAO.（2）解：①∵AD//OC ，∠DAO=105°,∴∠EOC=∠DAO=105°;∵∠E=30°,∴∠OCE=45°.②作OG ⊥CE 于点G,可得FG=CG,∵OC=22,∠OCE=45°.∴CG=OG=2,∴FG=2;∵在RT △OGE 中，∠E=30°，∴GE=23,∴EF=GE-FG=23-2.15. （2017浙江湖州第21题）（本小题8分）如图，O 为Rt C ∆AB 的直角边C A 上一点，以C O 为半径的O 与斜边AB 相切于点D ，交OA 于点E ．已知C 3B =C 3A =．（1）求D A 的长；（2）求图中阴影部分的面积．【答案】（132）6π （1）在Rt △ABC 中，22AC BC +223(3)+3∵BC ⊥OC∴BC 是⊙O 的切线∵AB 是⊙O 的切线∴3∴3（2）在Rt △ABC 中，sinA=31223BC AB == ∴∠A=30°∵AB 切⊙O 于点D∴OD ⊥AB∴∠AOD=90°-∠A=60° ∵tan =tan 30OD A AD = 33∴OD=1 ∴2601==3606S ππ⨯阴影 考点：1、切线的性质，2、勾股定理，3、解直角三角形，4、扇形的面积16. （2017浙江台州第22题） 如图，已知等腰直角三角形ABC ，点P 是斜边BC 上一点（不与,B C 重合），PE 是ABP ∆的外接圆⊙O 的直径.（1）求证：APE∆是等腰直角三角形；（2）若⊙O的直径为2，求22+的值.PC PB【答案】（1）证明见解析（2）4（1）证明：∵△ABC是等腰直角三角形，∴∠C=∠ABC=45°,∴∠PEA=∠ABC=45°又∵PE是⊙O的直径，∴∠PAE=90°,∴∠PEA=∠APE=45°,∴△APE是等腰直角三角形.（2）∵△ABC是等腰直角三角形，∴AC=AB,同理AP=AE,又∵∠CAB=∠PAE=90°,∴∠CAP=∠BAE,∴△CPA≌△BAE,∴CP=BE,在Rt△BPE中，∠PBE=90°,PE=2,∴PB2+BE2=PE2,∴CP2+PB2=PE2=4.考点：1、全等三角形的判定与性质，2、等腰三角形的判定与性质，3、勾股定理，4、圆心角、弧、弦的关系，5、等腰直角三角形14．（2017四川省南充市）如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F．（1）求证：DE是⊙O的切线；（2）若CF=2，DF=4，求⊙O直径的长．【答案】（1）证明见解析；（2）6．【解析】试题分析：（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案；（2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．试题解析：（1）如图，连接OD、CD．∵AC为⊙O的直径，∴△BCD是直角三角形，∵E为BC的中点，∴BE=CE=DE，∴∠CDE=∠DCE，∵OD=OC，∴∠ODC=∠OCD，∵∠ACB=90°，∴∠OCD+∠DCE=90°，∴∠ODC+∠CDE=90°，即OD⊥DE，∴DE是⊙O的切线；（2）设⊙O的半径为r，∵∠ODF=90°，∴OD2+DF2=OF2，即r2+42=（r+2）2，解得：r=3，∴⊙O的直径为6．考点：切线的判定与性质．15．（2017四川省广安市）如图，已知AB是⊙O的直径，弦CD与直径AB相交于点F．点E在⊙O外，做直线AE，且∠EAC=∠D．（1）求证：直线AE是⊙O的切线．（2）若∠BAC=30°，BC=4，cos∠BAD=34，CF=103，求BF的长．【答案】（1）证明见解析；（2）521．（1）连接BD，∵AB是⊙O的直径，∴∠ADB=90°，即∠ADC+∠CDB=90°，∵∠EAC=∠ADC，∠CDB=∠BAC，∴∠EAC+∠BAC=90°，即∠BAE=90°，∴直线AE是⊙O的切线；（2）∵AB 是⊙O 的直径，∴∠ACB=90°，Rt △ACB 中，∠BAC=30°，∴AB=2BC=2×4=8，由勾股定理得：AC=2284-=43，Rt △ADB 中，cos ∠BAD=34=AD AB ，∴34=8AD ，∴AD=6，∴BD=2286- =27，∵∠BDC=∠BAC ，∠DFB=∠AFC ，∴△DFB ∽△AFC ，∴BF BD FC AC =，∴2710433BF =，∴BF=5219．考点：1．切线的判定与性质；2．解直角三角形．。
2018年中考数学专题练习圆周角定理(含解析)-文档资料
2019中考数学专题练习-圆周角定理（含解析）、单选题1•如图，AB 是00的直径，弦CDO AB O CAB=40°连接BD, OD,则O AOD+O AB 的度数为（）CA.100 ° B.110 °C.120°D.150 2•已知A 、C B 是OO 上三点，若 O AOC=4,则O ABC 勺度数是（） A. 10 °B.20 °C.40 °3. 如图，OO 是O ABC 勺外接圆，O OCB=4,则OA 的度数等于（） A. 60°B.50°C.40°4. 如图，已知 EF 是OO 的直径，把 OA 为60。
的直角三角板 ABC 的一条直角边 BC 放在直线 EF 上，斜边AB 与OO 交于点P ,点B 与点O 重合•将三角板 ABC 沿OE 方向平移，使得点 B 与A. 30 < x < 60B. 30 < x w 90C. 30 w x w 120D. 60 w x w 120O BOC=100°则圆周角O BAC勺大小是（）点E 重合为止.设O PO R x°,则x 的取值范围是 B.100°C.130D. 200D.80D.306.下列各命题正确的是A.若两弧相等，则两弧所对圆周角相等B.有一组对边平行的四边形是梯形•C.垂直于弦的直线必过圆心D.有一边上的中线等于这边一半的三角形是直角三角形•7•某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为画一个直径为10的圆，把刻度尺CA的0刻度固定在半圆的圆心旋转•从图中所示的图尺可读出sin O AO的值是（）10.如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF则以AC和BC的11.如图，AB是O勺直径，点C是半径OA的中点，过点C作DE O AB交O于点D, E两点,1的半圆形量角器中，O处，刻度尺可以绕点OA.乙填空题B.7C.4D.则OA的度数为z SAC = ，则上£＞的大小是____________________ 度长为两根的一元二次方程是PC切O0于C.若OP=4409•如图，.山是半圆的直径,过点D 作直径DF ,连结AF ,贝U O DEA= ________ 。
中考专题复习——圆的相关证明(附答案)
中考复习专题——圆的相关证明题1．在⊙O 中，AB 为直径，C 为⊙O 上一点．（Ⅰ）如图①，过点C 作⊙O 的切线，与AB 的延长线相交于点P ，若P ∠︒=42，求∠CAB 的大小； （Ⅱ）如图②，D 为上一点，且OD 经过AC 的中点E ，连接DC 并延长，与AB 的延长线相交于点P ， 若∠CAB ︒=10，求∠P 的大小．2.已知AB 是⊙O 的直径，C 是⊙O 上一点，过点C 作⊙O 的切线，交AB 的延长线于点P ．（Ⅰ）如图①，连接AC ，BC ，若OB BP =，求A ∠和∠P 的大小；（Ⅱ）如图②，过点P 作⊙O 的切线PD ，切点为D ，连接CD ，BD ，若∠BDC ＝32°，求BDP ∠的大小．图①图②O B COB D CPE AC3.已知点A ，B ，C 是⊙O 上的三个点，︒=∠120AOB . （Ⅰ）如图①，若AC =BC ，求C ∠和CAO ∠的大小；（Ⅱ）如图②，过点C 作⊙O 的切线，交BA 的延长线于点D ，若AC =AD ，求CAO ∠的大小.4.已知AB 为⊙O 的直径，C 为⊙O 上一点，AD 和过点C 的切线互相垂直，垂足为D ，AD 交⊙O 于点E ．（Ⅰ）如图①，求证：AC 平分DAB ∠；（Ⅱ）如图②，过B 作BF AD ∥交⊙O 于点F ，连接CF ，若45AC =4DC =，求CF 和⊙O 半径的长． ABCDEO图①ABCDEO图②F5.已知，△DBC内接于⊙O，DB＝DC．（Ⅰ）如图①，过点B作射线BE交⊙O于点A，若∠EAD＝75°，求∠BDC的度数．（Ⅱ）如图②，分别过点B、点D作⊙O的切线相交于点E，若∠E=30°，求∠BDC的度数.①②6.已知P A，PB分别与⊙O相切于点A,B，PO交⊙O于点F，且其延长线交⊙O于点C，∠BCP=28°，E为CF上一点，延长BE交⊙O于点D.（Ⅰ）如图1，求∠CDB与∠APB的大小；（Ⅱ）如图2，当BC=CE时，求∠PBE的大小.7.在ABC △中90B ∠=︒D 为AC 上一点，以CD 为直径的⊙O 与AB 相切于点E ，与BC 相交于点F ，连接CE ．（Ⅰ）如图①，若27ACE ∠=︒，求A ∠和ECB ∠的大小； （Ⅱ）如图②，连接EF ，若//EF AC ，求A ∠的大小．8. 已知：在⊙O 中OA BC ⊥垂足为E ，点D 在⊙O 上．（Ⅰ）如图①若50AOB ∠=︒，求ADC ∠和∠CAO 的大小；（Ⅱ）如图②CD ∥AO ，过点D 作⊙O 的切线，与BC 的延长线相交于点P ，若26∠=︒ABC 求∠P 的大小．图①图②ABCF OED ABCOED F 图①O EDCBA图②POE DCBA9.如图，在⊙O 中，直径AB 与弦CD 相交于点E ，58ABC ∠=︒. （Ⅰ）如图①若85AEC ∠=︒，求BAD ∠和CDB ∠的大小；（Ⅱ）如图②若CD AB ⊥过点D 作⊙O 的切线DF ，与AB 的延长线相交于点F ，求F ∠的大小．10. 已知AB 是⊙O 的直径，CD 、CB 是⊙O 的弦，且AB CD ∥.（Ⅰ）如图①若25ABC ∠=︒，求BAC ∠和ODC ∠的大小；（Ⅱ）如图②过点C 作⊙O 的切线，与BA 的延长线交于点F 若OD CF ∥求ABC ∠的大小．图①图②EABO DCFE ABO DC图②图①11. 如图，⊙O 是△ABC 的外接圆，AE 切⊙O 于点A ，AE 与直径BD 的延长线相交于点E ．（Ⅰ）如图①，若∠C =71°，求∠E 的大小；（Ⅱ）如图②，当AE =AB ，DE =2时，求∠E 的大小和⊙O 的半径．12. 已知DA 、DC 分别与⊙O 相切于点A 点C ，延长DC 交直径AE 的延长线于点P ． （Ⅰ）如图①若DC =PC ，求∠P 的度数；（Ⅱ）如图②在⊙O 上取一点B ，连接AB 、BC 、BE ，当四边形ABCD 是平行四边形时，求∠P 及∠AEB 的大小． OEEDCBAD O C BA图①图②DECAPOB图① 图②ECAPOD13.如图①，AB 是⊙O 的弦，OE ⊥AB ，垂足为P ，交AB 于点E ，且OP =3PE ，AB =74．（Ⅰ）求⊙O 的半径；（Ⅱ）如图②过点E 作⊙O 的切线CD ，连接OB 并延长与该切线交于点D ，延长OA 交CD 于C ，求OC 的长． 图②图①EP A BCODP EOBA参考答案1.解：（Ⅰ）如图，连接OC∵ ⊙O 与PC 相切于点C ∴ OC PC ⊥，即90OCP ∠=︒ ∵ 42P ∠=︒∴ 9048COB P ∠=︒-∠=︒ 在Rt OPC △中，48CAB ACO COP ∠+∠=∠=︒ ∵OA =OC ∴∠CAB =∠ACO ∴ 24CAB ∠=︒（Ⅱ）∵ E 为AC 的中点∴ OD AC ⊥，即90AEO ∠=︒在Rt AOE △中，由10EAO ∠=︒得9080AOE EAO ∠=︒-∠=︒ ∴ 1402ACD AOD ∠=∠=︒∵ ACD ∠是ACP △的一个外角∴ 30P ACD CAP ∠=∠-∠=︒2. 解：（Ⅰ）如图①连接OC ∵PC 是⊙O 的切线∴︒=∠90OCP ∵OB BP =∴OB BC =∵OC OB =∴BOC ∆为等边三角形， ∴∠BOC=60° ∴︒=∠=∠3021BOC A ∠P=90°－∠COB ＝30°（Ⅱ）如图② 连接OC 、OD 设CD 交OP 于点E∵PC ，PD 是⊙O 的切线∴PD PC = ︒=∠=∠90ODP OCP ∵OD OC =∴OP 为CD 的垂直平分线 ∴︒=∠=∠90DEP CEP∵∠BDC ＝32°∴∠OBD ＝90°－∠BDC ＝58° ∵OB OD =∴∠ODB ＝∠OBD ＝58° ∴∠BDP ＝90°－58°＝32°3.解： （Ⅰ）∵︒=∠120AOB ∴∠ACB= 12 ∠AOB=60°如图① 连接OC∵AC =BC ∴∠AOC=∠BOC∵∠AOC+∠BOC +∠AOB=360° ∴∠AOC =12 （360°-120°）=120° ∵OA OC ∴∠CAO=∠ACO=12（180°-120°）=30°O AB PCOAB D CPE（Ⅱ）如图② 连接OC设∠ACD= x ∵ACAD ∴∠ACD =∠ADC= x∴∠CAB=2x ∵∠AOB=120°OAOB ∴∠OAB =∠OBA= 12（180°-120°）=30°∵CD 是⊙O 的切线∴∠OCD=90° ∵OAOC ∴∠OCA =∠OAC∴90°－x=2x －30° 解得x=40° ∴∠CAB=80°∴∠CAO=∠CAB －∠OAB =50°4.（Ⅰ）证明：连接OC ∵CD 为⊙的切线∴OC CD ⊥即90OCM OCD ∠=∠=︒ ∵AD CD ⊥垂足为D ∴90ADC ∠=︒ ∵90ADC OCM ∠=∠=︒∴OC AD ∥ ∴DAC ACO ∠=∠∵OC OA =∴CAO ACO ∠=∠∴DAC CAO ∠=∠∴AC 平分DAB ∠ （Ⅱ）解：连接AF 延长CO 交AF 于G ∵AB 为⊙的直径 ∴=90AFB ∠︒ ∵OC AD BF AD ∥，∥ ∴CO BF ∥∴90AFB AGC ∠=∠=︒ ∴OC AF ⊥由垂径定理可得AC=CF∴45AC CF == ∵90ADC ∠=︒22O O ABC DEOF GABCDEOM∴90ADC DCO AGC ∠=∠=∠=︒ ∴四边形ADCG 是矩形∴8AD CG == 4CD AG == 在Rt AGO 中，得222AG OG AO += 设OC x =则,8OA x OG x ==- 可得方程()22248x x +-=解得5x =． ∴⊙半径的长为545CF =．5.（Ⅰ）解：∵四边形ABCD 是⊙O 的内接四边形∴∠DAB +∠C ＝180° ∵∠EAD +∠DAB ＝180° ∴∠C ＝∠EAD ∵∠EAD ＝75° ∴∠C ＝75° ∵DB ＝DC∴∠DBC ＝∠C ＝75°∴∠BDC ＝180°﹣∠C ﹣∠DBC ＝30°（Ⅱ）解：连结OB OD∵EB ED 与⊙O 相切于点B 点D∴ED OD ⊥⊥，EB OB ∴ ︒=∠︒=∠90ODE 90，OBE∵︒=∠+∠+∠+∠360BOD ODE E OBE ︒=∠30E ∴︒=∠150BOD∴︒=∠=∠7521BOD C ∵DB ＝DC ，∴∠DBC ＝∠C ＝75°，∴∠BDC ＝180°﹣∠C ﹣∠DBC ＝30° O6. （I ）解：连接OB∵P A 、PB 与圆O 相切于点A 点,B∴PO 平分∠APB 且∠PBO ＝90° ∵∠BCP ＝28°∴∠BOP ＝2∠BCP ＝28°×2＝56° ∴∠BPO ＝90°－∠BOP ＝90°－56°＝34° ∴∠APB ＝2∠BPO ＝2×34°＝68°又∠BDC ＝BOC ∠21＝)180(21BOP ∠- ∴∠BDC = 62)56180(21=-∴∠APB =68°∠BDC= 62 （II ）连接OB∵BC ＝CE ∴∠CBE ＝∠CEB∵∠BCP ＝28° ∴∠CBE ＝76228180=-∵OB ＝OC ∴∠OBC ＝∠OCB ＝28° ∴∠EBO ＝∠CBE －∠OBC ＝76°－28°＝48° ∵P A 与圆O 相切于点A∴OB ⊥PB ∴∠PBO ＝90°∴∠PBE ＝90°－ ∠EBO ＝90°－48°＝42°7.解：（Ⅰ）如图连接OE ．∵ AB 与⊙O 相切∴ OE AB ⊥，即90AEO ∠=︒ ∵ 27ACE ∠=︒∴ 254AOE ACE ∠=∠=︒ ∴ 9036A AOE ∠=︒-∠=︒ ∵ OE OC =∴ OEC OCE ∠=∠∵ 90B ∠=︒∴ //OE BC ∴ ECB OEC ∠=∠ ∴ 27ECB ∠=︒ （Ⅱ）如图，连接OE OF∵ //OE BC //EF AC ∴ 四边形OEFC 为平行四边形 ∴ OE CF = ∴ OC OF CF == ∴ 60ACB ∠=︒∴ 9030A ACB ∠=︒-∠=︒ABCOED F ABCF OED8. 解：（Ⅰ）∵OA BC ⊥ ∴AB AC = 90∠=︒AEC∴∠=∠ACB ADC ∵1252∠=∠=︒ACB AOB∴25∠=∠=︒ADC ACB9065∠=︒-∠=︒CAO ACB（Ⅱ）连接BD . 由OA BC ⊥知，90∠=∠=︒AEB BEO∴ 9064∠=︒-∠=︒OAB ABC ∵AO ∥CD ∴90∠=∠=︒BCD BEO ∴BD 是⊙O 的直径又PD 与⊙O 相切∴⊥BD PD . 即90∠=︒BDP∵=OA OB ∴64∠=∠=︒OBA OAB∴642636∠=∠-∠=︒-︒=︒CBD ABO ABC ∴9052∠=︒-∠=︒P CBD9. （Ⅰ）∵∠AEC 是ΔBEC 的一个外角 58ABC ∠=︒85AEC ∠=︒27C AEC ABC ∴∠=∠-∠=︒∵在⊙O 中BAD C ∠=∠27BAD ∴∠=︒ AB 为⊙O 的直径90ADB ∴∠=︒ ∵在⊙O 中58ADC ABC ∠=∠=︒ 又CDB ADB ADC ∠=∠-∠32CDB ∴∠=︒（Ⅱ）连接OD∵CD ⊥AB 90CEB ∴∠=︒．9032E E CB BC =-∴∠=∠︒︒∴264DOB DCB ∠=∠=︒ ∵DF 是⊙O 的切线∴90ODF ∠=︒90906426F DOB ∴∠=︒-∠=︒-︒=︒图②POE DCBA图①O E DCBA10. 解：（Ⅰ）如图连接OC ∵ AB 是⊙O 的直径 ∴ 90ACB ∠=︒∴ 90BAC ABC ∠+∠=︒由25ABC ∠=︒得65BAC ∠=︒又AB CD ∥得25ABC BCD ∠=∠=︒ ∵ OB OC = ∴ 25OCB ABC ∠==∠=︒ 则50OCD OCB BCD ∠=∠+∠=︒ 由OC OD =得50ODC OCD ∠=∠=︒（Ⅱ）如图，连接OC∵CF 切⊙O 于点C ∴OC FC ⊥则90OCF ∠=︒∵ OD CF ∥ ∴ 90DOC OCF ∠=∠=︒ 又OC OD =则45ODC OCD ∠==∠=︒ 由AB CD ∥得45BOD ODC ∠=∠=︒∴135BOC DOC BOD ∠=∠+∠=︒ ∵ OC OB = ∴22.5ABC OCB ∠=∠=︒11. 解：（Ⅰ）连接OA .∵AE 切⊙O 于点A ∴OA ⊥AE ，∴∠OAE =90° ∵∠C =71° ∴∠AOB =2∠C =2×71°=142° 又∵∠AOB +∠AOE =180° ∴∠AOE =38° ∵∠AOE +∠E =90° ∴∠E =90°﹣38°=52° （Ⅱ）连接OA 设∠E = x .∵AB =AE ∴∠ABE =∠E = x ∵OA =OB ∴∠OAB =∠ABO = x ∴∠AOE =∠ABO +∠BAO =2x∵AE 是⊙O 的切线∴OA ⊥AE ，即∠OAE =90°在△OAE 中∠AOE +∠E =90°即2x +x =90°解得30x =︒∴∠E =30° 在Rt △OAE 中OA =21OE∵OA =OD ∴OA =OD =DE∵DE =2∴OA =2即⊙O 的半径为212.解：（Ⅰ）∵DA 、DC 是⊙O 的切线 ∴DA ＝DC OA ⊥DA ∴∠DAO ＝90°∵DC =PC ∴DA ＝DC =PC ∵∠DAP ＝90° ∴sin P=DP AD =21∴∠P=30° （Ⅱ）连接OC 、AC∵DA ，DC 是⊙O 的切线 ∴DA ＝DC∵四边形ABCD 是平行四边形∴□ABCD 是菱形 ∴DA =DC =CB =AB ∠ABC =∠ADC ∵∠AOC =2∠ABC ∴∠AOC =2∠ADC∵DA 、DC 是⊙O 的切线∴OA ⊥AD OC ⊥DC ∴∠DAO ＝∠DCO ＝90°∵∠ADC +∠DCO+∠AOC +∠DAO =360° ∴∠ADC +∠AOC =180°∴3∠ADC ＝180°∴∠ADC ＝60°∴∠P ＝90°－∠ADC ＝30°，∠ABC =60°又AB =BC ∴△ABC 是等边三角形 ∴∠ACB ＝60° ∴∠AEB ＝∠ACB=60°13. 解：（Ⅰ）∵OE ⊥AB∴1272APAB 设PE =x 则OP =3x OA =OE =4x在Rt OAP △中222OA OP AP =+即2216928x x =+ 解得x =2（负舍）∴4x =8 ∴半径OA 为8 （Ⅱ）∵ CD 为⊙O 的切线 ∴OE ⊥CD又∵OE ⊥AB ∴AB //CD ∴34OA OP OCOE∴323OCECAPODB。
初三数学专题02 圆的证明与计算题研究(含答案)
专题二：圆的证明与计算题研究【题型导引】题型一：与圆的性质有关的证明与计算（1）与圆内三角形、四边形为背景研究形状及其线段、周长面积等问题；（2）圆内多边形关于角的问题；（3）已知圆内特殊三角形背景下线段的长度计算等。
题型二：与圆的切线有关的证明与计算（1）已知圆的切线与特殊三角形的关系，计算半径、线段等问题；（2）已知圆与特殊三角形相关条件判定圆的切线及其线段计算等问题；（3）已知圆与特殊四边形相关条件判定圆的切线及其线段计算等问题。
题型三：与扇形、弧长等有关的计算（1）根据圆的性质及其相关条件进行计算弧长、扇形面积等问题；（2）根据圆的性质及其相关条件进行计算圆锥等问题； 【典例解析】类型一：与圆的性质有关的证明与计算例题1：（2019•湖北省荆门市•10分）已知锐角△ABC 的外接圆圆心为O ，半径为R ． （1）求证：sin ACB＝2R ； （2）若△ABC 中∠A ＝45°，∠B ＝60°，AC ＝3，求BC 的长及sin C 的值．【解答】解：（1）如图1，连接AO 并延长交⊙O 于D ，连接CD ， 则∠CD ＝90°，∠ABC ＝∠ADC ， ∵sin ∠ABC ＝sin ∠ADC ＝AC AD ＝2ACR∴sin ACB＝2R ； （2）∵sin ACB＝2R ，同理可得：sin AC B －sin AB C ＝sin BCA＝2R ，∴2R ＝3sin 60︒＝2，∴BC ＝2R •sin A ＝2sin45°＝2， 如图2，过C 作CE ⊥AB 于E ， ∴BE ＝BC •cos B ＝2cos60°＝22，AE ＝AC •cos45°＝62， ∴AB ＝AE ＋BE ＝622+， ∵AB ＝AR •sin C ，∴sin C ＝＝624+．技法归纳：圆的性质综合运用题中，经常用到的重要性质及技法：①运用圆是轴对称图形也是中心对称图形可以对相关结论作合理的猜测；②利用垂径定理，通过在由半弦、半径、弦心距组成的直角三角形，运用勾股定理或锐角三角函数进行计算；③在同圆或等圆中，圆心角、弧、弦、弦心距等量对等量关系，可以转化相等关系；④由直径所对的圆周角是直角构造直角三角形；⑤相似三角形、锐角三角函数、勾股定理是计算线段长度及其线段数量关系的重要手段． 类型二：与圆的位置关系有关的证明与计算例题2：(2018·娄底中考)如图，C ，D 是以AB 为直径的⊙O 上的点，AC ︵＝BC ︵，弦CD 交AB 于点E . (1)当PB 是⊙O 的切线时， 求证：∠PBD ＝∠DAB ； (2)求证：BC 2－CE 2＝CE ·DE ；(3)已知OA ＝4，E 是半径OA 的中点，求线段DE 的长．【解析】 (1)∵AB 是⊙O 的直径， ∴∠ADB ＝90°，∴∠BAD ＋∠ABD ＝90°. ∵PB 是⊙O 的切线，∴∠ABP ＝90°，∴∠PBD ＋∠ABD ＝90°， ∴∠BAD ＝∠PBD .(2)∵∠A ＝∠DCB ，∠AED ＝∠CEB ， ∴△ADE ∽△CBE ， ∴DE BE ＝AECE，即DE ·CE ＝AE ·BE . 如图，连接OC .设圆的半径为r ， 则OA ＝OB ＝OC ＝r ，则DE ·CE ＝AE ·BE ＝(OA －OE )(OB ＋OE )＝r 2－OE 2. ∵AC ︵＝BC ︵，∴∠AOC ＝∠BOC ＝90°， ∴CE 2＝OE 2＋OC 2＝OE 2＋r 2， BC 2＝BO 2＋CO 2＝2r 2，则BC 2－CE 2＝2r 2－(OE 2＋r 2)＝r 2－OE 2， ∴BC 2－CE 2＝DE ·CE .(3)∵OA ＝4，∴OB ＝OC ＝OA ＝4， ∴BC ＝OB 2＋OC 2＝4 2. 又∵E 是半径OA 的中点， ∴AE ＝OE ＝2，则CE ＝OC 2＋OE 2＝42＋22＝2 5. ∵BC 2－CE 2＝DE ·CE ， ∴(42)2－(25)2＝DE ·25，解得DE ＝655.技法归纳：与切线有关的证明与计算，最常用的辅助线是连接经过切点的半径，利用直径构造直角三角形，利用圆周角相等转移角的位置等．运用三角形全等、三角形相似、勾股定理、锐角三角函数等知识进行证明与计算．类型三：与扇形面积有关的证明与计算例题3：（2019•湖北武汉•8分）已知AB 是⊙O 的直径，AM 和BN 是⊙O 的两条切线，DC 与⊙O 相切于点E ，分别交AM 、BN 于D .C 两点． （1）如图1，求证：AB 2＝4AD •BC ；（2）如图2，连接OE 并延长交AM 于点F ，连接CF ．若∠ADE ＝2∠OFC ，AD ＝1，求图中阴影部分的面积．【解答】（1）证明：连接OC .OD ，如图1所示： ∵AM 和BN 是它的两条切线， ∴AM ⊥AB ，BN ⊥AB ， ∴AM ∥BN ，∴∠ADE ＋∠BCE ＝180° ∵DC 切⊙O 于E ， ∴∠ODE ＝12∠ADE ，∠OCE ＝12∠BCE ， ∴∠ODE ＋∠OCE ＝90°， ∴∠DOC ＝90°， ∴∠AOD ＋∠COB ＝90°， ∵∠AOD ＋∠ADO ＝90°， ∴∠AOD ＝∠OCB ， ∵∠OAD ＝∠OBC ＝90°， ∴△AOD ∽△BCO ，∴AD OA BO BC=,∴OA2＝AD•BC，∴（12AB）2＝AD•BC，∴AB2＝4AD•BC；（2）解：连接OD，OC，如图2所示：∵∠ADE＝2∠OFC，∴∠ADO＝∠OFC，∵∠ADO＝∠BOC，∠BOC＝∠FOC，∴∠OFC＝∠FOC，∴CF＝OC，∴CD垂直平分OF，∴OD＝DF，在△COD和△CFD中，，∴△COD≌△CFD（SSS），∴∠CDO＝∠CDF，∵∠ODA＋∠CDO＋∠CDF＝180°，∴∠ODA＝60°＝∠BOC，∴∠BOE＝120°，在Rt△DAO，AD 3 OA，Rt△BOC中，BC3OB，∴AD：BC＝1：3，∵AD＝1，∴BC＝3，OB3∴图中阴影部分的面积＝2S△OBC﹣S扇形OBE＝2×12×332120(3)π⨯3π．技法归纳：求与圆有关的阴影部分的面积时，常常是通过把不规则图形的面积，用扇形的面积和三角形的面积的和差来解决．特别地，对于旋转图形，要利用旋转的性质，确定旋转的中心(扇形的圆心)和旋转半径(相应的线段)的位置的变化，常常运用三角形全等进行面积的割补．【变式训练】1. 如图所示，在△ABC中，AB＝AC，其内切圆⊙O与边BC，AC，AB分别切于点D，E，F.(1)求证：BF＝CE；(2)若∠ACB＝30°，CE＝2 3，求AC的长．【解析】：(1)证明：连结AO并延长，∵AB＝AC，∴AO的延长线交BC于切点D，则BD＝CD.又由切线长定理，得BF＝BD，CD＝CE，∴BF＝CE.(2)∵CE＝2 3，∴CD＝2 3.又∵AD⊥BC，∴∠ADC＝90°.又∵∠ACB＝30°，∴AC＝CDcos∠ACB＝2 3cos30°＝2 332＝4.2. （2019•黑龙江省齐齐哈尔市•8分）如图，以△ABC的边BC为直径作⊙O，点A在⊙O上，点D在线段BC的延长线上，AD＝AB，∠D＝30°．（1）求证：直线AD是⊙O的切线；（2）若直径BC＝4，求图中阴影部分的面积．【解答】（1）证明：连接OA，则∠COA＝2∠B，∵AD＝AB，∴∠B＝∠D＝30°，∴∠COA＝60°，∴∠OAD＝180°﹣60°﹣30°＝90°，∴OA⊥AD，即CD是⊙O的切线；（2）解：∵BC＝4，∴OA＝OC＝2，在Rt△OAD中，OA＝2，∠D＝30°，∴OD＝2OA＝4，AD＝2，所以S△OAD＝OA•AD＝×2×2＝2，因为∠COA＝60°，所以S扇形COA＝＝π，所以S阴影＝S△OAD﹣S扇形COA＝2﹣．3. （2018辽宁抚顺）如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，点D为⊙O上一点，且CD ＝CB、连接DO并延长交CB的延长线于点E．（1）判断直线CD与⊙O的位置关系，并说明理由；（2）若BE＝4，DE＝8，求AC的长．【解答】（1）证明：连接O C．∵CB ＝CD ，CO ＝CO ，OB ＝OD ， ∴△OCB ≌△OCD ， ∴∠ODC ＝∠OBC ＝90°， ∴OD ⊥DC ， ∴DC 是⊙O 的切线． （2）解：设⊙O 的半径为r ． 在Rt △OBE 中，∵OE 2＝EB 2＋OB 2， ∴（8﹣r ）2＝r 2＋42， ∴r ＝3， ∵tan ∠E ＝＝，∴＝，∴CD ＝BC ＝6， 在Rt △ABC 中，AC ＝22AB BC +＝ 2266+＝62．4. （2019•甘肃庆阳•8分）已知：在△ABC 中，AB ＝A C ．（1）求作：△ABC 的外接圆．（要求：尺规作图，保留作图痕迹，不写作法） （2）若△ABC 的外接圆的圆心O 到BC 边的距离为4，BC ＝6，则S ⊙O ＝ ．【解答】解：（1）如图⊙O 即为所求．（2）设线段BC 的垂直平分线交BC 于点E ． 由题意OE ＝4，BE ＝EC ＝3， 在Rt △OBE 中，OB ＝2234 ＝5， ∴S 圆O ＝π•52＝25π． 故答案为25π．5. （2018云南昆明）如图，AB 是⊙O 的直径，ED 切⊙O 于点C ，AD 交⊙O 于点F ，∠AC 平分∠BAD ，连接BF ．（1）求证：AD ⊥ED ；（2）若CD ＝4，AF ＝2，求⊙O 的半径．【解答】（1）证明：连接OC ，如图， ∵AC 平分∠BAD ， ∴∠1＝∠2， ∵OA ＝OC ， ∴∠1＝∠3， ∴∠2＝∠3， ∴OC ∥AD ，∵ED 切⊙O 于点C ， ∴OC ⊥DE ， ∴AD ⊥ED ；（2）解：OC 交BF 于H ，如图， ∵AB 为直径， ∴∠AFB ＝90°，易得四边形CDFH 为矩形， ∴FH ＝CD ＝4，∠CHF ＝90°， ∴OH ⊥BF ， ∴BH ＝FH ＝4， ∴BF ＝8，在Rt △ABF 中，AB ＝ 22AF BF +＝ 2228+＝217，∴⊙O 的半径为17．6. （2019•四川省凉山州•8分）如图，点D 是以AB 为直径的⊙O 上一点，过点B 作⊙O 的切线，交AD 的延长线于点C ，E 是BC 的中点，连接DE 并延长与AB 的延长线交于点F ． （1）求证：DF 是⊙O 的切线； （2）若OB ＝BF ，EF ＝4，求AD 的长．【解答】解：（1）如图，连接OD ，BD ， ∵AB 为⊙O 的直径， ∴∠ADB ＝∠BDC ＝90°，在Rt△BDC中，∵BE＝EC，∴DE＝EC＝BE，∴∠1＝∠3，∵BC是⊙O的切线，∴∠3＋∠4＝90°，∴∠1＋∠4＝90°，又∵∠2＝∠4，∴∠1＋∠2＝90°，∴DF为⊙O的切线；（2）∵OB＝BF，∴OF＝2OD，∴∠F＝30°，∵∠FBE＝90°，∴BE＝EF＝2，∴DE＝BE＝2，∴DF＝6，∵∠F＝30°，∠ODF＝90°，∴∠FOD＝60°，∵OD＝OA，∴∠A＝∠ADO＝BOD＝30°，∴∠A＝∠F，∴AD＝DF＝6．7. （2019•山东省德州市•12分）如图，∠BPD＝120°，点A.C分别在射线PB.PD上，∠P AC＝30°，AC ＝3．（1）用尺规在图中作一段劣弧，使得它在A.C两点分别与射线PB和PD相切．要求：写出作法，并保留作图痕迹；（2）根据（1）的作法，结合已有条件，请写出已知和求证，并证明；（3）求所得的劣弧与线段P A .PC 围成的封闭图形的面积．【解答】解：（1）如图，（2）已知：如图，∠BPD ＝120°，点A .C 分别在射线PB .PD 上，∠P AC ＝30°，AC ＝3过A .C 分别作PB .PD 的垂线，它们相交于O ，以OA 为半径作⊙O ，OA ⊥PB ，求证：PB .PC 为⊙O 的切线；证明：∵∠BPD ＝120°，P AC ＝30°，∴∠PCA ＝30°，∴P A ＝PC ，连接OP ，∵OA ⊥P A ，PC ⊥OC ，∴∠P AO ＝∠PCO ＝90°，∵OP ＝OP ，∴Rt △P AO ≌Rt △PCO （HL ）∴OA ＝OC ，∴PB .PC 为⊙O 的切线；（3）∵∠OAP ＝∠OCP ＝90°﹣30°＝60°，∴△OAC 为等边三角形，∴OA ＝AC ＝3AOC ＝60°，∵OP 平分∠APC ，∴∠APO ＝60°，∴AP 33＝2，∴劣弧AC 与线段P A .PC 围成的封闭图形的面积＝S 四边形APCO ﹣S 形AOC ＝2×12×3×2260(23)360＝3﹣2π．8. （2019湖北省鄂州市）（10分）如图，P A是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O 于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC，P B．（1）求证：PB是⊙O的切线；（2）求证：E为△P AB的内心；（3）若cos∠P AB＝1010，BC＝1，求PO的长．【解答】（1）证明：连结OB，∵AC为⊙O的直径，∴∠ABC＝90°，∵AB⊥PO，∴PO∥BC∴∠AOP＝∠C，∠POB＝∠OBC，OB＝OC，∴∠OBC＝∠C，∴∠AOP＝∠POB，在△AOP和△BOP中，，∴△AOP≌△BOP（SAS），∴∠OBP ＝∠OAP ，∵P A 为⊙O 的切线，∴∠OAP ＝90°，∴∠OBP ＝90°，∴PB 是⊙O 的切线；（2）证明：连结AE ，∵P A 为⊙O 的切线，∴∠P AE ＋∠OAE ＝90°，∵AD ⊥ED ，∴∠EAD ＋∠AED ＝90°，∵OE ＝OA ，∴∠OAE ＝∠AED ，∴∠P AE ＝∠DAE ，即EA 平分∠P AD ，∵P A 、PD 为⊙O 的切线，∴PD 平分∠APB∴E 为△P AB 的内心；（3）解：∵∠P AB ＋∠BAC ＝90°，∠C ＋∠BAC ＝90°，∴∠P AB ＝∠C ，∴cos ∠C ＝cos ∠P AB在Rt △ABC 中，cos ∠C ＝BC AC ＝1AC ，∴AC AO ∵△P AO ∽△ABC ， ∴PO AO AC BC，∴PO ＝AO AC BC 5．9. 已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，若＝，如图1，．（1）判断△ABC的形状，并证明你的结论；（2）设AE与DF相交于点M，如图2，AF＝2FC＝4，求AM的长．【解答】解：（1）△ABC为等腰三角形，∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F，∴∠CFE＝∠CEF＝∠BDO＝∠BEO＝90°，∵四边形内角和为360°，∴∠EOF＋∠C＝180°，∠DOE＋∠B＝180°，∵＝，∴∠EOF＝∠DOE，∴∠B＝∠C，AB＝AC，∴△ABC为等腰三角形；（2）连接OB、OC、OD、OF，如图，∵等腰三角形ABC中，AE⊥BC，∴E是BC中点，BE＝CE，∵在Rt△AOF和Rt△AOD中，，∴Rt△AOF≌Rt△AOD，∴AF＝AD，同理Rt△COF≌Rt△COE，CF＝CE＝2，Rt△BOD≌Rt△BOE，BD＝BE，∴AD＝AF，BD＝CF，∴DF∥BC，∴＝，∵AE＝＝4，∴AM＝4×＝．10. （2019•山东威海•12分）（1）方法选择如图①，四边形ABCD是⊙O的内接四边形，连接AC，BD，AB＝BC＝A C．求证：BD＝AD＋C D．小颖认为可用截长法证明：在DB上截取DM＝AD，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN＝AD…请你选择一种方法证明．（2）类比探究【探究1】如图②，四边形ABCD是⊙O的内接四边形，连接AC，BD，BC是⊙O的直径，AB＝A C．试用等式表示线段AD，BD，CD之间的数量关系，井证明你的结论．【探究2】如图③，四边形ABCD是⊙O的内接四边形，连接AC，B D．若BC是⊙O的直径，∠ABC＝30°，则线段AD，BD，CD之间的等量关系式是．（3）拓展猜想如图④，四边形ABCD是⊙O的内接四边形，连接AC，B D．若BC是⊙O的直径，BC：AC：AB＝a：b：c，则线段AD，BD，CD之间的等量关系式是．【解答】解：（1）方法选择：∵AB＝BC＝AC，∴∠ACB＝∠ABC＝60°，如图①，在BD上截取DEMAD，连接AM，∵∠ADB＝∠ACB＝60°，∴△ADM是等边三角形，∴AM＝AD，∵∠ABM＝∠ACD，∵∠AMB＝∠ADC＝120°，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD＝BM＋DM＝CD＋AD；（2）类比探究：如图②，∵BC是⊙O的直径，∴∠BAC＝90°，∵AB＝AC，∴∠ABC＝∠ACB＝45°，过A作AM⊥AD交BD于M，∵∠ADB＝∠ACB＝45°，∴△ADM是等腰直角三角形，∴AM＝AD，∠AMD＝45°，∴DM2AD，∴∠AMB＝∠ADC＝135°，∵∠ABM＝∠ACD，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD ＝BM ＋DM ＝CD AD ；【探究2】如图③，∵若BC 是⊙O 的直径，∠ABC ＝30°， ∴∠BAC ＝90°，∠ACB ＝60°，过A 作AM ⊥AD 交BD 于M ，∵∠ADB ＝∠ACB ＝60°，∴∠AMD ＝30°，∴MD ＝2AD ，∵∠ABD ＝∠ACD ，∠AMB ＝∠ADC ＝150°，∴△ABM ∽△ACD ，∴BM CD ＝AB AC ，∴BM ，∴BD ＝BM ＋DM ＋2AD ；故答案为：BD CD ＋2AD ；（3）拓展猜想：BD ＝BM ＋DM ＝b c CD ＋ba AD ； 理由：如图④，∵若BC 是⊙O 的直径，∴∠BAC ＝90°，过A 作AM ⊥AD 交BD 于M ，∴∠MAD ＝90°，∴∠BAM ＝∠DAC ，∴△ABM ∽△ACD ， ∴BM CD ＝AB AC ＝bc ， ∴BM ＝b c CD ， ∵∠ADB ＝∠ACB ，∠BAC ＝∠NAD ＝90°，∴△ADM ∽△ACB ， ∴AD DM ＝AC BC ＝b a， ∴DM ＝b a AD ，∴BD ＝BM ＋DM ＝b c CD ＋v A D ． 故答案为：BD ＝b c CD ＋b a AD。
2018年中考数学全国用湘教版复习热点小专题(7)以圆为背景的综合计算与证明题
热点小专题(七)以圆为背景的综合计算与证明题类型一圆与切线有关的问题1．【2017·丽水】如图R7－1，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E.(1)求证：∠A＝∠ADE；(2)若AD＝16，DE＝10，求BC的长．图R7－12．【2017·枣庄】如图R7－2，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于E，F.(1)试判断直线BC与⊙O的位置关系，并说明理由；(2)若BD＝2 3，BF＝2，求阴影部分的面积(结果保留π)．图R7－23．【2017·宜昌】如图R7－3，四边形ABCD 中，E 是对角线AC 上一点，ED ＝EC ，以AE 为直径的⊙O 与边CD 相切于D ，B 点在⊙O 上，连接OB.(1)求证：DE ＝OE ；(2)若AB∥CD，求证：四边形ABCD 是菱形．图R7－34．已知A ，B ，C 是⊙O 上的三个点，四边形OABC 是平行四边形，过点C 作⊙O 的切线，交AB 的延长线于点D. (1)如图R7－4①，求∠ADC 的大小；(2)如图R7－4②，经过点O 作CD 的平行线，与AB 交于点E ，与AB ︵交于点F ，连接AF ，求∠FAB 的大小．图R7－45．如图R7－5，AB 是⊙O 的直径，PB 与⊙O 相切于点B ，连接PA 交⊙O 于点C ，连接BC. (1)求证：∠BAC＝∠CBP；(2)求证：PB 2＝PC·PA；(3)当AC ＝6，CP ＝3时，求sin ∠PAB 的值．图R7－56．【2016·雅安】如图R7－6①，AB 是⊙O 的直径，E 是AB 延长线上一点，EC 切⊙O 于点C ，OP ⊥AO 交AC 于点P ，交EC 的延长线于点D.(1)求证：△PCD 是等腰三角形；(2)CG⊥AB 于H 点，交⊙O 于G 点，过B 点作BF∥EC，交⊙O 于点F ，交CG 于Q 点，连接AF ，如图R7－6②，若sinE ＝35，CQ ＝5，求AF 的值．图R7－67．【2017·黄冈】已知：如图R7－7，MN 为⊙O 的直径，ME 是⊙O 的弦，MD 垂直于过点E 的直线DE ，垂足为点D ，且ME 平分∠DMN.求证：(1)DE 是⊙O 的切线；(2)ME 2＝MD·MN.图R7－78．【2017·苏州】如图R7－8，已知△ABC 内接于⊙O，AB 是直径，点D 在⊙O 上，OD ∥BC ，过点D 作DE⊥AB，垂足为E ，连接CD 交OE 边于点F.(1)求证：△DOE∽△ABC； (2)求证：∠ODF＝∠BDE；(3)连接OC ，设△DOE 的面积为S 1，四边形BCOD 的面积为S 2，若S 1S 2＝27，求sinA 的值．图R7－8参考答案1．解：(1)证明：如图，连接OD ，∵DE 是⊙O 的切线， ∴∠ODE ＝90°，∴∠ADE ＋∠BDO＝90°.∵∠ACB ＝90°，∴∠A ＋∠B＝90°， ∵OD ＝OB ，∴∠B ＝∠BDO. ∴∠ADE ＝∠A.(2)连接CD ，∵∠ADE ＝∠A， ∴AE ＝DE.∵BC 是⊙O 的直径，∠ACB ＝90°. ∴EC 是⊙O 的切线， ∴DE ＝EC ，∴AE ＝EC.∵DE＝10， ∴AC ＝2DE ＝20.在Rt △ADC 中，DC ＝202－162＝12.设BD ＝x ，在Rt △BDC 中，BC 2＝x 2＋122，在Rt △ABC 中，BC 2＝(x ＋16)2－202，∴x 2＋122＝(x ＋16)2－202， 解得x ＝9，∴BC ＝122＋92＝15.2．解：(1)BC 与⊙O 相切． 理由：连接OD.∵AD 是∠BAC 的平分线， ∴∠BAD ＝∠CAD. 又∵OD＝OA ， ∴∠OAD ＝∠ODA.∴∠CAD ＝∠ODA.∴OD∥AC.∴∠ODB ＝∠C＝90°，即OD⊥BC. 又∵BC 过半径OD 的外端点D ， ∴BC 与⊙O 相切．(2)设OF ＝OD ＝x ，则OB ＝OF ＋BF ＝x ＋2，根据勾股定理得：OB 2＝OD 2＋BD 2，即(x ＋2)2＝x 2＋12，解得：x ＝2，即OD ＝OF ＝2， ∴OB ＝2＋2＝4，∵在Rt △ODB 中，OD ＝12OB ，∴∠B ＝30°，∴∠DOB ＝60°，∴S 扇形DOF ＝60π×4360＝2π3.故阴影部分的面积为2 3－23π.3．证明：(1)连接OD ，∵CD 是⊙O 的切线， ∴OD ⊥CD ，∴∠2＋∠3＝∠1＋∠COD＝90°，又∵DE＝EC ，∴∠2＝∠1，∴∠3＝∠COD， ∴DE ＝EO.(2)∵OD＝OE ，∴OD ＝ED ＝OE ，∴∠3＝∠COD＝∠DEO＝60°，∴∠2＝∠1＝30°，∵OA ＝OB ＝OE ，而OE ＝DE ＝EC ，∴OA ＝OB ＝DE ＝EC ，又∵AB∥CD，∴∠4＝∠1，∴∠2＝∠1＝∠4＝∠OBA＝30°，∴△ABO ≌△CDE ，∴AB ＝CD ，∴四边形ABCD 是平行四边形．∵∠DAE ＝12∠DOE＝30°，∴∠1＝∠DAE，∴CD ＝AD ，∴四边形ABCD 是菱形．4．解：(1)∵CD 是⊙O 的切线，C 为切点， ∴OC ⊥CD ，即∠OCD＝90°. ∵四边形OABC 是平行四边形， ∴AB ∥OC ，即AD∥OC， ∴∠ADC ＋∠OCD＝180°，∴∠ADC ＝180°－∠OCD＝90°. (2)如图，连接OB ，则OB ＝OA ＝OC.∵四边形OABC 是平行四边形， ∴OC ＝AB ，∴OA ＝OB ＝AB ，即△AOB 是等边三角形， ∴∠AOB ＝60°.∵OF ∥CD ，由(1)知∠ADC＝90°， ∴∠AEO ＝∠ADC＝90°， ∴OF ⊥AB ， ∴BF ︵＝AF ︵，∴∠FOB ＝∠FOA＝12∠AOB＝30°，∴∠FAB ＝12∠FOB＝15°.5．解：(1)证明：∵AB 是⊙O 的直径，∴∠ACB ＝90°， ∴∠CAB ＋∠CBA＝90°， ∵PB 与⊙O 相切于点B ，∴∠PBA ＝90°，∴∠PBC ＋∠CBA＝90°， ∴∠BAC ＝∠PBC.(2)证明：∵∠PCB＝∠ABP＝90°，∠BAP ＝∠CBP，∴△ABP ∽△BCP ，∴AP PB ＝PBPC，∴PB 2＝PC·PA.(3)∵AC＝6，CP ＝3，∴PB 2＝PC·PA＝3×9＝27，即PB ＝3 3.在Rt △APB 中，AP ＝9，∴sin ∠PAB ＝PB PA ＝3 39＝33.∵EC 切⊙O 于点C ，∴OC ⊥DE. ∴∠1＋∠3＝90°ⓐ.又∵OP⊥OA，∴∠2＋∠4＝90°ⓑ. ∵OA ＝OC ，∴∠1＝∠2ⓒ. 由ⓐⓑⓒ可得，∠3＝∠4. 又∵∠4＝∠5，∴∠3＝∠5，∴DP ＝DC ，即△PCD 为等腰三角形．(2)如图②所示，连接BC ，OC ， ∵EC 切⊙O 于C 点，∴∠OCB ＋∠ECB＝90°①. 又∵OC＝OB ，∴∠OCB ＝∠OBC②. ∵CG ⊥AB ，∴∠OBC ＋∠BCG＝90°③. 由①②③可得∠BCE＝∠BCG④. 又∵BF∥DE，∴∠QBC ＝∠BCE⑤， 由④⑤，得∠BCG＝∠QBC， 又∵CQ＝5，∴BQ ＝5，又BF∥DE，∴∠ABF ＝∠E.又∵sinE ＝35，∴sin ∠ABF ＝35，即QH ＝3，BH ＝4.设⊙O 的半径为r ，则r 2－82＝(r －4)2， 解得r ＝10.又∵∠AFB＝90°，sin ∠ABF ＝35，∴AF ＝12.7．证明：(1)∵OM＝OE ，∴∠OME ＝∠OEM. ∵ME 平分∠DMN，∴∠OME ＝∠DME.∴∠OEM＝∠DME. ∵MD ⊥DE ，∴∠MDE ＝90°.∴在△MDE 中，∠DEM ＋∠DME＝90°. ∴∠DEM ＋∠OEM＝90°.即∠OED＝90°，∴OE ⊥DE. 又∵OE 为⊙O 的半径，∴∠MEN ＝90°.∴∠MEN ＝∠MDE＝90°.又由(1)可知，∠NME ＝∠DME. ∴△DME ∽△EMN. ∴MD ME ＝ME MN，∴ME 2＝MD·MN. 8．解：(1)证明：∵AB 是⊙O 的直径， ∴∠ACB ＝90°.∵DE ⊥AB ，∴∠DEO ＝90°. ∴∠DEO ＝∠ACB.∵OD∥BC，∴∠DOE ＝∠ABC， ∴△DOE ∽△ABC.(2)证明：∵△DOE∽△ABC，∴∠ODE ＝∠A.∵∠A 和∠BDC 是BC ︵所对的圆周角， ∴∠A ＝∠BDC，∴∠ODE ＝∠BDC. ∴∠ODF ＝∠BDE.(3)∵△DOE∽△ABC，∴S △DOE S △ABC ＝(OD AB )2＝14，即S △ABC ＝4S △DOE ＝4S 1，∵OA ＝OB ，∴S △BOC ＝12S △ABC ，即S △BOC ＝2S 1. ∵S 1S 2＝27，S 2＝S △BOC ＋S △DOE ＋S △DBE ＝2S 1＋S 1＋S △DBE ， ∴S △DBE ＝12S 1，∴BE ＝12OE ，即OE ＝23OB ＝23OD ，∴sinA ＝sin ∠ODE ＝OE OD ＝23.。
2018年中考复习圆的证明与计算#精选.
2017年中考复习圆的证明与计算一．解答题（共30小题）1．如图，AB为⊙O的直径，AE为⊙O的切线，若tan∠ABE=，AE=3，求BD 的长．2．如图，⊙O是△ABC的外接圆，∠A=45°，BD是直径，且BC=2，连接CD，求BD的长．3．如图，已知AD是⊙O的直径，BC是⊙O的弦，AD⊥BC，垂足为点E，AE=BC=16，求⊙O的直径．4．如图，△ABC中，CD⊥AB于点D，⊙D经过点B，与BC交于点E，与AB交与点F．已知tanA=，cot∠ABC=，AD=8．求（1）⊙D的半径；（2）CE的长．5．如图，AB是⊙O的直径，点C是⊙O上一点，AD和过点C的切线互相垂直，垂足为D，直线DC与AB的延长线相交于P．弦CE平分∠ACB，交直径AB于点F，连结BE．（1）求证：AC平分∠DAB；（2）探究线段PC，PF之间的大小关系，并加以证明；（3）若tan∠PCB=，BE=，求PF的长．6．如图，BC为⊙O的直径，A为圆上一点，点F为的中点，延长AB、AC，与过F点的切线交于D、E两点．（1）求证：BC∥DE；（2）若BC：DF=4：3，求tan∠ABC的值．7．如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E，F，连接EF．（1）求证：PF平分∠BFD；（2）若tan∠FBC=，DF=，求EF的长．8．如图，⊙O的弦AD∥BC，过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及延长线分别交AC、BC于点G、F．（1）求证：DF垂直平分AC；（2）若弦AD=10，AC=16，求⊙O的半径．9．如图所示，CD为⊙O的直径，点B在⊙O上，连接BC、BD，过点B的切线AE与CD的延长线交于点A，OE∥BD，交BC于点F，交AB于点E．（1）求证：∠E=∠C；（2）若⊙O的半径为3，AD=2，试求AE的长；（3）求△ABC的面积．10．如图，△ABC中，E是AC上一点，且AE=AB，∠EBC=∠BAC，以AB为直径的⊙O交AC于点D，交EB于点F．（1）求证：BC与⊙O相切；（2）若AB=8，sin∠EBC=，求AC的长．11．已知四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，∠DAB=45°．（Ⅰ）如图①，判断CD与⊙O的位置关系，并说明理由；（Ⅱ）如图②，E是⊙O上一点，且点E在AB的下方，若⊙O的半径为3cm，AE=5cm，求点E到AB的距离．12．如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O，与斜边AB交于点D、E为BC边的中点，连接DE．（1）求证：DE是⊙O的切线；（2）填空：①若∠B=30°，AC=2，则DE=；②当∠B=°时，以O，D，E，C为顶点的四边形是正方形．13．如图，AB是⊙O的直径，C是⊙O上一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且AC平分∠BAD．（1）求证：直线MN是⊙O的切线；（2）若CD=4，AC=5，求⊙O的直径．14．如图所示，△ABC的外接圆⊙O的半径为2，过点C作∠ACD=∠ABC，交BA 的延长线于点D，若∠ABC=45°，∠D=30°．（1）求证：CD是⊙O的切线；（2）求的长．15．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，经过点A作AE⊥OC，垂足为点D，AE与BC交于点F，与过点B的直线交于点E，且EB=EF．（1）求证：BE是⊙O的切线；（2）若CD=1，cos∠AEB=，求BE的长．16．如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D 是BC的中点，DE⊥AB，垂足为E，交AC的延长线于点F．（1）求证：直线EF是⊙O的切线；（2）CF=5，cos∠A=，求AE的长．17．如图，OA是⊙M的直径，点B在x轴上，连接AB交⊙M于点C．（1）若点A的坐标为（0，2），∠ABO=30°，求点B的坐标．（2）若D为OB的中点，求证：直线CD是⊙O的切线．18．已知：如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，∠PBA=∠C．（1）求证：PB是⊙O的切线．（2）若OP∥BC，且OP=8，∠C=60°，求⊙O的半径．19．如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，且BD=CD，过D作DF⊥AC，垂足为F．（1）求证：DF是⊙O的切线；（2）若AD=5，∠CDF=30°，求⊙O的半径．20．已知等边△ABC，M是边BC延长线上一点，连接AM交△ABC的外接圆于点D，延长BD至N，使得BN=AM，连接CN，MN，解答下列问题：（1）猜想△CMN的形状，并证明你的结论；（2）请你证明CN是⊙O的切线；（3）若等边△ABC的边长是2，求AD•AM的值．21．AB为⊙O直径，BC为⊙O切线，切点为B，CO平行于弦AD，作直线DC．①求证：DC为⊙O切线；②若AD•OC=8，求⊙O半径r．22．已知AB为⊙O的直径，OC⊥AB，弦DC与OB交于点F，在直线AB上有一点F，连接ED，且有ED=EF．（1）如图1，求证：ED为⊙O的切线；（2）如图2，直线ED与切线AG相交于G，且OF=2，⊙O的半径为6，求AG 的长．23．如图，已知⊙O的半径为2，AB是⊙O的直径，过B点作⊙O的切线BC，E 是BC的中点，AC交⊙O于点F，四边形AOEF是平行四边形．（1）求BC的长．（2）求证：EF是⊙O的切线．24．如图，在直角坐标系中，直线AB与x、y轴分别交于点A（4，0）、B（0，）两点，∠BAO的角平分线交y轴于点D，点C为直线AB上一点以AC为直径的⊙G经过点D，且与x轴交于另一点E．（1）求证：y轴是⊙G的切线．（2）求出⊙G的半径；（3）连结EC，求△ACE的面积．25．如图，已知圆O的直径AB垂直于弦CD于点E，连接CO并延长交AD于点F，且CF⊥AD．（1）请证明：E是OB的中点；（2）若AB=8，求CD的长．26．如图，AB是⊙O的直径，弦CD⊥AB于点E，且CD=24，点M在⊙O上，MD经过圆心O，联结MB．（1）若BE=8，求⊙O的半径；（2）若∠DMB=∠D，求线段OE的长．27．如图，在△ABC中，AB是⊙O的直径，AC与⊙O交于点D，点E在上，连接DE，AE，连接CE并延长交AB于点F，∠AED=∠ACF．（1）求证：CF⊥AB；（2）若CD=4，CB=4，cos∠ACF=，求EF的长．28．如图，AB是⊙O的直径，OD∥BC，∠A=30°，CD=2．求：（1）弦BC的长；（2）图中阴影部分的面积．29．如图，在⊙O中，弦AB⊥弦CD于E，弦AG⊥弦BC于F点，CD与AG相交于M点．（1）求证：=；（2）如果AB=12，CM=4，求⊙O的半径．30．如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E（1）求证：△ACE∽△CBE；（2）若AB=8，设OE=x（0＜x＜4），CE2=y，请求出y关于x的函数解析式．2017年中考复习圆的证明与计算参考答案一．解答题（共30小题）1．；2．；3．；4．；5．；6．；7．；8．；9．；10．；11．；12．3；45；13．；14．；15．；16．；17．；18．；19．；20．；21．；22．；23．；24．；25．；26．；27．；28．；29．；30．；最新文件仅供参考已改成word文本。
中考数学专题训练7.圆的证明与计算
圆的证明与计算1.如图，已知△ABC 内接于⊙O ， P 是圆外一点，P A 为⊙O 的切线，且P A ＝PB ，连接 OP ，线段 AB 与线段 OP 相交于点D . （1）求证：PB 为⊙O 的切线；（2）若P A ＝45PO ，⊙O 的半径为10，求线段 PD 的长.第1题图(1)证明：如解图，连接OA 、OB ，第1题解图∵P A ＝PB ，OA ＝OB ，OP ＝OP ， ∴△OAP ≌△OBP (SSS)， ∴∠OAP ＝∠OBP ， ∵P A 为⊙O 的切线， ∴∠OAP ＝90°， ∴∠OBP ＝90°， ∵OB 为⊙O 的半径， ∴PB 为⊙O 的切线；(2)解：∵P A ＝45PO ，⊙O 的半径为10，∴在Rt△AOP中，OA＝PO2－（45PO）2＝10，解得PO＝50 3，∴cos∠AOP＝AOOP＝ODAO，∴OD＝6，∴PD＝PO－OD＝32 3.2.如图，在△ABC中，AB＝AC，点D为BC上一点，且AD＝DC，过A，B，D 三点作⊙O，AE是⊙O的直径，连接DE.（1）求证：AC是⊙O的切线；（2）若cos C＝35，AC＝24，求直径AE的长.第2题图(1)证明：∵AB＝AC，AD＝DC，∴∠C＝∠B，∠DAC＝∠C，∴∠DAC＝∠B，又∵∠E＝∠B，∴∠DAC＝∠E，∵AE是⊙O的直径，∴∠ADE＝90°，∴∠E＋∠EAD＝90°，∴∠DAC＋∠EAD＝90°，即∠EAC＝90°，∴AE⊥AC，∵OA是⊙O的半径，∴AC是⊙O的切线；(2)解：如解图，过点D作DF⊥AC于点F，第2题解图∵DA＝DC，∴CF＝12AC＝12，在Rt△CDF中，∵cos C＝CFCD＝3 5，∴DC＝20，∴AD＝20，在Rt△CDF中，由勾股定理得1622==CFCDDF－，∵∠ADE＝∠DFC＝90°，∠E＝∠C，∴△ADE∽△DFC，∴AEDC＝ADDF，即AE20＝1620，解得AE＝25，即⊙O的直径AE为25.3．如图，在△ABC中，AB=BC，以AB为直径作⊙O，交BC于点D，交AC于点E，过点E作⊙O的切线EF，交BC于点F．（1）求证：EF⊥BC；（2）若CD=2，tan C=2，求⊙O的半径．第3题图（1）证明：如解图，连接BE，OE．第3题解图∵AB为⊙O的直径，∴∠AEB=90°．∵AB=BC，∴点E是AC的中点，∵点O是AB的中点，∴OE∥BC，∵EF是⊙O的切线，∴EF⊥OE．∴EF⊥BC；（2）解：如解图，连接AD，∵AB为⊙O的直径，∴∠ADB=90°，∵CD=2，tan C=CDAD2，∴AD=4．设AB=x，则BD=x－2．在Rt△ABD中，由勾股定理得AB2=AD2+BD2，即x2=42+（x－2）2，解得x=5，即AB=5，∴⊙O的半径为25．4.如图，已知⊙O是以AB为直径的△ABC的外接圆，过点A作⊙O的切线交OC的延长线于点D，交BC的延长线于点E.（1）求证：∠DAC＝∠DCE；（2）若AB＝2， sin D＝13，求AE的长.第4题图(1)证明：∵AD是⊙O的切线，∴∠DAB＝90°.∵AB是⊙O的直径，∴∠ACB＝90°.∵∠DAC＋∠CAB＝90°，∠CAB＋∠ABC＝90°，∴∠DAC ＝∠ABC . ∵OC ＝OB ， ∴∠ABC ＝∠OCB ， 又∵∠DCE ＝∠OCB ， ∴∠DAC ＝∠DCE ； (2)解：∵AB ＝2， ∴AO ＝1. ∵sin D ＝AO OD ＝13， ∴OD ＝3，DC ＝2， 在Rt △DAO 中，由勾股定理得AD ＝OD 2－OA 2＝22， ∵∠DAC ＝∠DCE ，∠D ＝∠D ， ∴△DEC ∽△DCA ， ∴DC DA ＝DE DC ， 即222＝DE2， 解得DE ＝2， ∴AE ＝AD －DE ＝ 2.5.如图，AB 是⊙O 的弦，D 为半径OA 的中点，过点D 作CD ⊥OA 交弦AB 于点E ，交⊙O 于点F ，且BC 是⊙O 的切线. （1）求证：CE ＝CB ；（2）连接AF ，BF ，求∠ABF 的度数；（3）若CD ＝15， BE ＝10，DE AE ＝513，求⊙O 的半径.第5题图(1)证明：如解图，连接OB，第5题解图∵BC是⊙O的切线，∴OB⊥BC，即∠OBC＝90°，∴∠OBA＋∠CBE＝90°，∵OA＝OB，∴∠OAB＝∠OBA，∴∠OAB+∠CBE＝90°，又∵CD⊥OA，∴∠OAB＋∠DEA＝90°，又∵∠CEB＝∠DEA，∴∠CBE＝∠CEB，∴CE＝CB；(2)解：如解图，连接OF，∵DA＝DO，CD⊥OA，∴AF＝OF，又∵OA＝OF，∴△AOF是等边三角形，∴∠AOF=60°，∴∠ABF＝12∠AOF＝30°；(3)解：如解图，过点C作CG⊥AB于点G，∵CD⊥OA，∴∠ADE＝∠CGE＝90°，又∵∠AED＝∠CEG，∴DE AE ＝EG CE ＝513， ∵CE ＝BC ，∴BG ＝EG ＝12BE ＝5， ∴CE ＝13，∴DE ＝CD －CE ＝2，∴AE ＝265，∴在Rt △ADE 中，由勾股定理得AD 22DE AE -=＝245， ∴OA ＝2AD ＝485， ∴⊙O 的半径为485.6.如图，四边形ABCD 内接于⊙O ，AB 是⊙O 的直径，AD ＝DC ，分别延长B A ，CD 交于点E ，作BF ⊥EC ，交EC 的延长线交于点F ，连接BD . （1）求证：△BFC ∽△BDA ； （2）若AE ＝AO ，求cos ∠ADE ；（3）在（2）的条件下，若BC ＝6，求BF 的长.第6题图(1)证明：∵AB 是⊙O 的直径， ∴∠BDA ＝90°. ∵BF ⊥EC ， ∴∠BFC ＝90°，∵四边形ABCD 是⊙O 的内接四边形， ∴∠BCF ＝∠BAD ，(2)解：如解图，连接OD ，AC ，第6题解图∵△BFC ∽△BDA ， ∴BF BD ＝BC AB ，∵OD 是⊙O 的半径，AD ＝CD ， ∴OD 垂直平分AC ， ∵AB 是⊙O 的直径， ∴∠ACB =90°， ∴OD ∥BC ， ∴△EOD ∽△EBC ， ∴OE BE ＝OD BC ，∵AE ＝AO ，即OE ＝2OB ，BE ＝3OB ， ∴OD BC ＝BE OE 23， ∴BC ＝32OD ， ∴BF BD ＝BC AB ＝32OD2OD ＝34， ∵∠ADB ＝90°， ∴∠ADE ＋∠BDF ＝90°， ∵∠BDF ＋∠DBF ＝90°， ∴∠ADE ＝∠DBF ，在Rt △BDF 中，cos ∠DBF ＝BF BD ＝34，∴cos ∠ADE ＝34；(3)解：∵BC ＝32OD ，BC ＝6， ∴OD ＝4， ∴AE ＝4，BE ＝12， ∵△EOD ∽△EBC ， ∴DE CE ＝OD BC ， ∴CE ＝32DE ，又∵∠EDA ＝∠EBC ，∠E ＝∠E ， ∴△AED ∽△CEB ， ∴AE CE ＝DE BE ， ∴DE ·CE ＝AE ·BE ， ∴DE ·32DE ＝4×12， ∴DE ＝42(负值舍去)， ∴CD ＝22，∴AD ＝22， ∵△BFC ∽△BDA ， ∴CF BC ＝AD AB ，∴CF 6＝228， ∴CF ＝322，在Rt △BCF 中，根据勾股定理得， BF ＝BC 2－CF 2＝3142.7.如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为H ，连接AC ，过»BD上一点E 作EG ∥AC 交CD 的延长线于点G ，连 接AE 交CD 于点F ，且EG =FG ，连接CE ．（1）求证：△ECF∽△GCE；（2）求证：EG是⊙O的切线；3，AH=3，（3）延长AB交GE的延长线于点M，若tan∠G=4求EM的值．第7题图（1）证明：∵AC∥EG，∴∠G=∠ACG，∵AB是⊙O的直径，AB⊥CD，∴»AD=»AC，∴∠CEF=∠ACD，∴∠G=∠CEF，∵∠ECF=∠ECG，∴△ECF∽△GCE；（2）证明：如解图，连接OE，第7题解图∵GF =GE ，∴∠GFE =∠GEF =∠AFH ，∵OA =OE ，∴∠OAE =∠OEA ，∵∠AFH +∠F AH =90°，∴∠GEF +∠AEO =90°，∴∠GEO =90°，∴GE ⊥OE ，∵OE 是⊙O 的半径，∴EG 是⊙O 的切线；（3）解：如解图，连接OC ，设⊙O 的半径为r ．在Rt △AHC 中，tan ∠ACH =tan ∠G =HC AH =43， ∵AH =3，∴HC =4．在Rt △HOC 中，∵OC =r ，OH =r －3，HC =4，∴（r －3）2+42=r 2，解得r =625， ∵GM ∥AC ，∴∠CAH =∠M ，∵∠OEM =∠AHC=90°，∴△AHC ∽△MEO ， ∴OE HC EM AH =， 即62543=EM， ∴825=EM ． 8．如图，AB 为⊙O 的直径，C 、G 是⊙O 上两点，过点C 的直线CD ⊥BG 交BG 的延长线于点D ，交BA 的延长线于点E ，连接BC ，交OD 于点F ，且BC 平分∠ABD ．（1）求证：CD 是⊙O 的切线；（2）若32=FD OF ，求∠E 的度数； （3）连接AD ，在（2）的条件下，若CD =23，求AD 的长．第8题图（1）证明：如解图，连接OC ，第8题解图∵OC =OB ，BC 平分∠ABD ，∴∠OCB =∠OBC ，∠OBC =∠DBC ，∴∠DBC =∠OCB ，∴OC ∥BD ，∴∠BDC =∠ECO ，∵CD ⊥BD ，∴∠BDC =90°，∴∠ECO =90°，∵OC 是⊙O 的半径，∴CD 是⊙O 的切线；（2）解：由（1）知，OC ∥BD ，∴∠OCF =∠DBF ，∠COF =∠BDF ，∴△OCF ∽△DBF ， ∴DB OC FD OF =， ∵32=FD OF ， ∴32=DB OC ， ∵OC ∥BD ，∴△EOC ∽△EBD ， ∴EB EO BD OC =， ∴32=EB EO ，设OE =2a ，则EB =3a ，∴OB =a ，∴OC =a ，∵∠OCE =90°，OC =21OE ，∴∠E =30°；（3）解：∵∠E =30°，∠BDE =90°，∴∠EBD =60°，∵BC 平分∠DBE ，∴∠OBC =∠DBC =EBD ∠21=30°，∵CD =23，∴BC =43，BD =6， ∵32=DB OC ， ∴OC =4，如解图，过点D 作DM ⊥AB 于点M ，∴∠DMB =90°，∵BD =6，∠DBM =60°，∴BM =3，DM =33，∵OC =4，∴AB =8，∴AM =AB －BM =5，∵∠DMA =90°，DM =33， ∴AD =13222=+AM DM ．9．如图，在△ABC 中，∠ACB =90°，O 是AB 上一点，以OA 为半径的⊙O 与BC 相交于点D ，与AB 交于点E ，AD 平分∠F AB ，连接ED 并延长交AC 的延长线于点F ．（1）求证：BC 为⊙O 的切线；（2）求证：AE =AF ；（3）若DE =3，sin ∠BDE =31，求AC 的长．第9题图（1）证明：如解图，连接OD ．第9题解图∵AD 平分∠F AB ，∴∠CAD =∠DAB ，∵OA =OD ，∴∠DAB =∠ODA ，∴∠CAD=∠ODA，∴AC∥OD，∴∠ODB=∠ACB=90°，∴OD⊥BC，∵OD为⊙O的半径，∴BC为⊙O的切线；（2）证明：由（1）知OD∥AC，∴∠ODE=∠F．∵OD=OE，∴∠OED=∠ODE，∴∠OED=∠F．∴AE=AF；（3）解：∵AE是⊙O的直径，∴∠ADE=90°．∴∠DAF+∠F=90°，∵AE=AF，∴DF=DE=3．∵∠ACB=90°，∴∠CDF+∠F=90°，∴∠DAF=∠CDF=∠BDE．在Rt △ADF 中， 31sin sin =∠=∠=BDE DAF AF DF ， ∴AF =3DF =9．在Rt △CDF 中，31sin sin =∠=∠=BDE CDF DF CF ， ∴131==DF CF ．∴AC =AF －CF =8．10．如图，在△ABC 中，AB =AC ，以AB 为直径作⊙O ，分别交BC 于点D ，交CA 的延长线于点E ，过点D 作DH ⊥AC 于点H ，连接DE 交线段OA 于点F ．（1）求证：DH 是⊙O 的切线；（2）若AE=AH ，求EF FD 的值； （3）若EA =EF =1，求⊙O 的半径．第10题图（1）证明：如解图，连接OD ，第10题解图∵OB =OD ，∴∠OBD =∠ODB ，∵AB =AC ，∴∠ABC =∠ACB ，∴∠ODB =∠ACB ，∴OD ∥AC ，∵DH ⊥AC ，∴DH ⊥OD ，∵OD 是⊙O 的半径，∴DH 是⊙O 的切线；（2）解：∵∠E =∠B ，AB =AC ，∴∠E =∠B =∠C ，∴ED =DC ，∵DH ⊥EC ，∴EH =CH ，∵AE =AH ，∴AE =31AC ，∵AO =BO ，OD ∥AC ，∴OD 是△ABC 的中位线，∴OD =21AC ， ∴23 AE OD ，∵AE ∥OD ，∴△AEF ∽△ODF ， ∴23==AE OD EF FD ； （3）解：设⊙O 的半径为r ，即OD =OB =r ， ∵EF =EA ，∴∠EF A =∠EAF ，∵OD ∥EC ，∴∠FOD =∠EAF ，则∠FOD =∠EAF =∠EF A =∠OFD ， ∴DF =OD =r ，∴DE =DF +EF =r +1，∴BD =CD =DE =r +1，在⊙O 中，∵∠BDE =∠EAB ，∴∠BFD =∠EF A =∠EAB =∠BDE ，∴BF =BD =r +1，∴AF =AB －BF =2OB －BF =2r －（1+r ）=r －1， ∵∠BFD =∠EF A ，∠B =∠E ，∴△BFD ∽△EF A ， ∴FD BF FA EF =， ∴r r r 111+=-，解得r=251+（负值已舍），∴⊙O的半径为251+．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（2017浙江衢州第19题）如图，AB 为半圆O 的直径，C 为BA 延长线上一点，CD 切半圆O 于点D 。
连结OD ，作BE ⊥CD 于点E ，交半圆O 于点F 。
已知CE=12，BE=9[来源:学#科#网Z#X#X#K]（1）求证：△COD ∽△CBE ；（2）求半圆O 的半径r 的长：试题解析： （1）∵CD 切半圆O 于点D ，∴CD ⊥OD ，∴∠CDO=90°， ∵BE ⊥CD ，∴∠E=90°=∠CDO ，又∵∠C=∠C ， ∴△COD ∽△CBE ．（2）在Rt △BEC 中，CE=12，BE=9，∴22CE BE +=15，∵△COD ∽△CBE ．∴OD OC BE BC=，即15915r r -=， 解得：r=458． 考点：1. 切线的性质；2.相似三角形的判定与性质.2.（2017山东德州第20题）如图，已知Rt ΔABC,∠C=90°，D 为BC 的中点.以AC 为直径的圆O 交AB 于点E.（1）求证：DE 是圆O 的切线.(2)若AE:EB=1:2,BC=6，求AE 的长.(1)如图所示，连接OE，CE∵AC是圆O的直径∴∠AEC=∠BEC=90°∵D是BC的中点∴ED＝12BC＝DC∴∠1=∠2∵OE=OC∴∠3=∠4∴∠1+∠3=∠2+∠4,即∠OED=∠ACD ∵∠ACD=90°∴∠OED=90°,即OE⊥DE又∵E是圆O上的一点∴DE是圆O的切线.考点：圆切线判定定理及相似三角形3.（2017甘肃庆阳第27题）如图，AN 是⊙M 的直径，NB ∥x 轴，AB 交⊙M 于点C ．（1）若点A （0，6），N （0，2），∠ABN=30°，求点B 的坐标；（2）若D 为线段NB 的中点，求证：直线CD 是⊙M 的切线．（1）∵A 的坐标为（0，6），N （0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：223AB AN -=，∴B （32）．（2）连接MC ，NC∵AN 是⊙M 的直径，∴∠ACN=90°，∴∠NCB=90°，在R t △NCB 中，D 为NB 的中点，∴CD=12NB=ND ， ∴∠CND=∠NCD ，∵MC=MN ，∴∠MCN=∠MNC ， ∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC ⊥CD ．∴直线CD 是⊙M 的切线．考点：切线的判定；坐标与图形性质．4.（2017广西贵港第24题）如图，在菱形ABCD 中，点P 在对角线AC 上，且PA PD =，O 是PAD ∆的外接圆.（1）求证：AB 是O 的切线；（2）若28,tan 2AC BAC =∠=求O 的半径. 【答案】(1)证明见解析；（2）364． （1）连结OP 、OA ，OP 交AD 于E ，如图，∵PA=PD ，∴弧AP=弧DP ，∴OP ⊥AD ，AE=DE ，∴∠1+∠OPA=90°，∵OP=OA ，∴∠OAP=∠OPA ，∴∠1+∠OAP=90°，∵四边形ABCD 为菱形，∴∠1=∠2，∴∠2+∠OAP=90°，∴OA ⊥AB ，∴直线AB 与⊙O 相切；（2）连结BD ，交AC 于点F ，如图，∵四边形ABCD 为菱形，∴DB 与AC 互相垂直平分，∵AC=8，tan ∠BAC=2，∴AF=4，tan ∠DAC=DF AF =2∴∴∴在Rt △PAE 中，tan ∠1=PE AE =2，∴设⊙O 的半径为R ，则OE=R OA=R ，在Rt △OAE 中，∵OA 2=OE 2+AE 2，∴R 2=（R 2+2，∴R=4，即⊙O的半径为364．考点：切线的判定与性质；菱形的性质；解直角三角形．5.（2017贵州安顺第25题）如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD 的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）设OE交⊙O于点F，若DF=1，BC=2 3，求阴影部分的面积．【答案】(1)证明见解析；（2）43﹣43π．（1）证明：连接OC，如图，∵CE为切线，∴OC⊥CE，∴∠OCE=90°，∵OD⊥BC，∴CD=BD，即OD垂中平分BC，∴EC=EB，在△OCE和△OBE中OC OBOE OEEC EB⎧=⎪=⎨⎪=⎩，∴△OCE≌△OBE，∴∠OBE=∠OCE=90°，∴OB⊥BE，∴BE与⊙O相切；（2）解：设⊙O的半径为r，则OD=r﹣1，在Rt△OBD中，BD=CD=12BC=3，∴（r﹣1）2+（3）2=r2，解得r=2，∵tan∠BOD=BDOD=3，∴∠BOD=60°，∴∠BOC=2∠BOD=120°，在Rt△OBE中，BE=3OB=23，∴阴影部分的面积=S四边形OBEC﹣S扇形BOC=2S△OBE﹣S扇形BOC=2×12×2×23﹣21202360π⨯⨯343π．考点：切线的判定与性质；扇形面积的计算．6.（2017湖北武汉第21题）如图，ABC∆内接于O，,AB AC CO=的延长线交AB于点D．（1）求证AO平分BAC∠；（2）若36,sin5BC BAC=∠=，求AC和CD的长．【答案】（1）证明见解析；（2）310；90 13.（2）过点C作CE⊥AB于E∵sin∠BAC=35,设AC=5m，则CE=3m∴AE=4m，BE=m在RtΔCBE中，m2+(3m)2=36∴m=3105，∴AC=310延长AO交BC于点H，则AH⊥BC，且BH=CH=3，过点O作OF⊥AH交AB于点F，∵∠HOC=∠BAC∴OH=4，OC=5∴AH=9∴tan∠BAH=13∴OF=13AO=53∵OF∥BC∴OF DOBC DC，即5DC-53=6DC∴DC=9013.考点：1.全等三角形的判定与性质；2.解直角三角形；3.平行线分线段成比例.7.（2017湖南怀化第23题）如图，已知BC是O⊙的直径，点D为BC延长线上的一点，点A为圆上一点，且AB AD，AC CD.(1)求证：ACD BAD△∽△；(2)求证：AD是O⊙的切线.试题解析：（1）∵AB=AD，∴∠B=∠D，∵AC=CD，∴∠CAD=∠D，∴∠CAD=∠B，∵∠D=∠D，∴△ACD∽△BAD；（2）连接OA，∵OA=OB，∴∠B=∠OAB，∴∠OAB=∠CAD，∵BC是⊙O的直径，∴∠BAC=90°，∴OA⊥AD，∴AD是⊙O的切线．考点：相似三角形的判定与性质；切线的判定．11.（2017江苏盐城第25题）如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE平分∠BAC交边BC于点E，经过点A、D、E的圆的圆心F恰好在y轴上，⊙F与y轴相交于另一点G．（1）求证：BC是⊙F的切线；（2）若点A、D的坐标分别为A（0，-1），D（2，0），求⊙F的半径；（3）试探究线段AG、AD、CD三者之间满足的等量关系，并证明你的结论．【答案】（1）证明见解析；（2）⊙F的半径为52；（3）AG=AD+2CD．证明见解析.试题解析：（1）连接EF，∵AE平分∠BAC，∴∠FAE=∠CAE，∵FA=FE，∴∠FAE=∠FEA，∴∠FEA=∠EAC，∴FE∥A C，∴∠FEB=∠C=90°，即BC是⊙F的切线；（2）连接FD，设⊙F的半径为r，则r2=（r-1）2+22，解得，r=52，即⊙F的半径为52；（3）AG=AD+2CD．证明：作FR⊥AD于R，则∠FRC=90°，又∠FEC=∠C=90°，∴四边形RCEF是矩形，∴EF=RC=RD+CD，∵FR⊥AD，∴AR=RD ，∴EF=RD+CD=12AD+CD ， ∴AG=2FE=AD+2CD ．.考点：圆的综合题．13.（2017甘肃兰州第27题）如图，ABC △内接于O ⊙，BC 是O ⊙的直径，弦AF 交BC 于点E ，延长BC 到点D ，连接OA ，AD ，使得FAC AOD ∠∠，D BAF ∠∠.(1)求证：AD 是O ⊙的切线；(2)若O ⊙的半径为5，2CE ，求EF 的长.（1）由BC 是⊙O 的直径，得到∠BAF+∠FAC=90°，等量代换得到∠D+∠AOD=90°，于是得到结论；（2）连接BF ，根据相似三角形的判定和性质即可得到结论．（2）连接BF ，∴∠FAC=∠AOD ，∴△ACE∽△DCA，∴AC AE CE OC OA AC==，∴255AC AEAC==，∴AC=AE=10，∵∠CAE=∠CBF，∴△ACE∽△BFE，∴AE BE CE EF=，∴1082EF=，∴EF=8105．考点：切线的判定与性质；相似三角形的判定与性质．14.（2017贵州黔东南州第21题）如图，已知直线PT与⊙O相切于点T，直线PO与⊙O相交于A，B两点．（1）求证：PT2=PA?PB；（2）若PT=TB=3，求图中阴影部分的面积．（1）证明：连接OT．∵PT是⊙O的切线，∴PT⊥OT，∴∠PTO=90°，∴∠PTA+∠OTA=90°，∵AB 是直径，∴∠ATB=90°，∴∠TAB+∠B=90°，∵OT=OA ，∴∠OAT=∠OTA ，∴∠PTA=∠B ，∵∠P=∠P ，∴△PTA ∽△PBT ， ∴PT PA PB PT=， ∴PT 2=PA?PB ．（2）∵∴∠P=∠B=∠PTA ，∵∠TAB=∠P+∠PTA ，∴∠TAB=2∠B ，∵∠TAB+∠B=90°，∴∠TAB=60°，∠B=30°，∴tanB=3AT TB = ∴AT=1，∵OA=OT ，∠TAO=60°，∴△AOT 是等边三角形，∴S 阴=S 扇形OAT ﹣S △AOT =226011360464ππ⨯-⨯=-. 考点：相似三角形的判定与性质；切线的性质；扇形面积的计算．16.（2017四川泸州第24题）如图，⊙O 与Rt △ABC 的直角边AC 和斜边AB 分别相切于点C 、D ，与边BC 相交于点F ，OA 与CD 相交于点E ，连接FE 并延长交AC 边于点G ．（1）求证：DF ∥AO ；（2）若AC=6，AB=10，求CG 的长．【答案】（1）证明见解析；（2）2.（1）证明：连接OD ．∵AB 与⊙O 相切与点D ，又AC 与⊙O 相切与点，∴AC=AD ，∵OC=OD ，∴OA ⊥CD ，∴CD ⊥OA ，∵CF 是直径，∴∠CDF=90°，∴DF ⊥CD ，∴DF ∥AO ．（2）过点作EM ⊥OC 于M ，∵AC=6，AB=10，∴22AB AC ，∴AD=AC=6，∴BD=AB-AD=4，∵BD 2=BF?BC ，∴BF=2，∴CF=BC-BF=6．OC=12CF=3，∴OA=22AC OC +=35， ∵OC 2=OE?OA ，∴OE=35， ∵EM ∥AC ，∴15EM OM OE AC OC OA ===， ∴OM=35，EM=65，FM=OF+OM=185， ∴ 3.6365EM FM CG FC ===， ∴CG=53EM=2． 考点：切线的性质．17.（2017四川宜宾第23题）如图，AB 是⊙O 的直径，点C 在AB 的延长线上，AD 平分∠CAE 交⊙O 于点D ，且AE ⊥CD ，垂足为点E ．（1）求证：直线CE 是⊙O 的切线．（2）若BC=3，CD=32，求弦AD 的长．（1）证明：连结OC ，如图，∵AD 平分∠EAC ，∴∠1=∠3，∵OA=OD，∴∠1=∠2，∴∠3=∠2，∴OD∥AE，∵AE⊥DC，∴OD⊥CE，∴CE是⊙O的切线；（2）∵∠CDO=∠ADB=90°，∴∠2=∠CDB=∠1，∵∠C=∠C，∴△CDB∽△CAD，∴CD CB BD CA CD AD==，∴CD2=CB?CA，∴（32）2=3CA，∴CA=6，∴AB=CA﹣BC=3，32262BDAD==,设BD=2K，AD=2K，在Rt△ADB中，2k2+4k2=5，∴k=306，∴AD=303．考点：切线的判定与性质．18.（2017新疆建设兵团第22题）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB=30°，延长CB至点D，使得CB=BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：BE是⊙O的切线；（2）当BE=3时，求图中阴影部分的面积．【答案】（1）证明见解析；（2）333-22π．（1）如图所示，连接BO，∵∠ACB=30°，∴∠OBC=∠OCB=30°，∵DE⊥AC，CB=BD，∴Rt△DCE中，BE=12CD=BC，∴∠BEC=∠BCE=30°，∴△BCE中，∠EBC=180°﹣∠BEC﹣∠BCE=120°，∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°，∴BE是⊙O的切线；（2）当BE=3时，BC=3，∵AC为⊙O的直径，∴∠ABC=90°，又∵∠ACB=30°，∴AB=tan30°×BC=3，∴AC=2AB=23，AO=3，∴阴影部分的面积=半圆的面积﹣Rt△ABC的面积=12π×AO2﹣12AB×BC=12π×3﹣12×3×3=33-22π．考点：切线的判定与性质；扇形面积的计算．1. (2017北京第24题)如图，AB 是O 的一条弦，E 是AB 的中点，过点E 作EC OA ⊥于点C ，过点B 作O的切线交CE 的延长线于点D .（1）求证：DB DE =；（2）若12,5AB BD ==，求O 的半径.（1）证明：∵DC ⊥OA, ∴∠1+∠3=90°, ∵BD 为切线，∴OB ⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2，∵∠3=∠4，∴∠4=∠5，在△DEB 中, ∠4=∠5，∴DE=DB.(2)作DF ⊥AB 于F,连接OE,∵DB=DE, ∴EF=12BE=3，在 RT △DEF 中，EF=3，DE=BD=5，EF=3 , ∴22534-=∴sin ∠DEF=DF DE = 45 , ∵∠AOE=∠DEF, ∴在RT △AOE 中，sin ∠AOE=45AE AO = , ∵AE=6, ∴AO=152. 考点：圆的性质，切线定理，三角形相似，三角函数2. (2017天津第21题)已知AB 是⊙O 的直径，AT 是⊙O 的切线，050=∠ABT ，BT 交⊙O 于点C ，E 是AB 上一点，延长CE 交⊙O 于点D .（1）如图①，求T ∠和CDB ∠的大小；（2）如图②，当BC BE =时，求CDO ∠的大小.：(1)如图，连接AC,21世纪教育网∵AB 是⊙O 的直径，AT 是⊙O 的切线， ∴AT ⊥AB,即∠TAB=90°.∵050=∠ABT ，∴∠T=90°-∠ABT=40°由AB 是⊙O 的直径，得∠ACB=90°， ∴∠CAB=90°-∠ABC=40°∴∠CDB=∠CAB=40°;（2）如图，连接AD,在△BCE 中，BE=BC ，∠EBC=50°， ∴∠BCE=∠BEC=65°,∴∠BAD=∠BCD=65°∵OA=OD∴∠ODA=∠OAD=65°∵∠ADC=∠ABC=50°∴∠CDO=∠ODA-∠ADC=15°.3. (2017福建第21题)如图，四边形ABCD 内接于O ，AB 是O 的直径，点P 在CA 的延长线上，45CAD ∠=．（Ⅰ）若4AB =，求弧CD 的长；（Ⅱ）若弧BC =弧AD ，AD AP =，求证：PD 是O 的切线．（Ⅰ）连接OC ，OD ，∵∠COD=2∠CAD ，∠CAD=45°，∴∠COD=90°，∵AB=4，∴OC=12 AB=2，∴CD 的长=902180π⨯⨯ =π；（Ⅱ）∵BC =AD ，∴∠BOC=∠AOD ，∵∠COD=90°，∴∠AOD=1802COD ︒-∠ =45°，∵OA=OD ，∴∠ODA=∠OAD ，∵∠AOD+∠ODA+∠OAD=180°，∴∠ODA=1802AOD ︒-∠=°，∵AD=AP ，∴∠ADP=∠APD ，∵∠CAD=∠ADP+∠APD ，∠CAD=45°，∴∠ADP=12∠CAD=°，∴∠ODP=∠ODA+∠ADP=90°，又∵OD 是半径，∴PD 是⊙O 的切线.4. (2017河南第18题)如图，在ABC ∆中， AB AC =，以AB 为直径的⊙O 交AC 边于点D ，过点C 作//CF AB ，与过点B 的切线交于点F ，连接BD .（1）求证：BD BF =；（2）若10AB =，4CD =，求BC 的长.(1)∵AB AC =∴∠ABC=∠ACB∵//CF AB∴∠ABC=∠FCB∴∠ACB=∠FCB ，即CB 平分∠DCF∵AB 为⊙O 直径∴∠ADB=90°，即BD AC ⊥∵BF 为⊙O 的切线∴BF AB ⊥∵//CF AB∴BF CF ⊥∴BD=BF考点：圆的综合题.6. （2017湖南长沙第23题）如图，AB 与⊙O 相切于C ，OB OA ,分别交⊙O 于点E D ,，CD CE =．（1）求证：OB OA =；（2）已知34=AB ，4=OA ，求阴影部分的面积．【答案】（1）证明见解析（2）2=233S π阴影试题解析：（1）连接OC ，则OC ⊥AB∵CD CE =∴∠AOC=∠BOC在△AOC 和△BOC 中，90AOC BOC OC OCOCA OCB ⎧∠=∠⎪=⎨⎪∠=∠=⎩∴△AOC ≌△BOC （ASA ）∴AO=BO（2）由（1）可得AC=BC=12AB=3∴在Rt △AOC 中，OC=2∴∠AOC=∠BOC=60° ∴11==232=2322BOC S BC OC ⋅⨯△ 26022==3603S ππ⨯⨯扇形BOC ∴2==233BOC S S S π-△阴影扇形BOC考点：1、切线的性质，2、三角形的面积，3、扇形的面积 7. （2017山东临沂第23题）如图，BAC ∠的平分线交ABC 的外接圆于点D ，ABC ∠的平分线交AD 于点E .（1）求证：DE DB =；（2）若90BAC ∠=︒，4BD =，求ABC 外接圆的半径.【试题解析：（1）AD 平分BAC ∠，BE 平分ABC ∠，,BAD CAD ABE CBE ∴∠=∠∠=∠，又BED ABE BAD ∠=∠+∠，DBE DBC CBE ∠=∠+∠，DBC DAC ∠=∠,BED DBE ∴∠=∠.DE DB ∴=.（2）解：连接CD ，90BAC ∠=，BC ∴是圆的直径.90BDC ∴∠=，90BDC ∴∠=.BAD CAD ∠=∠，BD CD ∴=，BD CD ∴=，BCD ∴∆是等腰直角三角形.4BD =，42BC ∴=.ABC ∴∆的外接圆的半径为22.考点：1、三角形的外接圆的性质，2、圆周角定理，3、三角形的外角性质，4、勾股定理8. (2017四川泸州第24题)如图，⊙O 与ABC Rt ∆的直角边AC 和斜边AB 分别相切于点;,D C 与边BC 相交于点F ,OA 与CD 相交于点E ，连接FE 并延长交AC 边于点G .（1）求证：DF AO ,10,6==AB AC CG（1）证明：AB 与⊙O 相切与点D BDF BCD ∠=∠∴ （弦切角定理）又AC 与⊙O 相切与点C由切线长定理得：;,DAO CAO AD AC ∠=∠= AO CD ⊥∴,;BDF DAO DAO CAO BCD ∠=∠∴∠=∠=∠∴ 即：DF E OC EM ⊥M 88,622=-=∴==AC AB BC AB AC 4,6=-=∴==AD AB BD AC AD ∴BCBF BD ⋅=2;2=BF ;321,6===-=∴FC OC BF BC FC 5322=+=∴OC AC OA 553,2=⋅=OE OA OE OC 解之得：235;5366.3;518;56,53;51==∴===∴=+===∴===∴EM CG FC FM CG EM OM OF FM EM OM OA OE OC OM AC EM (2017山东滨州第23题)（本小题满分10分）如图，点E 是△ABC 的内心，AE 的延长线交BC 于点F ，交△ABC 的外接圆⊙O 于点D ；连接BD ，过点D 作直线DM ，使∠BDM ＝∠DAC ．（1）求证：直线DM 是⊙O 的切线；（2）求证：DE 2＝DF ·DA ．【答案】详见解析.试题解析：证明：（1）如图1，连接DO ，并延长交⊙O 于点G ，连接BG ；∵点E 是△ABC 的内心，∴AD 平分∠BAC ，∴∠BAD ＝∠DAC ．21世纪教育网∵∠G ＝∠BAD ，∴∠MDB ＝∠G ，21世纪教育网∵DG 为⊙O 的直径，∴∠GBD ＝90°，∴∠G ＋∠BDG ＝90°．∴∠MDB ＋∠BDG ＝90°．∴直线DM 是⊙O 的切线；（2）如图2，连接BE．∵点E是△ABC的内心，∴∠ABE＝∠CBE，∠BAD＝∠CAD．∵∠EBD＝∠CBE＋∠CBD，∠BED＝∠ABE＋∠BAD，∠CBD＝∠CAD．∴∠EBD＝∠BED，∴DB＝DE．∵∠CBD＝∠BAD，∠ADB＝∠ADB，∴△DBF∽△DAB，∴BD2＝DF·DA．∴DE2＝DF·DA．10. (2017辽宁沈阳第22题)如图，在ABC∆中，以BC为直径的O交AC于点E，过点E做EF AB⊥于点F，延长EF交CB的延长线于点G，且2ABG C∠=∠.（1）求证：EF是O的切线；（2）若3sin5EGC∠=，O的半径是3，求AF的长.【答案】（1）详见解析；（2）24 5.试题解析：(1)连接OE，则2EOG C∠=∠,∵2ABG C∠=∠∴ABG EOG∠=∠∴//AB OE∵EF AB⊥∴090AFE∠=∴090GEO AFE∠=∠=∴OE EG⊥又∵OE是O的半径∴EF是O的切线；（2）∵2ABG C∠=∠，∵ABG C A∠=∠+∠∴C A∠=∠∴BA=BC又O的半径为3，∴OE=OB=OC∴BA=BC=2×3=6在Rt△OEG中，sin∠EGC=OEOG，即335OG=∴OG=5在Rt△FGB中，sin∠EGC=BFGB，即352FB=∴BF=6 5∴AF=AB-BF=6-65=245. 考点：圆的综合题.13. (2017山东菏泽第22题)如图，AB 是⊙O 的直径，PB 与⊙O 相切于点B ，连接PA 交⊙O 于点C .连接BC .（1）求证：CBP BAC ∠=∠；（2）求证：PA PC PB ⋅=2；（3）当3,6==CP AC 时，求PAB ∠sin 的值.【答案】(1)详见解析；（2）详见解析；（3）3.【解析】试题分析：（1）根据直径所对的圆周角为直角、切线的性质定理、同角的余角相等，即可证得CBP BAC ∠=∠；（2）先证△PB ∽C △ABP ，根据相似三角形的性质即可得结论； （3）利用PA PC PB ⋅=2，得33=PB ，从而求PAB ∠sin =3试题解析：【解】（1）∵AB 是⊙O 的直径∴∠ACB=90°∴∠A+∠ABC=90°∵PB 与⊙O 相切于点B∴∠CBP+∠ABC=90°∴CBP BAC ∠=∠(2)∵CBP BAC ∠=∠，∠P=∠P∴△PB ∽C △ABP∴BPPC AP PB =∴PA PC PB ⋅=2（3）∵3,6==CP AC ∴AP=9∵PA PC PB ⋅=2∴33=PB∴PAB ∠sin =3339==AP PB 14. (2017浙江金华第22题)如图，已知：AB 是O 的直径，点C 在O 上，CD 是O 的切线，AD CD ⊥于点,D E 是AB 延长线上的一点，CE 交O 于点F ，连接,OC AC ．(1)求证：AC 平分DAO ∠．(2)若105DAO ∠=，30E ∠=．①求OCE ∠的度数．②若O 的半径为2，求线段EF 的长．【答案】(1)详见解析；（2）①∠OCE=45°；②3（1）解：∵直线与⊙O 相切，∴OC ⊥CD ；又∵AD ⊥CD,∴AD （2）解：①∵AD ②作OG ⊥CE 于点G,可得FG=CG,∵2,∠OCE=45°.∴CG=OG=2,∴FG=2;∵在RT △OGE 中，∠E=30°，∴3,∴315. （2017浙江湖州第21题）（本小题8分）如图，O 为Rt C ∆AB 的直角边C A 上一点，以C O 为半径的O 与斜边AB 相切于点D ，交OA 于点E ．已知C 3B =，C 3A =．（1）求D A 的长；（2）求图中阴影部分的面积．【答案】（132）6π （1）在Rt △ABC 中，22AC BC +223(3)+3 ∵BC ⊥OC∴BC 是⊙O 的切线∵AB 是⊙O 的切线∴3∴3（2）在Rt △ABC 中，sinA=31223BC AB == ∴∠A=30°∵AB 切⊙O 于点D∴OD ⊥AB∴∠AOD=90°-∠A=60°∵tan =tan 30OD A AD=∴3 =3 3∴OD=1∴2601==3606 Sππ⨯阴影考点：1、切线的性质，2、勾股定理，3、解直角三角形，4、扇形的面积16. （2017浙江台州第22题）如图，已知等腰直角三角形ABC，点P是斜边BC上一点（不与,B C重合），PE是ABP∆的外接圆⊙O的直径.（1）求证：APE∆是等腰直角三角形；（2）若⊙O的直径为2，求22PC PB+的值.【答案】（1）证明见解析（2）4（1）证明：∵△ABC是等腰直角三角形，∴∠C=∠ABC=45°,∴∠PEA=∠ABC=45°又∵PE是⊙O的直径，∴∠PAE=90°,∴∠PEA=∠APE=45°,∴△APE是等腰直角三角形.（2）∵△ABC是等腰直角三角形，∴AC=AB,同理AP=AE,又∵∠CAB=∠PAE=90°,∴∠CAP=∠BAE,∴△CPA≌△BAE,∴CP=BE,在Rt△BPE中，∠PBE=90°,PE=2,∴PB2+BE2=PE2,∴CP2+PB2=PE2=4.考点：1、全等三角形的判定与性质，2、等腰三角形的判定与性质，3、勾股定理，4、圆心角、弧、弦的关系，5、等腰直角三角形14．（2017四川省南充市）如图，在Rt△ABC中，∠ACB=90°，以AC为直径作⊙O交AB于点D，E为BC的中点，连接D E并延长交AC的延长线于点F．（1）求证：DE是⊙O的切线；（2）若CF=2，DF=4，求⊙O直径的长．【答案】（1）证明见解析；（2）6．【解析】试题分析：（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案；（2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．试题解析：（1）如图，连接OD、CD．∵AC为⊙O的直径，∴△BCD是直角三角形，∵E为BC的中点，∴BE=CE=DE，∴∠CDE=∠DCE，∵OD=OC，∴∠ODC=∠OCD，∵∠ACB=90°，∴∠OCD+∠DCE=90°，∴∠ODC+∠CDE=90°，即OD⊥DE，∴DE是⊙O的切线；（2）设⊙O的半径为r，∵∠ODF=90°，∴OD2+DF2=OF2，即r2+42=（r+2）2，解得：r=3，∴⊙O的直径为6．考点：切线的判定与性质．15．（2017四川省广安市）如图，已知AB是⊙O的直径，弦CD与直径AB相交于点F．点E在⊙O外，做直线AE，且∠EAC=∠D．（1）求证：直线AE是⊙O的切线．（2）若∠BAC=30°，BC=4，cos∠BAD=34，CF=103，求BF的长．【答案】（1）证明见解析；（2）5219．（1）连接BD，∵AB是⊙O的直径，∴∠ADB=90°，即∠ADC+∠C DB=90°，∵∠EAC=∠ADC，∠CDB=∠BAC，∴∠EAC+∠BAC=90°，即∠BAE=90°，∴直线AE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ACB=90°，Rt△ACB中，∠BAC=30°，∴AB=2BC=2×4=8，由勾股定理得：AC=2284-=43，Rt△ADB中，cos∠BAD=34=ADAB，∴34=8AD，∴AD=6，∴BD=2286- =27，∵∠BDC=∠BAC，∠DFB=∠AFC，∴△DFB∽△AFC，∴BF BDFC AC=，∴2710433BF=，∴BF=521．考点：1．切线的判定与性质；2．解直角三角形．。