SAS学习系列26 Logistic回归
26. Logistic回归（一）Logistic回归一、原理二元或多元线性回归的因变量都是连续型变量，若因变量是分类变量（例如：患病与不患病；不重要、重要、非常重要），就需要用Logistic回归。
Logistic回归分析可以从统计意义上估计出在其它自变量固定不变的情况下，每个自变量对因变量取某个值的概率的数值影响大小。
Logistic回归模型有“条件”与“非条件”之分，前者适用于配对病例对照资料的分析，后者适用于队列研究或非配对的病例-对照研究成组资料的分析。
对于二分类因变量，y=1表示事件发生；y=0表示事件不发生。
事件发生的条件概率P{ y=1 | x i } 与x i之间是非线性关系，通常是单调的，即随着x i的增加/减少，P{ y=1 | x i } 也增加/减少。
Logistic函数F(x)=，图形如下图所示：该函数值域在(0,1)之间，x趋于-∞时，F(x)趋于0；x趋于+∞时，F(x)趋于1. 正好适合描述概率P{ y=1 | x i }. 例如，某因素x导致患病与否：x在某一水平段内变化时，对患病概率的影响较大；而在x较低或较高时对患病概率影响都不大。
记事件发生的条件概率P{ y=1 | x i } = p i，则p i ==记事件不发生的条件概率为1- p i =则在条件x i下，事件发生概率与事件不发生概率之比为=称为事件的发生比，简记为odds. 对odds取自然对数得到上式左边（对数发生比）记为Logit(y), 称为y的Logit变换。
可见变换之后的Logit(y)就可以用线性回归，计算出回归系数α和β值。
若分类因变量y 与多个自变量x i 有关，则变换后Logit(y)可由多元线性回归：11logit()ln()1k k p p x x p αββ==++-或 111()1(1|,,)1k k k x x p y x x e αββ-++==+ 二、回归参数的解释1. 三个名词 发生比（odds ）= =例如，事件发生概率为0.6，不发生概率为0.4，则发生比为1.5（发生比>1，表示事件更可能发生）。
发生比率（OR ）= = = = 即主对角线乘积/副对角线乘积，也称为交叉积比率，优势比。
例如，说明：大于1（小于1）的发生比率，表明事件发生的可能性会提高（降低），或自变量对事件概率有正（负）的作用；发生比率为1表示变量对事件概率无作用。
相对风险（RR）= =用来进行两组概率之间的比较。
当p1= p2时，相对风险为1，表明两组在事件发生方面没有差别。
2. 连续型自变量回归参数的解释截距α：基准发生比的对数，即当Logistic回归模型中没有任何自变量时（除常量外，所有自变量都取0值）所产生的发生比。
由于理解发生比，比理解对数发生比更容易，故将Logistic回归模型改写为：odds = =若βk>0（βk<0），则>1（<1）, 即x k每增加一个单位值时发生比会相应增加（减少）；若βk=0，则=1, 那么x k不论怎样变化发生比都不会变化。
反映了自变量x k增加一个单位时发生比所变化的倍数，即(x k+1)时的发生比与原发生比【(x k)时】之比。
自变量x k每变化一个单位，发生比率的变化率为注：由于βk是自变量x k的偏系数估计，故称为调整发生比率（AOR）的估计。
实际中，往往更关心的不是自变量变化1个单位，而是变化一段水平b-a个单位，例如年龄每增加5岁，此时调整发生比率为AOR =3. 二分类自变量回归参数的解释 二分类变量，例如性别，取值可以用0或1编码，也称为标志变量或虚拟变量。
若x k 为取值0或1的二分类变量，则有111ln()11k i x k ip x p αββ==+++⋅- 011ln()01k i x k i p x p αββ==+++⋅-两式作差得10 1 0ln()ln()ln(odds)11k k k k i i k x x x vs x i ip p p p β=====-=-- 可见βk 就是在控制其它变量条件下，x k =1与x k =0的对数发生比的差；也即是发生比率的对数，即调整发生比率的估计可表示为= 1 0(odds)k k x vs x ==注意，发生比率是，而不是两者概率比4. 多分类变量的处理与回归参数的解释当分类自变量多于两个类别时，需要建立一组虚拟变量来代表类型的归属性质。
若一个分类变量包括m 个类别，则可以产生m 个相应的虚拟变量，但建模需要的虚拟变量的数目为m-1. 省略的那个类别作为参照类。
例如，年龄是有序变量，按年龄段分为四个类别：x <40，40≤x <50，50≤x <60, x ≥60.设置3个虚拟变量Age1表示40≤x <50（属于该年龄段则Age1=1，否则Age1=0）；Age2表示50≤x <60（属于该年龄段则Age2=1，否则Age2=0）；Age3 表示x ≥60（属于该年龄段则Age3=1，否则Age3=0）；另一个不指定虚拟变量的x <40作为参照类（Age1，Age2，Age3都为0；哪一类作为参照类是随意的，取决于偏好或解释的方便）。
则模型为112233ln()Age Age Age 1p pαβββ=+++- 同二分类变量时一样，β1代表40≤x <50与参照类（Age0: x <40）在因变量上的差别，故β1 = ln(odds)Age1 vs Age0且40≤x <50对 x <40的发生比率为.注：（1）名义变量直接就是分类变量；连续变量也可以改为分类变量，例如考试成绩按分数段分为高、中、低三档。
（2）另外，也可采用效应变量编码，三种取值：-1, 0(参照类), 1.（3）用SAS 中CLASS 语句指定分类变量，可以自动进行效应编码，作为一组变量纳入模型，并对每一类别单独做显著性检验。
5. 用概率解释自变量的作用(1) 对事件发生概率的偏作用，可用Logit 函数求该自变量的偏导数来刻画：{1|}(1)k k kP y x p p x β∂==-∂ 其中p 为事件发生概率。
对于二元Logistic 回归，p =0.5时，斜率最陡，此时x=-α/β, 称为中位有效水平。
(2) 利用得到的Logistic 回归方程，可以预测概率：ˆˆˆˆodds ˆ1odds 1k k k k k k x x e p e αβαβ++∑==∑++ 有预测概率就可以计算某自变量值发生离散变化时，预测概率的离散变化：{1|,}{1|,}k k k P y x x x P y x x =+-=三、标准化系数通常在线性回归模型中的连续型自变量是以不同尺度度量的，这就使得某自变量中一个单位的变化并不等价于另一自变量上一个单位的变化。
因此，要使用标准化系数（使得因变量的作用具有可比性）。
标准化系数表示自变量的一个标准差的变化所导致的因变量上以其标准差为单位度量的变化。
有两种标准化的方法：（1）先回归再标准化；（2）先标准化x ，y 再回归；注：对于分类变量，例如性别、民族等，变量的标准化是没有意义的。
但其尺度标准要一致，比如0,1,2,3都变成1,2,3,4.四、偏相关偏相关，用来刻画在控制其他变量下，某自变量对Logistic 回归的贡献（依赖于其它变量）。
偏相关系数计算公式如下：r =其中，d.f.为自由度，分母为-2倍的截距模型（只有截距）的对数似然值。
五、回归参数的估计Logistic 回归参数的估计通常采用最大似然法，其基本思想是先建立似然函数与对数似然函数，再通过使对数似然函数最大求解相应的参数值，所得到的估计值称为参数的最大似然估计值。
假设有N 个案例构成的总体，Y 1, …, Y N . 从中随机抽取n 个案例作为样本，观测值标注为y 1 , …, y n . 设p i =P(y i =1 | x i )为给定x i 的条件下得到结果y i =1的条件概率，而在同样条件下得到结果为y i =0的条件概率为P(y i =0 | x i )=1-p i . 于是，得到一个观测值的概率为1()(1)i i y y i i i P y p p -=-其中，y i =1或y i =0. 当y i =1时，P(y i )= p i = P(y i =1 | x i ).由于各项观测相互独立，故它们的联合分布可表示为各边际分布的乘积：11()(1)i i ny y i i i L p p θ-==-∏称为n 个观测的似然函数。
对于Logistic 回归，/(1)i i x x i p e e αβαβ++=+. 根据最大似然原理，估计参数α和β使得似然函数L(θ)最大，令1ln[()][()ln(1)]i nx i i i L y x e αβθαβ+==+-+∑称为对数似然函数，也即让ln[L(θ)]最大。
令1ln[()][]01i i x n i x i L e y e αβαβθα++=∂=-=∂+∑ 1ln[()][]01i i x n i i x i L e y x e αβαβθβ++=∂=-=∂+∑ 采用牛顿迭代法解出α和β的估计值。
六、假设检验1. 似然比检验H 0：β1=β2=…=βp =0统计量201012(ln ln )2ln (2ln )LR L L L L χ=--=---服从自由度为变量个数该变量（从L 0到L 1）的卡方分布。
若P 值<0.05, 则拒绝原假设。
2. 比分检验以未包含某个或几个变量的模型为基础，保留模型中参数的估计值，并假设新增加的参数为零，计算似然函数的一价偏导数（也称“有效比分”）及信息距阵，两者相乘便得比分检验的统计量S. 样本量较大时，S 近似服从自由度为待检验因素个数的2χ分布。
3. Wald 检验即广义的T 检验，统计量为22ˆˆ[/SE ]kk W Z ββ== 其中ˆSE kβ为ˆk β的标准误。
H 0：βk =0为真时，Z 为标准正态分布，W 服从自由度为1的渐近2χ分布。
βk 的95%置信区间估计为：ˆˆˆˆSE 1.96SE k kk k Z αββββ±⋅=±. 发生比率的1-α置信区间为：ˆ/2ˆSE k k Z eαββ±⋅.注：上述三种方法中，似然比检验最可靠，比分检验一般与它相一致，但两者均要求较大的计算量；而Wald 检验未考虑各因素间的综合作用，在因素间有共线性时结果不如其它两者可靠。
为计算方便，通常向前选取变量用似然比或比分检验，而向后剔除变量常用Wald 检验。
七、模型的评价——拟合优度检验检查模型估计与实际数据的符合情况。
Spss软件之logistic回归分析
…
n
0
1
Xn01
X n02
…
1
0
X n11
X n12
…
2
0
Xn21
X n22
…
Xk X 10k X 11 k X 12k
X iMk
X n0k X n1 k X n2k
M
0
XnM1
XnM2
…
X nMk
Conditional logistic regression
用Pi表示第i层在一组危险因素作用下发病的概率, 条 件 logistic 模型可表示为
n
L
1
i1 1
M
k exp
j (X itj X i0 j )
t 1
j1
可以看出，条件logistic 回归分析只估计了表示危 险因素作用的βj值，表示匹配组效应的常数项βi0 则被自动地消去了。
Conditional logistic regression
对上述条件似然函数L取自然对数后，用非线性 迭代法求出参数的估计值bi及其标准误Sbi。回归 系数的假设检验及分析方法与非条件logistic回归 完全相同。
c1 1, c0 0,
Xj
1， 暴露
0，非暴露
ORj exp( j )
Logistic regression analysis
0,
ORj
1
无作用
ORj exp( j ), j >0, ORj 1 危险因子
0, ORj 1 保护因子
二、模型的参数估计
在logistic回归模型中，回归系数的估计通常用最大 似然法（MLE）。其基本思想是先建立一个样本 的似然函数，求似然函数达到最大值时参数的取 值，即为参数的极大似然估计值。
SAS学习系列26.Logistic回归
26. Logistic回归（一）Logistic回归一、原理二元或多元线性回归的因变量都是连续型变量，若因变量是分类变量（例如：患病与不患病；不重要、重要、非常重要），就需要用Logistic回归。
Logistic回归分析可以从统计意义上估计出在其它自变量固定不变的情况下，每个自变量对因变量取某个值的概率的数值影响大小。
Logistic回归模型有“条件”与“非条件”之分，前者适用于配对病例对照资料的分析，后者适用于队列研究或非配对的病例-对照研究成组资料的分析。
对于二分类因变量，y=1表示事件发生；y=0表示事件不发生。
事件发生的条件概率P{ y=1 | x i } 与x i之间是非线性关系，通常是单调的，即随着x i的增加/减少，P{ y=1 | x i } 也增加/减少。
Logistic函数F(x)=1，图形如下图所示：1+e−x该函数值域在(0,1)之间，x 趋于-∞时，F(x )趋于0；x 趋于+∞时，F(x )趋于1. 正好适合描述概率P{ y =1 | x i }. 例如，某因素x 导致患病与否：x 在某一水平段内变化时，对患病概率的影响较大；而在x 较低或较高时对患病概率影响都不大。
记事件发生的条件概率P{ y =1 | x i } = p i ，则p i =11+e −(α+βx i )=e α+βx i 1+e α+βx i记事件不发生的条件概率为1- p i =11+e α+βx i则在条件x i 下，事件发生概率与事件不发生概率之比为p i 1−p i= e α+βx i称为事件的发生比，简记为odds. 对odds 取自然对数得到ln (p i1−p i)= α+βx i 上式左边（对数发生比）记为Logit(y), 称为y 的Logit 变换。
可见变换之后的Logit(y)就可以用线性回归，计算出回归系数α和β值。
若分类因变量y 与多个自变量x i 有关，则变换后Logit(y)可由多元线性回归：11logit()ln()1k k pp x x p αββ==++-或 111()1(1|,,)1k k k x x p y x x eαββ-++==+二、回归参数的解释1. 三个名词发生比（odds）= 事件发生频数事件未发生频数= p k1−p k例如，事件发生概率为0.6，不发生概率为0.4，则发生比为1.5（发生比>1，表示事件更可能发生）。
SPSS做Logistic回归步骤
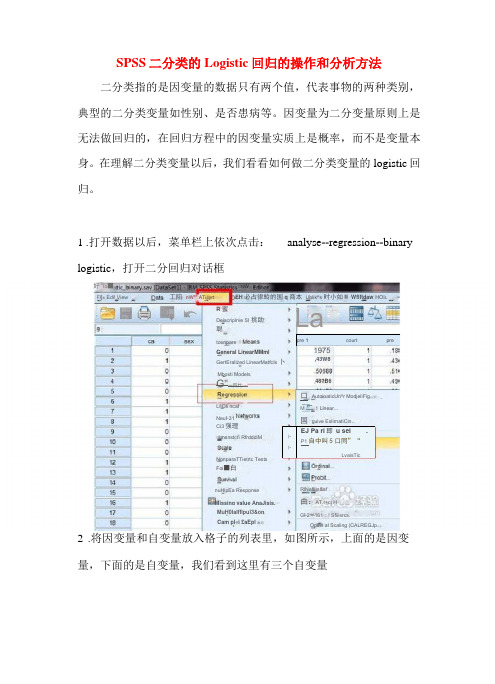
SPSS 二分类的Logistic 回归的操作和分析方法二分类指的是因变量的数据只有两个值，代表事物的两种类别， 典型的二分类变量如性别、是否患病等。
因变量为二分变量原则上是 无法做回归的，在回归方程中的因变量实质上是概率，而不是变量本 身。
在理解二分类变量以后，我们看看如何做二分类变量的logistic 回归。
1 .打开数据以后，菜单栏上依次点击： analyse --regression --binary logistic ，打开二分回归对话框2 .将因变量和自变量放入格子的列表里，如图所示，上面的是因变 量，下面的是自变量，我们看到这里有三个自变量pre 1courtpre卜 卜EJ Pa ri 即 u sei.P1自中叫5口同”“LvaisTic好 Io ■网 □N W□imsnstcri RfrdddiMNonparaTTietrtc Tests Foi ■白MuH0lalfflpul3&on Deiscriplrve SI 挑助聪LfiOli ncaf - Neuf-31 nuHlpEa ResponseMissing value AnaJisis. EH 必占律蛉的国q 商本 Ublik^s 时小如M Wflftdaw HOI LFl[« Edi! View工陷 nW"" ATiilyrtCam pl«i £aEpl 骷与Opsin al Scaling (CALREGJp..R 蜜GertEralized LinearMatfcIs 卜 Mbosti ModelsRlNafllin&af .曲：AT.r+ci HC] 2^^161；! Sfiiisrcs.tosnpareGeneral LinearMMml 48?B6Ci3强理 G"一四忙—一 3 La,43W8口 AutoioaticUn^r ModjeliFig..M 二1 Linear...国 guive EslirnatiCin...C>ep«n (lferit3 .设置回归方法，这里选择最简单的方法：enter ,它指的是将所有的 变量一次纳入到方程。
logistic回归模型
Logistic回归模型
• 列联表中的数据是以概率的形式把属性变量联系 起来的，而概率p的取值在0与1之间，因此，要把
概率 p (x)与 x 之间直接建立起函数关系是不合
适的。即 (x) x
Logistic回归模型
• 因此，人们通常把p的某个函数f(p)假设为变量的 函数形式，取 f ( p) ln (x) ln p
1 (x) 1 p
• 称之为logit函数，也叫逻辑斯蒂变换。 • 因此，逻辑斯蒂变换是取列联表中优势的对数。
当概率在0-1取值时，Logit可以取任意实数，避免 了线性概率模型的结构缺陷。
Logistic回归模型
假设响应变量Y是二分变量，令 p P(Y 1) ,影响Y
的因素有k个 x1, xk，则称：
多项logit模型
• 前面讨论的logit模型为二分数据的情况，有时候 响应变量有可能取三个或更多值，即多类别的属 性变量。
• 根据响应变量类型的不同，分两种情况：
–响应变量为定性名义变量； –响应变量为定性有序变量；
• 当名义响应变量有多个类别时，多项logit模型应 采取把每个类别与一个基线类别配成对，通常取 最后一类为参照，称为基线-类别logit.
• 为二分数据的逻辑斯ln 1蒂pp回归g(模x1,型,，xk简) 称逻辑斯蒂 回归模型。其中的k个因素称为逻辑斯蒂回归模型 的协变量。
• 最重要的逻辑斯蒂回归模型是logistic线性回归模 型，多元logit模型的形式为：
ln
p 1 p
0
1x1
k xk
Logistic回归模型
• 其中，0, 1, , k 是待估参数。根据上式可以得到
多项logit模型
logistic回归原理
logistic回归原理
Logistic回归是一种有效的、相对简单的数据分类技术，用于确定某个事件或观测值属于某类的概率。
它可以解释二元数据和多类数据，并且能够应用于各种场景，比如风险分析、金融建模、社会研究等等。
Logistic回归源自线性模型，它是一种称为逻辑斯蒂(logit)模型的回归模型，该模型基于概率理论。
Logistic回归模型是由概率对数函数构建而成的，即：
Y = log（P/(1-P)）
其中，P代表事件Y发生的概率。
Logistic归模型在数据分析中最主要的用途就是用于分类，它的原理是：假定输入的数据可以用一个线性函数来描述，并且拟合一条S型函数来获得概率，这个概率决定了每个样本点属于某一类的概率大小。
在使用Logistic回归之前，首先要处理好数据集，确保它具有足够的观测值，并且有合理的分类标签（例如“是”、“否”）。
接下来，要使用回归的模型，先把正确的观测值用正向的系数系数，将错误的观测值用负向的系数进行编码。
然后，确定正确的估计量结果，比如系数、拟合度指标和参数检验，以及误差分析。
最后，定义一个提升指标来评估结果，例如：准确率、召回率和精确率。
Logistic回归在机器学习中有各种应用，比如文本分类、情感分析和预测分析；在图像识别中，它可以用于目标检测、纹理识别和
边缘检测；在金融行业，它可以应用于信贷分析、欺诈检测和市场风险分析。
它也可以用于生物药物研究、病毒鉴别；在医学领域，它可以用于数据分析、诊断分析和临床预测等。
简而言之，Logistic回归是一种用于预测任意事件的概率发生的有效模型，可以用于多类数据的分类，在数据挖掘领域扮演着重要的角色，是结构化数据建模的常用工具。
logistic回归计算讲解
logistic回归计算讲解Logistic回归是一种广泛用于分类问题的机器学习算法。
它可以用于二分类问题，也可以通过一些修改用于多分类问题。
下面是Logistic回归的计算过程的简要讲解：1. 数据准备：首先，收集和准备用于训练和测试的数据集。
每个数据样本应该包括特征和对应的类别标签。
特征可以是连续值或离散值。
2. 特征缩放：如果特征具有不同的量纲或取值范围，可以对特征进行缩放，以便更好地使用Logistic回归算法。
常见的缩放方法包括标准化和归一化。
3. 参数初始化：初始化Logistic回归模型的参数，通常为权重（也称为系数）和偏置（也称为截距）。
4. 假设函数：定义Logistic回归的假设函数，它将特征值映射到预测的类别概率。
通常使用sigmoid函数作为Logistic回归的假设函数。
5. 成本函数：使用成本函数（也称为损失函数）来度量模型预测的错误程度。
对于Logistic回归，常用的成本函数是逻辑损失函数（Log Loss）或交叉熵损失函数。
6. 梯度下降：使用梯度下降算法或其他优化算法来最小化成本函数，从而找到最佳的模型参数。
梯度下降算法通过计算参数的梯度，沿着梯度的反方向更新参数，逐步调整参数值以降低成本。
7. 模型训练：使用训练数据集来训练Logistic回归模型。
通过迭代优化算法来更新参数，重复计算成本函数和梯度下降步骤，直到达到停止条件（如达到最大迭代次数或成本函数的变化很小）。
8. 模型预测：使用训练好的Logistic回归模型来进行预测。
将新的输入特征传递给假设函数，计算预测的类别概率。
通常，如果概率大于一个阈值，将样本预测为正类；否则，预测为负类。
常见的阈值是0.5。
以上是Logistic回归算法的主要计算步骤。
在实践中，还需要考虑特征选择、模型评估和调优等方面，以获得更好的分类性能。
(完整版)spss的logistic分析教程
Logistic回归主要分为三类，一种是因变量为二分类得logistic回归，这种回归叫做二项logistic回归，一种是因变量为无序多分类得logistic回归，比如倾向于选择哪种产品，这种回归叫做多项logistic回归。
还有一种是因变量为有序多分类的logistic回归，比如病重的程度是高，中，低呀等等，这种回归也叫累积logistic回归，或者序次logistic回归。
二值logistic回归：选择分析——回归——二元logistic，打开主面板，因变量勾选你的二分类变量，这个没有什么疑问，然后看下边写着一个协变量。
有没有很奇怪什么叫做协变量？在二元logistic回归里边可以认为协变量类似于自变量，或者就是自变量。
把你的自变量选到协变量的框框里边。
细心的朋友会发现，在指向协变量的那个箭头下边，还有一个小小的按钮，标着a*b，这个按钮的作用是用来选择交互项的。
我们知道，有时候两个变量合在一起会产生新的效应，比如年龄和结婚次数综合在一起，会对健康程度有一个新的影响，这时候，我们就认为两者有交互效应。
那么我们为了模型的准确，就把这个交互效应也选到模型里去。
我们在右边的那个框框里选择变量a，按住ctrl，在选择变量b，那么我们就同时选住这两个变量了，然后点那个a*b的按钮，这样，一个新的名字很长的变量就出现在协变量的框框里了，就是我们的交互作用的变量。
然后在下边有一个方法的下拉菜单。
默认的是进入，就是强迫所有选择的变量都进入到模型里边。
除去进入法以外，还有三种向前法，三种向后法。
一般默认进入就可以了，如果做出来的模型有变量的p值不合格，就用其他方法在做。
再下边的选择变量则是用来选择你的个案的。
一般也不用管它。
选好主面板以后，单击分类（右上角），打开分类对话框。
在这个对话框里边，左边的协变量的框框里边有你选好的自变量，右边写着分类协变量的框框则是空白的。
你要把协变量里边的字符型变量和分类变量选到分类协变量里边去（系统会自动生成哑变量来方便分析，什么事哑变量具体参照前文）。
利用 SPSS 进行 Logistic 回归分析简要步骤
利用SPSS 进行Logistic 回归分析简要步骤
现实中的很多现象可以划分为两种可能，或者归结为两种状态，这两种状态分别用0
和1 表示。
如果我们采用多个因素对0－1 表示的某种现象进行因果关系解释，就可能应用到logistic 回归。
Logistic 回归分为二值logistic 回归和多值logistic 回归两类.
第一步：整理原始数据。
数据整理内容包括两个方面：一
是对各地区按照三大地带的分类结果赋值，用0、1 表示，二是将城镇人口比重转换逻辑值，变量名称为“城市化”。
第二步：打开“聚类分析”对话框。
沿着主菜单的“Analyze→Regression→Binary Logistic
K
”的路径（图8-1-3）打开二值
Logistic 回归分析选项框.
第三步：选项设置。
首先，在源变量框中选中需要进行分析的变量，点击右边的箭头符号，将需要的变量调
入Dependent（因变量）和Covariates（协变量）列表框中（图8-1-5）。
在本例中，将名义变
量“城市化”调入Dependent（因变量）列表框，将“人均GDP”和“中部”调入Covariates （协变量）列表框中。
在Method（方法）一栏有七个选项。
采用第一种方法，即系统默认的强迫回归方法（Enter）。
接下来进行如下4 项设置：
⒈设置Categorical（分类）选项：定义分类变量.
⒉设置Save（保存）选项,
⒊设置Options
第四步,结果解读.。
saslogistic逻辑回归
如前所述，逻辑回归是一种用于解决 二元分类问题的机器学习算法，基于 逻辑函数拟合数据来预测事件发生的 概率。它在处理具有连续特征的数据 集时表现良好，并且可以用于预测概 率。
比较
支持向量机和逻辑回归在处理分类问 题时各有优缺点。SVM的优点在于其 强大的分类能力和对高维数据的处理 能力，尤其在处理线性可分的数据集 时表现优秀。而逻辑回归在处理具有 连续特征的数据集和预测概率方面表 现良好，且对于非线性数据集的处理 能力较强。
与决策树算法的比较
决策树算法
决策树算法是一种基于树的机器学习算法，通过递归地将数据集划分为更小的子集来构建 模型。它能够处理分类和回归问题，并且易于理解和解释。
逻辑回归
逻辑回归是一种用于解决二元分类问题的机器学习算法。它基于逻辑函数，通过拟合数据 来预测事件发生的概率。逻辑回归在处理具有连续特征的数据集时表现良好，并且可以用 于预测概率。
比较
决策树算法和逻辑回归在处理分类问题时各有优缺点。决策树算法可以处理更复杂的数据 集，但可能过拟合数据。逻辑回归在处理具有连续特征的数据集时表现良好，并且可以用 于预测概率，但可能不适用于具有大量特征的数据集。
与支持向量机算法的比较
支持向量机算法
逻辑回归
支持向量机（SVM）是一种监督学习 算法，用于分类和回归分析。它通过 找到能够将不同类别的数据点最大化 分隔的决策边界来实现分类。SVM对 于非线性数据集的处理能力有限，且 对于大规模数据集可能效率较低。
通过将自变量代入逻辑函数中，可以得到因变量的预测概率值，进而判断 其所属类别。
02 SASlogistic逻辑回归的 实现
SASlogistic逻辑回归的步骤
数据准备
对数据进行清洗、整理和转换， 确保数据的质量和可用性。
Logistic回归模型
Logistic 回归模型一、 分组数据的Logistic 回归模型针对0-1型因变量产生的问题，我们对回归模型应该作两个方面的改进。
第一， 回归函数应该用限制在[0，1]区间内的连续曲线，而不能再沿用沿用直线回归方程。
限制在[0，1]区间内的连续曲线很多，例如所有连续变量的分布函数都符合要求，我们常用的是Logistic 函数与正如分布函数，Logistic 函数的形式为：()1xxe f x e =+Logistic 函数的中文名称逻辑斯蒂函数，简称逻辑函数 第二、因变量y 本身只取0、1两个离散值，不适合直接作为回归模型中的因变量,由于回归函数01()i i i E y x πββ==+表示在自变量为i x 的条件下i y 的平均值,而i y 是0-1型随机变量,因而()i i E y π=就是在自变量为i x 的条件下i y 等于1的比例.这就提示我们可以用i y 等于1的比例代替i y 本身作为因变量.二,例子 在一次住房展销会上,与房地产商签订初步购房意向书的共有325n =名顾客,在随后的3个月的时间内,只有一部分顾客确实购买了房屋.购买了房屋的顾客记为1,没有购买房屋的顾客记为0,以顾客的年家庭收入为自变量x,对下面表所示的数据,序号年家庭收入（万元）x 签订意向书人数n 实际购房人数m 实际购房比例p逻辑变换p′=ln(p/(1-p))权重w=np(1-p)1 1.52580.32-0.7537718 5.442 2.532130.40625-0.37948967.718753 3.558260.448276-0.207639414.344834 4.552220.423077-0.310154912.692315 5.543200.465116-0.139761910.697676 6.539220.5641030.257829119.58974477.528160.5714290.287682076.85714388.521120.5714290.287682075.14285799.515100.6666670.693147183.333333建立Logistic 回归模型:c i x x p i i i,,2,1,)exp(1)exp(1010 =+++=ββββ,其中，c 为分组数据的组数，本例中c=9.将以上回归方程作线性变换，令)1ln(iii p p p -=' 该变换称为逻辑变换，变换后的线性回归模型为 i i i x p εββ++='10该式是一个普通的一元线性回归模型。