有限元分析材料
有限元分析在材料力学中的应用与优化设计

有限元分析在材料力学中的应用与优化设计材料力学是研究材料的力学性质、变形行为和破坏机制的学科,而有限元分析作为一种强大的计算工具,在材料力学领域中得到了广泛的应用。
本文将介绍有限元分析在材料力学中的应用,并探讨有限元分析在材料力学优化设计中的潜力。
一、有限元分析在材料力学中的应用1. 材料力学参数分析有限元分析可以通过建立材料模型,并引入相应的力学参数,来分析材料在加载过程中的力学响应。
通过改变材料的弹性模量、屈服强度等力学参数,可以预测材料的变形行为和破坏机制,为材料性能的改进和设计提供理论依据。
2. 材料疲劳寿命估计在材料力学中,疲劳是一个重要的研究方向。
有限元分析可以模拟材料在循环加载下的变形行为,通过计算应力、应变的变化,预测材料的疲劳寿命。
这有助于设计更加耐久和可靠的材料结构。
3. 材料失效分析有限元分析在材料失效分析中起到了关键的作用。
通过建立合适的失效准则,并将其应用于有限元模型中,可以确定材料的破坏位置和破坏形式。
这对于预测材料的寿命和改进设计具有重要的意义。
二、有限元分析在材料力学优化设计中的潜力1. 拓宽设计空间传统的材料力学设计往往依赖经验公式和试错法,设计空间有限。
而有限元分析可以通过模拟和分析不同材料参数、结构形式等因素对材料力学性能的影响,为设计师提供大量可行的设计方案,拓宽了设计空间。
2. 优化材料性能有限元分析结合材料力学的理论知识,可以帮助优化材料的性能。
通过优化材料的力学参数,例如提高弹性模量、降低应力集中等,可以实现材料的功能改进,提高材料的强度、韧性等性能。
3. 提高设计效率有限元分析可以模拟不同材料力学行为,通过计算机进行大规模计算,大大加快了设计过程。
设计师可以通过有限元分析快速评估不同设计方案的优劣,并进行参数敏感性分析,以指导设计方向。
4. 减少实验成本在传统的材料力学设计中,往往需要进行大量的实验来验证设计方案的可行性。
而有限元分析可以通过模拟不同材料参数和加载条件下的力学性能,减少实验的数量和成本。
复合材料用有限元分析

复合材料用有限元分析引言复合材料是由不同类型的材料组合而成的,具有优异的力学性能和轻质化的特点,在航空航天、汽车工程、建筑结构等领域得到广泛应用。
有限元分析是一种常用的工程分析方法,可用于预测复合材料结构在受力过程中的应力和变形情况。
本文将介绍复合材料用有限元分析的基本原理、建模过程、分析方法和结果解读。
有限元分析基本原理有限元分析基于有限元法,将复杂的结构分割成许多简单的单元,再利用数学方法求解这些单元的力学行为,最终得出整个结构的应力和变形情况。
复合材料的有限元分析一般采用3D固体单元或板单元,考虑复合材料的各向异性和层合板的分层结构。
有限元分析的基本原理可以总结为以下几个步骤:1.确定有限元模型:–根据复合材料结构的几何形状和材料性质,选择适当的有限元单元类型。
–确定网格划分方案,将结构划分为单元网格。
–确定边界条件和加载方式,包括约束条件和外部加载。
2.确定单元性质:–根据复合材料的材料力学性质,将其转化为有限元单元的材料刚度矩阵。
–考虑各向异性和分层结构,将材料刚度矩阵进行相应的转换。
3.确定单元相互连接关系:–根据结构的几何体系,确定单元之间的连接关系,包括单元之间的约束和边界条件。
4.求解方程组:–根据单元的刚度矩阵和边界条件,建立整个结构的刚度矩阵。
–考虑加载情况,求解结构的位移和应力。
5.结果后处理:–分析结构的应力和变形分布,评估结构的安全性和性能。
–对结果进行解读和优化。
复合材料有限元分析的建模过程复合材料的有限元分析建模过程与传统材料的有限元分析类似,但在材料性质和单元连接方面存在一些特殊性。
下面是复合材料有限元分析的建模过程的简要步骤:1.几何建模:–根据实际结构的几何形状,利用建模软件(如Solidworks或CATIA)进行3D建模。
–根据复合材料的分层结构,将各层材料的几何形状分别绘制。
2.材料定义:–根据复合材料的材料属性,定义合适的材料模型和参数。
–考虑复合材料的各向异性和分层结构,定义材料的力学参数。
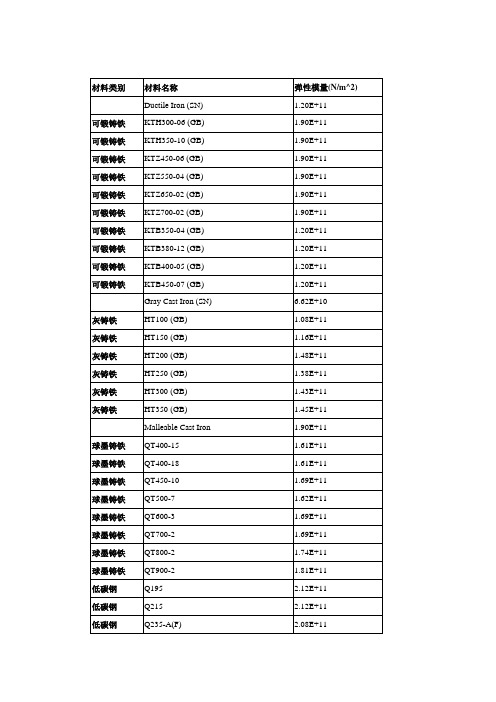
(完整版)有限元分析用的材料属性表
Cr4Mo4V# CrWMn 20CrMnMo 40CrMnMo 20CrMnTi 30CrMnTi 20CrMnSi 40CrMnSiMoV 5Cr21Mn9Ni2N 5Cr21Mn9Ni12N 20CrNiMo 20CrNi2MoA 2Cr12NiMoWV 28CrNiMoV# 30Cr2Ni4MoV# 40CrNiMo 40CrNiMoA 45CrNiMoV 45CrNiMoVA 10Cr2Mo1# 10Cr9Mo1VNb# 10CrMo910# 12Cr1MoV 12Cr1MoVTiB# 12Cr3MoVSiTiB# 12CrNi3 12Cr2Ni4 12Cr2Ni4H 12Cr2Ni4HA 12Cr18Ni9# 12Cr11MoV# 12Cr12Mo#
9Cr2Mo#
Cr12MoV
1.08E+11 2.10E+11 2.23E+11 2.10E+11 2.10E+11 2.10E+11 2.11E+11 2.11E+11 2.15E+11 2.06E+11 2.06E+11 2.06E+11 2.06E+11 2.06E+11 2.00E+11 2.07E+11 2.06E+11 2.11E+11 2.06E+11 2.06E+11 2.12E+11 2.10E+11 2.10E+11 2.11E+11 2.11E+11 2.20E+11 2.11E+11 2.13E+11 2.12E+11 2.25E+11 2.36E+11 2.18E+11
有限元分析用的材料属性表zy

可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁 可锻铸铁
灰铸铁 灰铸铁 灰铸铁 灰铸铁 灰铸铁 灰铸铁
材料名称 Ductile Iron (SN) KTH300-06 (GB) KTH350-10 (GB) KTZ450-06 (GB) KTZ550-04 (GB) KTZ650-02 (GB) KTZ700-02 (GB) KTB350-04 (GB) KTB380-12 (GB) KTB400-05 (GB) KTB450-07 (GB) Gray Cast Iron (SN) HT100 (GB) HT150 (GB) HT200 (GB) HT250 (GB) HT300 (GB) HT350 (GB)
常用工程材料属性( 弹性模量(N/m^2) 1.20E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.90E+11 1.20E+11 1.20E+11 1.20E+11 1.20E+11 6.62E+10 1.08E+11 1.16E+11 1.48E+11 1.38E+11 1.43E+11 1.45E+11
碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 碳素工具钢 铸钢 铸钢 铸钢 合金结构钢 合金结构钢 合金结构钢 合金结构钢
35Mn 45Mn 60Mn 65Mn 70Mn T2 T3 T7 T8 T8Mn T9 T10 ZG230-450 (GB) ZG20SiMn (GB) ZG40Cr (GB) Q295 Q345 Q390 Q420
有限元分析说明书

材料45号钢
强度较高,塑性和韧性尚好,用于制作承受负荷较大的小截面调质件和应力较小的大型正火零件,以及对心部强度要求不高的表面淬火零件,如曲轴、传动轴、齿轮、蜗杆、键、销等。水淬时有形成裂纹的倾向,形状复杂的零件应在热水或油中淬火。
弹性模量E=200GP,泊松比0.3,钢抗拉强度为600MPa,屈服强度为235MPa
求解结束
8.查看结果、分析、得出结论
接触摩擦应力
最大等效应力图
放大之后
最大位移图
结论:有计算结果可知,轮子的最大应力发生在与导轨接触近处,其值为168.745MP,小于235MP,最大位移为0.001555mm,发生在轮子轴孔处。满足使用要求。
组内评分:
卢亚宾5分
张雄4分
梁利闯6分
参考文献
【1】龚曙光,边炳【M】有限元基本原理及理论.武汉:华中科技出版社.
一、箱体
材料灰铸铁(HT200)
铸铁级别较高强度铸铁,基本组织为珠光体
主要特性强度、耐磨性、耐热性均较好,减震性也良好;铸铁性能较好,需要进行人工时效处理。
材料性能弹性模量E=120GP泊松比0.3最小抗拉强度200MP
Ansys分析计算
1.选择单元element type
选择实体,“Brick 8 node 185”类型
最大位移图
结论:有计算结果可知,凸轮的最大应力发生在键槽附近处,其值为51.56MP,小于335MP,最大位移为0.000757mm,发生在凸轮上下面。满足使用要求。
三、轴
材料45钢
轴类零件是机器中经常遇到的典型零件之一。它主要用来支承传动零部件,传递扭矩和承受载荷。45号钢为优质碳素结构用钢,硬度不高易切削加工,模具中常用来做模板,梢子,导柱等,但须热处理。
机械设计中有限元分析的几个关键问题

机械设计中有限元分析的几个关键问题机械设计中有限元分析是一种重要的工程分析方法,通过对机械结构进行有限元分析,可以评估结构的强度、刚度、稳定性等性能,为设计提供依据,提高产品的可靠性和安全性。
在进行有限元分析时,有一些关键问题需要特别注意,本文将就机械设计中有限元分析的几个关键问题进行探讨。
一、材料特性的选择在进行有限元分析时,首先需要确定材料的特性,例如弹性模量、屈服强度、断裂韧性等参数。
这些参数的选择对于有限元分析结果的准确性有着重要的影响。
在实际工程中,材料的特性往往是不确定的,因此需要根据实际情况进行合理的选择。
对于复合材料等非均质材料,其材料特性更为复杂,需要进行更为精细的分析和计算。
二、网格的生成和质量有限元分析是通过将结构划分为有限个小单元来进行分析计算的,这些小单元即为网格单元。
网格的生成和质量直接关系到分析结果的准确性。
不合理的网格划分可能会导致计算结果的误差,甚至影响到整个分析的可靠性。
合理的网格生成和质量的控制是进行有限元分析时的关键问题之一。
三、边界条件的确定在进行有限元分析时,需要明确结构的边界条件,包括约束边界和加载边界。
边界条件的确定关系到分析结果的可靠性和准确性。
合理的边界条件能够更好地模拟实际工况,得到真实的分析结果。
不合理的边界条件可能导致分析结果的失真,甚至无法得到可靠的结论。
四、材料非线性和接触非线性在实际工程中,材料的行为往往是非线性的,包括弹塑性、损伤、断裂等。
在一些结构的分析中,考虑到接触的影响也需要考虑到接触非线性。
这些非线性因素对于分析结果有着重要的影响,需要在有限元分析中予以充分考虑。
五、模态分析和稳定性分析除了结构的强度和刚度等静态性能外,对于一些关键结构还需要进行模态分析和稳定性分析。
模态分析用于评估结构的振动特性,稳定性分析则用于评估结构在受到外部载荷时的稳定性。
这些分析对于确保机械结构的安全性和可靠性至关重要。
六、敏感性分析和可靠度分析在进行有限元分析时,还需要进行敏感性分析和可靠度分析。
材料力学中的有限元方法分析

材料力学中的有限元方法分析材料力学是研究物质初始状态至最终破坏状态之间的力学行为及其规律的科学。
有限元分析是一种数值计算方法,可以求解各种工程问题的数学模型。
有限元方法在材料力学研究中有着重要的应用,本文将从有限元方法的基本原理、材料力学中的有限元分析、有限元模拟在材料力学中的应用等方面进行分析。
一、有限元方法的基本原理有限元方法是一种通过建立复杂结构的有限元模型,将一个复杂的连续问题转化为离散问题来求解的方法。
其基本思想是将一个连续物体分割成很多小的单元,使用一些简单的解析方法求解每个小单元内的力学问题,然后将所有小单元的解组合在一起来求解整体力学问题。
有限元方法求解的过程分为以下基本步骤:1.建立有限元模型2.离散化3.施加约束4.建立刚度矩阵和荷载向量5.求解未知量二、材料力学中的有限元分析材料力学中的有限元分析是指通过有限元方法对材料力学问题进行分析、计算和评估的方法。
材料力学问题中的目标是通过施加荷载或外界力,来得到物体内部的应力和应变状态,以及其随时间和载荷变化的规律。
在建立材料力学有限元模型时,需要考虑以下因素:1.应力集中和应变集中的位置和程度2.物理边界和几何结构3.材料的力学性质和力学参数材料力学中的有限元分析包含以下几个方面:1.静态分析:研究物体在静态等效荷载下的应力状态,计算物体的静态变形。
2.动态分析:研究物体在动态载荷下的应力和应变状态,计算物体的动力响应。
3.疲劳分析:研究物体在周期性载荷下的损伤状态、损伤机理和寿命预估。
4.热力耦合分析:研究物体在温度场和应力场的共同作用下的应力和应变状态。
5.多物理场分析:研究物体在电、磁、声、液、气、红外、光、辐射等多个物理场的共同作用下的应力和应变状态。
三、有限元模拟在材料力学中的应用有限元模拟在材料力学中的应用范围非常广泛,包括了以下几个方面:1.材料的结构设计和分析2.材料的性质和参数的测试和评估3.材料的制造和加工工艺的模拟4.材料的破坏和损伤机理的研究5.材料的寿命评估和振动疲劳分析最终,有限元分析的结果可以在材料设计、材料优化和制造流程等方面提供准确的数据支持,帮助人们更好地理解材料的力学行为和性质,促进材料科学的发展。
塑性材料的有限元分析

针对复杂材料和结构,需要深入研究材料的非线 性行为和多场耦合效应,建立更加完善的物理模 型和数值算法。
此外,应加强与实验研究的结合,通过实验验证 和修正有限元模型,提高模拟结果的可靠性。同 时,实验研究也能够为有限元分析提供更加真实 和全面的材料性能数据。
THANK YOU
03
有限元分析方法
有限元分析的基本原理
离散化
将连续的物理系统离散为有限个小的单元,每个 单元称为有限元。
近似解法
通过数学方法求解每个有限元的近似解,再通过 组合所有有限元的解得到整个系统的近似解。
平衡方程
建立每个有限元的平衡方程,通过求解平衡方程 得到每个节点的位移和应力。
有限元分析的实现过程
然而,塑性材料的有限元分析仍存在 一些挑战和限制,如模型的简化、边 界条件的确定、材料参数的获取等, 需要进一步研究和改进。
研究展望
未来研究应致力于发展更加精确和高效的有限元 分析方法,提高模拟结果的可靠性和精度。
在实际工程应用中,应加强有限元分析与其他数 值方法(如边界元、有限体积等)的结合,实现 优势互补,提高计算效率。
塑性变形的微观机
制
塑性变形是通过位错的滑移和攀 移等微观机制实现的,这些机制 在宏观上表现为塑性变形。
塑性变形的温度效
应
温度对塑性变形的影响较大,温 度升高会使材料的屈服强度降低, 塑性变形能力增强。
塑性变形的加工硬
化
在塑性变形过程中,材料的屈服 强度会随着变形程度的增加而逐 渐提高,这种现象称为加工硬化。
背景
随着计算机技术的不断发展,有限元分析已成为工程领域中解决复杂问题的常 用方法。通过有限元分析,可以模拟材料的变形、应力分布、应变等,为实际 工程提供重要的理论依据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.简述整体坐标的概念P25答:单元刚度矩阵的坐标变换式把平面刚架的所有单元在局部坐标系X’Y’z’下的单元刚度矩阵变换到一个统一的坐标系xoy下,这个统一的坐标系xoy称为整体坐标系。
12.P31答:平面钢架局部坐标系下的单元刚度矩阵与整体坐标系的下单元刚度矩阵的关系
有限元分析材料
篇一:有限元分析资料
1.什么是等参数单元?(教材)坐标变换和单元内的场函数采用相同数目的节点参数及相同的插值函数,这种变换方法是等参数变换,这种变换方式能满足坐标变换的相容性,采用等参数变换的单元称之为等参数单元。
2.等参数单元的特点、基本条件、划分单元应注意的问题(教材习题)
3.应用等参数单元时为什么要采用高斯积分,高斯积分点的数目如何确定?(教材习题)
5.梁单元和平面钢架结构单元的自由度由什么确定答:每个节点上有几个节点位移分量,就称每个节点有几个自由度
6.简述单元刚度矩阵的性质和矩阵元素的物理意义P9答:单元刚度矩阵是描述单元节点力和节点位移之间关系的矩阵单元刚度矩阵中元素aml的物理意义为单元第L个节点位移分量等于1,其他节点位移分量等于0时,对应的第m个节点力分量。
4.薄板弯曲问题的基本假设是什么?(其他参考书)(1)板弯曲钱垂直于中面的法线,在板弯曲后保持为直线,并垂直于弯曲后的中面。(2)板面各水平层之间相互挤压(3)薄板受垂直于中面的载荷时可以为中间层各点设有平行于板面的位移.
5.位移插值必须满足的三个条件:(教材)(1)位移插值函数应能满足单元的刚体位移(2)位移插值函数应能反映常量应变——常应变准则(3)位移插值函数应能保证单元内及相邻单元间位移的连续性——变形协调准则
15.什么叫平面应力问题?什么叫平面应力问题?什么叫平面应力问题设有很薄的薄板,只在边上受有平行于板面并且不沿厚度变化的面力,同时体积力也平行于板面并且不沿厚度变化,,这种有限元问题叫做平面应力问题。
1.诉述有限元法的定义P1答:有限元法是近似求解一般连续场问题的数值方法
2.有限元法的基本思想是什么P3答:首先,将表示结构的连续离散为若干个子域,单元之间通过其边界上的节点连接成组合体。其次,用每个单元内所假设的近似函数分片地表
7.刚度矩阵性质(总刚):(1)对称性,关于正对角线对称(2)稀疏性,矩阵中有大量的零元素(3)带状分布,矩阵中非零元素在主对角线两侧呈带状分布10.形函数的性质。(教材)(1)单元内任一点的三个形函数之和恒等于1,即ni+nj+nm=1.(2)在节点i:ni=1,nj=0,nm=0在节点j:ni=0,nj=1,nm=0在节点m:ni=0,nj=0,nm=111.有限元法的特点(其他参考书)(1)概念清楚,容易理解(2)适应性强,应用范围广。(3)有限元法采用矩阵形式表达,便于编制计算机程序,可以充分利用数字计算机的优势。(4)有限元法的主要缺点是解决工程问题必须首先编制计算机程序,必须运用计算机求解。
7.有限元法基本方程中的每一项的意义是什么P14答:,:整个结构的节点载荷列阵(外载荷、约束力),:整个结构的节点位移列阵,:结构的整体刚度矩阵,又称总刚度矩阵。
8.位移边界条件和载荷边界条件的意义是什么答:由于刚度矩阵的线性相关性不能得到解,从而引入边界条件。
9.简述整体刚度矩阵的性质和特点P14答:对称性;奇异性;稀疏性;带状性;对角线上的元素恒为正;每一行或者每一列相加为零。
6.什么是轴对称问题?(其他参考书):轴对称物体的形变及应力分布不一定是轴对称的,只有当约束和载荷都对称于旋转轴时,轴对称物体的变形及应力分布才是轴对称的。我们把满足上述条件的系统应力分析问题称为轴对称问题。(教材):如果弹性体的几何形状、约束情况以及所受的外力,都是绕某一轴对称的,则弹性体的应力、应变和位移也就对称于这一轴,这种问题称为轴对称问题。
13.虚功原理。(其他参考书)对于在力的用作下处于平衡状态的任何物体,不用考虑它是否真正发生了位移,而假想它发生了位移,那么物体上所有的力在这个虚位移上的总共必定等于零。
14.求解有限元七大步:(其他参考书)(1)选择坐标系,写出节点力的向量和位移向量
(2)选择合适的位移插值函数(3)求解出位移插值函数或形函数(4)求单元应变——位移——节点位移之间的关系(5)求单元应力——应变——节点位移之间的关系(6)求节点力——节点位移之间的关系,得到刚度矩阵(7)计算单元应力
示求解域内待求的未知厂变量。
3.有限元法的分类和基本步骤有哪些P3
答:分类:位移法、力法、混合法;步骤:结构的离散化,单元分析,单元集成,引入约束条件,求解线性方程组,得出节点位移。
4.有限元法有哪些优缺点P4答:优点:有限元法可以模拟各种几何形状复杂的结构,得出其近似解;通过计算机程序,可以广泛地应用于各种场合;可以从其他cad软件中导入建好的模型;数学处理比较方便,对复杂形状的结构也能适用;有限元法和优化设计方法相结合,以便发挥各自的优点。缺点:有限元计算,尤其是复杂问题的分析计算,所耗费的计算时间、内存和磁盘空间等计算资源是相当惊人的。对无限求解域问题没有较好的处理办法。尽管现有的有限元软件多数使用了网络自适应技术,但在具体应用时,采用什么类型的单元、多大的网络密度等都要完全依赖适用者的经验。
12.有限元法的基本思想。(必考题)(其他参考书):(1)假想把连续集合体来代替原来的连续系统。在节点上引进等效载荷,代替实际作用于系统上的外载荷。(2)对每个单元由分块近似的思想,按一定的规则建立求解未知量和节点相互作用之间的关系。(3)把所有单元的这种特性关系按一定条件集合起来,引入边界条件,构成一组一节点变量为未知量的代数方程组,求解之就得到有限个节点处的待求变量。(教材):有限元法的基本思想是里兹法的加分片近似,将原结构划分为许多小块,用这些离散单元的集合体代替原结构,用近似函数表示单元内的真实场变量,从而给出离散模型的数值解。
