2015-2016学年湖南省长沙市第一中学、雅礼中学、南雅中学三校高一下学期期末联考物理试题
湖南省长沙市第一中学2015-2016学年高一12月月考数学试题(解析版)

高一数学12月月考试卷一、选择题1. 已知集合A={-1,0,1},B={x|-1≤x<1},则A∩B=()A. {0}B. {-1,0}C. {0,1}D. {-1,0,1}【答案】B【解析】试题分析:由题意可得.故B正确.考点:集合的运算.【易错点睛】本题主要考查集合的运算,属容易题.已知集合中的元素的满足的条件为,所以,所以此题选项为C,否则极易错选D选项.2.lg+lg的值为()A. B. C. 1 D.【答案】C【解析】;故选C.3.下图中,能表示函数y=f(x)的图像的是( )A. B. C. D.【答案】D【解析】由函数的定义(对于非空数集中的任一个数,都有唯一的值相对应),得选项D符合要求;故选D.4.下列函数是偶函数的是:()A. B. C. D.【答案】B【解析】易知为奇函数,为偶函数,,为非奇非偶函数;故选B.5.函数f(x)=x+的零点个数为( )A. 0B. 1C. 2D. 3【答案】A【解析】令,即,显然该方程无解,即函数的零点个数为0;故选A.6.设是两个不同的平面,是一条直线,以下命题正确的是()A. 若,则B. 若,则C. 若,则D. 若,则【答案】C【解析】对于A、B、D均可能出现,而对于C是正确的.7.已知点A(2,-3),B(-3,-2),直线l过点P(1,1)且与线段AB有交点,设直线l的斜率为k,则k的取值范围是( )A. (-∞,-4]∪B.C. D.【答案】A【解析】由题意,得,由图象,得或;故选A.8.某几何体的三视图(均为直角三角形)及其尺寸如图所示,则该几何体的体积为( ).A. B. C. D. 1【答案】B【解析】由三视图可知该几何体是一个直三棱锥,其中高为1,底面是直角边为1,2的直角三角形,则该几何体的体积为;故选B.9.函数的图像大致是( )A. B. C. D.【答案】C【解析】因为,所以该函数的图象如选项C所示;故选C.10.如图,正方体的棱长为1,线段上有两个动点,且,则下列结论中错误的是()A. B. 平面C. 三棱锥的体积为定值D. 异面直线所成的角为定值【答案】D【解析】在正方体中,平面平面,故正确;平面平面平面平面,故正确;的面积为定值,,又平面为棱锥的高,三棱锥的体积为定值,故正确;利用图形设异面直线所成的角为,当与重合时;当与重合时异面直线所成角不是定值,错误,故选D.二、填空题11.函数的定义域为______________,值域为______________.【答案】(1). (2).【解析】若函数函数有意义,则,即,即函数的定义域为;因为,所以,即该函数的值域为.12.当a为任意实数时,直线ax-y+1-3a=0恒过定点_____.【答案】(3,1)将化为,即该直线恒过点.13.一条光线从点射出,与x轴相较于点,经x轴反射,则反射光线所在的直线方程为______【答案】【解析】由光学知识可得反射光线所在的直线过点和关于轴的对称点,其直线方程为,即.14.如图,二面角α-l-β的大小是60°,线段AB⊂α,B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是_____.【答案】【解析】过点A作面,,连接,易知,则是二面角的平面角,即,是与所成的角,即,是与平面所成的角,在中,设,则,,,即与平面所成的角的正弦值为.15.已知一几何体的三视图如图所示,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是(写出所有正确结论的编号)_____.①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.【答案】①③④⑤由三视图可知该几何体为一个长方体,其棱长分别为,各表面和对角面都为矩形,即①正确,是有三个面为直角三角形,有一个面为等腰三角形的四面体,即②正确,是每个面都是等腰三角形的四面体,即④正确,是每个面都是直角三角形的四面体,即⑤正确;故填①③④⑤.三、解答题:16.已知函数,(Ⅰ)证明f(x)在[1,+∞)上是增函数;(Ⅱ)求f(x)在[1,4]上的最大值及最小值.【答案】(1)见解析(2)【解析】试题分析:(Ⅰ)利用函数的单调性的定义进行证明; (Ⅱ)利用前一步所证的函数的单调性确定其最值.试题解析:(Ⅰ) 设,且,则∴∴,∴∴∴,即∴在上是增函数.(Ⅱ) 由(Ⅰ)可知在上是增函数∴当时,∴当时,综上所述,在上的最大值为,最小值为.17.设集合,,(1)若,求实数的值;(2)若,求实数的取值范围.【答案】(1)-1或-3;(2).【解析】(1)因为A={1,2},并且,所以,所以,从而求出a的值,然后再一一验证是否满足.(2)因为,所以可得,然后再讨论和两种情况,从方程的角度研究就是当时无实数根;时,有一个实数根和有两个实根两种情况. (1)有题可知:∵∴将2带入集合B中得:解得:当时,集合符合题意;当时,集合,符合题意综上所述:(2)若A∪B=A,则B⊆A,∵A={1,2},∴B=∅或B={1}或{2}或{1,2}.若B=∅,则△=4(a﹣1)2﹣4(a2﹣5)=24﹣8a<0,解得a>3,若B={1},则,即,不成立.若B={2},则,即,不成立,若B={1,2}.则,即,此时不成立,综上a>3.18.已知三角形三个顶点是,,,(1)求边上的中线所在直线方程;(2)求边上的高所在直线方程.【答案】(1)(2)【解析】试题分析:本题第(1)问,由中点公式得到中点,再求出边上的中线所在直线的斜率,然后由直线的点斜式方程求出边上的中线所在直线方程;第(2)问,先由和两点求出直线BC的斜率,由于边与高垂直,则由两直线垂直的结论求出高所在直线的斜率,再结合点,由直线的点斜式方程求出高所在直线方程。
2015-2016学年湖南省长沙一中高三(下)月考数学试卷(理科)(七)(解析版)

2015-2016学年湖南省长沙一中高三(下)月考数学试卷(理科)(七)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)已知集合U=R,A={x|0≤x≤2},B={y|y=2x,x∈R},则(∁U A)∩B=()A.(﹣∞,0)B.(0,1)C.(1,2]D.(2,+∞)2.(5分)“(m﹣1)(a﹣1)>0”是“log a m>0”的一个()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.(5分)若复数z满足z2+2z=﹣10,则|z|=()A.B. C.3 D.4.(5分)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.5.(5分)展开式中除常数项外的其余项的系数之和为()A.5377 B.﹣5377 C.5375 D.﹣53756.(5分)已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,1],∃x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是()A.a≤1 B.a≥1 C.a≤2 D.a≥27.(5分)将函数向右平移个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与,,x轴围成的图形面积为()A.B.C.D.8.(5分)已知不等式组表示平面区域Ω,过区域Ω中的任意一个点P,作圆x2+y2=1的两条切线且切点分别为A、B,当∠APB最大时,•的值为()A.2 B.C.D.39.(5分)已知向量满足:,则在上的投影长度的取值范围是()A.B.C.D.10.(5分)已知双曲线C与椭圆+=1有相同的焦点F1、F2,点P为双曲线C与椭圆的一个交点,且满足|PF1|=2|PF2|,则双曲线C的渐近线方程是()A.y=±x B.y=±x C.y=±x D.y=±x11.(5分)已知函数y=f(x)是R上的可导函数,当x≠0时,有,则函数的零点个数是()A.0 B.1 C.2 D.312.(5分)已知数列{a n}是等差数列,数列{b n}是等比数列,公比为q,数列{c n}中,c n=a n b n,S n是数列{c n}的前n项和,若S m=7,S2m=﹣201(m为正偶数),则S4m的值为()A.﹣1601 B.﹣1801 C.﹣2001 D.﹣2201二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13.(5分)5个人排成一排,其中甲与乙不相邻,而丙与丁必须相邻,则不同的排法种数为.14.(5分)将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量=(m,n),=(3,6),则向量与共线的概率为.15.(5分)如图是一个几何体的三视图,则该几何体的体积是.16.(5分)数列{a n}中,已知a1=5,a2=19,a3=41,当n≥3时,3(a n﹣a n﹣1)=a n+1﹣a n﹣2,则a10=.三、解答题:本大题共5小题,满分60分,解答应写出文字说明、证明过程或演算步骤17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin(x﹣A)+sinA(x ∈R)在x=处取得最大值.(1)当时,求函数f(x)的值域;(2)若a=7且sinB+sinC=,求△ABC的面积.18.(12分)某军区新兵50m步枪射击个人平均成绩X(单位:环)服从正态分布N(μ,σ2),从这些个人平均成绩中随机抽取,得到如下频率分布表:X 4 5 6 7 8 9频数 1 2 26 40 29 2(1)求μ和σ2的值(用样本书序期望、方差代替总数数学期望、方差);(2)如果这个军区有新兵10000名,试估计这个军区新兵步枪射击个人平均成绩在区间(7.9,8.8]上的人数.19.(12分)如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.(Ⅰ)求证:BD∥平面FGH;(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.20.(12分)已知离心率为的椭圆的右焦点F是圆(x﹣1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.(1)求椭圆方程;(2)求线段MN长的最大值,并求此时点P的坐标.21.(12分)已知函数f(x)=e2(lnx+a﹣1)(e=2.71828…为自然对数的底数在定义域上单调递增.(1)求实数a的取值范围;(2)当实数a取最小值时,设,证明:①;②.请考生在第(22)、(23)(24)三题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上.【选修4-1:几何证明选讲】22.(10分)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【选修4-4:坐标系与参数方程】23.在直角坐标系xOy中,直线l的参数方程为(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2sinθ.(Ⅰ)写出⊙C的直角坐标方程;(Ⅱ)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.【选修4-5:不等式选讲】24.若a>0,b>0,且+=.(Ⅰ)求a3+b3的最小值;(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.2015-2016学年湖南省长沙一中高三(下)月考数学试卷(理科)(七)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)(2016春•长沙校级月考)已知集合U=R,A={x|0≤x≤2},B={y|y=2x,x∈R},则(∁U A)∩B=()A.(﹣∞,0)B.(0,1)C.(1,2]D.(2,+∞)【分析】化简集合B,求出集合A的补集,再计算(∁U A)∩B即可.【解答】解:集合U=R,A={x|0≤x≤2},∴∁U A={x|x<0或x>2}=(﹣∞,0)∪(2,+∞),又B={y|y=2x,x∈R}={y|y>0}=(0,+∞),∴(∁U A)∩B=(2,+∞).故选:D.【点评】本题考查了集合的化简与运算问题,是基础题目.2.(5分)(2016春•长沙校级月考)“(m﹣1)(a﹣1)>0”是“log a m>0”的一个()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【分析】根据对数函数的图象和性质,解对数不等式,利用充分条件和必要条件的定义进行判断.【解答】解:当“(m﹣1)(a﹣1)>0”时,则或,此时log a m可能无意义,故“log a m>0”不一定成立,而当“log a m>0”时,则或,“(m﹣1)(a﹣1)>0”成立,故“(m﹣1)(a﹣1)>0”是“log a m>0”的一个必要不充分条件,故选:B【点评】本题主要考查充分条件和必要条件的判断,根据对数的性质是解决本题的关键,比较基础.3.(5分)(2016春•长沙校级月考)若复数z满足z2+2z=﹣10,则|z|=()A.B. C.3 D.【分析】设z=x+yi(x,y∈R),代入z2+2z=﹣10,利用复数的运算法则、复数相等即可得出.【解答】解:设z=x+yi(x,y∈R),∴(x+yi)2+2(x+yi)+10=0,∴x2﹣y2+2x+10+(2xy+2y)i=0,∴x2﹣y2+2x+10=2xy+2y=0,解得,∴|z|==.故选:D.【点评】本题考查了复数运算法则、复数相等、模的计算公式,考查了推理能力与计算能力,属于中档题.4.(5分)(2015•湖南)执行如图所示的程序框图,如果输入n=3,则输出的S=()A.B.C.D.【分析】列出循环过程中S与i的数值,满足判断框的条件即可结束循环.【解答】解:判断前i=1,n=3,s=0,第1次循环,S=,i=2,第2次循环,S=,i=3,第3次循环,S=,i=4,此时,i>n,满足判断框的条件,结束循环,输出结果:S===故选:B【点评】本题考查循环框图的应用,注意判断框的条件的应用,考查计算能力5.(5分)(2016春•长沙校级月考)展开式中除常数项外的其余项的系数之和为()A.5377 B.﹣5377 C.5375 D.﹣5375【分析】利用二项展开式中的通项公式,求出展开式的常数项,再令x=1可得展开式中各项系数和,由此求出展开式中除常数项外的其余项的系数和.【解答】解:(﹣x)9展开式中的通项公式为:T r+1=C9r•()9﹣r•(﹣1)r•x r=(﹣1)r•C9r•29﹣r•x,令=0,求得r=3,所以展开式中常数项为(﹣1)3•C93•26=﹣5376,令x=1可得展开式中各项系数之和为(2﹣1)9=1,所以展开式中除常数项外的其余项的系数之和为1+5376=5377.故选:A.【点评】本题主要考查二项式定理的应用问题,解题时应利用展开式的通项公式求出常数项,是基础题目.6.(5分)(2015•郑州一模)已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,1],∃x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是()A.a≤1 B.a≥1 C.a≤2 D.a≥2【分析】由∀x1∈[﹣1,2],都∃x2∈[1,2],使得f(x1)≥g(x2),可得f(x)=x2+1在x1∈[﹣1,2]的最小值不小于g(x)=ax+2在x2∈[1,2]的最小值,构造关于a的不等式组,可得结论.【解答】解:当x1∈[,1]时,由f(x)=x+得,f′(x)=,令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,∴f(x)在[,1]单调递减,∴f(1)=5是函数的最小值,当x2∈[2,3]时,g(x)=2x+a为增函数,∴g(2)=a+4是函数的最小值,又∵∀x1∈[,1],都∃x2∈[2,3],使得f(x1)≥g(x2),可得f(x)在x1∈[,1]的最小值不小于g(x)在x2∈[2,3]的最小值,即5≥a+4,解得:a≤1,故选:A.【点评】本题考查的知识是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.7.(5分)(2010•聊城二模)将函数向右平移个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与,,x轴围成的图形面积为()A.B.C.D.【分析】将函数向右平移个单位,推出函数解析式,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,利用积分求函数y=g(x)与,,x轴围成的图形面积.【解答】解:将函数向右平移个单位,得到函数=sin(2x+π)=﹣sin2x,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=﹣sinx的图象,则函数y=﹣sinx与,,x轴围成的图形面积:﹣+(﹣sinx)d x=﹣cosx+cosx=+1=故选B【点评】本题是中档题,考查三角函数图象的平移伸缩变换,利用积分求面积,正确的变换是基础,合理利用积分求面积是近年高考必考内容.8.(5分)(2015•天水校级模拟)已知不等式组表示平面区域Ω,过区域Ω中的任意一个点P,作圆x2+y2=1的两条切线且切点分别为A、B,当∠APB最大时,•的值为()A.2 B.C.D.3【分析】作出不等式组对应的平面区域,根据数形结合求确定当α最小时,P的位置,利用向量的数量积公式,即可得到结论.【解答】解:作出不等式组对应的平面区域如图,要使∠APB最大,则P到圆心的距离最小即可,由图象可知当OP垂直直线x+y﹣2=0,此时|OP|==2,|OA|=1,设∠APB=α,则sin=,=此时cosα=,•==.故选:B【点评】本题主要考查线性规划的应用,考查学生分析解决问题的能力,利用数形结合是解决本题的关键.9.(5分)(2015•东阳市模拟)已知向量满足:,则在上的投影长度的取值范围是()A.B.C.D.【分析】由=≤12可求的范围,进而可求的范围,然后由在上的投影||cosθ可求【解答】解:设向量的夹角为θ∵||=13,||=1∴===≤12∴≥5∴=≥∴∵在上的投影||cosθ=cosθ故选D【点评】本题主要考查了向量的数量积的性质及投影的定义的简单应用,解题的关键是弄清楚基本概念.10.(5分)(2014秋•湖南校级期末)已知双曲线C与椭圆+=1有相同的焦点F1、F2,点P为双曲线C与椭圆的一个交点,且满足|PF1|=2|PF2|,则双曲线C的渐近线方程是()A.y=±x B.y=±x C.y=±x D.y=±x【分析】通过椭圆、双曲线的定义直接计算即可.【解答】解:由椭圆定义可知:|PF1|+|PF2|=6,又∵|PF1|=2|PF2|,∴3|PF2|=6,即|PF2|=2,由双曲线定义可知:|PF1|﹣|PF2|=2a,又∵|PF1|=2|PF2|,∴|PF2|=2a,即a=1,由已知,双曲线的焦半距c=2,则b=,∴双曲线的渐近线方程为:y=±x,故选:A.【点评】本题考查求椭圆的离心率,注意解题方法的积累,属于基础题.11.(5分)(2016•永州模拟)已知函数y=f(x)是R上的可导函数,当x≠0时,有,则函数的零点个数是()A.0 B.1 C.2 D.3【分析】将函数=0,转化为xf(x)=﹣,然后利用函数和导数之间的关系研究函数g(x)=xf(x)的单调性和取值范围,利用数形结合即可得到结论.【解答】解:由=0,得xf(x)=﹣,设g(x)=xf(x),则g′(x)=f(x)+xf′(x),∵x≠0时,有,∴x≠0时,,即当x>0时,g'(x)=f(x)+xf'(x)>0,此时函数g(x)单调递增,此时g(x)>g(0)=0,当x<0时,g'(x)=f(x)+xf'(x)<0,此时函数g(x)单调递减,此时g(x)>g(0)=0,作出函数g(x)和函数y=﹣的图象,(直线只代表单调性和取值范围),由图象可知函数的零点个数为1个.故选:B.【点评】本题主要考查方程根的个数的应用,利用方程和函数之间的关系,作出函数的图象,利用数形结合是解决本题的关键.12.(5分)(2016春•长沙校级月考)已知数列{a n}是等差数列,数列{b n}是等比数列,公比为q,数列{c n}中,c n=a n b n,S n是数列{c n}的前n项和,若S m=7,S2m=﹣201(m为正偶数),则S4m的值为()A.﹣1601 B.﹣1801 C.﹣2001 D.﹣2201【分析】令A=S m,B=S2m﹣S m,C=S3m﹣S2m,结合等差数列和等比数列的特征得到:B﹣q m•A=(a m+1﹣a1)b m+1+…+(a2m﹣a m)b2m=md(b m+1+…+b2m).同理C﹣q m•B=md(b2m+1+…+b2m)=md(b m+1+…+b2m)•q n,故C﹣q m•B=q m(B﹣q m•A)代值可得11(q m)2+8q m﹣208=0,求得q m的值后,代入(S4m﹣S3m),从而求得S4m的值.【解答】解:令A=S m,B=S2m﹣S m,C=S3m﹣S2m,则q m•A=(a1b1+a2b2+…+a m b m)q m=a1b m+1+…+a m b2m.故B﹣q m•A=(a m+1﹣a1)b m+1+…+(a2m﹣a m)b2m=md(b m+1+…+b2m),其中,d是数列{a n}的公差,q数列{b n}的公比.同理C﹣q m•B=md(b2m+1+…+b2m)=md(b m+1+…+b2m)•q n,故C﹣q m•B=q m(B﹣q m•A)代值可得11(q m)2+8q m﹣208=0,q m=4或q m=﹣(舍去,因m为正偶数),又S4m﹣S3m=(a1b1+a2b2+…+a m b m)q3m+3md(b m+1+…+b2m)q2m,=11×43+3(B﹣q m•A)×42,=11×43﹣3×12×43,=﹣1600.故S4m=S3m﹣1600=﹣1801.故选:B.【点评】该题考查等差数列、等比数列的通项公式、前n项和公式,考查学生的运算求解能力,熟记相关公式是解题关键.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13.(5分)(2016•商丘二模)5个人排成一排,其中甲与乙不相邻,而丙与丁必须相邻,则不同的排法种数为24.【分析】由题设中的条件知,可以先把丙与丁必须相邻,可先将两者绑定,又甲与乙不相邻,可把丙与丁看作是一个人,与甲乙之外的一个人作一个全排列,由于此两个元素隔开了三个空,再由插空法将甲乙两人插入三个空,由分析过程知,此题应分为三步完成,由计数原理计算出结果即可【解答】解:由题意,第一步将丙与丁绑定,两者的站法有2种,第二步将此两人看作一个整体,与除甲乙之外的一人看作两个元素做一个全排列有A22种站法,此时隔开了三个空,第三步将甲乙两人插入三个空,排法种数为A32则不同的排法种数为2×A22×A32=2×2×6=24故答案为:24.【点评】本题考查排列、组合及简单计数问题,解题的关键是掌握并理解计数原理,计数时的一些技巧在解题时很有用,如本题中所用到的绑定,与插空,这些技巧都是针对某一类计数问题的,题后应注意总结一下,不同的计数问题中所采用的技巧,将这些技巧与具体的背景结合起来,熟练掌握这些技巧.14.(5分)(2012•东莞二模)将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m,第二次出现的点数为n,向量=(m,n),=(3,6),则向量与共线的概率为.【分析】本题是一个古典概型,试验发生包含的事件是一颗骰子掷两次,共有6×6种结果,满足条件事件是向量共线,根据向量共线的条件得到6m﹣3n=0即n=2m,列举出所有的结果数,得到概率.【解答】解:由题意知本题是一个古典概型,∵试验发生包含的事件是一颗骰子掷两次,共有6×6=36种结果,满足条件事件是向量=(m,n)与=(3,6)共线,即6m﹣3n=0,∴n=2m,满足这种条件的有(1,2)(2,4)(3,6),共有3种结果,∴向量与共线的概率P=,故答案为:【点评】本题考查古典概型及其概率公式,考查向量共线的充要条件,考查利用列举法得到所有的满足条件的事件数,本题是一个比较简单的综合题目.15.(5分)(2016春•长沙校级月考)如图是一个几何体的三视图,则该几何体的体积是.【分析】由已知中的三视图,可知该几何体是一个底面为三角形的三棱柱,切去了一个三棱锥.该几何体的体积等于三棱柱体积减去三棱锥的体积.【解答】解:由三视图可知,该几何体是一个底面为三角形的三棱柱,切去了一个三棱锥.该几何体的体积等于三棱柱体积减去三棱锥的体积.如图三棱柱体积=三棱锥的体积=那么该几何体的体积为:故答案为:【点评】本题考查了对三视图的认识和理解,解决本题的关键是得到该几何体的形状是如何而来的,才能解决此题.属于中档题.16.(5分)(2016春•长沙校级月考)数列{a n}中,已知a1=5,a2=19,a3=41,当n≥3时,3(a n﹣a n﹣1)=a n+1﹣a n﹣2,则a10=419.【分析】判断数列{a n﹣a n﹣1}是等差数列,求出通项公式,然后求解a10即可.【解答】解:数列{a n}中,已知a1=5,a2=19,a3=41,当n≥3时,3(a n﹣a n﹣1)=a n+1﹣a n﹣2,可得:2(a n﹣a n﹣1)=(a n+1﹣a n)+(a n﹣1﹣a n﹣2),所以数列{a n﹣a n﹣1}是等差数列,d=a3﹣a2﹣a2+a1=8,a2﹣a1=14,a3﹣a2=22,…a n+1﹣a n=8n+6,累加可得a n=2n(2n+1)﹣1,又a10=419.故答案为:419.【点评】本题考查等差数列通项公式的应用,数列的递推关系式的应用,考查转化思想以及计算能力.三、解答题:本大题共5小题,满分60分,解答应写出文字说明、证明过程或演算步骤17.(12分)(2015•衡水四模)在△ABC中,角A,B,C所对的边分别为a,b,c,函数f(x)=2cosxsin (x﹣A)+sinA(x∈R)在x=处取得最大值.(1)当时,求函数f(x)的值域;(2)若a=7且sinB+sinC=,求△ABC的面积.【分析】利用三角函数的恒等变换化简函数f(x)的解析式为sin(2x﹣A),由于函数在处取得最大值.令,其中k∈z,解得A的值,(1)由于A为三角形内角,可得A的值,再由x的范围可得函数的值域;(2)由正弦定理求得b+c=13,再由余弦定理求得bc的值,由△ABC的面积等于,算出即可.【解答】解:∵函数f(x)=2cosxsin(x﹣A)+sinA=2cosxsinxcosA﹣2cosxcosxsinA+sinA=sin2xcosA﹣cos2xsinA=sin(2x﹣A)又∵函数f(x)=2cosxsin(x﹣A)+sinA(x∈R)在处取得最大值.∴,其中k∈z,即,其中k∈z,(1)∵A∈(0,π),∴A=∵,∴2x﹣A∴,即函数f(x)的值域为:(2)由正弦定理得到,则sinB+sinC=sinA,即,∴b+c=13由余弦定理得到a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA即49=169﹣3bc,∴bc=40故△ABC的面积为:S=.【点评】本题主要考查三角函数的恒等变换,正、余弦定理的应用,正弦函数的值域,属于中档题.18.(12分)(2016春•长沙校级月考)某军区新兵50m步枪射击个人平均成绩X(单位:环)服从正态分布N(μ,σ2),从这些个人平均成绩中随机抽取,得到如下频率分布表:X 4 5 6 7 8 9频数 1 2 26 40 29 2(1)求μ和σ2的值(用样本书序期望、方差代替总数数学期望、方差);(2)如果这个军区有新兵10000名,试估计这个军区新兵步枪射击个人平均成绩在区间(7.9,8.8]上的人数.【分析】(1)由题意得随机抽取的100个成绩的分布列,由此求出E(X),D(X),由此能求出μ,σ2=.(2)由(1)知X~N(7,0.8),从而P(7.9<X≤8.8)=[P(5.2<X≤8.8)﹣P(6.1<X≤7.9)]=0.1359.由此能求出这个军区新兵50m步枪射击个人平均成绩在区间(7.9.8.8]上的人数.【解答】解:(1)由题意得随机抽取的100个成绩的分布列为:X 4 5 6 7 8 9频率0.01 0.02 0.26 0.40 0.29 0.02∴E(X)=4×0.01+5×0.02+6×0.26+7×0.40+8×0.29+9×0.02=7.D(X)=(4﹣7)2×0.01+(5﹣7)2×0.02+(6﹣7)2×0.26+(7﹣7)2×0.40+(8﹣7)2×0.29+(9﹣7)2×0.02=0.8.∵样本成绩是随机得到的,∴由样本估算总体得:μ=E(X)=7,σ2=D(X)=0.8.(2)由(1)知X~N(7,0.8),∵≈0.9,∴σ=0.9,∴P(7.9<X≤8.8)=[P(5.2<X≤8.8)﹣P(6.1<X≤7.9)]==0.1359.∴这个军区新兵50m步枪射击个人平均成绩在区间(7.9.8.8]上的人数约为:10000×0.1359=1359.【点评】本题考查总体数学期望、方差的求法,考查概率的求法及应用,是中档题,解题时要认真审题,注意离散型随机变量的分布列的性质的合理运用.19.(12分)(2015•山东)如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.(Ⅰ)求证:BD∥平面FGH;(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.【分析】(Ⅰ)根据AB=2DE便可得到BC=2EF,从而可以得出四边形EFHB为平行四边形,从而得到BE ∥HF,便有BE∥平面FGH,再证明DE∥平面FGH,从而得到平面BDE∥平面FGH,从而BD∥平面FGH;(Ⅱ)连接HE,根据条件能够说明HC,HG,HE三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,然后求出一些点的坐标.连接BG,可说明为平面ACFD的一条法向量,设平面FGH的法向量为,根据即可求出法向量,设平面FGH与平面ACFD所成的角为θ,根据cosθ=即可求出平面FGH与平面ACFD所成的角的大小.【解答】解:(Ⅰ)证明:根据已知条件,DF∥AC,EF∥BC,DE∥AB;△DEF∽△ABC,又AB=2DE,∴BC=2EF=2BH,∴四边形EFHB为平行四边形;∴BE∥HF,HF⊂平面FGH,BE⊄平面FGH;∴BE∥平面FGH;同样,因为GH为△ABC中位线,∴GH∥AB;又DE∥AB;∴DE∥GH;∴DE∥平面FGH,DE∩BE=E;∴平面BDE∥平面FGH,BD⊂平面BDE;∴BD∥平面FGH;(Ⅱ)连接HE,则HE∥CF;∵CF⊥平面ABC;∴HE⊥平面ABC,并且HG⊥HC;∴HC,HG,HE三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设HC=1,则:H(0,0,0),G(0,1,0),F(1,0,1),B(﹣1,0,0);连接BG,根据已知条件BA=BC,G为AC中点;∴BG⊥AC;又CF⊥平面ABC,BG⊂平面ABC;∴BG⊥CF,AC∩CF=C;∴BG⊥平面ACFD;∴向量为平面ACFD的法向量;设平面FGH的法向量为,则:,取z=1,则:;设平面FGH和平面ACFD所成的锐二面角为θ,则:cosθ=|cos|=;∴平面FGH与平面ACFD所成的角为60°.【点评】考查棱台的定义,平行四边形的定义,线面平行的判定定理,面面平行的判定定理及其性质,线面垂直的性质及线面垂直的判定定理,以及建立空间直角坐标系,利用空间向量求二面角的方法,平面法向量的概念及求法,向量垂直的充要条件,向量夹角余弦的坐标公式,平面和平面所成角的定义.20.(12分)(2016春•长沙校级月考)已知离心率为的椭圆的右焦点F是圆(x﹣1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.(1)求椭圆方程;(2)求线段MN长的最大值,并求此时点P的坐标.【分析】(1)根据圆方程可求得圆心坐标,即椭圆的右焦点,根据椭圆的离心率进而求得a,最后根据a,b和c的关系求得b,则椭圆方程可得;(2)P(x0,y0),M(0,m),N(0,n),把椭圆方程与圆方程联立求得交点的横坐标,进而可推断x0的范围,把直线PM的方程化简,根据点到直线的距离公式表示出圆心到直线PM和PN的距离.求得x0和y0的关系式,进而求得m+n和mn的表达式,进而求得|MN|.把点P代入椭圆方程根据弦长公式求得MN|.记f(x)=2﹣,根据函数的导函数判断函数的单调性,进而确定函数f(x)的值域,进而求得当x0=﹣,时,|MN|取得最大值,进而求得y0,则P点坐标可得.【解答】解:由圆(x﹣1)2+y2=1的圆心坐标为:(1,0),∴c=1,由e==,即a=,∴b2=a2﹣c2=1,∴椭圆方程;(2)设P(x0,y0),M(0,m),N(0,n),由,解得:x=2﹣,x=2+(舍去),∴x0=(﹣,0)∪(0,2﹣),直线PM的方程为:y﹣m=x,即(y0﹣m)x﹣x0y+mx0=0,∴=1,∴(x0﹣2)m2+2y0m﹣x0=0,同理可知:(x0﹣2)n2+2y0n﹣x0=0,∴m和n是方程:(x0﹣2)t2+2y0t﹣x0=0的两个根,∴m+n=﹣,mn=,∴丨MN丨=丨m﹣n丨==,∴,∴丨MN丨=,记f(x)=2﹣,则f′(x)=,∴x∈(﹣,0)时,f'(x)<0;x∈(0,2﹣)时,f'(x)<0,∴f(x)在(﹣,0)上单调递减,在(0,2﹣)内也是单调递减,显然,由f(x)的单调性可知:f(x)max=2,∴丨MN丨max=2,此时x0=﹣,故P点坐标为(﹣,0),为椭圆左顶点.【点评】本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查了椭圆的标准方程、简单几何性质、一元二次方程根与系数的关系和利用导数研究函数的单调性等知识,属于中档题.21.(12分)(2016春•长沙校级月考)已知函数f(x)=e2(lnx+a﹣1)(e=2.71828…为自然对数的底数在定义域上单调递增.(1)求实数a的取值范围;(2)当实数a取最小值时,设,证明:①;②.【分析】(′1)先求导函数,再构造函数lnx+a﹣1+,则y min≥0,再求导,根据导数和函数最值的关系即可求出;(2)①先求导,再构造函数h(x)=e x(ex﹣2)+ex2,根据导数和函数单调性的关系得到故存在唯一x0>0,使h(x0)=0,再求出端点值,即可证明,②令F(x)=lnx+,G(x)=e﹣x,根据导数和函数单调性的关系得到lnx+﹣e﹣x>F()﹣G(),利用放缩法即可证明【解答】解:(1)∵f(x)=e2(lnx+a﹣1),∴f′(x)=e2(lnx+a﹣1+)≥0,对x>0恒成立,∴lnx+a﹣1+≥0,对x>0恒成立,令y=lnx+a﹣1+,则y min≥0,又y′=,当0<x<1时,y′<0,当x>1时,y′>0,故y min=a≥0,(2)①由(1)可知,g(x)=lnx+﹣e﹣x﹣1,则g′(x)=﹣+e﹣x=,x>0,令h(x)=e x(ex﹣2)+ex2,则h′(x)=e x(ex+e﹣2)+2ex>0,∴h(x)在(0,+∞)上单调递增,又h(0)=﹣2,h()=,故存在唯一x0>0,使h(x0)=0,故g(x)在(0,x0)上递减,在(x0,+∞)上递增,又h()=(﹣2+)=<0,h()=e(﹣2)+e=e(﹣2+),∵e x≥1+x,∴=•>(1﹣)=,∴﹣2+>+﹣2=>=>0故g(x)≥min{y|y=g(x),x∈[,]}②令F(x)=lnx+,G(x)=e﹣x,则F′(x)=,可知F(x)在(0,)上递减,又<,故F(x)在[,]上递减,又G(x)在[,]上也递减,故当x∈[,]时,lnx+﹣e﹣x>F()﹣G()=ln+﹣e=﹣e﹣ln,∵ln=ln7﹣ln4=dx,又当x∈[,]时,≤,∴dx<dx=故﹣e﹣ln﹣>﹣﹣﹣=>=>0,再由①可知g(x)+1>对一切正数x成立【点评】本题考查了导数和函数单调性和最值的关系,以及恒成立的问题,采用放缩法和构造法是关键,计算量很大,属于难题.请考生在第(22)、(23)(24)三题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上.【选修4-1:几何证明选讲】22.(10分)(2015•新课标II)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N 两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【分析】(1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;(2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC﹣S△AEF计算即可.【解答】(1)证明:∵△ABC为等腰三角形,AD⊥BC,∴AD是∠CAB的角平分线,又∵圆O分别与AB、AC相切于点E、F,∴AE=AF,∴AD⊥EF,∴EF∥BC;(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,又∵EF为圆O的弦,∴O在AD上,连结OE、OM,则OE⊥AE,由AG等于圆O的半径可得AO=2OE,∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,∵AE=2,∴AO=4,OE=2,∵OM=OE=2,DM=MN=,∴OD=1,∴AD=5,AB=,∴四边形EBCF的面积为×﹣××=.【点评】本题考查空间中线与线之间的位置关系,考查四边形面积的计算,注意解题方法的积累,属于中档题.【选修4-4:坐标系与参数方程】23.(2015•陕西)在直角坐标系xOy中,直线l的参数方程为(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2sinθ.(Ⅰ)写出⊙C的直角坐标方程;(Ⅱ)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.【分析】(I)由⊙C的极坐标方程为ρ=2sinθ.化为ρ2=2,把代入即可得出;.(II)设P,又C.利用两点之间的距离公式可得|PC|=,再利用二次函数的性质即可得出.【解答】解:(I)由⊙C的极坐标方程为ρ=2sinθ.∴ρ2=2,化为x2+y2=,配方为=3.(II)设P,又C.∴|PC|==≥2,因此当t=0时,|PC|取得最小值2.此时P(3,0).【点评】本题考查了极坐标化为直角坐标方程、参数方程的应用、两点之间的距离公式、二次函数的性质,考查了推理能力与计算能力,属于中档题.【选修4-5:不等式选讲】24.(2014•新课标I)若a>0,b>0,且+=.(Ⅰ)求a3+b3的最小值;(Ⅱ)是否存在a,b,使得2a+3b=6?并说明理由.【分析】(Ⅰ)由条件利用基本不等式求得ab≥2,再利用基本不等式求得a3+b3的最小值.(Ⅱ)根据ab≥4及基本不等式求的2a+3b>8,从而可得不存在a,b,使得2a+3b=6.【解答】解:(Ⅰ)∵a>0,b>0,且+=,∴=+≥2,∴ab≥2,当且仅当a=b=时取等号.∵a3+b3 ≥2≥2=4,当且仅当a=b=时取等号,∴a3+b3的最小值为4.(Ⅱ)∵2a+3b≥2=2,当且仅当2a=3b时,取等号.而由(1)可知,2≥2=4>6,故不存在a,b,使得2a+3b=6成立.【点评】本题主要考查基本不等式在最值中的应用,要注意检验等号成立条件是否具备,属于基础题.2016年11月5日。
湖南省长郡中、雅礼中学等长沙名校联盟2015-2016学年高一数学暑假第一次阶段性测试试题

2015年长沙名校联盟高一年 级暑假第一次阶段性测试试卷数 学(湖南卷版)本试卷包括三个大题,共6页,总分150分,考试时量120分钟注意事项:1. 答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2. 必须在答题卡上答题,在草稿纸、试题卷上答题无效;3. 答题时,请考生注意各大题题号后面的答题提示;4. 请勿折叠答题卡,保持字体工整、笔记清晰、卡面清洁;5. 答题卡上不准使用涂改液涂改。
一、选择题(每小题5分,共50分)1. 已知数列}{n a 是等差数列,且48111032=+++a a a a ,则76a a +等于( ) A. 12 B. 18 C. 24 D. 302. 下列命题中,错误的个数有________个①平行于同一条直线的两个平面平行. ②平行于同一个平面的两个平面平行.③一个平面与两个平行平面相交,交线平行.④一条直线与两个平行平面中的一个相交,则必与另一个平面相交.A. 0个B. 1个C. 2个D. 3个3.已知圆:C x y x y +++-=2212880与圆:C x y x y +---=2224420相交,则圆C 1与圆C 2的公共弦所在的直线的方程为( )A .210x y ++=B .210x y +-=C .210x y -+=D .210x y --=4. 把正方形ABCD 沿对角线AC 折起,当以,,,A B C D 四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成的角的大小为( )A .90B .60C .45D .305. 设偶函数f (x )的定义域为R ,当[0,)x ∈+∞时f (x )是增函数,则(2),(),(3)f f f π--的大小关系是( )A.()f π>(3)f ->(2)f -B.()f π>(2)f ->(3)f -C.()f π<(3)f -<(2)f -D.()f π<(2)f -<(3)f -6. 1sin 2y αα=+的最大值为( ) A. 12C. 1D. 27. 若任取[]12121212()(),,,,()22x x f x f x x x a b x x f ++∈≠>且都有成立,则称()f x 是[],a b 上的凸函数.试问:在下列图像中,是凸函数图像的为( )8. 已知n 次多项式f (x )=a n x n +a n -1x n -1+…+a 1x +a 0,用秦九韶算法求f (x 0)的值,需要进行的乘法运算、加法运算的次数依次是( )A .n ,nB .2n ,nC .21+)(n n ,n D .n +1,n +19. 设向量a 与b 的夹角为θ,定义a 与b 的“向量积”:a b ⨯是一个向量,它的模sin a b a b θ⨯=⋅⋅,若()()3,1,1,3a b =--=,则a b ⨯=( )A .2B .C .D .410. 已知等比数列{n a }中,n a =2×31-n ,则由此数列的偶数项所组成的新数列的前n 项和nS 的值为( )A .3n-B .3(3n-C .419-n D .4)19(3-n二、填空题(每小题5分,共25分)11. 函数213log log y x=()的定义域为_______________. 12. 如图,在长方体ABCD —A 1B 1C 1D 1中,棱锥A 1——ABCD的体积AABC D D BAC与长方体的体积之比为_______________.13. 按照程序框图(如右图)执行,第3个输出的数是_______________. 14. 已知函数()sin()cos()f x x x =+θ++θ是偶函数,且[0,]2πθ∈,则θ的值为_______________.15.在ABC ∆中,0601,,A b ==,则a b cA B C++=++sin sin sin _______________.三、解答题(共75分) 16.(本小题满分12分)已知函数2π()sin sin 2f x x x x ωωω⎛⎫=++ ⎪⎝⎭(0ω>)的最小正周期为π. (Ⅰ)求ω的值;(Ⅱ)求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦,上的取值范围.17.(本小题满分12分)如图,在三棱锥P —ABC 中,PC ⊥底面ABC ,AB ⊥BC ,D ,E 分别是AB ,PB 的中点. (Ⅰ)求证:DE ∥平面PAC . (Ⅱ)求证:AB ⊥PB ;(Ⅲ)若PC =BC ,求二面角P —AB —C 的大小.CPE18.(本小题满分12分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.(Ⅰ)求取出的两个球上标号为相同数字的概率; (Ⅱ)求取出的两个球上标号之积能被3整除的概率.19.(本小题满分13分) 已知函数2π()cos 12f x x ⎛⎫=+⎪⎝⎭,1()1sin 22g x x =+. (Ⅰ)设0x x =是函数()y f x =图象的一条对称轴,求0()g x 的值; (Ⅱ)求函数()()()h x f x g x =+的单调递增区间.20.(本小题满分13分)设关于x 的一元二次方程n a 2x -1n a +x 1+0= (n N *∈)有两根α和β,且满足6263ααββ-+=.(Ⅰ)试用n a 表示1n a +;(Ⅱ)求证:数列23n a ⎧⎫-⎨⎬⎩⎭是等比数列; (Ⅲ)当176a =时,求数列{}n a 的通项公式,并求数列}{n na 的前n 项和n T .21.(本小题满分13分)已知()()()f x x x a x b =--,点A(s, f(s)), B(t, f(t)) (Ⅰ)若1a b ==,求函数()f x 的单调递增区间;(Ⅱ)若函数()f x 的导函数()f x '满足:当|x |≤1时,有|()f x '|≤23恒成立,求函数()f x 的解析表达式;(Ⅲ)若0<a<b, 函数()f x 在x s =和x t =处取得极值,且a b +=证明:与不可能垂直.2015年长沙名校联盟高一年级暑假第一次阶段性测试试卷数学参考答案1C 2B 3B 4C 5A 6C 7C 8A 9A 10D11.(0,1) 12. 1:3 13.5 14.4π 15.15o 或75o16.112cos 222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭. 因为函数()f x 的最小正周期为π,且0ω>,所以2ππ2ω=,解得1ω=.(Ⅱ)由(Ⅰ)得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭.因为2π03x ≤≤,所以ππ7π2666x --≤≤,所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤,因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤,即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦,.17. (1)证明:因为D ,E 分别是AB ,PB 的中点,所以DE ∥PA .因为PA ⊂平面PAC ,且DE ⊄平面PAC , 所以DE ∥平面PAC . (2)因为PC ⊥平面ABC ,且AB ⊂平面ABC ,所以AB ⊥PC .又因为AB ⊥BC ,且PC ∩BC =C . 所以AB ⊥平面PBC . 又因为PB ⊂平面PBC ,所以AB ⊥PB . (3)由(2)知,PB ⊥AB ,BC ⊥AB ,所以,∠PBC 为二面角P —AB —C 的平面角.ACPBDE(第17题)因为PC =BC ,∠PCB =90°, 所以∠PBC =45°,所以二面角P —AB —C 的大小为45°.18. 解:设从甲、乙两个盒子中各取1个球,其数字分别为x ,y .用(x ,y )表示抽取结果,则所有可能的结果有16种,即(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4), (3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4). (1)设“取出的两个球上的标号相同”为事件A , 则A ={(1,1),(2,2),(3,3),(4,4)}. 事件A 由4个基本事件组成,故所求概率P (A )=164=41. (2)设“取出的两个球上标号的数字之积能被3整除”为事件B , 则B ={(1,3),(3,1),(2,3),(3,2),(3,3),(3,4),(4,3)} 事件B 由7个基本事件组成,故所求概率P (A )=167. 19.解:(I )由题设知1π()[1cos(2)]26f x x =++. 因为0x x =是函数()y f x =图象的一条对称轴,所以0π26x +πk =, 即0 π2π6x k =-(k ∈Z ). 所以0011π()1sin 21sin(π)226g x x k =+=+-.当k 为偶数时,01π13()1sin 12644g x ⎛⎫=+-=-= ⎪⎝⎭, 当k 为奇数时,01π15()1sin 12644g x =+=+=. (II )1π1()()()1cos 21sin 2262h x f x g x x x ⎡⎤⎛⎫=+=++++ ⎪⎢⎥⎝⎭⎣⎦ 1π31313cos 2sin 2sin 22622222x x x x ⎛⎫⎡⎤⎛⎫=+++=++ ⎪ ⎪⎢⎥ ⎪⎝⎭⎣⎦⎝⎭1π3sin 2232x ⎛⎫=++ ⎪⎝⎭. 当πππ2π22π232k x k -++≤≤,即5ππππ1212k x k -+≤≤(k ∈Z )时,函数1π3()sin 2232h x x ⎛⎫=++ ⎪⎝⎭是增函数, 故函数()h x 的单调递增区间是5ππππ1212k k ⎡⎤-+⎢⎥⎣⎦,(k ∈Z ).20.解:(1)根据韦达定理,得1n n a a αβ++=, 1na αβ⋅=, 由6263ααββ-+=得 1263n n n a a a +⋅-=,故11123n n a a +=+ (2)证明:121112()32323n n n a a a +-=-=-,若203n a -=,则1203n a +-=,从而123n n a a +==,这时一元二次方程n a 2x -1n a +x 1+0=无实数根,故1203n a +-≠, 所以1213223n n a a +-=-,数列23n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列. (3)设23n n b a =-,则数列{}n b 是公比12q =的等比数列,又1127213632b a =-=-=,所以111111222n nn n b b q--⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭, 所以2132nn a ⎛⎫-= ⎪⎝⎭,2132nn a ⎛⎫=+ ⎪⎝⎭.n n n n na 232+=则由错位相减法可得=n T n n n n 22232+-++. 21.解:(I) f (x)=x 3-2x 2+x, f '(x)=3x 2-4x+1,因为f(x)单调递增,所以f '(x )≥0, 即 3x 2-4x +1≥0,解得,x ≥1, 或x ≤31, 故f(x)的增区间是(-∞,31)和 (II) f '(x)=3x 2-2(a+b)x+ab.当x ∈时,恒有|f '(x)|≤23 故有23-≤f '(1)≤23,23-≤f '(-1)≤23,23-≤f '(0)≤23即⎪⎪⎪⎩⎪⎪⎪⎨⎧-+++-++--③.23 ≤ab ≤23②,23 ≤ ab )b a (23 ≤23①,23 ≤ ab )b a (23 ≤23①+②,得29-≤ab ≤23-, 又由③,得 ab=23-, 将上式代回①和②,得 a+b=0, 故f(x)=x 323-x (III) 假设⊥,即OA OB ⋅=))(,())(,(t f t s f s ⋅ = st+f(s)f(t)=0, (s-a)(s-b)(t-a)(t-b)=-1, =-1,由s ,t 为f '(x)=0的两根可得, s+t=32(a+b), st=31, (0<a<b),从而有ab(a-b)2=9这样(a+b)2=(a-b)2+4ab =ab9+4ab ≥236=12,即 a+b≥23,这样与a+b<23矛盾故与不可能垂直.。
2015-2016学湖南省长沙市第一中学、雅礼中学、南雅中学三校年高一下学期期末联考地理试题
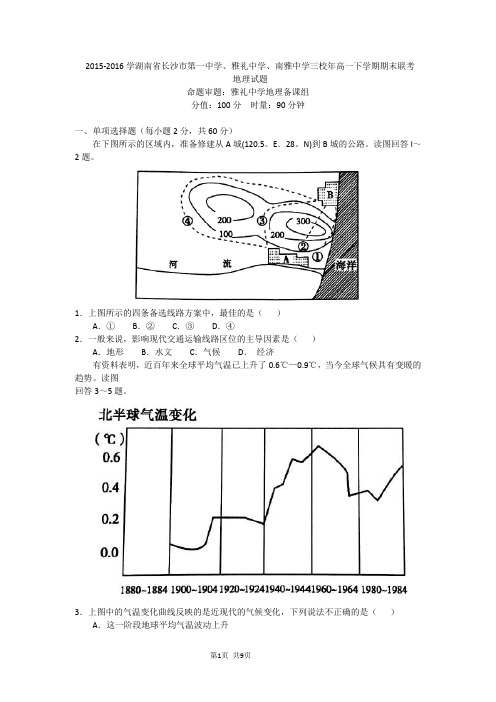
2015-2016学湖南省长沙市第一中学、雅礼中学、南雅中学三校年高一下学期期末联考地理试题命题审题:雅礼中学地理备课组分值:100分时量:90分钟一、单项选择题(每小题2分,共60分)在下图所示的区域内,准备修建从A城(120.5。
E.28。
N)到B城的公路。
读图回答l~2题。
1.上图所示的四条备选线路方案中,最佳的是()A.①B.②C.③D.④2.一般来说,影响现代交通运输线路区位的主导因素是()A.地形B.水文C.气候D.经济有资料表明,近百年来全球平均气温已上升了0.6℃—0.9℃,当今全球气候具有变暖的趋势。
读图回答3~5题。
3.上图中的气温变化曲线反映的是近现代的气候变化,下列说法不正确的是()A.这一阶段地球平均气温波动上升B.20世纪80年代的气温高于20世纪40年代的气温C.该曲线变化的总趋势与地球大气中温室气体增加的趋势大体一致D.近百年来的气温明显低于距今7万年至距今l万年的气温4.该图反映的问题是全球变暖,下列对策可以缓解气候变暖的是( )①减少化石燃料的使用量②大面积植树造林③发展技术,提高燃科的燃烧效率④开发新能源,改善能源结构A.①②③B.①③④C.①②D.①②③④5.上述气温变化对人类来说,既有正面影响也有负面影响,下列叙述正确的是( ) A.气温升高将使森林树种大量增加B.商山冰川将改变规模,有些地方出现减少和退缩C.各地农作物产最都会大幅度减少D.气候变暖,会使各地人们的新陈代谢变慢,增强身体活力近年来,每年农历新年过后,都会形成农民离乡外出打工大潮,与往年不同的是2011年春节后,浙江、江苏、广东等传统用工大省出现了“用工荒”。
而在湖北、四川等劳务输出大省,当地政府和企业出台了更多的措施“截留”农民工。
据此完成6~7题。
6.导致“用工荒”出现的主要原因有( )A.地方政府出台政策限制民工的流动B.沿海省份对外来务工人员需求量大幅上升C.沿海劳动密集型产业能提供相对更好的工资待遇D.劳务输出省份加工制造业和服务业对民工需求量增大7.关于“用工荒”影响的叙述,正确的是()A.成为沿海中低端制造业转移的一大推力B.导致沿海经济出现整体下滑的趋势C.促进中西部地区高新技术产业的发展D.制约中西部地区的社会经济发展下图为我国东部沿海某市2010年和2014年人口变化统计图,读图完成8-9题。
湖南省长郡中学、雅礼中学等长沙名校联盟2015-2016学年高一语文暑假第一次阶段性测试试题

2015年长沙名校联盟高一年级暑假第一次阶段性测试试卷语文(湖南卷版)本试卷包括六个大题,共8页,总分150分,考试时量150分钟注意事项:1. 答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2. 必须在答题卡上答题,在草稿纸、试题卷上答题无效;3. 答题时,请考生注意各大题题号后面的答题提示;4. 请勿折叠答题卡,保持字体工整、笔记清晰、卡面清洁;5. 答题卡上不准使用涂改液涂改。
参考学校长郡中学雅礼中学长沙市一中田家炳实验中学师大附中周南中学明德中学麓山国际实验学校2015年长沙名校联盟高一年级暑假第一次阶段性测试试卷语文一、语言运用(每小题3分,共12分)1.下面各组词语中加点字正确的一项是()A.楔.子(xiē)蝥.贼(máo)勾.当(gōu)昧.心(mèi)B.堤.沙(dī)天堑.(qiàn)乍.暖(zhà)祠.堂(cí)C.脑髓.(suǐ)囊.括(náng)追溯.(shuò)刹.那(chà)D.吝啬.(sè)专横.(hèng)蹩.进(bié)单.于(chán)2.依次在下列横线处填入词语,最恰当的一项是()(1)“黑洞”是宇宙空间中存在的一种质量极大的天体,产生的引力场如此强大,________任何物体包括光线都无法逃逸。
(2)国家发改委决定降低行政事业性收费标准,包括与企业________的受理商标注册费、机动车抵押登记费等都相应下调。
(3)美国“棱镜门”事件泄密者斯诺登选择俄罗斯避难最安全,因为在莫斯科美国的情报机构________,无法动他一根汗毛。
A. 以至息息相关鞭长莫及B. 以致休戚相关望尘莫及C. 以至休戚相关望尘莫及D. 以致息息相关鞭长莫及3. 下列各项中,没有语病的一项是()A. 肖复兴认为,如今少数网络作品的走红,依然掩盖不了整体网络文学创作水准和思想含量不高,因此,我们要辨证地看待网络作品的火热现象。
【百强校】2015-2016学年湖南省长沙一中等三校高一下期末化学试卷(带解析)
绝密★启用前【百强校】2015-2016学年湖南省长沙一中等三校高一下期末化学试卷(带解析)试卷副标题考试范围:xxx ;考试时间:44分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、设N A 为阿伏伽德罗常数的值,下列说法正确的是 A .2.0gH 218O 与D 2O 的混合物中所含中子数为N A B .常温常压下,4.4g 乙醛所含单键数目为0.7N AC .标准状况下.5.6 LCO 2与足量Na 2O 2反应转移的电子数为0.5N AD .50mL1 2mol/L 盐酸与足量MnO 2共热,转移的电子数为0.3N A2、下列各组金属最适合用H 2或CO 把它从化合物中还原出来的是 A .Ca 、Mg B .Al 、Fe C .Fe 、Cu D .Hg 、Ag3、美国科学家将铅和氪两种元素的原子核对撞,获得了一种质子数为118、质量数为293的新元素,该元素原子核内的中子数和核外电子数之差为 A .47 B .175 C .61 D .574、铜和镁的合金2.14 g完全溶于一定浓度的硝酸,若反应中硝酸被还NO2、NO、N2O 三种气体而且在标准状况下它们的体积均为0.224 L。
在反应后的溶液中,加人足量的氢氧化钠溶液,生成的沉淀经过滤、洗涤、干燥后称量,质量为A.4.18 g B.3.12 g C.4.68 g D.5.08 g5、已知某主族元素X的原子获得一个电子成为X-离子,则该元素在周期表中所在的族为①ⅦA族②ⅥA族③IA族A.只可能是①B.只可能是③C.可能是①或③D.可能是①或②或③6、X、Y、Z三种元素原子的核电荷数在11-17之间。
它们的最高价氧化物对应的水化物是HXO4、H2YO4、H3ZO4。
2015-2016学年湖南省长沙市一中高一第二学期期末考试英语试题【word】

2015-2016学年湖南省长沙市一中高一第二学期期末考试英语试题【word】命题审题:雅礼中学英语备课组分值:150分时量:120分钟第I卷第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the man doing?A. Watching TVB. CookingC. Preparing to go out2. Where is Lisa most probably now?A. At workB. At homeC. In the hospital3. What did David do yesterday?A. He did his homeworkB. He went swimmingC. He had an exam4. When is the plane leaving?A. At 4:40B. At 5:40C. At 6:405. How will Bella go to Shanghai?A. By planeB. By carC. By train第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6--7题。
6. What is included in the rent?A. GasB. Internet accessC. Electricity7. How much did the man’s friend pay in rent?A. $1,200B. $1,000C. $800听第7段材料,回答第8-9题。
2015-2016学年湖南省长沙市第一中学高一下学期第二次阶段测试化学试题

2015-2016学年湖南省长沙市第一中学高一下学期第二次阶段测试化学试题时间:90分钟满分:100分可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Si~28 S-32 Cl-35.5 Cu-64一、单项选择题(本大题包括16小题,每小题3分,共48分,每题只有一个正确答案)1.下列化学用语的书写正确的是A:氮气的电子式:B.硫原子的结构示意图:C.CH4的比例模型:D.乙烯的结构简式:CH2CH22.绿色化学对于化学反应提出了“原子经济性”的新概念及要求。
理想的原子经济性反应是原料中的原子全部转变成所需产物,不产生副产物,实现零排放。
下列几种生产乙苯()的方法中,原子经济性最好的是3.下列由相关实验现象所推出的结论正确的是A.Cl2、SO2均能使品红溶液褪色,说明二者均有氧化性B.向溶液中滴加酸化的Ba(NO3)2溶液出现白色沉淀,说明该溶液一定有SO42-C.Fe与稀HNO3、稀H2SO4反应均有气泡产生,说明Fe与两种酸均发生置换反应D.分别充满HCl、NH3的烧瓶倒置于水中后液面均迅速上升,说明二者均易溶于水4.下列各组物质中,化学键全部为共价键的是A.NH4Cl、CO2、HClB.O2、KF、SO2C.HCl、CH3COOH、CH4D.Na2O2、N2、H2O5.化学式为C3H6Cl2的有机物,若再有一个氢原子被氯原子取代,则产物有两种可能的结构,原有机物的结构简式为A.CH2Cl-CH2-CH2ClB.CHCl2-CH2-CH3C.CH2Cl-CHCl-CH3D.CH3-CCl2-CH36.下列物质性质的变化规律与分子间作用力有关的是A.HF、HCl、HBr、HI的热稳定性依次减弱B.金刚石的硬度大于硅,其熔沸点也高于硅C.NaF、NaCl、NaBr、NaI的熔点依次降低D.F2、Cl2、Br2、I2的熔沸点逐渐升高7.既可以用来鉴别乙烷和乙烯,又可以用来除去乙烷中混有的乙烯的试剂是A.溴水B.氧气C.酸性高锰酸钾溶液D.氢气8.一定能使化学反应速率加快的因素是①扩大容器容积②使用正催化剂③增大反应物的物质的量④升高温度⑤缩小容积⑥增大压强A.②③B.②③④⑥C.②③③⑤D.②④9.如右下图所示的装置中,观察到电流计指针偏转,M棒变粗,N棒变细,并测得电解质溶液的质量减小,由此判断下表中所列M、N、P物质,其中可以成立的是10.X、Y、Z、W均为短周期元素,它们在元素周期表中的位置如右图所示,若Y原子的最外层电子数是次外层电子数的3倍,下列说法正确的是A、原子半径:W>Z>Y>XB、最高价氧化物对应水化物的酸性:Z>W>XC、四种元素的单质中,Z单质的熔沸点最低D、W的单质能与水反应,生成一种具有漂白性的物质11.N A为阿伏伽德罗常数,下列说法中正确的是A、高温下60gSiO2与足量纯碱反应,最多释放出2N A个气体分子B、1molC5H12分子中共价键总数为14N AC、78gNa2O2固体与足量的H2O反应转移的电子数为N AD、标准状况下,2.24LNH3和CH4的混合气体,所含电子总数为2N A12.肼(H2NNH2)是一种高能燃料,有关化学反应的能量变化如图所示,已知断裂1mol化学键所需能量(KJ):N≡N为942、O=O为500、N-N为154,则断裂1molN-H键所需的能量(KJ)是A.194B.391C.516D.65813.对于有机物的命名正确的是A.2-乙基-戊烷B.2-丙基-丁烷C.2-甲基-3-乙基丁烷D.3-甲基-己烷14.下图表示球棍模型,小球表示原子序数小于10的原子,短线表示化学键,每个原子都到达稳定结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015级高一下学期期末三校联考物理命题审题:一中物理备课组 分值:100分时间 : 90分钟一、选择题:(本题包括13小超,每小题4分,共52分.其中11-13三个小题,每小题给出的四个选项中,有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错的得0分) 1.下列说法符合史实的是( ) A.牛顿发现了行星的运动规律 B.开普勒发现了万有引力定律C.卡文迪许第一次在实验室里测出了万有引力常量D.牛顿发现了海王星和冥王星2.真空中两个完全相同的金属小球,分别带有+3Q 和一Q 的电量,当它们相距r 时,它们之间的库仑力是F.若把它们接触后分开,再置于相距r/3的两点,则它们的库仑力的大小为() A.F/3 B. F C. 9F D. 3F3.如图所示的皮带传动装置中,皮带与轮之间不打滑,两轮半径分别为R 和r ,且R=3r, A, B 分别为两轮边缘上的点,则皮带轮运动过程中,关于A, B 两点下列说法正确的是()3.如图所示的皮带传动装置中,皮带与轮之间不打滑,两轮半径分别为R 和r ,且R=3r, A, B 分别为两轮边缘上的点,则皮带轮运动过程中,关于A, B 两点下列说法正确的是( ) A.向心加速度之比a A :a B =1:3 B.角速度之比ωA : ωB =3 : 1 C.议线速度大小之比v A :v B =1:3D.在相同的时间内通过的路程之比S A::S B =3:14.如图所示,倾角为8的斜面长为L ,在顶端水平抛出一小球,小球刚好落在斜面的底端,那么,小球初速度vo 的大小为().cos 2sin gL A θ.cos sin gL B θ .sin 2cos gL C θ .sin cos gLD θ5.如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中匀速上浮。
在红蜡块从玻璃管的下端以速度v 匀速上浮的同时,使玻璃管水平向右以速率v 匀速运动。
红蜡块由管口上升到顶端.所需时间为t,相对地面通过的路程为L 。
则下列说法正确的是() A. v 增大时,t 增大 B. v 增人时,t 不变 C. v 增大时,L 增大D.v增大时,L减小6.我国载人飞船“神舟七号”的顺利飞天,极大地振奋了民族精神。
“神七“,在轨道飞行过程中,宇航员翟志钢跨出飞船,实现了“太空行走”,当他出舱后相对于飞船静止不动时,以下说法正确的是()A.他处于平衡状态B.他不受任何力的作用C.他的加速度不为零D.他的加速度恒定不变7.关于圆周运动,以下说法正确的是()A.做匀速圆周运动的物体,所受各力的合力一定是向心力B.做匀速圆周运动的物体除了受到其它物体的作用,还受到一个向心力C.物体做离心运动时,是因为它受到了离心力的作用D.汽车转弯时速度过小,会因离心运动造成交通事故8.如图所示,滑块A和B叠放在固定的斜面体上,从静止开始以相同的加速度一起沿斜面加速下滑.己知B与斜面体间光滑接触,则在AB下滑的过程中,下列说法正确的是()A.B对A的支持力不做功;B.. B对A的作用力做负功;C. B对A的摩擦力做正功;D. B, A的重力做功的平均功率相同:9.一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图甲所示,曲线上的:4点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半经ρ叫做A点的曲率半径.现将一物体沿水平方向抛出,落地时速度v与水平面成α角,如图乙所示.则在其轨迹最高点P处的曲率半径是( )2222222sin cos cos ....sin v v v v A B C D gggg αααα10.起重机的钢索将重物由地面吊到空中某个高度,其速度图象如图甲所示,则钢索拉力的功率随时间变化的图象可能是图乙中的哪一个?( )11. .如图所示,a 、b 、c 是北斗卫星导航系统中的3颗卫星,下列说法正确的是() A .b 、c 的向心加速度大小相等,且小于a 的向心加速度B .c 加速可追上同一轨道上的b ,b 减速可等候同一轨道上的cC .b 卫星由于某原因,轨道半径缓慢减小,其线速度增大,机械能增大D .b 卫星由于某原因,轨道半径缓慢减小,其线速度增大,机械能减小12.蹦床运动要求运动员在一张绷紧的弹性网上蹦起、腾空并做空中动作.为了测量运动员跃起的高度,训练时可在弹性网上安装压力传感器,利用传感器记录弹性网的压力,并在计算机上作出压力一时间图象,假设作出的图象如图所示.设运动员在空中运动时可视为质点,忽略空气阻力,则根据图象判断下列说法正确的是(g 取10 m/s2)() A.在1.1 s-2.3s 时系统的弹性势能保持不变 B.运动员在5.5s 时刻运动方向向上 C.运动员跃起的最大高度为5.0 mD.运动员在空中的机械能在增大13.如图所示,一轻质弹簧的下端,固定在水平面上,上端叠放着两个质量均为M的物体B(物体B与弹簧栓接),弹簧的劲度系数为k,初始时物体处于静止状态.现用竖直向上的拉力F 作用在物体A上,使物体A开始向上做加速度为a的匀加速运动,测得两个物体的v-t图像如图乙所示(重力加速度为g),则()A.施加外力的瞬间,A、B间的弹力大小为M(g-a)B.A、 B在t时刻分离,此时弹簧弹力大小不为零1C.弹簧恢复到原长时,物体B的速度达到最大值D. B与弹簧组成的系统的机械能先逐渐减小,后保持不变二、填空题及实验题:(每空2分,共计14分)14.“用DIS研究机械能守恒定律”的实验中,让轻杆连接摆锤由A点释放,用光电门测定摆锤在某一位置的瞬时速度,从而求得摆锤在该位置的动能,同时输入摆锤的高度(实验中A,B,C,D四点高度为0.150m, 0.100 m, 0.050 m, 0.000 m,己由计算机默认),求得摆锤在该位置的重力势能,进而研究势能与动能转化时的规律。
1)实验时,把点作了零势能点。
(2)(单选)若实验测得D点的机械能明显偏大,造成该误差的原因可能是( )A、摆锤在运动中受到空气阻力的影响B、光电门放在D点上方C、摆锤在A点不是由静止释放的D、摆锤释放的位置在AB之间15.某同学查资料得知,弹簧的弹性势212P E kx =,其中k 是弹簧的劲度系数,x 是弹簧长度的变化量.于是设想用压缩的弹簧推静止的小球(质量为m)运动来初步探究“外力做功与物体动能变化的关系”.为了研究方便,把小球放在水平桌面上做实验,让小球在弹力作用下运动,即只有弹簧弹力做功.(重力加速度为g)该同学设计实验如下: (1)首先进行如图甲所示的实验:将轻质弹簧竖直挂起来,在弹簧的另一端挂上小球,静止时测得弹簧的伸长量为d.在此步骤中,目的是要确定弹簧的劲度系数k ,用m 、 d 、 g 表示为 。
(2)接粉进行如图乙所示的实验:将这根弹簧水平放在桌面上,另一端被小球压缩,测得压缩量为x ,释放弹簧,小球被推出去,从高为h 的水平桌面上抛出,小球在空中运动的水平距离为L.小球的初动能1k E = 。
小球离开桌面的动能2k E = (用m 、g 、L 、h )。
弹簧对小球做的功W= (用m 、x 、d 、g 表示)对比W 和21k k E E -就可以得出”外力做功与物体动能变化的关系”. 需要验证的关系为(用所测物理最d,x 、h 、L 表示)三、计算题:(本题4个大题共34分,其中第16-18题均为8分,第19题10分)16.( 8分)有三根长度皆为l=0.30 m 的不可伸长的绝缘轻线,其中两根的一端固定在天花板的O 点,另一端分别栓有质量皆为m=1.0 X 10-2kg 的带电小球A 和B ,它们的电荷量分别为-q 和+q ,q=1.0×10-6C.A 、B 之间用第三根线连接起来,空间中存在大小为E=2.0 X 105 N/C 的匀强电场,电场强度的方向水平向右.平衡时A, B 球的位置如图所示.已知静电力常量k=9 X 109N ·m 2/C 2重力加速度g=10 m/s 2. 求:(I) A, B 间的库仑力的大小(2)连接A, B的轻线的拉力大小.17. (8分)滑板运动是一种陆地上的“冲浪”运动,滑板运动员可在不同的滑坡上滑行,做出各种动作,给人以美的享受.如图是模拟的滑板组合滑行轨道,该轨道由足够长的斜直轨道、半径R1=1m的凹形圆弧轨道和半径R2=1.6m的凸形圆弧轨道组成,这三部分轨道处于同一竖直平面内且依次平滑连接,其中M点为凹形圆弧轨道的最低点,N点为凸形圆弧轨道的最高点,凸形圆弧轨道的圆心0点与M点处在同一水平面上。
一质量为m=1 kg可看作质点的滑板,从斜直轨道上的P点无初速滑下,经过M点滑向N点,P点距M点所在水平面的高度h=1.8m不计一切阻力g取1 Om/s2.(1)滑板滑到M点时的速度多大?(2)滑板滑到M点时,滑板对轨道的压力多大?(3)改变滑板无初速下滑时距M点所在水平面的高度,,用压力传感器测出滑板滑至N点时对轨道的压力大小F,求当F为零时滑板的下滑高度h1.18. (8分)某星球可视为球体,其绕过两极的转轴自转的周期为T,若在它的两极处用弹簧秤测得某物体的重力为F,在赤道上用弹簧秤测得同一物体的重力为0.9F,己知万有引力常量为G,则此星球的平均密度是多少?19. (10分)如图所示,原长为L的轻质弹簧一端固定在O点,另一端与质量为,的圆环相连,圆环套在粗糙竖直固定杆上的A处,环与杆间动摩擦因数μ= 0.5,此时弹簧水平且处于原长。
让圆环从A处由静止开始下滑,经过B处时速度最大,到达C处时速度为零。
过程中弹簧始终在弹性限度之内。
重力加速度为g。
求(1)圆环在A处的加速度为多大?(2)若AB间距离为3L/4,则弹簧的劲度系数k为多少?(3)若圆环到达C 处时弹簧弹性势能为Ep ,且AC =h ,使圆环在C 处时获得一个竖直向上的初速度,圆环恰好能到达A 处。
则这个初速度应为多大?长沙市一中高一下期期水考试物理答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 选项CDAADCACCBADBCABD二·填空题及实验题:(每空2分,共计14分) 14.D C15. 222(1)(2)0,,24mgmgL hx dL dh=16.1(1)0.1(2)0.042F N T N ==17. '1(1)6/(2)46(3) 2.4N v m sF N h m===18. 230GT πρ=19. (1)4(2)(3)2Pa gmg kLmgh E v m=-=以下为部分题目解析。
