2019年海口市高考调研考试-理数试卷
海南省海口市2019年高三高考调研测试数学(理)试卷 PDF版含答案

15.(0,12
) ∵犳(狓)>1+log2犪,∴1+log2犪<0,@0<犪<
1 2
.
16.槡3300 M犗犃,犗犅,犗犆 O,@4π×12+142+犿4=6π,@ 犿2=2,犃→犅=(2,0,-1),@cos〈犃→犅,
犗→犇〉=
1= 槡5×6
槡3300.
17.:(1)∵tan犆=
2;
“¹º4»),¼½42»´µ¶· 犡∈[26,30)”Y¾¿犃,
@
犘(犃)=1-犘(犃珡)=1-[C14×
1 5
×(45
)3+C04×(45
)4]=161235.
5;
(2)犃 ÀÁ/ÀÂîÄÅÃcdY犢(Æ·:Ç).
①ÈÉk³ÊË,@犢 /;²ÌY
5.A ∵狓(狓-5)=(狓+10)2,∴狓=-4,狓+10=6,AB狇=-
3 2
,∴犪狀=-4×(-
3 2
)狀-1.
6.D ∵sin40°<1<log34,ln0.4<0<tan226°,cos(-20°)=cos20°=sin70°>sin65°,∴ C D A,B,C,
tan410°=tan50°>1>sin80°>
犅1犉 ® w 犃犈犉 a ¯ Y θ,@ sinθ= cos〈犅1→犉,狀〉 =
#
$
犅1→犉·狀 犅1→犉 狀
=3槡65130. 12; *
!
)
19.:(1)"°±;²O³KHM´µ¶·
犡∈[26,30)/¸±Y(0.075+0.025)×2=
1 5
.
,∴烅烄狓30 =犽①,
"①?犽狓0=3,gh②?1+3ln狓0=1,
烆犽狓0-2=1+3ln狓0②,
2019年海南高考理科数学真题(含详细完整解析)
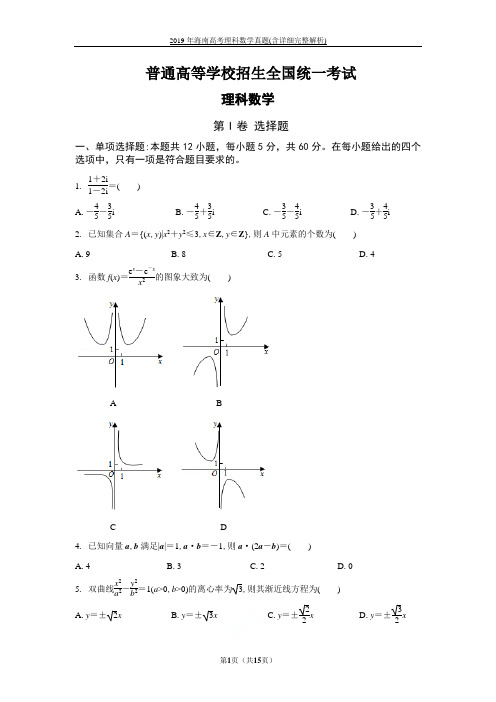
普通高等学校招生全国统一考试理科数学第I 卷 选择题一、单项选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.1+2i1-2i=( ) A .-45-35iB .-45+35iC .-35-45iD .-35+45i2. 已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( ) A .9 B .8C .5D .43. 函数f (x )=e x -e -xx 2的图象大致为( )A BC D4. 已知向量a ,b 满足|a |=1,a ·b =-1,则a ·(2a -b )=( ) A .4 B .3C .2D .05. 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y =±2xB .y =±3xC .y =±22x D .y =±32x6. 在△ABC 中,cos c 2=55,BC =1,AC =5,则AB =( )A .4 2B .30C .29D .2 57. 为计算S =1-12+13-14+…+199-1100,设计了如图的程序框图,则在空白框中应填入( )A .i =i +1?B .i =i +2?C .i =i +3?D .i =i +4?8. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ) A .112B .114C .115D .1189. 在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22 10. 若f (x )=cos x -sin x 在[0,a ]是减函数,则a 的最大值是( ) A .π4 B .π2C .3π4D .π11. 已知f (x )是定义域为(-∞,+∞)的奇函数,满足f (1-x )=f (1+x ),若f (1)=2,则f (1)+f (2)+f (3)+…+f (50)=( )A .-50B .0C .2D .5012. 已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A .23 B .12 C .13D .14第II 卷 非选择题二、填空题:本题共4小题,每小题5分,共20分。
2019年海南高考理科数学真题(含详细完整解析)

普通高等学校招生全国统一考试理科数学第I 卷 选择题一、单项选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.1+2i1-2i=( ) A .-45-35iB .-45+35iC .-35-45iD .-35+45i2. 已知集合A ={(x ,y )|x 2+y 2≤3,x ∈Z ,y ∈Z },则A 中元素的个数为( ) A .9 B .8C .5D .43. 函数f (x )=e x -e -xx 2的图象大致为( )A BC D4. 已知向量a ,b 满足|a |=1,a ·b =-1,则a ·(2a -b )=( ) A .4 B .3C .2D .05. 双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,则其渐近线方程为( )A .y =±2xB .y =±3xC .y =±22x D .y =±32x6. 在△ABC 中,cos c 2=55,BC =1,AC =5,则AB =( )A .4 2B .30C .29D .2 57. 为计算S =1-12+13-14+…+199-1100,设计了如图的程序框图,则在空白框中应填入( )A .i =i +1?B .i =i +2?C .i =i +3?D .i =i +4?8. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( ) A .112B .114C .115D .1189. 在长方体ABCD -A 1B 1C 1D 1中,AB =BC =1,AA 1=3,则异面直线AD 1与DB 1所成角的余弦值为( )A .15B .56C .55D .22 10. 若f (x )=cos x -sin x 在[0,a ]是减函数,则a 的最大值是( ) A .π4 B .π2C .3π4D .π11. 已知f (x )是定义域为(-∞,+∞)的奇函数,满足f (1-x )=f (1+x ),若f (1)=2,则f (1)+f (2)+f (3)+…+f (50)=( )A .-50B .0C .2D .5012. 已知F 1,F 2是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,△PF 1F 2为等腰三角形,∠F 1F 2P =120°,则C 的离心率为( ) A .23 B .12 C .13D .14第II 卷 非选择题二、填空题:本题共4小题,每小题5分,共20分。
2019届高三入学调研理科数学试卷(1)含答案.doc

(2)公司决定再采购_,_两款车扩大市场,_,_两款车各100辆的资料如表:
平均每辆车每年可为公司带来收入500元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命都是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的期望值作为决策依据,应选择采购哪款车型?
即,此时最小,为;
即的取值范围是,故答案为.
15.已知,,则__________.
【答案】
【解析】∵,,∴,
则_,解得_.
∴_.
故答案为_.
16.四棱锥_中,底面_是边长为2的正方形,侧面_是以_为斜边的等腰直角三角形,若四棱锥_的体积取值范围为_,则该四棱锥外接球表面积的取值范围是______.
【答案】_
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数_等于()
A._B._C._D._
【答案】C
【解析】_,故选C.
2.已知集合_,_,则_()
A.B.
C.D.
【答案】C
【解析】集合_,,
∴,故选C.
3.函数的图象是()
A.B.C.D.
【答案】A
【解析】
根据_,由平面向量加法法则,
则有_为平行四边形_的对角线,故_,
联立椭圆_、直线_方程,
可得_,∵_,则_,
_,
可得_,∴_,故选A.
二、填空题:本大题共4小题,每小题5分.
13.曲线_在点_处的切线方程为__________.
【答案】_.
海口市高考数学一诊试卷(理科)(I)卷

海口市高考数学一诊试卷(理科)(I)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2019高二下·凤城月考) 若集合,则()A .B .C .D .2. (2分)复数为虚数单位的虚部为()A .B .C .D .3. (2分) (2019高二下·吉林月考) 完成下列两项调查:从某社区户高收入家庭、户中等收入家庭、户低收入家庭中选出户,调查社会购买能力的某项指标;从某中学的名艺术特长生中选出名调查学习负担情况.这两项调查宜采用的抽样方法依次是()A . 简单随机抽样,系统抽样B . 分层抽样,简单随机抽样C . 系统抽样,分层抽样D . 都用分层抽样4. (2分)已知直线∥平面,,那么过点P且平行于直线的直线()A . 只有一条,不在平面内B . 有无数条,不一定在内C . 只有一条,且在平面内D . 有无数条,一定在内5. (2分)设是等差数列的前n项和,若,则()A . 1B . -1C . 2D .6. (2分)某几何体的三视图如图所示,则该几何体的体积是()A . (+2)πB . (+4)πC . (+2)πD . (+2)π7. (2分)若直线经过点,则()A .B .C .D .8. (2分) (2018高二下·乌兰月考) 如图所示,程序的输出结果为S=132,则判断框中应填()A . i≥10?B . i≥11?C . i≤11?D . i≥12?9. (2分)已知满足不等式设,则的最大值与最小值的差为()A . 4B . 3C . 2D . 110. (2分) (2019高一上·沈阳月考) 要得到函数的图象,只需将函数的图象上所有的点的()A . 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动个单位长度B . 横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动个单位长度C . 横坐标缩短到原来的倍(纵坐标不变),再向左平行移动个单位长度D . 横坐标缩短到原来的倍(纵坐标不变),再向右平行移动个单位长度11. (2分)设抛物线的焦点为F,准线为l,P为抛物线上的一点,,垂足为A.若直线AF的斜率为,则= ()A . 4B . 8C .D .12. (2分) (2018高二下·辽宁期末) 已知是定义在上的奇函数,对任意的,均有 .当时,,则()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高一下·苏州期末) 已知| |=2,• =1,,的夹角θ为60°,则| |为________.14. (1分)(x2+ )6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形面积为________.15. (1分)已知函数f(x)满足f(﹣x)=f(x),且f(x+2)=f(x)+f(2),当x∈[0,1]时,f(x)=x,那么在区间[﹣1,3]内,关于x的方程f(x)=kx+k+1(k∈R)且k≠﹣1恰有4个不同的根,则k的取值范围是________16. (1分)(2017·石嘴山模拟) 已知数列{an}的前n项和为Sn , a1=2,an+1﹣Sn=2(n∈N*)则an=________.三、解答题 (共7题;共60分)17. (10分) (2018高一下·佛山期中) 在锐角中,角,,的对边分别为,,,且.(1)求角;(2)若,求周长的取值范围.18. (5分)(2017·南开模拟) 某仪器经过检验合格才能出厂,初检合格率为:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为.每台仪器各项费用如表:项目生产成本检验费/次调试费出厂价金额(元)10001002003000(Ⅰ)求每台仪器能出厂的概率;(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润=出厂价﹣生产成本﹣检验费﹣调试费);(Ⅲ)假设每台仪器是否合格相互独立,记X为生产两台仪器所获得的利润,求X的分布列和数学期望.19. (10分)(2017·烟台模拟) 如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,.(1)证明:DE⊥AB;(2)求二面角D﹣BE﹣A的余弦值.20. (10分)(2020·河南模拟) 已知椭圆:过点,过坐标原点作两条互相垂直的射线与椭圆分别交于,两点.(1)证明:当取得最小值时,椭圆的离心率为 .(2)若椭圆的焦距为2,是否存在定圆与直线总相切?若存在,求定圆的方程;若不存在,请说明理由.21. (10分) (2018高二下·牡丹江期末) 已知函数/ ,其中 .(1)当时,求曲线在处的切线方程;(2)若函数在区间内恰有一个极大值和一个极小值,求实数的取值范围.22. (5分)(2017·息县模拟) 在直角坐标系xOy中,直线l的参数方程为(t为参数,α∈[0,π)).以原点O为极点,以x轴正半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程为ρcos2θ=4sinθ.(Ⅰ)设M(x,y)为曲线C上任意一点,求x+y的取值范围;(Ⅱ)若直线l与曲线C交于两点A,B,求|AB|的最小值.23. (10分)(2017·赣州模拟) 已知函数f(x)=|x|﹣|x﹣1|.(1)若关于x的不等式f(x)≥|m﹣1|的解集非空,求实数m的取值集合M.(2)记(1)中数集M中的最大值为k,正实数a,b满足a2+b2=k,证明:a+b≥2ab.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共60分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、23-1、23-2、。
2019年全国统一高考数学试卷(理科)(新课标Ⅱ)(海南卷)-普通用卷

2019年全国统一高考数学试卷(理科)(新课标Ⅱ)(海南卷)副标题一、选择题(本大题共12小题,共60.0分)1. 设z =−3+2i ,则在复平面内z 对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. 设函数f(x)的定义域为R ,满足f(x +1)=2f(x),且当x ∈(0,1]时,f(x)=x(x −1).若对任意x ∈(−∞,m],都有f(x)≥−89,则m 的取值范围是( )A. (−∞,94]B. (−∞,73] C. (−∞,52] D. (−∞,83] 3. 若a >b ,则( )A. ln(a −b)>0B. 3a <3bC. a 3−b 3>0D. |a|>|b|4. 若抛物线y 2=2px(p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =( )A. 2B. 3C. 4D. 85. 设F 为双曲线C :x 2a 2−y 2b 2=1(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ|=|OF|,则C 的离心率为( )A. √2B. √3C. 2D. √56. 演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )A. 中位数B. 平均数C. 方差D. 极差7. 下列函数中,以π2为周期且在区间(π4,π2)单调递增的是( )A. f(x)=|cos2x|B. f(x)=|sin2x|C. f(x)=cos |x|D. f(x)=sin |x|8. 设集合A ={x|x 2−5x +6>0},B ={x|x −1<0},则A ∩B =( )A. (−∞,1)B. (−2,1)C. (−3,−1)D. (3,+∞) 9. 已知α∈(0,π2),2sin2α=cos2α+1,则sinα=( ).A. 15B. √55 C. √33 D. 2√5510. 已知AB ⃗⃗⃗⃗⃗ =(2,3),AC ⃗⃗⃗⃗⃗ =(3,t),|BC ⃗⃗⃗⃗⃗ |=1,则AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =( ) A. −3 B. −2 C. 2 D. 3 11. 设α,β为两个平面,则α//β的充要条件是( )A. α内有无数条直线与β平行B. α内有两条相交直线与β平行C. α,β平行于同一条直线D. α,β垂直于同一平面12. 2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日L2点的轨道运行.L2点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,L2点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:M1(R+r)2+M2r2=(R+r)M1R3.设α=rR .由于α的值很小,因此在近似计算中3α3+3α4+α5(1+α)2≈3α3,则r的近似值为().A. √M2M1R B. √M22M1R C. 3√3M2M1R D. 3√M23M1R二、填空题(本大题共4小题,共20.0分)13.△ABC的内角A,B,C的对边分别为a,b,c.若b=6,a=2c,B=π3,则△ABC的面积为______.14.已知f(x)是奇函数,且当x<0时,f(x)=−e ax.若f(ln2)=8,则a=.15.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为______.16.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.三、解答题(本大题共7小题,共84.0分)17.已知数列{a n}和{b n}满足a1=1,b1=0,4a n+1=3a n−b n+4,4b n+1=3b n−a n−4.(1)证明:{a n+b n}是等比数列,{a n−b n}是等差数列;(2)求{a n}和{b n}的通项公式.18.如图,长方体ABCD−A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B−EC−C1的正弦值..记M的19.已知点A(−2,0),B(2,0),动点M(x,y)满足直线AM与BM的斜率之积为−12轨迹为曲线C.(1)求C的方程,并说明C是什么曲线;(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.(i)证明:△PQG是直角三角形;(ii)求△PQG面积的最大值.20.11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.(1)求P(X=2);(2)求事件“X=4且甲获胜”的概率.21.已知函数.(1)讨论f(x)的单调性,并证明f(x)有且仅有两个零点;(2)设x0是f(x)的一个零点,证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=e x的切线.22.在极坐标系中,O为极点,点M(ρ0,θ0)(ρ0>0)在曲线C:ρ=4sinθ上,直线l过点A(4,0)且与OM垂直,垂足为P.(1)当θ0=π时,求ρ0及l的极坐标方程;3(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.23.已知f(x)=|x−a|x+|x−2|(x−a).(1)当a=1时,求不等式f(x)<0的解集;(2)若x∈(−∞,1)时,f(x)<0,求a的取值范围.答案和解析1.【答案】C【解析】【分析】本题主要考查共轭复数的代数表示及其几何意义,属于基础题.求出z 的共轭复数,根据复数的几何意义求出复数所对应点的坐标即可. 【解答】解:∵z =−3+2i , ∴z =−3−2i ,∴在复平面内z 对应的点为(−3,−2),在第三象限. 故选C .2.【答案】B【解析】【分析】本题考查了函数与方程的综合运用,属中档题.由f(x +1)=2f(x),得f(x)=2f(x −1),分段求解析式,结合图象可得. 【解答】解:因为f(x +1)=2f(x), ∴f(x)=2f(x −1),∵x ∈(0,1]时,f(x)=x(x −1)∈[−14,0],∴x ∈(1,2]时,x −1∈(0,1],f(x)=2f(x −1)=2(x −1)(x −2)∈[−12,0]; ∴x ∈(2,3]时,x −1∈(1,2],f(x)=2f(x −1)=4(x −2)(x −3)∈[−1,0], 当x ∈(2,3]时,由4(x −2)(x −3)=−89解得x =73或x =83, 若对任意x ∈(−∞,m],都有f(x)≥−89,则m ≤73. 故选B .3.【答案】C【解析】【分析】本题考查了不等式的基本性质,利用特殊值法可迅速得到正确选项,属基础题.取a =0,b =−1,利用特殊值法可得正确选项. 【解答】解:取a =0,b =−1,则: ln (a −b)=ln1=0,排除A ; 3a =30=1>3b =3−1=13,排除B ;令f (x )=x 3,则f(x)在上单调递增,又a >b ,故C 对; |a|=0<|−1|=|b |,排除D . 故选C . 4.【答案】D【解析】【分析】本题考查了抛物线与椭圆的性质,属基础题. 根据抛物线的性质以及椭圆的性质列方程可解得. 【解答】解:由题意可得3p −p =(p2)2,解得p =8. 故选D . 5.【答案】A【解析】【分析】本题考查双曲线的简单性质,考查数形结合的解题思想方法.由题意画出图形,先求出PQ ,再由|PQ|=|OF|列式求C 的离心率. 【解答】 解:如图,由题意,把x =c2代入x 2+y 2=a 2,得PQ =2√a 2−c 24,再由|PQ|=|OF|,得2√a 2−c 24=c ,即2a 2=c 2,∴c 2a 2=2,解得e =ca =√2. 故选A .6.【答案】A【解析】解:根据题意,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,最中间的一个数不变,即中位数不变, 故选:A .根据题意,由数据的数字特征的定义,分析可得答案.本题考查数据的数字特征,关键是掌握数据的平均数、中位数、方差、极差的定义以及计算方法,属于基础题. 7.【答案】A【解析】【分析】本题主要考查了正弦函数、余弦函数的周期性及单调性,考查了排除法的应用,属于中档题.根据正弦函数、余弦函数的周期性及单调性依次判断,利用排除法即可求解. 【解答】解:f(x)=sin |x|不是周期函数,可排除D 选项; f(x)=cos |x|的周期为2π,可排除C 选项;f(x)=|sin 2x|在π4处取得最大值,不可能在区间(π4,π2)上单调递增,可排除B . 故选A . 8.【答案】A【解析】【分析】本题考查交集的计算,关键是掌握交集的定义,涉及到不等式的求解,属于基础题. 根据题意,求出集合A 、B ,由交集的定义计算可得答案. 【解答】解:根据题意,A ={x|x 2−5x +6>0}={x|x >3或x <2}, B ={x|x −1<0}={x|x <1},则A ∩B ={x|x <1},即A ∩B =(−∞,1). 故选A . 9.【答案】B【解析】【分析】本题主要考查了二倍角的三角函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.由二倍角公式化简已知条件可得4sinαcosα=2cos 2α,结合角的范围可求得sinα>0,cosα>0,可得cosα=2sinα,根据同角三角函数基本关系式即可解得sinα的值. 【解答】解:∵2sin2α=cos2α+1,由二倍角公式可得4sinαcosα=2cos 2α, ∵α∈(0,π2),∴sin α>0,cos α>0,∴cosα=2sinα.则有sin 2α+cos 2α=sin 2α+(2sinα)2=5sin 2α=1, 解得sinα=√55.故选B .10.【答案】C【解析】【分析】本题主要考查了向量数量积的定义及性质的坐标表示,属于基础题. 由BC⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ 先求出BC ⃗⃗⃗⃗⃗ 的坐标,然后根据|BC ⃗⃗⃗⃗⃗ |=1,可求t ,结合向量数量积定义的坐标表示即可求解. 【解答】解:∵AB⃗⃗⃗⃗⃗ =(2,3),AC ⃗⃗⃗⃗⃗ =(3,t),∴BC ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ −AB⃗⃗⃗⃗⃗ =(1,t −3). ∵|BC ⃗⃗⃗⃗⃗ |=1,∴t −3=0,即BC ⃗⃗⃗⃗⃗ =(1,0), 则AB⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =2. 故选C . 11.【答案】B【解析】【分析】本题考查了充要条件的定义和面面平行的判定定理,考查了推理能力,属于基础题. 由充要条件的定义结合面面平行的判定定理可得结论. 【解答】解:对于A ,α内有无数条直线与β平行,α与β相交或α//β; 对于B ,α内有两条相交直线与β平行,则α//β;对于C ,α,β平行于同一条直线,α与β相交或α//β; 对于D ,α,β垂直于同一平面,α与β相交或α//β. 故选B .12.【答案】D【解析】【分析】本题考查点到月球的距离的求法,考查函数在我国航天事业中的灵活运用,考查化归与转化思想、函数与方程思想,考查运算求解能力,是中档题. 由α=r R ,推导出M2M 1=3α3+3α4+α5(1+α)2≈3α3,由此能求出r =αR =√M23M13R .【解答】解:∵α=rR , ∴r =αR , 且r 满足方程M 1(R+r)2+M 2r 2=(R +r)M1R 3,∴M 2M 1=3α3+3α4+α5(1+α)2≈3α3,∴r =αR =√M23M13R .故选:D .13.【答案】6√3【解析】【分析】本题考查了余弦定理和三角形的面积公式,属基础题. 利用余弦定理得到c 2,然后根据面积公式求出结果即可.【解答】解:由余弦定理有,∵b =6,a =2c ,B =π3, ∴36=(2c)2+c 2−4c 2cos π3, ∴c 2=12,.故答案为6√3.14.【答案】−3【解析】【分析】本题主要考查函数奇偶性的应用,对数的运算性质,属于基础题.奇函数的定义结合对数的运算可得结果【解答】解:∵f(x)是奇函数,∴f(−ln2)=−8,又∵当x<0时,f(x)=−e ax,∴f(−ln2)=−e−aln2=−8,∴−aln2=ln8,∴a=−3.故答案为−3.15.【答案】0.98【解析】【分析】本题考查经停该站高铁列车所有车次的平均正点率的估计值的求法,考查加权平均数公式等基础知识,考查推理能力与计算能力,属于基础题.利用加权平均数公式直接求解.【解答】解:∵经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,∴经停该站高铁列车所有车次的平均正点率的估计值为:x−=110+20+10(10×0.97+20×0.98+10×0.99)=0.98.故答案为0.98.16.【答案】26;√2−1【解析】【分析】本题考查了几何体的内接多面体,属中档题.中间层是一个正八棱柱,有8个侧面,上层是有8+1个面,下层也有8+1个面,故共有26个面;中间层正八棱柱的棱长加上两个棱长的√22倍等于正方体的棱长.【解答】解:该半正多面体中间层是一个正八棱柱,有8个侧面,故该半正多面体共有8+8+8+ 2=26个面;设其棱长为x,因为每个顶点都在边长为1的正方体上,则x+√22x+√22x=1,解得x=√2−1.故答案为26;√2−1.17.【答案】(1)证明:∵4a n+1=3a n−b n+4,4b n+1=3b n−a n−4,∴4(a n+1+b n+1)=2(a n+b n),4(a n+1−b n+1)=4(a n−b n)+8,即a n+1+b n+1=12(a n+b n),a n+1−b n+1=a n−b n+2;又a1+b1=1,a1−b1=1,∴{a n+b n}是首项为1,公比为12的等比数列,{a n−b n}是首项为1,公差为2的等差数列;(2)解:由(1)可得:a n+b n=(12)n−1,a n−b n=1+2(n−1)=2n−1,∴a n =(12)n +n −12,b n =(12)n −n +12.【解析】本题主要考查了等差、等比数列的定义和通项公式,考查学生的计算能力和推理能力,属于简单题. (1)定义法证明即可;(2)由(1)结合等差、等比的通项公式可得.18.【答案】解:证明:(1)长方体ABCD −A 1B 1C 1D 1中,B 1C 1⊥平面ABA 1B 1, ∴B 1C 1⊥BE , ∵BE ⊥EC 1,∵B 1C 1∩EC 1=C 1, ∴BE ⊥平面EB 1C 1,(2)以C 为坐标原点,建立如图所示的空间直角坐标系,设AE =A 1E =1, ∵BE ⊥平面EB 1C 1, ∴BE ⊥EB 1, ∴AB =1,则E(1,1,1),A(1,1,0),B 1(0,1,2),C 1(0,0,2),C(0,0,0), ∵BC ⊥EB 1,BE ⊥EB 1,且BC ∩BE =E , ∴EB 1⊥面EBC ,故取平面EBC 的法向量为m ⃗⃗ =EB 1⃗⃗⃗⃗⃗⃗⃗ =(−1,0,1),设平面ECC 1 的法向量n⃗ =(x,y ,z), 由{n ⃗ ⋅CC 1⃗⃗⃗⃗⃗⃗⃗ =0n ⃗ ⋅CE ⃗⃗⃗⃗⃗ =0,得{z =0x +y +z =0, 取x =1,得n⃗ =(1,−1,0), ∴cos <m ⃗⃗ ,n ⃗ >=m⃗⃗⃗ ⋅n ⃗ |m ⃗⃗⃗ |⋅|n ⃗ |=−12, ∴二面角B −EC −C 1的正弦值为√32.【解析】本题主要考查线面垂直的证明,考查二面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理能力与计算能力,属于中档题. (1)推导出B 1C 1⊥BE ,BE ⊥EC 1,由此能证明BE ⊥平面EB 1C 1.(2)以C 为坐标原点,建立如图所示的空间直角坐标系,利用向量法能求出二面角B −EC −C 1的正弦值.19.【答案】解:(1)由题意得y x+2·y x−2=−12,整理得曲线C 的方程:x 24+y 22=1(y ≠0),∴曲线C 是焦点在x 轴上不含长轴端点的椭圆;(2)(i)设P(x 0,y 0),则Q(−x 0,−y 0),E(x 0,0),G(x G ,y G ),∴直线QE 的方程为:y =y 02x 0(x −x 0),与x 24+y 22=1联立消去y ,得(2x 02+y 02)x 2−2x 0y 02x +x 02y 02−8x 02=0,∴−x 0x G =x 02y 02−8x 022x 02+y 02, ∴x G =(8−y 02)x 02x 02+y 02, ∴y G =y 02x 0(x G −x 0)=y 0(4−x 02−y 02)2x 02+y 02,∴k PG =y G −y 0x G −x 0 =y 0(4−x 02−y 02)2x 02+y 02−y 0x 0(8−y 02)2x 02+y 02−x 0 =4y 0−y 0x 02−y 03−2y 0x 02−y 038x 0−x 0y 02−2x 03−x 0y 02 =y 0(4−3x 02−2y 02)2x 0(4−y 02−x 02),把x 02+2y 02=4代入上式, 得k PG =y 0(4−3x 02−4+x 02)2x 0(4−y 02−4+2y 02)=−y 0×2x 022x 0y 02=−x 0y 0, ∴k PQ ·k PG =y 0x 0·(−x0y 0)=−1,∴PQ ⊥PG ,故△PQG 为直角三角形;(ii)S △PQG =12|PE|·(x G −x Q ) =12y 0(x G +x 0)=12y 0[(8−y 02)x 02x 02+y 02+x 0] =12y 0x 0×8−y 02+2x 02+y 022x 02+y 02 =y 0x 0(4+x 02)2x 02+y 02 =y 0x 0(x 02+2y 02+x 02)2x 02+y 02 =2y 0x 0(x 02+y 02)2x 02+y 02 =8y 0x 0(x 02+y 02)(2x 02+y 02)(x 02+2y 02)=8(y 0x 03+x 0y 03)2x 04+2y 04+5x 02y 02 =8(x 0y 0+y 0x 0)2(x 0y 0+y 0x 0)2+1 令t =x 0y 0+y0x 0,则t ≥2, S △PQG =8t 2t 2+1=82t +1t 利用“对勾”函数f(t)=2t +1t 在[2,+∞)的单调性可知,f(t)≥4+12=92(t =2时取等号), ∴S △PQG ≤892=169(此时x 0=y 0=2√33), 故△PQG 面积的最大值为169.【解析】此题考查了直接法求曲线方程,直线与椭圆的综合,换元法等,对运算能力考查尤为突出,计算难度大.(1)利用直接法不难得到方程;(2)(i)设P(x 0,y 0),则Q(−x 0,−y 0),E(x 0,0),利用直线QE 的方程与椭圆方程联立求得G 点坐标,进而证得PQ ,PG 斜率之积为−1;(ii)利用S =12|PE|×(x G +x 0),代入已得数据,并对x 0y 0+y 0x 0换元,利用“对勾”函数可得最值. 20.【答案】解:(1)设双方10:10平后的第k 个球甲获胜为事件A k (k =1,2,3,…),则P(X =2)=P(A 1A 2)+P(A 1−A 2−)=P(A 1)P(A 2)+P(A 1−)P(A 2−)=0.5×0.4+0.5×0.6=0.5;(2)P(X =4且甲获胜)=P(A 1−A 2A 3A 4)+P(A 1A 2−A 3A 4)=P(A 1−)P(A 2)P(A 3)P(A 4)+P(A 1)P(A 2−)P(A 3)P(A 4)=(0.5×0.4+0.5×0.6)×0.5×0.4=0.1.【解析】本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查推理能力与计算能力,是中档题.(1)设双方10:10平后的第k 个球甲获胜为事件A k (k =1,2,3,…),则P(X =2)=P(A 1A 2)+P(A 1−A 2−)=P(A 1)P(A 2)+P(A 1−)P(A 2−),由此能求出结果;(2)P(X =4且甲获胜)=P(A 1−A 2A 3A 4)+P(A 1A 2−A 3A 4)=P(A 1−)P(A 2)P(A 3)P(A 4)+P(A 1)P(A 2−)P(A 3)P(A 4),由此能求出事件“X =4且甲获胜”的概率. 21.【答案】解析:(1)函数f(x)=lnx −x+1x−1,定义域为:(0,1)∪(1,+∞); f′(x)=1x +2(x−1)2>0,(x >0且x ≠1),∴f(x)在(0,1)和(1,+∞)上单调递增,①在(0,1)区间取值1e 2,1e 代入函数,由函数零点的定义得,∵f(1e 2)<0,f(1e )>0,f(1e 2)⋅f(1e )<0,∴f(x)在(0,1)有且仅有一个零点,②在(1,+∞)区间取值e ,e 2代入函数,由函数零点的定义得,又∵f(e)<0,f(e 2)>0,f(e)⋅f(e 2)<0,∴f(x)在(1,+∞)上有且仅有一个零点,故f(x)在定义域内有且仅有两个零点;(2)x 0是f(x)的一个零点,则有lnx 0=x 0+1x 0−1, 曲线y =lnx ,则有y′=1x ,曲线y =lnx 在点A(x 0,lnx 0)处的切线方程为:y −lnx 0=1x 0(x −x 0), 即y =1x 0x −1+lnx 0, 可得y =1x 0x +2x 0−1,而曲线y =e x 的切线在点(ln 1x 0,1x 0)处的切线方程为:y −1x 0=1x 0(x −ln 1x 0),即y =1x 0x +2x 0−1,故曲线y =lnx 在点A(x 0,lnx 0)处的切线也是曲线y =e x 的切线.故得证.【解析】本题考查f(x)的单调性,函数导数,在定义域内根据零点存在性定理求零点个数,以及利用曲线的切线方程定义证明.(1)讨论f(x)的单调性,求函数导数,在定义域内根据零点存在性定理求零点个数,(2)运用曲线的切线方程定义可证明y =lnx 在点A(x 0,lnx 0)处的切线方程为y =1x 0x +2x 0−1,曲线y =e x 在点(ln 1x 0,1x 0)处的切线方程为y = 1x 0x +2x 0−1 ,得证.22.【答案】解:(1)如图:∵M(ρ0,θ0)(ρ0>0)在曲线C :ρ=4sinθ上,当θ0=π3时,,且由图得|OP|=|OA|cosθ0=2,在直线l 上任取一点(ρ,θ),则有,即,故l 的极坐标方程为ρcos(θ−π3)=2;(2)设P(ρP ,θP ),则在Rt △OAP 中,有|OP|=|OA|cosθP即ρP =4cosθP ,∵P 在线段OM 上,且AP ⊥OM ,∴θP ∈[π4,π2],其中π4为P 点与M 点重合时的角度,由4cosθP =4sinθP 得到,故P 点轨迹的极坐标方程为ρ=4cosθ,θ∈[π4,π2].【解析】本题考查曲线的极坐标方程及其应用,数形结合能力,是中档题.(1)由θ0=π3可得|OP|=2,在直线l 上任取一点(ρ,θ),利用三角形中边角关系即可求得l 的极坐标方程;(2)设P(ρ,θ),在Rt △OAP 中,根据边与角的关系得答案.23.【答案】解:(1)当a =1时,f(x)=|x −1|x +|x −2|(x −1),∵f(x)<0,∴当x <1时,f(x)=−2(x −1)2<0,恒成立,∴x <1;当x ≥1时,f(x)=(x −1)(x +|x −2|)≥0恒成立,∴x ∈⌀;综上,不等式的解集为(−∞,1).(2)∵x ∈(−∞,1)时,f(x)=|x −a|x −(x −2)(x −a).当a ≥1时,f(x)=2(a −x)(x −1)<0在x ∈(−∞,1)上恒成立;当a <1时,若x ∈(−∞,a),f(x)=2(a −x)(x −1)<0,∴f(x)<0,成立;若x∈(a,1),则f(x)=2(x−a)>0,不满足题意;所以当a<1时,不满足题意;综上,a的取值范围为[1,+∞).【解析】本题考查了绝对值不等式的解法,考查了分类讨论思想,关键是掌握相关知识,逐一分析解答即可,属于中档题.(1)将a=1代入得f(x)=|x−1|x+|x−2|(x−1),然后分x<1和x≥1两种情况讨论f(x)<0即可;(2)根据条件分a≥1和a<1两种情况讨论即可.。
2019年海南省高考理科数学试卷及答案解析【word版】

2019年普通高等学校招生全国统一考试(新课标Ⅱ卷)理科数学注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合{}0,1,2M =,{}2=320N x x x -+≤,则MN =(A) {}1 (B) {}2 (C) {}0,1(D) {}1,2解析:∵{}{}2=32012N x x x x x -+≤=≤≤,∴MN ={}1,2答案:D(2)设复数1z ,2z 在复平面内的对应点关于虚轴对称,12i z =+,则12z z =(A) 5-(B) 5(C) 4i -+(D) 4i --解析:∵12i z =+,∴22i z =-+,∴2212(2i)(2i)i 25z z =+-+=-=-答案:A(3)设向量a ,b 满足+=a b -=a b =⋅a b(A) 1(B) 2(C) 3(D) 5解析:∵+=a b -=a b 2()10+=a b ……①,2()6-=a b ……②. 由①-②得:1=⋅a b答案:A(4)钝角三角形ABC 的面积是12,1AB =,BC =AC =(A) 5(C) 2 (D) 1解析:∵1||||sin 2ABC S AB BC B ∆=⋅⋅,即:111sin 22B =⋅,∴sin B = 即45B =或135.又∵222||||||2||||cos AC AB BC AB BC B =+-⋅⋅∴2||1AC =或5,又∵ABC ∆为钝角三角形,∴2||5AC =,即:AC答案:B(5)某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 (A) 0.8 (B) 0.75 (C) 0.6 (D) 0.45解析:此题为条件概率,所以0.60.80.75P == 答案:A(6)如图,格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件有一个底 面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则 切削掉部分的体积与原来毛坯体积的比值为(A) 1727 (B) 59(C)1027(D)13解析:原来毛坯体积为:223654(cm )ππ⋅⋅=,由三视图得,该零件由左侧底面半径为2cm ,高为4cm 的圆柱和右侧底面半径为3cm ,高为2cm 的圆柱构成,所以该零件的体积为:222243234(cm )πππ⋅⋅+⋅⋅=,则切削掉部分的体积为2543420(cm )πππ-=,所以切削掉部分的体积与原来毛坯体积的比值为20105427ππ= 答案:C(7)执行右面的程序框图,如果输入的x ,t 均为2,则输出的S = (A) 4 (B) 5 (C) 6 (D) 7 解析:输入的x ,t 均为2.12≤是,1221M =⋅=,235S =+=,112k =+=;22≤是,2222M =⋅=257S =+=,213k =+=,32≤否,输出7S = 答案:D(8)设曲线ln(1)y ax x =-+在点(0,0)处的切线方程为2y x =,则a = (A) 0(B) 1(C) 2解析:∵1'1y a x =-+,且在点(0,0)处的切线的斜率为2,∴01'|201x y a ==-=+,即3a = 答案:D(9)设x ,y 满足约束条件70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩,则2z x y =-的最大值为(A) 10(B) 8(C) 3(D) 2解析:作出x ,y 满足约束条件70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩表示的平面区域如图阴影部分:做出目标函数0l :2y x =,∵2y x z =-,∴当2y x z =-的截距 最小时,z 有最大值。
2019年普通高等学校招生全国统一考试5月调研测试卷—理科数学(附参考答案)

2021年普通高等学校招生全国统一测试5月调研测试卷理科数学本试卷共23题,共150分,共4页.测试结束后,将本试卷和做题卡一并交回.求的.A.C.D.两条不同的直线a, b和一个平面 ,那么使得“ a//b〞成立的一个必要条件是6. C.D.a//a//且b//a, b与所成角相同某几何体的三视图如下图,那么该几何体的外表积为A. 4 2 2俯视图C. 8 2.2、选择题: 本大题共12小题,每题5分,共60分. 在每题给出的四个备选项中,只有一项为哪一项符合题目要假设复数z满足—zi其中i是虚数单位,那么z1.—i 2C. D.2. 集合[2, ), B {x|1 w x w a} , AI ,那么实数a的取值范围是3.4. A. (2,函数f(x) 2x,那么曲线y f (x)在点(1,C. (1, 2)f(1))处的切线的倾斜角是C. 23某中学数学竞赛培训班共有10人,分为两个小组,在一次模拟测试中两个小组成绩的茎叶图如下图,甲乙两组同学成绩的平均数相同, 那么甲乙两组同学成绩的中位数之差为D.D.(1, 2]3_45.10.某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有 3男3女参加三所单位的招聘,那么不同的录取方案种数为. ................................................. -.* ... .........一、,、, 一 ■ ■ 一 •2 ,对任意k N , a 2k , a 2k 1, a 2k 2成等差数列,公差为2k 1,那么a 1017. 执行如下图的程序框图,假设输出i 的值为7,那么框图中①处可以填入8. 9. B.C. D.S>7S> 21S> 28S>36uuu 等腰梯形 ABCD 中,AB G 为EF 的中点,假设记 3r 3r A. — a — b8 4函数 f(x) Acos( xuur rAB a, UUUT2DC , E, ULUT r AD b, F 分别为AD, BC 的中点,UULf 那么AGB. 3r-a8 3r —b 4D.3r b 8)(A0,0,局部图象如下图,要得到函数 Asin x 的图象,只需将函数f(x)的图象A .向左平移一12B. 向左平移一6C.向右平移一12D.向右平移一6A. 36B. 72C. 108D. 14411.假设函数f (x)(cosx sin x) e x , x (0, 10 ),那么f (x)的所有极大值点之和与所有极小值点之和的差为B. 5C. 55D. 5522x y12.直线l 与椭圆C 1:一 —8 421切于点P ,与圆C 2: x 2y 2 16交于点A, B ,圆C 2在点A, B 处的切线交于点Q , O 为坐标原点,那么OPQ 的面积的最大值为二、填空题:本大题共 13.在平面直角坐标系B.C. ,2D. 14小题,每题5分,共20分.xOy 中,角 的终边上有一点 P(1,2),贝U sin214 .在圆 x 2 y 2 2x15 .双曲线— a1上任取一点,那么该点到直线 x 、3y一 一 3 一 2 0的距离不小于一的概率为2斗 1 (a 0, b 0)的左焦点为F 1 ,过点F 1作斜率为J2的直线与y 轴及双曲线的右支分 b 2别交于A, B 两点,假设uur uuuF 1A AB,那么双曲线的离心率为16.数列{a n }中,a 2三、解做题:共70分.解容许写出文字说明、证实过程或演算步骤.第17〜21题为必考题,每个试题考生都必须作答.第22、23为选考题,考生根据要求作答.(一)必考题:共60分.17. (12 分)锐角ABC中,角A, B, C所对的边分别为a, b, c, sin A cosC(sin B J3cosB) 0 .(1)求角C ;(2)假设b J2, c J3,求AB边上的高长.18. 〔12 分〕中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加效劳的志愿者分“嘉宾〞、“法医〞等假设干小组.2021年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的功能厅参加了500名学生在重庆科技馆多“志愿者培训〞,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2021年中国国际智博会效劳的志愿者.(1)假设“嘉宾〞小组需要2名志愿者,求这2人分别来自不同大学的概率(结果用分数表示) ;(2)假设“法医〞小组的3名志愿者只能从重庆医科大学或西南政法大学抽出, 用表示抽出志愿者来自重庆医科大学的人数, 求的分布列和数学期望.19. (12 分)如图,在四^^锥S ABCD中,底面ABCD是矩形,M 是AB的中点,AC与DM交于点O , SO 平面ABCD , AB 2芯,AD 2石,SO 2.(1)求证:平面SAC 平面SDM ;(2)求直线SB与平面SAD所成角的正弦值.A M B20. (12 分)2 2x y 点P 在椭圆 —— — 1上,过点P 作PP x 轴于点P . 2 4(1)求线段PP 的中点的轨迹 C 的方程;(2)设A 、B 两点在(1)中轨迹C 上,点M(0, 1),两直线MA 与MB 的斜率之积为uur uur迹C 上存在点D 满足|DA| |DB|,当 ABD 面积最小时,求直线 AB 的方程.21 . (12 分)a R,函数f(x) x 2 2ax (4 a)ln x 有两个不同的极值点 x1, x 2. (1)求a 的取值范围;(2)证实:f(x 1)f(x 2) 16ln 2 24 .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,那么按所做的第一题计分. 22 .[选彳4-4:坐标系与参数方程](10分)x tcos在直角坐标系xOy 中,曲线C 1的参数方程为 (t 为参数且t 0 ,[0,)),曲线C 2的参数y tsin、一 x cos 万程为(为参数),以.为极点,x 轴正半轴为极轴建立极坐标系,曲线 C 3的极坐标方程为y 1 sin4cos(1)求C 2的普通方程及C 3的直角坐标方程;(2)假设曲线C I 与曲线C 2, C 3分别交于点A, B,求|AB|的最大值.23 .[选彳4—5:不等式选讲](10分)设函数 f (x) | x 1| | x a |, a R .(1)假设不等式 “刈为6的解集为(,4]U [b, ) (b 4),求a, b 的值;(2)假设f(x)> a|x|对任意x R 恒成立,求a 的取值范围.1 一 …一,且(1)中轨22021年普通高等学校招生全国统一测试5月调研测试卷理科数学参考答案一、选择题 1 〜6 DBDCDD 7 〜12 CBCDAA9 .解析:由题意知:A 2,又由于f(0) 2cos 1一,3,22又由于f(——)2——— 2,33 3所以 f(x) 2cos(2x —) 2sin(2 x —) 2sin[2( x )]. 361211 2 12 2 1...10 .解析:分两类:甲单位一男一女或两男: C 3 C 3 C 4 C 2 C 3 C 4 C 2 144.11 .解析:f (x)2sin x e x 0 x ( , 2) U (3 , 4)U(5 , 6 )U(7 , 8 )U(9 , 10 ),所以极大值点为:2 , 4 , 6 , 8 ,极小值点为: ,3 , 5 , 7 , 9 ,那么差值为 5 .12 .解析:设 Q(x 〔,y 〔),P(x 2, y 2),那么有:% 272cos , y ? 2sin ,又由替换法那么有:x 〔x y 〔y 16与x 2x 至y 1表示同一条线, 8 4 1 所以 x 1 2x 2, y 1 4y 2S —x 1y 2x 2y 1 2j2sin2,所以取大值2J2 .2、填空题__ BF b -22_ 一 _所以 tan BF 1F 2 ------------------ ------------- 、、2 c a 2.2ac 0F 1F 2 2ac三、解做题 17. (12 分)解:(1)由于 sin A cosC(sin B J3cosB) 0所以 cosB(sinC 、3 cosC) 0 tanC(2)由余弦定理有:c 2 a 2 b 22abcosC4 13. 515.解析:14. 115.2 .3 16. 51013uur uur F 1A ABy B 2YA ,即A 为F 〔B 中点,那么AO 为中位线,所以BF 2FR,16.解析:a 100 a 2 2 (3 599) 5000a 101 5000 101 5101 .e 2 W.sin( B C) cosC(sin B 73cosB) 0 , 33C — . (6 分)3a 2 \ 2a 1 0 a那么分布列为:所以E( ) 2. (12分)19. (12 分)〔1〕以A 为原点,AB 为x 轴,AD 为y 轴建立平面直角坐标系,uur _ _ uuuin _ _ uur Luur那么 AC 〔2褥,2黎〕,DM 〔® 2阴〕,由于 AC DM 0 AC DM又由于SO 面ABCD SO DM ,又由于 AC I SO O 所以DM 面SAC 平面SAC 平面SDM . 〔6分〕 〔2〕以.为原点,OC, OD, OS 分别为x, v, z 轴建立坐标系由于 AC DM ,所以 DO 20M 2应,OC 2OA 4,T 设平面SAD 的法向量n 〔x, y, z 〕,所求线面角为UULT T AD n 0UUU TAS n 0uur uur uuuu那么 SB SA 2AM (2,UULT2), AD (2, 2.2,ULU0), AS (2, 0, 2),T ULT 那么 sin cos n,SBT UUT n SB ---- U LT3.10 八------- .(12 分)10由等面积法有:S 1absinC -ch h 上«3.〔12分〕22 218. 〔12 分〕解:〔1〕由题意知:重庆大学、西南大学、重庆医科大学、西南政法大学志愿者分别为15, 20, 10, 5人.C 15C 20C 10C 5c 5o57 . (6 分)〔2〕 的可能取值为:0, 1, 2, 3P( 0)P( 2)C 3C ;5 29? P 〔 1)CfC 10 C 35 20 91' C 5c 210 45C ;5P(3)C 30 C 3524 91解: n ( -: 2, 1, x 2).解:X21〕设中点坐标〔x, y〕,那么P〔x, 2y〕,所以——2(2y)24 1 (4 分)解: 〔2〕设直线AB: y kx m,联立椭圆得:(1 2 k2 )x2 4kmx 2m2 2 0.设A〔x1,y1〕,B〔x2,y2〕,贝u有:k MA由于S VABD2y11y2 1 k x1x2 k(m 1)(x1 x2) (m 1)2x1 x2 x1x2m 12(m 1)m 0.kx ,解得2S VOAD,所以S V ABD最小时,所以直线AB为y(12 分)(D f (x) 2x 2a所以4a24(2) f (x)f (x1)令为由于2X A一1同理2 2kX D—2k2.S VOAD1-OA2OD 2T x D1 1 22k2k2252k2 2k2a-i22 (44 a2x 2a - xx. (12分)2x22ax (4a)2x22ax (4x4.a)(4分)x2a, x1x22f (x2) (X I x2) 2x1x2 2a(x1 x2) (4 a)ln x1x24 a4 (4 a)ln ------------ ,2f(x2) 2tlnt 4t214t 16,h(t),2那么有h(t) 2ln t 8t 16 h (t) - 8,h (t) 0,所以h(t),所以h(t) h(4) 0,所以h(t)所以h(t) h(4) 16ln 2 24. (12 分)解: 2(1) C 2:x (y1)22cos .2sin21 , C 3 :4 cos 2y 4x2 2(x 2) y4.(5 分)23. 解: ⑵C i :C 2 : 2sin 由图像可知: (10 分)(1) f( 4) 5f(b) b ABOBOA2sin 4cos 2、5sin((10 分)〔经检验,舍〕4 〔经检验,舍〕(5分)(2)①.当a< 0时:②.当a 0时:由图像知a 2 w f( a) aw a综上所述,a〔10分〕。
