2020-2021福州一中高三下学期理科数学开学质量检查考试及答案最终版

合集下载

福建省福州市第一中学2020-2021学年高一化学下学期在线自测自评质检试题

734 4福建省福州市第一中学2020-2021学年高一化学下学期在线自测自评质检试题一、选择题（每题 3 分，共 60 分）1．在 NO 2 被水吸收的反应中，发生还原反应和发生氧化反应的物质质量比为A ．3∶1B ．1∶3C ．1∶2D ．2∶12．鉴别二氧化氮和溴蒸气，可选用的试剂是A ．NaOH 溶液B ．淀粉/KI 试纸C ．硝酸银溶液D ．石蕊溶液3．所含微粒种类最少的液体是A ．液氨B ．氯水C ．氨水D ．盐酸4．下列可作为氨气干燥剂的是A ．浓硫酸B ．碱石灰C ．无水氯化钙D ．氢氧化钠溶液5．将导出的氨气接近下列物质时，不会产生白烟的是A ．氯气B ．浓 H 2SO 4C ．浓 HClD ．浓 HNO 36．下列实验用来证明 SO 2 的存在，其中正确的是①能使品红溶液褪色②能使湿润的蓝色石蕊试纸变红③能使澄清的石灰水变浊④通入足量的 NaOH 溶液中，再滴入 BaCl 2 溶液，有白色沉淀生成，该沉淀溶于盐酸 ⑤通入溴水使其褪色，再滴入 Ba(NO 3)2 溶液，有白色沉淀 A ．都能证明B ．都不能证明C ．①⑤能证明D ．只有⑤能证明7．对于某些离子的检验及结论一定正确的是A ．加入稀盐酸产生无色气体，将气体通入澄清石灰水中，溶液变浑浊，一定有 CO 2-B ．加入氯化钡溶液有白色沉淀产生，再加盐酸，沉淀不消失，一定有 SO 2-C ．加入氢氧化钠溶液并加热，产生的气体能使湿润红色石蕊试纸变蓝，一定有 NH +D ．加入碳酸钠溶液产生白色沉淀，再加盐酸白色沉淀消失，一定有 Ba 2+8．下述实验中均有红棕色气体产生，对比分析所得结论不正确的是①②③A ．由①中的红棕色气体，推断产生的气体一定是混合气体B ．红棕色气体不能表明②中木炭与浓硝酸发生了反应C ．由③说明浓硝酸具有挥发性，生成的红棕色气体为还原产物8D ．③的气体产物中检测出 CO 2，由此说明木炭一定与浓硝酸发生了反应9．在下图装置中，烧瓶中充满干燥气体 a ，将滴管中的液体 b 挤入烧瓶内，轻轻振荡烧瓶，然后打开弹簧夹 f ，烧杯中的液体 b呈喷泉状喷出，最终几乎充满烧瓶。

福州市2020届高三1月质量检查(数学理)

准考证号姓名.〔在此卷上答题无效〕绝密★启用前2021 — 2021学年度第一学期福州市高三期末质量检测数学〔理科〕试题〔完卷时间120 分钟；总分值150 分〕本试卷分第Ⅰ卷〔选择题〕和第Ⅰ卷〔非选择题〕两局部．第Ⅰ卷1至2页，第Ⅰ卷3至4 页．总分值 150 分.考前须知：1.答题前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名〞与考生本人准考证号、姓名是否一致．2.第Ⅰ卷每题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．第Ⅰ卷用 0.5 毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．3.考试完毕，考生必须将试题卷和答题卡一并交回．第Ⅰ卷一、选择题：本大题共 12小题，每题 5 分，共 60 分．在每题给出的四个选项中，只有一项为哪一项符合题目要求的．1.设复数 z 1i ,那么zi 12A ． 5B．10 2C．5D．542 22.集合 A x | x ≤ 0或 x ≥ 2， B x | x2x 2 ≤ 0 ，那么A ．AüB B．BüAC．AI B D． AUB R3.执行如下图的程序框图，假设输入的a,b 分别为 4,2 ,那么输出的 nA ．6B． 5C．4D． 34.向量 a(2, ),b(,2) ,那么“ 2 〞是“ a //(a2b) 〞的A ．充分不必要条件B ．充要条件C．必要不充分条件 D ．既不充分又不必要条件5.假设x5a0a1 (x 2)a2 (x 2)2a5 ( x 2)5,那么a0=A． 32B．2C． 1D． 326.假设实数 a, b 满足 0 ＜ a2＜ b ＜ a ＜ 1, 且m log a b, n2log a b2 , 那么m,n, p的log a b , p大小关系为A ． m＞ p ＞ n B． p ＞ n ＞ m C． n ＞ p ＞ m D． p ＞ m＞ n7.假设2cos2x1 sin2 x ，那么 tanxA ．1B．1C．1或1D．1或1或33338.假设 x, y 满足约束条件3≤ x y ≤ 1,x y 的最小值为9≤ 3x y ≤那么z3,A ． 1B． 3C． 5D． 69.把函数 f x sin x cos x 图象上各点的横坐标缩短到原来的1倍〔纵坐标不变〕，再2把得到的图象向左平移π个单位长度，所得图象对应的函数为g x，那么8A ．g x 2 cos 2xB ． g x 2 sin 2 x3C． g x 2 sin 1x5 D ． g x 2 sin 1 x3 212810.四边形 ABCD 为正方形， GD平面 ABCD ，四边形 DGEA 与四边形 DGFC 也都为正方形，连接 EF,FB,BE ，点 H 为 BF 的中点，有下述四个结论：① DE BF ；② EF 与 CH 所成角为 60；③ EC平面 DBF ；④ BF 与平面 ACFE 所成角为 45．其中所有正确结论的编号是A ．①②B．①②③C．①③④D．①②③④11. 双曲线 E :x 2y 21 〔 a 0,b 0 〕的左、右焦点分别为 F 1, F 2，假设E 上点 A满a 2b 2足 AF 12 AF 2 uuur uuuur，那么 E 的离心率取值范围，且向量 AF 1 , AF 2 夹角的取值范围为,3是A ． 3,5B ． 7,3C ． 3,5D ． 7,912. 函数 f (x)x 22ax, g( x)1，假设存在点Ax 1 , f x 1 , B x 2 , g x 2，使得直线xAB 与两曲线 y f x 和 yg x 都相切，当实数 a 取最小值时， x 1x 2A ．232B ．332C ．32D ． 3 3224绝密★启用前2021 — 2021学年度第一学期福州市高三期末质量检测数学〔理科〕试题第一卷考前须知：用 0.5 毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．二、填空题：本大题共 4 小题，每题 5 分，共 20 分．把答案填在题中的横线上．函数 f ( x)x,x ＜ 0,f113.e x1,那么 f (2)．x ≥ 0,14.设抛物线 y22px 上的三个点 A2, y1, B 1, y2 , C3, y3到该抛物线的焦点距离分别32为 d1 , d2 , d3．假设 d1 , d2 , d3中的最大值为3，那么p的值为．15. S 为数列 { a } 前n 项和，假设a15，且 a n 1 2a n2，那么S．n n21216.农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子〞，古称“角黍〞，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原 .如图，平行四边形形状的纸片是由六个边长为 1 的正三角形构成的，将它沿虚线折起来，可以得到如下图粽子形状的六面体，那么该六面体的体积为；假设该六面体内有一球，那么该球体积的最大值为．三、解答题：本大题共 6 小题，共 70 分．解容许写出文字说明、证明过程或演算步骤．第17～ 21 题为必考题，每个试题考生都必须作答．第22、 23 题为选考题，考生根据要求作答．〔一〕必考题：共60 分．17.〔本小题总分值 12 分〕在△ABC 中，AC1,BC7 ．（1〕假设 A 150 ，求 cos B ；〔 2〕D为AB边上一点，且BD 2 AD 2CD ，求△ ABC 的面积．18.〔本小题总分值 12 分〕等差数列 a n的公差为 2,a2 , a4, a8分别等于等比数列b n的第 2 项，第 3 项，第 4 项.〔 1〕求数列a n和 b n的通项公式；〔 2〕假设数列c n满足c1c2c n b n 1 ,求数列 c n的前 2021 项的和．a1a2a n19.〔本小题总分值12 分〕如图，在四棱锥 P ABCD 中，底面 ABCD 为正方形，PA底面 ABCD ，PA AB ， E 为线段 PB 的中点， F 为线段BC上的动点．（1〕求证：平面AEF平面 PBC ．（2〕试确定点F的位置，使平面AEF与平面 PCD 所成的锐二面角为 30 ．20.〔本小题总分值12 分〕圆 O : x2y24，椭圆 C : x2y2221〔a＞b＞0〕的短轴长等于圆O半径的 63a b倍， C 的离心率为 2 ．2（1〕求 C 的方程；（2〕假设直线 l 与 C 交于 A, B 两点，且与圆 O 相切，证明：△ AOB 为直角三角形．21.〔本小题总分值12 分〕函数 f x cos x ax2 1.1〔 1〕当a时，证明：f x ⋯0 ；2〔 2〕假设f x在 R 上有且只有一个零点，求 a 的取值范围．〔二〕选考题：共10 分．请考生在第22， 23 两题中任选一题作答．如果多做，那么按所做第一个题目计分，作答时请用 2B 铅笔在答题卡上将所选题号后的方框涂黑．22.〔本小题总分值 10 分〕选修4 4：坐标系与参数方程x53 t,在直角坐标系 xOy 中，直线l的参数方程为2〔 t为参数〕．以坐标原点为1y3t2极点， x 轴的正半轴为极轴建立极坐标系，曲线 C 的极坐标方程为2cos．〔 1〕求 C 的直角坐标方程；11〔 2〕设点 M 的直角坐标为5, 3， l 与曲线 C 的交点为A, B，求的值．MA MB23.〔本小题总分值 10 分〕选修4 5 ：不等式选讲函数 f (x) 2x 1 x1的最小值为 m ．2〔 1〕求 m 的值；〔 2〕假设 a,b,c 为正实数，且a b c m ，证明： a2b2c2 ≥1．32021－2021 学年度第一学期福州市高三期末质量检测数学〔理科〕参考答案及评分细那么评分说明：1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考察内容比照评分标准制定相应的评分细那么。

福建省福州第一中学高三数学下学期开学质检试题理(含解析)

(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．
二、填空题（每小题5分，共20分）
13.中国有个名句“运筹帷幄之中，决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如下表：
∴轨迹为抛物线,且点C1为焦点，BC为准线；
故排除C，D，
同理可得，
在平面ABB1A1上，
点P到点B的距离与到直线C1D1的距离相等，
从而排除A，
本题选择B选项.
12.已知函数，其中，为自然对数的底数，若，是的导函数，函数在区间内有两个零点，则的取值范围是（）
A. B. C. D.
5.一次数学考试后，某老师从甲，乙两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学成绩的中位数为73，则的值为（）
A. 2B. -2C. 3D. -3
【答案】D
【解析】
由茎叶图知，解得，
所以，故选D.
6.《中国诗词大会》（第二季）亮点颇多，十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下，百人团齐声朗诵，别有韵味．若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场，且《将进酒》排在《望岳》的前面，《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后，则后六场的排法有（）
【详解】抛物线：焦点为
则抛物线焦点为，，
所以，即，
因为线段的中点在轴上，
所以点横坐标为，
则轴
所以，即
则
根据双曲线定义可知

福建省福州一中2020届高三数学(理)下学期第一次质检试卷

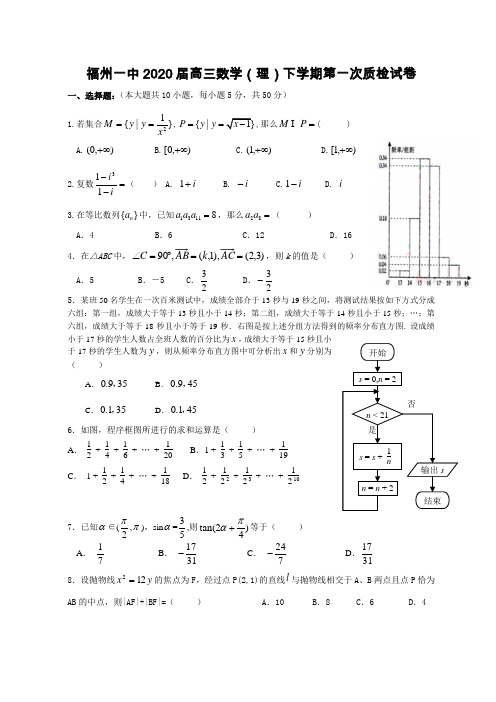
福州一中2020届高三数学（理）下学期第一次质检试卷一、选择题：（本大题共10小题，每小题5分，共50分） 1.若集合}1|{2xy y M ==,{|1}P y y x ==-,那么=P M I ( ) A.),0(+∞ B.),0[+∞ C.),1(+∞ D.),1[+∞2.复数=--ii 113（） A. i +1 B. i - C.i -1 D. i 3.在等比数列{}n a 中，已知13118a a a =，那么28a a =（） A ．4B ．6C ．12D ．164．在△ABC 中，)3,2(),1,(,90==︒=∠AC k AB C ，则k 的值是（） A ．5B ．－5C ．23 D ．23-5．某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；…；第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒的学生人数占全班人数的百分比为x ，成绩大于等于15秒且小于17秒的学生人数为y ，则从频率分布直方图中可分析出x 和y 分别为（）A ．0.935，B ．0.945，C ．0.135，D ．0.145，6．如图，程序框图所进行的求和运算是（） A ． 12 + 14 + 16 + … + 120 B ．1 + 13 + 15 + … + 119C ． 1 + 12 + 14 + … + 118D ． 12 + 12 2 + 12 3 + … + 12 107．已知α∈(2π,π)，sin α=53,则)42tan(πα+等于（）A ． 71B ． 3117-C ． 724-D ．31178．设抛物线y x 122=的焦点为F ，经过点P(2,1)的直线l 与抛物线相交于A 、B 两点且点P 恰为AB 的中点，则|AF|+|BF|=（） A ．10 B ．8 C ．6 D ．4开始 s = 0,n = 2n < 21 是否s = s + 1nn = n + 2输出s结束9.设βα,为互不重合的平面，n m ,为互不重合的直线，给出下列四个命题： ①若αα⊂⊥n m ,,则n m ⊥；②若ββαα//,//,,n m n m ⊂⊂，则βα//；③若m n n m ⊥⊂=⊥,,,αβαβαI ，则β⊥n ； ④ 若,//,,n m m βαα⊥⊥则β//n . 其中所有正确命题的序号是（）A ．①③B ．②④C ．①④D ．③④ 10．若直线1+=kx y 与圆0422=-+++my kx y x 交于N M ,两点,且N M ,关于直线 0=-y x 对称,动点P ()b a ,在不等式组200-+≥⎧⎪-≤⎨⎪≥⎩kx y kx my y 表示的平面区域内部及边界上运动，则21b w a -=-的取值范围是（）A ．),2[+∞B ．]2,(--∞C ．]2,2[-D ．),2[]2,(+∞⋃--∞ 二、填空题：（本大题共有5个小题，每小题4分，共计20分） 11. 一个几何体的三视图如图所示，则该几何体的体积等于__________.12．62)x展开式中，常数项是__________.13.=-⎰-dx x 0224 .14. 抛掷3个骰子，当至少有一个5点或一个6点出现时，就说这次试验成功，则在54次试验中成功次数n 的期望为 . 15.在圆中有结论:如图,“AB 是圆O 的直径,直线AC,BD 是圆O 过A,B 的切线,P 是圆O 上任意一点,CD 是过P 的切线,则有PD PC PO ⋅=2”. 类比到椭圆：“AB 是椭圆的长轴, O 是椭圆的中心，21,F F 是椭圆的的焦点，直线AC,BD 是椭圆过A,B 的切线,P 是椭圆上任意一点,CD 是过P 的切线,则有 .”三、解答题（本大题共有6个小题，共计80分） 16．( 本题满分13分)函数()sin()(0,0,||)2f x A x B A πωϕωϕ=++>><的图像上一个最高点的坐标为(,3)12π，与之相邻的一个最低点的坐标为7(,1)12π-. （Ⅰ）求()f x 的表达式； (Ⅱ) 当,2x ππ⎡⎤∈⎢⎥⎣⎦,求函数)(x f 的单调递增区间和零点.主视图左视图俯视图17．( 本题满分13分)如图，五面体11A BCC B -中，41=AB ．底面ABC 是正三角形，2=AB .四边形11BCC B 是矩形，二面角1A BC C --为直二面角.（Ⅰ）D 在AC 上运动，当D 在何处时，有//1AB 平面1BDC ,并且说明理由；（Ⅱ）当//1AB 平面1BDC 时，求二面角D BC C --1的余弦值.18．( 本题满分13分)某企业2020年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n 年（今年为第一年）的利润为500(1+n 21)万元（n 为正整数）. （Ⅰ）设从今年起的前n 年，若该企业不进行技术改造的累计纯利润为A n 万元，进行技术改造后的累计纯利润为B n 万元（须扣除技术改造资金），求A n 、B n 的表达式；（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？19．( 本题满分13分)已知双曲线22221x y -=的两个焦点为F 1，F 2，P 为动点，若21PF PF +=4.（Ⅰ）求动点P 的轨迹E 的方程；（Ⅱ）求12cos F PF ∠的最小值；（Ⅲ）设点M （-2，0），过点N （27-，0）作直线l 交轨迹E 于A 、B 两点，判断AMB ∠的大小是否为定值？并证明你的结论.20．（本题满分14分）C 1B 1D CB已知函数)1ln()ln(1)ln()(++-+=x ax x ax x f , ),0(R a a ∈≠ （Ⅰ）求函数()f x 的定义域；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）当a >0时，若存在x 使得()ln(2)f x a ≥成立，求a 的取值范围.21．（本题满分14分，共3小题，任选其中2题作答，每小题7分） (1) 选修4－2：矩阵与变换设矩阵MN A =，求矩阵A 的特征值以及属于每个特征值的一个特征向量．其中 M = ⎝⎛11 ⎪⎪⎭⎫42 ，N = ⎝⎛-11 ⎪⎪⎭⎫12 (2) 选修4－5：不等式选讲已知函数()24---=x x x f ．（Ⅰ）作出函数()x f y =的图像；（Ⅱ）解不等式124>---x x (3) 选修4－4：坐标系与参数方程求极坐标系中，圆2=ρ上的点到直线()6sin 3cos =+θθρ的距离的最小值．福州一中2020届高三数学（理）下学期第一次质检试卷参考答案二、填空题 11. 8 +4π3； 12. 60； 13.π； 14. 38； 15. PD PC PF PF ⋅=⋅21. 三、解答题16. 解：（Ⅰ）依题意的2121272πππ=-=T ,所以π=T ,于是22==Tπω……………2分由⎩⎨⎧-=+-=+13B A B A 解得⎩⎨⎧==12B A ……………………………………………4分把)3,12(π代入()2sin(2)1f x x ϕ=++,可得1)6sin(=+ϕπ,所以226ππϕπ+=+k ,所以32ππϕ+=k ,因为2||πϕ<,所以3πϕ=综上所述，1)32sin(2)(++=πx x f ………………………………7分（Ⅱ）令0)(=x f ，得21)32sin(-=+πx ，又Θ,2x ππ⎡⎤∈⎢⎥⎣⎦373234πππ≤+≤∴x 61132ππ=+∴x 故43π=x 函数)(x f 的零点是43π=x ……………10分373234πππ≤+≤x Θ ∴由373223πππ≤+≤x 得ππ≤≤x 127∴函数)(x f 的单调递增区间是⎥⎦⎤⎢⎣⎡ππ,127 ……………13分17. 解：（Ⅰ）当D 为AC 中点时,有//1AB 平面1BDC ………2分证明:连结1B C 交1BC 于O ,连结DO ∵四边形11BCC B 是矩形 ∴O 为1B C 中点又D 为AC 中点,从而1//DO AB ……………………………4分 ∵1AB ⊄平面1BDC ,DO ⊂平面1BDC∴//1AB 平面1BDC …………………………………………6分（Ⅱ）建立空间直角坐标系B xyz -如图所示,则(0,0,0)B ,A ,(0,2,0)C ,3,0)2D ,1C …………7分所以3,0)2BD =u u u r ,1BC =u u u u r . ………………………………8分设),,(1z y x n =为平面1BDC 的法向量,则有30220x y y+=⎨⎪+=⎩,即3x zy =⎧⎪⎨=⎪⎩令1=z ,可得平面1BDC 的一个法向量为1(3,n =u r ,而平面1BCC 的一个法向量为2(1,0,0)n =u u r (11)分所以121212cos ,||||n n n n n n ⋅<>===u r u u ru r u u r u r u u r 所以二面角D BC C --1的余弦值为13133…………………………13分 18. 解: (Ⅰ)依题意知，数列n A 是一个以500为首项，－20为公差的等差数列，所以2(1)480(20)490102n n n A n n n -=+⨯-=-，…………………3分 2111500(1)500(1)500(1)600222n n B =++++++-L ＝2111500500()600222n n ++++-L＝11[1()]22500500600112n n -+⨯--＝5005001002n n -- …………………6分 (Ⅱ)依题意得，n n B A >，即2500500100490102nn n n -->-，可化简得250102n n n <+-，…………………8分 ∴可设n n f 250)(=，2()10g n n n =+-又+∈N n Θ，∴可设)(n f 是减函数，)(n g 是增函数，又5050(3)(3)2,(4)(4)8816f g f g =>==<= 则4n =时不等式成立，即4年…………………12分答：略 ……………13分19．（Ⅰ）解：依题意双曲线方程可化为1212122=-y x 则221=F F ∴21PF PF +=4>221=F F ∴点P 的轨迹是以21,F F 为焦点的椭圆，其方程可设为22221(0)x y a b a b+=>>∴由22,42==c a 得1,2==c a 3142=-=∴b 则所求椭圆方程为13422=+y x ，故动点P 的轨迹E 的方程为13422=+y x ；………………3分（Ⅱ）设0,021>=>=n PF m PF ,θ=∠21PF F 则由4=+n m ，221=F F 可知在21PF F ∆中162212242)(24cos 222-=-=--+=-+=mnmn mn mn mn n m mn n m θ 又mn n m n m 24,0,0≥+=>>Θ4≤∴mn 即411≥mn 21146cos =-≥∴θ 当且仅当2==n m 时等号成立．故12cos F PF ∠的最小值为21………………6分（Ⅲ）当l 与x 轴重合时，构不成角AMB ，不合题意．当l x ⊥轴时，直线l 的方程为27x =-，代入22143x y +=解得A 、B 的坐标分别为212,77⎛⎫- ⎪⎝⎭、212,77⎛⎫-- ⎪⎝⎭ 而127MN =，∴90AMB ∠=o，猜测90AMB ∠=o为定值．………8分证明：设直线l 的方程为27my x =+，由 22273412x my x y ⎧=-⎪⎨⎪+=⎩ ，得2212576(34)0749m y my +--= ∴122127(34)m y y m +=+ ，12257649(34)y y m =-+ ………10分 ∴11221212(2,)(2,)(2)(2)MA MB x y x y x x y y ⋅=++=+++u u u r u u u rg11121212()()77my my y y =+++2121212144(1)()749m y y y y =++++2225761212144(1)49(34)77(34)49m m m m m -=++⋅+++49144)43(49)34(14422+++-=m m 0= ∴ 90AMB ∠=o为定值。

2021年高三下学期开学考试数学(理)试题含答案

2021年高三下学期开学考试数学（理）试题含答案一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合，，且有4个子集，则实数的取值范围是（）A. B. C. D.2．复数等于（）A. B. C. D.03. 函数的单调递减区间是（）A. B.C. D.4．等比数列中，，前3项和为，则公比的值是（）A. 1B.－C. 1或－D. -1或－5. 已知关于的二项式展开式的二项式系数之和为32，常数项为80，则的值为（）A．1 B．C．2 D．6. 若两个正实数满足，且不等式有解，则实数的取值范围是（）A. B.C. D.7. 执行如图所示的程序框图，若输入的值为8，则输出的值为（）A. 4B. 8C. 10D. 128．若为不等式组表示的平面区域，则当从－2连续变化到1时，动直线扫过中的那部分区域的面积为 ( )A．1 B． C．D．9. 如图，一个空间几何体的正视图、侧视图都是面积为，一个内角为的菱形，俯视图为正方形，那么这个几何体的表面积为（）A. B. C. D.10. 已知为正三角形内一点，且满足，若的面积与的面积比值为3，则的值为（）A. B. C. 2 D. 311. 过双曲线的左焦点作圆的切线，切点为，延长交抛物线于点,为原点，若，则双曲线的离心率为（）A. B. C. D.12．定义在上的单调函数，则方程的解所在区间是（）A. B. C. D.第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分，第13题~第21题为必考题，每个试题考生都必须做答，第22题~24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13. 已知等差数列中，,那么 . 14. 5位同学排队，其中3位女生，2位男生.如果2位男生不能相邻，且女生甲不能排在排头，则排法种数为 . 15. 已知球的直径，是球球面上的三点,，是正三角形，则三棱锥的体积为 . 16. 给出下列四个结论：（1）如图中，是斜边上的点，. 以为起点任作一条射线交于点，则点落在线段上的概率是；（2）设某大学的女生体重与身高具有线性相关关系，根据一组样本数据，用最小二乘法建立的线性回归方程为，则若该大学某女生身高增加，则其体重约增加；（3）若是定义在上的奇函数，且满足,则函数的图像关于对称;（4）已知随机变量服从正态分布则.其中正确结论的序号为三、解答题：本大题共70分，解答应写出必要的文字说明，证明过程或演算步骤． 17．（本小题满分12分）“德是”号飞船返回舱顺利到达地球后，为了及时将航天员救出，地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心（记为）．当返回舱距地面1万米的点时（假定以后垂直下落，并在点着陆），救援中心测得飞船位于其南偏东方向，仰角为，救援中心测得飞船位于其南偏西方向，仰角为．救援中心测得着陆点位于其正东方向．（1）求两救援中心间的距离；（2）救援中心与着陆点间的距离．A BCD E北 A P东B C D18．(本小题满分12分)我国新修订的《环境空气质量标准》指出空气质量指数在为优秀，各类人群可正常活动.市环保局对我市xx 年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为，，，，由此得到样本的空气质量指数频率分布直方图，如图.(1) 求的值；(2) 根据样本数据，试估计这一年度的空气质量指数的平均值；(3) 如果空气质量指数不超过，就认定空气质量为“特优等级”，则从这一年的监测数据中随机抽取天的数值，其中达到“特优等级”的天数为，求的分布列和数学期望.空气质量指数0.0320.020 0.018O 5 15 25 35 4519. （本小题满分12分）如图，在四棱锥中，平面平面，，在锐角中，并且，.（1）点是上的一点，证明：平面平面；（2）若与平面成角，当面平面时，求点到平面的距离．20.（本小题满分12分）已知椭圆的左，右顶点分别为，圆上有一动点,点在轴的上方，，直线交椭圆于点，连接.(1)若,求△的面积;(2)设直线的斜率存在且分别为,若,求的取值范围.21. (本小题满分12分)设函数.（1）若函数在处有极值，求函数的最大值；（2）①是否存在实数，使得关于的不等式在上恒成立？若存在，求出的取值范围；若不存在，说明理由；②证明：不等式考生在题（22）（23）（24）中任选一题作答，如果多做，则按所做的的第一题计分．做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑．22.（本小题满分10分）选修4—1：几何证明选讲如图，已知点在⊙直径的延长线上，切⊙于点，是的平分线，交于点，交于点．（Ⅰ）求的度数；（Ⅱ）若，求．23.（本小题满分10分）选修4—4：坐标系与参数方程在平面直角坐标系中，直线的参数方程为（为参数），直线与曲线交于两点.（1）求的长；（2）在以为极点，轴的正半轴为极轴建立极坐标系，设点的极坐标为，求点到线段中点的距离．24.（本小题满分10分）选修4—5：不等式选讲已知实数满足，且.（Ⅰ）证明：；（Ⅱ）证明：.哈尔滨市第六中学xx 届高三第三次模拟考试数学试卷（理工类）答案一．选择题1.B2.D3.B4.C5.C6.B7.B8.D9.D 10.A 11.A 12.C 二．填空题13. 14. 15.40 16.②③④ 三．解答题17. 解：（1）由题意知，则均为直角三角形………………1分在中，，解得…………………………2分在中，，解得…………………………3分又，万米. …………………………5分（2），，…………………………7分又，所以.…………………………9分在中，由正弦定理，…………………………10分万米…………………………12分18.(1) 解：由题意，得， ……………1分解得. ……………2分（2）解：个样本中空气质量指数的平均值为0.2100.32200.3300.184024.6X =⨯+⨯+⨯+⨯= ……………3分由样本估计总体，可估计这一年度空气质量指数的平均值约为. …………4分（3）解：利用样本估计总体，该年度空气质量指数在内为“特优等级”，且指数达到“特优等级”的概率为，则. ………5分的取值为， ………6分，，，. ……………10分 ∴的分布列为：……11分∴6448121301231251251251255E ξ=⨯+⨯+⨯+⨯=. ………12分（或者）19.解法一（1）因为，，由勾股定理得，因为平面平面，平面平面 =，面，所以平面面，所以平面平面 ………6分12M（2）如图，因为平面，所以平面平面，所以，做于，所以面，，设面面=，面平面所以面面，所以，取中点，得为平行四边形，由平面边长得为中点，所以………12分解法二（1）同一（2）在平面过做垂线为轴，由（1），以为原点，为轴建立空间直角坐标系,设平面法向量为，设，锐角所以，由，解得，，，解得或（舍）设，解得因为面平面，，所以面法向量为，所以，解得，所以到平面的距离为竖坐标．………12分20.（1）依题意，.设，则.由得, ,, 解得, . …………5分(2)设, 动点在圆上, .又, , 即====.又由题意可知,且,则问题可转化为求函数的值域.由导数可知函数在其定义域内为减函数, 函数的值域为从而的取值范围为……12分21.（1）由已知得：，且函数在处有极值∴，即∴∴当时，，单调递增；当时，，单调递减；∴函数的最大值为（2）①由已知得：(i)若，则时，∴在上为减函数，∴在上恒成立；(ii)若，则时，∴在上为增函数，∴，不能使在上恒成立；(iii)若，则时，，xyz当时，，∴在上为增函数，此时， ∴不能使在上恒成立；综上所述，的取值范围是 …………8分 ②由以上得：取得：令，则，()1222111ln 101111n n n n x x n n n n n n-⎛⎫-=-+<-=-< ⎪+-++⎝⎭. 因此. 又()1211ln ln ln 1ln1ln 1nn k k n k k k -==⎛⎫=--+=+⎡⎤ ⎪⎣⎦⎝⎭∑∑ 故1122211111ln 1ln 1111nn n n k k k k k n x k k k k n --===⎡⎤⎛⎫⎛⎫=-+=-++ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎣⎦∑∑∑ ()()11122111111111111n n n k k k kk k k kn k k ---===⎛⎫>-=-≥=-+>- ⎪+++⎝⎭∑∑∑ ……12分22．（1）因为为⊙的切线，所以…………1分因为是的平分线，所以…………2分所以，即，…………3分又因为为⊙的直径，所以…………4分. 所以.…………5分（2）因为，所以，所以∽，所以，………7分在中，又因为，所以，………8分中，………10分23.解:（1）直线的参数方程化为标准型（为参数） …… 2分代入曲线方程得设对应的参数分别为，则，，所以 …… 5分（2）由极坐标与直角坐标互化公式得直角坐标， …… 6分所以点在直线，中点对应参数为，由参数几何意义，所以点到线段中点的距离 ……10分 24.(1) ，相乘得证——————5分（2），，相加得证——————10分40095 9C9F 鲟Zx5P34375 8647 虇x29910 74D6 瓖22319 572F 圯•B35268 89C4 规34290 85F2 藲24190 5E7E 幾精品文档实用文档。

2020届福建省高三毕业班质量检查测试数学(理)试题(解析版)

2021届福建省高三毕业班质量检查测试数学〔理〕试题一、单项选择题21 .集合A xy ln x 1 ,B xx 4 0 那么AI B =A. xx 2B. x 1 x 2C. x 1 x 2 D【答案】C【解析】可求出集合A, B,然后进行交集的运算即可.【详解】. . ,・, 2 ■八人A x y ln x 1 {x|x> 1} ,B x x 4 0 x 2 x,An B={x|1 <x< 2}.应选：C.【点睛】考查描述法的定义,对数函数的定义域,一元二次不等式的解法,交集的运算.2.假设复数z满足Z 1 i 1 i,那么zA. iB. 1 iC. & D【答案】D【解析】把等式变形,利用复数代数形式的乘除运算化简求得z,算公式求解.【详解】1 i 1 i i由〔z+1〕 i=1 + i,得z+1 ----------------------- 2——1 i,i iz= - i,贝U | z| = 1.应选D.【点睛】此题考查复数代数形式的乘除运算,考查复数模的求法,是根底题.3.经统计,某市高三学生期末数学成绩X : N 85, 2,且P 80 X该市任选一名高三学生,其成绩不低于90分的概率是A. 0.35 B, 0.65 C, 0.7 D 再由复数模的计90 0.3,那么从0.85【答案】A【解析】由直接利用正态分布曲线的对称性求解.【详解】•••学生成绩X服从正态分布N (85, 02),且P (80VXV90) =0.3,•- P (X>90) 1[1 - P (80vXv90) ] - 1 0.3 0.35 ,2 2・•・从该市任选一名高三学生,其成绩不低于90分的概率是0.35.应选A.【点睛】此题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量科和b的应用,考查曲线的对称性,属于根底题.x y 1 04 .假设x, y满足约束条件x y 1 0 ,那么z x 2y的最小值是y 1 0A.—5B. —4C. 0D.2【答案】B【解析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.【详解】作出不等式组对应的平面区域如图：(阴影局部)由z= x+2y 得y 1x — z2 2平移直线y 1x 1z, 2 2由图象可知当直线y -x 1z经过点A ( - 2, - 1)时, 2 2直线y工x 工z的截距最小, 2 2此时z最小.将A (-2, - 1)的坐标代入目标函数z=x+2y,得z= -4.即z= x+2y的最小值为一4;应选：B.【点睛】此题主要考查线性规划的应用, 结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的根本方法.5.某简单几何体的三视图如下图 ,假设该几何体的所有顶点都在球 .的球面上,那么球OB. 4V3 D- 3273【解析】由三视图复原几何体,可知该几何体为直三棱柱,底面为等腰直角三角形,直角边长为2,侧棱长为2,然后将其放入正方体进行求解.8.2 3的体积是由三视图复原原几何体如可知该几何体为直三棱柱,底面为等腰直角三角形,直角边长为 2,侧棱长为2.把该三棱锥补形为正方体,那么正方体体对角线长为 j 22 2 22 2J3 .,该三棱柱外接球的半径为 J 3. 体积V 4〔括3 473 .3应选B. 【点睛】此题考查空间几何体的三视图,考查多面体外接球外表积与体积的求法,是中档题.6.将函数y sin 2x — 的图象向右平移 —个单位长度后,所得图象的一个对称中 6 6心为〔〕A.—,0B. 一, 0C. 一, 0D.1, 0 12432【答案】A【解析】根据平移法那么得到 f x sin 2x —,再计算对称中央横坐标满足 6 k -一一、x — — , k Z ,斛仔答案. 12 2 【详解】函数y sin 2x 一的图象向右平移 —个单位长度得到函数： 6 6f x sin 2 x —— sin 2x —,对称中央横坐标满足： 66 6此题考查了三角函数平移, 三角函数的对称中央, 意在考查学生对于三角函数知识的综合应用.7• a V 2,b 5/5,c 7/7,那么A. a b cB acbC bac D. c b aKk. ,,k - 2k -6一120时,对称中央为一,012【答案】A【解析】根据募函数的单调性即可求出. 【详解】a 盘,b 5/5,c 7/7,贝U a 70=235=( 25) 7= 327= ( 27)5=1285, b70=514= ( 52) 7= 257c 70= 710= ( 72) 5= 495, . . a>c, a>b,又 b 70= 514= ( 57) 2= ( 78125) 2c 70= 710= ( 75) 2= ( 16807) 2,b>c,a> b>c,应选A. 【点睛】此题考查了不等式的大小比拟,掌握嘉函数的单调性是关键,属于根底题8 .某商场通过转动如下图的质地均匀的6等分的圆盘进行抽奖活动,当指针指向阴影区域时为中奖.规定每位顾客有 3次抽奖时机,但中奖1次就停止抽奖.假设每次抽奖相互独立,那么顾客中奖的概率是1【解析】由题意应用几何概型面积之比得一次中奖概率 -,分为三类讨论中奖可能得答3案. 【详解】由题意应用几何概型面积之比得一次中奖概率 -3. ......... . , 一 1 第一次就中奖的概率 -,3 .2 1 2第二次中奖概率为-1 2 ,3 3 9 一2 2 14第三次中奖概率为 --1,3 3 3 27_.. ......... . (1)2 419A.C.4 27 5B.D.3 19 27所以顾客中奖的概率为-2——3 9 27 27应选D.【点睛】此题考查了几何概型求概率及互斥事件的概率问题, 应用面积比是解决问题的关键, 属于简单题.9 .设椭圆E的两焦点分别为F1, F2,以F1为圆心,F1F2为半径的圆与E交于P, Q两点,假设PF1F2为直角三角形,那么E的离心率为〔〕A. B. 2i1 C.巨 D. 72 12 2【答案】B【解析】由PFR为直角三角形,得PF1F2 900,可得|PF- 2c,| PF2 2j2c,利用椭圆的定义和离心率的概念,即可求解^【详解】如下图,由于PF1F2为直角三角形,所以PF1F2 90°,所以P E| 2c,|PF2 2j2c,贝U 2c 272c 2a,解得e | J2 1 ,应选 B【点睛】此题主要考查了椭圆的标准方程及其简单的几何性质的应用, 其中解答中合理利用椭圆的定义和离心率的概念求解是解答的关键,着重考查了运算与求解水平,属于根底题10.如图,AB是圆锥SO的底面O的直径,D是圆O上异于A, B的任意一点,以AO为直径的圆与AD的另一个交点为C,P为SD的中点.现给出以下结论:① SAC为直角三角形②平面SAD 平面SBD③平面PAB必与圆锥SO的某条母线平行其中正确结论的个数是A. 0B. 1C. 2 D . 3【答案】C【解析】①根据线面垂直的判定定理证实AC,平面SOC即可②假设平面SAD,平面SBD,根据面面垂直的性质定理推出矛盾即可③连接DO并延长交圆于E,连接PO, SE,利用中位线的性质进行判断即可【详解】①; SO,底面圆O,SOX AC,C在以AO为直径的圆上,. ACXOC,. OCASO=O,. AC,平面SOC, AC± SC,即①△ SAC为直角三角形正确,故①正确,②假设平面SAD,平面SBD,在平面SA D中过A作AH,SD交SD于H,那么AH,平面SBD, AH ± BD,又•「BDLAD , BD,面SAD,又CO//BD , • . CO,面SAD, . COX SC又在△ SOC中,SO± OC,在一个三角形内不可能有两个直角,故平面SAD,平面SBD不成立, 故②错误,③连接DO并延长交圆于E,连接PO, SE,••• P为SD的中点,O为ED的中点,OP是△ SDE的中位线,PO// SE,即SE//平面APB,即平面PAB必与圆锥SO的母线SE平行.故③正确, 故正确是①③,应选C.涉及空间直线平行和垂直的判断, 结合相应的判定定理1< a< 1可得g (x)为奇函数且在(-1,1)上为增函数,据此f (a)+ f(a +1) >2? 1< a 1<1 ,a> a 1解可得a 的取值范围,即可得答案.1 x根据题意,函数f (x) = lnL^1 x的定义域为(-1,1),应选：C.此题考查函数的奇偶性与单调性的综合应用,关键构造新函数是解决此题的关键. 11.函数f2,那么a 的取值范围是A.1, 2C.- ,02【解析】根据题意, 由函数的解析式求出函数的定义域,设g (x) = f (x) - 1,分析x +1 ,有1―x>0,解可得-1vxv 1,即函数1 xf (x)设 g (x) = f (x)-g (x),那么函数/ । 1 x—1 = In —1 xg (x)为奇函数;1 x. 1 xx,贝U g ( - x) = In ---------( - x) = - [In ----------x]=分析易得：g (x)=In 1-x x 在(-1, 1)上为增函数,1 xf (a) + f (a +1 ) > 2? f(a) — 1 > — [f(a+1) - 1]? g (a) >- g(s+1 ) ?g (a)>g 1< a< 1(—a — 1)1<a a 〉解可得: 1八-< a< 0, 2 即a 的取值范围为(-,0);2g (x) = f (x) — 1,属BE此题主要考查命题的真假判断,于中档题.12.在 ABC 中,B 30o ,BC 3, AB 2褥,点D 在边BC 上,点巳C 关于直线AD 的对称点分别为B ,C ,那么 BBC 的面积的最大值为【解析】解三角形,建立坐标系,设 AD 斜率为k,用k 表示出B'纵坐标,代入面积公式得出面积关于 k 的函数,根据k 的范围和函数单调性求出面积最大值.由余弦定理可得 AC 2= AB 2+BC 2— 2AB ?BC Cos B= 12+9—2X273 3 — 3,. AC 网,且 AC 2+ BC 2=AB 2, . ACXBC,以C 为原点,以CB, CA 为坐标轴建立平面直角坐标系,如下图: 设直线AD 的方程为y= kx J3 ,6k 2.3k 2・ CC' // BB',石时,,(k) >0,当 73V k< £ 时,F (k)<0,A. 9_^32B.述7当D 与线段AB 的端点重合时,B, B', C '在同一条直线上,不符合题意, 旦设B ,〔 m,3n),显然 n< 0,S>A BB' C = Sk BB'BC 236k 2.3 k 2 19k 3 32,令 f (k)9k k 2 1(k<鱼),贝U f' (k)33k 2 23k 3-------------------- 5 (k 2 1)2令 f' ( k)=0可得k也或k 近〔舍〕,3• ・当 k<,当k J 3时,f (k)取得最大值f ( 73)法,属于较难题.二、填空题13 .向量此题考查了根据向量垂直求参数,意在考查学生的计算水平..91 n .................................... ..........................14 .假设(2x 2 —)n 展开式的二项式系数之和为64,那么展开式中的常数项是x【答案】60【解析】由题意利用二项式系数的性质求得 n 的值,在二项展开式的通项公式中,令的哥指数等于0,求出r 的值,即可求得常数项.假设(2x 2 l)n 展开式的二项式系数之和为64,那么2n =64, n=6.x那么展开式中的通项公式为 T r +1C ；?( - 1) r ?26「r ?x 12丁令12-3r=0,求得r=4,49可得常数项为C 6 ?22= 60,3.3 2函数单调性判断与最值计算, 考查了用解析法解决几何问题的方rb 1,且根据0, 化简计算得到答案.故答案为:r,那么a r 2 a2.2.此题考查了余弦定理,故答案为60.【点睛】此题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.15.在平面直角坐标系xOy中,角的顶点为坐标原点,始边与x轴的非负半轴重合, 终边交单位圆O于第一象限的点p a,b,且a b 7,那么cos5 —的值是2【答案】-3或-5 5【解析】根据a b 7且a2 b2 5公式和任意角三角函数定义可求得结果【详解】a b 7 35 a a由a2b21得：5或4a 0,b 0 b b 5cos - sin b 2 1及P a,b位于第一象限可求得a的值；根据诱导45352 5 5,一______ 3 4此题正确结果：-3或45 5【点睛】此题考查根据终边上的点求解三角函数值和诱导公式的应用,属于根底题^16.如图为陕西博物馆收藏的国宝一一唐・金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯型几何体的主体局部可近似看作是双曲2 2线C：—匕1的右支与直线x 0,y 4,y 2围成的曲边四边形MABQ绕y 3 9轴旋转一周得到的几何体,如图N,P分别为C的渐近线与y 4,y 2的交点,曲边五边形MNOPQ绕y轴旋转一周得到的几何体的体积可由祖恒原理〔祖恒原理：哥势既同,那么积不容异〕.意思是：两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,那么这两个几何体的体积相等〕,据此求得该金杯的容积是由双曲线方程及定积分的几何意义,求得答案.2 2—1,得 X 2 3 —, 9 3由祖的I 原理可知,金杯的容积与曲形四边形 MABQ 绕y 轴旋转一周得到的几何体的体 ,金杯的容积是 26兀. 故答案为26兀.此题考查祖的I 原理的应用及定积分的几何意义的应用,考查了求旋转体的体积的方法, 表达了等价转化、数形结合的数学思想,属于中档题.三、解做题17.数列 a n 的前n 项和S n 满足S n 2a n n . (1)求证数列a n 1是等比数列,并求a n ；(2)假设数列b n 为等差数列,且b 3 a 2,b 7 a 3,求数列a n b n 的前n 项T n .【答案】(1) a n 2n 1 (2) n 1 2n1 n n 1 22【解析】(1)由数列的递推式和等比数列的定义和通项公式,可得所求；(2)运用等差数列的通项公式可得bn 及&bn 的公式,由数列的错位相减法和等差数列、等比数列的求和公式,可得所求和. 【详解】(1)当 n 1 时,S 2a 1 1 ,所以 a 1 1.由双曲线2C:—3 积相同,而曲形四边形MABQ 绕y 轴旋转一周得到的几何体的体积为:44Vx 2dy2223 dy3y64 8 12 -6 - 26兀,99.(杯壁厚度忽略不计) 26【解由于S n 2a n n ①,所以当n 2时,S n i 2am n 1②, ①-②得 a n 2a n 2 a n i 1,所以 a n 2a n i 1.所以a n 1是首项为2,公比为2的等比数列. 所以4 1 2 2n ;所以a n 2n 1.(2)由(1)知,a 2 3 , a 3 7 ,所以 b 3 a 2 3, b 7 a 3 7 ,设b n 的公差为d ,那么＞ b 3所以 b n b 3 n 3 d n, 所以 a n b n n 2n 1 n 2n n .设数列 n 2n 的前n 项和为K n ,数列 n 的前n 项和为T n , 所以 K n 2 2 22 3 23 L n 2n ③,234n 1 _2K n 22 23 2 L n 2 ④,③-④得n2 1 2 … …2 3 nn 1n 1n 1K n 22 2L 2 n 2------------ n 21 n 22.1 2n 1所以 K n n 1 2 2,n n 1又由于T n 1 2 3 L n,2所以 K n T n n 1 2n 1 n n 1 2. 2 所以a n b n 的前n 项和为 n 1 2n 1 n n 1 2.2【点睛】此题考查等差数列和等比数列的通项公式和求和公式的运用, 求和,考查方程思想和运算水平,属于中档题.18 .如图,三棱柱ABC AB 1C 1中,底面ABC 是等边三角形所以 a n 1 a n 112am 1 1a n 112a n1 2 a n 11考查了数列的错位相减法侧面BCC 1B 1是矩形,AB ARN 是B i C 的中点,M 是棱AA i 上的点,且AA 〔 CM(1)证实：MN//平面ABC;(2)假设AB A i B ,求二面角A CM N 的余弦值.【答案】(1)见解析(2) 巫5【解析】(1)连结BM,推导出BCXBB i, AA i^BC,从而AA i±MC,进而AA i ,平面BCM, AA i ± MB,推导出四边形 AMNP 是平行四边形,从而 MN//AP,由此能证实 MN //平面 ABC.(2)推导出△ ABA i 是等腰直角三角形,设 AB J2a ,那么AA i=2a, BM = AM = a,推导出 MCXBM, MCXAAi, BMXAAi,以 M 为坐标原点, MAi, MB, MC 为 x, y, z 轴,建立空间直角坐标系,利用向量法能求出二面角 A-CM-N 的余弦值.【详解】(i)如图i,在三棱柱ABC A i B i C i 中,连结BM ,由于BCC i B i 是矩形,所以 BC BB i ,由于 AA //BB i ,所以 AA i BC , 又由于AA i MC , BC MC C ,所以AA i 平面BCM , 所以AA i MB ,又由于AB AB ,所以M 是AA i 中点,i ―取BC 中点P,连结NP, AP ,由于N 是B 1c 的中点,那么NP//BB 1且NP - BB i ,2所以NP//MA 且NP MA,所以四边形 AMNP 是平行四边形,所以 MN//AP, 又由于MN 平面ABC, AP 平面ABC,所以MN//平面ABC .A i B,所以 ABA i 是等腰直角三角形,设 AB J2a ,〔2〕由于AB〔图1〕〔图2〕那么 AA i 2a, BM AM a 在 Rt ACM 中,AC J2a ,所以 MC a .贝U cosn 1, n 2此题考查线面平行的证实,考查了利用空间向量法求解二面角的方法, 线面、面面间的位置关系等根底知识,考查运算求解水平,是中档题.219 .在平面直角坐标系 xOy 中,圆F ： x 1y 2 1外的点P 在y 轴的右侧运动,H P到圆F 上的点的最小距离等于它到 y 轴的距离,记P 的轨迹为E .(1)求E 的方程；(2)过点F 的直线交E 于A ,B 两点,以AB 为直径的圆D 与平行于y 轴的直线相切于点M ,线段DM 交E 于点N ,证实： AMB 的面积是 AMN 的面积的四倍.2【答案】(1) y 4x x 0 (2)见解析【解析】法—：(1)设P (x, y), x> 0, F (1, 0).由点P 在OF 外,可得点P 到.F 上的点的最小距离为|PF| - 1,由题意可得：|PF| - 1=x,利用两点之间的距离公式即在 BCM 中,CM 2BM 2 2a 2 BC 2,所以 MCBM ,由(1)知,那么MC AA1 , BM AA1 ,如图2,以M 为坐标原点,uuuv MA 1 ,uuuv uuuv MB ,MC的方向分别为x 轴, y 轴,z 轴的正方向建立空间直角坐标系, 那么 M 0,0,0 , C0,0,a , B i 2a,a,0 .~ a a 一所以N a,-,-,那么uuuv0,0,a , MN设平面 CMN 的法向量为x, y,z ,那么? n 1 uuu v MC uuu v0,即 0, axaz 0, a 2y2z 0.2.故平面CMN 的一个法向量为1, 2,0 ,由于平面ACM 的一个法向量为n 20,1,0 ,由于二面角A CM 所以二面角ACMN 的余弦值为考查空间中线线、可得出.(2)设 N (xo, yo), A (xi, yi), B (X 2, v2 .那么 D ( ^1一x 2, -y 1一y 2 ).由题意可 2 2设直线AB 的方程为：y= k (x- 1) (kw .).与抛物线方程联立化为：k 2x 2- (2k 2+4)x +k 2=0.利用根与系数的关系、中点坐标公式可得D, M, N 的坐标.再利用三角形面积计算公式即可得出.法二：(1)由题意得,点P 到圆F 1,0的距离PF 等于P 到直线x 1的距离,根据抛物线的定义求得轨迹方程.(2)设A x 1,y 1 , B x 2,y 2 ,由题意可设直线 AB 的方程为：x ty 1 t 0与抛物线方程联立,利用根与系数的关系、中点坐标公式可得D 的坐标,结合1 _,1 ___ ___________________ _ _______ _______ _____ ____________________DM — AB ,可得m 1,进而求出N 的坐标,利用点的位置关系得到面积的关2系.(2)设A K,y 1 , B x 2,y 2 ,由题意可设直线 AB 的方程为:x ty 1 t 0与抛物线方程联立,利用根与系数白关系、中点坐标公式可得 D, M的坐标,利用斜率公式计算得到 k M F k AB 1 ,再利用长度关系得到面积的关系.【详解】解法一：(1)设P x,y ,依题意x o, F 1,0 .由于P 在圆F 外,所以P 到圆F 上的点的最小距离为 PF 1 依题意得PF | 1 x,即J x 1 2 y 2 1 x , 化简得E 的方程为y 2 4x x 0 .(2)设 N 刈,丫0 , A K,y 1 ,B x 2,y 2 ,那么 D依题意可设直线 AB 的方程y k x 1 k 0 ,法三：(1)与法一同; x 〔 x 2 y 〔 y 22 , 2由 yyk ］得k 2x 22k 24x k2 0.2由于 2k 4 4k 16k16 0,k 2 2 2 k 2 ,k、…一 2 一设M X M ,y M ,依题意得y M —,所以MDk又由于MD 网,所以匚工x M 马2 , 2 k k一 ~2 解得X M1 ,所以M 1k故 S AMB4s AMN-所以x 1 x 22k 2 4 k 2由抛物线的定义知 AB x 1 x 2 24k 2 4 k 2由于 2 x0,— k 在抛物线上,所以1 2k 2,k所以 S AMB y 2 k 2k 2y 1S AMNMN yy D 1一MN2y 1 y 2 k 2 1 4k 2y 1解法二: (1)设 P x,y 0.由于P 在圆F 外,所以 P 到圆F 上的点的最小距离为PF 1.依题意彳#,点P 到圆F 1,0的距离PF 等于P 到直线1的距离,那么有y 1 y 2k 2 2~~2~X M.k所以P 在以F 1,0为焦点,x 1为准线的抛物线上所以E 的方程为y 2 4x x 0〔2〕设 A x i , y i , B X 2, y 2 ,由于直线 AB 过F 1,0 ,依题意可设其方程 x ty 1 t 0 x ty 1, 2由 2 得 y 24ty 4 0, y 4x由于 16t 2 16 0,所以 y 〔 y 2 4t, .一. . . 2_那么有 x 1 x 2ty 1 1 ty 214t 2.由于D 是AB 的中点,所以 D 2t 2 1,2t . ................................. 2 由抛物线的定义得 ABx 1 1 x 2 1 4t 4.,设圆D 与l ：x m 相切于M ,由于DM 与抛物线相交于 N ,所以m 0,且DM l , 〜,、,― 1 _ 一 2 1 2 .一 ■一所以DM-AB ,即22 1 m — 4t 2 4 ,解得m 1,22、一一.一一 2 一一 .2设 N x c , y ° ,那么 y 0 2t,且 2t 4x 0,所以 x ° t ,t 2 ,所以N 为DM 的中点,所以S AMD 2S AMN ,又由于D 为AB 的中点,S AMB 2s AMD ,所以S AMB 4s AMN解法三：〔1〕同解法一.2t 2 11由于2—1 ------------------1 2(2)设 A X i , y i , B X 2, y 2 ,连结 MF , NF .由于直线AB 过F 1,0 ,依题意可设其方程 x ty 1 t 0 x ty 1, 2由 2 得 y 4ty 4 0., y 4x 由于 16t 2 16 0,所以 y i y 4t , 所以 y My D 2t .…AB _ 一. 由于MD ---------- , AB X 1 x 2 2,又由于MD2所以x 1 x 2 2学1—2 X M ,解得X M1 ,所以M 1,2t ,2 2 2t 1, w所以 k MF k AB -------------------- -1 ,故 MFD 90 .1 1 t所以 S AMN 二 S AMD ,21又 S AMD 二 S AMB ,所以 S AMB 4s AMN .2【点睛】此题考查了抛物线与圆的标准方程及性质的应用,考查了一元二次方程的根与系数的关系、中点坐标公式、三角形面积计算公式、两点之间的距离公式,考查了推理水平与计算水平,属于中档题.20 .“工资条里显红利,个税新政人民心〞 .随着2021年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税〔简称个税〕改革迎来了全面实施的阶段 .2021年1月1日实施的个税新政主要内容包括：〔1〕个税起征点为5000元；〔2〕每月应纳税所得额〔含税〕=收入一个税起征点-专项附加扣除；〔3〕专项附加扣除包括住房、子女教育和赡养老人等新旧个税政策下每月应纳税所得额〔含税〕计算方法及其对应的税率表如下:又由于NMNF ,所以NF ND ,从而 MN NDX M ,随机抽取某市1000名同一收入层级的IT从业者的相关资料,经统计分析,预估他们2021 年的人均月收入24000元统计资料还说明,他们均符合住房专项扣除；同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为：住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等.假设该市该收入层级的IT从业者都单独享受专项附加扣除,将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入根据样本估计总体的思想,解决如下问题：〔1〕设该市该收入层级的IT从业者2021年月缴个税为X元,求X的分布列和期望；〔2〕根据新旧个税方案,估计从2021年1月开始,经过多少个月,该市该收入层级的IT 从业者各月少缴交的个税之和就超过2021年的月收入？【答案】〔1〕见解析〔2〕经过12个月,该收入层级的IT从业者少缴交的个税的总和就超过2021年的月收入【解析】〔1〕求出4种人群的每月应缴个税额,得出分布列和数学期望；〔2〕计算两种政策下的每月应缴个税额度差即可得出结论.(1)既不符合子女教育扣除也不符合赡养老人扣除的人群每月应纳税所得额为24000 5000 1000 18000,月缴个税X 3000 0.03 9000 0.1 6000 0.2 2190；只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为24000 5000 1000 1000 17000,月缴个税X 3000 0.03 9000 0.1 5000 0.2 1990；只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为24000 5000 1000 2000 16000,月缴个税X 3000 0.03 9000 0.1 4000 0.2 1790;既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为24000 5000 1000 1000 2000 15000,月缴个税X 3000 0.03 9000 0.1 3000 0.2 1590；所以X的可能值为2190, 1990, 1790, 1590,依题意,上述四类人群的人数之比是2:1:1:1,2 1所以P X 2190 — , P X 1990 —,5 51 1P X 1790 一,P X 1590 —.,5 5_ _ _ 2 _ 1 _ 1 一1 一所以E X 2190 — 1990 — 1790 — 1590 — 1950.. 5 5 5 5(2)由于在旧政策下该收入层级的IT从业者2021年每月应纳税所得额为24000 3500 20500,其月缴个税为1500 0.03 3000 0.1 4500 0.2 11500 0.25 4120,由于在新政策下该收入层级的IT从业者2021年月缴个税为1950,所以该收入层级的IT从业者每月少缴交的个税为4120 1950 2170.,设经过x个月,该收入层级的IT从业者少缴交的个税的总和就超过24000,那么2170x 24000,由于x N ,所以x 12,所以经过12个月,该收入层级的IT从业者少缴交的个税的总和就超过2021年的月收【点睛】此题考查了离散型随机变量的分布列与数学期望计算,考查样本估计总体的统计思想,属于中档题.2x21.函数f x x e a.(1)假设y 2x是曲线y f x的切线,求a的值；(2)假设f x 1 x In x,求a的取值范围.【答案】(1) a 1⑵,1【解析】法—：(1)根据题意,设切点的坐标为( 与,力),求出函数的导数,由导数的y1 2x1几何意义分析可得y X e2x1 ax1,解可得a的值,即可得答案；2x1 1 e2" a 2(2)根据题意,f (x) > 1 + x+lnx IP x (S x-a) > 1+x+lnx,结合x的取值范围变形可得a+1 <e2x LJnx,设F (x) = e2x LJnx,利用导数分析F (x)在(0, +oo)上x x的最小值,据此分析可得答案.2x . 法二：(1)同解法一.(2)设F x x e a 1 x Inx ,求导后,先研究a=1时导函数的最小值, 从而得到结论成立, 再研究a>1和a<1时情况,利用变换主元的方法进行放缩后分别说明成立及不成立.法三：(1)同解法一.(2)先考查函数mt e t t 1,通过导函数证实mt 0,利用此引理进行放缩,分a 1及a 1去证实,分别去证实成立与说明不成立,得到a的范围.【详解】2x 2x解法一：(1)由于f x x e a ,所以f x 2x 1 e a ,设直线y 2x与y f x的图象的切点为x1,y1 ,那么2斗1 e2x1 a 2.①y xe2x1ax,②由于切点既在切线上又在曲线上,所以y1 11'V1 2.③由①②③得a 1.2x 2x(2)由题意得xe 1 lnx a 1 x,即xe 1 Inx a 1 x,由于x 0,所以e 2x1-lnx a 2、几 l2x1 lnx nrt设 F x e ------------------ ,贝U F x2考查函数h x2x 2e 2x lnx,1由于 h x 4xe x 1— 0, x 又由于h e 11ee 1 1e ee1 .故存在x 0— ,1 ,使得h xo ( e1,c 2x lnx2x 2e 2x lnx2e不 ------------------------ -x x所以h x 在0, 单调递增.1 2 1 0 ,且 h 12 e 2 0,e,即 2x 02e 2x 0 lnx .0 ,0 , F x 单调递增.2x 01 lnx 0 e --------------x 0由题意得,a 1 F x 0 .令x 02e 2x 0 t0,取对数2% 2lnx ° lnt 得,④由 2x 02e 2x 0 lnx 0 由④⑤得 2x 0 lnx 0 2t lnt, 设函数 x lnx 2x,那么有 x 0 t , 由于 x lnx 2x 在0, 单调递增,所以 x ° t ,即 lnx 02x 0, l2x01 lnx 0 11 2x 0 -所以 F x ° e x 0-------------- 0--------- 0 2,故 a 1 2,解得 a 1 . x ° x °x °故a 的取值范围是 ,1 .解法二：(1)同解法一.(2)设 F x x e 2x a 1 x lnx , x 0,2x2x 1 e所以当x0,x 0时,h x 0, F x 0 , F x 单调递减;当 x x °,所以 F X min F x 0①当a 1时,令G x2xxe 2x lnx 1,G x 2x 1 e 2x - x、几2 x12 x1设g x e 一,x 0.由于 g x 2e — 0, xx1-故存在x °-,0 ,使得g x 0 0,4 2x 01...............所以e 一,两边取对数得2x 0lnx 0.,x .②当a 1时,由于x 0,所以a 1不符合题意. ③当a 1时,F x 综上,a 的取值范围是 ,1 .解法三：(1)同解法一.(2)考查函数 m t e t t 1,由于m t e t 1 ,所以当t 0时,m t 当 t ,0 时,m t 0;当 t 0, 时,m t 0, 所以m t 在 ,0单调递减,在 0, 单调递增.所以m t m 00.①当a 1 2,即a 1时,由于x 0, 所以 xe 2x e 2x lnx 2x Inx 1 a 1 x Inx 1,符合题意； ②当 a 12 ,即 a 1 时,设 g xe 2x Inx Inx a 1 x1,所以g x 在0,、…一一. 1 单调递增,又由于g - 4Te 4 0, g 1 e 2 1 0所以当x 0,x 0 , g x 0, G x 0 , G x 单调递减. x x 0,0, G x 0 , G x 单调递增. 所以G x 由访G x 0 x 0e 2x 02x 0 lnx 0 1 0.即a 1时,有x e 2x11 x Inx 所以a 1符合题意,所以 F x x e 2x a2x1 x Inx x e 1由①知,存在x 00, ,使得 F x 0G x 0 0,0,由于 x 0,所以 g x e 2x 1nx Inx 2x 1, 令 h xe 2x 1nx Inx 2x 1 ,考察 t x2x Inx x 0 .…1~、…,〜由于t x 2 — 0,所以t x 在0, 单调递增. x 12 .. 一八由于 t —— 1 0,t12 0,e e1 .故存在 x 0-,1 ,使得 t x 0 0,即 2x 0 1nx 0 0,e所以存在 x 0 1,1 ,使得 h x 0 e 2x 0lnx 02x 0 1nx 0 1 0,e1 ,由于g x h x ,故存在x 0- ,1 ,使信g x 0 h x 0 0,e所以a 1不符合题意. 综上,a 的取值范围是 ,1 .【点睛】此题考查利用导数分析函数的最值以及计算切线的方程,考查了利用导数研究函数的恒成立问题,关键是掌握导数的定义,正确计算函数的导数,属于综合题.(2)设1与C 交于A ,B 两点,线段 AB 的中点为M ,求PM ._ . 一 x 2 o 55【答案】(1) — y 21, 1,1 (2) PM 一 241【解析】(1)利用互化公式把曲线 C 化成直角坐标方程,把点P 的极坐标化成直角坐标;(2)把直线l 的参数方程的标准形式代入曲线C 的直角坐标方程,根据韦达定理以及参数t 的几何意义可得.22.在直角坐标系xOy 中,直线1的参数方程为为极点,x 轴的正半轴为极轴建立极坐标系,曲线点P 的极坐标为 72,-.(1)求C 的直角坐标方程和 P 的直角坐标；t 为参数),以坐标原点C 的极坐标方程为2 2~21 sino2 . c c c . c c c (1)由p 2—2-^得p 2+ p 2sin 2 0 =2,将p 2= x 2+y 2,y=psin 0代入上式并整理得曲线 C1 sin2的直角坐标方程为 —y 2=i,2设点P 的直角坐标为(x, y),由于P 的极坐标为(J ], 7)2— y 2=1,并整理得 41t 2+110t +25 = 0, 2由于△= 1102- 4X 41X 25= 8000>0,故可设方程的两根为t 1, t 2,… _ ,一110那么t 1, t 2为A, B 对应的参数,且t 1 + t 2 ——,41依题意,点M 对应的参数为, 2所以 I PM I = I t 1__k| 55.2 41此题考查了简单曲线的极坐标方程,属中档题. 23.函数 f x x 1 ax 3 a 0 .(1)当a 2时,求不等式f x 1的解集；(2)假设y f x 的图像与x 轴围成直角三角形,求a 的值. 【答案】(1) x 1 x 3 (2)我【解析】(1)分3段去绝对值解不等式组,再求并； (2)将y= f (x)去绝对值写出分段函数,根据其图象与 x 轴围成直角三角形,转化为(a- 1) (a+1) =- 1 或(*1) (1-a) = - 1,可解得. 【详解】(1)当 a= 2 时,不等式 f (x) > 1,即 | x+1| - |2 x- 3| >1,当xw - 1时,原不等式可化为- x- 1+2x- 3> 1,解得x>5,由于x< - 1,所以此时原不等式无解；, 3 ........................... .一一 3 当-1<x —时,原不等式可化为 x +1+2x- 3> 1,解得x> 1,所以1v x —；22所以 x= pcos 0 . 2 cos — 所以点P 的直角坐标为(1, y= psin 0 ..2sin - 1, 1,1).3x 1 -t(2)将5代入4 y 1 t5当x>3时,原不等式可化为 x +1 - 2x +3>1, 2 综上,原不等式的解集为 {x[1 <x<3}.那么a 1 a 11 ,解得a 0,舍去;当a 1时,y f x 的图象与x 轴不能围成三角形,不符合题意,舍去; 当a 1时,要使得y f x 的图象与x 轴围成直角三角形, 那么1 a a 11 ,解得a J 2,由于a 1 ,所以a J 2.【点睛】此题考查了绝对值不等式的解法, 考查了数形结合思想及函数与方程思想的转化, 属于中档题.解得xv 3,所以3<xv3.2a 1 x 4, x 1,一 , 3(2)由于a 0,所以—0 ,所以f x a3a 1 x 2, 1 x —, a , 3 1 a x 4, x 一 a由于a 0,所以f 1c c. 3 ,3八 a 30, f — 1 — 0,a a当0 a 1时,要使得y f x 的图象与x 轴围成直角三角形,综上,所求a 的值为72.gft 】 q 61。

2021届福州市高中毕业班第三次质量检查(理科数学)详细解答

2021届福州市高中毕业班第三次质量检查数学（理科）详细解答一、选择题：本大题共12小题，每小题5分，共60分． 1. 已知纯虚数z 满足(1i)2i z a -=+，则实数a 等于A ．2B ．1C ．1-D ．2-【命题意图】本小题考查复数的概念与运算等基础知识；考查运算求解能力；考查函数与方程思想；考查数学运算等核心素养，体现基础性．【答案】A ．【解析】解法一：设i(,z b b =∈R 且0),b ≠则(1i)i i 2i.b b b a -=+=+ 因为a ∈R ，所以2,,b a b =⎧⎨=⎩所以2a =，故选A ．解法二：2i (2i)(1i)22i 1i 222a a a a z +++-+===+-．因为z 为纯虚数,所以20,20,a a -=⎧⎨+≠⎩解得2a =，故选A.2. 已知集合{}(){}2220,log 2A x x x B x y x =+-==-＜，则()AB =RA ．∅B ．(]2,2-C ．()1,2D ．()2,1-【命题意图】本小题考查解一元二次不等式、函数的定义域，集合的交集、补集运算等基础知识；考查运算求解能力；考查数学运算核心素养，体现基础性．【答案】D ．【解答】依题意，{}{}21,2A x x B x x =-=＜＜＞，所以B =R{}2x x ≤，所以()AB =R()2,1-．3. 执行右面的程序框图，则输出的m =A ．1B ．2C ．3D ．4【命题意图】本小题考查程序框图等基础知识；考查推理论证能力；考查逻辑推理核心素养，体现基础性．【答案】C ．【解答】该框图的功能为求小于12的正整数中3的倍数的个数，故输出的m 值应为3，故选C ． 4.5. 函数()2e 2x f x x x =--的图象大致为ABCD【命题意图】本小题考查函数的图象与性质等基础知识；考查运算求解能力；考查数形结合思想，考查直观想象、数学运算等核心素养，体现基础性．【答案】B ．【解答】解法一：因为()()e 22,e 2x x f x x f x '''=--=-，令()e 20x f x ''=-=，得ln2x =，当ln 2x ＜时()0f x ''＜，()f x '为减函数；当ln 2x ＞时，()0f x ''＞，()f x '为增函数，而()ln 222ln 222ln 20f '=--=-＜，所以原函数存在两个极值点，故淘汰选项C 和D ．将1x =代入原函数，求得()1e 120f =--＜，淘汰选项A ，故选B ．解法二：()1e 210f =--＜，淘汰选项A ，D ；当x →-∞时，()e x f x =-()2x x +→-∞，淘汰选项C ．故选B ．6. 甲、乙、丙、丁四名同学在某次军训射击测试中，各射击10次．四人测试成绩对应的条形图如下：以下关于四名同学射击成绩的数字特征判断不正确．．．的是 A ．平均数相同B ．中位数相同C ．众数不完全相同D ．丁的方差最大【命题意图】本小题考查统计图表、数字特征的概念等基础知识；考查运算求解能力；考查数形结合思想、统计与概率思想；考查直观想象、数据处理、数学运算等核心素养，体现基础性、应用性．【答案】D ．【解析】由图的对称性可知，平均数都为5；由图易知，四组数据的众数不完全相同，中位数相同；记甲、乙、丙、丁图所对应的方差分别为22221234,,,s s s s ，则()()2221450.5650.51s =-⨯+-⨯=，()()()22222450.3550.4650.30.6s =-⨯+-⨯+-⨯=，()()()()()2222223350.3450.1550.2650.1750.3 2.6s =-⨯+-⨯+-⨯+-⨯+-⨯=， ()()()()()2222224250.1450.3550.2650.3850.1 2.4s =-⨯+-⨯+-⨯+-⨯+-⨯=，所以丙的方差最大．故选D ． 7. 已知角θ的终边在直线3y x =-上，则2sin 21cos θθ=+ A ．611-B ．311-C ．311D ．611【命题意图】本小题考查三角函数的定义、三角恒等变换等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想；考查数学运算、直观想象等核心素养，体现基础性．【答案】A ．【解析】解法一：依题意，tan 3θ=-，所以原式2222sin cos 2tan 6sin 2cos tan 211θθθθθθ===-++，故选A ．解法二：不妨在直线3y x =-上取一点()1,3P -，则r，所以cosθsin θ=所以6sin 22sin cos 10θθθ==-，原式6610111110-==-+，故选A ．8. 数独是源自18世纪瑞士的一种数学游戏．如图是数独的一个简化版，由3行3列9个单元格构成．玩该游戏时，需要将数字1,2,3（各3个）全部填入单元格，每个单元格填一个数字，要求每一行、每一列均有1,2,3这三个数字，则不同的填法有 A ．12种 B ．24种 C ．72种D ．216种【命题意图】本小题考查计数原理等基础知识；考查运算求解能力、应用意识；考查数学抽象、数学建模、逻辑推理等核心素养，体现综合性和应用性．【答案】A ．【解答】先填第一行，有336A =种不同填法，再填第二行第一列，有2种不同填法，当该单元格填好后，其它单元格唯一确定．根据分步乘法计数原理，共有6212⨯=种不同的填法．故选A ．9. 已知函数()()sin 06f x x ωωπ⎛⎫=+ ⎪⎝⎭＞图象上相邻两条对称轴的距离为2π，把()f x 图象上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的图象向右平移35π个单位长度，得到函数()g x 的图象，则 A ．()cos 4g x x =- B ．()cos 4g x x =C ．()cos g x x =-D ．()cos g x x =【命题意图】本小题考查三角函数图象的变换、诱导公式等基础知识；考查运算求解能力；考查数形结合思想；考查数学运算、直观想象等核心素养，体现基础性．【答案】D ．【解析】依题意，2T =2π，所以T =π，所以2ωπ=π，解得ω=2，所以()f x =sin 26x π⎛⎫+ ⎪⎝⎭．把()f x 图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到曲线sin 6y x π⎛⎫=+ ⎪⎝⎭，再把曲线sin 6y x π⎛⎫=+ ⎪⎝⎭向右平移35π个单位长度，得到曲线sin 63y x π5π⎛⎫=+- ⎪⎝⎭，即cos y x =，故()cos g x x =，故选D ． 10. 已知椭圆2222:1x y C a b+=（0a b ＞＞）的焦距为2，右顶点为A ．过原点与x 轴不重合的直线交C 于,M N 两点，线段AM 的中点为B ，若直线BN 经过C 的右焦点，则C 的方程为A ．22143x y +=B ．22165x y +=C ．22198x y +=D ．2213632x y +=【命题意图】本小题考查直线与椭圆的位置关系等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想、函数与方程思想等；考查数学运算、直观想象等核心素养，体现基础性．【答案】C ．【解析】解法一：设()00,M x y ，则()00,N x y --，因为(),0A a 且线段AM 的中点为B ，所以00,22a x y B +⎛⎫⎪⎝⎭，由,,B F N 三点共线得FN FB ∥，依题意，()1,0F ，故FN =()001,,x y ---001,22a x y FB +⎛⎫=-⎪⎝⎭即()000011022y a x x y +⎛⎫-++-= ⎪⎝⎭，又00y ≠，解得3=a ，所以222318b =-=，所以椭圆C 的标准方程为22198x y +=，故选C ．解法二：设()00,M x y ，则()00,N x y --，依题意，(),0A a ，AO NB 和是AMN △的中线，所以()1,0F 为AMN △的重心，故0013x x a-+=，解得3a =，所以222318b =-=，所以椭圆C 的标准方程为22198x y +=．故选C ．11. 已知函数()1ln f x x x x=-+，给出下列四个结论： ①曲线()y f x =在1x =处的切线方程为10x y +-=； ②()f x 恰有2个零点；③()f x 既有最大值，又有最小值；④若120x x ＞且()()120f x f x +=，则121x x =．其中所有正确结论的序号是 A ．①②③B ．①②④C ．①②D ．③④【命题意图】本小题考查函数的图象性质、导数的应用等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想、函数与方程思想等；考查数学运算、直观想象等核心素养，体现基础性、综合性．【答案】B ．【解答】依题意，()f x 的定义域为()(),00,-∞+∞．当0x ＞时，()2221111x x f x x x x-+-'=--=，所以()11f '=-，可知曲线在点()1,0处的切线方程为()01y x -=--，即10x y +-=，所以①正确；因为0x ＞时，()2213240x f x x ⎛⎫---⎪⎝⎭'=＜，所以()f x 区间()0,+∞上单调递减．同理可求()f x 在区间(),0-∞上单调递减．所以③错误；又()()10,10f f -==，所以②正确；对于④，若120x x ＞0,＞，由()()120f x f x +=得()()122221ln f x f x x x x ⎛⎫=-=--+=⎪⎝⎭21lnx +2221111f x x x ⎛⎫-= ⎪⎝⎭，即()121f x f x ⎛⎫= ⎪⎝⎭．因为()f x 在()0,+∞上为减函数，所以121x x =，即121x x =．同理可证当120,0x x ＜＜时，命题也成立．故④正确．综上，故选B ．12. 三棱锥P ABC -中，顶点P 在底面ABC 的投影为ABC △的内心，三个侧面的面积分别为12,16,20，且底面面积为24，则三棱锥P ABC -的内切球的表面积为 A ．43π B ．12π C ．163πD ．16π【命题意图】本小题考查空间点、线、面位置关系，空间几何体的侧面积、体积等基本知识；考查空间想象能力、运算求解能力、论证推理能力；考查化归与转化思想；考查直观想象、数学运算等核心素养，体现基础性、创新性．【答案】C ．【解答】解法一：不妨设12,16,20,PBC PAC PAB S S S ===△△△设P 在底面ABC 的投影为H ，分别作HD BC ⊥于点D ，HE AB ⊥于点E ，HF AC ⊥于点F ，则,PD BC ⊥,PE AB ⊥PF AC ⊥．依题意，H 为ABC △的内心，则Rt Rt Rt PDH PFH PEH △≌△≌△，故PD PF PE ==，又12PBC S BC PD =⋅△，12PAC S AC PF =⋅△，12PAB S AB PE =⋅△，所以::::12:16:203:4:5PBC PAC PAB S S S BC AC AB ===△△△，所以90ACB ∠=︒．令3,4,5BC x AC x AB x ===. 所以11342422ABC S BC AC x x =⋅=⋅⋅=△，解得2x =，所以6,8,10BC AC AB ===. 设ABC △内切圆半径为r ，则()12ABC BC AC AB r S ++=△，即()16810242r ⨯++=，解得2r =，故2HD =．由112,62PBC S BC PD BC =⋅==△，得4PD =，所以2223PH PD HD =-=，所以11242316333P ABC ABC V S PH -=⋅=⨯⨯=△，设三棱锥P ABC -的内切球的半径为R ，则()13P ABC PBC PAC PAB ABC V S S S S R -=+++△△△△，即()1163121620243R =⨯+++，解得23R =，所以三棱锥P ABC -的内切球的表面积为21643R ππ=，故选C ．解法二：不妨设12,16,20,PBC PAC PAB S S S ===△△△设P 在底面ABC 的投影为H ，分别作HD BC ⊥于点D ，HE AB ⊥于点E ，HF AC ⊥于点F ，则,PD BC ⊥,PE AB ⊥PF AC ⊥．依题意，H 为ABC △的内心，则Rt Rt Rt PEH PFH PDH △≌△≌△，故PD PF PE ==，且PEH PFH PDH ∠=∠=∠，记为θ．所以cos HE HF HDPE PF PDθ===，故cos HAC HBC HAB PAB PAC PBC S S S S S S θ===△△△△△△，所以1cos 2BC PABPAC PBC S S S S θ==++△A △△△，所以π3θ=．又12PBC S BC PD =⋅△，12PAC S AC PF =⋅△， 12PAB S AB PE =⋅△，所以::::12:16:203:4:5PBC PAC PAB S S S BC AC AB ===△△△，所以90ACB ∠=︒．令3,4,5BC x AC x AB x ===. 所以11342422ABC S BC AC x x =⋅=⋅⋅=△，解得2x =，所以6,8,10BC AC AB ===. 设ABC △内切圆半径为r ，由直角三角形内切圆半径公式得681022r +-==．由题意知三棱锥内切球的球心在PH 上，设为点O ．由条件知点O 也在PDH ∠的角平分线上，所以内切球半径tan30R r =︒=所以三棱锥P ABC -的内切球的表面积为21643R ππ=，故选C ．二、填空题：本大题共4小题，每小题5分，共20分．13. 已知向量()1,2AB =，()2,5CB =，(),1t MN =．若AC MN ∥，则实数t = ．【命题意图】本小题考查平面向量坐标运算等基础知识；考查运算求解能力；考查数形结合思想、函数与方程思想等；考查数学运算、直观想象等核心素养，体现基础性．【答案】13．【解析】因为()()()1,22,51,3AC AB CB =-=---=，又因为(),1t MN =，AC MN ∥，所以()113t -⨯=-，解得13t =． 14. 正方体1111ABCD A B C D -中，P 为1BC 中点，Q 为1A D 中点，则异面直线DP 与1C Q 所成角的余弦值为．【命题意图】本小题考查空间直线与直线的位置关系等基本知识；考查空间想象能力、运算求解能力、推理论证能力；考查化归与转化思想；考查直观想象、数学运算等核心素养，体现基础性．【答案】23．【解答】解法一：连结11,CB QB ，因为四边形11BCC B 为正方形，P 为1BC 中点，所以1112B P BC =．因为11//A B CD ，所以四边形11CDA B 为平行四边形，所以11//B C A D ，又Q 为1A D 中点，所以1//B P DQ ，所以四边形1DPB Q 为平行四边形，所以1B Q DP ∥，所以11B QC ∠为异面直线DP 与1C Q 所成角或其补角．设正方体的棱长为2，在1Rt BAQ △中，221111246B Q AQ A B =+=+=；同理可求16C Q =．在11B C Q △中，222111111112cos 23266B Q C Q B C C QB B Q C Q +-∠===⋅⨯⨯，故异面直线DP 与1C Q 所成角的余弦值为23．解法二：如图，以D 为原点，分别以1,,DA DC DD 的方向为,,x y z 轴的正方向，建立空间直角坐标系D xyz -．设正方体的棱长为2，则各点的坐标为()()0,0,0,1,2,1,D P ()10,2,2,C ()1,0,1Q ，所以()()11,2,1,1,2,1DP C Q ==--，所以1cos ,DP C Q =11DP C Q DP C Q⋅=66=⨯23-．所以异面直线DP 与1C Q 所成角的余弦值为23．解法三：设正方体的棱长为2，1,,,DA DC DD ===a b c 则()111222DP =++=++b a c a b c ，()1111222C Q =-+-=--b a c a b c ，由1,,DA DC DD 三条直线两两垂直得0⋅=⋅=⋅=a b b c a c ，所以2222222211111112224224444DP C Q ⎛⎫⎛⎫⋅=-+=--=⨯--⨯=- ⎪ ⎪⎝⎭⎝⎭a b c a b c ，222222111116,64444DP C Q =++==++=a b c a b c ，所以1cos ,DP C Q =11DP C Q DP C Q⋅=66=⨯23-．所以异面直线DP 与1C Q 所成角的余弦值为23． 15. 在ABC △中，内角,,A B C 的对边分别为,,a b c ，若22sin cos 1A B +=，则cb a-的取值范围为．【命题意图】本小题考查解三角形等基础知识；考查运算求解能力；考查数形结合思想、函数与方程思想、化归与转化思想等；考查数学运算、直观想象等核心素养，体现基础性．【答案】()2,3．【解析】在ABC △中，因为22sin cos 1A B +=，所以cos cos2B A =，所以2B A =. 由正弦定理及题设得()sin sin sin cos2cos sin 2sin sin sin sin sin 2sin A B c CA A A A b aB A B A A A++====----()22sin 2cos 12sin cos 2sin cos sin A A A AA A A-+=-24cos 12cos 12cos 1A A A -=+-，由02π,0π3πB A C A =⎧⎨=-⎩＜＜＜＜得π03A ＜＜，故1cos 12A ＜＜，所以cb a-的取值范围为()2,3． 16. 已知梯形ABCD 满足,45AB CD BAD ∠=︒∥，以,A D 为焦点的双曲线Γ经过,B C 两点．若7CD AB =，则Γ的离心率为．【命题意图】本小题考查直线与双曲线的位置关系等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想、函数与方程思想；考查数学运算、直观想象等核心素养，体现基础性、综合性．【解答】解法一：如图所示，以AD 中点O 为原点，以AD 为x 轴，建立直角坐标系．设点C 关于点O 对称的点为C '，由对称性知，B ,A ,C '三点共线．设Γ的方程为)00(12222>>=-b a b y a x ，，)0,(c A -,11(,)B x y ,22(,)C x y '，则直线BC '方程为c x y +=，由2222,1y x c x y ab =+⎧⎪⎨-=⎪⎩得22224()20b a y b cy b --+=，所以()4242240b c b b a ∆=--＞，24121222222,b c b y y y y b a b a +==--，由7CD AB =，所以217y y =，因为12,y y 异号，所以217y y =-，由21212227,2,y y b c y y b a =-⎧⎪⎨+=⎪-⎩，解得⎪⎪⎩⎪⎪⎨⎧-=--=)(37)(322222221a b c b y a b cb y ，代入22421ab b y y -=，得)(97222a bc -=-，因为222a c b -=，所以2289c a =，所以Γ的离心率324c e a ==．解法二：如图所示，以AD 中点O 为原点，以AD 为x 轴，建立直角坐标系．设Γ的方程为)00(12222>>=-b a by a x ，，)0,(c A -．依题意，设(),B m m c -，则()7,7C c m m +，()()222222221,(1)7491,(2)m c m a bc m ma b ⎧--=⎪⎪⎨+⎪-=⎪⎩由()()1492⨯-得()2223377c a b m cc-==，将237b m c=代入（1）得422491780a a c c -+=，解得2298a c =或22a c =（舍去），所以Γ的离心率324c e a ==．解法三：如图，连接,AC BD ．设该双曲线的焦距2AD c =，实轴长为2a ，则BD -2AB AC CD a =-=．设AB m =，则7CD m =，2,27BD a m AC a m =+=+．依题意，45,135BAD ADC ∠=︒∠=︒，在ABD △中，由余弦定理及题设得()2222422a m m c mc +=+-，在ACD △中，由余弦定理及题设得()22227494142a m m c mc +=++，A DCB))22,c a m c -=+))227c a mc -=-，两式相除得18c =，故Γ的离心率c e a =．三、解答题：本大题共6小题，共70分． 17. （本小题满分12分）已知数列{}n a 和{}n b 的前n 项和分别为n S ,n T ，12a =，11b =，且112n n a a T +=+．（1）若数列{}n a 为等差数列，求n S ；（2）若112n n b b S +=+，证明：数列{}n n a b +和{}n n a b -均为等比数列．【命题意图】本小题考查等差数列、等比数列等基础知识；考查运算求解能力、推理论证能力；考查化归转化思想；考查数学运算、逻辑推理等学科素养；体现基础性．满分12分．【解答】（1）由112n n a a T +=+，得2112a a b =+，又12a =，11b =，解得24a =. ································································· 1分因为数列{}n a 为等差数列，所以该数列的公差为21a a -=2， ························ 2分所以()21222n n n S n n n -=+⋅=+．··························································· 4分（2）当2n ≥时，112n n a a T -=+，因为1n n n T T b --=，所以12n n n a a b +-=，即12n n n a a b +=+， ···························· 5分同理可得：12n n n b b a +=+． ···································································· 6分则113()n n n n a b a b +++=+，所以113n n n na b a b +++=+（2n ≥）， ································· 7分又21121124,25a a b b b a =+==+=，所以22114533a b a b ++==+，所以113n n n na b a b +++=+（*n ∈N ）， ································································ 8分所以数列{}n n a b +是以3为首项，3为公比的等比数列. ································ 9分因为11()n n n n a b a b ++-=--，所以111n n n na b a b ++-=--（2n ≥）， ·························· 10分又221145121a b a b --==---，所以111n n n na b a b ++-=--（*n ∈N ）， ······························ 11分所以数列{}n n a b -是以1-为首项，1-为公比的等比数列． ························· 12分 18. （本小题满分12分）如图，在多面体PABCD 中，平面ABCD ⊥平面PAD ，AD BC ∥，90BAD ∠=︒，120PAD ∠=︒，1BC =，2AB AD PA ===．（1）求平面PBC 与平面PAD 所成二面角的正弦值；（2）若E 是棱PB 的中点，求证：对于棱CD 上任意一点F ，EF 与PD 都不平行．【命题意图】本小题考查直线与平面垂直的判定与性质，直线与平面平行、平面与平面平行的判定与性质，二面角等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查化归与转化思想、函数与方程思想；考查直观想象、逻辑推理等核心素养，体现基础性、综合性．满分12分．【解析】解法一：（1）因为AB AD ⊥，平面ABCD ⊥平面PAD ，平面ABCD 平面PAD AD =，AB ⊂平面ABCD ，所以AB ⊥平面PAD . ·········································· 1分作AH AD ⊥交PD 于H ，则,,AB AD AH 三条直线两两垂直．以A 为坐标原点O ，分别以AH AD AB ，，所在直线为,,x y z 轴，建立空间直角坐标系，如图所示． ················ 2分因为120PAD ∠=︒，1BC =，2AB AD PA ===．所以()()()())0,0,0,0,0,2,0,1,2,0,2,0,1,0A B C D P-， ····························· 3分设平面PBC 的法向量为(),,x y z =n ，因为()()0,1,0,3,1,2BC BP ==--，所以0,0,BC BP ⎧⋅=⎪⎨⋅=⎪⎩n n 所以0,20,y y z =⎧⎪--=令2x =，所以(=n ， ·············· 4分由z 轴⊥平面PAD 知()0,0,1=m 为平面PAD 的一个法向量, ··························· 5分所以cos ,⋅<>===⋅n m n m n m， ················································· 6分P ADCBP所以PBC 与平面PAD． ··································· 7分（2）因为E 是棱PB 的中点，由（1）可得1,12E ⎫-⎪⎪⎝⎭.假设棱CD 上存在点F ，使得EF PD ， ·················································· 8分设DF DC λ=，01λ≤≤，所以()55,10,1,2,1222EF ED DF λλλ⎛⎫⎛⎫=+=-+-=--+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ·········· 9分因为EF PD，所以()EF tPD t ==， ·· 10分所以53,2120,t λλ⎧=⎪⎪⎪⎪-=⎨⎪⎪-+=⎪⎪⎩这个方程组无解， ···············11分所以假设不成立，所以对于棱CD 上任意一点F ，EF 与PD 都不平行. ·········· 12分解法二：（1）如图，在平面PAD 内，过点P 作DA 的垂线，垂足为M ；在平面ABCD 内，过M 作AD 的垂线，交CB 的延长线于点N ．连接PN ．因为MN PM M =，所以AD ⊥平面PMN ． ············· 1分因为AD BC ∥，BC ⊂平面PBC ，AD ⊄平面PBC ，所以AD ∥平面PBC ， ··········································· 2分设平面PBC平面PAD l =，则AD l ∥，故l ⊥平面PMN ． ········································································································ 3分所以NPM ∠为平面PBC 与平面PAD 所成二面角的平面角． ························· 4分因为120PAD ∠=︒，2AB AD PA ===，所以60MAP ∠=︒，在Rt PAM △中，2sin 60PM =︒ ····················································· 5分又2MN AB ==，所以在Rt PMN △中，PN = ················ 6分所以sin MN MPN PN =∠ 所以PBC 与平面PAD． ··································· 7分PAB CDPNM（2）假设棱CD 上存在点F ，使得EF PD ，显然F 与点D 不同， ··································································· 8分所以,,,P E F D 四点共面，记该平面为α，所以P α∈，PE α⊂，FD α⊂， ···················································· 9分又B PE ∈，C FD ∈，所以B α∈，C α∈，所以α就是点,,B C D 确定的平面， ························································ 10分这与P ABCD -为四棱锥相矛盾，所以假设不成立，所以对于棱CD 上任意一点F ，EF 与PD 都不平行. ·································· 12分解法三：（1）同解法一． ······································································· 7分（2）假设棱CD 上存在点F ，使得EF PD ． ·········································· 8分连接BD ，取BD 的中点M ，在△BPD 中，因为,E M 分别为,BP BD 的中点，所以EMPD . ···················································· 9分因为过直线外一点有且只有一条直线和已知直线平行，所以EM 与EF 重合. ······················································································· 10分又点F 在线段CD 上，所以F BD CD =，又BD CD D =，所以F 是BD 与CD 的交点D ，即EF 就是ED ， ······································ 11分而ED 与PD 相交，所以与EFPD 相矛盾，所以假设不成立，所以对于棱CD 上任意一点F ，EF 与PD 都不平行． ································ 12分 19. （本小题满分12分）已知抛物线2:4C y x =，直线:2l x my =+（0m ＞）与C 交于,A B 两点，M 为AB 的中点，O 为坐标原点．（1）求直线OM 斜率的最大值；（2）若点P 在直线2x =-上，且PAB △为等边三角形，求点P 的坐标．【命题意图】本题考查抛物线方程、直线与抛物线的位置关系等基础知识；考查运算求解能力；考查数形结合思想、函数与方程思想；考查直观想象、数学运算等核心素养，体现基础性、综合性．满分12分．【解析】解法一：（1）设1122(,),(,)A x y B x y ，由22,4x my y x =+⎧⎨=⎩，消去x 得，2480y my --=， ··········································· 1分AB CP CEFABCPCEAM216320,m ∆=+>且12124,8y y m y y +==-. ················································ 2分所以21212()44 4.x x m y y m +=++=+ 因为M 为AB 的中点，所以M 的坐标为1212(,)22x x y y ++，即2(22,2)m m +, ···································· 3分又因为0m >，所以2221112212OM m m k m m m m ====+++, ·················· 5分（当且仅当1m m=，即1m =等号成立.）所以OM 的斜率的最大值为12． ······························································ 6分（2）由（1）知，12|AB y y -== ····································································· 8分由PM AB ⊥得22||22(2)|2(PM m m +--=+， ·············· 9分因为PAB △为等边三角形，所以||||PM AB ， ··································· 10分所以22(m +=21m =，解得1,m =±又0m ＞，所以1m =， ······································································· 11分则(4,2)M ，直线MP 的方程为2(4)y x -=--，即6y x =-+，所以2x =-时，8y =，所以所求的点P 的坐标为(2,8)-． ························································· 12分解法二：（1）设112200(,),(,),(,)A x y B x y M x y ，因为M 为AB 的中点，且直线:2(0)l x my m =+>，所以0122,y y y =+1212,x x m y y -=- ································································ 1分由2112224,4,y x y x ⎧=⎪⎨=⎪⎩得22121244,y y x x -=-所以()1212124,x x y y y y -+=-所以024,y m =即02y m =. ······································· 2分所以200222,x my m =+=+即2(22,2)M m m +， ·········································· 3分又因为0m >，所以2221112212OM m m k m m m m ====+++, ················· 5分（当且仅当1m m=，即1m =等号成立.）所以OM 的斜率的最大值为12． ······························································ 6分（2）由22,4x my y x=+⎧⎨=⎩，消去x 得2480y my --=，所以216320,m ∆=+>且12124,8y y m y y +==-. ·········································· 7分AB =====····································································· 8分由（1）知，AB 的中点M 的坐标为2(22,2)m m +，所以线段AB 的垂直平分线方程为：()2222y m m x m -=---.令2x =-，得线段AB 的垂直平分线与直线2x =-交点坐标为()32,26,P m m -+所以22(m M P + ·························· 9分。

2021年福州一中高三下学期开学质量检查考试数学试题与答案

3 ，且 ACD 的面积为 3
3
，求线
3
4
段 BD 的长度．
（18）（本小题满分 12 分）
如图，在四棱锥 P ABCD 中，底面 ABCD 为菱形， BAD 60 ， APD 90 ，且 AD PB ． (I)求证：平面 PAD ⊥平面 ABCD ； (II)若 AD PB ，求二面角 D PB C 的余弦值．
范围是（）
A． [
1 2e
，8 3e 2
)
B． [
64 5e4
，27 4e3
)
C． [
27 4e3
，8 3e 2
)
D． [ 0 ，1 ) 2e
二、选择题：本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多项符合
题目要求。全部选对的得 5 分，有选错的得 0 分，部分选对的得 2 分。
藏，若不及时处理，打上来的鱼会很快失去新鲜度.已知某种鱼失去的新鲜度 h 与其出水后
1
时间 t （分）满足的函数关系式为 h= 1 a t ．若出水后10 分钟，这种鱼失去的新鲜度为 20
10% ．那么若不及时处理，打上来的这种鱼在多长时间后开始失去全部新鲜度（已知 lg 2 0.3 ，结果取整数）（）
D．3
3.某地为了解居民的每日总用电量 y（万度）与气温 x（°C）之间的关系，收集了四天的每
日总用电量和气温的数据如表：
气温 x（°C）
19
13
9
1
每日总用电量 y（（万度） 24
34
38
64
经分析，可用线性回归方程
拟合 y 与 x 的关系．据此预测气温为 14°C 时，
该地当日总用电量 y （万度）为（）

2020-2021年福建省福州市质检一：福州市2020届高三第一次质量检测数学(理)试题含答案

福建省福州市2020届高三第一次质量检测
理科数学
注意事项：
1.答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类填写到答题卡和试卷规定的位置上。

2.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3.必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

第Ⅰ卷（共60分）
一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A＝{x|x2﹣x﹣6＜0}，集合B＝{x|x﹣1＞0}，则（∁R A）∩B＝（）
A．（1，3）B．（1，3]C．[3，+∞）D．（3，+∞）2．（5分）若iz＝1+i（其中i是虚数单位），则复数z的共轭复数在复平面内对应的点位于（）
A．第一象限B．第二象限C．第三象限D．第四象限
第1页（共23页）。

2020-2021学年福建省福州市高一下学期期末数学试题

福州市2020-2021年第二学期质量检查数学试卷（完卷时间：120分钟；满分：150分）友情提示：请将所有答案填写到答题卡上！请不要错位、越界答题！注意事项：1．答题前，考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名．考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．3．考试结束，考生必须持试题卷和答题卡一并交回一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知复数z 满足，12z ii i+=++，则复数z =（）.A.2i + B.12i+ C.3i+ D.32i-【答案】B2.设D ，E ，F 分别为ABC 的三边BC ，CA ，AB 的中点，则EB ＋FC等于（）A.BCB.12AD C.ADD.12BC 【答案】C3.若2log 31x =，求33x x -+=（）A.52B.136 C.103D.32【答案】A4.某校新成立3个社团，规定每位同学只能参加其中一个社团，假定每位同学参加各个社团的可能性相同，则该校甲、乙两位同学参加同一个社团的概率为（）A.19B.16 C.23D.13【答案】D5.已知复数1z ，2z ，则“12z z R ⋅∈”是“12z z =”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B6.将曲线1:2sin C y x =上各点的横坐标缩短到原来的12倍（纵坐标不变），得到的曲线2C ，把2C 向左平移6π个单位长度，得到曲线()3:C y f x =，则下列结论正确的是（）A.()f x 的最小正周期为4πB.12x π=是()f x 的一条对称轴C.()f x 在,36ππ⎛⎫-⎪⎝⎭D.()f x 在,36ππ⎛⎫- ⎪⎝⎭上单调递增【答案】B7.在我国国旗的正五角星图形中有许多黄金分割点，如图所示的正五角星几何图形中，CDE △是顶角为36︒的等腰三角形，C ，D 为线段AB 上的两个黄金分割点，则有AC BD CD AB AB BC ===cos 216︒=（）A.512+ B.12- C.514+-D.14--【答案】C8.如图所示的一个圆锥形的金瓜配件，重75.06克，其轴截面是一个等边三角形，现将其打磨成一个体积最大的球形配件，则该球形配件的重量约为（）A.34.37克B.34.03克C.33.36克D.32.69克【答案】C二、选择题：本题共4小题，每小陋5分，共20分，在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．9.某地区经过一年的新农村建设，农村的经济收入增加了一倍，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：则下面结论中正确的是（）A .新农村建设后，种植收入减少了B .新农村建设后，养殖收入增加了一倍C.新农村建设后，其他收入增加了一倍以上D.新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半【答案】BCD10.已知a ，b 是平面内夹角为3π的两个单位向量，向量c在该平面内，且()0a b c ⋅-= ，则下列结论正确的是（）A.1a b += B.1a b -= C.()a c b-⊥D.c的最小值为12【答案】BD11.在棱长为1的正方体1111ABCD A B C D -中，点P 、E 、F 分别为1CC 、BC 、CD 的中点，则下列说法正确的是（）A.AP 与EF 所成角为60︒B.点1A 到平面PEF 的距离为334C.直线1A B 与平面PEF 所成角的正弦值为3D.平面1PED 截正方体得到的截面图形是梯形【答案】CD12.在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若()2c b a b =+，则以下结论正确的是（）A.c b > B.2C B= C.a c > D.04B π<<【答案】AB三、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中的横线上．13.“幸福感指数”是某个人对自己目前生活状态满意程度的主观指标数值，常用区间[]0,10内的一个数来表示，该数越接近10表示满意程度越高，现随机抽取6位小区居民进行调查，他们的“幸福感指数”分别为5，6，7，8，9，5，则这组数据的第80百分位数是______．【答案】814.已知一个正六棱柱的所有顶点都在球面上，若正六棱柱的底面边长与侧棱长均为2，则这个球的表面积为_____．【答案】20π15.设向量()11,0e =u r ，()20,1e =u r ．若1227a e e =-+ ，1243b e e =+ ，则a b ⋅= ______，向量a 在向量b上的投影向量为______．【答案】①.13②.1252392525e e +16.某小微企业生产一种如下图所示的电路子模块：要求三个不同位置1，2，3接入三个不同的电子元件A ，B ，C ，它们正常工作的概率分别为0.9，0.8，0.7，假设接入三个位置的元件能否正常工作相互独立，当且仅当3号位元件正常工作同时1号位与2号位元件中至少有一件正常工作时，电路子模块才能正常工作，则该电路子模块能正常工作的概率最大值为______．【答案】0.846四、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤．17.如图，在三棱锥A BCD -中，AB AD ⊥，BC BD ⊥，平面ABD ⊥平面BCD ．（1）求证：AD AC ⊥；（2）已知2DE EA =，2DF FC =，则棱BD 上是否存在点G ，使得平面//EFG 平面ABC ？若存在，确定点G 的位置；若不存在，请说明理由．【答案】（1）证明见解析；（2）存在；2DG GB =．18.已知1sin cos 5αα+=，()0,απ∈，（1）求tan α的值；（2）若2sin 10β=，0,2πβ⎛⎫∈ ⎪⎝⎭，求αβ+的值．【答案】（1）4tan 3α=-；（2）34αβπ+=．19.2021年是“十四五”规划开局之年，也是建党100周年．为了传承红色基因，某学校开展了“学党史，担使命”的知识竞赛．现从参赛的所有学生中，随机抽取100人的成绩作为样本，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示．（1）求频率分布直方图中a 的值，并估计该校此次竞赛成绩的平均分x （同一组中的数据用该组区间中点值代表）；（2）若根据成绩对该样本进行分层，用分层随机抽样的方法，从成绩不低于75分的学生中随机抽取7人查看他们的答题情况，再从这7人中随机抽取2人进行调查分析，求这2人中至少有1人成绩在[)85,95内的概率．【答案】（1）0.035a =；71；（2）1121．20.已知函数()e e xxf x -=+．（1）根据函数单调性的定义，研究()f x 的单调性；（2）若()()221g x x x af x =-+-有唯一零点，求a 的值．【答案】（1）()f x 在区间()0,∞+上单调递增，在区间(),0-∞上单调递减；（2）12a =．21.如图，AB 是底部不可到达的一个建筑物，A 为建筑物的最高点．某学习小组准备了两种工具：测角仪（可测量仰角与俯角）与米尺（测量长度）．请你利用准备好的工具，设计一种测量建筑物高度AB 的方案，包括：（1）指出要测量的数据（用字母表示，并标示在图中）；（2）用文字和公式写出计算AB 的步骤．【答案】（1）答案见解析；（2）答案见解析．22.如图，已知正四棱锥S ABCD -与正四面体S A B C ''''-所有的棱长均为a ．（1）若M 为SB 的中点，证明：//SD 平面MAC ；（2）把正四面体S A B C ''''-与正四棱锥S ABCD -全等的两个面重合，排成一个新的几何体，问该几何体由多少个面组成？并说明理由．【答案】（1）证明见解析；（2）由5个面组成；理由见解析．。

福州一中2020届高三教学反馈检测试卷理科数学试卷

（1）解不等式 f (x) g(x) ；
（2）若 3 f (x) + g(x) ax + 4 对任意的实数 x 恒成立，求实数 a 的取值范围。
5
A. a b c
B. a c b
C. c a b
D. b c a
4. 已知 , 是两个不重合的平面，直线 AA1 = A, AA1 = A1 ，直线 BB1 = B ，
BB1 = B1 ， AA1 / /BB1 ， p : / / ， q : AA1 = BB1 ，则 p 是 q 的（）
ABC 的外接圆方程为 ( )
A． x2 + y2 + 6x − 4y −16 = 0
B． x2 + y2 + 6x −16 = 0
C． x2 + y2 + 5x − 6y −12 = 0
D． x2 + y2 − 4y −16 = 0
12.
已知函数
f (x) = aex
−
x
+
3e2 x ex − x
10. 在棱长为 6 的正方体 ABCD − A1B1C1D1 中，点 E 满足 BE = 2EC ，则三棱锥
D1 − AEC 的外接球的表面积是（）
A． 54
B. 70
C. 108
D.140
11．过点 A(−8, 4) 作抛物线 y2 = 8x 的两条切线 l1,l2 ，设 l1,l2 与 y 轴分别交于点 B,C ，则
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
5. A4 纸是由国际标准化组织的 ISO 216 定义的，其纸张尺
A

2020-2021学年高三数学(理科)教学质量检测试题及答案解析

最新普通高中高三教学质量监测理科数学注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

l ．已知集合A ＝{x ｜y ，B ＝{x ｜2x －1＞0}，则A ∩B ＝A ．（－∞，－1）B ．[0，1）C ．（1，＋∞）D ．[0，＋∞）2．已知复数z ＝2＋i ，则221z z z －－＝A ．1322i ＋B ．1322i －－C ．1122i －－D ．1122i ＋3．已知双曲线C ：22221x y a b－＝（a ＞0，b ＞0）的离心率为2，且经过点（2，则双曲线C 的标准方程为A ．22123x y －＝B ．22139x y －＝C ．22146x y －＝ D ．221x y －＝ 4．已知等差数列{n a }，满足a 1＋a 5＝6，a 2＋a 14＝26，则{n a }的前10项和S 10＝ A ．40 B ．120 C ．100 D ．805．下列命题中正确的是A ．x ＝1是2x －2x ＋1＝0的充分不必要条件B ．在△ABC 中，A ＞B 是cosA ＜cosB 的必要不充分条件 C ．n ∃∈N ﹡，22n ＋5n ＋2能被2整除是假命题D ．若p ∧（q ⌝）为假，p ∨（q ⌝）为真，则p ，q 同真或同假6．已知定义在R 上的函数f （x ）在[1，＋∞）上单调递增，且f （x ＋1）为偶函数，则 A ．f （0）＜f （12） B ．f （－2）＞f （2） C ．f （－1）＜f （3） D ．f （－4）＝f （4） 7．执行如图所示的程序框图，输出的结果是A ．56B ．36C ．54D ．648．若x ，y 满足不等式组2010080x y x y x y ⎧⎪⎨⎪⎩－＋＞－5＋≤＋－≤，则z ＝｜x －3｜＋2y 的最小值为A ．4B ．265C ．6D ． 79．某几何体的三视图如图所示，则该几何体的体积是A ．8＋73πB ．8＋83πC ．8＋103πD ．8＋3π10．已知函数f （x ）＝｜sinx ｜＋｜cosx ｜，则下列结论中错误的是 A ．f （x ）是周期函数 B ．f （x ）的对称轴方程为x ＝4k π，k ∈Z C ．f （x ）在区间（4π，34π）上为增函数D ．方程f （x ）＝65在区间[32π－，0]有6个根11．已知抛物线Γ：2x ＝8y 的焦点为F ，直线l 与抛物线Γ在第一象限相切于点P ，并且与直线y ＝－2及x 轴分别交于A 、B 两点，直线PF 与抛物线Γ的另一交点为Q ，过点B作BC ∥AF 交PF 于点C ，若｜PC ｜＝｜QF ｜，则｜PF ｜＝A 5 1B ．25C ．35D ．5512．若关于x 的不等式xlnx ＋x －kx ＋3k ＞0对任意x ＞1恒成立，则整数k 的最大值为 A ．4 B ．3 C ．2 D ．5第Ⅱ卷本卷包括必考题和选考题两部分。

2021年福建省福州市市第一中学高三数学理测试题含解析

2020-2021学年福建省福州市市第一中学高三数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1.已知△ABC的三个内角A,B、C所对的三边分别为a，b、c，若△ABC的面积则tan等于A．1/2 B．1/4C．1/8 D．1参考答案：答案：B2. ( )A． B． C． D．参考答案：C略3. 已知下图（1）中的图像对应的函数为，则下图（2）中的图像对应的函数在下列给出的四个式子中，只可能是（）A． B． C． D．参考答案：D略4. 早在公元前三百多年我国已经运用“以度审容”的科学方法，其中商鞅铜方升是公元前344年商鞅督造的一种标准量器，其三视图如图所示(单位：寸)，若π取3，其体积为12.6(立方寸)，则图中的x为A．1.2 B．1.6 C．1.8 D．2.4参考答案：B由三视图知，商鞅铜方升是由一个圆柱和一个长方体组合而成的，故其体积为，又故.故选B．5. 已知，则（）A. B. C. D.参考答案：D.考点：诱导公式.6. 某公司门前有一排9个车位的停车场，从左往右数第三个，第七个车位分别停着A车和B车，同时进来C，D两车，在C，D不相邻的条件下，C和D至少有一辆与A和B车相邻的概率是（）A．B．C． D．参考答案：B【考点】列举法计算基本事件数及事件发生的概率．【分析】先求出基本事件总数n==34，C和D至少有一辆与A和B车相邻的对立事件是C和D都不与A和B车相邻，由此能求出C和D至少有一辆与A和B车相邻的概率．【解答】解：某公司门前有一排9个车位的停车场，从左往右数第三个，第七个车位分别停着A车和B车，同时进来C，D两车，在C，D不相邻的条件下，基本事件总数n==34，C和D至少有一辆与A和B车相邻的对立事件是C和D都不与A和B车相邻，∴C和D至少有一辆与A和B车相邻的概率：p=1﹣=．故选：B．【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．7. 执行如图所示的程序框图，若输出，则框图中①处可以填入（）参考答案：C8. 下列选项中，说法正确的是( )A．命题“?x∈R，x2﹣x≤0”的否定是“?x∈R，x2﹣x＞0”B．命题“p∨q为真”是命题“p∧q为真”的充分不必要条件C．命题“若am2≤bm2，则a≤b”是假命题D．命题“在△ABC中，若sinA＜，则A＜”的逆否命题为真命题参考答案：C【考点】命题的真假判断与应用．【专题】简易逻辑．【分析】根据特称命题的否定，充要条件的定义，四种命题的关系，逐一分析四个答案是否成立，最后综合讨论结果，可得结论．【解答】解：对于A，命题“?x∈R，x2﹣x≤0”的否定是“?x∈R，x2﹣x＞0”，故错误；对于B，命题“p∨q为真”是命题“p∧q为真”的必要不充分条件，故错误；对于C，命题“若am2≤bm2，则a≤b”在m=0时，不一定成立，故是假命题，故正确；对于D，“在△ABC中，若sinA＜，则A＜或A＞”为假命题，故其逆否命题也为假命题，故错误；故选：C【点评】本题考查的知识点是命题的真假判断与应用，特称命题的否定，充要条件的定义，四种命题的关系，难度不大，属于基础题．9. 若函数，函数，则的最小值为（）A． B． C． D．参考答案：B【知识点】利用导数研究曲线上某点切线方程；利用导数求闭区间上函数的最值．B11 B12解析：设z=（x1﹣x2）2+（y1﹣y2）2，则z的几何意义是两条曲线上动点之间的距离的平方，求函数y=sin2x﹣（x∈[0，π]）的导数，f′（x）=2cos2x，直线y=x+3的斜率k=1，由f′（x）=2cos2x=1，即cos2x=，即2x=，解得x=，此时y=six2x﹣=﹣=0，即函数在（，0）处的切线和直线y=x+3平行，则最短距离d=，∴（x1﹣x2）2+（y1﹣y2）2的最小值d2=（）2=，故选：B【思路点拨】根据平移切线法，求出和直线y=x+3平行的切线方程或切点，利用点到直线的距离公式即可得到结论．10. （5分）若a，b，c为实数，且a＜b＜0，则下列命题正确的是（）A． ac2＜bc2 B．＜ C．＞ D． a2＞ab＞b2参考答案：D【考点】：不等式比较大小；不等关系与不等式．【专题】：不等式的解法及应用．【分析】：本题可以利用基本不等关系，判断选项中的命题是否正确，正确的可加以证明，错误的可以举反例判断，得到本题结论．解：选项A，∵c为实数，∴取c=0，ac2=0，bc2=0，此时ac2=bc2，故选项A不成立；选项B，=，∵a＜b＜0，∴b﹣a＞0，ab＞0，∴＞0，即，故选项B不成立；选项C，∵a＜b＜0，∴取a=﹣2，b=﹣1，则，，∴此时，故选项C 不成立；选项D ， ∵a＜b ＜0，∴a 2﹣ab=a （a ﹣b ）＞0， ∴a 2＞ab ．∴ab﹣b 2=b （a ﹣b ）＞0， ∴ab＞b 2．故选项D 正确，故选D ．【点评】：本题考查了基本不等关系，本题难度不大，属于基础题．二、填空题:本大题共7小题,每小题4分,共28分11. 为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则选择的3天恰好为连续3天的概率是（结构用最简分数表示）。

福建省福州第一中学2020届高三下学期开学质检数学(理)试题

福建省福州第一中学2020届高三下学期开学质检数学（理）试题注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、单选题1．已知全集U =R ，集合{|lg }A x y x ==, 集合{|1}B y y ==，那么U A C B ⋂= （）A ．φB ．(]0,1C ．()0,1D ．()1,+∞ 2．复数()2211i i +++的共轭复数是 A ．1i + B ．1i - C ．1i -+ D ．1i --3．下列命题中假命题是( )A ．∃x 0∈R ，ln x 0＜0B ．∀x ∈(－∞，0)，e x ＞x ＋1C ．∀x ＞0,5x ＞3xD ．∃x 0∈(0，＋∞)，x 0＜sin x 04．执行如图所示的程序框图，输出S 的值为（）A ．2log 101-B ．22log 31-C ．92D ．65．一次数学考试后，某老师从甲，乙两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学成绩的中位数为73，则x y -的值为（）A ．2B ．-2C ．3D ．-36．《中国诗词大会》（第二季）亮点颇多，十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下，百人团齐声朗诵，别有韵味．若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场，且《将进酒》排在《望岳》的前面，《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后，则后六场的排法有（） A ．288种 B ．144种 C ．720种 D ．360种7．在平面直角坐标系中，不等式组{x +y ≤0x −y ≤0x 2+y 2≤r 2(r 为常数)表示的平面区域的面积为π，若x ，y 满足上述约束条件，则z ＝x+y+1x+3的最小值为( ) A ．－1 B ．－5√2+17 C ．13 D ．－758．已知数列{}n a 的前n 项和为n S ，点(,3)n n S +*()n N ∈在函数32x y =⨯的图象上，等比数列{}n b 满足1n n n b b a ++=*()n N ∈，其前n 项和为n T ，则下列结论正确的是（）A ．2n n S T =B ．21n n T b =+C ．n n T a >D ．1n n T b +<9．双曲线2222:1(0,0)x y M a b a b-=>>的左、右焦点为1F ，2F ，抛物线N ：()220y px p =>的焦点为2F ，点P 为双曲线M 与抛物线N 的一个交点，若线段1PF 的中点在y 轴上，则该双曲线的离心率为（）A 1B 1C ．12D ．1210．已知函数1()cos 2626f x x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭，若存在123,,,,n x x x x 满足12306n x x x x π≤<<<<≤，且()()()()()()12231n n f x f x f x f x f x f x --+-++-()*122,n n N =≥∈，则n 的最小值为（）A ．6B ．10C ．8D ．1211．如图，点P 在正方体1111ABCD A B C D -的表面上运动，且P 到直线BC 与直线11C D 的距离相等，如果将正方体在平面内展开，那么动点P 的轨迹在展开图中的形状是（）A ．B ．C ．D ．12．已知函数22()1x f x e ax bx =-+-，其中,a b ∈R ，e 为自然对数的底数，若(1)0f =，'()f x 是()f x 的导函数，函数'()f x 在区间(0,1)内有两个零点，则a 的取值范围是（）A ．22(3,1)e e -+B ．2(3,)e -+∞C ．2(,22)e -∞+D ．22(26,22)e e -+ 第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题13．中国有个名句“运筹帷幄之中，决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如下表：表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推，例如6613用算筹表示就是：，则7288用算筹式可表示为__________.14．若随机变量()2~2,3X N ，且()()1P X P x a ≤=≥，则()52x a ax⎛+⋅ ⎝展开式中3x 项的系数是__________．15．已知P 是圆224x y +=上一点，且不在坐标轴上，(2,0)A ，(0,2)B ，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，则||2||AN BM +的最小值为__________． 16．如图，在ABC ∆中，三内角A ，B ，C 的对边分别为a ，b ，c ，且222a b c bc =++，a S 为ABC ∆的面积，圆O 是ABC ∆的外接圆，P 是圆O 上一动点，当cos S B C 取得最大值时，PA PB ⋅的最大值为_______.三、解答题17．已知等差数列{}n a 的前n 项和为n S ，且11a =，345S S S +=.（1）求数列{}n a 的通项公式；（2）令11(1)n n n n b a a -+=-，求数列{}n b 的前2n 项和2n T .18．如图，在四边形ABCD 中，//AB CD ，23BCD π∠=，四边形ACFE 为矩形，且CF ⊥平面ABCD ，AD CD BC CF ===.（1）求证：EF ⊥平面BCF ；（2）点M 在线段EF 上运动，当点M 在什么位置时，平面MAB 与平面FCB 所成锐二面角最大，并求此时二面角的余弦值.19．噪声污染已经成为影响人们身体健康和生活质量的严重问题，为了了解强度D （单位：分贝）与声音能量I （单位：2/W cm ）之间的关系，将测量得到的声音强度i D 和声音能量()1,2,,10i I i =数据作了初步处理，得到下面的散点图及一些统计量的值.表中lg i i W I =，101110i i W W ==∑ （1）根据表中数据，求声音强度D 关于声音能量I 的回归方程lg D a b I =+；（2）当声音强度大于60分贝时属于噪音，会产生噪声污染，城市中某点P 共受到两个声源的影响，这两个声源的声音能量分别是1I 和2I ，且10121410I I +=.已知点P 的声音能量等于声音能量1I 与2I 之和.请根据（1）中的回归方程，判断P 点是否受到噪声污染的干扰，并说明理由.附：对于一组数据()()()1122,,,,,n n v v v μμμ，其回归直线v αβμ=+的斜率和截距的最小二乘估计分别为：()()()121i i i i i u u u u v v u u β∧==--=-∑∑，v u αβ∧∧=-20．已知12P ⎫⎪⎭在椭圆2222:1(0)x y C a b a b+=>>上，F 为右焦点，PF x ⊥轴，,,,A B C D 为椭圆上的四个动点，且AC ，BD 交于原点O .（1）判断直线:()(,)2m n l x m n y m n R ++-=+∈与椭圆的位置关系；（2设()11,A x y ，()22,B x y 满足12124y y x x =，判断AB BC k k +的值是否为定值，若是，请求出此定值，并求出四边形ABCD 面积的最大值，否则说明理由.21．已知函数()()()21'0x f x ax x e f =+-+. （1）讨论函数()f x 的单调性；（2）若()()()ln ,x x g x e f x x h x e -=+=，过()0,0O 分别作曲线()y g x =与()y h x =的切线12,l l ，且1l 与2l 关于x 轴对称，求证: ()321222e e a e ++-<<-. 22．已知直线112:2x t l y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），以坐标原点为极点，x 轴的非负半轴为极轴且两坐标系中具有相同的长度单位，建立极坐标系，曲线C的极坐标方程为2sin (3)a a ρθ-=>-.（1）将曲线C 的极坐标方程化为直角坐标方程；（2）若曲线C 与直线l 有唯一公共点，求实数a 的值.23．已知0a >，0b >，记A =，B a b =+.（1B -的最大值；（2）若4ab =，是否存在,a b ，使得6A B +=？并说明理由.参考答案1．C【解析】【分析】先化简集合A 和B,再求U U C B A C B ⋂和.【详解】由题得A={x|x>0},B={y|y≥1}，所以{|1},(0,1)U U C B y y A C B =<∴⋂=.故答案为C【点睛】(1)本题主要考查集合的化简和运算，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 集合的运算要注意灵活运用维恩图和数轴，一般情况下，有限集的运算用维恩图分析，无限集的运算用数轴，这实际上是数形结合的思想的具体运用.2．B【解析】()()22121121112i i i i i ⋅-++=+-+=++ ，故其共轭复数是1i - ，选B 3．D 【解析】【分析】【详解】∃x 0∈R ，lnx 0＜0，的当x ∈（0，1）时，恒成立，所以正确；x ∈（﹣∞，0），令g （x ）＝e x ﹣x ﹣1，可得g ′（x ）＝e x ﹣1＜0，函数是减函数，g （x ）＞g （0）＝0，可得∀x ∈（﹣∞，0），e x ＞x +1恒成立，正确；由指数函数的性质的可知，∀x ＞0，5x ＞3x 正确；令f (x )＝sin x －x (x ＞0)，则f ′(x )＝cos x －1≤0，所以f (x )在(0，＋∞)上为减函数，所以f (x )＜f (0)，即f (x )＜0，即sin x ＜x (x ＞0)，故∀x ∈(0，＋∞)，sin x ＜x ，所以D 为假命题，故选D. 4．B【解析】【分析】【详解】第一次循环，23log 2S i =+=；第二次循环，223log log 3S i =+=；以此类推得第七次循环，222293log log log 3log ,82S i =++=+==；结束循环输出229log 2log 312=-，选B. 点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.5．D【解析】由茎叶图知727786(80)908157073x y +++++⎧=⎪⎨⎪+=⎩，解得0,3x y ==，所以3x y -=-，故选D .6．B【解析】【分析】根据题意分2步进行分析：①用倍分法分析《将进酒》，《望岳》和另外两首诗词的排法数目；②用插空法分析《山居秋暝》与《送杜少府之任蜀州》的排法数目，由分步计数原理计算可得答案【详解】根据题意分2步进行分析：①将《将进酒》，《望岳》和另外两首诗词的4首诗词全排列，则有4424A =种顺序《将进酒》排在《望岳》的前面，∴这4首诗词的排法有44122A =种 ②，这4首诗词排好后，不含最后，有4个空位，在4个空位中任选2个，安排《山居秋暝》与《送杜少府之任蜀州》，有3412A =种安排方法则后六场的排法有1212144⨯=种故选B 【点睛】本题考查的是有关限制条件的排列数的问题，第一需要注意先把不相邻的元素找出来，将剩下的排好，这里需要注意定序问题除阶乘，第二需要将不相邻的两个元素进行插空，利用分步计数原理求得结果，注意特殊元素特殊对待． 7．D 【解析】作出不等式组表示的平面区域，如图所示，由题意，知14πr 2=π，解得r =2．因为目标函数z =x+y+1x+3=1+y−2x+3表示区域内上的点与点P(−3,2)连线的斜率加上1，由图知当区域内的点与点P 的连线与圆相切时斜率最小．设切线方程为y −2=k(x +3)，即kx −y +3k +2=0，则有√k 2+1=2，解得k =−125或k =0（舍），所以z min =1−125=−75，故选D ．8．D 【解析】【分析】【详解】由题意可得：332,323n nn n S S +=⨯=⨯- ，由等比数列前n 项和的特点可得数列{}n a 是首项为3，公比为2的等比数列，数列的通项公式：132n n a -=⨯ ，设11n nb b q -= ，则：111132n n n b q b q --+=⨯ ，解得：11,2b q == ，数列{}n b 的通项公式12n nb -= ，由等比数列求和公式有：21nn T =- ，考查所给的选项：13,21,,n n n n n n n n S T T b T a T b +==-<< .本题选择D 选项. 9．B 【解析】【分析】先根据抛物线焦点为2F ，求得2p c =;再根据线段1PF 的中点在y 轴上，可得P 点横坐标，分析可知2PF x ⊥轴.由双曲线通经公式可得22PF p c ==，即可由勾股定理及双曲线定义得,a c 关系，进而求得离心率. 【详解】抛物线N ：()220y px p =>的焦点为2F则抛物线焦点为,02p ⎛⎫⎪⎝⎭，()2,0F c ，()1,0F c - 所以2pc =，即2p c =，因为线段1PF 的中点在y 轴上，所以P 点横坐标为c ，则2PF x ⊥轴所以22PF p c ==，即212PF F F =则12PF =根据双曲线定义可知122PF PF a -=所以22c a -=解得1ce a ===故选:B 【点睛】本题考查了双曲线离心率的求法，抛物线焦点与双曲线焦点的关系，双曲线的几何意义，中点坐标公式的应用，属于中档题. 10．C 【解析】【分析】由辅助角公式先将函数()f x 化简，当()()()()1max min n n f x f x f x f x --=-时n 取得最小值，由正弦函数的性质即可求得n x 的值即可求解. 【详解】函数1()sin cos 2626f x x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭，根据助辅助角公式化简可得 ()sin sin 66f x x x ππ⎛⎫=+-= ⎪⎝⎭因为()()()()1max min 2n n f x f x f x f x --=-= 所以当()()()()()()12231n n f x f x f x f x f x f x --+-++-()*122,n n N =≥∈时，n 的取值满足12330,,22x x x ππ===，4557,22x x ππ==，678911,,622x x x πππ=== 所以此时n 的最小值为8 故选:C 【点睛】本题考查了正弦函数的图像与性质应用，辅助角化简三角函数式的应用，属于中档题. 11．B 【解析】在平面BCC 1B 1上，P 到直线C 1D 1的距离为|PC 1|，∵P 到直线BC 与直线C 1D 1的距离相等， ∴点P 到点C 1的距离与到直线BC 的距离相等， ∴轨迹为抛物线,且点C 1为焦点，BC 为准线；故排除C，D，同理可得，在平面ABB1A1上，点P到点B的距离与到直线C1D1的距离相等，从而排除A，本题选择B选项.12．A【解析】【分析】利用f（1）＝0得出a，b的关系，根据f′（x）＝0有两解可知y＝2e2x与y＝2ax+a+1﹣e2的函数图象在（0，1）上有两个交点，做出两函数图象，根据图象判断a的范围．【详解】解：∵f（1）＝0，∴e2﹣a+b﹣1＝0，∴b＝﹣e2+a+1，∴f（x）＝e2x﹣ax2+（﹣e2+a+1）x﹣1，∴f′（x）＝2e2x﹣2ax﹣e2+a+1，令f′（x）＝0得2e2x＝2ax﹣a﹣1+e2，∵函数f′（x）在区间（0，1）内有两个零点，∴y＝2e2x与y＝2ax﹣a﹣1+e2的函数图象在（0，1）上有两个交点，作出y＝2e2x与y＝2ax﹣a﹣1+e2＝a（2x﹣1）+e2﹣1函数图象，如图所示：若直线y＝2ax﹣a﹣1+e2经过点（1，2e2），则a＝e2+1，若直线y＝2ax﹣a﹣1+e2经过点（0，2），则a＝e2﹣3，∴e2﹣3＜a＜e2+1．故选：A ．点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解． 13．【解析】【分析】根据题意，分别用横式或纵式表示出7288的各位数字，合并后即可得解. 【详解】根据题意， 7288用算筹式表示时: 千位需要用横式表示，即7用来表示; 百位需要用纵式表示，即2用来表示; 十位需要用横式表示，即8用来表示; 个位需要用纵式表示，即8用来表示. 所以7288用算筹式可表示为；故答案为:.【点睛】本题考查了数学在中国传统文化中的应用，对所给条件分析清晰，进行合理运用，属于基础题. 14．1620 【解析】随机变量()2~2,3X N ，均值是2，且()()1P X P x a ≤=≥，∴3a =；∴()()()55522233693x a ax x x x x x⎛⎛⎛+=+-=++ ⎝⎝⎝；又53x⎛- ⎝展开式的通项公式为()()35552155313rrr r r r r r T C x C x ---+⎛=⋅⋅=-⋅⋅⋅ ⎝，令3512r -=，解得83r =，不合题意，舍去；令3522r -=，解得2r ，对应2x 的系数为()232512270C -⋅⋅=；令3532r -=，解得43r =，不合题意，舍去；∴展开式中3x 项的系数是62701620⨯=，故答案为1620.点睛：本题考查了正态分布曲线的特点及其几何意义，也考查二项式系数的性质与应用问题，是基础题；根据正态分布的概率性质求出a 的值，再化()()5522693x a ax x x x ⎛⎛+=++- ⎝⎝；利用(53x ⎛- ⎝展开式的通项公式求出含2x 的系数，即可求出对应项的系数. 15．8 【解析】设点(2cos ,2sin )P θθ，则直线PA 的方程：sin (2)cos 1y x θθ=--，则2sin (0,)cos 1M θθ--同理2cos (,0)sin 1N θθ--，则2AN BM +2cos 4sin 6sin 1cos 1θθθθ=++--的最小值为8.16．32+【解析】试题分析：∵222a b c bc =++，∴2221cos 22b c a A bc +-==-，∴23A π=，设圆O 的半径为R，则222sin sin 3a R A π===，∴1R =，∴1cos sin cos 2S B C bc A B C =cos B C =+sin cos )B C B C B C ==-，当6B C π==时，cos S B C +取得最大值，建立如图直角坐标系，则(0,1)A，1()2B，1)2C ，设(cos ,sin )P θθ，则1(cos ,sin 1)(cos )2PA PB θθθθ⋅=-+-333cos sin )22223πθθθ=-+=++，当且仅当cos()13πθ+=时，PA PB ⋅取最大值32考点：1.正余弦定理解三角形；2.三角恒等变形；3.平面向量数量积的坐标运算. 17．（Ⅰ）21n a n =-（Ⅱ）284n n -- 【解析】试题分析: （Ⅰ）求等差数列通项公式,一般方法为待定系数法,即根据条件列出关于首项与公差的方程组,解出首项与公差再代入通项公式即可,（Ⅱ）涉及符号数列求和,一般方法为分组求和,即按奇偶,项的正负重新组合,利用平方差公式转化为求特殊数列(如等差数列)的和.试题解析: （Ⅰ）设等差数列{}n a 的公差为d ，由345S S S +=可得1235a a a a ++=，即253a a =，所以3(1)14d d +=+，解得2d =．∴ 1(1)221n a n n =+-⨯=-．（Ⅱ）由（Ⅰ）可得：112(1)(21)(21)(1)(41)n n n b n n n --=-⋅-+=-⋅-.∴ 22222122(411)(421)(431)(441)(1)4(2)1n n T n -⎡⎤=⨯--⨯-+⨯--⨯-++-⋅⨯-⎣⎦22222241234(21)(2)n n ⎡⎤=-+-++--⎣⎦22(21)4(1234212)4842n n n n n n +=-+++++-+=-⨯=--．点睛：本题采用分组转化法求和，即通过两个一组进行重新组合，将原数列转化为一个等差数列. 分组转化法求和的常见类型有分段型（如,{2,n n n n a n =为奇数为偶数）及本题的符号型（如2(1)n n a n =- ）18．（1）见解析；（2【解析】【分析】【详解】试题分析：（Ⅰ）在梯形ABCD 中，设1AD CD BC ===，题意求得2AB =,再由余弦定理求得23AB =,满足222AB AC BC =+,得则BC AC ⊥.再由CF ⊥平面ABCD 得AC CF ⊥，由线面垂直的判定可.进一步得到AC 丄平面BCF ;（Ⅱ）分别以直线,,CA CB CF 为:x 轴，y 轴轴建立如图所示的空间直角坐标系，设1AD CD CF === ,令FM λ=(0λ≤≤得到,,,C A B M 的坐标，求出平面MAB 的一法向量.由题意可得平面的FCD 一个法向量，求出两法向量所成角的余弦值，可得当λ0=时，,此时点M 与点F 重合.试题解析：（Ⅰ）证明：在梯形ABCD 中，∵//AB CD ,设1AD CD BC ===，又∵23BCD π∠=,∴2AB =,∴2222cos603AC AB BC AB BC =+-⋅⋅︒= ∴222AB AC BC =+.则BC AC ⊥. ∵CF ⊥平面ABCD ,AC ⊂平面ABCD ， ∴AC CF ⊥,而CFBC C =,∴AC ⊥平面BCF .∵//EF AC ,∴EF ⊥平面BCF .（Ⅱ）解：分别以直线,,CA CB CF 为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，设1AD CD BC CD ====，令(0FM λλ=≤≤，则())()()0,0,0,,0,1,0,,0,1C AB M λ，∴()()3,1,0,,1,1AB BM λ=-=- 设(),,n x y z =为平面MAB 的一个法向量，由00n AB n BM ⎧⋅=⎨⋅=⎩得300x y x y z λ⎧-+=⎪⎨-+=⎪⎩，取1x=，则()1,3,n λ=，∵()1,0,0m =是平面FCB 的一个法向量，∴1cos ,13n m n m n m⋅===+∵03λ≤≤，∴当0λ=时，cos θ有最小值为7， ∴点M 与点F 重合时，平面MAB 与平面FCB 所成二面角最大，此时二面角的余弦值为. 19．（1）10lg 160.7i D I =+（2）会受到干扰,理由见解析. 【解析】【分析】（1）令lg i i W I =，建立D 与W 的线性回归方程，结合所给公式求得b .代入样本中心点求得a ，即可得声音强度D 关于声音能量I 的回归方程.（2）由点12P I I =+，结合10121410I I +=，利用基本不等式求得点P 能量的最小值.由（1）得声音强度D 的预报值，比较大小即可判断. 【详解】（1）令lg i i W I =，则i D a bW =+由表中参考数据可得()()()10110215.1100.51i i i i i W W D D b W W==--===-∑∑ 将45.7,11.5D W ==-代入i D a bW =+ 可得()45.71011.5160.7a D bW =-=+⨯-= 所以10160.7D W =+即声音强度D 关于声音能量I 的回归方程为10lg 160.7i D I =+ （2）已知点P 的声音能量等于声音能量1I 与2I 之和，所以12P I I =+而10121410I I +=，即101214101I I -⎛⎫⨯+= ⎪⎝⎭所以12P I I =+()1012121410I I I I -⎛⎫=+⨯⨯+ ⎪⎝⎭1021124105I I I I -⎛⎫=⨯++ ⎪⎝⎭10910-≥⨯由（1）可知点P 的声音强度预报值为()10min 10lg 910160.710lg960.760D -=⨯+=+>所以点P 会受到噪声污染的干扰【点睛】本题考查了非线性回归方程的求法，利用线性回归方程进行预报与判断，属于中档题. 20．（1）直线l 与椭圆相切或相交.（2）AB BC k k +的值是定值，0AB BC k k +=；()max 1ABCD S = 【解析】【分析】（1）将直线l 变形，可确定直线l 所过定点的坐标，可得该定点坐标在椭圆上，即可判断出直线l 与椭圆的位置关系.（2）先根据条件，求得椭圆的标准方程.讨论直线AB 的斜率情况可知当斜率不存在或斜率为0时不满足12124y y x x =.进而设直线AB 的方程为y kx m =+，联立椭圆方程，利用韦达定理及等式12124y y x x =，化简即可求得k 的值，确定AB BC k k +为定值；由点到直线距离公式求得d ，利用弦长公式求得AB ，即可用m 表示出AOB S ∆，由二次函数性质求得AOB S ∆的最大值，并根据4ABCD AOB S ∆=即可求得ABCD S 的最大值. 【详解】（1）直线11:()(,)222m n l x m n y m n m n R ++-=+∈，将直线方程化简变形可得022x x y m y n ⎛⎛++--= ⎝⎭⎝⎭，因为,m n R ∈，令10221022x y x y ⎧+-=⎪⎪⎨⎪--=⎪⎩，解得12x y ⎧=⎪⎨=⎪⎩ ，所以直线l过定点12P ⎫⎪⎭，而由P 在椭圆上，可知直线l 与椭圆相切或相交.（2）12P ⎫⎪⎭在椭圆2222:1(0)x yC a b a b+=>>上，PF x ⊥轴，由椭圆性质可得212b c a ==，则222212c b aa b c ⎧=⎪⎪=⎨⎪=+⎪⎩解得2,1a b == ，所以椭圆的标准方程为2214x y +=，因为()11,A x y ，()22,B x y ，,,,A B C D 为椭圆上的四个动点且AC ，BD 交于原点O .所以()11,C x y --，()22,D x y --，当直线AB 的斜率不存在时，不满足12124y y x x =，因而直线AB 的斜率一定存在. 当直线AB 斜率存在且为0时，不满足12124y y x x =，所以直线AB 的斜率一定存在且不为0.设直线AB 的方程为y kx m =+.则2214y kx m x y =+⎧⎪⎨+=⎪⎩，化简可得()()222418410k x kmx m +++-=，所以()2121222418,4141m km x x x x k k -+=-⋅=++，()()()()2222284414416410,km k m k m ∆=-+-=-+>①因为1122,kx m y kx m y =+=+，所以()()()2212121212y y kx m kx m k x x km x x m =++=+++，则()()2222222414184414141m m km k km m k k k ⎡⎤--⎛⎫⎢⎥⨯+⨯-+= ⎪⎢⎥+++⎝⎭⎢⎥⎣⎦，整理可得241k =，解得12k =±.由题意可知A B C D 、、、的位置等价，所以不妨设12AB k =，则12BC k =-，则11022AB BC k k +=-=，即AB BC k k +为定值.直线AB 的方程为12y x m =+.即102x y m -+= 则点O 到直线AB的距离为d =因为()2121222418,4141m km x x x x k k -+=-⋅=++代入可得()212122,21x x m x x m +=-⋅=-则由弦长公式可得AB =所以1122AOB S AB d ∆=⋅⋅====当21m =时取等号.而21m =时满足①. 所以()max 1AOB S ∆= 此时44ABCD AOB S ∆==故四边形ABCD 面积的最大值的最大值为4 【点睛】本题考查了直线过定点的求法，直线与椭圆位置关系的判断，椭圆标准方程的求法，韦达定理在求弦长公式中的应用，椭圆中的四边形面积问题综合应用，属于难题. 21．(1)见解析；(2) 见解析.【解析】试题分析：(1) 求出()'f x ，分五种情讨论，分别令()'0f x >得增区间， ()'0f x <得减区间；（2）根据导数的几何意义可求出两切线的斜率分别为,e e -，根据切点处两函数纵坐标相等可得关于1,x a 的两个等式，由其中一个等式求得1x 的范围，再根据另一个等式利用导数求得a 的范围. 试题解析：由已知得()()()2'21,'00xf x ax a x e f ⎡⎤=++=⎣⎦，所以()()21x f x ax x e =+-.(1) ()()()2'2121x xf x ax a x e x ax a e ⎡⎤⎡⎤=++=++⎣⎦⎣⎦. ① 若0a >，当12x a<--或0x >时， ()'0f x >；当120x a--<<时， ()'0f x <，所以()f x 的单调递增区间为()1,2,0,a ⎛⎫-∞--+∞ ⎪⎝⎭；单调递减区间为12,0a ⎛⎫-- ⎪⎝⎭. ②若()()()0,1,'x x a f x x e f x xe ==-=，当0x >时，()'0f x >；当0x <时， ()'0f x <，所以()f x 的单调递增区间为()0,+∞；单调递减区间为(),0-∞. ③ 若102a -<<，当12x a>--或0x <时， ()'0f x <；当102x a <<--时， ()'0f x >，所以()f x 的单调递增区间为10,2a ⎛⎫-- ⎪⎝⎭；单调递减区间为()1,0,2,a ⎛⎫-∞--+∞ ⎪⎝⎭.④若()211,'022x a f x x e =-=-≤，故()f x 的单调递减区间为(),-∞+∞.⑤若12a <-，当12x a<--或0x >时， ()'0f x <；当120x a --<<时， ()'0f x >，所以()f x 的单调递增区间为12,0a ⎛⎫-- ⎪⎝⎭；单调递减区间为()1,2,0,a ⎛⎫-∞--+∞ ⎪⎝⎭.当0a >时， ()f x 的单调递增区间为()1,2,0,a ⎛⎫-∞--+∞ ⎪⎝⎭；单调递减区间为12,0a ⎛⎫--⎪⎝⎭. 当0a =时， ()f x 的单调递增区间为()0,+∞；单调递减区间为(),0-∞.当102a -<<时， ()f x 的单调递增区间为10,2a ⎛⎫-- ⎪⎝⎭；单调递减区间为()1,0,2,a ⎛⎫-∞--+∞ ⎪⎝⎭. 当12a =-时， ()f x 的单调递减区间为(),-∞+∞；当12a <-时， ()f x 单调递增区间为12,0a ⎛⎫-- ⎪⎝⎭ ；单调递减区间为1,2a ⎛⎫-∞-- ⎪⎝⎭,()0,+∞；(2) ()()()22ln 1ln 1ln x x x g x e f x x e ax x e x ax x x --=+=-+-+=+-+,设2l 的方程为2y k x =，切点为()22,x y ，则222222,x x y y e k e x ===，所以2221,,x y e k e ===.由题意知12k k e =-=-，所以1l 的方程为y ex =-，设1l 与()y g x =的切点为()11,x y ，则()111121111111'21,22y e k g x ax e a x x x x +==++==-=--. 又2111111ln y ax x x ex =++-+=-,即1113ln 022e x x ++-=，令()()1311ln ,'222e e u x x x u x x++=+-=+，在定义域上， ()'0u x >，所以()0,+∞上， ()u x 是单调递增函数，又()2310,ln 021212e e ee u u e e -⎛⎫=>=+-< ⎪++⎝⎭，所以()1?01e u u e ⎛⎫< ⎪+⎝⎭，即111e x e <<+，令11t x =，则()()2111,12e t a t t e t e +⎡⎤<<=-++⎣⎦，所以()()32112,122e e e a a a a e e +++⎛⎫>=-<=- ⎪⎝⎭，故 ()321222e e a e ++-<<-. 【方法点睛】本题主要考查利用导数研究函数的单调性以及不等式的证明，属于难题.不等式证明问题是近年高考命题的热点，命题主要是和导数、绝对值不等式及柯西不等式相结合，导数部分一旦出该类型题往往难度较大，要准确解答首先观察不等式特点，结合已解答的问题把要证的不等式变形，并运用已证结论先行放缩，然后再化简或者进一步利用导数证明.22．（1）(223y x a -+=+,()3a >- （2）94a =-【解析】【分析】（1）由极坐标方程与直角坐标方程转化公式，代入即可得解.（2）将直线参数方程化为普通方程，利用直线与圆相切的性质即可求得a 的值. 【详解】（1）曲线C的极坐标方程为2sin (3)a a ρθ-=>-.化为直角坐标方程可得22a y x -=+化为标准方程可得(223y x a -+=+，()3a >-（2）直线112:x t l y ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数），0y -= 由（1）可知曲线C:(223y x a +=+为圆因为曲线C 与直线l 有唯一公共点，由点到直线距离公式可知d ==解得94a =- 【点睛】本题考查了极坐标与直角坐标方程的转化，参数方程化为普通方程，直线与圆的位置关系应用，属于中档题.23．（1）1 （2）存在,理由见解析. 【解析】【分析】（1）将A =，B a b =+B -中，配成二次函数形式，结合二次函数性质即可求得最大值.（2）假设存在,a b ，使得6A B +=和4ab =,x y ==将方程组化简后再令,t x y =+可得关于t 的一元二次不等式.结合判别式即可判断是否存在正数解，即可判断是否存在,a b .【详解】（1）0a >，0b >，记A =+，B a b =+B -()a b =-+a b =--+221212-+≤⎭⎭=- 当且仅当12a b ==时取等号B -的最大值为1（2）存在,a b ，使得6A B +=.理由如下: 假设存在,a b ，使得6A B +=.则64A B a b ab ⎧+=+=⎪⎨=⎪⎩,0,0x y x y ==>>则方程组可化为2262x y x y xy ⎧+++=⎨=⎩令,0t x y t =+>将上述方程组化为2100t t +-=则1410410∆=+⨯=>且12100t t =-<所以2100t t +-=由正实数根，即存在正数t 满足方程因此存在,x y 使得t 为正数也就是存在,a b ，使得6A B +=，4ab =同时成立【点睛】本题考查了方程和不等式的综合应用，由二次函数性质求最值，一元二次方程的根与判别式关系的应用，属于中档题.。

福建省福州第一中学2020届高三下学期教学反馈检测数学(理)试题(含答案)

1 / 15福州一中2020届高三教学反馈检测理科数学试卷本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分满分150分，考试时间120分钟第I 卷一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1.已知i 是虚数单位，若32i a z i+=+是纯虚数，则实数a=() A.1B.12C.12-D.-22.已知向量,a b r r 满足2||1,||2,()3a b a b ==+=r r r r ，则||a b -=r r ()C.3D.73.已知0.5lg 0.5,,0.5e a b e c ===,e 为自然对数的底数，则() A.a<b<cB.a<c<bC.c<a<bD.b<c<a4.已知α，β是两个不重合的平面，直线111,AA A AA A αβ⋂=⋂=，直线1BB B α⋂=,111111,//,://,:BB B AA BB p q AA BB βαβ⋂==，则p 是q 的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.A4纸是由国际标准化组织的ISO216定义的，其纸张尺寸的长宽比都是2:1,这种规格的纸张不管对折多少次，都仍是长宽比还是2:1的长方形，世界上多数国家所使用的纸张尺寸都是采用这一国际标准。

如图是一个A4尺寸的长方形工ABCD 内接于一个半圆，AB>AD,在这个半圆中随机取一点，此点取自长方形ABCD 区域的概率P=22 32 42 2 6.若将函数()2sin(2)02f x x πθθ⎛⎫=+<< ⎪⎝⎭图象上的每一个点都向左平移π6个单位，得到y =g(x)的图象，若函数y=g(x)是偶函数，则函数y=g(x)的单调递减区间为() A.,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦ B.,()222k k k Z πππ⎡⎤+∈⎢⎥⎣⎦ C.,()222k k k Z πππ⎡⎤-∈⎢⎥⎣⎦ D.,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦7.211++A.1A A =+B.1A A =C.2A A =D.2A A =+8.已知数列{}{}*,,n n a b n N ∈都是公差为1的等差数列，且*11113,,a b a b N +=∈,设()*n n a c b n N =∈，则数列{c n }的前7项和等于（）A.17B.26C.35D.44 9.奥运会乒乓球单打的淘汰赛采用七局四胜制，猜先后由一方先发球，双方轮流先发球，当一方赢得四局胜利时，该方获胜，比赛结束，现有甲、乙两人比赛，根据前期比赛成绩，单局甲先发球并取胜的概率为0.8，乙先发球并取胜的概率为0.4，且各局比赛的结果相互独立；如果第一局由乙先发球，则甲以4:0获胜的概率是（）A.0.1024B.0.2304C.0.2048D.0.460810.在棱长为6的正方体ABCD-A 1B 1C 1D 1中，点E 满足2BE EC =u u u r u u u r ，则三棱锥D 1-AEC 的外接球的表面积是（）A.54πB.70πC.108πD.140π 11.过点A （-8,4）作抛物线y 2=8x 的两条切线l 1,l 2，设l 1,12与y 轴分别交于点B,C ，则△ABC 的外接圆方程为（）A.x 2+y 2+6x-4y-16=0B.x 2+y 2+6x-16=0C.x 2+y 2+5x-6y-12=0D.x 2+y 2-4y-16=0 12.已知函数23()xxx e f x ae x e x =-+-有三个不同的零点123,,x x x ,且123x x x <<，则3122312111x x x x x x e e e ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为（） A.1B.3C.4D.9第Ⅱ卷二、填空题：本题共4小题，每小题5分，共20分。

福建省福州一中2021届高三数学5月校质检理(1)

福建省福州一中数学(理科)本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部份（总分值150分考试时刻120分钟）第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每题5分，共50分．在每题给出的四个选项中有且只有一项为哪一项符合题目要求的，把答案填在答题卡的相应位置．） 1. 已知命题p ：x R ∃∈，21x =．那么p ⌝是A ．x R ∀∉，21x ≠ B. x R ∀∈，21x ≠ C ．x R ∃∉，21x ≠D. x R ∃∈，21x ≠2. 设集合{}1,1M =-，{}2N a =，那么“1a =”是“MN M =”的A ．充分没必要要条件B ．必要不充分条件C ．充分必要条件D ．既不充分又没必要要条件3. 执行如下图的程序框图，假设输入A 的值为2，那么输出的P 值为A ．2B ．3C ．4D ．54. 设变量,x y 知足约束条件01030y x y x y ≥⎧⎪-+≥⎨⎪+-≤⎩，那么2z x y =+的最大值为A.2-B. 3C. 4D. 65. 在等差数列{}n a 中，已知1232,13,a a a =+=则456a a a ++等于A ．40B ．42C ．43D ．456. 若2sin 44πα⎛⎫+= ⎪⎝⎭，那么sin2α等于 A ．34 B ．34- C ．12 D ．12- 7. 函数()412x xf x +=的图象A ．关于y 轴对称B ．关于x 轴对称C ．关于直线y x =对称D ．关于原点对称8. 已知平面α外不共线的三点,,A B C 到α的距离都相等，那么正确的结论是A ．平面ABC 必平行于αB ．平面ABC 必与α相交C ．平面ABC 必不垂直于αD ．存在ABC ∆的一条中位线平行于α或在α内9. 已知共核心的椭圆和双曲线，核心为12,F F ，记它们其中的一个交点为P ，且12120F PF ∠=，那么该椭圆离心率1e 与双曲线离心率2e 必然知足的关系式为A ．1213144e e += B. 221231144e e += C ．221231144e e += D. 221213144e e += 10．设12,,,n A A A 为集合{}1,2,,S n =的n 个不同子集()4n ≥，为了表示这些子集，作n 行n 列的数阵，规定第i 行与第j 列的数为0,,1,,j ij j i A a i A ∉⎧⎪=⎨∈⎪⎩ 那么以下说法正确的个数是①数阵中第1列的数满是0当且仅当1A =∅; ②数阵中第n 列的数满是1当且仅当n A S =; ③数阵中第j 行的数字和说明元素j 属于12,,,n A A A 中的几个子集;④数阵中所有的2n 个数字之和不小于n ; ⑤数阵中所有的2n 个数字之和不大于21n n -+.A ．2 B. 3 C ．4 D. 5 第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，每题4分，共20分．把答案填在答题卡的相应位置． 11．假设复数1iz i=+，那么z 的共轭复数z ＝___________. 12．已知多项式()()()22012111nn n x x x b b x b x b x ++++++=++++，且知足12n b b b +++26=，那么正整数n 的一个可能值为___________.13．已知圆22:440C x y x y +--=，直线:36230l x y ++-=，在圆C 上任取一点A ，那么点A 到直线l 的距离小于2的概率为________． 14. 已知()ln ln 1x x x '=+，那么1ln exdx =⎰___________.知15.已知两个非零向量a 和b 所成的角为()0θθπ≤≤，规定向量c a b =⨯，足：（1）模：sin c a b θ=；（2）方向：向量c 的方向垂直于向量a 和b （向量a 和b 组成的平面），且符合“右手定那么”：用右手的四指表示向量a 的方向，然后手指朝着手心的方向摆动角度θ到向量b 的方向，大拇指所指的方向确实是向量c 的方向.如此的运算就叫向量的叉乘，又叫外积、向量积. 关于向量的叉乘运算，以下说法正确的选项是___________.①0a a ⨯=; ②0a b ⨯=等价于a 和b 共线; ③叉乘运算知足互换律，即a b b a ⨯=⨯;④叉乘运算知足数乘结合律，即()()()a b a b a b λλλ⨯=⨯=⨯.三、解答题：本大题共6小题，共80分．解答写在答题卡相应位置，应写出文字说明、证明进程或演算步骤． 16．（本小题总分值13分）某学校随机抽取部份新生调查其上学所需时刻（单位：分钟），并将所得数据绘制成频率散布直方图（如图），其中上学所需时刻的范围是[]100,0，样本数据分组为[)20,0，[)40,20，[)60,40，[)80,60，[]100,80，学校规定上学所需时刻不小于1小时的学生能够申请在学校住宿. （Ⅰ）求频率散布直方图中x 的值；（Ⅱ）依照频率散布直方图估量样本数据的中位数；（Ⅲ）用那个样本的频率散布估量整体散布，将频率视为概率，从能够住宿的学生当中随机抽取3人，记ξ为其中上学所需时刻不低于80分钟的人数，求ξ的散布列及其数学期望. 17. （本小题总分值13分）已知几何体A BCED -的三视图如下图，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（Ⅰ）求二面角E AD B --的余弦值;（Ⅱ）试探讨在棱DE 上是不是存在点Q ，使得 AQ BQ ⊥，假设存在，求出DQ 的长；假设不存在，请说明说明理由. 18. （本小题总分值13分）如图，直角三角形ABC 中，90B ∠=，1,3AB BC ==．点,M N 别离在边AB 和AC 上(M 点和B 点不重合)，将AMN ∆沿MN 翻折，AMN ∆变成A MN '∆，使极点A '落在边BC 上(A '点和B 点不重合).设AMN θ∠=．（Ⅰ）用θ表示线段AM 的长度，并写出θ的取值范围；（Ⅱ）求线段A N '长度的最小值． 19. （本小题总分值13分）已知抛物线C 的极点为坐标原点,其核心()(),00F c c >到直线l 20x y -+=的距离为322. （Ⅰ）求抛物线C 的方程;（Ⅱ）若M 是抛物线C 上异于原点的任意一点，圆M 与y 轴相切. （i ）试证：存在必然圆N 与圆M 相外切，并求出圆N 的方程；（ii ）假设点P 是直线l 上任意一点，,A B 是圆N 上两点，且AB BN λ=，求PA PB ⋅的取值范围. 20. （本小题总分值14分）已知函数()ln f x ax x x =+的图象在点x e =(e 为自然对数的底数)处的切线斜率为3．（Ⅰ）求实数a 的值；（Ⅱ）假设k Z ∈，且()f x kx k >-对任意1x >恒成立，求k 的最大值；（III ）假设()*2ln 23ln3ln 3,k a k k k k N =+++≥∈，证明：311nk ka =<∑()*,n k n N ≥∈． 21. 此题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，总分值14分．若是多做，那么按所做的前两题记分．作答时，先用2B 铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．（1）（本小题总分值7分）选修4-2：矩阵与变换已知矩阵2413M ⎛⎫=⎪⎝⎭，2010N ⎛⎫= ⎪⎝⎭，（Ⅰ）求二阶矩阵X ，使MX N =；（Ⅱ）求圆221xy 在矩阵X 变换下的曲线方程.（2）（本小题总分值7分）选修4-4：坐标系与参数方程在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建坐标系,已知曲线()2:sin2cos 0C a a ρθθ=>，已知过点()2,4P --的直线l的参数方程为：()2242x t y t ⎧=-+⎪⎪⎨⎪=-+⎪⎩是参数，直线l 与曲线C 别离交于,M N ．（Ⅰ）写出曲线C 和直线l 的一般方程；（Ⅱ）若,,PM MN PN 成等比数列，求a 的值．（3）（本小题总分值7分）选修4-5：不等式选讲已知,a b 为正实数.（Ⅰ）求证22a b a b b a+≥+；（Ⅱ）利用（Ⅰ）的结论求函数()()221011x x y x xx-=+<<-的最小值.福州一中高考模拟数学试卷（2021年5月）参考答案（理科）一．选择题 BACDB BADCC 二．填空题 11.12i -；12. 4；13. 14；14. 1；15. ①②④ 三．解答题16.解：（I ）由直方图可得：200.025200.0065200.0032201x ⨯+⨯+⨯+⨯⨯=.因此0.0125x. …………………………………3分（II ）设中位数为y ，那么()200.0125200.0250.5y ⨯+-⨯=，解得30y =因其中位数估量为30分钟. .……………6分（III ）依题意得13,2B ξ⎛⎫⎪⎝⎭，ξ的所有可能取值为0,1,2,3, .……………7分 ()311328P ξ⎛⎫=== ⎪⎝⎭.……………11分因此ξ的散布列为ξ 0 1 2 3P18 38 38 18因此ξ的数学期望是13322E ξ=⨯=..……………13分17. 解：（I ）由三视图知，,,CA CB CE 两两两垂直，以C 为原点，以,,CA CB CE所在直线为,,x y z 轴成立空间直角坐标系．……………1分则A （4，0，0），B （0，4，0），D （0，4，1），E （0，0，4）∴(0,4,3),(4,4,0)DE AB =-=-，x()()4,4,1,0,0,1DA BD =--=……………3分设面ADE 的法向量为(),,n x y z =，面ABD 的法向量为(),,m x y z '''=那么有00n DE n DA ⎧⋅=⎪⎨⋅=⎪⎩，即430440y z x y z -+=⎧⎨--=⎩，取1z =得31,,14n ⎛⎫= ⎪⎝⎭，m AB m BD ⎧⋅=⎪⎨⋅=⎪⎩，即4400x y z -+=⎧⎨=⎩，取1x =得()1,1,0m =，……………… 6分设二面角E AD B --的大小为θ，由图可知θ为钝角故317824cos cos ,8241216n m n m n mθ+⋅=-=-=-=-⋅∴二面角E AD B --的余弦值为78282-．…………………………… 8分（II ）∵点Q 在棱DE 上，∴存在()01λλ≤≤使得DQ DE λ=………………… 9分同理()4,44,31AQ λλ=--+………………… 11分即()()()2444+3+1=0λλλ--解得15λ=因此知足题设的点Q 存在，DQ 的长为1.…………………………13分 18. 解：（I ）设MA MA x '==，那么1MB x =-．在Rt MBA '∆中，()1cos 2xxπθ--=， …………………………………2分 ∴2111cos22sin MA x θθ===-． …………………………………4分 ∵点M 在线段AB 上，M 点和B 点不重合，A '点和B 点不重合， ∴42ππθ⎛⎫∈⎪⎝⎭，．…………………………………5分（II ）在AMN ∆中，23ANM πθ∠=- 2sin sin 3ANMAπθθ=⎛⎫- ⎪⎝⎭,21sin sin 12sin 222sin sin 2sin sin 333MA AN θθθπππθθθθ⋅===⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．…………… 8分令22132sin sin 2sin sin cos sin 3sin cos 322t πθθθθθθθθ⎛⎫⎛⎫=-=+=+ ⎪ ⎪⎝⎭⎝⎭1311sin 2cos2sin 222226πθθθ⎛⎫=+-=+- ⎪⎝⎭………………… 11分 ∵42ππθ<<， ∴52366πππθ<-<．当且仅当262ππθ-=，即3πθ=时， t 有最大值32. ∴3πθ=时，AN '有最小值23．………………… 13分 19.解：(Ⅰ) 依题意,设抛物线C 的方程为24y cx =,由023222c -+=结合0c >,解得1c =. 因此抛物线C 的方程为24y x =. …………4分点(Ⅱ) （i ）设圆M 与y 轴的切点是点M ',连结MM '交抛物线C 的准线于的圆M ''，那么1M MF MM r ''==+，因此圆M 与以F 为核心，1为半径相切，圆N 即为圆F ，圆N 的方程为()2211x y -+=;…………8分(ii)由AB BN λ=可知，AB 为圆N 直径，…………9分从而因此PA PB ⋅的取值范围是7,2⎡⎫+∞⎪⎢⎣⎭.…………13分20.解：（I ）因为()ln f x ax x x =+，因此()ln 1f x a x '=++．………………… 1分因为函数()ln f x ax x x =+的图像在点e x =处的切线斜率为3，因此()e 3f '=，即lne 13a ++=．因此1a =．………………… 2分（II ）由（1）知，()ln f x x x x =+，因此()1f x k x <-对任意1x >恒成立，即ln 1x x xk x +<-对任意1x >恒成立．………………… 3分令()ln 1x x xg x x +=-，则()()2ln 21x x g x x --'=-，………………… 4分令()ln 2h x x x =--()1x >，则()1110x h x x x-'=-=>，因此函数()h x 在()1,+∞上单调递增．………………… 5分因为()()31ln30,422ln 20h h =-<=->，因此方程()0h x =在()1,+∞上存在唯一实根0x ，且知足()03,4x ∈．当01()0x x h x <<<时，，即()0g x '<，当0()0x x h x >>时，，即()0g x '>，6分因此函数()ln 1x x xg x x +=-在()01,x 上单调递减，在()0,x +∞上单调递增．因此()()()()()000000min001ln 123,411x x x x g x g x x x x ++-====∈⎡⎤⎣⎦--．……… 7分因此()()0min 3,4k g x x <=∈⎡⎤⎣⎦．故整数k 的最大值是3．………………… 8分（III ）由（II ）知()ln 231x x x x >->，取()*2,x k k k N =≥∈，那么有将上面各式相加得即()21k a k >-，故()()()211131(2)1k k a k k k <=≥---，因此 …………………14分21.（1）解：（Ⅰ）法１：由于24213=，∴M -1=1322112M -⎛⎫- ⎪= ⎪ ⎪-⎝⎭, ∴1X M N -==32201021100012⎛⎫- ⎪⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪-⎝⎭；…………………3分（Ⅱ）设圆上任意一点(),x y 在矩阵1M-对应的变换作用下变成(),x y ''则10000x x x y y '⎛⎫⎛⎫⎛⎫⎛⎫== ⎪⎪ ⎪ ⎪'⎝⎭⎝⎭⎝⎭⎝⎭那么0x x y '=⎧⎨'=⎩，因此作用后的曲线方程为0(11)yx .…………………7分（2）解：（Ⅰ）2,22-==x y ax y …………………4分（Ⅱ）直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=+-=t y t x 224222（t 为参数）,代入ax y 22=取得0)4(8)4(222=+++-a t a t ,那么有)4(8),4(222121a t t a t t +=⋅+=+，因为2MN PM PN =，因此()21212t t t t -=，即()212125t t t t += ，即()()284404a a +=+解得1=a …………………7分（3）（Ⅰ）证明：0,0a b >>，由柯西不等式得=a b =. 因此22a b a b b a+≥+.…………………4分（Ⅱ）解：01,10x x <<∴->由（Ⅰ）知，()221111x x y x x xx-=+≥-+=-，当且仅当1x x -=，即12x =时等号成立. 因此函数()()221011x x y x xx-=+<<-的最小值为1. …………………7分。