板裂缝及挠度计算
悬挑雨棚板结构计算小工具Exce版

计算界限相对受压区高度ξb
0.518
满足最大配筋率要求
四、裂缝验算
MK=(gK+qK)ln2/2+FgKln (kN· m) Mq=(gK+ψqqK)l2/2+FgKln (KN·m) σsk=MK/0.87h0AS (N/mm2) σsq=Mq/0.87h0AS (N/mm2) 6.60 6.52 257.70 254.58
2.00 1.00 1.43 14.3 25 75
7× qk
10 200 392.7 满足 0.52 0.20 2.06
筋率要求
筋率要求
2.01 1.00% 10.0 5 0.587 0.17 满足
3.00E+04 2.00 203.63 203.73 203.63 满足
悬挑雨棚板配筋、裂缝及挠度计算
一、常规数据
混凝土容重(kN/m3) 基本雪压(kN/m2) 积雪分布系数μr 板 厚 底板根部厚(mm) 底板端部厚(mm) 计算跨度L0(mm) 端部翻边高出板面h'(mm) 端部翻边宽b'(mm) 构件受力特征系数αcr 纵向受拉钢筋表面特征系数νi 混凝土强度等级 受拉钢筋强度设计值fy (N/mm2) 积水荷载标准值 (kN/m) 板保护层厚度c(mm) 26 0.3 1.00 100 100 400 600 80 1.90 1.00 C30 360 2.00 20 雪荷载标准值(kN/m2) 检修集中荷载标准值 (kN/m) 活荷载准永久值系数ψq 钢筋弹性模量ES(N/mm2)
五、挠度验算
受压翼缘面积与腹板有效面积的比值 γ'f
0.00 6.667 404.79 407.46 1/200度的影响系数θ
钢筋混凝土构件抗裂度和裂缝计算(第二课)

混凝土结构
Concrete Structure
第九章 钢筋混凝土构件裂缝宽度和挠度验算 Deformation and Crack Width of RC Beam
整理ppt
第九章 变形和裂缝宽度的计算
第九章 钢筋混凝土构件的变形、裂缝和耐久性
§9. 3 §9. 4 §9. 5
(3) 腹板竖直裂缝:
位置:腹板较薄处 方向:垂直于梁轴线 分布:由梁的半高线上下延伸,裂缝中间宽两端窄
整理ppt
第九章 变形和裂缝宽度的计算
2、 成因
• 未凝固的混凝土下沉引起沿钢筋方向的裂缝。 • 由于混凝土体积变化受到内部或外部约束,在混凝土内 产生拉应力,导致开裂。 • 外力作用使混凝土产生拉应力,引起裂缝。 • 由于温度应力引起裂缝或其它因素。
整理ppt
第九章 变形和裂缝宽度的计算
§9. 3 钢筋混凝土构件裂缝宽度验算 9.3.1 裂缝的主要形式、成因及危害
1、 主要形式
(1) 受拉翼缘裂缝:
位置:受拉翼缘的侧面和底面 方向:垂直于受拉主筋 分布:临近跨中部分较密,渐向两端较稀
整理ppt
第九章 变形和裂缝宽度的计算
(2) 斜裂缝:
位置:距支座一定距离的梁的受拉区 方向:向跨中倾斜约45~60° 分布:两端近支座处较密,渐向跨中较稀
★裂缝间距的计算公式即是以该阶段的受力分析建立的。
★裂缝出齐后,随着荷载的继续增加,裂缝宽度不断开展。裂 缝的开展是由于混凝土的回缩,钢筋不断伸长,导致钢筋与混 凝土之间产生变形差,这是裂缝宽度计算的依据。
★由于混凝土材料的不均匀性,裂缝的出现、分布和开展具有 很大的离散性,因此裂缝间距和宽度也是不均匀的。但大量的 试验统计资料分析表明,裂缝间距和宽度的平均值具有一定规 律性,是钢筋与混凝土之间粘结受力机理的反映。
钢筋混凝土受弯构件的裂缝宽度和挠度验算
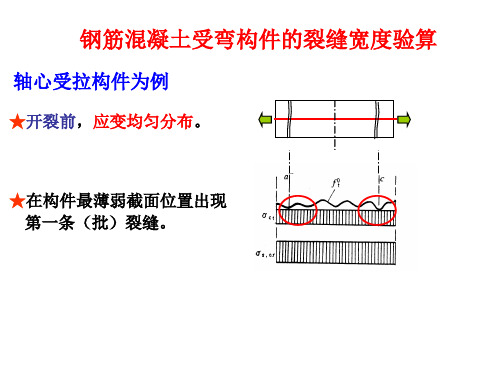
受压翼缘加强系数
3、钢筋应变不均匀系数
sm sk s sm s sk
钢筋应力不均匀系数 是反映裂缝间混凝土参加受拉工作 程度的影响系数。 越小,裂缝之间的混凝土协助钢筋抗拉的
作用越强。
1.1 0.65 ftk s sk te
sk分布图
1.1 0.65 ftk s sk te
sm sk
Sm cm cck
sm
cm
c
(
' f
Mk
0 )bh02Ec
cm
Mk
bh02 Ec
sm
Mk
Ash0 Es
ቤተ መጻሕፍቲ ባይዱ
Bs
Mk
M k h0
sm cm
cm
Mk
bh02 Ec
Bs
1
Ash02 Es
1
bh03 Ec
Bs
Es Ash02
E
E 0.2 6 E
1 3.5 f
Bs
1.15
Es Ash02 0.2
6E
1 3.5 f
1.1 0.65 ftk s sk te
在短期弯矩Mk=(0.5~0.7)Mu范围,三个参数、 和 中, 和 为常数,而 随弯矩增长而增大。
wm smlm cmlm
εsm、εcm——分别为裂缝间钢筋及砼的平均应变; lm——裂缝间距。
平均裂缝宽度wm
wm smlm cmlm
sm
(1
cm sm
梁裂缝、挠度计算表

=(As+Ap)/Ate; Ate=0.5bh= 0.0419
钢筋应变不均匀系数ψ =1.1-0.65*ftk/ρ te/σ sk(0.2<ψ <1)= 0.912 梁裂缝宽度(mm)ω max=α cr*ψ *σ sk/Es*(1.9c+0.08deq/ρ te)= 0.1214 裂缝控制值(mm)ω lim = 0.4000 裂缝验算结果:满足?OK!!! OK!!! 梁跨中挠度计算 支承情况(两端简支,一端简支一端固端,两端固端) 两端简支 梁受压纵向钢筋实配面积(mm)A's= 510 梁受拉纵向钢筋配筋率ρ =As/bh0= 0.023787879 钢筋与砼弹性模量比值α e=Es/Ec= 6.666666667 受拉翼缘面积与腹板有效面积比值γ 'f=(bf-b)hf/bh0= 0.00 短期刚度(mm4)Bs=EsAsh02/(1.15ψ +0.2+(6α eρ /(1+3.5γ 'f))= 4143484349352.5700
梁裂缝宽度、挠度计算书
梁截面特征
பைடு நூலகம்
9/18/18
(红色为输入数值)
梁宽(mm)b= 180 梁高(mm)h= 250
梁压区翼缘板计算宽度(mm)b'f= 0 梁压区翼缘板计算高度(mm)h'f= 0 受拉钢筋合力点距离(mm)a(单排35;双排60~80)= 30 梁钢筋保护层厚度(mm)C(25<C<32)= 20 材料特性 梁砼强度等级C?(20,25,30,35,40)= 30 砼轴心抗压强度(N/mm2)fc= 14.3 砼轴心抗拉强度(N/mm2)ftk= 2.01 砼的弹性模量(N/mm2)Ec= 30000 钢筋的抗拉强度(N/mm2)fy = 360 钢筋的弹性模量(N/mm2)Es= 200000 梁上荷载计算 楼板恒载(Kn/m2)Gk= 3.6 楼板活载(Kn/m2)Qk= 0 梁跨中集中恒荷载Pk= 0 梁跨中集中活荷载Pk= 40 活载准永久值系数ψ f= 0.6 梁荷载分布计算宽度(m)= 0.19 梁计算跨度(m)l0= 4.3 梁自重(Kn/m)= 1.125 内力计算 标准组合弯矩(Kn*m)Mk= 47.18 准永久值组合弯矩(Kn*m)Mq= 29.98 梁跨中裂缝计算 梁受拉纵向钢筋实配面筋(mm)As= 942 梁受拉纵向钢筋等效直径deq= 20 梁纵向钢筋的应力σ sk=Mk/0.87/h0/As= 166.29 有效钢筋配筋率ρ
板裂缝及挠度计算

板裂缝及挠度计算1.平板的应力分析平板的应力分析可以基于弹性力学的理论进行。
假设平板是均匀的、各向同性的,那么在不受外力作用时,平板内部的应力是各向均匀分布的。
根据弹性力学理论,在弹性范围内,平板内部的应力满足以下关系:σx=Ex*εx+νy*εyσy=νx*εx+Ey*εyτxy = Gxy * γxy其中,σx和σy为平板沿x和y方向的正应力,τxy为平板剪应力,εx和εy为平板的应变,Ex和Ey分别为平板沿x和y方向的杨氏模量,νx和νy为平板沿x和y方向的泊松比,Gxy为平板剪切模量,γxy为平板剪切应变。
2.材料性能参数材料性能参数是计算板裂缝及挠度的重要输入参数。
常用的材料性能参数有杨氏模量(Ex、Ey)、泊松比(νx、νy)和剪切模量(Gxy)等。
这些参数可以通过材料试验或文献资料获得。
3.荷载和边界条件的确定对于板裂缝及挠度计算,需要确定荷载情况和边界条件。
荷载包括集中力、均布力、分布力等。
边界条件包括固支、自由支座、边界固定、边界自由等。
荷载和边界条件的确定需根据具体问题进行分析。
4.板裂缝计算板裂缝的计算可以采用弹性力学理论或断裂力学理论。
在弹性力学理论中,采用裂纹模型,假设裂缝是一个分开的两个平行板,然后应用应力分析,计算得到裂缝的应力集中因子,再根据应力集中因子和材料断裂力学参数计算得到裂缝的长度和深度。
在断裂力学理论中,采用线弹性断裂力学理论,根据材料断裂力学参数和荷载情况计算得到裂缝的长度和深度。
5.板挠度计算板挠度的计算也可以基于弹性力学理论。
通常,挠度可以通过解析方法、数值方法或实验方法计算得到。
解析方法包括弯曲弹性平板理论和细长板理论等。
数值方法主要利用有限元法进行计算。
实验方法包括挠度量测和拟静力试验等。
综上所述,板裂缝及挠度计算是一个较为复杂的问题,需要采取适当的理论和方法进行分析。
在实际工程中,需要根据具体问题的要求和具体材料的性能参数来选择合适的计算方法。
钢筋混凝土受弯构件的裂缝宽度和挠度计算

钢筋混凝土受弯构件的裂缝宽度和挠度计算【最新版】目录1.钢筋混凝土受弯构件裂缝宽度和挠度计算的背景和意义2.裂缝宽度和挠度计算的理论基础3.裂缝宽度和挠度计算的方法和步骤4.计算结果的分析和应用5.结论和展望正文钢筋混凝土受弯构件的裂缝宽度和挠度计算是建筑结构设计中的重要环节,关系到结构的安全性、稳定性和耐久性。
在实际工程中,裂缝宽度和挠度通常是混凝土结构受弯构件的主要设计控制参数,因此,对它们的精确计算和分析具有重要的现实意义。
一、钢筋混凝土受弯构件裂缝宽度和挠度计算的理论基础裂缝宽度和挠度是受弯构件的两个主要变形参数。
其中,裂缝宽度是指混凝土受弯构件在弯曲过程中,由于内部应力达到极限而产生的裂缝的宽度;而挠度则是指受弯构件在弯曲过程中,构件的中性轴线偏离原位置的距离。
二、裂缝宽度和挠度计算的方法和步骤在实际工程中,裂缝宽度和挠度的计算通常采用以下的方法和步骤:1.确定受弯构件的材料性能参数,包括混凝土的抗压强度、抗拉强度、弹性模量等;2.根据受弯构件的几何参数和荷载条件,确定构件的截面几何形状和尺寸;3.采用适当的数学方法(如有限元法、矩方法等)计算受弯构件在荷载作用下的应力和应变分布;4.根据计算结果,确定裂缝宽度和挠度的数值。
三、计算结果的分析和应用裂缝宽度和挠度的计算结果可以反映受弯构件在弯曲过程中的变形情况,为结构设计提供重要的依据。
通常,我们需要对计算结果进行以下的分析和应用:1.检验裂缝宽度和挠度是否符合设计规范的要求;2.如果不符合要求,则需要调整设计参数(如增加截面尺寸、改变材料性能等)重新计算,直到满足设计要求;3.根据裂缝宽度和挠度的计算结果,确定受弯构件的耐久性和安全性。
四、结论和展望钢筋混凝土受弯构件的裂缝宽度和挠度计算是建筑结构设计的重要内容。
随着计算机技术和数学方法的发展,计算方法和工具也越来越精确和便捷。
受弯构件的裂缝与变形验算

第十章受弯构件的裂缝与变形验算第一节概述1.一、钢筋混凝土受弯构件在使用阶段的计算特点:1.使用阶段一般指梁带裂缝工作阶段。
2.使用阶段计算是按照构件使用条件对已设计的构件进行计算,以保证在使用情况下的应力、裂缝和变形小于正常使用极限状态的限值。
当构件验算不满足要求时,必须按承载能力极限状态要求对已设计好的构件进行修正、调整,直至满足两种极限状态的设计要求。
3.使用阶段计算中涉及到的内力,是各种使用荷载在构件截面上各自产生的同类型内力,按荷载组合原则简单叠加,不带任何荷载系数。
二、结构按正常使用极限状态设计采用的两种效应组合:1 1.作用短期效应组合。
永久作用标准值效应与可变作用频遇值效应相组合,其效应组合表达式为:2 2.作用长期效应组合。
永久作用标准值效应与可变作用准永久值效应相组合,其效应组合表达式为:第二节换算截面一、基本假定二、截面变换三、换算截面的几何特性表达式一、基本假定1.平截面假定。
2.弹性体假定。
3.受拉区出现裂缝后,受拉区的混凝土不参加工作,拉应力全部由钢筋承担。
4.同一强度等级的混凝土,其拉、压弹性模量视为同一常值,不随应力大小而变,从而钢筋的弹性模量和混凝土的弹性模量之比值为一常数值,即/。
与混凝土的强度等级有关。
《公桥规》规定钢筋混凝土构件的截面换算系数。
二、截面变换将截面受拉区纵向受拉钢筋的截面面积换算成假想的能承受拉应力的混凝土截面面积,如图。
并满足:1、虚拟混凝土块仍居于钢筋的重心处且应变相同,即2、虚拟混凝土块与钢筋承担的内力相同,即由虎克定律(Hookelaw)得:根据换算截面面积承受拉力的作用应与原钢筋的作用相同的原则可得所以,上式表明,截面面积为的纵向受拉钢筋的作用相当于截面面积为的受拉混凝土的作用,即称为钢筋的换算截面面积。
<top>三、换算截面的几何特性表达式(一)、单筋矩形截面1、换算截面面积:2、换算截面对中性轴的静矩:2、换算截面对中性轴的静矩:受压区:受拉区:3、换算截面对中性轴的惯性矩4、受压区高度x:对于受弯构件,开裂截面的中性轴通过其换算截面的形心轴,即若将符号(受压区相对高度)及(配筋率)代入上式,则可得到5、受压区边缘混凝土应力6、受拉钢筋应力(二)、双筋矩形截面对于双筋矩形截面,截面换算的方法就是将受拉钢筋的截面和受压钢筋截面分别用两个虚拟的混凝土块代替,形成换算截面。
预应力裂缝和挠度计算
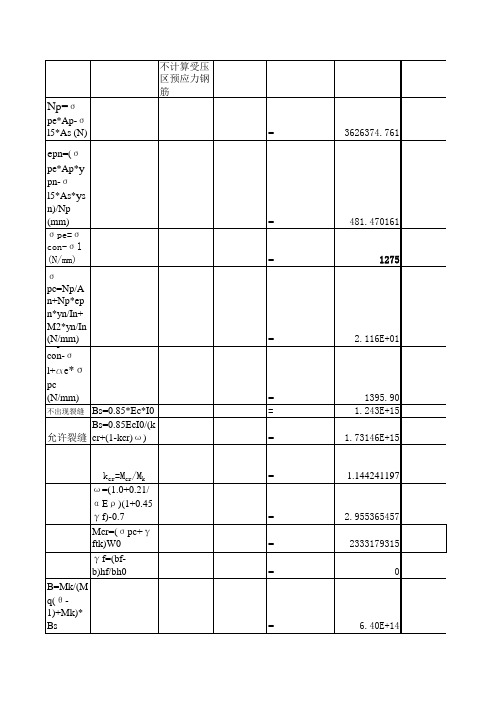
3626374.761 481.470161 1275 2.116E+01 1395.90 1.243E+15 1.73146E+15 1.144241197 2.955365457 2333179315 0 6.40E+14
epn=(σpe*Ap*ypn-σl5*As*ysn)/Np (mm)
三级 标准组合并考虑长期作用的最大裂宽 ωmax≤ω1im ω1im-最大裂缝宽度限值按第3.3.4条采用 ωmax=αcr*ψ*σsk/Es*(1.9c+0.08deq/ρte)= ψ=1.1-0.65ftk/(ρte*σsk)= deq=Σni*(di)^2/Σni*vi*di= V1 V2 按表8.1.2-2 1 ρte=(As+Ap)/Ate= ok Ate=0.5bh+(bf-b)hf= 暂时不考虑bf.hf σsk=(Mk±M2-Np0(z-ep))/((Ap+As)z)=
σpe=σcon-σl (N/mm) σpc=Np/An+Np*epn*yn/In+M2*yn/In (N/mm) σp0=σcon-σl+ae*σpc (N/mm) 不出现裂缝 Bs=0.85*Ec*I0 允许裂缝 Bs=0.85EcI0/(kcr+(1-kcr)ω) kcr=Mcr/Mk ω=(1.0+0.21/αEρ)(1+0.45γf)-0.7 Mcr=(σpc+γftk)W0 γf=(bf-b)hf/bh0 B=Mk/(Mq(θ-1)+Mk)*Bs
C35
3.150E+04
M设计值 2.51E+09 M恒 1.70E+09 M活 3.38E+08 短期弯矩 Ms 2.04E+09 长期弯矩 Ml 1.92E+09 M2 -5.06E+08
