比例谐振控制算法分析(1)
比例谐振控制在永磁同步电机调速中的应用研究

比例谐振控制在永磁同步电机调速中的应用研究1. 引言1.1 研究背景永磁同步电机是一种应用广泛、性能优越的电机类型,广泛应用于工业生产中的众多领域,如风力发电、汽车电动化等。
随着电气化技术的不断发展,永磁同步电机调速技术也日益成熟。
随着电力需求的不断增长和对电机性能要求的提高,需要更加高效的控制方法来实现永磁同步电机的精密调速。
目前对比例谐振控制在永磁同步电机调速中的应用研究还比较有限,需要进一步深入探讨。
本研究旨在通过分析比例谐振控制的原理和方法,探讨其在永磁同步电机调速中的应用,为提升永磁同步电机的控制性能和应用前景提供理论支持和实验数据。
1.2 研究目的本研究的主要目的是探究比例谐振控制在永磁同步电机调速中的具体应用效果,并对其在电机控制领域中的潜在价值进行分析。
通过对比例谐振控制原理及方法的深入研究,结合永磁同步电机调速技术的现状,希望能够验证比例谐振控制在提高永磁同步电机性能和效率方面的有效性,并探讨其在实际应用中可能遇到的挑战和问题。
本研究也旨在为永磁同步电机调速技术的进一步发展提供新的思路和方法,为提高电机系统的稳定性和效率提供技术支持和参考。
通过实验设计和结果分析,将为比例谐振控制在永磁同步电机调速中的应用提供实际数据支持,验证其在实际工程中的可行性和效果,为电机控制领域的研究和发展做出贡献。
1.3 研究意义研究比例谐振控制在永磁同步电机调速中的应用可以提高永磁同步电机的性能指标,如提高调速精度、降低谐波扭矩、减小振动等。
这对于提高永磁同步电机的工作效率和负载能力具有重要意义。
研究比例谐振控制在永磁同步电机调速中的应用可以为工程实践提供技术支持和参考。
通过实验设计和结果分析,可以验证比例谐振控制在永磁同步电机调速中的有效性,为工程应用提供重要参考。
2. 正文2.1 永磁同步电机调速技术及现状永磁同步电机调速技术是现代电力传动领域的重要技术之一,其具有高效率、高功率因数、高控制精度等优点,得到了广泛的应用。
矩阵变换器输出电流比例谐振控制研究

矩阵变换器输出电流比例谐振控制研究1.引言:介绍矩阵变换器和其在电力转换中的应用,介绍谐振控制的目的,说明文章研究的重要性和意义。
2.矩阵变换器的谐振控制理论:介绍矩阵变换器的结构和原理,介绍其在谐振控制中的应用,探讨谐振控制理论及电流比例谐振控制的原理。
3.模型及仿真:建立矩阵变换器的数学模型,利用Matlab/Simulink进行仿真,地面系统平台进行实验验证。
利用电流比例控制方法实现谐振控制。
4.实验及分析:从实验数据中提取必要的参数,对比实验结果和仿真结果,分析实验数据,探究电流比例控制谐振控制在矩阵变换器中的应用,分析问题所在,提出改进方案。
5.总结及展望:总结全文,归纳本文研究内容、方法和结论,指出本文的不足之处及未来研究的可能方向。
随着电力系统的发展和新能源的普及,矩阵变换器作为一种新型的电力转换器件,在电力转换领域得到了广泛的应用。
与传统的单相桥等电压变换器相比,矩阵变换器具有功率密度高、功率因数高、体积小等优点。
然而,在矩阵变换器的运行过程中,由于其独特的结构和工作方式,容易出现谐振现象,导致设备的损坏和系统的不稳定。
因此,如何有效地控制谐振问题已成为矩阵变换器研究领域的一个热点问题。
谐振问题在电力转换器中一直存在,如何解决问题成为了研究领域的重要任务。
利用谐振控制的技术可以有效地解决矩阵变换器的谐振问题。
谐振控制可以通过对谐振频率和振幅的监测来实现,通过改变控制系统的参数实现控制。
这种方法可以使系统更加灵活、稳定和可靠。
本文将针对矩阵变换器的谐振问题进行研究,通过分析控制系统的结构和控制策略,进一步研究电流比例谐振控制方法在矩阵变换器中的应用。
文章的研究意义在于为解决矩阵变换器谐振问题提供了一种全新的思路和方法,同时能够提升谐振控制能力。
本研究的目的在于寻找一种合适的电流比例谐振控制方案,并通过模拟实验和模型验证研究效果。
本章节主要对研究主题进行综合介绍。
第一节将详细介绍矩阵变换器和其在电力转换中的应用,包括其优点和缺点以及目前存在的问题。
谐振详解[1]
![谐振详解[1]](https://img.taocdn.com/s3/m/4a98e42c192e45361066f5cb.png)
∙在rlc电路中。
当电路的阻抗z(jw)的虚部为0时,此时z(jw)=r在频率w下最小。
此时电流i=u/|z|最大,此时可将频率为w的电流选出。
反之y=g往掉该频率,这是它们的关键点选频电路:利用lc串联电路。
和lc并联电路的谐振办到的,当w=1/√(lc)。
即f=1/2π√(lc)时,lc串联电路z=r发生谐振。
lc相当于短路。
谐振是什么意思可将频率为w的电流选出当w=1/√(lc),即f=1/2π√(lc)时。
lc并联电路z=g+j(wc-1/wl)的虚部为0,即j(wc-1/wl)=0。
此时导纳g 最小,即阻抗z最大。
lc并联电路相当于开路,可将频率为w的电流往掉,选频电路就就是lc的串并联用上面的关系达到选频的。
谐振电路振荡电路:就是有rlc 或电源的电路。
其中只有lc的串联电路w=1/√(lc),谐振电路:应该就是串联谐振和并联谐振吧。
滤波电路:应该跟选频电路差未几吧,串联谐振和并联谐振的区别:上面有讲到。
lc串联电路中z(jw)=r+j(wl-1/wc),lc并联电路中导纳y=g+j(wc-1/wl)。
所以w=1/√(lc),即f=1/2π√(lc)时前者电流最大。
被选出,后者电流最小。
被过滤,我只是大学生的啦知识有限。
不知对你有不有用,对了 w是指频率。
j是虚部符号,其他符号都有注明。
呵呵怕你的版本跟我的不一样∙谐振即物理的简谐振动,物体在跟偏离平衡位置的位移成正比。
且总是指向平衡位置的回复力的作用下的振动,其动力学方程式是f=-kx。
谐振是什么∙谐振的现象是电流增大和电压减小,越接近谐振中心。
电流表电压表功率表转动变化快,但是和短路得区别是不会出现零序量,∙在物理学里。
有一个概念叫共振:当策动力的频率和系统的固有频率相等时,系统受迫振动的振幅最大。
这种现象叫共振。
谐振器电路里的谐振实在也是这个意思:当电路的激励的频率即是电路的固有频率时,电路的电磁振荡的振幅也将达到峰值,实际上。
带LC滤波的三相逆变器的比例谐振控制

第45卷第6期2011年6月电力电子技术PowerElectronicsV01.45,No.6June2011带LC滤波的三相逆变器的比例谐振控制李永坚,黄绍平(湖南工程学院,电气信息学院,湖南湘潭411104)摘要:针对带LC输出滤波器的三相电压型逆变器,提出一种新的无电流传感器比例谐振(PR)控制策略,仅需检测输出滤波电容电压。
无需检测其电流。
相比于同步旋转坐标系的PR控制器,提出的PR控制器基于静止坐标系.无需进行复杂的坐标变换,减少了计算量,能对正序与负序电流进行统一调节。
仿真和实验结果表明,该控制策略具有良好的动静态性能,可实现正弦交流指令的零稳态误差控制,利用其谐振控制器的特性对特定次谐波进行补偿.在逆变器带平衡负载和不平衡非线性负载时都能适用。
关键词:逆变器;比例谐振控制;滤波中图分类号:TM464文献标识码:A文章编号:1000一lOOX(2011)06—0076—03Proportinal.resonantControlforThree-phaseInverterwithLCFiltersLIYong-jian,HUANGShao・ping(HunanInstituteofEngineering,Xiangtan411104,China)Abstract:Anovelcurrentsensor]essproportional・resonant(PR)controlschemeforthree・phaseinverterwithLCout—putfiltersispresented.Theproposedcontrolschemewithuseofcurrentsensorlessonlyrequiesvoltagemeasuredacrosscapacityinsteadofcurrentmeasured.ComparedwithPRcontrollerinsynchronousframe,theproposedPRcon—trollerisimplementedinstationaryframewithoutcomplexreferenceframetransforms,itisabletoadjustpositiveandnegativesequencecomponentsoftheoutputcurrentsimultaneously.Simulationandexperimentalresultsshowthatthecontrolschemehasgooddynamicandstaticperformances,theproposedschemecarlachievezerosteady—stateerrorforsinusoidalreferencecommand,specificharmonicscanbecompensatedbyuseoftheresonantcharacteristicsofthecontroller,thecontrolledinvertercanoperatewellinblanceloadsornonlinearunbalanceloads.Keywords:inverter;proportinal—resonantcontrol;tiltingFoundationProject:SupportedbyScienceandTechnologyPlanningFundofHunanProvince(No.2010GK3100);CollegesandUniversitiesOpenInnovationPlatformFundofHunanProvince(No.2009K100)1引言逆变器按输出波形可分为正弦波逆变器与方波逆变器.前者在实际中应用较多。
比例谐振控制算法阐明

比例谐振控制算法分析
目录
0 前言........................................................................................................................................2 1 PR 控制器...............................................................................................................................2 2 准 PR 控制器.........................................................................................................................5 3 准 PR 控制器的参数设置.....................................................................................................6
3.1 ������������ = 0, ������������变化 ..........................................................................................................6 3.2 ������������变化, ������������ = 1 ..........................................................................................................6 4 准 PR 控制器的离散化.........................................................................................................7 附录 A 数字滤波器设计..........................................................................................................9 A.1 脉冲响应不变法........................................................................................................9 A.2 双线性变换法..........................................................................................................10 附录 B 双线性变换法原理....................................................................................................13 B.1 连续时间系统 H(s)的最基本环节..........................................................................13 B.2 积分的数值计算与离散一阶系统..........................................................................13 B.3 连续时间一阶环节的离散实现..........................................................................Байду номын сангаас...14 B.4 高阶连续时间系统的离散实现..............................................................................14
400_Hz中频电源波形多重比例谐振控制策略

" ** "
研究与分析
电器与能效管理技术!"!#$%&!
\N控制策略在工程中应用最广$但 \N控制器 不能实现对正弦信号的无静差控制$受制于中频 电源较小的带宽$又需兼顾稳定裕度的要求$使得 \N控 制 器 的 低 频 增 益 较 低$ 稳 态 误 差 较 大$ 控 制 的稳态和动态特性不能满足要求)#7%* % 重复控制 具有消除周期性扰动的特性$稳态时可以实现无 静差控制$得到较好的输出电压波形$但重复控制 器设计过程复杂$理论设计参数可能与实际相差 较大$降低了设计的有效性% 另外$其无法实现少 于一个周期的动态响应$因此采用其进行控制的 系统动态特性较差$不能满足高性能中频电源的 动态指标要求)'7$* % 无差拍控制通过采用状态观 测器将控制作用提前一拍进行$能够得到较好的 输出品质$但其控制效果对控制对象的数学模型 及参数精确度的依赖性很大$控制系统的鲁棒性 不强% 滑模变结构控制具有较好的动&静态性能$ 但对于逆变电源系统而言$理想的滑模切换面选 取难度大及较高的采样频率要求限制了应用$而 目前只停留在试验阶段)"* % \Y控制器在谐振频 率处理论上的增益是无限的$又能够迅速滤除谐 振频率之外的信号$可以实现对正弦交流信号的 无静差控制$能够满足中频电源对稳态精度的要 求$此外$\Y控制器还具备良好的动态特性$能够 满足中频电源的动态特性要求%
7"""滤波电容(
H"""等效电阻! 考虑电感电阻&死区效
应# (
(>"""负载( '>"""负载电流% 由式!!#可得到相应的连续时间模型% 单相
利用pid求谐振频率的方法

利用pid求谐振频率的方法(原创实用版3篇)《利用pid求谐振频率的方法》篇1PID 控制器是一种常用的控制器设计方法,可以用于控制各种系统,包括谐振系统。
在谐振系统中,PID 控制器可以用来调整系统的谐振频率,以实现所需的控制目标。
以下是利用PID 控制器求谐振频率的一般步骤:1. 确定谐振系统的参数:确定谐振系统的质量、刚度、阻尼等参数。
这些参数可以通过实验或理论计算得到。
2. 设计PID 控制器:根据系统的参数和控制目标,设计PID 控制器的增益和时间常数。
PID 控制器的增益和时间常数可以通过实验或Ziegler-Nichols 方法等方法进行调整。
3. 调整谐振频率:通过调整PID 控制器的增益和时间常数,调整谐振系统的谐振频率。
具体来说,可以通过增加或减小控制器增益来调整谐振频率,或者通过增加或减小控制器时间常数来调整谐振频率。
4. 验证控制效果:通过实验或仿真验证PID 控制器的控制效果,确保控制目标得到满足。
在实际应用中,谐振系统的参数和控制目标可能会发生变化,因此需要对PID 控制器进行调整以保持控制效果。
《利用pid求谐振频率的方法》篇2PID(Proportional-Integral-Derivative,比例-积分-微分)控制是一种常用的控制算法,它在许多领域,如机械、化工、航空等都有广泛的应用。
在电子电路中,PID 控制可以用于谐振频率的测量和调节。
利用PID 求谐振频率的方法主要包括以下几个步骤:1. 搭建实验电路:设计一个包含谐振器的电路,并将其连接到示波器和PID 控制器上。
通过示波器观察谐振器的振荡波形,从而获取有关谐振频率的信息。
2. 确定PID 参数:根据电路的特性和实际需求,设置PID 控制器的参数。
比例(P)term 决定控制器的输出与误差之间的比例关系;积分(I)term 用于处理系统的累积误差,以消除稳态误差;微分(D)term 用于处理误差的高频分量,以抑制谐振器的振幅波动。
LLC 谐振分析说明
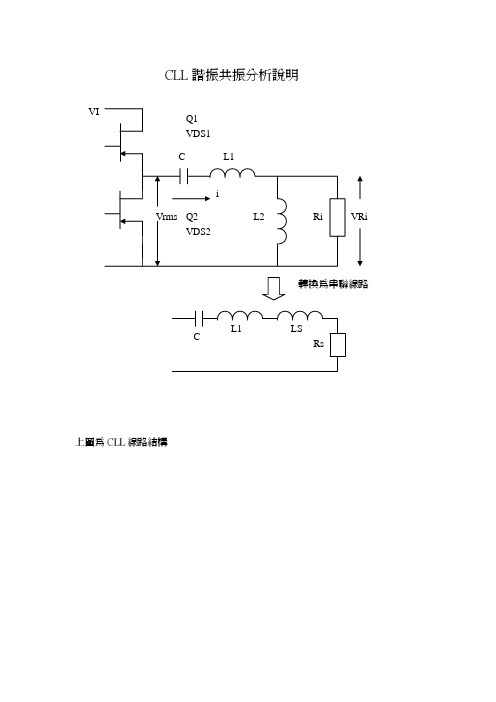
由等效電路圖,我們定義 ac 對 ac 的電壓轉換方程 MVR 為
MVR = V Ri ( rms ) Vrms = Ri XL2 Z
----------(20)
而 Ri xL2 =
Ri jwL2 = Ri + jwL2
Ri Ri 將(6)式 L2 = 代入 Ri (1 + A) w0 QL 1+ jwL2
2 2
k4A 2 2 + k 2 [QL (1 + A) 2 − 1] − QL (1 + A) 2 = 0 1+ A k4A 2 2 + k 2 QL (1 + A) 2 − k 2 − QL (1 + A) 2 = 0 1+ A
1 − Q L (1 + A) 2 ± [Q L (1 + A) 2 − 1] 2 − 4 AQ L (1 + A) 解 k 得k = 2A 1+ A
QL w0 Ri
L 1+ A
1
LC 以上列各項帶入(10)的各項因數中並簡化之 (A) 項 以 L2 跟 C 帶入
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
0 前言............................................................................................................................................ 3 1 PR 控制器 .................................................................................................................................. 3 2 准 PR 控制器............................................................................................................................ 6 3 准 PR 控制器的参数设置 ....................................................................................................... 7
对于同频的输入信号M sin(ωt + φ),该环节的时域响应分析如下:
输入信号的拉普拉斯变换为:
L(M sin(ωt + φ))
=
L(M
sin(ωt)cosφ
+
Mcos(ωt)sinφ)=
Mcosφ
∗
ω s2+ω2Βιβλιοθήκη +Msinφ
∗
s s2+ω2
经过s2K+Rωs 02后的表达式为:
(Mcosφ
∗
ω s2+ω2
1 PR 控制器
PR 控制器,即比例谐振控制器,由比例环节和谐振环节组成,可对正弦量实现无静差
控制。理想 PR 控制器的传递函数如下式所示:
G(s)
=
Kp
+
KRs s2+ω02
式中Kp为比例项系数,KR为谐振项系数,ω0为谐振频率。PR 控制器中的积分环节又
称广义积分器,可以对谐振频率的正弦量进行幅值积分。
+
Msinφ
PR 控制器可以实现对交流输入的无静差控制。将 PR 控制器用于网侧变换器的控制系 统中,可在两相静止坐标系下对电流进行调节。可以简化控制过程中的坐标变换,消除两相 静止坐标系下对电流进行调节。可以简化控制过程中的坐标变换,消除电流 d、q 轴分量之 间的耦合关系,且可以忽略电网电压对系统的扰动作用。此外,应用 PR 控制器,易于实现 低次谐波补偿,这些都有助于简化控制系统的结构。
3.1 ωc = ������, KR变化........................................................................................................... 7 3.2 ωc变化, KR = 1........................................................................................................... 7 4 准 PR 控制器的离散化 ........................................................................................................... 8 附录 A 数字滤波器设计...........................................................................................................10 A.1 脉冲响应不变法......................................................................................................... 10 A.2 双线性变换法.............................................................................................................12 附录 B 双线性变换法原理 .......................................................................................................15 B.1 连续时间系统 H(s)的最基本环节 ...........................................................................15 B.2 积分的数值计算与离散一阶系统............................................................................15 B.3 连续时间一阶环节的离散实现................................................................................16 B.4 高阶连续时间系统的离散实现................................................................................17
0 前言
在整流器和双馈发电机的矢量控制系统中广泛地采用了坐标变换技术,将三相静止坐标 系下的电流电压等正弦量转化为同步旋转坐标系下的直流量,这一方面是为了简化系统的模 型,实现有功功率和和无功功率的解耦,另一方面是因为 PI 控制器无法对正弦量实现无静 差控制。坐标变换简化了控制系统外环的设计,却使电流分量互相耦合,造成内环结构复杂, 设计困难。
