考研数学知识网络图
2021年考研数学高数考点解析

2021年考研数学高数考点解析高等数学作为硕士研究生招生考试的内容之一,主要考查考生对高等数学的基本概念、基本理论、基本方法的理解和掌握以及考生的抽象思维能力、逻辑推理能力、综合运用能力和解决实际问题的能力。
依据数学考试大纲中的考试要求,包新卓老师在下面的表格中简要罗列了高等数学在数学(一)、数学(二)和数学(三)这三个卷种中所涵盖的考试内容。
接下来,包新卓老师就从数学(一)、数学(二)、数学(三)的公共部分开始。
一、函数、极限、连续高等数学在考研中,也被称为微积分学。
微积分学的研究对象是函数,许多重要的概念都需要用极限理论精确定义,因此极限是微积分学的重要基础,这部分内容对后续内容的学习影响深远,故应重点掌握。
在这一部分,由于数学(一)、数学(二)、数学(三)的考试要求完全一样,故这里不做分类。
考纲内容:1、函数的概念及表示法、函数关系的建立;2、函数的有界性、单调性、周期性和奇偶性;3、复合函数、反函数、分段函数和隐函数;4、基本初等函数的性质及其图形,初等函数;5、数列极限与函数极限的定义及其性质;6、函数的左极限和右极限;7、无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷大量的比较;8、极限的四则运算:掌握极限的四则运算法则;9、极限存在的两个准则(单调有界准则和夹逼准则),两个重要极限;10、函数连续的概念,函数间断点的类型;11、初等函数的连续性,闭区间上连续函数的性质;根据往年改卷反馈回来的数据可知,大部分考生对函数、极限、连续这一部分的内容普遍掌握得比较好,但由于这部分内容与后续内容多有交叉,因此考生要注意前后知识的融会贯通。
二、一元函数微分学一元函数微分学不仅在微积分的学习中占有着极其重要的地位,而且它也是考研数学考查的重点。
在这里,对于数学(一)和数学(二)单独考点,包新卓老师会在相应的内容后面予以标出,未做任何标出的内容则为数学(一)、数学(二)、数学(三)的公共考点。
考研数学二经典知识点技巧总结(高数线代)

高等数学(数二)一. 重点知识标记高等数学科目大纲章节知识点题型重要度等级高等数学第一章函数、极限、连续1 .等价无穷小代换、洛必达法则、泰勒展开式求函数的极限★★★★★2 .函数连续的概念、函数间断点的类型3 .判断函数连续性与间断点的类型★★★第二章一元函数微分学1 .导数的定义、可导与连续之间的关系按定义求一点处的导数,可导与连续的关系★★★★2 .函数的单调性、函数的极值讨论函数的单调性、极值★★★★3.闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用★★★★★第三章一元函数积分学1 .积分上限的函数及其导数变限积分求导问题★★★★★2 .有理函数、三角函数有理式、简单无理函数的积分计算被积函数为有理函数、三角函数有理式、简单无理函数的不定积分和定积分★★第四章多元函数微分学1 .隐函数、偏导数、的存在性以及它们之间的因果关系2 .函数在一点处极限的存在性,连续性,偏导数的存在性,全微分存在性与偏导数的连续性的讨论与它们之间的因果关系★★3 .多元复合函数、隐函数的求导法求偏导数,全微分★★★★★第五章多元函数积分学1. 二重积分的概念、性质及计算2.二重积分的计算及应用★★第六章常微分方程1.一阶线性微分方程、齐次方程,2.微分方程的简单应用,用微分方程解决一些应用问题★★★★一、函数、极限、连续部分:极限的运算法则、极限存在的准则(单调有界准则和夹逼准则)、未定式的极限、主要的等价无穷小、函数间断点的判断以及分类,还有闭区间上连续函数的性质(尤其是介值定理),这些知识点在历年真题中出现的概率比较高,属于重点内容,但是很基础,不是难点,因此这部分内容一定不要丢分。
二、微分学部分:主要是一元函数微分学和多元函数微分学,其中一元函数微分学是基础亦是重点。
一元函数微分学,主要掌握连续性、可导性、可微性三者的关系,另外要掌握各种函数求导的方法,尤其是复合函数、隐函数求导。
考研数学 知识结构思维导图(数二)
1.分离变量,物以类聚人以群分 2.y'在等式左侧,右侧应写成乘积形式
一阶微分方程的求解
齐次型
y'=f(y/x)
对x求导
1/y'=f(x/y)
对y求导
换元后分离变量,交换x和y的地位
一阶线性型(或可换元为它)
y'+p(x)y=q(x) 伯努利方程
y'+p(x)y=q(x)的特殊形式
伯努利方程可理解为一 阶线性方程的普遍形式
符号函数 抽象函数
复合函数
偏导函数
换元法
一元函数积分换元法 二元函数积分换元法
应用
面积
1.积分变化口诀:后积先定限,限内画直 线,先交先下限,后交写上限;
2.注意对称性得0的应用可以极大地化简计 算
微分方程
可分离变量
y'=f(x).g(y)
分离变量
y'=f(ax+by+c)
换元后再分离变量
一般一层积分不易处理,化成两层积分,在交换 积分次序
分部积分法
换序型
反常积分的计算
研究对象
常规题型取绝对值时取值范围
曲线平移时相关符号不同取值范围所对应的面积
切线综合
函数列综合
题型总结
在平面极坐标系中,如果极径ρ随极角θ的 增加而成比例增加(或减少),这样的动
点所形成的轨迹叫做螺线。
阿基米德螺旋线
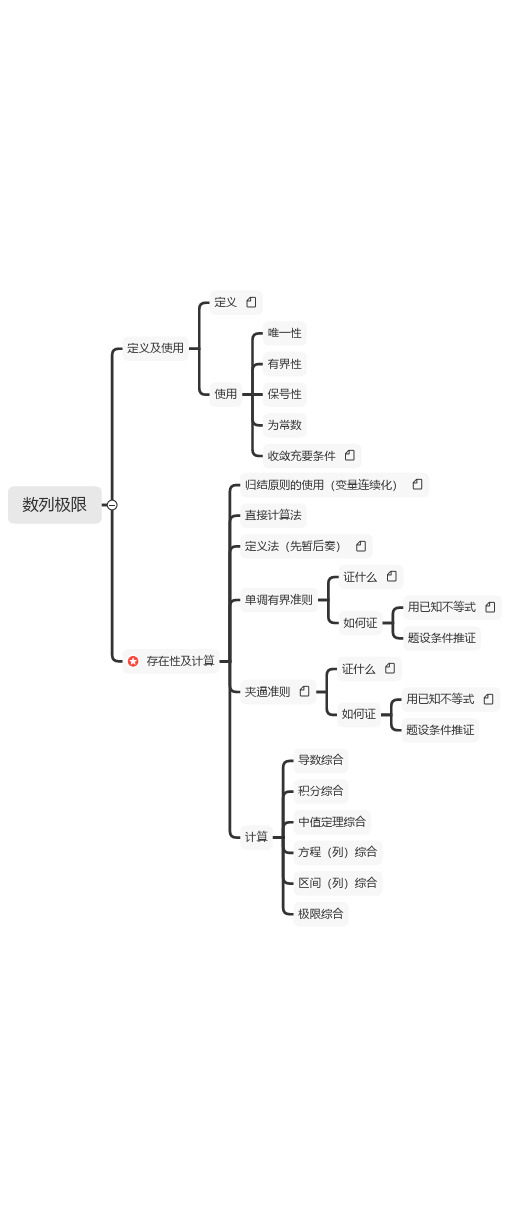
数列极限
定义
定义及使用
唯一性 有界性
使用
保号性
为常数
收敛充要条件
归结原则的使用(变量连续化)
直接计算法
定义法(先暂后奏)
考研数学备考题型及分值情况

考研数学备考题型及分值情况考研数学题型及分值情况解读若是数一:试卷满分为150分,考试时间为180分钟. 。
高等数学56% 线性代数22% 概率论与数理统计 22% 。
试卷题型结构为:单选题 8小题,每题4分,共32分,填空题 6小题,每题4分,共24分,解答题(包括证明题) 9小题,共94分若是数二:高等数学 78% ,线性代数22% 。
试卷题型结构为:单项选择题选题 8小题,每题4分,共32分,填空题 6小题,每题4分,共24分,解答题(包括证明题) 9小题,共94分若是数三:微积分 56% ,线性代数 22% ,概率论与数理统计 22% ,试卷题型结构为:单项选择题选题8小题,每题4分,共32分,填空题 6小题,每题4分,共24分,解答题(包括证明题) 9小题,共94分考研数学冲刺如何归纳总结高等数学分为5大知识模块:1、一元微积分学 ;2、多元微积分学;3、曲线、曲面积分;4、无穷级数;5、微分方程。
这里面的曲线、曲面积分是数一的同学特有的,其他内容是所有考数学的同学都要考查的。
线性代数分为3大知识模块:1、行列式和矩阵;2、向量和线性方程组;3、特征值、特征向量和二次型。
线性代数部分从考纲来看各个卷种的差别不大,近些年的变化也不大,是考研数学相对稳定的一部分考查内容。
概率论与数理统计分为3大知识模块:1、概率、概率基本性质及简单的概型,2、随机变量及其分布与数字特征,3、统计基本概念、参数估计及假设检验,这部分是数二的同学不要求的,而数一和数三大纲的要求还是有些差距的,比如数一要求假设检验而数三不要求。
建议大家可以按下面提供的方法进行四个不同层次的归纳总结:第一个层次是概念、性质、公式、定理及相关知识之间的联系、区别的归纳与总结。
我们的方法是:首先按照自己认为的重要到次重要的顺序进行回忆,之后比照考试大纲所规定的考试内容,看自己有哪些遗漏了,从而形成完整的知识网络。
我们还要对遗漏的知识点进行分析,要搞清楚这个知识点是由于和这个小的知识模块关系不紧密而没有联系起来,还是自己在复习过程中忽略了。
数学分析第二章极限与连续知识网络思维导图及复习
量求极限。 6、 理解函数连续的概念,会判断函数不连续点的类型。 7、 掌握用基本定理证明闭区间上连续函数的最大值、最小值、介值性定理的基本思路和方
法。 8、 理解一致连续的概念,并会应用其证明相关命题。 三、知识点梳理 1、数列极限的概念、性质与定理
不一致连续: 0
0,
xn
,xn
,
lim(
n
xn
x)
0 ,而 lim( n
f
(xn )
f
( xn)
c
0.
四、典型例题分析
基本题型 I 利用定义证明数列的极限
例
证明
lim
n
n 2n
0
证 明 : 0, 要 使 得
n 2n
0
成立,只要
n 2n
0
n 2n
2 n
(这是因为
2n (11)n 1 n n(n 1) ... n2
(ii) 同 阶 无 穷 小 : lim f (x) a 0 , 则 称 f (x) 是 g(x) 的 同 阶 无 穷 小 , 记 为 xx0 g(x)
f (x) Og(x) x x0 ,
0
特别地,如果 f (x) 在 O(x0 ) 有界,记作 f (x) O(1), (x x0 )
③ 函数的不连续点
(i)第一类不连续点: f (x0 0), f (x0 0) 存在,但不相等。
(ii)第二类不连续点: f (x0 0), f (x0 0) 中至少有一个不存在.
(iii)可移不连续点:
f (x0
0)
f
(x0
线性代数各知识脉络图

线性代数各知识脉络图————————————————————————————————作者:————————————————————————————————日期:一、行列式知识结构网络图概念性质展开式计算证明0A =应用经转置行列式的值不变; 某行有公因数k ,可把k 提到行列不同行、不同列的n 个1nn ik ikk D a A ==∑(按i 行展开) 1n n kj kjk D a A ==∑(按j 行余子式、给定(i ,j )未给定(i ,j )化三角形-加边法、爪用行列式性质计算; 克拉默法则;判断方阵的可逆,利用伴随几()n n R n⨯<A ;0是方阵A 的特征值;行列行列式是线性代数中的重要工具,在求解线性方程组、求逆矩阵、判断向量组的线性相关性、求矩阵的特征值、判断二次型的正定性等方面都要用到.本章的重点是应用行列式的性质和展开定理计算行列式.行列式的计算除了利用性质及展开定理外,还有三角化法、升阶法、递推法和数学归纳法等,计算方法多,技巧性强,这是难点所在.要掌握好这些方法,首先必须具体分析所求行列式元素分布的规律,针对其特点采取适当的方法;其次是要注意总结、积累经验,不断提高运算能力.行列式的性质【例】:已知531,252,234都是9的倍数,利用行列式的性质(而不是展开),证明522353124也是9的倍数。
解答:522353124231321010r r ,r r ++522353531252234139r 5229353582726【例】:如果除最后一行外,从每一行减去后面的一行,而从最后一行减去原先的第一行,问行列式值如何变化?解答:设原行列式为⎪⎪⎪⎭⎫ ⎝⎛=n A ααM 1det ,则新的行列式为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----=-113221det ααααααααn n n B M, ()00,,3,2det 11321113221=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=--ααααααααααααααn n n i n n n n i r r B MΛM特殊行列式1、(主)对角行列式、上(下)三角行列式1111111111221122221111111niii nnnnnna a a a a a a a a a a a a a a a ====∏L LOM M O OM L2、(次)对角行列式、上(下)三角行列式()()12111111212212121111111n n nnn n n,n ,n,n ,n iii n n,n nn n n a a a a a a a a a a aa a a a a ----=-===-∏LL N N M N L3、分块三角行列式 形式简记为:*==⨯*A O A AB BO B,()1k n⨯*==-⨯*O A AA B BB O4、范德蒙德行列式()211112112122222221212121111111121121111111,,,11n n n n n n n n n n n n n n n n n n nn n x x x x x x x x x x f x x x x x x x x x x x x x x x x x --------------==L L L L L L M M M M M M M M L LL()()121,,,n ijn i j f x x x x x ≥>≥=-∏L ()()()()()1213211212111,,,n nj n j j j n j n j j j f x x x xx xx xx x x --≥≥-≥≥≥≥≥≥=-⋅---∏∏∏∏L L()()()()1221n n n n n n x x x x x x x x --=----L()()()()()()()12131211323121n n n n n n x x x x x x x x x x x x x x -------------L L认识范德蒙德行列式可以将n 阶范德蒙德行列式看成式关于n 个变量12,,,n x x x L 的函数,即()12,,,n n D f x x x =L 。
考研高等数学思维导图

则在开区间(a,b)内至少有一点 ξ,使f (ξ ) = 0.
③ 设函数f (x)在闭区间[a,b]上连续,且在这区间的端点取不同的函数值,f (a) = A, f (b) = B,
则对于A与B之间的任意一个数C,在开区间(a,b)内至少有一点ξ,使得f (ξ) = C(a < ξ < b).
可去间断点:(1)=(2)≠(3) 跳跃间断点:(1)≠(2)
第二类间断点,(1)、(2)至少有一个不存在 无穷间断点、振当间断点都属于第二类
常考:无定义点一定是间断点;分段点可能是间断点
渐近线 水平渐近线、铅直渐近线、斜渐近线
1/31
① 在闭区间上连续的函数在该区间上有界且一定能取得它的最小值和最大值
数列极限总结 ........................................................................ 3
第六章 定积分的应用 ....................................................................17
④ ∀ε > 0, ∃δ > 0,当0 < x − x0 < δ时,有 f (x) − A < ε ⇔ lim f (x) = A x→ x0
第二章 导数与微分.......................................................................... 5
第八章 向量代数与空间解析几何(数一).....................................20
高等数学考研复习思维导图 脑图

高等数学函数特性:有界性、单调性、奇偶性、周期性反函数、复合函数、分段函数初等函数极限无穷小两个重要极限间断点连续零点定理、介值定理洛必达法则、泰勒公式导数和微分求导反函数求导复合函数求导高阶导数隐函数求导参数方程求导拐点、凹凸性最大值、最小值微分微分中值定理罗尔定理朗格拉日中值定理*柯西中值定理曲率、弧微分不定积分换元法分部积分法定积分反常积分微分方程可分离变量的微分方程齐次方程一阶线性微分方程齐次非齐次伯努利方程可降阶的高阶微分方程高/二阶线性微分方程解的结构常系数齐次线性微分方程常系数非齐次线性微分方程欧拉方程空间解析几何向量数量积向量积混合积曲面一次曲面二次曲面柱面圆柱面椭圆住吗抛物柱面椭圆锥面椭球面单叶双曲面双叶双曲面椭圆抛物面双曲抛物面(马鞍面)空间曲线空间曲线的一般方程空间曲线的参数方程空间曲线在坐标面上的投影平面及方程平面一般方程两平面夹角平面束方程空间直线及方程空间直线的一般方程空间直线的对称式方程空间直线的参数方程两直线夹角直线与平面的夹角多元函数微分法多元函数点集极限连续性偏导数全微分多元函数复合求导隐函数求导一个方程的情况方程组的情况几何应用一元向量值函数及导数空间曲线的切线和法平面曲面的切平面和法线(偏导数有关)方向导数和梯度(偏导数有关)多元函数的极值(偏导数有关)条件极值重积分二重积分性质极坐标计算二重积分三重积分柱面坐标计算三重积分球面坐标计算三重积分曲线积分对弧长的曲线积分(线密度)对坐标的曲线积分(力做功)两类曲线积分之间的关系格林公式路径无关原函数的一个全微分曲面积分对面积的曲面积分对坐标的曲面积分两类曲面积分之间的联系高斯公式无穷级数基本知识常数项级数、收敛、发散收敛级数的基本性质正项级数定义审敛比较审敛法比较审敛法的极限形式比值审敛法*根值审敛法(柯西审敛法)极限审敛法交错级数绝对收敛、条件收敛幂级数阿贝尔定理性质和运算收敛半径函数展开成幂级数傅立叶级数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
第八单元矩阵代数
5
壳虫分享论坛,想您所想,做您所想!
第九单元矩阵的特征值和特征向量
第十一单元随机事件和概率
6
壳虫分享论坛,想您所想,做您所想!
7
壳虫分享论坛,想您所想,做您所想!
第
8
壳虫分享论坛,想您所想,做您所想!
第十四单元中心极限定理
壳虫分享论坛,想您所想,做您所想!
考研数学知识网络图
第一单元极限和一元函数微分学
1
壳虫分享论坛,想您所想,做您所想!
第二单元一元函数积分学
2
壳虫分享论坛,想您所想,做您所想!
第三单元多元函数微积分学
3
壳虫分享论坛,想您所想,做您所想!
第六单元行列式
第七单元向量与线性方程组
4
壳虫分享论坛,想您所想,做您所想!
