专题1-第4讲
专题1“概念辨析”专题第4讲——水圈、自然带答案
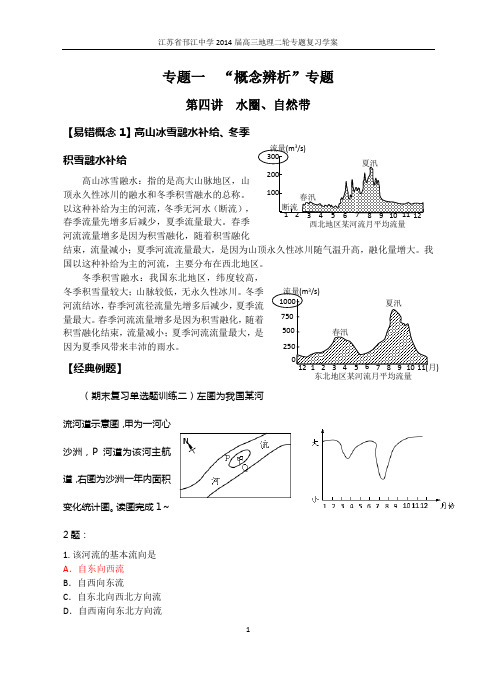
专题一 “概念辨析”专题第四讲 水圈、自然带【易错概念1】高山冰雪融水补给、冬季积雪融水补给高山冰雪融水:指的是高大山脉地区,山顶永久性冰川的融水和冬季积雪融水的总称。
以这种补给为主的河流,冬季无河水(断流),春季流量先增多后减少,夏季流量最大。
春季河流流量增多是因为积雪融化,随着积雪融化结束,流量减小;夏季河流流量最大,是因为山顶永久性冰川随气温升高,融化量增大。
我国以这种补给为主的河流,主要分布在西北地区。
冬季积雪融水:我国东北地区,纬度较高,冬季积雪量较大;山脉较低,无永久性冰川。
冬季河流结冰,春季河流径流量先增多后减少,夏季流量最大。
春季河流流量增多是因为积雪融化,随着积雪融化结束,流量减小;夏季河流流量最大,是因为夏季风带来丰沛的雨水。
【经典例题】(期末复习单选题训练二)左图为我国某河流河道示意图,甲为一河心沙洲,P 河道为该河主航道,右图为沙洲一年内面积变化统计图。
读图完成1~2题: 1. 该河流的基本流向是 A .自东向西流 B .自西向东流C .自东北向西北方向流D .自西南向东北方向流 2. 根据图中信息判断,关于该河流说法正确的是①位于我国西北地区 ②有春汛现象 ③夏季以雨水补给为主 ④河流含沙量大 A .①③ B .②③ C .①④ D .②④【易错概念2】凌汛凌汛指的是冰凌堵塞河道,河水上涨的现象。
凌汛的产生,需要同时具备两个条件:①河流有结冰期;②河流由较低纬度流向较高纬度。
【经典例题】(期末复习双选题训练)青藏高原拥有庞大的淡水资源,“藏水北调”的设想引起极大关注和争论。
读图回答第3-4题。
)东北地区某河流月平均流量西北地区某河流月平均流量3.(双选)下列天于雅鲁藏布江的描述,正确的是A.径流量年际变化小B.常发生凌汛C.雨水补给为主D.径流量从上游往下游递增4.(双选)“藏水北调”工程可能会A.诱发沿线地质灾害B.加剧青藏地区冰川消融C.改善调入地生态环境D.降低我国水资源利用率【易错概念3】内流河、外流河最终能够汇入海洋的河流,称为外流河。
高考英语二轮专题训练模块2专题1第4讲主旨大意题模拟精练巧押题含解析新人教版

专题1 第4讲A阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项。
(2020·北京通州一模)Infectious diseases and associated deaths have reduced,but they remain a significant threat throughout the world.Infectious diseases outbreaks and the fear and panic that accompany them present various economic risks.First,there are costs to the health system,both public and private,of medical treatment of the infected and of outbreak control.Concern over the spread of a relatively contained outbreak can lead to decreased trade.Travel and tourism to regions affected by outbreaks are also likely to decline.Some long-running outbreaks,such as HIV,prevent foreign direct investment.The economic risks are large.It is estimated that the expected yearly cost of infectious diseases is at roughly $500 billion.Even when the health impact of an outbreak is relatively limited,its economic consequences can quickly become expanded.Liberia,for example,saw GDP growth decline 8 percentages from 2013 to 2014 during the Ebola outbreak in Africa.The risk is complex,but policymakers have tools in response.Investing in improved health care,supply of clean water,and better health systems can reduce the frequency of human contact with viruses.Investment in reliable disease monitoring in both human and animal populations is also critical.Within formal global watch systems,instead of discouraging reporting possible outbreaks,it may be beneficial to develop incentives for reporting suspected cases,as countries may reasonably fear the effects of such reporting on trade,tourism,and other economic rmal monitoring systems,social media for example,which collect information from official reports,media reports,online discussions,and eyewitness observations,can also help national health systems and international responders get ahead of the outbreak news during the early stages.Cooperations for monitoring infectious diseases readiness at the national level provide information national governments can use to react timely to their outbreaks.There is a significant market failure when it comes to vaccines(疫苗) against individual low-probability viruses that collectively are likely to cause panic.Giventhe low probability that any single vaccine of this type will be needed,high Research and Development(R&D) costs,and delayed returns,medical companies hesitate to invest in their development.However,responsible international corporations such as CFPI can overcome this market failure.Its goals include advancing candidate vaccines against specific low-probability,high-severity viruses through proof of concept to enable rapid clinical testing in the event of outbreaks.It also aims to fund development of institutional and technical platforms to speed R&D in response to outbreaks for which there are no vaccines.Undoubtedly,humans and infectious viruses will coexist.However,we can take effective measures to manage the risk of the diseases.Joint action now at the local,national,and multinational levels can go a long way toward protecting our collective well-being in the future.1.What does the underlined word “incentives” in Paragraph 5 probably mean?A.Habits. B.Opinions.C.Arguments D.Rewards.2.CFPI is a special company which .A.is able to predict the trend of the marketB.develops vaccines against infectious virusesC.makes huge profits by selling general medicineD.employs staff who graduate from famous universities3.What does the passage imply?A.More importance should be attached to health care systems.B.All-level cooperations are required to handle infectious diseases.C.It will not be long before mankind thoroughly defeats the viruses.D.Technologies hold the key to the settlement of medical problems.4.Which of the following would be the best title for the passage?A.Health Risks and Research of Infectious DiseasesB.Global Cooperation and Spread of Infectious DiseasesC.Economic Impact and Solutions of Infectious DiseasesD.Medical Service and Development of Infectious Diseases【答案】 1.D 2.B 3.B 4.C【解析】这是一篇说明文。
2014高考历史一轮复习配套课件:必修1 专题1 第4讲 明清君主专制的加强

【参考答案】 (1)理解:宋代的官与差遣分开,有官位不一定有差 遣,也就是没任务。但朝廷也会支付俸禄给他们, 结果造成官员过剩;地方上的监察官很多。结果官 员都人浮于事,相互推卸责任,产生冗官。原因: 北宋初年加强中央集权导致的后果。 (2)明朝初年实行特务统治,加强对大臣的监察。废 丞相,权分六部。
(3)军机处简化了处理政务的手续,办事快捷,提高 了清王朝的行政效率;军机处完全听命于皇帝,军 国大事完全由皇帝一人裁决,是专制皇权发展到顶 峰的标志。 (4)特点:皇权不断加强、相权不断遭到压制。评析: 专制皇权的不断强化是传统官僚体制发展的产物, 可以提高决策效率;导致一人独尊,将国家命运系 于一人,成为社会发展的桎梏。
(4)总体评价: ①便于集权,办理政务迅速、机密,君主旨意畅通 无阻,是皇权高度膨胀的产物。 ②由于军机大臣只起上传下达的作用,这一机构的 设置表明皇权得到空前的加强,它标志着我国的封 建君主专制主义中央集权发展到了顶点。
考点1:明朝君主专制的加强 【1—1】(2013· 山东基能)在中国古代,“中央政府的 组织,皇权相权是划分的,期间比重纵有不同,但总 不能说一切由皇帝专制”。这一状况被彻底改变始于 ( )
二、清朝加强君主专制的措施 1.议政王大臣会议:清初,军国机要由议政王大臣 会议定夺。议政王大臣会议的权力凌驾于内阁、六 部之上。皇权受到很大限制。 2.南书房的设置:康熙亲政后,为扩大皇权,在宫 内设南书房,挑选翰林院学士入值。当值的翰林院 学士实际上是参与机务,替皇帝起草谕旨。中枢机 构一分为三,内阁、议政王大臣会议与南书房三足 鼎立,互相制约,最后集权于皇帝。
(4)影响: ①废丞相,权分六部。此措施解决了长期以来存在 的君权与相权之间的矛盾,进一步强化了皇权,历 时1600多年的丞相制度被废除。 ②废行省,设三司。三司是中央在地方的派出机关, 互不统属,分权鼎立,互相牵制,遇有重大事宜, 由三司合议,上报中央部院,从而便于中央垂直领 导,加强了朝廷对地方的控制,形成了极端的君主 专制统治。
2023届高考化学一轮复习 第4讲 元素周期表 化学键 分子结构与性质 课件(103张PPT)

逐渐__增_强___
逐渐__减_弱___
酸性_增__强___
酸性_减__弱___
碱性_减__弱___
碱性_增__强___
_增_强__
_减_弱__
(1) 元素主要化合价 ①F 无正价,O 无最高正价。 ②主族元素最高正价=原子核外最外层电子数(O、F 除外)。 ③非金属元素的最低化合价=原子核外最外层电子数-8(H 除外);最高正化合价 +|最低负化合价|=8(H、B 除外)。
族序数等于周期序数 3 倍的元素 根据金属性、非 金属性最强的元素
金属性推断
非金属性最强的元素
空气中含量最多的元素
根据含量推断 地壳中含量最多的元素
地壳中含量最多的金属元素
元素 _____H_、_B_e_、__A_l ______
___C_、_S_____ __O____
___N_a____ ___F___ ___N___ ___O___
类型 6 利用元素在周期表中的位置推断元素 (2021·南京、盐城一模)图为元素周期表中短周期的一部分,下列说法不正
确的是( A ) A. 离子半径:M->Z2->Y- B. 电负性:Y>M>Z C. 简单气态氢化物的稳定性: Y>M>Z D. Y 元素基态原子的简化电子排布式:[X]2s22p5
逐渐_减__弱___
逐渐__增_强___
非金属性
逐渐__增_强___
逐渐__减_弱___
元素性质 化合物性质
内容 第一电离能 电负性
最高价氧化物对应水化物 氢化物稳定性
同周期(从左到右) 同主族(自上而下)
总体呈现__增__大____的
趋势,但__Ⅱ_A___族和 逐渐__减__小__
专题一 第4讲 现代诗歌的表达技巧

返回
2.下面对诗歌艺术特色的赏析,不正确的一项是(3分) ( ) A.这首诗由三部分组成,每部分均以这样两句诗开头: “雪落在中国的土地上,/寒冷在封锁着中国呀……”它 重复叠现,构成了这首诗的主旋律。 B.“雪落在中国的土地上”,这里的“土地”,是一种单 纯的客观景物,是作者抒情的载体。 C.“寒冷”“封锁”等词语虽然简洁,但极富弹力与表现 力,它们蕴涵着深深的历史和现实的思考,使诗的意象 和内涵增添了极大的重量。 D.“沿着雪夜的河流……——啊,你/蓬发垢面的少妇”, 这一环境描写为后面创设了凄凉又阴沉的氛围。
返回
(3)要指明表达的作用。分析完了修辞手法只能算是答了一 半,其表意作用则是另一半。表意作用要紧扣修辞手法作 答。如本题中的拟人则要扣住“变无情的自然为有情”这一 角度作答。 [参考答案] 用了拟人的修辞手法。“倦意”“黎明的 眼”“湿草的懒味”等词语,不仅真切地呈现了黎明的情 景,且把无情的自然万物变得富有人情味,很好地折射了 “我”的内在情感。
《再别康桥》的 参考答案:(1)结构上:首尾呼应,结构严谨,并且造成
第一节和最后一 了全诗回环往复的韵律美。
节,语意相似, (2)内容上:诗人无限的情思,由一个“轻轻的招手”这 节奏相同,这样 样的动作牵动出来,并以“挥一挥衣袖”这样的动作结 写有什么作用? 束,貌似复唱,实际上情感已得到深化,渲染了伤别的 请简要赏析。 氛围,构成了主题的回旋。
返回
(3)画面描写
画面
分析
总结
诗人把笔触指向了女性的悲 在这首诗中,诗人勾
惨遭遇,“蓬发垢面的少妇”“垂 勒 了 两 幅 饥 馑 流 亡 第一
着头”坐在“破烂的乌篷船里”, 图,表现了人民所遭 幅
专题一第4讲 切线及函数零点问题

第4讲导数与函数图象的切线及函数零点问题一、选择题1.曲线y=xx+2在点(-1,-1)处的切线方程为() A.y=2x+1 B.y=2x-1 C.y=-2x-3 D.y=-2x-2解析易知点(-1,-1)在曲线上,且y′=x+2-x(x+2)2=2(x+2)2,所以切线斜率k=y′|x=-1=21=2.由点斜式得切线方程为y+1=2(x+1),即y=2x+1.答案 A2.(2015·雅安诊断)若曲线f(x)=a cos x与曲线g(x)=x2+bx+1在交点(0,m)处有公切线,则a+b的值为()A.-1 B.0 C.1 D.2解析∵f′(x)=-a sin x,∴f′(0)=0.又g′(x)=2x+b,∴g′(0)=b,∴b=0.又g(0)=1=m,∴f(0)=a=m=1,∴a+b=1.答案 C3.(2015·威海模拟)直线y=kx+1与曲线y=x3+ax+b相切于点A(1,3),则2a +b的值为()A.2 B.-1 C.1 D.-2解析∵y′=3x2+a.∴y′|x=1=3+a=k,又3=k+1,∴k=2,∴a=-1.又3=1+a+b,∴b=3,∴2a+b=-2+3=1.答案 C4.(2015·武汉模拟)曲线y=x ln x在点(e,e)处的切线与直线x+ay=1垂直,则实数a的值为()A .2B .-2 C.12 D .-12解析 依题意得y ′=1+ln x ,y ′|x =e =1+ln e =2,所以-1a ×2=-1,a =2,故选A.答案 A5.已知e 是自然对数的底数,函数f (x )=e x +x -2的零点为a ,函数g (x )=ln x+x -2的零点为b ,则下列不等式中成立的是( ) A .f (a )<f (1)<f (b ) B .f (a )<f (b )<f (1) C .f (1)<f (a )<f (b )D .f (b )<f (1)<f (a )解析 由题意,知f ′(x )=e x +1>0恒成立,所以函数f (x )在R 上是单调递增的,而f (0)=e 0+0-2=-1<0,f (1)=e 1+1-2=e -1>0,所以函数f (x )的零点a ∈(0,1);由题意,知g ′(x )=1x +1>0,所以g (x )在(0,+∞)上是单调递增的,又g (1)=ln 1+1-2=-1<0,g (2)=ln 2+2-2=ln 2>0,所以函数g (x )的零点b ∈(1,2).综上,可得0<a <1<b <2. 因为f (x )在R 上是单调递增的, 所以f (a )<f (1)<f (b ).答案 A二、填空题6.已知f (x )=x 3+f ′⎝ ⎛⎭⎪⎫23x 2-x ,则f (x )的图象在点⎝ ⎛⎭⎪⎫23,f ⎝ ⎛⎭⎪⎫23处的切线斜率是________.解析 f ′(x )=3x 2+2f ′⎝ ⎛⎭⎪⎫23x -1,令x =23,可得f ′⎝ ⎛⎭⎪⎫23=3×⎝ ⎛⎭⎪⎫232+2f ′⎝ ⎛⎭⎪⎫23×23-1,解得f ′⎝ ⎛⎭⎪⎫23=-1,所以f (x )的图象在点⎝ ⎛⎭⎪⎫23,f ⎝⎛⎭⎪⎫23处的切线斜率是-1.答案 -17.(2015·青岛模拟)关于x 的方程x 3-3x 2-a =0有三个不同的实数解,则实数a的取值范围是________.解析 由题意知使函数f (x )=x 3-3x 2-a 的极大值大于0且极小值小于0即可,又f ′(x )=3x 2-6x =3x (x -2),令f ′(x )=0,得x 1=0,x 2=2.当x <0时,f ′(x )>0;当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0,所以当x =0时,f (x )取得极大值,即f (x )极大值=f (0)=-a ;当x =2时,f (x )取得极小值,即f (x )极小值=f (2)=-4-a ,所以⎩⎨⎧-a >0,-4-a <0,解得-4<a <0.答案 (-4,0)8.(2015·安徽卷)设x 3+ax +b =0,其中a ,b 均为实数,下列条件中,使得该三次方程仅有一个实根的是________(写出所有正确条件的编号). ①a =-3,b =-3;②a =-3,b =2;③a =-3,b >2; ④a =0,b =2;⑤a =1,b =2.解析 令f (x )=x 3+ax +b ,f ′(x )=3x 2+a ,当a ≥0时,f ′(x )≥0,f (x )单调递增,必有一个实根,④⑤正确;当a <0时,由于选项当中a =-3,∴只考虑a =-3这一种情况,f ′(x )=3x 2-3=3(x +1)(x -1),∴f (x )极大=f (-1)=-1+3+b =b +2,f (x )极小=f (1)=1-3+b =b -2,要使f (x )=0仅有一个实根,则而f (x )极大<0或f (x )极小>0,∴b <-2或b >2,①③正确,所有正确条件为①③④⑤.答案 ①③④⑤三、解答题9.已知曲线C :y =e ax . (1)若曲线C 在点(0,1)处的切线为y =2x +m ,求实数a 和m 的值;(2)对任意实数a ,曲线C 总在直线l :y =ax +b 的上方,求实数b 的取值范围. 解 (1)y ′=a e ax ,因为曲线C 在点(0,1)处的切线为y =2x +m , 所以1=2×0+m 且y ′|x =0=2,解得m =1,a =2.(2)法一 对于任意实数a ,曲线C 总在直线y =ax +b 的上方,等价于∀x ,a ∈R ,都有e ax >ax +b , 即∀x ,a ∈R ,e ax -ax -b >0恒成立. 令g (x )=e ax -ax -b ,①若a =0,则g (x )=1-b ,所以实数b 的取值范围是b <1;②若a ≠0,g ′(x )=a (e ax -1),由g ′(x )=0得x =0,g ′(x ),g (x )的变化情况如下:所以g (x ) 所以实数b 的取值范围是b <1. 综上,实数b 的取值范围是b <1.法二 对于任意实数a ,曲线C 总在直线y =ax +b 的上方,等价于∀x ,a ∈R ,都有e ax >ax +b ,即∀x ,a ∈R ,b <e ax -ax 恒成立.令t =ax ,则等价于∀t ∈R ,b <e t -t 恒成立. 令g (t )=e t -t ,则g ′(t )=e t -1.由g ′(t )=0得t =0,g ′(t ),g (t )的变化情况如下:所以g (t )所以实数b 的取值范围是b <1.10.(2015·济南模拟)已知函数f (x )=2ln x -x 2+ax (a ∈R ). (1)当a =2时,求f (x )的图象在x =1处的切线方程;(2)若函数g (x )=f (x )-ax +m 在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点,求实数m 的取值范围.解 (1)当a =2时,f (x )=2ln x -x 2+2x , f ′(x )=2x -2x +2,切点坐标为(1,1), 切线的斜率k =f ′(1)=2,则切线方程为y -1=2(x -1),即y =2x -1. (2)g (x )=2ln x -x 2+m ,则g ′(x )=2x -2x =-2(x +1)(x -1)x.因为x ∈⎣⎢⎡⎦⎥⎤1e ,e ,所以当g ′(x )=0时,x =1.当1e <x <1时,g ′(x )>0;当1<x <e 时,g ′(x )<0. 故g (x )在x =1处取得极大值g (1)=m -1. 又g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2,g (e)=m +2-e 2,g (e)-g ⎝ ⎛⎭⎪⎫1e =4-e 2+1e 2<0,则g (e)<g ⎝ ⎛⎭⎪⎫1e ,所以g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上的最小值是g (e).g (x )在⎣⎢⎡⎦⎥⎤1e ,e 上有两个零点的条件是⎩⎪⎨⎪⎧g (1)=m -1>0,g ⎝ ⎛⎭⎪⎫1e =m -2-1e 2≤0,解得1<m ≤2+1e 2,所以实数m 的取值范围是⎝ ⎛⎦⎥⎤1,2+1e 2.11.(2014·四川卷)已知函数f (x )=e x -ax 2-bx -1,其中a ,b ∈R ,e =2.718 28…为自然对数的底数. (1)设g (x )是函数f (x )的导函数,求函数g (x )在区间[0,1]上的最小值; (2)若f (1)=0,函数f (x )在区间(0,1)内有零点. 证明:e -2<a <1.解 (1)由f (x )=e x -ax 2-bx -1,有g (x )=f ′(x )=e x -2ax -b . 所以g ′(x )=e x -2a .当x ∈[0,1]时,g ′(x )∈[1-2a ,e -2a ].当a ≤12时,g ′(x )≥0,所以g (x )在[0,1]上单调递增, 因此g (x )在[0,1]上的最小值是g (0)=1-b ; 当a ≥e2时,g ′(x )≤0,所以g (x )在[0,1]上单调递减, 因此g (x )在[0,1]上的最小值是g (1)=e -2a -b ; 当12<a <e2时,令g ′(x )=0,得x =ln(2a )∈(0,1).所以函数g (x )在区间[0,ln(2a )]上单调递减,在区间(ln(2a ),1]上单调递增.于是,g(x)在[0,1]上的最小值是g(ln(2a))=2a-2a ln(2a)-b.综上所述,当a≤12时,g(x)在[0,1]上的最小值是g(0)=1-b;当12<a<e2时,g(x)在[0,1]上的最小值是g(ln(2a))=2a-2a ln(2a)-b;当a≥e2时,g(x)在[0,1]上的最小值是g(1)=e-2a-b.(2)证明设x0为f(x)在区间(0,1)内的一个零点,则由f(0)=f(x0)=0可知f(x)在区间(0,x0)上不可能单调递增,也不可能单调递减.则g(x)不可能恒为正,也不可能恒为负,故g(x)在区间(0,x0)内存在零点x1. 同理g(x)在区间(x0,1)内存在零点x2.所以g(x)在区间(0,1)内至少有两个零点.由(1)知,当a≤12时,g(x)在[0,1]上单调递增,故g(x)在(0,1)内至多有一个零点.当a≥e2时,g(x)在[0,1]上单调递减,故g(x)在(0,1)内至多有一个零点.所以12<a<e2.此时g(x)在区间[0,ln(2a)]上单调递减,在区间(ln(2a),1]上单调递增.因此x1∈(0,ln(2a)],x2∈(ln(2a),1),必有g(0)=1-b>0,g(1)=e-2a-b>0.由f(1)=0有a+b=e-1<2,由g(0)=a-e+2>0,g(1)=1-a>0.解得e-2<a<1.所以,函数f(x)在区间(0,1)内有零点时,e-2<a<1.。
专题一 第4讲 氧化还原反应

应10NaN3+2KNO3 === K2O+xNa2O+16N2↑,下列说法错误的是
()
关闭
根据A.原x=子5 守恒可知x=5,A正确;题给反应中硝酸钾是氧化剂,氮元素的化合 价从B.+每5价生降成低16到m0价ol ,N所2以转每移生10成m16olm电o子l N2转移10 mol电子,B正确;题给反 应中CD..NN反a2N应既3中后是的氧氧N化化元产产素物物的化与又合还是价原还升产原高物产,作的物还质原量剂之,硝比酸为钾1中∶氮15元素化合价降低,
3.(2019 江苏海安高级中学月考)现有下列氧化还原反应:① 关闭
2由Br反-+应Cl①2 2BBr-+r2C+l22Cl- Br②2+22FCel2-可++B知r2还原性2FeB3+r-+>2CBl-r,-由反③应②
22MFen2O++4- B+1r20Cl-2+F1e63H+++2Br-2可M知n2还++原5C性l2↑F+e82H+>2BOr。-,由根反据应上③述反应,判断下
高频考点
-3-
考点一
考点二
考点三
氧化还原反应概念辨析及规律应用
真题示例
1.(2019北京理综,10)下列除杂试剂选用正确且除杂过程不涉及
氧化还原反应的是( )
关闭
A 项物,Fe质粉(括和号F内eC为l3杂的质反)应 Fe+2Fe除Cl杂3 试3剂FeCl2 属于氧化还原反
应A,AF不eC选l2 溶;B液项(,F加eC入l3)足量 NaOH 溶F液e 粉发生复分解反应生成 MBg(ONHaC)2l沉溶淀液,(过Mg滤C后l2)用盐酸中和过Na量OH的溶N液aO、H稀得盐到酸不含 MgCl2 的CNCaCl2l(H溶C液l) ,B 正确;C 项,除去 ClH2 中2O的、浓H硫Cl酸,可将混合气体通过 饱D和N食O盐(N水O2,然) 后再用浓硫酸干燥,HC2O不、选无;D水项C,aNCOl22 和 H2O 的反
2023年高考英语二轮复习第一部分阅读能力突破篇专题一阅读理解第4讲主旨大意题

lovely gatekeepers welcomed her and kick-started what was to be a trip
Ginni would never forget.
Ever since her childhood, Ginni, now 71, has had a deep love for
第一部分 专题一 阅读理解
高考二轮总复习 • 英语 新教材
返回导航
【解题示范】 第一步:阅读文章,概括文章大意。文章主要介绍 了一种会识别形状的凤头鹦鹉;
第二步:分析各选项,进行斟酌判断,揣摩哪个选项能准确概括主 旨。通读全文,再结合第一段“Coffinʼs cockatoos, a kind of small parrot native to Australasia, have been shown to have similar shaperecognition abilities to a human two-year-old.(科芬的凤头鹦鹉是一种原 产于大洋洲的小鹦鹉,它的形状识别能力与两岁的人类相似。)”可知, 本 文 主 要 介 绍 了 会 识 别 形 状 的 凤 头 鹦 鹉 。 选 项 “Cockatoos: Skilful Shape-Sorters (凤头鹦鹉:识别形状的熟练工)”符合文意,最适合作为 本文标题。故选D。
第一部分 专题一 阅读理解
高考二轮总复习 • 英语 新教材
返回导航
技法点拨 1.定位主题句确定文章大意 文章由段落组成,段落的中心思想服务于文章的中心思想,因此找 到每个段落的主题句,总结概括后便不难得出文章的主旨大意。 一般情况下,段落的主题句通常在该逻辑段落的首尾,但也有些难 度较大的试题会隐含在段落之中,此时要理解全文结构,找到支撑性细 节内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.设f (x )是定义在R 上的奇函数,当x <0时,f ′(x )>0,且f (0)=0,f ⎝ ⎛⎭⎪⎫-12=0,则不等式f (x )<0的解集为( )A.⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫x <12 B.⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫0<x <12C.⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x <-12或0<x <12 D.⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫-12≤x ≤0或x ≥12【解析】 如图所示,根据图象得不等式f (x )<0的解集为⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫x <-12或0<x <12.【答案】 C2.已知函数f (x )=13x 3-2x 2+3m ,x ∈[0,+∞),若f (x )+5≥0恒成立,则实数m 的取值范围是( )A.⎣⎢⎡⎭⎪⎫179,+∞ B.⎝ ⎛⎭⎪⎫179,+∞ C .(-∞,2]D .(-∞,2)【解析】 f ′(x )=x 2-4x ,由f ′(x )>0,得x >4或x <0. ∴f (x )在(0,4)上递减,在(4,+∞)上递增, ∴当x ∈[0,+∞)时,f (x )min =f (4).∴要使f (x )+5≥0恒成立,只需f (4)+5≥0恒成立即可,代入解得m ≥179. 【答案】 A3.若存在正数x 使2x (x -a )<1成立,则a 的取值范围是( ) A .(-∞,+∞) B .(-2,+∞) C .(0,+∞)D .(-1,+∞)【解析】 ∵2x (x -a )<1,∴a >x -12x . 令f (x )=x -12x ,∴f ′(x )=1+2-x ln 2>0. ∴f (x )在(0,+∞)上单调递增, ∴f (x )>f (0)=0-1=-1,∴a 的取值范围为(-1,+∞),故选D. 【答案】 D4.(2017·安徽黄山一模,12)已知函数f (x )=m ⎝ ⎛⎭⎪⎫x -1x -2ln x (m ∈R ),g (x )=-mx ,若至少存在一个x 0∈[1,e],使得f (x 0)<g (x 0)成立,则实数m 的取值范围是( )A.⎝ ⎛⎦⎥⎤-∞,2e B.⎝ ⎛⎭⎪⎫-∞,2e C .(-∞,0]D .(-∞,0)【解析】 由题意,不等式f (x )<g (x )在[1,e]上有解,∵mx <2ln x 在[1,e]上有解,即m 2<ln x x 在[1,e]上有解,令h (x )=ln xx ,则h ′(x )=1-ln x x 2,当1≤x ≤e 时,h ′(x )≥0,∴在[1,e]上,h (x )max =h (e)=1e ,∴m 2<1e ,∴m <2e .∴m 的取值范围是⎝ ⎛⎭⎪⎫-∞,2e .故选B.【答案】 B5.(2017·山东师范大学附中二模)已知定义在R 上的可导函数f (x )的导函数为f ′(x ),满足f ′(x )<f (x ),且f (x +2)为偶函数,f (4)=1,则不等式f (x )<e x 的解集为( )A .(-2,+∞)B .(0,+∞)C .(1,+∞)D .(4,+∞)【解析】 由f (x +2)为偶函数可知函数f (x )的图象关于x =2对称,则f (4)=f (0)=1.令F (x )=f (x )e x ,则F ′(x )=f ′(x )-f (x )e x<0.∴函数F (x )在R 上单调递减.又f (x )<e x 等价于f (x )e x <1,∴F (x )<F (0),∴x >0.【答案】 B 二、填空题6.已知不等式e x -x >ax 的解集为P ,若[0,2]⊆P ,则实数a 的取值范围是________.【解析】 由题意知不等式e x -x >ax 在x ∈[0,2]上恒成立. 当x =0时,显然对任意实数a ,该不等式都成立.当x ∈(0,2]时,原不等式即a <e x x -1,令g (x )=e xx -1,则g ′(x )=e x (x -1)x 2,当0<x <1时,g ′(x )<0,g (x )单调递减,当1<x <2时,g ′(x )>0,g (x )单调递增,故g (x )在(0,2]上的最小值为g (1)=e -1,故a 的取值范围为(-∞,e -1).【答案】 (-∞,e -1)7.若在区间[0,1]上存在实数x 使2x (3x +a )<1成立,则a 的取值范围是________.【解析】 2x (3x +a )<1可化为a <2-x -3x ,则在区间[0,1]上存在实数x 使2x (3x +a )<1成立,等价于a <(2-x -3x )max ,而2-x -3x 在[0,1]上单调递减,∴2-x -3x 的最大值为20-0=1,∴a <1,故a 的取值范围是(-∞,1). 【答案】 (-∞,1) 8.已知函数f (x )=x -1x +1,g (x )=x 2-2ax +4,若对于任意x 1∈[0,1],存在x 2∈[1,2],使f (x 1)≥g (x 2),则实数a 的取值范围是________.【解析】 由于f ′(x )=1+1(x +1)2>0,因此函数f (x )在[0,1]上单调递增,所以x ∈[0,1]时,f (x )min =f (0)=-1.根据题意可知存在x ∈[1,2],使得g (x )=x 2-2ax +4≤-1,即x 2-2ax +5≤0,即a ≥x 2+52x 能成立,令h (x )=x 2+52x ,则要使a ≥h (x )在x ∈[1,2]上能成立,只需使a ≥h (x )min ,又函数h (x )=x 2+52x 在x ∈[1,2]上单调递减,所以h (x )min =h (2)=94,故只需a ≥94.【答案】 ⎣⎢⎡⎭⎪⎫94,+∞三、解答题9.已知f(x)=x ln x,g(x)=-x2+ax-3.(1)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;(2)证明:对一切x∈(0,+∞),都有ln x>1e x-2e x成立.(1)【解】∀x∈(0,+∞),有2x ln x≥-x2+ax-3,则a≤2ln x+x+3 x,设h(x)=2ln x+x+3x(x>0),则h′(x)=(x+3)(x-1)x2,①当x∈(0,1)时,h′(x)<0,h(x)单调递减,②当x∈(1,+∞)时,h′(x)>0,h(x)单调递增,所以h(x)min=h(1)=4.因为对一切x∈(0,+∞),2f(x)≥g(x)恒成立,所以a≤h(x)min=4,即a的取值范围为(-∞,4].(2)【证明】问题等价于证明x ln x>xe x-2e(x∈(0,+∞))成立.f(x)=x ln x(x∈(0,+∞))的最小值是-1 e,当且仅当x=1e时取到.设m(x)=xe x-2e(x∈(0,+∞)),则m′(x)=1-xe x,易知m(x)max=m(1)=-1e,当且仅当x=1时取到.从而对一切x∈(0,+∞),都有ln x>1e x-2e x成立.10.(2017·潍坊一模)已知函数f(x)=ln x+x2-ax(a为常数).(1)若x=1是函数f(x)的一个极值点,求a的值;(2)当0<a≤2时,试判断f(x)的单调性;(3)若对任意的a∈(1,2),x0∈[1,2],不等式f(x0)>m ln a恒成立,求实数m 的取值范围.【解】f′(x)=1x+2x-a.(1)由已知得:f′(1)=0,所以1+2-a=0,所以a=3.(2)当0<a≤2时,f′(x)=1x+2x-a=2x2-ax+1x=2⎝⎛⎭⎪⎫x-a42+1-a28x.因为0<a≤2,所以1-a28>0,而x>0,即f′(x)=2x2-ax+1x>0,故f(x)在(0,+∞)上是增函数.(3)当a∈(1,2)时,由(2)知,f(x)在[1,2]上的最小值为f(1)=1-a,故问题等价于:对任意的a∈(1,2),不等式1-a>m ln a恒成立,即m<1-a ln a恒成立.记g(a)=1-aln a(1<a<2),则g′(a)=-a ln a-1+aa(ln a)2.令M(a)=-a ln a-1+a,则M′(a)=-ln a<0,所以M(a)在(1,2)上单调递减,所以M(a)<M(1)=0,故g′(a)<0,所以g(a)=1-aln a在a∈(1,2)上单调递减,所以m≤g(2)=1-2ln 2=-log2e,即实数m的取值范围为(-∞,-log2e].11.已知函数f(x)=ax+bx+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.(1)用a表示出b,c;(2)若f(x)≥ln x在[1,+∞)上恒成立,求a的取值范围;(3)证明:1+12+13+…+1n>ln(n+1)+n2(n+1)(n≥1).(1)【解】 f ′(x )=a -bx 2,则有⎩⎨⎧f (1)=a +b +c =0,f ′(1)=a -b =1,解得⎩⎨⎧b =a -1,c =1-2a .(2)【解】 由(1)知,f (x )=ax +a -1x +1-2a .令g (x )=f (x )-ln x =ax +a -1x +1-2a -ln x ,x ∈[1,+∞),则g (1)=0,g ′(x )=a -a -1x 2-1x =ax 2-x -(a -1)x 2=a (x -1)⎝⎛⎭⎪⎫x -1-a a x 2,(ⅰ)当0<a <12时,1-a a >1.若1<x <1-aa ,则g ′(x )<0,g (x )是减函数, 所以g (x )<g (1)=0,即f (x )<ln x . 故f (x )≥ln x 在[1,+∞)上不成立. (ⅱ)当a ≥12时,1-a a ≤1.若x >1,则g ′(x )>0,g (x )是增函数, 所以g (x )>g (1)=0,即f (x )>ln x ,故当x ≥1时,f (x )≥ln x . 综上所述,所求a 的取值范围为⎣⎢⎡⎭⎪⎫12,+∞.(3)【证明】 法一 由(2)知:当a ≥12时,有f (x )≥ln x (x ≥1). 令a =12,有f (x )=12⎝ ⎛⎭⎪⎫x -1x ≥ln x (x ≥1),且当x >1时,12⎝ ⎛⎭⎪⎫x -1x >ln x .令x =k +1k ,有ln k +1k <12⎝ ⎛⎭⎪⎫k +1k -k k +1=12⎣⎢⎡⎦⎥⎤⎝ ⎛⎦⎥⎤1+1k -⎝ ⎛⎭⎪⎫1-1k +1, 即ln(k +1)-ln k <12⎝ ⎛⎭⎪⎫1k +1k +1,k =1,2,3,…,n .将上述n个不等式依次相加得ln(n+1)<12+⎝⎛⎭⎪⎫12+13+…+1n+12(n+1),整理得1+12+13+…+1n>ln(n+1)+n2(n+1).法二用数学归纳法证明.①当n=1时,左边=1,右边=ln 2+14<1,不等式成立.②假设n=k时,不等式成立,即1+12+13+…+1k>ln(k+1)+k2(k+1).那么1+12+13+…+1k+1k+1>ln(k+1)+k2(k+1)+1k+1=ln(k+1)+k+22(k+1).由(2)知:当a≥12时,有f(x)≥ln x(x≥1).令a=12,有f(x)=12⎝⎛⎭⎪⎫x-1x≥ln x(x≥1).令x=k+2k+1,得:12⎝⎛⎭⎪⎫k+2k+1-k+1k+2≥lnk+2k+1=ln(k+2)-ln(k+1).∴ln(k+1)+k+22(k+1)≥ln(k+2)+k+12(k+2).∴1+12+13+…+1k+1k+1>ln(k+2)+k+12(k+2).这就是说,当n=k+1时,不等式也成立.根据①和②,可知不等式对任何n∈N*都成立.。
