气体分子热运动速率和能量的统计分布律
第三章气体分子热运动速率

C
0
2021/3/31
v v 0崎山苑工作室
28
(2)常数 C 由归一化条件求得
0v0 f (v)dv 1
0v0 Cdv 1
C v0 1
C
1 v0
(3)平均速率:
v
2021/3/31
0
1
v0
vf (v)dv
v02 2
1 2
v0
崎山苑工作室
0v0
v
1 dv v0
29
例3. 由麦氏分布律导出理想气体分子按平动动能的分布律,并找
f vx ,vy ,vz
m e 2
m
vx2
v
2 y
vz2
2kT
2kT
2021/3/31
dvx、dvy、dvz为速度空间的一个体积元
崎山苑工作室
32
*速度空间(velocity space)的概念 v 表示分子的速度
以其分量vx、 vy、 vz为轴可构成一直角坐标系,
由此坐标系所确定的空间为速度空间。
崎山苑工作室
15
气体的三种统计速率
(1)最可几速率: 速率分布函数 f (v)中的极大值对应
的分子速率 v p 。
d f (v)
极值条件
0
f
(v)
4
dv
m
2kT
3
2
e
mv2 2kT
v
2
vp
2kT
m
2RT
1.41
RT
温度超高,vp越大;分子的质量越大, vp越小
2021/3/31
崎山苑工作室
h
dN(h) Nf (h)dh
h
《气体分子运动的统计规律》 讲义

《气体分子运动的统计规律》讲义一、气体分子的热运动在我们的日常生活中,气体无处不在,比如我们呼吸的空气、充满气球的氢气等。
那么,这些气体分子是如何运动的呢?气体分子处于永不停息的无规则运动之中,这种运动被称为热运动。
想象一下,在一个封闭的容器中,充满了气体分子,它们就像一群顽皮的孩子,四处乱跑,相互碰撞,没有固定的方向和轨迹。
气体分子的热运动具有以下几个特点:速度的多样性:不同的气体分子具有不同的速度。
有的分子运动速度快,有的则慢。
无规则性:它们的运动方向是随机的,无法预测下一刻某个分子会往哪个方向跑。
频繁的碰撞:分子之间会不断地发生碰撞,这使得它们的运动状态不断改变。
二、气体分子运动的统计规律既然气体分子的运动如此复杂和无规则,那我们要如何去描述和理解它们的整体行为呢?这就需要依靠统计规律。
什么是统计规律呢?简单来说,就是通过对大量个体行为的观察和分析,总结出的总体的、平均的规律。
对于气体分子,我们无法确切知道每个分子在每一时刻的具体运动状态,但我们可以通过统计方法来了解它们的一些总体特征。
比如,我们可以统计在一定温度和压强下,气体分子的速度分布情况。
麦克斯韦速度分布律就是描述气体分子速度分布的重要规律。
它告诉我们,在一定条件下,气体分子的速度分布呈现出一定的规律性,速度较小和较大的分子较少,而具有中等速度的分子较多。
再比如,气体分子对容器壁的压强,也是通过对大量分子撞击容器壁的行为进行统计得出的。
三、麦克斯韦速度分布律麦克斯韦速度分布律是描述气体分子运动速度分布的关键规律。
假设在一个容器中充满了理想气体,处于平衡态。
麦克斯韦速度分布律表明,分子速度在三个方向上(x、y、z)的分量的分布都是独立的,且满足一定的概率分布。
具体来说,速度分量 vx 的分布函数为 f(vx) , vy 和 vz 的分布函数类似。
通过对这些分布函数的积分,可以得到分子速度的大小 v 的分布函数 f(v) 。
麦克斯韦速度分布律在许多方面都有重要的应用。
热学-统计物理3 第3章 气体分子热运动速率和能量的统计分布律
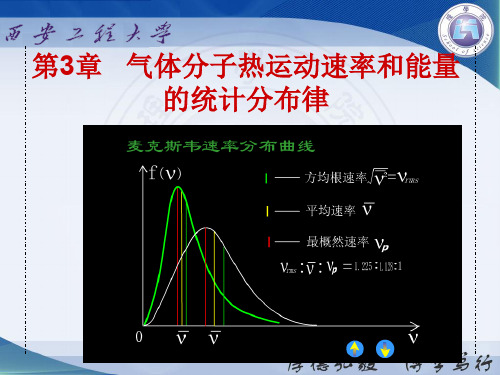
v v pv v 2
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确?
(A) vp 是气体分子中大部分分子所具有的速率. (B) vp 是速率最大的速度值. (C) vp 是麦克斯韦速率分布函数的最大值.
(D) 速率大小与最概然速率相近的气体分子的比 率最大.
例1 计算在 27 C 时,氢气和氧气分子的方均
M
3.方均根速率 v2
v2
N
0
v2dN N
0
v2Nf N
(v)dv
o
v
v2 v2 f (v)dv 4 ( m )3 2 e mv2 2kT v4dv
0
2 kT
0
v4ev2 dv 3
0
8 5
v2 3kT m
v2 3kT 3RT
2kT
v
麦克斯韦速率分布函数的物理意义: f (v) dNv
Nd v
既反映理想气体在热动平衡条件下,分布在速率 v 附近单
位速率区间内的分子数占总分子数的百分比,又表示任意
一分子的速率出现在 v附近单位速率区间内的概率。
如果以速率为横坐标轴,速率分布函数为纵坐标轴,画 出的一条表示f(v) —v之间关系的曲线,称为气体分子的麦 克斯韦速率分布曲线。 ,它形象地描绘出气体分子按速率 分布的情况。
大量分子的速率的算术平均值叫做分子的平均速率.
v
vNf (v)dv
0
vf (v)dv
v 4 (
m
)3 e2 mv2 2kT v2dv
N
0
0
第三章 气体分子热运动速率和能量的统计分布规律

Ndv
2kT
1.麦克斯韦速率分布函数f()的物理意义
由 dN f (υ)dυ N
f (υ) dN Ndυ
f()表示:在速率附近的单位速率区间内的分子数占总 分子数的百分比。或分子速率出现在附近的单位速率区间内
的概率概率密度。
f (υ)dυ dN
N
—在速率区间 ~ +d 内的分子数占
例 (1) n f()d 的物理意义是什么?(n是分子的数密度)
(2) 写出速率不大于最可几速率p的分子数占总分子数
的百分比。
解 nf (υ)dυ Nf (υ)dυ dN
V
V
n f()d —表示单位体积中,速率在 ~+d 内的分子数。
(2) 写出速率不大于最可几速率p的分子数占总分子数的
dN v y N
g(y )dy
dNvz N
g(z )dz
(2)由独立概率相乘原理,粒子出现在x ~x+dx,y ~y+dy,z ~z+dz的
概率为:
dNv N
g(x )g(y )g(z )dxdydz
F • dxdydz
F就是速度分布函数
(3)由于粒子在任何方向上运动的概率相等,所以F应该与速度的方向 无关,应该是速度的大小的函数。
dNv N
1
3 3
e dv dv dv (vx2 vy2 vz2 ) / 2 xyz
转化成球坐标:
dvxdvydvz v2 sin dddv
vx2
v
2 y
vz2
v2
麦克斯韦速度分布:dNv 1 v2ev2 / 2 sin dddv N 3 3
热力学-3.气体分子动理论速率与能量

1.59 RT M
一般用于计算分子运动的平均距离;
同理,方均根速率
v2 v2 f (v)dv
3kT
3RT 1.73 RT
0
m
M
M
方均根速率用来计算分子平均动能。
最概然速率
2kT 2RT
RT
vp
m
1.41
M
M
最概然速率用在讨论分子速率分布。
f(v)
O
vp v v2
•在气体动理论方面,他提出气体分子按 速率分布的统计规律。
1。由于分子受到频繁的碰撞,每个分子热运动的速率是变化的, 要某一分子具有多大的运动速率没有意义,所以只能估计在某 个速率间隔内出现的概率;
2。哪怕是相同的速率间隔,但是不同的速率附近,其概率是不 等的。
速率接近为0的可能性很小,速率非常大的可能性也很小, 而居中速率的可能性则较大。
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点: 1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的;
2.范围:(速率v附近的)单位速率间隔,所以要除以dv; 3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
f (v)dv dN N
N v1 v2
v2
f (v)dv
第三章 气体分子热运动 速率和能量的统计分布律
内容回顾
第一章 平衡态和温度 第二章 压强和温度的微观本质
平均效果
气体分子按速率分布的统计规律最早是由麦克斯韦于
1859年在概率论的基础上导出的,1877年玻耳兹曼由经典统 计力学中导出,1920年斯特恩从实验中证实了麦克斯韦分子 按速率分布的统计规律。
热学[李椿 章立源 钱尚武]习题解答_第三章气体分子热运动速率与能量的统计分布律
![热学[李椿 章立源 钱尚武]习题解答_第三章气体分子热运动速率与能量的统计分布律](https://img.taocdn.com/s3/m/581192a543323968001c927e.png)
第 三 章 气体分子热运动速率和能量的统计分布律3-1 设有一群粒子按速率分布如下:试求(1)平均速率V ;(2)方均根速率2V (3)最可几速率Vp解:(1)平均速率:18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=ii i N V N V(m/s)3-2 计算300K 时,氧分子的最可几速率、平均速率和方均根速率。
解:s m RTV P /395103230031.8223=⨯⨯⨯==-μs m RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμs m RTV/483103230031.83332=⨯⨯⨯==-μ3-3 计算氧分子的最可几速率,设氧气的温度为100K 、1000K 和10000K 。
解:μRTV P 2=代入数据则分别为:T=100K 时 s m V P /1028.22⨯= T=1000K 时 s m V P /1021.72⨯= T=10000K 时 s m V P /1028.23⨯=3-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率,求T 2/T 1。
解:因μRTV32=πμ28RT V =由题意得:μRT3πμ28RT =∴T 2/T 1=83π3-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数(在计算中可将dv 近似地取为△v=1m/s )解:设1.0cm 3氮气中分子数为N ,速率在500~501m/s 之间内的分子数为△N ,由麦氏速率分布律:△ N=V V e KTm N V KTm∆⋅⋅⋅-22232)2(4ππ ∵ V p2= 2KTm ,代入上式 △N=VV V ppe V V VN∆--⋅⋅222214ρπ因500到501相差很小,故在该速率区间取分子速率V =500m/s , 又s m V P /402102827331.823≅⨯⨯⨯=- △V=1m/s (vv p=)代入计算得:△N=×10-3N 个3-6 设氮气的温度为300℃,求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。
热学-第三章气体分子热运动速率和能量分布

等概率性
在平衡态下,系统从任意一个微观状态转移到另一个 微观状态的概率相等。
宏观态与微观态等概率性的意义
平衡态是系统内部最混乱的状态,即系统内部各个分 子运动状态的分布最均匀,没有明显的有序性。
热力学概率与宏观态的等概率性
热力学概率
宏观态等概率性与热力学概 率的关系
在平衡态下,系统处于各个宏观态的概率相等,即 热力学概率相等。
了解气体分子的能量分布和速度分布有助于深入理解热力学的基本原理,如温度 、内能、熵等概念。
03 气体分子的碰撞和动量传 递
气体分子间的碰撞频率
总结词
气体分子间的碰撞频率与气体分子的速度分布和分子间的距离有关,是气体分子热运动的重要参数。
详细描述
气体分子间的碰撞频率是指在单位时间内,两个分子相互碰撞的次数。由于气体分子的速度分布和分 子间的距离不同,碰撞频率也会有所差异。在理想气体中,碰撞频率可以用公式计算,它与气体分子 的平均自由程和分子速度有关。
定义
气体分子在热运动中具有的 平均能量是指所有气体分子 的总能量除以分子总数。
计算公式
平均能量 = (总能量) / (分子 总数)
影响因素
温度和物质的种类会影响气 体分子的平均能量。
气体分子的最可几能量
01
定义
气体分子在热运动中具有的最可 几能量是指一定温度下,占据一 定数量的分子的主要能量的值。
熵与自然过程的不可逆性
熵与自然过程的不可逆性密切相关,因为高熵状态对应于无序程度较高的状态,低熵状态对应于有序 程度较高的状态。
在自然过程中,由于熵增加原理的作用,系统总是向着高熵状态发展,即从有序向无序发展。因此,许 多自然过程都是不可逆的。
例如,物体受热会膨胀,但自发地收缩;化学反应会进行到底,但自发地逆向反应很困难;生物体衰老 和死亡后不能自发地恢复青春等。这些都是由于系统内部熵增加导致的不可逆过程。
分子热运动的速度和速率统计分布规律

C 1 vo
vvf(v)dvvoC vdvCvo 2
0
0
2
1
v
2 o
vo
vo 2 2
v20 v2f(v)dv0 voC v2dv1 3vo 2
v2
3 3 vo
9.4.2 分子的速度分布函数:
速度空间(如图) 速度空间的体积元 dVxdVydVz 代表如下速度范围
Vz dVxdVy dVz
-
p
a
A
π
a
-
3 2
v
2 x
v
2 x
e
-
a
v
2 x
d
v
x
-
e
-
a
v
2 x
d
v
x
kT m
-
a m 2kT
F (V x,V y,V z)(2π m kT)3 2e-2m kT(V x2+ V y2+ V z2)
麦克斯韦速度分布函数
2. 麦克斯韦速率分布律
处于平衡态的理想气体系统,速率满足下列分布规律
处于平衡态的理想气体系统利用系统的各向同性性三个速度分量的相互独立性dvdvdvdvdvdvdvdvdvaevvvktfvvvkt麦克斯韦速度分布函数处于平衡态的理想气体系统速率满足下列分布规律麦克斯韦速率分布律分子速率处于vdv间的几率是分子速度矢量端点落在和vdv为内外半径球壳内的几率
9.4.1 分子的速率分布函数
2RT M
1.41 kT m
V 0 Vf (V)dV
V 8kT 8RT 1 .6 0 k T
πm πM
m
V2 V2f(V)dV 0
or 1mV2 3kT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 二 章 分子动理学理论的平衡态理论2-1 设有一群粒子按速率分布如下:试求(1)平均速率V ;(2)方均根速率2V(3)最可几速率Vp解:(1)平均速率:18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速率37.322≅∑∑=iii NV N V(m/s)2-2 计算300K 时,氧分子的最可几速率、平均速率和方均根速率。
解:sm RTV P/395103230031.8223=⨯⨯⨯==-μsm RTV /446103214.330031.8883=⨯⨯⨯⨯==-πμsm RTV /483103230031.83332=⨯⨯⨯==-μ2-3 计算氧分子的最可几速率,设氧气的温度为100K 、1000K 和10000K 。
解:μRTV P2=代入数据则分别为:T=100K 时 sm V P /1028.22⨯= T=1000K 时 sm V P/1021.72⨯= T=10000K 时 sm V P/1028.23⨯=2-4 某种气体分子在温度T 1时的方均根速率等于温度T 2时的平均速率,求T 2/T 1。
解:因μRTV32=πμ28RTV=由题意得:μRT3πμ28RT=∴T 2/T 1=83π2-5 求0℃时1.0cm 3氮气中速率在500m/s 到501m/s 之间的分子数(在计算中可将dv 近似地取为△v=1m/s )解:设1.0cm 3氮气中分子数为N ,速率在500~501m/s 之间内的分子数为△N ,由麦氏速率分布律: △ N=VVeKTm NVKTm ∆⋅⋅⋅-22232)2(4ππ∵ V p2= 2KT m ,代入上式△N=VVV ppeVV VN∆--⋅⋅222214ρπ因500到501相差很小,故在该速率区间取分子速率V =500m/s , 又sm V P/402102827331.823≅⨯⨯⨯=- △V=1m/s(vv p =1.24)代入计算得:△N=1.86×10-3N 个2-6 设氮气的温度为300℃,求速率在3000m/s 到3010m/s 之间的分子数△N 1与速率在1500m/s 到1510m/s 之间的分子数△N 2之比。
解: 取分子速率为V 1=3000m/s V 2=1500m/s, △V 1=△V 2=10m/s由5题计算过程可得: △V 1=12212214V VV pppeV V VN∆--⋅⋅π△N 2=22222214V VV pppeVV VN∆--⋅⋅π∴ △N/△N 2=2121)(21)(21)()(pppVV VV peVV eVV --⋅其中V P =331018.210257331.82⨯=⨯⨯⨯-m/sv 1v p =1.375,v 2v p =0.687∴969.0687.0375.122687.02375.1221≅⨯⨯=∆∆--ee NN解法2:若考虑△V 1=△V 2=10m/s 比较大,可不用近似法,用积分法求△N 1,△N 2dN=dVVVV pPeVN22234--⋅π△N 1=⎰⎰⎰-=122100V V V V dN dN dN △N 2=⎰⎰⎰-=34430V V V V dNdN dN令X i =v iv pi=1、2、3、4利用16题结果:22)([0iix i i V ex x erf N dN--=⎰π∴ △N 1=]2)([]2)([2122112x x i ex x erf N ex x erfN -----ππ(1)△N 2=]2)([]2)([23243344x x ex x erf N ex x erfN -----ππ(2)其中V P =sm RT/10182.223⨯=μ375.111==P V V x 379.122==PV V x687.033==PV V x 6722.044==PV V x查误差函数表得:erf(x 1)=0.9482 erf(x 2)=0.9489 erf(x 3)=0.6687 erf(x 4)=0.6722将数字代入(1)、(2)计算,再求得:703.021=∆∆NN2-7 试就下列几种情况,求气体分子数占总分子数的比率: (1) 速率在区间v p ~1.0v p 1内 (2) 速度分量v x 在区间v p ~1.0v p 1内(3) 速度分量v p 、v p 、v p 同时在区间v p ~1.0v p 1内解:设气体分子总数为N ,在三种情况下的分子数分别为△N 1、△N 2、△N 3 (1) 由麦氏速率分布律: △ N=⎰⎰⎰-=1221V V V V dNdN dN 令v 2=1.01v p ,v i =v p ,pi i v v x =,则111==pv v x ,01.122==pv v x ,利用16题结果可得;2122112212)(2)(x x ex x erf ex x erf NN --+--=∆ππ查误差函数表:erf (x 1)=0.8427 erf (x 2)=0.8468 ∴008.01=∆NN(2) 由麦氏速率分布律:xvv pxdvevNdNpx 221--=π∴xvv v pxvv v pdve vNdve vNN px px 2122)(1)(12----⎰⎰-=∆ππ)(])(exp[1)(])(exp[122212px px vv pxpx vv vv d vv vv d vv NN pp⎰⎰---=∆ππ令px v v x=, 111==pv v x ,01.122==p v v x∴dxe dx e NN xx xx ⋅-=∆--⎰⎰2122211ππ利用误差函数:dxx xp e x erf x)(2)(2-=⎰π%21.0]8427.08468.0[21)()([21122=-=-=∆x erf x erf N N(3)令px v v x=,由麦氏速度分布律得:zyxvv v v pdvdvdve vNdN pzy x ⋅=++--2222331ππ8332333108.0)002.0()(][)1(211222---⨯==∆=-=∆⎰⎰NN dx edx eN N x x x x π2-8根据麦克斯韦速率分布函数,计算足够多的点,以dN/dv 为纵坐标,v 为横坐标,作1摩尔氧气在100K 和400K 时的分子速率分布曲线。
解:由麦氏速率分布律得:22232)2(4ve KTm N dvdN vKTm -=ππ将π=3.14,N=N A =6.02×1023T=100K m=32×10-3代入上式得到常数: A=eKTm N A23)2(4ππ KTm B2=∴22VAe dvdN BV⋅=- (1)为了避免麻烦和突出分析问题方法,我们只做如下讨论:由麦氏速率分布律我们知道,单位速率区间分布的分子数随速率的变化,必然在最可几速率处取极大值,极大值为: 令22VAedvdN y BV⋅==-则)]2(2[222=-⋅+⋅=--BV eV V e A dv dy BVBV得BV VP 1==又在V=0时,y=0,V →∞时,y →0 又mKT B V P 11121==mKT B V P 22221==∵T 1=100K <T 2=400K ∴1P V <2P V 由此作出草图2-9根据麦克斯韦速率分布律,求速率倒数的平均值v 1。
解:VKT m emKT KTm VKTm d VemKT KT m VdVeKT m dvV f VvKTmV KTm KTmvππππππππ42)()2(4)2()()2(4)2(4)(1102232222322322==⋅-⋅=-⋅⋅-===∞-∞-∞-∞⎰⎰⎰2-10一容器的器壁上开有一直径为0.20mm 的小圆孔,容器贮有100℃的水银,容器外被抽成真空,已知水银在此温度下的蒸汽压为0.28mmHg 。
(1) 求容器内水银蒸汽分子的平均速率。
(2) 每小时有多少克水银从小孔逸出?解:(1))/(1098.11020114.337331.88823s m RTV ⨯=⨯⨯⨯⨯==-πμ(2)逸出分子数就是与小孔处应相碰的分子数,所以每小时从小孔逸出的分子数为:ts V n N ⋅⋅=41其中KTV P V n ⋅=4141是每秒和器壁单位面积碰撞的分子数,2)2(d sπ=是小孔面积,t=3600s ,故ts V KTP N ⋅⋅⋅=41,代入数据得:N=4.05×1019(个) ∴)(1035.11005.41002.610201219233g N NmNMA--⨯=⨯⨯⨯⨯===μ2-11如图3-11,一容器被一隔板分成两部分,其中气体的压强,分子数密度分别为p 1、n 1、p 2、n 2。
两部分气体的温度相同,都等于T 。
摩尔质量也相同,均为μ。
试证明:如隔板上有一面积为A 的小孔,则每秒通过小孔的气体质量为:)(221P P A RTM-=πμ证明:设p 1>p 2,通过小孔的分子数相当于和面积为A 的器壁碰撞的分子数。
从1跑到2的分子数:tA V n N ⋅⋅=11141 从2跑到1的分子数:tA V n N ⋅⋅=22241实际通过小孔的分子数:(从1转移到2))221121(41Vn V n At NN N -=-=∆因t=1秒,KTP n =,πμRTV8=T 1=T 2=T∴)(2)(841)(841212121P P A RTP P RTRTAKT P KTP RTAmn m M -=-=-==∆=πμπμμπμ若P 2>P 1,则M <0,表示分子实际是从2向1转移。
2-12 有N 个粒子,其速率分布函数为)0()(0〉〉==v v C NdvdN v f)(0)(0v v v f 〈=(1)作速率分布曲线。
(2)由N 和v 0求常数C 。
(3)求粒子的平均速率。
解:(1) )0()(0〉〉=v v C v f)(0)(0v v v f 〈=得速率分布曲线如图示(2)∵1)(0=⎰∞dv v f∴10)(0==⎰⎰∞v cdv dv v f即1=cv 01v c=(3)0202121)(v cv dv v vf v===⎰∞2-13 N 个假想的气体分子,其速率分布如图3-13所示(当v >v 0时,粒子数为零)。
(1)由N 和V 0求a 。
(2)求速率在1.5V 0到2.0V 0之间的分子数。
(3) 求分子的平均速率。
解:由图得分子的速率分布函数: NV Va 0 (00V V 〈〈)Na (02VV V 〈〈)f(v)= 0 (02V V 〉)(1) ∵dvV NfdN)(=∴aV aVV V a advdV V Va dV V f N NVVV0020202321)(0=+=+==⎰⎰⎰∞32V N a =(2) 速率在1.5V 0到2.0V 0之间的分子数33221)5.12()(000025.125.10N V V N V V a adVdV V NfN VVVV=⋅=-===∆⎰⎰2-14 证明:麦克斯韦速率分布函数可以写作:)(2x F dxdN =其中pvv x=mKT v p2=2224)(xexNx F -⋅=π证明:dxx eNvv d ve Ndvv e vN dvv eKTm N dvv Nf dNxpvpvv vv p KTmvpp222323222322222224)(44)2(4)(------⋅=⋅=⋅⋅===ππππππ∴)(4222x F xeNdxdN x=⋅⋅=-π2-15设气体分子的总数为N ,试证明速度的x 分量大于某一给定值v x 的分子数为:)](1[2x erf N N xv-=∆∞∝(提示:速度的x 分量在0到∞之间的分子数为2N )证明:由于速度的x 分量在区间v x ~v x +dv x 内的分子数为:xvv pxdvevNdNvpx ⋅=--221π故在v x ~∞范围内的分子数为:⎰⎰⎰-==∆∞∞∞→xxxxx vv xv v V dNdNdNN由题意:2N dNxv =⎰∞xvv v pvv dve vNdNpx xxx⋅=--⎰⎰22010π令px vv x=利用误差函数得:)(2222x erf N dxeN dN xxvv xx=⋅=⎰⎰-π∴)](1[2)(22x erf N x erf N N Nx V -=-=∞→2-16 设气体分子的总数为N ,试证明速率在0到任一给定值v 之间的分子数为:]2)([20xvex erf N N-→-=∆π其中pvv x=,v p 为最可几速率。
