专题四-方程(组)、不等式(组)及其实际应用-(共34张)
七年级方程(组)、不等式(组)复习资料

7、甲、乙两件服装的成本共 500 元,商店老板为获取利润,决定将甲服装按 50﹪的利润定价, 乙服装按 40﹪的利润定价。在实际出售时,应顾客要求,两件服装均按 9 折出售,这样商店共 获利 157 元,求甲、乙两件服装的成本各是多少元?
(1)a+l
b+l; (2)a-5
b-5;
2-3x≤ 8 的解集是
1 x-1< 1 2
(3)-3a
-3b; (4)6-a
3、写出适合不等式 2x+3<9 的正整数解_____________________。
1-x≥ 0
4、不等式组
的整数解是
.
2x-1>-3
5 、 代 数 式 1 - k 的 值 大 于 - 1 而 又 不 大 于 3 ,则k的取值范围是
10、某玩具工厂广告称:“本厂工人工作时间:每天工作 8 小时,每月工作 25 天;待遇:熟练 工人按计件付工资,多劳多得,计件工资不少于 800 元,每月另加福利工资 100 元,按月结 算;……”该厂只生产两种玩具:小狗和小汽车。熟练工人晓云元月份领工资 900 多元,她记 录了如下表的一些数据:
2、 当 x取 什 么 值 时 , 代 数 式 2x +1 -1的 值 不 小 于 3x − 8 +2的 值 ?
2
11. 为节约能源,某单位按以下规定收取每月电费:用电不超过 140 度,按每度 0.43 元收费; 如果超过 140 度,超过部分按每度 0.57 元收费。若某用电户四月份的电费平均每度 0.5 元,问 该用户四月应交电费多少元?
部编九年级下数学专题四 方程(组)、不等式(组)的实际应用

专题四 方程(组)、不等式(组)的实际应用方程(组)的实际应用【例1】 (2016·济南)学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40千克,了解到这些蔬菜的种植成本共42元,还了解到如下信息:(1)请问采摘的黄瓜和茄子各多少千克?(2)这些采摘的黄瓜和茄子可赚多少元?分析:(1)设采摘黄瓜x 千克,茄子y 千克,根据题中两个等量关系,列出二元一次方程组求解即可;(2)根据黄瓜和茄子的斤数,再求出每斤黄瓜和茄子赚的钱数,列式计算即可.解:(1)设采摘黄瓜x 千克,茄子y 千克.根据题意得⎩⎨⎧x +y =40,x +1.2y =42,解得⎩⎨⎧x =30,y =10,则采摘的黄瓜和茄子分别为30千克、10千克(2)30×(1.5-1)+10×(2-1.2)=23(元),则这些采摘的黄瓜和茄子可赚23元【例2】 (2016·淮安)王师傅检修一条长600米的自来水管道,计划用若干小时完成,在实际检修过程中,每小时检修管道长度是原计划的1.2倍,结果提前2小时完成任务,王师傅原计划每小时检修管道多少米?分析:设原计划每小时检修管道为x m ,根据题中等量关系列出分式方程进行求解.解:设原计划每小时检修管道x 米,由题意得600x -6001.2x=2,解得x =50,经检验,x =50是原方程的解,且符合题意,则原计划每小时检修管道50米方程(组)与不等式(组)的综合应用【例3】 (2016·永州)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.(1)求该种商品每次降价的百分率;(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?分析:(1)设该种商品每次降价的百分率为x%,根据题中等量关系列出一元二次方程进行求解;(2)设第一次降价后售出该种商品m 件,根据题中不等关系列出一元一次不等式进行求解.解:(1)设该种商品每次降价的百分率为x%,依题意得400×(1-x%)2=324,解得x =10,或x =190(舍去),则该种商品每次降价的百分率为10%(2)设第一次降价后售出该种商品m 件,则第二次降价后售出该种商品(100-m)件,第一次降价后的单件利润为400×(1-10%)-300=60(元),第二次降价后的单件利润为324-300=24(元).依题意得60m +24×(100-m)≥3210,即36m +2400≥3210,解得m ≥22.5,∴m ≥23,则第一次降价后至少要售出该种商品23件1.(2016·宜宾)2016年“母亲节”前夕,某花店用4 000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知第二批所购花的束数是第一批所购花的束数的1.5倍,且每束花的进价比第一批的进价少5元,求第一批花每束的进价是多少?解:设第一批花每束的进价是x 元,依题意得4 000x ×1.5=4 500x -5,解得x =20.经检验x =20是原方程的解,且符合题意,则第一批花每束的进价是20元2.(2016·包头)如图,一幅长20 cm ,宽12 cm 的图案,其中有一横两竖的彩条,横、竖彩条的宽度比为3∶2.设竖彩条的宽度为x cm ,图案中三条彩条所占面积为y cm 2.(1)求y 与x 之间的函数关系式;(2)若图案中三条彩条所占面积是图案面积的25,求横、竖彩条的宽度. 解:(1)根据题意可知横彩条的宽度为32x cm ,∴y =20×32x +2×12x -2×32x 2,即y =-3x 2+54x(2)根据题意得-3x 2+54x =25×20×12,整理得x 2-18x +32=0,解得x 1=2,x 2=16(舍去),∴32x =3,则横彩条的宽度为3 cm ,竖彩条的宽度为2 cm 3.(2016·沈阳)倡导健康生活,推进全民健身,某社区要购进A ,B 两种型号的健身器材若干套,A ,B 两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.(1)若购买A ,B 两种型号的健身器材共50套,且恰好支出20000元,求A ,B 两种型号健身器材各购买多少套?(2)若购买A ,B 两种型号的健身器材共50套,且支出不超过18000元,求A 种型号健身器材至少要购买多少套?解:(1)设购买A 种型号健身器材x 套,B 型器材健身器材y 套,根据题意得⎩⎨⎧x +y =50,310x +460y =20000,解得⎩⎨⎧x =20,y =30,则购买A 种型号健身器材20套,B 型器材健身器材30套(2)设购买A 型号健身器材m 套,根据题意得310m +460(50-m)≤18000,解得m ≥3313,∵m 为整数,∴m 的最小值为34,则A 种型号健身器材至少要购买34套1.(2015·深圳)下表为深圳市居民每月用水收费标准(单位:元/立方米):用水量 单价x ≤22 a(1)某用户用水10立方米,(2)在(1)的前提下,该用户5月份交水费71元,请问该用户用水多少立方米?解:(1)由题意得10a =23,解得a =2.3,则a 值为2.3(2)设该用户用水x 立方米,∵用水22立方米时,水费为22×2.3=50.6<71,∴x >22,∴22×2.3+(x -22)×(2.3+1.1)=71,解得x =28,则该用户用水28立方米2.(2016·贵港)为了经济发展的需要,某市2014年投入科研经费500万元,2016年投入科研经费720万元.(1)求2014至2016年该市投入科研经费的年平均增长率;(2)根据目前经济发展的实际情况,该市计划2017年投入的科研经费比2016年有所增加,但年增长率不超过15%,假定该市计划2017年投入的科研经费为a 万元,请求出a 的取值范围.解:(1)设2014至2016年该市投入科研经费的年平均增长率为x ,根据题意得500(1+x)2=720,解得x 1=0.2=20%,x 2=-2.2(舍去),则2014至2016年该市投入科研经费的年平均增长率为20%(2)根据题意得a -720720×100%≤15%,解得a ≤828,又∵该市计划2017年投入的科研经费比2016年有所增加,∴a 的取值范围为720<a ≤8283.(导学号 59042294)(2016·重庆)近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%.某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?(2)5月20日,猪肉价格为每千克40元.5月21日,某市决定投入储备猪肉并规定其销售价在每千克40元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的34,两种猪肉销售的总金额比5月20日提高了110a%,求a 的值.解:(1)设今年年初猪肉价格为每千克x 元,根据题意得2.5×(1+60%)x ≥100,解得x ≥25,则今年年初猪肉的最低价格为每千克25元(2)设5月20日两种猪肉总销量为1,根据题意得40(1-a%)×34(1+a%)+40×14(1+a%)=40(1+110a%),令a%=y ,原方程化为40(1-y)×34(1+y)+40×14(1+y)=40(1+110y),整理得5y 2-y =0,解得y =0.2,或y =0(舍去),则a%=0.2,∴a =20,即a 的值为204.(导学号 59042295)(2016·日照)随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A 型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%.(1)A 型自行车去年每辆售价多少元?(2)该车行今年计划新进一批A 型车和新款B 型车共60辆,且B 型车的进货数量不超过A 型车数量的两倍.已知A 型车和B 型车的进货价格分别为1500元和1800元,计划B 型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?解:(1)设去年A 型车每辆售价x 元,则今年每辆售价为(x -200)元,由题意得80000x=80000(1-10%)x -200,解得x =2000,经检验,x =2000是原方程的根,则去年A 型车每辆售价为2000元(2)设今年新进A 型车a 辆,则B 型车(60-a)辆,获利y 元,由题意得y =(1800-1500)a +(2400-1800)(60-a),即y =-300a +36000.∵B 型车的进货数量不超过A 型车数量的两倍,∴60-a ≤2a ,∴a ≥20.∵k =-300<0,∴y 随a 的增大而减小,∴a =20时,y 最大=30000元.此时B 型车的数量为60-20=40(辆),∴当新进A 型车20辆,B 型车40辆时,这批车获利最大。
专题03方程(组)、不等式(组)的解法(解析版)

专题03方程(组)、不等式(组)的解法一、选择题1、一元一次方程20x -=的解是( )A. 2x =B. 2x =-C. 0x =D. 1x =答案:A分析:直接利用一元一次方程的解法得出答案. 解答:20x -=, 解得:2x =. 选A .2、以2和4为根的一元二次方程是( ) A. 2680x x ++= B. 2680x x -+=C. 2680x x +-=D. 2680x x --=答案:B分析:根据已知两根确定出所求方程即可. 解答:以2和4为根的一元二次方程是x 2-6x +8=0, 选B .3、已知点M (2m -1,1-m )在第四象限,则m 的取值范围在数轴上表示正确的是( ) A.B.C.D.答案:A分析:根据第四象限内点的坐标特点列出关于m 的不等式组,求出m 的取值范围,并在数轴上表示出来即可.解答:解:∵点M (2m -1,1-m )在第四象限,∴21010m m ->⎧⎨-<⎩①②由①得,m >0.5; 由②得,m >1, 在数轴上表示为:选A .4、关于x 的分式方程2x a1x 1+=+的解为负数,则a 的取值范围是( )A. a 1>B. a 1<C. a 1<且a 2≠-D. a 1>且a 2≠答案:D分析:分式方程去分母转化为整式方程,表示出整式方程的解,根据分式方程解为负数列出关于a 的不等式,求出不等式的解集即可确定出a 的范围. 解答:分式方程去分母得:x 12x a +=+,即x 1a =-, 因为分式方程解为负数,所以1a 0-<,且1a 1-≠-, 解得:a 1>且a 2≠, 选D.5、已知方程组2325x y x y +=⎧⎨-=⎩,则26x y +的值是( )A. -2B. 2C. -4D. 4答案:C分析:两式相减,得32x y +=﹣,所以234x y +()=﹣,即264x y +=﹣. 解答:解:两式相减,得32x y +=﹣, ∴234x y +()=﹣, 即264x y +=﹣, 选C .6、小刚在解关于x 的方程ax ²+bx +c =0(a ≠0)时,只抄对了a =1,b =4,解出其中一个根是x =-1.他核对时发现所抄的c 比原方程的c 值小2.则原方程的根的情况是( ) A. 不存在实数根 B. 有两个不相等的实数根C. 有一个根是x =-1D. 有两个相等的实数根答案:A分析:直接把已知数据代入进而得出c 的值,再解方程求出答案.解答:解:∵小刚在解关于x 的方程ax 2+bx +c =0(a ≠0)时,只抄对了a =1,b =4,解出其中一个根是x =-1,∴(-1)2-4+c =0, 解得:c =3, 故原方程中c =5,则∆=b 2-4ac =16-4×1×5=-4<0, 则原方程的根的情况是不存在实数根. 选A .7、若不等式组11324x xx m+⎧<-⎪⎨⎪<⎩无解,则m 的取值范围为( )A. 2m ≤B. 2m <C. 2m ≥D. 2m >答案:A分析:求出第一个不等式的解集,根据口诀:大大小小无解了可得关于m 的不等式,解之可得. 解答:解不等式1132x x+<-,得:x >8, ∵不等式组无解, ∴4m ≤8, 解得m ≤2, 选A.8、由方程组43x m y m +=⎧⎨-=⎩,可得出x 与y 的关系是( )A. x y l?+=B. x y 1+=-C. x y 7+=-D.x y 7+= 答案:D分析:先把方程组化为43x m y m +=⎧⎨-=⎩的形式,再把两式相加即可得到关于x 、y 的关系式.解答:原方程可化为43x m y m +=⎧⎨-=⎩①②①+②得,x +y =7. 选D.9、小华在做解方程作业时,不小心将方程中的一个常数弄脏了而看不清楚,被弄脏的方程是11()1323x xx▲---+=-,这该怎么办呢?他想了一想,然后看了一下书后面的答案,知道此方程的解是x=5,于是,他很快便补好了这个常数,并迅速地做完了作业.同学们,你能补出这个常数吗?它应该是()A. 2B. 3C. 4D. 5答案:D分析:设这个数是a,把x=5代入方程得出一个关于a的方程,求出方程的解即可.解答:设这个数是a,把x=5代入得:13(-2+5)=1-5a3-,∴1=1-5a3-,解得:a=5.选D.10、若x1是方程ax2+2x+c=0(a≠0)的一个根,设M=(ax1+1)2,N=2-ac,则M与N的大小关系为()A. M>NB. M=NC. M<ND. 不能确定答案:C分析:把x1代入方程ax2+2x+c=0得ax12+2x1=-c,作差法比较可得.解答:∵x1是方程ax2+2x+c=0(a≠0)的一个根,∴ax12+2x1+c=0,即ax12+2x1=-c,则M-N=(ax1+1)2-(2-ac)=a2x12+2ax1+1-2+ac=a(ax12+2x1)+ac-1=-ac+ac-1=-1,∵-1<0,∴M-N<0,∴M<N.选C.11、如果解关于x 的分式方程2122m xx x-=--时出现增根,那么m 的值为( )A. -2B. 2C. 4D. -4答案:D分析:本题考查了分式方程的增根. 解答:2122m xx x-=--,去分母,方程两边同时乘以(x -2),得: m +2x =x -2,由分母可知,分式方程的增根可能是2. 当x =2时,m +4=2-2,m =-4, 选D . 二、填空题12、方程2x -4=0的解也是关于x 的方程x 2+mx +2=0的一个解,则m 的值为______. 答案:-3分析:先解一元一次方程,再把解代入一元二次方程求出m 的值即可. 解答:2x −4=0, 解得:x =2,把x =2代入方程x 2+mx +2=0得: 4+2m +2=0, 解得:m =−3. 故答案为−3.13、已知x ,y 满足方程组x 2y 5x 2y 3-=⎧⎨+=-⎩,则22x 4y -的值为______.答案:-15分析:观察所求的式子以及所给的方程组,可知利用平方差公式进行求解即可得.解答:∵x 2y 5x 2y 3-=⎧⎨+=-⎩,∴22x 4y -=(x +2y )(x -2y )=-3×5=-15, 故答案为:-15.14、已知一元二次方程2430x x -+=的两根1x ,2x ,则211124x x x x -+=______.答案:0分析:本题考查了一元二次方程的根与系数的关系. 解答:∵12x x 、是方程24+30x x -=的两个根,∴211124303x x x x ,-+=⋅=, ∴21143x x -=-,∴211124330x x x x -+⋅=-+=.15、关于x 的一元二次方程(a -1)x 2-2x +3=0有实数根,则整数a 的最大值是______. 答案:-2分析:本题考查了根的判别式.解答:解:根据题意得:a +1≠0且△=(-2)2-4×(a +1)×3≥0,解得a ≤23-且a ≠-1,所以整数a 的最大值为-2.故答案为-2. 16、关于x 的一元二次方程ax 2-x -14=0有实数根,则a 的取值范围为______. 答案:a ≥-1且a ≠0分析:本题考查了根的判别式:一元二次方程ax 2+bx +c =0(a ≠0)的根与△=b 2-4ac 有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.利用一元二次方程的定义和判别式的意义得到≠0且△=(-1)2-4a •(-14)≥0,然后求出两个不等式的公共部分即可. 解答:根据题意得a ≠0且△=(-1)2-4a •(-14)≥0,解得:a ≥-1且a ≠0.故答案为a ≥-1且a ≠0.17、如果不等式组()2131x x x m ⎧->-⎨<⎩的解集是1x <,那么m 的值是______.答案:1分析:先求出第一个不等式的解集,再根据“同小取小”解答即可.解答:()213x 1x x m ①②⎧->-⎨<⎩,解不等式①,x <2, 解不等式②,x <m ,∵不等式组的解集是x <1, ∴m =1, 故答案为:1.18、设1x 、2x 是方程2320x x -+=的两个根,则1212x x x x +-=______. 答案:1分析:根据一元二次方程根与系数的关系公式,可直接求得12x x +和12x x .解答:如果方程()200++=≠ax bx c a 的两个实数根是12x x 、,那么12=b x x a+-,12=c x x a .可知:1212323,211x x x x -+=-=⋅==,所以1212321x x x x +-=-=. 19、若一元二次方程220x x k -+=有两个不相等的实数根,则k 的取值范围是______. 答案:k <1分析:本题考查了根的判别式.解答:∵一元二次方程220x x k -+=有两个不相等的实数根, ∴△=24b ac -=4-4k >0, 解得:k <1,则k 的取值范围是:k <1. 故答案为k <1. 20、关于x 的分式方程12122a x x-+=--的解为正数,则a 的取值范围是______. 答案:a <5且a ≠3分析:直接解分式方程,进而利用分式方程的解是正数得出a 的取值范围,进而结合分式方程有意义的条件分析得出答案. 解答:去分母得:122a x -+=-, 解得:5x a =-,50a ->,解得:5a <,当52x a =-=时,3a =不合题意, 故5a <且3a ≠. 故答案为:5a <且3a ≠.21、已知α,β是关于x 的一元二次方程x 2+(2m +3)x +m 2=0的两个不相等的实数根,且满足11αβ+=-1,则m 的值是______.答案:3分析:可以先由韦达定理得出两个关于α、β的式子,题目中的式子变形即可得出相应的与韦达定理相关的式子,即可求解. 解答:得α+β=-2m -3,αβ=m 2,又因为211+-2m-3+===-1mαβαβαβ,所以m 2-2m -3=0,得m =3或m =-1,因为一元二次方程()22230x m x m +++=的两个不相等的实数根,所以△>0,得(2m +3)2-4×m 2=12m +9>0,所以m >4-3,所以m =-1舍去,综上m =3. 三、解答题 22、(1)解方程:11322x x x--=---. (2)解不等式组:312215(1)x x x x -⎧<-⎪⎨⎪+≥-⎩答案:(1)无解;(2)-1<x ≤2.分析:(1)分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可. 解答:(1)去分母得:1-x +1=-3x +6, 解得:x =2,经检验x =2是增根,分式方程无解;(2)()3122151x x x x -⎧<-⎪⎨⎪+≥-⎩①②, 由①得:x >-1, 由②得:x ≤2,则不等式组的解集为-1<x ≤2.23、先化简,再求值:22221(1)11a a a a a a --÷---+,其中a 是方程x 2+x =6的一个根.答案:11a -,14-. 分析:原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出已知方程的解得到a 的值,代入计算即可求出值.解答:解:原式=()2(2)1211(1)1a a a a a a a ---+÷+-+ =()(2)1•1(1)(2)a a a a a a a -++--=11a -, 方程x 2+x =6,解得:x =-3或x =2(舍去), 当a =x =-3时,原式=-14. 24、解方程(1)2250x x --=(2)1421x x =-+答案:(1)1211x x ==(2)3x =是方程的解. 分析:(1)利用配方法进行求解即可;(2)方程两边同时乘以(x -2)(x +1),化为整式方程,解整式方程后进行检验即可得. 解答:(1)x 2-2x =5, x 2-2x +1=5+1, (x -1)2=6,x ,∴1211x x ==(2)方程两边同时乘以(x -2)(x +1),得 x +1=4(x -2), 解得:x =3,检验:当x =3时,(x -2)(x +1)≠0, 所以x =3是原方程的解. 25、关于x 的方程22210x x m -+-=有实数根,且m 为正整数,求m 的值及此时方程的根.答案:1m =,此时方程的根为121x x ==分析:直接利用根的判别式△≥0得出m 的取值范围进而解方程得出答案. 解答:解:∵关于x 的方程x 2-2x +2m -1=0有实数根, ∴b 2-4ac =4-4(2m -1)≥0, 解得:m ≤1, ∵m 为正整数, ∴m =1,∴此时二次方程为:x 2-2x +1=0,则(x -1)2=0,解得:x 1=x 2=1.26、己知关于x ,y 的二元一次方程组2352x y x y k-=⎧⎨-=⎩的解满足x y >,求k 的取值范围.答案:5k <.分析:先用加减法求得x y -的值(用含k 的式子表示),然后再列不等式求解即可. 解答:2352x y x y k -=⎧⎨-=⎩①②,①-②得:5x y k -=-,∵x y >,∴0x y ->.∴50k ->.解得:5k <.27、已知关于x 的方程22220x mx m m -++-=有两个不相等的实数根.(1)求m 的取值范围;(2)当m 为正整数时,求方程的根.答案:(1)m <2;(2)x 1=0,x 2=2.分析:(1)利用判别式的意义得到=(-2m )2-4(m 2+m -1)>0,,然后解不等式即可;(2)利用m 的范围确定m 的正整数值为1,则方程化为x 2-2x =0,然后利用因式分解法解方程.解答:解:(1)()22442m m m ∆=-+-22444848m m m m =--+=-+∵方程有两个不相等的实数根,480m ∆=-+>.2m <.(2)∵m 为正整数,且2m <,1m =.原方程为220x x -=.∴()20x x -=.∴120,2x x ==.28、(1)解一元二次方程:x 2-4x +1=0(2)解分式方程:11322xx x -+=--答案:(1)1222x x ==(2)无解分析:(1)根据配方法或公式法即可求解一元二次方程;(2)先去分母化为整式方程,即可求解.解答:(1)2443x x -+=2(2)3x -=2x -=12x =22x =或1,4,1a b c ==-=,2416412b ac ∆=-=-=4222b x a -===±±±1222x x ==(2)13(2)(1)x x +-=--1361x x +-=-+24=x2x =检验2x =时,20x -=2x ∴=不是原方程的解∴原方程无解.29、先化简,再求值:231111x x x x -⎛⎫+÷ ⎪+-⎝⎭,其中x 是不等式组11210x x x --⎧->⎪⎨⎪-+<⎩的整数解.答案:原式=44x -;原式=4分析:先化简式子为44x -,再求解不等式的整数解为2x =,最后将2x =代入化简的式子中即可求解. 解答:解:231111x x x x -⎛⎫+÷ ⎪+-⎝⎭ 131(+1)(1)=1x x x x x x ++--⎛⎫⨯ ⎪+⎝⎭ 4(+1)(1)=+1x x x xx -⨯ =44x - 解不等式组11210x x x --⎧->⎪⎨⎪-+<⎩解得31x x ⎧⎨⎩<> ∴1<x <3,∴不等式组的整数解是2x =,∴当2x =时,原式=42-4=4⨯.30、如果方程x 2+px +q =0的两个根是x 1、x 2,那么x 1+x 2=-p ,x 1·x 2=q .请根据以上结论,解决下列问题:(1)已知关于x 的方程x 2+mx +n =0(n ≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;(2)已知a 、b 满足a 2-15a -5=0,b 2-15b -5=0,求a b b a+的值; (3)已知a 、b 、c 均为实数,且a +b +c =0,abc =16,求正数c 的最小值.答案:(1)nx 2+mx +1=0;(2)-47或2;(3)c 的最小值为4.分析:(1)设x 2+mx +n =0(n ≠0)的两根为x 1、x 2,根据根与系数的关系可得x 1+x 2=-m ,x 1·x 2=n ,将以上两式变形可得1211+x x 和1211x x ⋅,即可求出答案. (2)根据a 、b 满足a 2-15a -5=0,b 2-15b -5=0,得出a ,b 是x 2-15x -5=0的解,求出a +b 和ab 的值,即可求结果;(3)根据a +b +c =0,abc =16,得出a +b =-c ,ab =16c,a 、b 是方程x 2+cx +1211+x x =0的解,再根据c 2-4×1211+x x ≥0,即可求出c 的最小值. 解答:解:(1)设x 2+mx +n =0(n ≠0)的两根为x 1、x 2.∴x 1+x 2=-m ,x 1·x 2=n ∴1211+x x =1212x x x x +=-m n ,1211x x ⋅=1n∴所求一元二次方程为x2+mnx+1n=0,即nx2+mx+1=0;(2)①当a≠b时,由题意知a、b是一元二次方程x2-15x-5=0的两根,∴a+b=15,ab=-5∴ab+ba=22a bab+=2()2a b abab+-=2152(5)5-⨯--=-47②当a=b时,ab+ba=1+1=2综上,ab+ba=-47或2;(3)∵a+b+c=0,abc=16,∴a+b=-c,ab=16 c∴a、b是方程x2+cx+16c=0的两根,∴Δ=c2-416c⨯≥0∵c>0,∴c3≥64,∴c≥4,∴c的最小值为4.。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
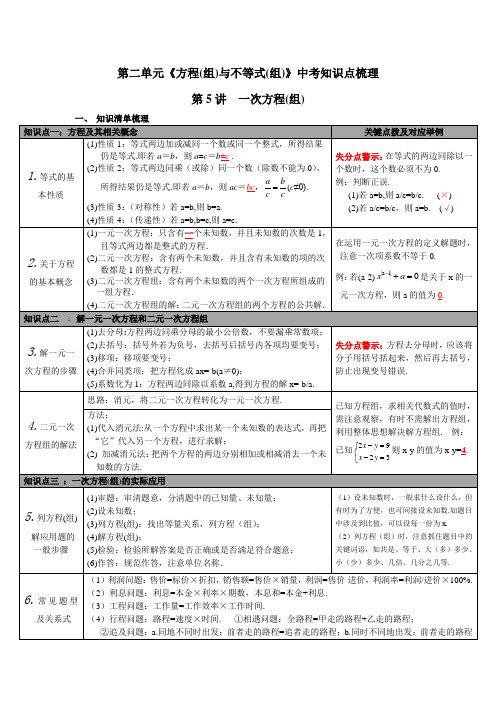
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
2024年中考数学复习专题课件(共30张PPT)一元一次不等式(组)及其应用

解:设普通水稻的亩产量是 x kg,则杂交水稻的亩产量是 2x kg,依题 意得 7 200 9 600
x - 2x =4,解得 x=600, 经检验,x=600 是原分式方程的解,且符合题意,则 2x=2×600=1 200(kg). 答:普通水稻的亩产量是 600 kg,杂交水稻的亩产量是 1 200 kg.
__00__.
6.[2023·贵州第 17(2)题 6 分]已知 A=a-1,B=-a+3.若 A>B,求 a 的取值范围. 解:由 A>B 得 a-1>-a+3, 解得 a>2, 即 a 的取值范围为 a>2.
7.[2021·贵阳第 17(1)题 6 分]有三个不等式 2x+3<-1,-5x>15, 3(x-1)>6,请在其中任选两个不等式, 组成一个不等式组,并求出它 的解集.
4.风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞 ,该 大桥限重标志牌显示,载重后总质量超过 30 t 的车辆禁止通行,现有一 辆自重 8 t 的卡车,要运输若干套某种设备,每套设备由 1 个 A 部件和 3 个 B 部件组成,这种设备必须成套运输,已知 1 个 A 部件和 2 个 B 部件 的总质量为 2.8 t,2 个 A 部件和 3 个 B 部件的质量相等. (1)求 1 个 A 部件和 1 个 B 部件的质量各是多少; (2)卡车一次最多可运输多少套这种设备通过此大桥?
解:(1)设出售的竹篮 x 个,陶罐 y 个,依题意有 5x+12y=61, x=5, 6x+10y=60,解得y=3. 答:小钢出售的竹篮 5 个,陶罐 3 个.
(2)设购买鲜花 a 束,依题意有 0<61-5a≤20, 解得 8.2≤a<12.2, ∵a 为整数, ∴共有 4 种购买方案, 方案一:购买鲜花 9 束; 方案二:购买鲜花 10 束; 方案三:购买鲜花 11 束; 方案四:购买鲜花 12 束.
专题04 二元一次方程组(真题测试)(解析版)

专题04 二元一次方程组(真题测试)一、单选题1. (2019 湖南邵阳) 某出租车起步价所包含的路程为0~2km,超过2km的部分按每千米另收费.津津乘坐这种出租车走了7km,付了16元;盼盼乘坐这种出租车走了13km,付了28元.设这种出租车的起步价为x元,超过2km后每千米收费y元,则下列方程正确的是()A. {x+7y=16x+13y=28 B. C. D.【答案】D【考点】二元一次方程组的解【解答】设这种出租车的起步价为x元,超过2km后每千米收费y元,则所列方程组为,故答案为:D.【分析】设这种出租车的起步价为x元,超过2km后每千米收费y元,根据二人坐车产生的费用进行计算即可。
2. (2019 山东菏泽) 已知是方程组的解,则a+b的值是()A. ﹣1B. 1C. ﹣5D. 5【答案】A【考点】二元一次方程组的解【解答】将代入,可得:,两式相加:a+b=−1,故答案为:A.【分析】将x、y的值代入方程组后方程组中两式相加即可得到a+b的值。
3. (2019 湖北荆门) 已知实数x,y满足方程组则的值为()A. B. 1 C. 3 D.【答案】A【考点】二元一次方程的解【解答】解:,故答案为:A【分析】先解方程组,把x和y的值代入求值式即可。
4. (2018 北京) 方程组的解为()A. B. C. D.【答案】D【考点】二元一次方程组的解【解答】解:将4组解分别代入原方程组,只有D选项同时满足两个方程,故答案为:D.【分析】根据方程组的解能使方程组中的每一个方程都成立,故将4组解分别代入原方程组,一一判断即可得出答案。
5. (2019 湖北孝感) 已知二元一次方程组{x+y=12x+4y=9,则的值是()A. B. 5 C. D. 6【答案】C【考点】利用分式运算化简求值,解二元一次方程组【解答】,得,2y=7,解得y=72,把y=72代入①得,x+72=1,解得x=−52,① ,故答案为:C.【分析】利用加减消元法求出二元一次方程组的解,再将代数式的分子分母进行因式分解,进行约分化简,然后代入求值。
中考数学专题复习四--分式方程和不等式

中考数学专题复习四--分式方程和不等式(组)(总6页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除中考数学专题复习(四)分式方程和不等式(组)【知识梳理】1.分式方程:分母中含有的方程叫分式方程.2.解分式方程的一般步骤:(1)去分母,在方程的两边都乘以,约去分母,化成整式方程;(2)解这个整式方程;(3)验根,把整式方程的根代入,看结果是不是零,使最简公分母为零的根是原方程的增根,必须舍去.3. 用换元法解分式方程的一般步骤:①设辅助未知数,并用含辅助未知数的代数式去表示方程中另外的代数式;②解所得到的关于辅助未知数的新方程,求出辅助未知数的值;③把辅助未知数的值代入原设中,求出原未知数的值;④检验作答.4.分式方程的应用:分式方程的应用题与一元一次方程应用题类似,不同的是要注意检验:(1)检验所求的解是否是所列;(2)检验所求的解是否 . 5.易错知识辨析:(1)去分母时,不要漏乘没有分母的项.(2)解分式方程的重要步骤是检验,检验的方法是可代入最简公分母, 使最简公分母为0的值是原分式方程的增根,应舍去,也可直接代入原方程验根.(3)如何由增根求参数的值:①将原方程化为整式方程;②将增根代入变形后的整式方程,求出参数的值.6.不等式的有关概念:用连接起来的式子叫不等式;使不等式成立的的值叫做不等式的解;一个含有的不等式的解的叫做不等式的解集.求一个不等式的的过程或证明不等式无解的过程叫做解不等式.7.不等式的基本性质:(1)若a <b ,则a +c c b +; (2)若a >b ,c >0则ac bc (或ca cb ); (3)若a >b ,c <0则ac bc (或c a cb ). 8.一元一次不等式:只含有 未知数,且未知数的次数是 且系数 的不等式,称为一元一次不等式;一元一次不等式的一般形式为 或ax b <;解一元一次不等式的一般步骤:去分母、 、移项、 、系数化为1.9.一元一次不等式组:几个 合在一起就组成一个一元一次不等式组.一般地,几个不等式的解集的 ,叫做由它们组成的不等式组的解集.10.由两个一元一次不等式组成的不等式组的解集有四种情况:(已知a b <)x a x b <⎧⎨<⎩的解集是x a <,即“小小取小”; x a x b >⎧⎨>⎩的解集是x b >,即“大大取大”;x a x b >⎧⎨<⎩的解集是a x b <<,即“大小小大中间找”; x a x b <⎧⎨>⎩的解集是空集,即“大大小小取不了”.11.易错知识辨析:(1)不等式的解集用数轴来表示时,注意“空心圆圈”和“实心点”的不同含义.(2)解字母系数的不等式时要讨论字母系数的正、负情况.如不等式ax b >(或ax b <)(0a ≠)的形式的解集: 当0a >时,b x a >(或b x a <); 当0a <时,b x a <(或b x a>); 当0a <时,b x a <(或b x a>). 12.求不等式(组)的特殊解:不等式(组)的解往往有无数多个,但其特殊解在某些范围内是有限的,如整数解,非负整数解,求这些特殊解应先确定不等式(组)的解集,然后再找到相应答案.13.列不等式(组)解应用题的一般步骤:①审:审题,分析题中已知什么、求什么,明确各数量之间的关系;②设:设未知数(一般求什么,就设什么为x );③找:找出能够表示应用题全部含义的一个不等关系;④列:根据这个不等关系列出需要的代数式,从而列出不等式(组);⑤解:解所列出的不等式(组),写出未知数的值或范围;⑥验:检验所求解是否符合题意;⑦答:写出答案(包括单位).14.易错知识辨析:判断不等式是否成立,关键是分析不等号的变化,其根据是不等式的性质.【真题回顾】一、选择题1.(2010年山东菏泽全真模拟1)下列运算中,错误..的是( ) A.(0)a ac c b bc =≠ B.1a b a b--=-+2(4)4-= D.x y y x x y y x --=++ 2.(2010年江西省统一考试样卷)若分式21x x +有意义,则x 的取值范围是( )A .x >1B .x >-1C .x ≠0D .x ≠-13.(2009年孝感)关于x 的方程211x a x +=- 的解是正数,则a 的取值范围是( ) A .a >-1 B .a >-1且a≠0 C .a <-1 D .a <-1且a≠-24.(2011.鸡西)分式方程)2)(1(11+-=--x x m x x 产生增根,则m 的值是( ) A. 0和3 B. 1 C. 1和-2 D. 35.(2009年安徽)甲志愿者计划用若干个工作日完成社区的某项工作,从第三个工作日起,乙志愿者加盟此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲志愿者计划完成此项工作的天数是( )A .8 B.7 C .6 D .5二、填空题1.(2010年西湖区月考)若分式22221x x x x --++的值为0,则x 的值等于 2.(2010年江苏省泰州市中考模拟题)使代数式43--x x 有意义的x 的取值范围是 . 3.(2009年滨州)解方程2223321x x x x --=-时,若设21x y x =-,则方程可化为 . 4.(2011襄阳)已知关于x 的分式方程1131=-+-xx m 的解是正数,则m 的取值范围为 5.(2010新疆乌鲁木齐)在数轴上,点A 、B 对应的数分别为2 ,15+-x x ,且A 、B 两点关于原点对称,则x 的值为 。
2023年广东中考数学二轮专题复习——方程(组)与不等式(组)(含答案)

2023年广东中考数学专题复习——方程(组)与不等式(组)(时间:90分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分)1.已知两数x,y之和是10,x比y的3倍大2,则下面所列方程组正确的是( )A.{x+y=10y=3x+2B.{x+y=10y=3x-2C.{x+y=10x=3y+2 D.{x+y=10x=3y-22.若把不等式组{2-x≥-3,x-1≥-2的解集在数轴上表示出来,则其对应的图形为A.长方形 B.线段 C.射线 D.直线3.用配方法解方程x2-2x-1=0时,配方后所得的方程为( )A.(x-1)2=2 B.(x-1)2=0C.(x+1)2=2 D.(x+1)2=04.计算2x-2-xx-2的结果是( )A.0 B.1 C.x D.-15.已知关于x的方程x2-kx-6=0的一个根为x=3,则实数k的值为( ) A.1 B.-1 C.2 D.-26.不等式x≥2的解集在数轴上表示为( )A BC D7.已知方程组{2x+y=4,x+2y=5,则x+y的值为( )A.-1 B.0 C.2 D.38.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数k的取值范围是( )A.k>-1 B.k<1且k≠0C.k≥-1且k≠0D.k>-1且k≠09.小朱要到距家1 500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,并且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱的速度是x 米/分,则根据题意所列方程正确的是( )A .1 440x -100-1 440x =10B .1 440x =10+1 440x +100C .1 440x =1 440x -100+10D .1 440x +100-1 440x =1010.设x 1,x 2是方程x 2+3x -3=0的两个实数根,则x 2x 1+x 1x 2的值为( )A .5 B .-5 C .1 D .-1二、填空题(本大题共5小题,每小题3分,共15分)11.要使分式5x -1有意义,则x 的取值范围是 .12.一元二次方程x 2-3x =0的根是 .13.已知a|a |+b|b |=0,则ab|ab |的值为 .14.如果4x a +2b -5-2y 3a -b -3=8是二元一次方程,那么a -b = .15.对于实数a ,b ,定义运算“*”:a*b ={a 2-ab (a ≥b ),ab -b 2(a <b ).例如:4*2,因为4>2,所以4*2=42-4×2=8.若x 1,x 2是一元二次方程x 2-5x +6=0的两个根,则x 1*x 2= .三、解答题(一)(本大题共3小题,每小题8分,共24分)16.解方程:x 2-10x +9=0.17.解不等式组:{9x +5<8x +7,43x +2>1-23x ,并写出其整数解.18.解方程:2xx-2=1-12-x.四、解答题(二)(本大题共3小题,每小题9分,共27分)19.先化简,再求值:x-2x-1÷(x+1-3x-1),其中x=3-2.20.某条高速的建设正在紧张地进行,现有大量的沙石需要运输.某车队有载重为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石.(1)该车队载重为8吨和10吨的卡车各有多少辆?(2)随着工程的进展,该车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.21.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.(1)求证:该方程有两个不相等的实数根;(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.五、解答题(三)(本大题共2小题,每小题12分,共24分)22.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2013年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.(1)若该商城前4个月的自行车销量的月平均增长率相同,该商城4月份卖出多少辆自行车?(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车的进价为1 000元/辆,售价为1 300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?23.关于x的一元二次方程(m-1)x2-2mx+m+1=0.(1)求方程的根;(2)m为何整数时,此方程的两个根都为正整数?2023年广东中考数学专题复习——方程(组)与不等式(组) 答案版(时间:90分钟 满分:120分)一、选择题(本大题共10小题,每小题3分,共30分)1.已知两数x,y之和是10,x比y的3倍大2,则下面所列方程组正确的是(C)A.{x+y=10y=3x+2B.{x+y=10y=3x-2C.{x+y=10x=3y+2 D.{x+y=10x=3y-22.若把不等式组{2-x≥-3,x-1≥-2的解集在数轴上表示出来,则其对应的图形为(B)A.长方形 B.线段 C.射线 D.直线3.用配方法解方程x2-2x-1=0时,配方后所得的方程为(A)A.(x-1)2=2 B.(x-1)2=0C.(x+1)2=2 D.(x+1)2=04.计算2x -2-xx -2的结果是(D )A .0B .1C .xD .-15.已知关于x 的方程x 2-kx -6=0的一个根为x =3,则实数k 的值为(A )A .1B .-1C .2D .-26.不等式x≥2的解集在数轴上表示为(C )AB CD 7.已知方程组{2x +y =4,x +2y =5,则x +y 的值为(D )A .-1 B .0 C .2 D .38.若关于x 的一元二次方程kx 2-2x -1=0有两个不相等的实数根,则实数k 的取值范围是(D )A .k>-1B .k<1且k≠0C .k≥-1且k≠0D .k>-1且k≠09.小朱要到距家1 500米的学校上学,一天,小朱出发10分钟后,小朱的爸爸立即去追小朱,并且在距离学校60米的地方追上了他.已知爸爸比小朱的速度快100米/分,求小朱的速度.若设小朱的速度是x 米/分,则根据题意所列方程正确的是(B )A .1 440x -100-1 440x=10 B .1 440x =10+1 440x +100C .1 440x =1 440x -100+10 D .1 440x +100-1 440x =1010.设x 1,x 2是方程x 2+3x -3=0的两个实数根,则x 2x 1+x 1x 2的值为(B )A .5 B .-5 C .1 D .-1二、填空题(本大题共5小题,每小题3分,共15分)11.要使分式5x -1有意义,则x 的取值范围是x≠1.12.一元二次方程x 2-3x =0的根是x 1=0,x 2=3.13.已知a|a |+b|b |=0,则ab|ab |的值为-1.14.如果4x a +2b -5-2y 3a -b -3=8是二元一次方程,那么a -b =0.15.对于实数a ,b ,定义运算“*”:a*b ={a 2-ab (a ≥b ),ab -b 2(a <b ).例如:4*2,因为4>2,所以4*2=42-4×2=8.若x 1,x 2是一元二次方程x 2-5x +6=0的两个根,则x 1*x 2=3或-3.三、解答题(一)(本大题共3小题,每小题8分,共24分)16.解方程:x 2-10x +9=0.解:方法一(配方法):将方程x 2-10x +9=0变形为x 2-10x =-9,配方,得x 2-10x +25=-9+25,整理,得(x -5)2=16,解得x 1=1,x 2=9.方法二(求根公式法):因为a =1,b =-10,c =9,Δ=100-36=64>0,由求根公式解得x 1=1,x 2=9.方法三(因式分解法):将方程x 2-10x +9=0变形为(x -1)(x -9)=0,解得x 1=1,x 2=9.17.解不等式组:{9x +5<8x +7,43x +2>1-23x ,并写出其整数解.解:{9x +5<8x +7, ①43x +2>1-23x , ②解不等式①得x<2,解不等式②得x>-12.把①②的解集表示在数轴上,如图.故原不等式组的解集是-12<x<2.其整数解是0和1.18.解方程:2x x -2=1-12-x.解:方程的两边同时乘(x -2),得2x =x -2+1,解得x =-1.检验:当x =-1时,x -2≠0,故x =-1是原方程的解.四、解答题(二)(本大题共3小题,每小题9分,共27分)19.先化简,再求值:x -2x -1÷(x +1-3x -1),其中x =3-2.解:原式=x -2x -1÷(x 2-1x -1-3x -1)=x -2x -1×x -1(x +2)(x -2)=1x +2.当x =3-2时,原式=33.20.某条高速的建设正在紧张地进行,现有大量的沙石需要运输.某车队有载重为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石.(1)该车队载重为8吨和10吨的卡车各有多少辆?(2)随着工程的进展,该车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.解:(1)设该车队载重为8吨和10吨的卡车分别有x 辆、y 辆,根据题意得{x +y =12,8x +10y =110,解得{x =5,y =7.故该车队载重为8吨的卡车有5辆,载重为10吨的卡车有7辆;(2)设载重为8吨的卡车增加了z 辆,依题意得8(5+z)+10(7+6-z)>165,解得z<52.∵z≥0且为整数,∴z =0,1,2;∴6-z =6,5,4,∴车队共有3种购车方案:①载重为8吨的卡车不购买,载重为10吨的卡车购买6辆;②载重为8吨的卡车购买1辆,载重为10吨的卡车购买5辆;③载重为8吨的卡车购买2辆,载重为10吨的卡车购买4辆.21.已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.(1)求证:该方程有两个不相等的实数根;(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.(1)证明:∵Δ=[-(2k+1)]2-4×1×(k2+k)=1>0,∴方程有两个不相等的实数根;(2)解:∵由x2-(2k+1)x+k2+k=0,得(x-k)[x-(k+1)]=0,∴x1=k,x2=k+1.即AB,AC的长为k,k+1,当AB=BC时,即k=5,满足三角形构成条件;当AC=BC时,k+1=5,解得k=4,满足三角形构成条件.综上所述,k=4或k=5.五、解答题(三)(本大题共2小题,每小题12分,共24分)22.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2013年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.(1)若该商城前4个月的自行车销量的月平均增长率相同,该商城4月份卖出多少辆自行车?(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车的进价为1 000元/辆,售价为1 300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?解:(1)设前4个月自行车销量的月平均增长率为x,根据题意列方程,得64(1+x)2=100,解得x1=-225%(不合题意,舍去),x2=25%,100×(1+25%)=125(辆).故该商城4月份卖出125辆自行车.(2)设购进B 型车x 辆,则购进A 型车30 000-1 000x 500辆,根据题意得不等式组2x≤30 000-1 000x 500≤2.8x ,解得12.5≤x≤15,因为自行车辆数为整数,所以13≤x≤15,销售利润W =(700-500)×30 000-1 000x 500+(1 300-1 000)x.整理得W =-100x +12 000,因为W 随着x 的增大而减小,所以当x =13时,销售利润W 有最大值,此时,30 000-1 000×13500=34,所以该商城应购进A 型车34辆,B 型车13辆.23.关于x 的一元二次方程(m -1)x 2-2mx +m +1=0.(1)求方程的根;(2)m 为何整数时,此方程的两个根都为正整数?解:(1)方法一:根据题意得m≠1.Δ=(-2m)2-4(m -1)(m +1)=4.∴x 1=2m +22(m -1)=m +1m -1,x 2=2m -22(m -1)=1.方法二:根据题意得m≠1.原方程可化为(x -1)[(m -1)x -(m +1)]=0,∴x 1=m +1m -1,x 2=1.(2)由(1)知x 1=m +1m -1=1+2m -1,∵方程的两个根都是正整数,∴2m -1是正整数,∴m -1=1或2.∴m =2或3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例 1】(1)(2017·黄冈)解方程:x+3 1+1=x-x-2 1.
(1)求男式单车和女式单车的单价; (2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置 两种单车的费用不超过50 000元,该社区有几种购置方案?怎样购置才能使 所需总费用最低,最低费用是多少?
【思路引导】(1)根据“购买3辆男式单车与4辆女式单车费用相同,购买5 辆男式单车与4辆女式单车共需16 000元”列方程组求解可得;(2)设购置女 式单车m辆,则购置男式单车(m+4)辆,根据“两种单车至少需要22辆、购 置两种单车的费用不超过50 000元”列不等式组求解,即可确定购置方案; 再列出购置总费用关于m的函数解析式,利用一次函数的性质结合m的范围 可得其最值情况.
3x-1<x+5, (2)(2017·淮安)解不等式组:x-2 3<x-1, 并写出它的整数解.
3.(2017·黄石)已知关于 x 的一元二次方程 x2-4x-m2=0. (1)求证:该方程有两个不相等的实数根; (2)若该方程的两个实数根 x1,x2 满足 x1+2x2=9,求 m 的值.
4.(导学号)(2017·哈尔滨)威丽商场销售A,B两种商品,售出1件A种商品和 4件B种商品所得利润为600元,售出3件A种商品和5件B种商品所得利润为1 100元. (1)求每件A种商品和每件B种商品售出后所得利润分别为多少元; (2)由于需求量大,A,B两种商品很快售完,威丽商场决定再一次购进A,B 两种商品共34件.如果将这34件商品全部售完后所得利润不低于4 000元, 那么威丽商场至少需购进多少件A种商品?
方法归纳
1.判别式与根的关系: (1)当b2-4ac>0⇔方程有两个不相等的实数根; (2)当b2-4ac=0⇔方程有两个相等的实数根; (3)当b2-4ac<0⇔方程没有实数根.
2.利用根与系数的关系解决求值问题,常见变形有: (1)x12+x22=(x1+x2)2-2x1x2; (2)x11+x12=xx1+1x2x2; (3)|x1-x2|= (x1+x2)2-4x1x2.K
1.解方程(组): (1)(2017·宁夏)xx+ -33-x+4 3=1;
x+y=2, (2)2x-13y=53.
2.解不等式(组): (1)(2017·长沙)解不等式组25xx≥ -- 1>93-(xx,+1), 并把它的解集在数轴上表示出来;
解:25xx≥ -- 1>93-(xx①+,1)②,解不等式①,得 x≥-3,解不等式②, 得 x>2,所以不等式组的解集为 x>2,将解集表示在数轴上如下:
解:(1)∵关于 x 的方程 x2+(2k-1)x+k2-1=0 有两个实数根 x1,x2, ∴Δ=(2k-1)2-4(k2-1)=-4k+5≥0,解得 k≤54.
∴实数 k 的取值范围为 k≤54.
(2)∵关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2,∴x1+x2=1 -2k,x1·x2=k2-1.∵x12+x22=(x1+x2)2-2x1·x2=16+x1·x2,∴(1-2k)2- 2×(k2-1)=16+(k2-1),即k2-4k-12=0,解得k=-2或k=6(不符合题 意,舍去).∴实数k的值为-2.
方法归纳
1.构建方程(组)或不等式解决实际问题,一般需要注意以下步骤:审题、设 未知数、列方程(组)或不等式(组)、解、检验、答.按照这样的程序,可以 避免出现失误. 2.解决这类问题的关键是从问题情境中找等量关系和不等关系,其中不等 关系有非常明显的标志语,如“大于”、“小于”、“不少于”、“不超 过”等等.
解:(1)设男式单车 x 元/辆,女式单车 y 元/辆,
根据题意,得35xx=+44yy,=16
x=2 000,解得y=1
000, 500.
答:男式单车 2 000 元/辆,女式单车 1 500 元/辆.
(2)设购置女式单车 m 辆,则购置男式单车(m+4)辆, 根据题意,得m2 0+00m(+m4+≥42)2,+1 500m≤50 000,解得 9≤m≤12. ∵m 为整数,∴m 的值可以是 9,10,11,12,即该社区有四种购置方案; 设购置总费用为 W,则 W=2 000(m+4)+1 500m=3 500m+8 000. ∵W 随 m 的增大而增大,∴当 m=9 时,W 取得最小值,最小值为 39 500. 答:该社区共有 4 种购置方案,其中购置男式单车 13 辆、女式单车 9 辆 时所需总费用最低,最低费用为 39 500 元.
【例 3】(2017·岳阳)我市某校组织爱心捐书活动,准备将一批捐赠的书打
包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的23,结果 打了 16 个包还多 40 本;第二次他们把剩下的书全部取来,连同第一次打包剩 下的书一起,刚好又打了 9 个包,那么这批书共有多少本?
【例4】(2017·恩施州)为积极响应政府提出的“绿色发展·低碳出行”号召, 某社区决定购置一批共享单车.经市场调查得知,购买3辆男式单车与4辆女 式单车费用相同,购买5辆男式单车与4辆女式单车共需16 000元.
解:(1)设每件 A 种商品售出后所得利润为 x 元, 每件 B 种商品售出后所得利润为 y 元. 由题意,得x3+ x+4y5=y=60101,00,解得xy==210000,. 答:每件 A 种商品售出后所得利润为 200 元,每件 B 种商品售出后所得 利润为 100Байду номын сангаас元.
(2)(2017·枣庄)x 取哪些整数值时,不等式 5x+2>3(x-1)与12x≤2-32x 都 成立?
【例2】(2017·十堰)已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数 根x1,x2.
(1)求实数k的取值范围; (2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
