概率统计基础训练题
概率与统计的基础练习题

概率与统计的基础练习题在概率与统计学中,练习题是帮助学生巩固知识和提高技能的重要方式。
通过解答练习题,学生可以加深对概率和统计理论的理解,掌握基本的解题方法和技巧。
本文将为您提供一系列概率与统计的基础练习题,帮助您巩固相关知识。
1. 骰子问题假设有一个六面骰子,每个面上的数字分别为1、2、3、4、5和6。
现从中抽取一个骰子,并投掷5次,每次记录下骰子的面数。
请计算以下概率:a) 出现奇数的次数为3次的概率。
b) 至少出现一次6的概率。
c) 第一次出现4的概率。
解答:a) 出现奇数的次数为3次的概率=(投掷出奇数的次数为3次)/(总共投掷的次数为5次)= C(5, 3) * (1/2)^3 * (1/2)^2 = 10/32 = 5/16。
b) 至少出现一次6的概率= 1 - 不出现6的概率= 1 - (5/6)^5 = 1 - 3125/7776 = 4651/7776。
c) 第一次出现4的概率= (第一次投掷出现4,后面四次不出现4)= 1/6 * (5/6)^4 = 625/7776。
2. 选课问题某高中学生共有20门选修课可供选择,但该学生只能选择其中5门课。
假设该学生随机选课,求以下概率:a) 至少选择一门语言课的概率。
b) 选择4门以上的概率。
c) 选课中不包含数学和科学课的概率。
解答:a) 至少选择一门语言课的概率= 1 - 全选非语言课的概率 = 1 - (C(15,5) / C(20, 5)) = 1 - 3003/15504 = 12501/15504。
b) 选择4门以上的概率= (选择4门课的情况数 + 选择5门课的情况数) / 总共的情况数 = (C(20, 4) + C(20, 5)) / C(20, 5) = (4845 + 15504) / 15504 = 20349/15504 = 462/351。
c) 选课中不包含数学和科学课的概率= (C(8, 5) / C(20, 5)) =56/15504。
概率与统计基础训练题(有详解)

概率与统计基础训练题(有详解)概率与统计基础训练题(有详解)
问题一
某班级有30名学生,其中20名男生和10名女生。
如果从这个班级中随机选取一名学生,求选中的学生是女生的概率。
解答:
女生人数为10,总人数为30,所以概率为女生人数除以总人数,即 10/30 = 1/3。
问题二
一批产品的质量控制数据显示,产品正常的概率为80%。
某个客户购买了5个这种产品,以该概率计算,求这5个产品中至少有2个正常产品的概率。
解答:
可以使用二项分布来求解。
根据二项分布的公式,可以得出至少有2个正常产品的概率为P(X≥2) = 1 - P(X=0) - P(X=1)。
计算 P(X=0) = (1-0.8)^5 = 0.
计算 P(X=1) = C(5, 1) * (0.8^1) * (1-0.8)^4 = 0.
所以P(X≥2) = 1 - 0. - 0. = 0.。
问题三
一批电视机中有10%的次品。
现在从中随机选取3台电视机进行检测,求这3台电视机中至少有1台次品的概率。
解答:
可以使用二项分布来求解。
根据二项分布的公式,可以得出至少有1台次品的概率为P(X≥1) = 1 - P(X=0)。
计算 P(X=0) = (1-0.1)^3 = 0.729
所以P(X≥1) = 1 - 0.729 = 0.271。
以上是概率与统计基础训练题的解答,希望对您有所帮助。
中职数学概率统计练习题

中职数学概率统计练习题
练一:概率计算
1. 某班级有50名学生,其中30人擅长篮球,20人擅长足球,10人既擅长篮球又擅长足球。
从该班级中随机选一个学生,请计算该学生擅长篮球或足球的概率。
练二:条件概率
2. 一家电子产品公司生产电视机和电冰箱两种产品。
该公司的统计数据显示,电视机的次品率是5%,而电冰箱的次品率是3%。
另外,该公司生产的电视机和电冰箱的比例为3:2。
从该公司中随机选一个产品,请计算该产品是电视机的概率,且是次品的条件概率。
练三:二项分布
3. 一枚硬币正面向上的概率是0.6。
现在进行5次抛硬币的实验,请计算恰好有3次正面朝上的概率。
练四:正态分布
4. 某市一所高中的学生成绩服从正态分布,其平均分为80分,标准差为10分。
请计算学生中成绩大于90分的比例。
练五:抽样与估计
5. 某公司的员工数量为1000人。
为了对该公司员工的平均年
龄进行估计,从中随机抽取了100人并统计了他们的年龄。
请计算
在95%的置信水平下,对于该公司员工平均年龄的置信区间。
练六:相关与回归
6. 一个研究人员想要了解身高和体重之间的关系。
他在200名
成年男性中测量了他们的身高(单位:厘米)和体重(单位:千克)。
请计算身高和体重之间的相关系数,并解释其意义。
概率与统计基础过关题(附答案)
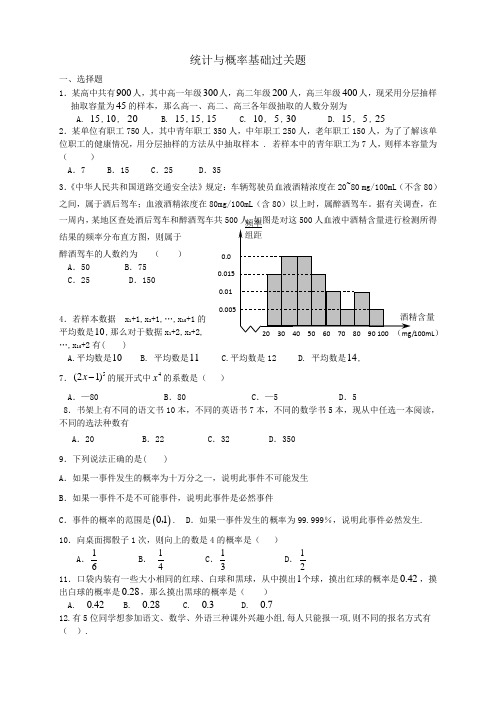
统计与概率基础过关题一、选择题1.某高中共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取容量为45的样本,那么高一、高二、高三各年级抽取的人数分别为A. 15,10, 20B. 15,15,15C. 10, 5,30D. 15, 5,252.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为( )A .7B .15C .25D .353.《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100mL (不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100mL (含80)以上时,属醉酒驾车。
据有关调查,在一周内,某地区查处酒后驾车和醉酒驾车共500人.如图是对这500人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为 ( ) A .50 B .75C .25D .1504.若样本数据 x 1+1,x 2+1,…,x 10+1的平均数是10,那么对于数据x 1+2,x 2+2, …,x 10+2有( )A.平均数是10B. 平均数是11C.平均数是12D. 平均数是14, 7.5(21)x -的展开式中4x 的系数是( )A .—80B .80C .—5D .58.书架上有不同的语文书10本,不同的英语书7本,不同的数学书5本,现从中任选一本阅读,不同的选法种数有A .20B .22C .32D .350 9.下列说法正确的是( )A .如果一事件发生的概率为十万分之一,说明此事件不可能发生B .如果一事件不是不可能事件,说明此事件是必然事件C .事件的概率的范围是()01,. D .如果一事件发生的概率为99.999%,说明此事件必然发生. 10.向桌面掷骰子1次,则向上的数是4的概率是( )A.C11个球,摸出红球的概率是0.42,摸出白球的概率是0.28,那么摸出黒球的概率是( ) A. 0.42 B. 0.28 C. 0.3 D. 0.712.有5位同学想参加语文、数学、外语三种课外兴趣小组,每人只能报一项,则不同的报名方式有( ).) 0.0150.01 0.00.0250.0150.010.005频率组距A.8种B.15种C.53种D.35种二、填空题13.抛掷一枚均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6),则事件“出现点数大于4”的概率是_____________.14.甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、0.5,则三人都达标的概率是 ,三人中至少有一人达标的概率是 。
2024年数学高三下册概率统计基础练习题(含答案)

2024年数学高三下册概率统计基础练习题(含答案)试题部分一、选择题:1. 已知一组数据的方差是9,那么这组数据的标准差是()A. 3B. 9C. 3²D. 1/32. 下列哪个图形能够表示一个离散型随机变量X的概率分布()A. 直方图B. 折线图C. 散点图D. 条形图3. 抛掷一枚质地均匀的硬币三次,恰好出现两次正面朝上的概率是()A. 1/2B. 1/3C. 3/8D. 1/44. 已知随机变量X服从二项分布,且P(X=0)=0.16,P(X=1)=0.32,则P(X=2)等于()A. 0.16B. 0.32C. 0.48D. 0.645. 下列关于正态分布的说法,错误的是()A. 正态分布是连续型概率分布B. 正态分布曲线呈钟形C. 正态分布的均数等于0,标准差等于1D. 正态分布曲线关于x轴对称6. 设随机变量X的分布列为:X=1的概率为0.2,X=2的概率为0.3,X=3的概率为0.5,则E(X)等于()A. 1B. 2C. 2.5D. 37. 已知一组数据的平均数为50,标准差为5,那么这组数据的中位数()A. 一定大于50B. 一定小于50C. 一定等于50D. 无法确定8. 在一组数据中,众数与众数的频率之和等于()A. 1B. 0C. 数据总数D. 频率9. 下列关于概率的说法,正确的是()A. 必然事件的概率为0B. 不可能事件的概率为1C. 随机事件的概率介于0和1之间D. 互斥事件的概率之和等于110. 在一个箱子中有5个红球,3个蓝球,2个绿球,随机取出一个球,取到红球或绿球的概率是()A. 2/5B. 3/5C. 4/5D. 1/2二、判断题:1. 样本方差越大,说明数据的波动越大。
()2. 两个互斥事件的概率之和一定等于1。
()3. 随机变量X的期望值E(X)一定等于它的众数。
()4. 在二项分布中,如果n固定,p越大,概率分布越集中。
()5. 正态分布曲线下,面积等于1的部分对应的横坐标范围是负无穷到正无穷。
概率基础测试题及答案解析

概率基础测试题及答案解析一、选择题(每题3分,共30分)1. 随机变量X服从标准正态分布,那么P(X>0)等于多少?A. 0.5B. 0.6826C. 0.8413D. 0.5000答案:A解析:标准正态分布的均值为0,标准差为1,对称轴为X=0,因此P(X>0)等于0.5。
2. 已知随机变量X服从二项分布B(n, p),其中n=10,p=0.3,那么E(X)等于多少?A. 1.5B. 3C. 2.7D. 0.3答案:B解析:二项分布的期望值E(X)=np,所以E(X)=10*0.3=3。
3. 一组数据的平均数是5,方差是4,那么这组数据的中位数是多少?A. 4B. 5C. 6D. 无法确定答案:B解析:平均数是所有数据的总和除以数据的个数,而中位数是将数据按大小顺序排列后位于中间的数。
在没有具体数据的情况下,无法确定中位数,但根据平均数的定义,可以推断中位数为5。
4. 已知随机变量X和Y相互独立,且P(X=1)=0.5,P(Y=1)=0.3,那么P(X=1且Y=1)等于多少?A. 0.15B. 0.5C. 0.3D. 0.6答案:A解析:由于X和Y相互独立,所以P(X=1且Y=1)=P(X=1)*P(Y=1)=0.5*0.3=0.15。
5. 一组数据的样本容量为100,样本均值为50,样本方差为25,那么这组数据的标准差是多少?A. 5B. 10C. 20D. 25答案:A解析:标准差是方差的平方根,所以标准差=√25=5。
6. 已知随机变量X服从泊松分布,其参数λ=4,那么P(X=3)等于多少?A. 0.182B. 0.273C. 0.409D. 0.546答案:B解析:泊松分布的概率质量函数为P(X=k)=e^(-λ)λ^k/k!,代入λ=4和k=3,计算得到P(X=3)=e^(-4)4^3/3!=0.273。
7. 已知随机变量X服从均匀分布U(0,1),那么P(0.5<X<0.6)等于多少?A. 0.1B. 0.05C. 0.15D. 0.2答案:B解析:均匀分布的概率等于区间长度,所以P(0.5<X<0.6)=0.6-0.5=0.1,但因为题目中区间长度为0.1,所以答案为0.05。
2024年数学九年级上册概率统计基础练习题(含答案)
2024年数学九年级上册概率统计基础练习题(含答案)试题部分一、选择题:1. 下列事件中,哪一个属于随机事件?A. 太阳从西边升起B. 掷一枚硬币,正面朝上C. 1+1=2D. 今天的天气是晴天2. 下列数据中,哪一个不是频数?A. 某班有50名学生,其中30名学生喜欢打篮球B. 某班有50名学生,其中男生25名C. 某班有50名学生,考试及格的有40名D. 某班有50名学生,平均身高160cm3. 抛掷两个骰子,下列哪个事件的概率为1/6?A. 两个骰子的点数和为7B. 两个骰子的点数和为12C. 两个骰子的点数相同D. 两个骰子的点数之和小于64. 下列哪个图形的面积可以用概率公式计算?A. 正方形B. 长方形C. 圆形D. 三角形5. 一个袋子里有5个红球,3个蓝球,2个绿球,从中随机抽取一个球,下列哪个事件的概率最大?A. 抽到红球B. 抽到蓝球C. 抽到绿球D. 抽到红球或蓝球6. 下列哪个统计量不受极端值影响?A. 平均数B. 中位数C. 众数D. 方差A. 70分B. 75分C. 80分D. 85分8. 下列哪个图形的面积不能表示概率?A. 长方形B. 正方形C. 圆形D. 梯形9. 一个班级有40名学生,其中有30名学生参加了数学竞赛,20名学生参加了英语竞赛。
如果每名学生最多参加一个竞赛,那么至少有多少名学生没有参加任何竞赛?A. 0B. 10C. 15D. 2010. 下列哪个事件的概率为0?A. 抛掷一枚硬币,正面朝上B. 抛掷一枚硬币,反面朝上C. 抛掷一枚硬币,正面和反面同时朝上D. 抛掷一枚硬币,正面和反面同时朝下二、判断题:1. 概率值越大,事件发生的可能性越大。
()2. 概率值越小,事件发生的可能性越小。
()3. 抛掷一枚硬币,正面朝上的概率是1/2。
()4. 在一组数据中,众数只有一个。
()5. 平均数、中位数和众数都是描述数据集中趋势的统计量。
()6. 方差越小,数据的波动越小。
概率统计第一章概率论的基础知识习题与答案
概率统计第一章概率论的基础知识习题与答案概率论与数理统计概率论的基础知识习题一、选择题1、下列关系正确的是( )。
A、0∈∅B、{0}∅=∅⊂D、{0}∅∈C、{0}答案:C2、设{}{}2222=+==+=,则( )。
P x y x y Q x y x y(,)1,(,)4A、P Q⊂B、P Q<C、P Q⊂与P Q⊃都不对D、4P Q=答案:C二、填空1、6个学生和一个老师并排照相,让老师在正中间共有________种排法。
答案:6!720=2、5个教师分配教5门课,每人教一门,但教师甲只能教其中三门课,则不同的分配方法有____________种。
答案:723、编号为1,2,3,4,5的5个小球任意地放到编号为A、B、C、D、E、F的六个小盒子中,概率论的基础知识第 1 页(共 19 页)每一个盒至多可放一球,则不同的放法有_________种。
答案:()65432720⨯⨯⨯⨯=4、设由十个数字0,1,2,3, ,9的任意七个数字都可以组成电话号码,则所有可能组成的电话号码的总数是_______________。
答案:710个5、九名战士排成一队,正班长必须排在前头,副班长必须排在后头,共有_______________种不同的排法。
答案:77!5040P==6、平面上有10个点,其中任何三点都不在一直线上,这些点可以确定_____个三角形。
答案:1207、5个篮球队员,分工打右前锋,左前锋,中锋,左后卫右后卫5个位置共有_____________种分工方法?答案:5!120=8、6个毕业生,两个留校,另4人分配到4个概率论的基础知识第 2 页(共 19 页)不同单位,每单位1人。
则分配方法有______种。
答案:(6543)360⨯⨯⨯=9、平面上有12个点,其中任意三点都不在一条直线上,这些点可以确定_____________条不同的直线。
答案:6610、编号为1,2,3,4,5的5个小球,任意地放到编号为A,B,C,D,E,F,的六个小箱子中,每个箱子中可放0至5个球,则不同的放法有___________种。
概率统计基础训练题
第一章基础训练题一、填空1、设}1),({},4),({2222>+=≤+=y x y x B y x y x A ,则=⋂B A 。
2、事件A 、B 、C 至少有一个发生可表示为 ,至少有两个发生 ,三个都不发生 。
3、设}6,5,4,3,2,1{},7,5,3,1{==B A ,则=-B A 。
4、设事件A 在10次试验中发生了4次,则事件A 的频率为 。
5、设,)(),()(p A p B A p AB p ==则=)(B p 。
6、A 、B 二人各抛一枚硬币3次,则出现国徽一面次数相同的概率是 。
7、筐中有4个青苹果和5个红元帅,随机地从中取出2个,则取出的苹果为同一品种的概率为 ,恰好取出2个青苹果的概率为 ,恰好取出1个青苹果和1个红元帅的概率为 。
8、从一批由45件正品,5件次品组成的产品中任取3件产品,其中恰有一件次品的概率为 ,至少有一件正品的概率为 。
9、从一筐装有95个一等品,5个二等品的苹果中,每次随机取一个,记录它的等级后放回原筐搅匀后再取一个,共取50次,则无二等品的概率为 。
10、已知,3.0)(,4.0)(==B p A p 5.0)(=⋃B A p ,则=)(B A p 。
11、已知,8.0)(,6.0)(,5.0)(===A B p B p A p 则=)(AB p ,=⋃)(B A p 。
12、对任意二事件B A ,,=-)(B A p 。
13、已知,3.0)(,4.0)(==B p A p (1)当A ,B 互不相容时,=⋃)(B A p ,=)(AB p(2)当A ,B 相互独立时,=⋃)(B A p ,=)(AB p ;(3)当A B ⊂时,=)(A p ,=)(A B p ,=⋃)(B A p ,=)(AB p ,=-)(B A p 。
14、设C B A ,,为三事件,A 与B 都发生而C 不发生,则用C B A ,,的运算关系可表示为 。
设A ,B ,C 都发生,则用C B A ,,的运算关系可表示为 。
概率统计习题集(含答案)
第一章 随机事件及其概率一、选择题:1.设A 、B 、C 是三个事件,与事件A 互斥的事件是: ( )A .AB AC + B .()A B C + C .ABCD .A B C ++2.设B A ⊂ 则 ( )A .()P AB =1-P (A ) B .()()()P B A P B A -=-C . P(B|A) = P(B)D .(|)()P AB P A =3.设A 、B 是两个事件,P (A )> 0,P (B )> 0,当下面的条件( )成立时,A 与B 一定独立A .()()()P AB P A P B = B .P (A|B )=0C .P (A|B )= P (B )D .P (A|B )= ()P A4.设P (A )= a ,P (B )= b, P (A+B )= c, 则 ()P AB 为: ( )A .a-bB .c-bC .a(1-b)D .b-a5.设事件A 与B 的概率大于零,且A 与B 为对立事件,则不成立的是 ( )A .A 与B 互不相容 B .A 与B 相互独立C .A 与B 互不独立D .A 与B 互不相容6.设A 与B 为两个事件,P (A )≠P (B )> 0,且A B ⊃,则一定成立的关系式是( )A .P (A|B )=1 B .P(B|A)=1C .(|A)1p B =D .(A|)1p B =7.设A 、B 为任意两个事件,则下列关系式成立的是 ( )A .()AB B A -= B .()A B B A -⊃C .()A B B A -⊂D .()A B B A -=8.设事件A 与B 互不相容,则有 ( )A .P (AB )=p (A )P (B ) B .P (AB )=0C .A 与B 互不相容D .A+B 是必然事件9.设事件A 与B 独立,则有 ( )A .P (AB )=p (A )P (B ) B .P (A+B )=P (A )+P (B )C .P (AB )=0D .P (A+B )=110.对任意两事件A 与B ,一定成立的等式是 ( )A .P (AB )=p (A )P (B ) B .P (A+B )=P (A )+P (B )C .P (A|B )=P (A )D .P (AB )=P (A )P (B|A )11.若A 、B 是两个任意事件,且P (AB )=0,则 ( )A .A 与B 互斥 B .AB 是不可能事件C .P (A )=0或P (B )=0D .AB 未必是不可能事件12.若事件A 、B 满足A B ⊂,则 ( )A .A 与B 同时发生 B .A 发生时则B 必发生C .B 发生时则A 必发生D .A 不发生则B 总不发生13.设A 、B 为任意两个事件,则P (A-B )等于 ( )A . ()()PB P AB - B .()()()P A P B P AB -+C .()()P A P AB -D .()()()P A P B P AB --14.设A 、B 、C 为三事件,则AB BC AC 表示 ( )A .A 、B 、C 至少发生一个 B .A 、B 、C 至少发生两个C .A 、B 、C 至多发生两个D .A 、B 、C 至多发生一个15.设0 < P (A) < 1. 0 < P (B) < 1. P(|B)+P(A B A )=1. 则下列各式正确的是( )A .A 与B 互不相容 B .A 与B 相互独立C .A 与B 相互对立D .A 与B 互不独立16.设随机实际A 、B 、C 两两互斥,且P (A )=0.2,P (B )=0.3,P (C )=0.4,则PA B C -= ()( ). A .0.5 B .0.1 C .0.44 D .0.317掷两枚均匀硬币,出现一正一反的概率为 ( )A .1/2B .1/3C .1/4D .3/418.一种零件的加工由两道工序组成,第一道工序的废品率为 1p ,第二道工序的废品率为2p ,则该零件加工的成品率为 ( )A .121p p --B .121p p -C .12121p p p p --+D .122p p --19.每次试验的成功率为)10(<<p p ,则在3次重复试验中至少失败一次概率为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章基础训练题一、填空1、设}1),({},4),({2222>+=≤+=y x y x B y x y x A ,则=⋂B A 。
2、事件A 、B 、C 至少有一个发生可表示为 ,至少有两个发生 ,三个都不发生 。
3、设}6,5,4,3,2,1{},7,5,3,1{==B A ,则=-B A 。
4、设事件A 在10次试验中发生了4次,则事件A 的频率为 。
5、设,)(),()(p A p B A p AB p ==则=)(B p 。
6、A 、B 二人各抛一枚硬币3次,则出现国徽一面次数相同的概率是 。
7、筐中有4个青苹果和5个红元帅,随机地从中取出2个,则取出的苹果为同一品种的概率为 ,恰好取出2个青苹果的概率为 ,恰好取出1个青苹果和1个红元帅的概率为 。
8、从一批由45件正品,5件次品组成的产品中任取3件产品,其中恰有一件次品的概率为 ,至少有一件正品的概率为 。
9、从一筐装有95个一等品,5个二等品的苹果中,每次随机取一个,记录它的等级后放回原筐搅匀后再取一个,共取50次,则无二等品的概率为 。
10、已知,3.0)(,4.0)(==B p A p 5.0)(=⋃B A p ,则=)(B A p 。
11、已知,8.0)(,6.0)(,5.0)(===A B p B p A p 则=)(AB p ,=⋃)(B A p 。
12、对任意二事件B A ,,=-)(B A p 。
13、已知,3.0)(,4.0)(==B p A p (1)当A ,B 互不相容时,=⋃)(B A p ,=)(AB p(2)当A ,B 相互独立时,=⋃)(B A p ,=)(AB p ;(3)当A B ⊂时,=)(A p ,=)(A B p ,=⋃)(B A p ,=)(AB p ,=-)(B A p 。
14、设C B A ,,为三事件,A 与B 都发生而C 不发生,则用C B A ,,的运算关系可表示为 。
设A ,B ,C 都发生,则用C B A ,,的运算关系可表示为 。
15、设B A ,为互斥事件,且,8.0)(=A p 则)(B A p = 。
16、从一批由10件正品,3件次品组成的产品中,任取一件产品,取得次品的概率为 。
17、设B A ,为两事件,则=)(AB p 。
若B A ,为互斥事件,则=⋃)(B A p 。
18、设2.0)(,5.0)(=-=A B p A p ,则=⋃=)()(B A p B A p 。
(7.0)()()(),()()(=⋃=-+-=-B A p A B p A p AB p B p A B p )二、判断1、(1)B B A B A ⋃=⋃(对);(2)B A B A ⋃=(错);(3)Φ=))((B A AB (对)2、若A B ⊂,则B A A AB B ⋃==,。
(对)3、若A B ⊂,则A B ⊂。
(错)4、事件A 与B 互不相容,则A 与B 互逆。
(错)5、设A ,B 为任意二事件,则)()()(B P A P B A p +=+。
(错)6、设A ,B 为任意二事件,则)()()(B P A P B A p -=-。
(错)7、若A ,B 相互独立,则)()(B A P A p =。
(对)8、若A ,B 相互独立,则)()()(B p A p AB p ⋅=。
(对)9、如果B A ⊂,那么AB A =。
(对)10、如果B A ⊂,那么A B ⊂。
(对)11、如果B A ⊂,那么B B A =⋃。
(对)12、如果φ=AB ,且A C ⊂,那么φ=BC 。
(对)13、B A B A ⋃=。
(错)14、事件C B A ,,都发生可表示为C B A ⋃⋃。
(错)15、对于事件B A ,,满足)()()(B p A p B A p +≤+。
(对)16、如果φ=AB ,则称事件B A ,相互独立。
(错)17、设1)()(0≤=<B p A p ,且0)(≠AB p ,则)()(A B p B A p =。
(对)18、如果)()(B A p B A p =,则B A ,相互独立。
(对)19、某人射击中靶率为0.9,则他射击10次恰有9次击中的概率为100%。
(错)三、计算1、从一批由47件正品,3件次品组成的产品中,任取一件产品,求取得正品的概率。
2、某射手的命中率为0.95,他独立重复地向目标射击5次,求:(1)恰好命中4次的概率;(2)至少命中3次的概率。
3、两射手彼此独立地向一目标射击,设甲击中的概率为0.8,乙击中的概率为0.7,则目标被击中的概率是多少?4、一批产品共有10个正品和4个次品,每次抽取一个,抽取后不放回,任意抽取两次,求第二次抽出的是次品的概率。
5、电话号码由7个数字组成,每个数字可以是9,,1,0 中的任一个,求电话号码由完全不相同的数字组成的概率。
6、从一箱装有40个合格品,10个次品的苹果中任意抽取10个,试求所抽取的10个苹果中恰有2个次品的概率。
7、设A ,B 为任意二事件,且知4.0)()(==B p A p ,28.0)(=B A p ,求)(),(B A p B A p ⋃。
8、已知一批玉米种子的出苗率为0.9,现每穴种两粒,问一粒出苗一粒不出苗的概率是多少?9、袋中有3个黑球,3个白球,一次随机地摸出2个球,求恰有一白一黑的概率。
10、从0,1,2,3这四个数字中任取三个进行排列,求“取得的三个数字排成的数是三位数且是偶数”的概率。
11、一批零件共100个,次品率为10%,每次从中任取一个零件,取出的零件不再放回,求第三次才取得正品的概率。
12、设一仓库中有12箱同种规格的产品,其中由甲、乙、丙三厂生产的分别有5箱、4箱、3箱,三厂产品的废品率依次为0.1,0.15,0.18,从这12箱产品中任取一箱,再从这箱中任取一件,求取得合格品的概率;若取得合格品,问该产品为哪个厂生产的可能性大?13、设有甲、乙、丙三个车间生产同一种零件,每车间的产量分别占总产量的50%,30%,20%,各车间的正品率分别为93%,94%,95%,求:(1)任意抽查一零件是废品的概率;(2)如果抽出的零件是废品,此零件是哪个车间生产的可能性大?14、某工厂有甲、乙、丙三个车间生产同一种产品,每个车间的产量分别占全厂的25%,35%,40%,各车间产品的次品率分别为5%,4%,2%,求:(1)全厂的次品率;(2)如果抽出的产品是次品,此产品是哪个车间生产的可能性大?15、假定某工厂甲、乙、丙3个车间生产同一种螺钉,产量依次占全厂的45%、35%、20%。
如果各车间的次品率依次为4%、2%、5%,求产品的次品率,并求哪个车间生产的可能性大。
第二章基础训练题一、填空1、设随机变量ξ的分布函数为}{)(x p x F ≤=ξ,则=>}{x p ξ ,=≤<}{b a p ξ 。
2、设⎩⎨⎧<>=-000)(~x x Ae x x ϕξ,则A = ,=<<}40{ξp ,=)(x F 。
3、设⎩⎨⎧<<=其它010)(~2x Ax x ϕξ,则A = ,=<}21{ξp ,=)(x F 。
4、设),(~2b a N ξ,则密度函数=)(x ϕ 。
5、),(~p n B ξ,则=k 时,}{k p =ξ最大。
6、设),(~p n B ξ,则}{k p =ξ= 。
7、设连续型随机变量ξ的密度函数为)(x ϕ,则⎰+∞∞-=dx x )(ϕ 。
8、设某电话总机交换台每分钟收到的呼唤次数)3(~p ξ,则在1分钟内恰有4次呼唤的概率是 。
9、对于二项分布),(~p n B ξ,当n 很大,p 很小时,可近似用 来计算。
10、概率密度函数222)(21)(σμπϕ--=x e x 的图形位置完全由 来决定。
11、设),(~211σμξN 与),(~222σμηN 相互独立,则~ηξ+ 。
12、设~),,(~2σμξησμξ-=N 。
13、若ηξ,相互独立且服从相同的分布)1,0(N ,则~ηξ+ 。
14、 若ηξ,相互独立且依次服从)(),(21λλp p ,则~ηξ+ 。
二、判断1、分布函数0)(≥x F 。
(错)2、离散型随机变量ξ与η相互独立的充要条件是 ,2,1,)2()1(=⋅=j i p p p j i ij 。
(对) 3、设η为随机变量ξ的函数,则η的分布就是ξ的分布。
(错)4、已知}{)(x p x F ≤=ξ,则)()(}{a F b F b a p -=≤≤ξ。
(对)5、离散型随机变量的所有可能取的值是有限个或可列个数值。
(对)6、若)1.0,10(~B ξ,则)1(~p ξ (错)7、若)2(~p ξ,则)4(~2p ξη= (错) 三、计算1、已知随机变量ξ的分布如右表,求系数c 及}00{≠<ξξp2、已知随机变量ξ的分布如右表,求1,12221-=+=ξηξη的分布。
3、一批产品包括7件正品,3件次品,从中任取3件,求取出次品ξ的概率分布及其分布函数。
4、设),(ηξ的联合分布为下表(1),求 ηξ, 的边缘分布,}1{},0{==ξηηξp p 。
(1)5、设⎩⎨⎧<≥=-000)(~x x e x xϕξ,求2ξη=的概率密度。
6、设⎩⎨⎧<<=其它0102)(~x x x ϕξ,求1;2+-ξξ的密度函数。
7、设+∞<<∞-+=x xA x 21)(~ϕξ,求A ;}10{<<ξp ;41}{,=>a p a ξ使。
8、设⎪⎩⎪⎨⎧≥<≤<=111000)(~2x x Ax x x F ξ,求:(1)A ;(2)概率密度函数。
9、设⎩⎨⎧->=-其它01)(~2x ce x xϕξ,求:ξ;}21{;<<x p c 的分布函数。
10、设随机变量)5,0(~U ξ,求方程02442=+++k kx x 有实根的概率。
11、设)25,4(~N ξ,求}80{<<ξp ,(其中7881.0)54(=Φ)12、设ξ服从泊松分布,已知}4{},2{}1{====ξξξp p p 求。
13、连续型随机变量ξ的概率密度为kx x =)(ϕ()10<<x ,试计算:(1)k ;(2)}5.02.0{<<ξP 。
第三章基础训练题一、填空1、设)4,(~μξN ,且52=ξE ,则=μ ,ξ的密度函数=)(x ϕ 。
2、设)(~λξp ,且2=ξE ,则=ξD ,==}1{ξp 。
3、设),(~2b a N ξ,则密度函数=)(x ϕ ,=ξE ,ξD = 。
4、随机变量ξ与η相互独立,则=),cov(ηξ ,ξηρ= 。
