对数函数 - 简单 - 讲义
9对数函数 - 简单 - 讲义

对数函数知识讲解一、对数函数的图像与性质①函数log a y x =(0a >,1a ≠)叫做对数函数,其中x 是自变量,图像如下1a > 01a <<图 象性 质定义域:(0,+∞) 值域:R过点(1,0),即当时,时 时时 时在(0,+∞)上是增函数在(0,+∞)上是减函数1oyx 1oyx1=x 0=y )1,0(∈x 0<y ),1(+∞∈x 0>y )1,0(∈x 0>y ),1(+∞∈x 0<y②对数函数的性质:定义域:(0,)+∞;值域:R ;过点(1,0),即当1x =时,0y =. 当0a >时,在(0,+∞)上是增函数;当01a <<时,在(0,+∞)上是减函数.二、对数函数与指数函数的关系关系:对数函数log a y x =与指数函数x y a =图像关于直线y x =对称. 类型:指数方程和对数方程主要有以下几种类型:()()log ,log ()()f x b a a a b f x b f x b f x a =⇔==⇔=(定义法)()()()(),log ()log ()()()0f x g x a a a a f x g x f x g x f x g x =⇔==⇔=>(转化法) ()()()log ()log f x g x m m a b f x a g x b =⇔= (取对数法)三、对数函数有关的性质(1)xy a =与log a y x =;2x x a a y --=与(l g ()ay o x x R =+∈;11x x a y a -=+与1log 1a xy x+=- 关于y x =对称,(2)已知1()lg 1x f x x +=-,,(1,1)a b ∈-则()()1a b f a f b f ab +⎛⎫+= ⎪+⎝⎭(3)指数函数与对数函数可以有两个或一个交点.典型例题一.选择题(共8小题)1.下列函数中,是对数函数的是( )①y=lg x a (x >0且x ≠1)②y=log 2x ﹣1③y=2lg 8x ④y=log 5x . A .① B .②C .③D .④【解答】解:由对数函数的定义可知:④y=log 5x 是对数函数,其余3个都不是对数函数. 故选:D .2.使对数log a (一2a +1)有意义的a 的取值范围为( ) A .a >12且a ≠1B .0<a <12C .a >0且a ≠1D .a <12【解答】解:要使对数有意义,则{−2a +1>0a >0a ≠1,解得0<a <12,故选:B .3.(2018•辽宁模拟)函数f (x )=log 3(x 2﹣x ﹣2)的定义域为( ) A .{x |x >2或x <﹣1} B .{x |﹣1<x <2}C .{x |﹣2<x <1}D .{x |x >1或x <﹣2}【解答】解:由题意得:x 2﹣x ﹣2>0,解得:x >2或x <﹣1, ∴函数的定义域是:{x |x >2或x <﹣1}, 故选:A .4.(2016秋•邹平县期中)函数y=2+log 2x (x ≥1)的值域为( ) A .(2,+∞) B .(﹣∞,2)C .[2,+∞)D .[3,+∞)【解答】解:∵函数y=2+log 2x 在[1,+∞)上单调递增, ∴当x=1时,y 有最小值2,即函数y=2+log 2x (x ≥1)的值域为[2,+∞). 故选:C .5.(2018•天津)已知a=log 372,b=(14)13,c=log 1315,则a ,b ,c 的大小关系为( ) A .a >b >c B .b >a >cC .c >b >aD .c >a >b【解答】解:∵a=log 372,c=log 1315=log 35,且5>72>3,∴log 35>log 372>1,则b=(14)13<(14)0=1,∴c >a >b . 故选:D .6.(2017秋•黄陵县校级期末)若a >0且a ≠1,则函数y=log a (x +1)的图象一定过点()A.(1,1)B.(1,0)C.(﹣1,0)D.(0,0)【解答】解:令x+1=1,求得x=0,y=0,故函数y=log a(x+1)的图象一定过点(0,0),故选:D.7.(2017秋•定边县校级期末)函数y=log a(x+2)+1的图象过定点()A.(1,2)B.(2,1)C.(﹣2,1)D.(﹣1,1)【解答】解:由函数图象的平移公式,我们可得:将函数y=log a x(a>0,a≠1)的图象向左平移2个单位,再向上平移1个单位,即可得到函数y=log a(x+2)+1(a>0,a≠1)的图象.又∵函数y=log a x(a>0,a≠1)的图象恒过(1,0)点,由平移向量公式,易得函数y=log a(x+2)+1(a>0,a≠1)的图象恒过(﹣1,1)点,故选:D.8.(2016秋•秀屿区校级期末)若函数y=log a(x+1)(a>0,a≠1)的图象过定点,则x值为()A.﹣1B.0C.1D.无法确定【解答】解:因为y=log a x的图象恒过(1,0)点,又y=log a (x +1)的图象是把y=log a x 的图象左移1个单位得到的, 所以y=log a (x +1)的图象必过定点(0,0). 故选:B .二.填空题(共4小题)9.(2012•黄浦区二模)函数f (x )=log 12(2x +1)的定义域为 (﹣12,+∞) .【解答】解:∵2x +1>0∴x >﹣12即函数f (x )=log 12(2x +1)的定义域为(﹣12,+∞)故答案为:(﹣12,+∞)10.(2012秋•东台市校级期中)集合A={1,log 2x }中的实数x 的取值范围为 (0,2)∪(2,+∞) .【解答】解:∵集合A={1,log 2x }, ∴{log 2x ≠1x >0,解得x ∈(0,2)∪(2,+∞),故答案为:(0,2)∪(2,+∞);11.(2017秋•昆山市期中)已知a=log 20.3,b=20.3,c=0.32,则小到大排列 a <c <b .【解答】解:a=log 20.3<0,b=20.3>1,c=0.32∈(0,1). ∴a <c <b .故答案为:a <c <b .12.(2016春•浦东新区期中)若对数函数y=log a x 的图象过点(9,2),则a= 3 . 【解答】解:∵对数函数y=log a x 的图象经过点P (9,2), ∴2=log a 9, ∴a=3, 故答案为:3.三.解答题(共2小题)13.当log x ﹣1(x 2﹣5x ﹣6)有意义时,求x 的取值范围.【解答】解:当log x ﹣1(x 2﹣5x ﹣6)有意义时,满足{x 2−5x −6>0x −1>0x −1≠1,解得x>6.∴x ∈(6,+∞).14.已知1<x <10,且a=lg 2x ,b=lgx 2,c=lg (lgx ),那么求a ,b ,c 的大小顺序. 【解答】解:∵1<x <10, ∴0<lgx <1.c=lg (lgx )<0.∴a ﹣b=(lgx ﹣2)lgx <0,∴0<a <b , ∴c <a <b .。
对数函数及其性质知识点总结讲义

对数函数及其性质知识点总结讲义一、对数基本概念1.对数的定义:对数是数学中的一种运算,用一个数的指数表示另一个数。
2. 对数的表示方法:如果a^x = b,则记作x = loga(b)。
3.对数函数:对数函数是指以对数的形式来表示函数的函数。
二、对数函数的性质1.定义域和值域:-对数函数的定义域为正实数集,即x>0。
-对数函数的值域为实数集,即y∈R。
2.对称性:- 设a > 1,则loga(x) = y当且仅当a^y = x。
- 设0 < a < 1,则loga(x) = y当且仅当a^y = x。
3.基本性质:- loga(1) = 0,其中a ≠ 0。
- loga(a) = 1,其中a ≠ 1- loga(x · y) = loga(x) + loga(y),其中x > 0,y > 0。
- loga(x / y) = loga(x) - loga(y),其中x > 0,y > 0。
- loga(x^p) = p · loga(x),其中x > 0,p ∈ R。
- loga(b) = logc(b) / logc(a),其中a,b > 0,且a ≠ 1,c ≠14.基本图像:- 对数函数y = loga(x)的图像为一条曲线,也称为对数曲线。
-当0<a<1时,对数曲线在第一象限上严格递减。
-当a>1时,对数曲线在第一象限上严格递增。
5.特殊对数函数:- 以2为底的对数函数y = log2(x)常用于衡量信息的位数及计算机科学中。
- 自然对数函数y = ln(x)常用于微积分和其它分支的数学中。
三、对数函数的应用1.指数增长与对数函数:对数函数的性质使得它在描述指数增长的问题中非常有用。
-对数函数可以用来模拟人口增长、投资收益、疾病传播等指数增长的过程。
2.对数函数在数据处理中的应用:-对数函数可以用来处理大量数据、极大值、极小值等情形。
指数函数与对数函数(讲义)

(一)基础知识回顾:1.二次函数:当¹a 0时,y =ax 2+bx +c 或f (x )=ax 2+bx +c 称为关于x 的二次函数,其对称轴为直线x =-a b 2,另外配方可得f (x )=a (x -x 0)2+f (x 0),其中x 0=-ab 2,下同。
,下同。
2.二次函数的性质:当a >0时,f (x )的图象开口向上,在区间(-∞,x 0]上随自变量x 增大函数值减小(简称递减),在[x 0, -∞)上随自变量增大函数值增大(简称递增)∞)上随自变量增大函数值增大(简称递增)。
当a <0时,情况相反。
情况相反。
3.当a >0时,方程f (x )=0即ax 2+bx +c =0…①和不等式ax 2+bx +c >0…②及ax 2+bx +c <0…③与函数f (x )的关系如下(记△=b 2-4ac )。
1)当△>0时,方程①有两个不等实根,设x 1,x 2(x 1<x 2),不等式②和不等式③的解集分别是{x |x <x 1或x >x 2}和{x |x 1<x <x 2},二次函数f (x )图象与x 轴有两个不同的交点,f (x )还可写成f (x )=a (x -x 1)(x -x 2). 2)当△=0时,方程①有两个相等的实根x 1=x 2=x 0=ab2-,不等式②和不等式③的解集分别是{x |x ab2-¹}和空集Æ,f (x )的图象与x 轴有唯一公共点。
轴有唯一公共点。
3)当△<0时,方程①无解,不等式②和不等式③的解集分别是R 和Æ.f (x )图象与x 轴无公共点。
共点。
当a <0时,请读者自己分析。
时,请读者自己分析。
4.二次函数的最值:若a >0,当x =x 0时,f (x )取最小值f (x 0)=ab ac 442-,若a <0,则当x =x 0=a b 2-时,f (x )取最大值f (x 0)=ab ac 442-.对于给定区间[m,n ]上的二次函数f (x )=ax 2+bx +c (a >0),当x 0∈[m, n ]时,f (x )在[m, n ]上的最小值为f (x 0); 当x 0<m 时。
对数函数及其性质知识点总结经典讲义

对数函数及其性质知识点总结经典讲义对数函数是指以一些正数b为底的函数,表示为logb(x),其中x为自变量,b为底数。
对数函数是指数函数的逆运算,可以用于解决指数方程和指数不等式问题。
对数函数的一些重要性质如下:1.对数函数的定义域是正实数集R+。
2.对数函数的值域是实数集R。
3.对数函数的自变量必须大于0,即x>0。
4.底数b必须大于0且不等于1,即b>0,b≠15.对数函数的图像在直线y=x左侧,与x轴交于点(1,0)。
6. 对数函数是单调递增函数,即当自变量x1 > x2时,有logb(x1) > logb(x2)。
7. 对数函数的特殊值:logb(1) = 0,logb(b) = 18. 对数函数的运算规则:logb(x·y) = logb(x) + logb(y),logb(x/y) = logb(x) - logb(y),logb(x^n) = n·logb(x),其中x、y 为正实数,n为任意实数。
9. 对数函数的函数性质:logb(1/x) = -logb(x),logb√x =(1/2)·logb(x)。
10. 对数函数的性质:logb(m/n) = logb(m) - logb(n),logb(m^n) = n·logb(m),logb(m) = (logc(m))/(logc(b)),其中b、c为正实数,m、n为正实数。
11. 对数函数的解析式:logb(x) = logc(x)/logc(b),其中c为任意正实数,c ≠ 112. 对数函数的性质:logb(x) = 1/(logx(b))。
13. 对数函数与指数函数的关系:y = logb(x)是函数y = b^x的反函数,两者互为反函数。
对数函数在数学、科学和工程等领域中具有广泛的应用。
它可以用于求解指数方程和指数不等式,简化复杂的计算和求解过程。
在数学中,对数函数是指数函数的重要补充,它们互为反函数,可以相互转化,应用更加灵活。
第六讲 对数与对数函数新人教版高中数学经典复习讲义
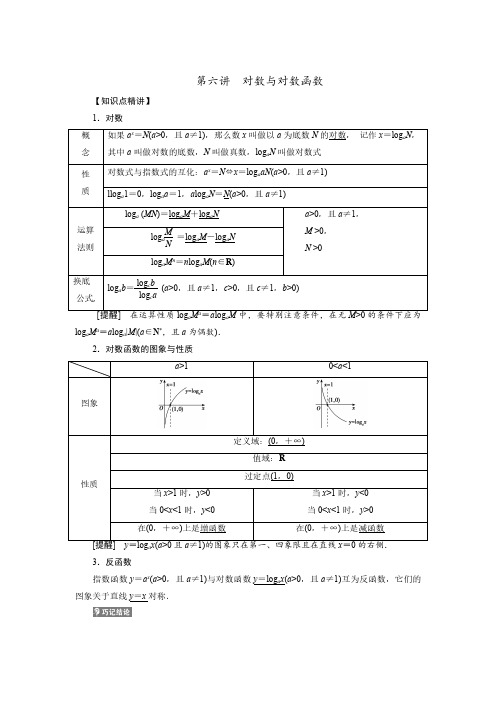
第六讲对数与对数函数【知识点精讲】1.对数概念如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底数N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数,log a N 叫做对数式性质对数式与指数式的互化:a x =N ⇔x=log a aN (a >0,且a ≠1)llog a 1=0,log a a =1,a log a N =N (a >0,且a ≠1)运算法则log a (MN )=log a M +log a Na >0,且a ≠1,M >0,N >0log a MN =log a M -log a Nlog a M n =n log a M (n ∈R )换底公式,log a b =log c blog c a(a >0,且a ≠1,c >0,且c ≠1,b >0)[提醒]在运算性质log a M a =a log a M 中,要特别注意条件,在无M >0的条件下应为log a M a =a log a |M |(a ∈N *,且a 为偶数).2.对数函数的图象与性质a >10<a <1图象性质定义域:(0,+∞)值域:R过定点(1,0)当x >1时,y >0当0<x <1时,y <0当x >1时,y <0当0<x <1时,y >0在(0,+∞)上是增函数在(0,+∞)上是减函数[提醒]y =log a x (a >0且a ≠1)的图象只在第一、四象限且在直线x =0的右侧.3.反函数指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数,它们的图象关于直线y =x 对称.【题型归纳及思路提示】考点01对数与对数运算例1(1)lg27+lg 8-3lg10lg 1.2=___.(2)(log 32+log 92)·(log 43+log 83)=___.(3)(2021·保定模拟)设2a =5b =m ,且1a +1b =2,则m =___.(4)若log a 2=m ,log a 3=n ,则a 2m +n =___,用m ,n 表示log 46为___.考点02对数函数的图象与性质考向1对数函数的图象及其应用——师生共研例2(1)函数y =lg|x -1|的图象是()(2)当0<x ≤12时,4x <log a x (a >0且a ≠1),则实数a 的取值范围是()名师点拨应用对数型函数的图象可求解的问题(1)对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想.(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.考向2对数函数的性质及其应用——多维探究角度1比较对数值的大小例3(1)已知a=log23+log23,b=log29-log23,c=log32,则a,b,c的大小关系是()A.a=b<c B.a=b>c C.a<b<c D.a>b>c(2)已知a=log52,b=log0.50.2,c=0.50.2,则a,b,c的大小关系为()A.a<c<b B.a<b<c C.b<c<a D.c<a<b角度2利用对数函数单调性求参数的取值范围例4已知函数f(x)=log0.5(x2-ax+3a)在[2,+∞)上单调递减,则实数a的取值范围是()A.(-∞,4]B.[4,+∞)C.[-4,4]D.(-4,4]角度3简单对数不等式的解法例5设函数f(x)2x,x>0,12(-x),x<0.若f(a)>f(-a),则实数a的取值范围是()A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)名师点拨1.比较对数式的大小的关系:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断;若底数为同一字母,则需要对底数进行分类讨论;(2)若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较;(3)若底数与真数都不同,则常借助1,0等中间量进行比较.2.解决与对数函数有关的函数的单调性问题的步骤。
对数函数讲义

对数函数教学设计一、 问题情境1、情境:我们研究指数函数时,曾经讨论过细胞分裂问题.某种细胞分裂时,得到的细胞的个数y 是分裂次数x 的函数,这个函数可以用指数函数y =2x表示.2、问题:现在,我们来研究相反的问题,如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞?这个问题就相当于已知y =2x 中的y 求x ,我们将y =2x改写成对数式为y =log 2x ,对于每一个给定的y 值,都有唯一的x 值与之相对应。
把y 看作自变量,分裂次数x 就是细胞个数y 的函数。
这样就得到了一个新的函数。
习惯上,仍用x 表示自变量,用y 表示它的函数。
上面的这个函数就写成y =log 2x 。
二、 新授:1、对数函数概念: 一般地,函数x y alog =(a >0且a ≠1)叫做对数函数.思考1:函数x y alog=(a >0且a ≠1)与函数xa y =(a >0且a ≠1)的定义域、值域之间有什么关系? (函数x y alog=(a >0且a ≠1)的定义域、值域分别是函数xa y =(a>0且a ≠1)的值域和定义域)2、对数函数的图像与性质: ①学生自主活动探究 在同一坐标轴下画出对数函数x y 2log=与指数函数xy 2=的图像观察图像有什么特征?思考2:一般地,当a >0且a ≠1时,函数x y alog =与函数xa y =的图像有什么关系?(函数x y alog=与函数xa y =的图像关于直线y=x 对称)总结:我们发现函数x y alog=(a >0且a ≠1)的定义域、值域分别是函数xa y =(a >0且a ≠1)的值域和定义域,它们的图像关于直线y=x 对称。
这样我们把xa y =称为x yalog=的反函数,同样x y alog=称为xa y =的反函数。
一般地,如果函数)(x f y =存在反函数,那么它的反函数记作)(1x fy -=在同一坐标轴下画出对数函数x y 3log =与x y 31log=的图像,并观察函数图像,说说图像的特征。
《对数的概念》 讲义

《对数的概念》讲义一、引入在数学的世界里,我们常常会遇到各种各样的数和运算。
其中,有一种非常重要的数学概念,那就是对数。
想象一下,你正在计算一个数的乘方,比如 2 的 3 次方等于 8。
但如果反过来,已知结果是 8,要找出是 2 的几次方得到 8 呢?这时候,对数就派上用场了。
二、什么是对数对数,简单来说,就是在一个等式中,表示要得到某个数,需要对另一个固定的数(底数)进行多少次乘方运算。
如果 a 的 b 次幂等于 N(a>0,且a≠1),那么数 b 叫做以 a 为底N 的对数,记作 b =logₐN。
例如,因为 2³= 8,所以 3 就是以 2 为底 8 的对数,记作 log₂8 =3。
再比如,因为 10²= 100,所以 2 就是以 10 为底 100 的对数,记作log₁₀100 = 2。
这里,a 叫做对数的底数,N 叫做真数。
三、对数的性质1、零和负数没有对数。
因为对数是指数运算的逆运算,而任何数的任何次幂都不可能是零或负数。
2、 1 的对数是 0。
因为 a⁰= 1(a>0,且a≠1),所以logₐ1 = 0。
3、底数的对数是 1。
即logₐa = 1。
四、对数的运算1、对数的加法logₐ(MN) =logₐM +logₐN例如,log₂(4×8) = log₂4 + log₂8 = 2 + 3 = 52、对数的减法logₐ(M / N) =logₐM logₐN比如,log₃(9 / 3) = log₃9 log₃3 = 2 1 = 13、对数的乘方logₐ(Mⁿ) =n logₐM例如,log₅(25²) = 2 log₅25 = 4五、常用对数和自然对数1、常用对数以 10 为底的对数叫做常用对数,简记为 lg。
例如,lg100 = 2。
2、自然对数以无理数 e(约等于 271828)为底的对数叫做自然对数,简记为 ln。
例如,ln e = 1,ln e²= 2。
《对数函数 y=log2 x 的图象和性质》 讲义

《对数函数 y=log2 x 的图象和性质》讲义《对数函数 y=log₂ x 的图象和性质》讲义一、对数函数的定义在数学中,如果 a 的 x 次方等于 N(a>0,且a≠1),那么数 x 叫做以 a 为底 N 的对数,记作 x =logₐN。
当底数 a = 2 时,我们就得到了对数函数 y = log₂ x。
二、对数函数 y = log₂ x 的图象1、图象的绘制要绘制对数函数 y = log₂ x 的图象,我们可以通过列表、描点、连线的方法来完成。
选取一些 x 的值,比如 x = 1/8 、1/4 、1/2 、1、2、4、8 等等,然后分别计算出对应的 y 值。
当 x = 1/8 时,y = log₂(1/8) =-3 ;当 x = 1/4 时,y = log₂(1/4) =-2 ;当 x = 1/2 时,y = log₂(1/2) =-1 ;当 x = 1 时,y = log₂ 1 = 0 ;当 x = 2 时,y = log₂ 2 = 1 ;当 x = 4 时,y = log₂ 4 = 2 ;当 x = 8 时,y = log₂ 8 = 3 。
将这些点(1/8,-3)、(1/4,-2)、(1/2,-1)、(1,0)、(2,1)、(4,2)、(8,3)在平面直角坐标系中描出,然后用平滑的曲线连接起来,就得到了对数函数 y = log₂ x 的图象。
2、图象的特征(1)对数函数 y = log₂ x 的图象位于 y 轴右侧。
(2)图象经过点(1,0),因为 log₂ 1 = 0 。
(3)从左往右看,图象逐渐上升。
三、对数函数 y = log₂ x 的性质1、定义域对数函数 y = log₂ x 的定义域为(0,+∞),因为对数中的真数必须大于 0 。
2、值域对数函数 y = log₂ x 的值域为(∞,+∞)。
当 x 趋近于 0 时,y 趋近于负无穷;当 x 趋近于正无穷时,y 趋近于正无穷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对数函数
知识讲解
一、对数函数的图像与性质
①函数log a y x =(0a >,1a ≠)叫做对数函数,其中x 是自变量,图像如下
②对数函数的性质:定义域:(0,)+∞;值域:R ;过点(1,0),即当1x =时,0y =. 当0a >时,在(0,+∞)上是增函数;当01a <<时,在(0,+∞)上是减函数.
1a > 01a <<
图 象
1
o
y
x
1
o
y
x
性 质
定义域:(0,+∞) 值域:R
过点(1,0),即当1=x 时,0=y
)1,0(∈x 时 0<y ),1(+∞∈x 时 0>y
)1,0(∈x 时 0>y ),1(+∞∈x 时0<y
在(0,+∞)上是增函数
在(0,+∞)上是减函数
二、对数函数与指数函数的关系
关系:对数函数log a y x =与指数函数x y a =图像关于直线y x =对称. 类型:指数方程和对数方程主要有以下几种类型:
()()log ,log ()()f x b a a a b f x b f x b f x a =⇔==⇔=(定义法)
()()()(),log ()log ()()()0f x g x a a a a f x g x f x g x f x g x =⇔==⇔=>(转化法) ()()()log ()log f x g x m m a b f x a g x b =⇔= (取对数法)
三、对数函数有关的性质
(1)x
y a =与log a y x =;2
x x a a y --=
与(l g ()a y o x x R =∈;11x x a y a -=+与
1log 1a x
y x
+=- 关于y x =对称,
(2)已知1()lg 1x f x x +=-,,(1,1)a b ∈-则()()1a b f a f b f ab +⎛⎫
+= ⎪+⎝⎭
(3)指数函数与对数函数可以有两个或一个交点.
典型例题
一.选择题(共8小题)
1.下列函数中,是对数函数的是()
①y=lg x a(x>0且x≠1)②y=log2x﹣1③y=2lg8x④y=log5x.
A.①B.②C.③D.④
2.使对数log a(一2a+1)有意义的a的取值范围为()
A.a>且a≠1 B.0<a<C.a>0且a≠1 D.a<
3.(2018•辽宁模拟)函数f(x)=log3(x2﹣x﹣2)的定义域为()A.{x|x>2或x<﹣1}B.{x|﹣1<x<2}C.{x|﹣2<x<1}D.{x|x>1或x <﹣2}
4.(2016秋•邹平县期中)函数y=2+log2x(x≥1)的值域为()A.(2,+∞)B.(﹣∞,2)C.[2,+∞)D.[3,+∞)
5.(2018•天津)已知a=log3,b=(),c=log,则a,b,c的大小关系为()
A.a>b>c B.b>a>c C.c>b>a D.c>a>b
6.(2017秋•黄陵县校级期末)若a>0且a≠1,则函数y=log a(x+1)的图象一定过点()
A.(1,1) B.(1,0) C.(﹣1,0)D.(0,0)
7.(2017秋•定边县校级期末)函数y=log a(x+2)+1的图象过定点()A.(1,2) B.(2,1) C.(﹣2,1)D.(﹣1,1)
8.(2016秋•秀屿区校级期末)若函数y=log a(x+1)(a>0,a≠1)的图象过定
点,则x值为()
A.﹣1 B.0 C.1 D.无法确定
二.填空题(共4小题)
9.(2012•黄浦区二模)函数f(x)=的定义域为.10.(2012秋•东台市校级期中)集合A={1,log2x}中的实数x的取值范围为.
11.(2017秋•昆山市期中)已知a=log20.3,b=20.3,c=0.32,则小到大排列.
12.(2016春•浦东新区期中)若对数函数y=log a x的图象过点(9,2),则a=.三.解答题(共2小题)
13.当log x﹣1(x2﹣5x﹣6)有意义时,求x的取值范围.
14.已知1<x<10,且a=lg2x,b=lgx2,c=lg(lgx),那么求a,b,c的大小顺序.。
