上海暑假数学八升九第1讲-四边形当中的证明
初三数学四边形的证明
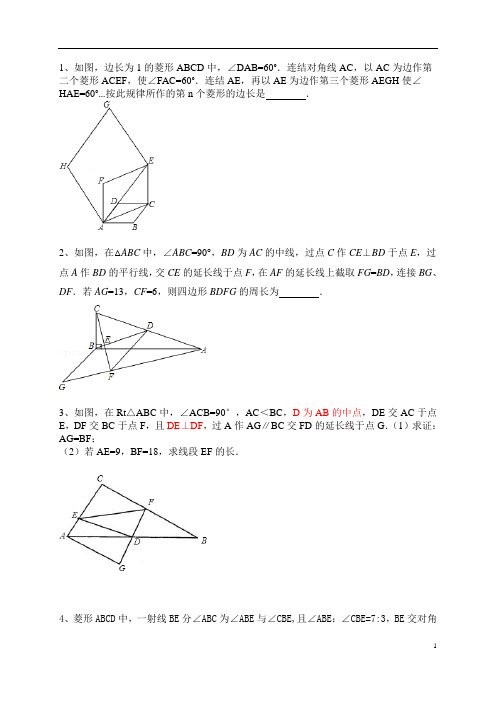
1、如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是.
2、如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为.
3、如图,在Rt△ABC中,∠ACB=90°,AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过A作AG∥BC交FD的延长线于点G.(1)求证:AG=BF;
(2)若AE=9,BF=18,求线段EF的长.
4、菱形ABCD中,一射线BE分∠ABC为∠ABE与∠CBE,且∠ABE:∠CBE=7:3,BE交对角
线AC于F交CD于E,过B作BK⊥AD于K点,交AC于M,且∠DAC=15°。
(1)求∠DEB的度数;
(2)求证:2CF=CM+2FB.
6.如图,在平行四边形ABCD中,延长CD到E,使DE=DC,连接BE交AD于F,交AC
G F E D C
B A
E
M F
D
C B A
于G .
(1)若BE 为∠ABC 的平分线,求证:BC=AF+DE; (2)若BC=2AB,DE=1,∠ABC=60°,求GF 的长.
7.已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF 与对角线AC 交于点M ,过M 作ME ⊥CD 于点E,∠1=∠2。
(1)若CE=1,求BC 的长; (2)求证AM=DF+ME 。
沪教版(上海)八年级第一学期 第十九章 第1讲 几何证明

例
逆命题:如果一个角是钝角,那么这个角是两个钝角的和.
4
逆命题:直角三角形其中一边上中线等于这边的一半.
逆命题:如果两个三角形关于某点成中心对称,那么这两个三角形全等. 逆命题:如果两个三角形全等,那么其中两边及第三边上的高对应相等.
逆命题:如果两个角不相等,那么这两个角不是对顶角.
例 5
例
逆命题:如果三角形两腰上的中线相等,那么这个三角形是等腰三角形.
第一讲
几何证明
命题 可以判断正误的陈述句
滚出去! 站起来.
命题的组成
如果两条直线互相平行, 那么这两条直线被第三条直线所截得的内错角相等.
如果一个人骑着白马,那么他一定是唐僧。
对顶角相等.
逆命题
原命题: 如果两条直线互相平行, 那么这两条直线被第三条直线所截得的内错角相等.
逆命题: 如果两条直线被第三条直线所截得的内错角相等, 那么这两条直线互相平行.
l
例 6
例 6
例 6
例 7
例 7
例 8
练 习 1
练 习 2
练 习 3练 习 4练 习 5练 习 6
对顶角相等.
相等的角是对顶角.
如果一个人骑着白马,那么他一定是唐僧。
如果一个人是唐僧,那么他骑着白马。
例 1
例 1
例 2
例 2
如果一个四边形有三个角是直角,那么这个四边形是矩形.
如果两个角是同一个角的补角,那么这两个角相等.
如果两个数都是无理数,那么他们的积是无理数.
例 3
例 3
例 4
5
逆命题:两直线平行,内错角相等. 逆命题:等角对等边.
逆命题:如果两条直线被第三条直线所截得的同旁内角的角平分线互相垂直,那么这两条直线平行. 逆命题:如果 a+b 为奇数,那么a,b两数一奇一偶.
八年级数学暑假专题四边形上海科技版知识精讲

初二数学暑假专题——四边形上海科技版【本讲教育信息】一、教学内容:暑假专题之五四边形(上)多边形内角和、平行四边形二、教学重点、难点重点:平行四边形的判定和性质难点:平行四边形的性质和判定的应用三、具体教学内容:1、n边形的内角和等于︒-180)2n(,任意多边形的外角和等于︒360,n边形的对角线条数为2)3n(n-。
2、有两组对边互相平行的四边形叫做平行四边形。
3、平行四边形的对边平行且相等,对角相等,对角线互相平分,平行线之间的距离处处相等。
4、对角线互相平分的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
一组对边平行且相等的四边形是平行四边形。
两组对边分别相等的四边形是平行四边形。
5、连接三角形两边中点的线段,叫做三角形的中位线,三角线的中位线平行于第三边,并且等于它的一半。
【典型例题】例1、一个多边形截去一个角后,形成一个新多边形,新多边形的内角和为︒2520,则原多边形的边数是多少?分析:多边形截去一个角时,有三种情况(以五边形为例)(1)截后少一边(2)截后多一边(3)截后边数不变(1)(2)(3)设新多边形的边数为n,则︒=︒⋅-2520180)2n(。
解得n=16,因为截去一个角时有三种情况,所以原多边形可能是十五边形或十六边形或十七边形。
例2、一个n边形的n个内角中,至多有锐角()个。
A、1个B、2个C、3个D、)3n(-个分析:若多边形的内角为锐角,则相邻的外角为钝角,而n边形的外角和为360°,因此是钝角的外角不能超过3个,否则外角和大于360°,因此n 边形的n 个内角中至多有3个锐角。
故选C 。
例3、如图,M 是平行四边形ABCD 的一边AD 上任意一点,若△CMB 的面积为S ,△CDM 的面积为S 1,△ABM 的面积为S 2,则下列关于S ,S 1,S 2的大小关系中正确的是( )。
A 、21S S S +>B 、21S S S +=C 、21S S S +<D 、无法确定分析:由平行线间的距离处处相等知,△CDM 、△ABM 及△BCM 的高相等,设为h∵h DM 21S 1⋅= h AM 21S 2⋅= h BC 21S ⋅= 又 DM+AM=AD=BC∴h )AM DM (21S S 21⋅+=+ S h BC 21=⋅= 故选B 。
沪教版 九年级数学 暑假同步讲义 第1讲 相似形与比例线段(提高版)
放缩与相似形是九年级上学期第一章第一节的内容,主要对相似多边形的概念和性质进行讲解,重点是理解相似形的相关概念和相似多边形性质的运用.通过对相似多边形的学习,为后面学习相似三角形的知识奠定基础.比例线段是九年级上学期第一章第二节的内容,主要对比例线段的有关概念和性质进行讲解,重点是理解不同概念和性质之间的联系和区别,熟练比例线段之间的转换,并能结合具体图形,运用比例线段的性质进行解题.通过对比例线段的学习,一方面为之后学习平行线分线段成比例做好准备,另一方面服务于之后相似三角形知识的学习.相似形与比例线段内容分析知识结构2 / 111、 相似形的概念相似形:我们把形状相同的两个图形称为相似的图形,简称相似形. 2、 相似多边形的性质如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例.当两个相似的多边形是全等形时,它们对应边的长度的比值为1.【例1】 下列说法不一定正确的是( )A .所有的等边三角形都相似B .有一个角是100︒的等腰三角形都相似C .所有等腰直角三角形都相似D .所有的直角三角形都相似【例2】 下列各组中的两个图形一定相似的有( )(1)两个等腰三角形; (2)两个直角三角形; (3)两个等腰直角三角形; (4)两个等边三角形; (5)两个矩形;(6)两个菱形; (7)两个正方形;(8)两个等腰梯形;(9)两个圆. A .3组B .4组C .5组D .6组【例3】 已知四边形ABCD 和四边形''''A B C D 是相似的图形,并且点A 与点'A 、点B与点'B 、点C 与点'C 、点D 与点'D 分别是对应顶点,已知4BC =, 3.6CD =,'' 3.3A B =,''3B C =,75B ∠=︒,105C ∠=︒,95D ∠=︒,求AB ,''C D 的长和'A ∠的度数.模块一:相似形的概念及性质知识精讲例题解析ABED C【例4】 如图,ABC ∆和ADE ∆是相似形,顶点A 、B 、C 分别与点A 、D 、E 对应,已知35A ∠=︒,65B ∠=︒, 1.2AE =, 2.5AB =,2AC =,1ED =.求AD 、BC 的长和AED ∠的度数.【例5】 已知ABC ∆的三边长分别是3、4、5,与其相似的'''A B C ∆的最大边长是15,求'''A B C ∆的最小边长.【例6】 已知甲、乙两个三角形相似,甲三角形的三边长分别为4、6、8,乙三角形其中一边的长为2,求乙三角形的另外两边的长.【例7】 如图,矩形ABCD 中,2AB CD =,线段10EF =,在EF 上取一点M ,分别以EM 、MF 为一边作矩形EMNH 、矩形MFGN ,使矩形MFGN 与矩形ABCD 相似,且点M 与点A 、点F 与点B ,点G 与点C ,点N 与点D 分别是对应顶点,令MN x =.求出矩形EMNH 的面积S 与x 的函数关系式.NC B AD EH G FM4 / 111、 比和比例一般来说,两个数或两个同类的量a 与b 相除,叫做a 与b 的比,记作:a b (或表示为a b); 如果::a b c d =(或a cb d=),那么就说a 、b 、c 、d 成比例. 2、 比例的性质(1) 基本性质:如果a cb d=,那么ad bc =;如果a cb d =,那么b d ac =,a b cd =,c da b=. (2) 合比性质: 如果a c b d =,那么a b c d b d++=; 如果a cb d =,那么a bc db d--=. (3) 等比性质: 如果a c k b d ==,那么a c a c k b d b d+===+.【例8】 (1)若23x y =,则x y y -=______; (2)若45a b =,则2a ba b +=- ______; (3)若250x y -=,则()()3:43x y x y +-=______.模块二:比例的性质知识精讲例题解析【例9】 (1)已知:23a b a -=,求243a ba b -+的值; (2)已知:357x y z==,求332y z y z +-的值;(3)已知:32x y z ==,求22x y zx y z-++-的值.【例10】 设线段x 、y 、z 满足23418x y z x y zx y z +++⎧==⎪⎨⎪++=⎩,求x 、y 、z 的值.【例11】 设()()23a b b c c aa b b c c a +++==---,求895a b c ++的值.【例12】 若333333x y y z z xm z x y +++===,求m 的值.A DE BF C【例13】已知a b ckb c a c a b===+++,则一次函数3y kx=-的图像一定经过第几象限?1、比例线段的概念对于四条线段a、b、c、d,如果::a b c d=(或表示为a cb d=),那么a、b、c、d叫做成比例线段,简称比例线段.2、黄金分割如果点P把线段AB分割成AP和PB(AP PB>)两段(如下图),其中AP是AB和PB的比例中项,那么称这种分割为黄金分割,点P称为线段AB的黄金分割点.其中,510.6182APAB-=≈,称为黄金分割数,简称黄金数.【例14】如图,已知在四边形ABCD中,点E、F分别在AB、CD上,AB DC AE DF=.求证:(1)AB DCEB FC=;(2)AB DC AB DCEB FC EB FC+-=+-.模块三:比例线段知识精讲例题解析A P B6/ 11【例15】 如果ABC ∆和'''A B C ∆面积相等,且:''9:25AB A B =,那么边AB 与边''A B 上的高的比为( ) A .9:25B .25:9C .3:5D .5:3【例16】 已知有三条线段的长分别为3cm ,6cm ,9cm 的线段,请再添一条线段,使这四条线段成比例,求所添线段的长度.【例17】 在ABC ∆中,点D 、E 分别在边AB 、AC 上,且34AD AE DE AB AC BC ===,则AEEC=______,若ADE ∆的周长为90厘米,则ABC ∆的周长为______厘米.【例18】 如图,在梯形ABCD 中,AD //BC ,对角线AC 、BD 相交于点O .(1)图中有哪几对三角形的面积相等?为什么?(2)求证:AO DOCO BO=.【例19】 如图,在ABC ∆中,BD AC ⊥,垂足为D ,E 是BC 边上的一点,EF AC ⊥,垂足为F ,:2:3ABD ABED S S ∆=,求:AD AF 的值.AB CDOABCDEF8 / 11【例20】 已知线段AB 的长度为l ,点P 在线段上,PB APAP AB=,求线段AP 的长.【例21】 (1)点P 是线段AB 的黄金分割点,AP BP >,6AB =厘米,求BP 的长;(2)已知点P 是线段AB 的黄金分割点,51AB =+,求AP 的值.【例22】 如图,乐器上的一根弦80AB =厘米,两个端点A 、B 固定在乐器面板上,支撑点C 是靠近点B 的黄金分割点,支撑点D 是靠近点A 的黄金分割点,求CD 的长.【例23】 如图,在矩形ABCD 中截取正方形ABMN ,已知MN 是BC 和CM 的比例中项,35CM =-,求AD 的长.A B C DA B CDN M【例24】 如图,以长为2的线段AB 为边作正方形ABCD ,取AB 的中点P ,连接PD .在BA 的延长线上取点F ,使PF PD =.以AF 为边作正方形AMEF ,点M 在AD上.(1)求线段AM 、DM 的长; (2)求证:2AM AD DM =; (3)请指出图中的黄金分割点.【习题1】已知点D 是边BC 上一点,且ABC ∆与DAC ∆是相似形,点A 、B 、C 分别与点D 、A 、C 对应,:3:2CB CA =,求:CD DB 的值.【习题2】 若()()::a b x y x y =+-,则:x y =______.【习题3】直线l 上顺次有四点A 、B 、C 、D ,且3AB AD BC DC ==,则BCAD= ______;ABCD=______.随堂检测ABCDEFMP【习题4】点P是线段AB的黄金分割点,求APAB的值.【作业1】下列各组四边形中是相似多边形的是()A.一组邻边为2厘米和5厘米与一组邻边为3厘米和6厘米的矩形B.有一个内角为30︒的两个菱形C.边长分别为3厘米和4厘米的两个菱形D.两个高相等的等腰梯形【作业2】已知ABC∆的三边长分别是4、5、6,与其相似的'''A B C∆的最小边长是12,求'''A B C∆的周长.【作业3】7a cm=,0.08b m=, 1.5c dm=,求线段a、b、c的第四比例项.【作业4】舞台的形状是一个矩形,宽AB为12米,如果主持人站立的位置是宽AB 的黄金分割点,那么主持人从台侧点A沿AB走到主持的位置至少需走______米.【作业5】若222222b c a c a bka b c+++===,求直线y kx k=+经过的象限.课后作业10/ 11【作业6】 已知a 、b 、c 是非零实数,且满足a b c a b c a b c c b a+--+-++==,求()()()a b b c c a abc +++的值.。
四边形证明总结范文

四边形证明总结范文四边形是由四条线段组成的几何图形,它有一些特殊性质和定理。
在这篇文章中,我们将总结和证明一些常见的四边形定理。
1.平行四边形定理:如果一个四边形的对边是平行的,那么它是一个平行四边形。
证明:设ABCD是一个四边形,AB∥CD。
我们需要证明AD∥BC。
假设AD与BC不平行,那么它们会相交于一点E。
由于AB∥CD,所以∠ABE=∠CDE(平行线之间的内错角相等)。
同理,也可以得到∠AEB=∠CDE。
但是根据角分线定理,∠ABE+∠AEB=180°,与∠CDE+∠CDE=180°矛盾。
所以AD∥BC,四边形ABCD是一个平行四边形。
2.等腰梯形定理:如果一个四边形的两边平行并且另外两边长度相等,那么它是一个等腰梯形。
证明:设ABCD是一个四边形,AB∥CD,AB=CD,我们需要证明BC=AD。
根据平行四边形定理,AD∥BC。
如果BC≠AD,那么它们会相交于一点E。
由于AB∥CD,并且线段BE与线段AE与AB、CD相交,所以∠ABE=∠AEB (平行线之间的内错角相等)。
同理,也可以得到∠CDE=∠CED。
由于AB=CD,所以∠ABE=∠CDE。
但是根据角分线定理,∠ABE+∠CDE=180°,与∠CDE+∠CED=180°矛盾。
所以BC=AD,四边形ABCD是一个等腰梯形。
3.矩形定理:如果一个四边形的四个角都是直角,那么它是一个矩形。
证明:设ABCD是一个四边形,∠A=∠B=∠C=∠D=90°。
我们需要证明AB∥CD以及AD∥BC。
由于∠A=∠B,所以直角三角形ABC与直角三角形DAB是相似的(直角三角形的两个角相等即为相似)。
根据相似三角形的性质,我们可以得到BC/AB=AB/AD,即BC·AD=AB·AB。
同理,也可以得到AD/AB=AB/BC,即AD·BC=AB·AB。
将这两个等式相加,得到BC·AD+AD·BC=2·AB·AB,即(BC+AD)·AD=2·AB·AB。
四边形证明
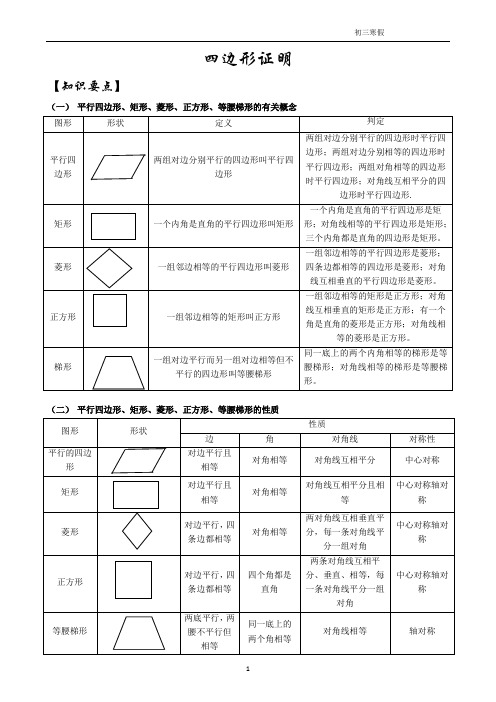
四边形证明【知识要点】(一)平行四边形、矩形、菱形、正方形、等腰梯形的有关概念(二)平行四边形、矩形、菱形、正方形、等腰梯形的性质【精典例题】例1.已知∆ABC 中,AE 平分∠BAC ,BC 平分∠EBF ,若AB=AC 。
求证四边形BECF 是菱形。
例2.已知直角梯形ABCD 中,//AB DC ,90oDAB ∠=,1AD=DC=2AB ,E 时AB 的中点.(1)求证:四边形AECD 时正方形.(2)求B ∠的度数.例3.已知如图,在梯形ABCD中,//AD BC ,AB=DC,点E,F,G分别在边AB、BC、CD上,AE=GF=GC .(1)求证:四边形AEFG 使平行四边形;(2)当2FGC EFB ∠=∠时,求证:四边形AEFG 时矩形.例4.已知:如图,将矩形纸片ABCD 沿着对角线BD 折叠,点C 落在点E 处,BE 交AD 于点F ,连接AE.证明:(1)BF=DF.(2)//AE BD例5.如图,在正方形ABCD 中,点F 在CD 边上,射线AF 交BD 于点E ,交BC的延长线于点G.(1)求证: ADE CDE ∆≅∆;(2)过点C作CH⊥CE,交FG于点H,求证:FH=GH;(3)设AD=1,DF=x ,试问是否存在x 的值,使ECG ∆为等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.课堂训练一、选择题(''4520⨯=)1.已知边长为a 的正方形,以它的对角线底作一个三角形,使其面积等于此正方形的面积,则三角形底边上的高为( ) A 、2a B 、2aC 、a 2D 、a 22.矩形、菱形和正方形都具有的性质是( ) A 、对角线相等B 、对角线互相平分C 、对角线平分一组对角D 、对角线互相垂直 3.在下列图形中,是轴对称图形但不是中心对称的图形是( )A 、矩形B 、平行四边形C 、圆D 、等腰梯形4.若菱形的周长为16cm ,两相邻角的度数之比是1:2,则菱形的面积是( )ADCB EO(A ) 4 3 cm (B )8 3 cm (C )16 3 cm (D )20 3 cm5.一菱形的一边上高的垂足是这边的中点,这菱形中的最大内角的度数是( )A 、︒150B 、︒135C 、︒120D 、︒100二、填空题(''4520⨯=)1.矩形ABCD 中,DE ⊥AC ,∠ADE=︒36,那么∠ACD= 度。
八年级数学下册(沪科版)《四边形》讲义
八年级下册数学讲义第19章 四边形 知识脉络:1.四边形的内角和与外角和定理: (1)四边形的内角和等于360°; (2)四边形的外角和等于360°.2.多边形的内角和与外角和定理: (1)n 边形的内角和等于(n-2)180°; (2)任意多边形的外角和等于360°.3.平行四边形的性质:因为ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;(4.平行四边形的判定: 是平行四边形)对角线互相平分()一组对边平行且相等()两组对角分别相等()两组对边分别相等()两组对边分别平行(ABCD 54321⎪⎪⎪⎭⎪⎪⎪⎬⎫.A BCD 1234AB CDABDOCABDOC两组对边平行四边行一 基本概念:四边形,四边形的内角,四边形的外角,多边形,平行线间的距离,平行四边形,矩形,菱形,正方形,中心对称,中心对称图形,梯形,等腰梯形,直角梯形,三角形中位线,梯形中位线.二 公式:1.S 菱形 =21ab=ch.(a 、b 为菱形的对角线 ,c 为菱形的边长 ,h 为c 边上的高) 2.S 平行四边形 =ah. a 为平行四边形的边,h 为a 上的高)三 常识: ※1.若n 是多边形的边数,则对角线条数公式是:2)3n (n -.2.规则图形折叠一般“出一对全等,一对相似”.3.如图:平行四边形、矩形、菱形、正方形的从属关系.n 边形的的性质: (1)n 边形的内角和等于ο180)2(⋅-n . (2)任意多边形的外角和等于ο360 (3)n 边形共有2)3(-n n 条对角线 (4)在平面内,内角都相等且边都相等的多边形叫做正多边形。
(5)正多边形的每个内角等于nn 180).2(- 平行四边形矩形菱形正方形图1FED CBA 图2FE D CBA四边形:四边形的内角和等于360°, 外角和等于360°1、四边形内角中最多有三个钝角,四个直角,三个锐角;2、四边形外角中最多有三个钝角、四个直角、三个锐角,最少没有钝角,没有直角,没有锐角;3、四边形内角与同一个顶点的一个外角互为邻补角. 平行四边形的性质:(1)平行四边形的邻角互补,对角相等. (2)平行四边形的对边平行且相等. (3)夹在两条平行线间的平行线段相等. (4)平行四边形的对角线互相平分. 平行四边形的判定:(1)定义:两组对边分别平行的四边形是平行四边形. (2)定理1:两组对角分别相等的四边形是平行四边形. (3)定理2:两组对边分别相等的四边形是平行四边形. (4)定理3:对角线互相平分的四边形是平行四边形. (5)定理4:一组对边平行且相等的四边形是平行四边形.两条平行线的距离两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离.平行线间的距离处处相等 平行四边形的面积:ABCD S Y =BC·AE=CD·BF同底(等底)同高(等高)的平行四边形面积相等.ABCD S Y =BCFE S Y矩形的性质:(1)对边平行且相等。
沪教版八年级四边形证明题及综合题部分答案
四边形证明题及综合题答案1.证明:(1)∵正方形ABCD ,∴AB=AD ,∠B =∠D =90°…………………………(2分)∵∠BAE = ∠DAF∴△ABE ≌△ADF ……………………………………………………………(1分)∴BE = DF ……………………………………………………………………(2分)(2)∵正方形ABCD ,∴∠BAC =∠DAC ………………………………………(1分) ∵∠BAE =∠DAF ∴∠EAO =∠FAO ……………………………………(1分)∵△ABE ≌△ADF ∴AE = AF …………………………………………(1分)∴EO=FO ,AO ⊥EF …………………………………………………………(2分)∵OM = OA ∴ 四边形AEMF 是平行四边形……………………………(1分)∵AO ⊥EF ∴四边形AEMF 是菱形……………………………………(1分)2.(1)证明:联结EG ,∵ 梯形ABCD 中,AD BC ∥,且E 、G 分别是AB 、CD 的中点,∴ EG //B C ,且)(21BC AD EG +=,…………………………(2分) 又∵)(21BC AD BF += ∴ EG =BF .……………………………………………………(1分)∴ 四边形AEFG 是平行四边形.…………………(2分)(2)证明:设AF 与EG 交于点O ,∵ EG //AD ,∴∠DAG =∠AGE∵AG 平分FAD ∠,∴∠DAG =∠GAO∴∠GAO =∠AGE∴ AO=GO .………………………………(2分)∵四边形AEFG 是平行四边形,∴ AF =EG ,四边形AEFG 是矩形…………………………(2分)3.证明:(1)∵梯形ABCD 是等腰梯形,AD ∥BC∴ ∠BAE=∠ADF ………………………………………………(1分)∵AD = DC ∴ AE=DF …………………………………………(1分)∵BA=AD ∴△BAE ≌△ADF , …………………………………(1分)∴BE=AF . …………………………………………………………(1分)(2)猜想∠BPF=120°.……………………………………………………(1分)∵由(1)知△BAE ≌△ADF ,∴∠ABE=∠DAF .…………………(1分)∴∠BPF=∠ABE+∠BAP=∠BAE .……………………………………(1分)而AD ∥BC ,∠C=∠ABC=60°,∴=120°.∴∠BPF=∠BAE =120°.………………………………………………(1分)4、证:(1)∵四边形ABCD 是矩形,∴AD ∥BC ,AD =BC .∴∠DAC =∠BCA .又∵DN ⊥AC ,BM ⊥AC ,∴∠DNA =∠BMC .∴⊿DAN ≌⊿BCM , ---------------------------------------------------(3分)∴AN =CM . ---------------------------------------------------------------(1分)(2)联结BD 交AC 于点O ,∵AN = NM =2,∴AC = BD =6,又∵四边形ABCD 是矩形,∴AO =DO =3,在⊿ODN 中,OD =3,ON =1,∠OND =︒90,∴DN =2222=-ON OD ,--------------------------------------(2分)∴矩形ABCD 的面积=212=⨯DN AC .-----------------------(1分)5.解:(1)方法1:延长EF 交AD 于G (如图1).……………1分在平行四边形ABCD 中,AD ∥BC ,BC AD =.∵EF ∥CA ,EG ∥CA ,∴四边形ACEG 是平行四边形.∴ CE AG =.……………1分 又∵BC CE 21=,BC AD =, ∴ GD AD BC CE AG ====2121.……………1分 ∵AD ∥BC ,∴ECF ADC ∠=∠.在CEF △和DGF △中,∵DFG CFE ∠=∠,ECF ADC ∠=∠,DG CE =, ∴CEF △≌DGF △(A.A.S ). ∴DF CE =.…………………1分∵四边形ABCD 是平行四边形,∴OD OB =.∴OF ∥BE . ………………1分方法2:将线段BC 的中点记为G ,联结OG (如图2). ………………1分∵四边形ABCD 是平行四边形,∴OD OB =.∴OG ∥CD . …………1分∴FCE OGC ∠=∠.∵EF ∥CA ,∴FEC OCG ∠=∠. A B (第5题图1) D C OEF G A B (第5题图2)D C O EF G∵BC GC 21=,BC CE 21=, ∴CE GC =.在OGC △和FCE △中,∵FEC OCG ∠=∠,CE GC =,FCE OGC ∠=∠,∴OGC △≌FCE △(A.S.A ). …………………1分∴FC OG =.又∵OG ∥CF ,∴四边形OGCF 是平行四边形. …………………1分∴OF ∥GC . …………………1分其他方法,请参照上述标准酌情评分.(2)如果梯形OBEF 是等腰梯形,那么四边形ABCD 是矩形. ……………1分∵OF ∥CE ,EF ∥CO ,∴四边形OCEF 是平行四边形.∴OC EF =.……………1分又∵梯形OBEF 是等腰梯形,∴EF BO =.∴OC OB =.(备注:使用方法2的同学也可能由OGC △≌FCE △找到解题方法;使用方法1的同学也可能由四边形ACEG 是平行四边形找到解题方法).∵四边形ABCD 是平行四边形,∴OC AC 2=,BO BD 2=.∴BD AC =.……………1分∴平行四边形ABCD 是矩形. ……………1分6.证明:(1)∵在正方形ABCD 中,AD //BC ,∴∠A =∠HBE ,∠ADE =∠H ,…(1分)∵AE =BE ,∴△ADE ≌△BHE .………………………………………(1分)∴BH =AD =BC .…………………………………………………………(1分)∵CM =GM ,∴BM //GH .………………………………………………(1分)(2)∵在正方形ABCD 中,AB =AD =CD ,∠A =∠ADC =90º,又∵DF =21AD ,AE =21AB ,∴AE =DF .∴△AED ≌△DFC .………(1分) ∴∠ADE =∠DCF .………………………………………………………(1分)∵∠ADE +∠GDC =90º,∴∠DCF +∠GDC =90º.∴∠DGC =90º.…(1分)∵BM //GH ,∴∠BMG =∠DGC =90º,即BM ⊥CF .…………………(1分)7、证明:∵AC 平分∠BAD , ∴∠BAC=∠CAD .又 ∵AE ∥BF , ∴∠BCA=∠CAD . --------------------------1分∴∠BAC=∠BCA .∴ AB=BC . --------------------1分同理可证AB=AD .∴ AD=BC . ----------------------1分又 AD ∥BC ,∴ 四边形ABCD 是平行四边形. -----1分又AB=BC ,∴□ABCD 是菱形. -----1分8. 证明:(1)∵正方形ABCD∴90A EBH ∠=∠=︒ AD BC =…………1′ ∵E 是AB 的中点 ∴ AB BE =…………1′∵AED BEH ∠=∠∴AED BEH ≅ …………1′∴AD BH = ∴BC BH =…………1′∵M 是CG 的中点 ∴//BM GH …………1′ (2)证AED CDF ≅ …………1′ ∴ADE DCF ∠=∠∵90DCF CDE ∠+∠=︒ ∴90CGH ∠=︒ ………1′∵//BM GH ∴90CMB CGH ∠=∠=︒∴BM CF ⊥ …………1′9.证法一: ∵在梯形ABCD 中,AD //BC ,又∵EF =AD∴四边形AEFD 是平行四边形.………………………………………(1分) ∴AD //DF ,∴∠AEF =∠DFC .………………………………………(1分)∵AB =CD ,∴∠B =∠C .………………………………………………(1分)又∵BE =CF ,∴△ABE ≌△DCF .……………………………………(1分)∴∠AEB =∠DFC ,……………………………………………………(1分)∴∠AEB =∠AEF .………………………………………………………(1分)∵∠AEB +∠AEF =180º,∴∠AEF =90º.……………………………(1分)∴四边形AEFD 是矩形.………………………………………………(1分)证法二: 联结AF 、DE .…………………………………………………………(1分)∵在梯形ABCD 中,AD //BC ,又∵EF =AD ,∴四边形AEFD 是平行四边形.………………………………………(1分) M H G FE D CB A∵AB =CD ,∴∠B =∠C .………………………………………………(1分)∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE ,…………………………(1分)∴△ABF ≌△DCE .……………………………………………………(1分)∴AF =DE ,………………………………………………………………(2分)∴四边形AEFD 是矩形.………………………………………………(1分)10、证明:(1)∵□ABCD ,∴A B ∥CD ,AB =CD -----------------------------------1分∵E 、F 分别为AB 、CD 的中点,∴DF =12DC ,BE =12AB ∴DF ∥BE ,DF =BE ---------------------------------------------------------------------1分∴四边形DEBF 为平行四边形∴DE ∥BF -----------------------------------------------------------------------------------1分(2)证明:∵AG ∥BD ,∴∠G =∠DBC =90°,∴∆DBC 为直角三角形---1分又∵F 为边CD 的中点.∴BF =12DC =DF ------------------------------------------1分 又∵四边形DEBF 为平行四边形,∴四边形DEBF 是菱形----------------------1分11.证明:∵在梯形ABCD 中,AD //BC ,∴∠DAE =∠FAE ,∠ADE =∠CFE .……(1分)又∵AE =EC ,∴△ADE ≌△CFE .…………………………………………(1分)∴AD =FC ,…………………………………………………………………(1分)∴四边形AFCD 是平行四边形.……………………………………………(1分)∵BC =2AD ,∴FC =AD =21BC .……………………………………………(1分) ∵AC ⊥AB ,∴AF =21BC .…………………………………………………(1分) ∴AF =FC ,……………………………………………………………………(1分)∴四边形AFCD 是菱形.……………………………………………………(1分)12.(1)解:线段AD 与BC 的长度之间的数量为:3BC AD =.…………………(1分)证明:∵ AD // BC ,DE // AB ,∴ 四边形ABED 是平行四边形.∴ AD = B E .………………………………………………………(2分)同理可证,四边形AFCD 是平行四边形.即得 AD = FC .……(1分)又∵ 四边形AEFD 是平行四边形,∴ AD = EF .……………(1分)∴ AD = BE = EF = FC .∴ 3B C A D =.……………………………………………………(1分)(2)证明:∵ DE // AB ,∴ ∠B =∠DEC .…………………………………(1分)∵ ∠B +∠C = 90°,∴ ∠DEC +∠C = 90°.即得 ∠EDC = 90°.………………………………………………(2分)又∵ EF = FC ,∴ DF = EF .……………………………………(2分)∵ 四边形AEFD 是平行四边形,∴ 四边形AEFD 是菱形.…………………………………………(1分)13.(1) ⊿MBN ≌⊿MPN (1)∵⊿MBN ≌⊿MPN∴MB=MP,∴22MP MB =∵矩形ABCD∴AD=CD (矩形的对边相等)∴∠A=∠D=90°(矩形四个内角都是直角) ………………………………1 ∵AD=3, CD=2, CP=x, AM=y∴DP=2-x, MD=3-y ………………………………1 Rt ⊿ABM 中,42222+=+=y AB AM MB同理 22222)2()3(x y PD MD MP -+-=+= (1)222)2()3(4x y y -+-=+ (1)∴ 6942+-=x x y ....................................1 (3)︒=∠90BMP (1)当︒=∠90BMP 时,可证DMP ABM ∆≅∆ ………………………………1 ∴ AM=CP ,AB=DM∴ 1,32=-=y y ………………………………1 ∴ 1,21=-=x x ………………………………1 ∴当CM=1时,︒=∠90BMP14.(1)证:过P 作MN ⊥AB ,交AB 于点M ,交CD 于点N∵正方形ABCD ,∴ PM=AM ,MN=AB ,从而 MB=PN ………………………………(2分)∴ △PMB ≌△PNE ,从而 PB=PE …………(2分)(2) 解:PF 的长度不会发生变化,设O 为AC 中点,联结PO ,∵正方形ABCD , ∴ BO ⊥AC ,…………(1分)从而∠PBO =∠EPF ,……………………(1分)∴ △POB ≌△PEF , 从而 PF=BO 22= …………(2分)。
四边形的性质与证明
平形四边形复习由此得到平行四边形性质名称 平行四边形 示意图定义性质边角对角线(1)在平行四边形ABCD 中,∠A=500,求∠B 、∠C 、∠D 的度数。
(2)在平行四边形ABCD 中,若∠A :∠B=2:3,求∠C 、∠D 的度数。
(3)如图,AD ∥BC ,AE ∥CD ,BD 平分∠ABC ,求证AB=CE图(5)E DCBA1.填空:(1)在ABCD 中,∠A=︒50,则∠B = 度,∠C = 度,∠D = 度.(2)如果ABCD 中,∠A —∠B=240,则∠A= 度,∠B= 度,∠C= 度,∠D= 度.(3)如果ABCD 的周长为28cm ,且AB :BC=2∶5,那么AB= cm ,BC= cm ,CD= cm ,CD= cm . 2.如图4.3-9,在ABCD 中,AC 为对角线,BE ⊥AC ,DF ⊥AC ,E 、F 为垂足,求证:BE =DF . 四、课后练习1.(选择)在下列图形的性质中,平行四边形不一定具有的是( ). (A )对角相等(B )对角互补(C )邻角互补 (D )内角和是︒3602.在ABCD 中,如果EF ∥AD ,GH ∥CD ,EF 与GH 相交与点O ,那么图中的平行四边形一共有( ). (A )4个 (B )5个 (C )8个 (D )9个3.如图,AD ∥BC ,AE ∥CD ,BD 平分∠ABC ,求证AB=CE .1.复习提问:(1)什么样的四边形是平行四边形?四边形与平行四边形的关系是:(2)平行四边形的性质:①具有一般四边形的性质(内角和是 360). ②角:平行四边形的对角相等,邻角互补. 边:平行四边形的对边相等.结论:(1)平行四边形是中心对称图形,两条对角线的交点是对称中心; (2)平行四边形的对角线互相平分. 三、随堂练习1.在平行四边形中,周长等于48, ① 已知一边长12,求各边的长 ② 已知AB=2BC ,求各边的长③ 已知对角线AC 、BD 交于点O ,△AOD 与△AOB 的周长的差是10,求各边的长2.如图,ABCD 中,AE⊥BD,∠EAD=60°,AE=2cm ,AC+BD=14cm ,则△OBC 的周长是____ ___cm . 3.ABCD 一内角的平分线与边相交并把这条边分成cm 5,cm 7的两条线段,则ABCD 的周长是_____cm .四、课后练习 1.判断对错(1)在ABCD 中,AC 交BD 于O ,则AO=OB=OC=OD . ( ) (2)平行四边形两条对角线的交点到一组对边的距离相等. ( ) (3)平行四边形的两组对边分别平行且相等. ( ) (4)平行四边形是轴对称图形. ( ) 2.在 ABCD 中,AC =6、BD =4,则AB 的范围是__ ______.3.在平行四边形ABCD 中,已知AB 、BC 、CD 三条边的长度分别为(x+3),(x-4)和16,则这个四边形的周长是 .4.公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB =15cm ,AD =12cm ,AC ⊥BC ,求小路BC ,CD ,OC 的长,并算出绿地的面积.平行四边形的判定平行四边形判定方法1 两组对边分别相等的四边形是平行四边形。
四边形原理
四边形原理
四边形原理是数学中的一个概念,指的是四边形的两条对角线平分彼此的交点角。
具体来说,如果一个四边形的两条对角线交于一点,并且这个交点将对角线分成两段,那么这个交点所对应的四个角度的度数之和为180度。
四边形原理可以用来证明一些与四边形相关的性质。
例如,如果一个四边形是矩形,那么它的对角线相等,且交于90度的角。
又如,如果一个四边形是菱形,那么它的对角线互相垂直,且交于90度的角。
利用四边形原理,我们可以求解一些未知的角度。
例如,如果一个四边形的两条对角线交于一点,已知其中一个角度的度数,可以利用四边形原理求解其他角度的度数。
只需将已知的角度度数与180度相减,再将结果平分即可得到其他角度的度数。
四边形原理在几何学的证明和问题求解中具有重要的应用价值。
它不仅可以帮助我们理解四边形的性质,还可以拓展至其他形状的图形中,进一步推导出更多的数学定理。
通过深入研究四边形原理,我们可以在几何学的学习中更加深入地理解和应用相关知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精锐教育辅导讲义
问题1:平行四边形有哪些性质?矩形、菱形各自有哪些特有性质?从边,角,对角线角度说明。
问题2:平行四边形的判定方法有哪些?矩形的判定方法有哪些?菱形的判定方法有哪些?
问题3:正方形有哪些性质?从边、角、对角线角、对称性角度来说明。
问题4:正方形的判定方法有哪些?
问题5:证明梯形或等腰梯形的方法
☆总结:解决梯形问题常用的方法
①作高法:使两腰在两个直角三角形中,如图(e)
②移腰法:使两腰在同一个三角形中,如图(b)梯形两个下底角是互余的,那么一般会用到这种添辅助线的
方式,构造直角三角形;
③延腰法:构造具有公共角的两个等腰三角形,如图(d);
④等积变形法:联结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形,如图(f).
⑤移对角线法:如图(g)平移对角线,可以构造特殊的图形,如平行四边形,如果是对角线互相垂直的
等腰梯形,那么在平移的过程中,还可构造等腰直角三角形,结合三线合一,求梯形的高等.
例题1:已知:如图,在梯形ABCD中,AD//BC,AB=DC.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC=2∠EFB时,求证:四边形AEFG是矩形。
试一试:在等边△ABC中,AB=8,点D在边BC上,△ADE为等边三角形,且点E与点D在直线AC的两侧,过点E作EF//BC,EF与AB、AC分别相交于点F、G.
(1)如图,求证:四边形BCEF是平行四边形;
(2)设BD=x,FG=y,求y关于x的函数解析式,并写出定义域;
A
E
C
B
A D
G
F
※(3)如果AD 的长为7时,求线段FG 的长.
例题2:如图,△ABC 中,点D 、E 分别是边BC 、AC 的中点,过点A 作AF//BC 交线段DE 的延长线相交于
F 点,取AF 的中点
G ,如果BC = 2 AB . 求证:(1)四边形ABDF 是菱形;
(2)AC = 2DG .
试一试:如图,在ABC △中,90A ∠=o ,AH BC ⊥于H ,B ∠的平分线交AC 于D ,DF BC ⊥ 于F .
求证:四边形AEFD 是菱形.
A
C C
B
F
D E
G
试一试:如图,四边形ABCD 为直角梯形,AD BC BC CD BC AD 2,,//=⊥,对角线相交于点E ,EF//BC 交AB 于点F 。
求证:四边形BCFE 为等腰梯形。
1、已知:如图,O 为正方形ABCD 对角线的交点,点E 在边CB 的延长线上,联结EO ,OF ⊥OE 交BA 延长线于点F ,联结EF 。
(1) 求证:EO =FO ;
(2) 若正方形的边长为2, OE =2OA ,求BE 的长.
E
F
D
A
B
C
B
A
F
E
【巩固练习】
1.已知:如图,点E 、G 在平行四边形ABCD 的边AD 上,EG =ED ,延长CE 到点F ,使得EF =EC . 求证:AF ∥BG .
2.已知:在矩形ABCD 中,AE 平分∠BAD ,∠AOD =120°,求:∠BOE
3.在△ABC 中,AD 是中线,将△ADC 沿直线AD 翻折后点C 落在E 处,联结BE 和DE ,若AC =DC 。
(1)求证:四边形AEDC 是菱形;
(2)判断四边形AEBD 的形状,并证明你的结论。
F
E
D
C
A
B
G
E
O
A
B
C D
11/ 11。
