(河北专版)2017年中考数学总复习第5单元四边形第23课时多边形与命题课件
合集下载
中考数学冲刺复习 第五章 四边形 第23课 多边形与平行四边形课件

=180°. 求证(qiúzhèng):四边形ABCD是平行四边形.
证明:∵∠A+∠B=180°,∠A+∠D=180°,
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
第八页,共十二页。
B组
4.已知:如图,E,F分别是▱ABCD的边AD,BC 的中点(zhōnɡ diǎn).求证:AF=CE.
第十页,共十二页。
C组
6.如图,在平行四边形ABCD中,∠C=60°,M,N分别(fēnbié)
是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD= MN.
3
证明(zhèngmíng):(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC, ∵M,N分别是AD,BC的中点,∴MD=NC.MD∥NC,
∵在△ADF和△CBE中,∠BEC=∠DFA,∠ADF=∠CBE,AF=CE, ∴△ADF≌△CBE(AAS)∴BE=DF. 又∵BE∥DF,∴四边形DEBF是平行四边形.
【变式3】如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求
证:四边形DECF是平行四边形.
证明:∵D,F,E是△ABC各边的中点, ∴DF,DE是△ABC的中位线.
∴DF∥BC,DE∥AC. ∴四边形DECF是平行四边形.
第七页,共十二页。
三、过关(guò 〃guān)训练 A组
1.六边形的内角(nèi jiǎo)和为7_2_0_°___,外角和为___3_6_0_°____.
2.一个平行四边形的一个外角是38°,这个平行四边形的内角的度数分 别是_____________3_8_°__,_1_4_2.°,38°,142° 3.如图,在四边形ABCD中,∠A+∠B=180°,∠A+∠D
证明:∵∠A+∠B=180°,∠A+∠D=180°,
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
第八页,共十二页。
B组
4.已知:如图,E,F分别是▱ABCD的边AD,BC 的中点(zhōnɡ diǎn).求证:AF=CE.
第十页,共十二页。
C组
6.如图,在平行四边形ABCD中,∠C=60°,M,N分别(fēnbié)
是AD,BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD= MN.
3
证明(zhèngmíng):(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC, ∵M,N分别是AD,BC的中点,∴MD=NC.MD∥NC,
∵在△ADF和△CBE中,∠BEC=∠DFA,∠ADF=∠CBE,AF=CE, ∴△ADF≌△CBE(AAS)∴BE=DF. 又∵BE∥DF,∴四边形DEBF是平行四边形.
【变式3】如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求
证:四边形DECF是平行四边形.
证明:∵D,F,E是△ABC各边的中点, ∴DF,DE是△ABC的中位线.
∴DF∥BC,DE∥AC. ∴四边形DECF是平行四边形.
第七页,共十二页。
三、过关(guò 〃guān)训练 A组
1.六边形的内角(nèi jiǎo)和为7_2_0_°___,外角和为___3_6_0_°____.
2.一个平行四边形的一个外角是38°,这个平行四边形的内角的度数分 别是_____________3_8_°__,_1_4_2.°,38°,142° 3.如图,在四边形ABCD中,∠A+∠B=180°,∠A+∠D
(河北)中考数学总复习:5.1《多边形与平行四边形》ppt课件

5.(2014·邯郸模拟)如图,在四边形ABCD中,AB∥CD,要使得四 边 形 ABCD 是 平 行 四 边 形 , 应 添 加 的 条 件 是 ___________________________________ . ( 只填写一个条件 , 不使 用图形以外的字母和线段)
答案不唯一,如:AB=CD
平行四边形的面积及三角形的中位线
1.平行四边形的面积等于________. 2.三角形的中位线平行于第三边且等于 ________.
【例1】(1)(2013·资阳)一个正多边形的每个外角都等于36°,那么它是( C) A.正六边形 B.正八边形 C.正十边形 D.正十二边形 (2)(2013·烟台)一个多边形截去一个角后,形成另一个多边形的内角和为720°,那 么原多边形的边数为( ) A.5 B.5或6 C.5或7 D.5或6或7
多边形的内角和与外角和
D
(1)多边形的外角和等于360°; (2)截去一个角,分三种情况:含多边形一个顶点、二个顶点、三个顶点 ,由新多边形的内角和推出原多边形的边数.
平行四边形的性质与判定 【例2】(1)四边形ABCD中,对角线AC,BD相交于点O, 下列条件不能判定这个四边形是平行四边形的是 ( ) A.AB∥CD,AD∥BC D B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
C
3.(2012·河北)如图,在▱ABCD中,∠A=70°,将▱ABCD折叠,使 点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN ,则∠AMF等于( B ) A.70° B.40° C.30° D.20° 4.(2013· 河北)用4个全等的正八边形进行拼接,使相邻的两个正八边 形有一条公共边,围成一圈后中间形成一个正方形,如图①.用n个全等 的正六边形按这种方式拼接,如图②,若围成一圈后中间也形成一个正 多边形,则n的值为__6__.
中考数学第五单元四边形第23课时多边形及平行四边形市赛课公开课一等奖省名师优质课获奖PPT课件

证实:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF.
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
图 23-5
∴△ABE≌△CDF,
∴AE=CF.
第16页
高频考向探究
探究二 平行四边形判定
例 2 [2018·大庆] 如图 23-6,在 Rt△ABC 中,∠ACB=90°,D,E 分别是 AB,AC 的中点,连结 CD,DE,过点 E 作 EF
第30页
6.[2018·温州] 如图 23-12,在四边形 ABCD 中,E 是 AB 的中点,AD∥EC,∠AED=∠B.
(1)求证:△AED≌△EBC;
证实:∵AD∥EC,∴∠A=∠BEC,
∵E是AB中点,∴AE=BE,
∵∠AED=∠B,∴△AED≌△EBC(ASA).
图 23-12
第29页
当堂效果检测
∴AB2=52+(25-AB)2,解得AB=13,
即线段AB长度为13 cm.
第19页
高频考向探究
【方法模型】
判定一个四边形是平行四边形时,应依据条件选择适当判定定理,当四边形中包括中点连线时,可考
虑应用三角形中位线定理,由一组对边平行且相等四边形是平行四边形来证实.
第20页
高频考向探究
针 对 训 练
40°
.
图 23-1
第7页
课前双基巩固
3.[2018·临沂] 如图 23-2,在▱ABCD 中,AB=10,AD=6,AC⊥BC.则
[答案] 4 13
BD=
[解析] ∵AB=10,AD=BC=6,AC⊥BC,
.
∴AC= 102 -62 =8,∵四边形 ABCD 是
中考数学复习 第5单元 四边形 第23课时 多边形与平行四边形课件 湘教版.pptx

考点聚焦
考点1 多边形及其性质
多边形 在同一平面内,若干条不在同一直线上的线段首__尾__顺__次__相
的定义 接组成的图形叫作多边形
内角和 n边形的内角和为(_n_-__2_)_1_8_0°
多边形 外角和 n边形的内角和为__3_6_0_°___
的性质
对角线 定义
n一边共形可从以一画个_顶__n点_(_出_n_-发_条3可)对以角画线_(_n_-__3_)__条对角线, 各边__相__等____,各内2 角__相__等____的多边形叫作正
(4)AO=OD;( × )
回归教材
(7)AO⊥AB.( × )
考点聚焦
11
考向探究
第五单元┃ 四边形
|针对训练| [2017·益阳]如图23-5,四边形ABCD为平行四边形,F是 CD的中点,连接AF并延长与BC的延长线交于点E. 求证:BC=CE.
图23-5
证明:∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC. ∴∠DAF=∠E,∠ADF=∠ECF, 又∵F是CD的中点,即DF=CF, ∴△ADF≌△ECF,∴AD=CE.∴BC=CE.
边形的每个内角都相等,等于540°÷5=108°.因此答案
是108°.
【方法模型】 (1)多边形的内角中最多有三个锐角;(2)多边形的边数每 增加一,内角和度数增加180°;(3)多边形的外角和与边 数n无关.
回归教材
考点聚焦
10
考向探究
第五单元┃ 四边形 探究2 平行四边形的性质 命题角度
(1)证明平行四边形中的三角形全等或线段相等;
回归教材
考点聚焦
12
考向探究
第五单元┃ 四边形 探究3 平行四边形的判定 命题角度 (1)根据条件判定一个四边形是平行四边形; (2)添加条件,使四边形为平行四边形; (3)以平行四边形为基础,给出正确的结论并证明. 例3 如图23-6,四边形ABCD中,对角线AC与BD相交于O, 在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条 件,“四边形ABCD是平行四边形”为结论构成命题.
中考数学 第五单元 四边形 第23课时 多边形及平行四边形课件浙教级数学课件
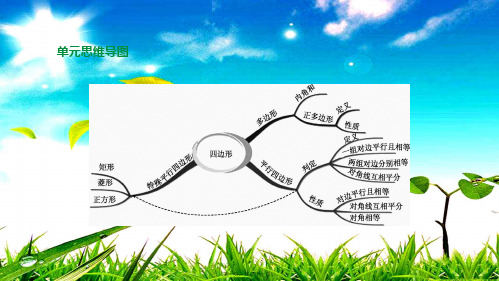
坐标为(1,2),则点 B 的坐标为
形,A(3,0),C(1,2),所以 BC=OA=3.得点
.
c
B 的横坐标为 3+1=4,纵坐标为
2,所以
点 B(4,2).
图 23-10
第二十六页,共三十一页。
当堂效果检测
5.如图 23-11,四边形 ABCD 的对角线相交于点 O,AO=CO,请添加一个条件 答案(dáàn)不唯一,如BO=DO
中,OB= 2 + 2 =2 13,
∴BD=4 13.
第八页,共三十一页。
课前双基巩固
知识梳理
平行四边形的对边
,对角线
相等
相等(xiāngděng)
且
,对角ng)
(duì jiǎo)
平行(pí
ngxí
第九页,共三十一页。
.
互相平分
课前双基巩固
考点(kǎo diǎn)三
平行四边形的判定
图 23-4
∴DF∥BE.
第十四页,共三十一页。
高频考向探究
例 1 如图 23-4,在▱ABCD 中,BE 平分∠ABC,交 AD 于点 E,F 是 BC 上一点,且 CF=AE,连结 DF.
(2)若∠ABC=70°,求∠CDF 的度数.
∵四边形 ABCD 是平行四边形,
∴AD=BC,AD∥BC.
第三页,共三十一页。
(
)
D
课前双基巩固
2.[2018·台州] 正十边形的每一个内角的度数为 (
)
[答案] D
A.120°
B.135°
[解析] 方法一:首先利用内角和公式计
C.140°
D.144°
算出正十边形的内角和,然后再计算每
中考数学复习方案 第五单元 四边形 第23课时 多边形与平行四边形课件
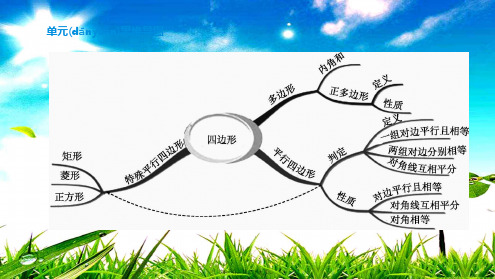
解:(1)证明(zhèngmíng):∵四边形ABCD是平行四边形,
∴AE∥CD,AB=CD,
图23-13
∴∠EBF=∠DCF,∠BEF=∠CDF.
∵AB=BE,∴BE=CD,
∴△BEF≌△CDF,∴BF=CF.
第二十七页,共二十九页。
6. [2019·张家界]如图23-13,平行四边形ABCD中,连结对角线AC,延长(yáncháng)AB至点E,使
diǎn),△BEO的周长是8,则△BCD的周长为
A.15
B.16
(
C.24)D.18 Nhomakorabea图23-9
第二十三页,共二十九页。
B
3.如图 23-10,在四边形 ABCD 中,∠A+∠D=α,∠ABC 的平分线与∠BCD 的平分线
交于点 P,则∠P= (
1
A.90°-2α
C
)
1
B.90°+2α
1
C.2α
图23-10
2. [2019·广东]一个(yī ɡè)多边形的内角和是1080°,这个多边形的边数是
3.正n边形的每个内角为120°,这个正n边形的对角线条数为
第四页,共二十九页。
条. 9
8.
知识(zhī shi)梳理
定义
各边都相等,各内角都相等的多边形称为正多边形
n边形的内角和为 (n-2)·180°
任意多边形的外角和为
例1 如图23-5,已知△ABC,分别(fēnbié)以△ABC的三边为边在△ABC的同侧作三个等边三角
形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
图23-5
第十二页,共二十九页。
证明:∵△ABE,△BCD 都是等边三角形,∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴AE∥CD,AB=CD,
图23-13
∴∠EBF=∠DCF,∠BEF=∠CDF.
∵AB=BE,∴BE=CD,
∴△BEF≌△CDF,∴BF=CF.
第二十七页,共二十九页。
6. [2019·张家界]如图23-13,平行四边形ABCD中,连结对角线AC,延长(yáncháng)AB至点E,使
diǎn),△BEO的周长是8,则△BCD的周长为
A.15
B.16
(
C.24)D.18 Nhomakorabea图23-9
第二十三页,共二十九页。
B
3.如图 23-10,在四边形 ABCD 中,∠A+∠D=α,∠ABC 的平分线与∠BCD 的平分线
交于点 P,则∠P= (
1
A.90°-2α
C
)
1
B.90°+2α
1
C.2α
图23-10
2. [2019·广东]一个(yī ɡè)多边形的内角和是1080°,这个多边形的边数是
3.正n边形的每个内角为120°,这个正n边形的对角线条数为
第四页,共二十九页。
条. 9
8.
知识(zhī shi)梳理
定义
各边都相等,各内角都相等的多边形称为正多边形
n边形的内角和为 (n-2)·180°
任意多边形的外角和为
例1 如图23-5,已知△ABC,分别(fēnbié)以△ABC的三边为边在△ABC的同侧作三个等边三角
形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
图23-5
第十二页,共二十九页。
证明:∵△ABE,△BCD 都是等边三角形,∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
河北省中考数学总复习第五单元四边形第23课时矩形、菱形、正方形课件
∵BD=DC,∴AE 平行且等于 DC,故四边形 ADCE 是平行四边形.
又∵∠ADC=90°,∴平行四边形 ADCE 是矩形.
图 23-4
高频考向探究
探究一 矩形的性质与判定6年1次单独考,3次涉及
例 1 [2018·青岛] 已知:如图 23-5,
ABCD,对角线 AC 与 BD 相
交于点 E,点 G 为 AD 的中点,连接 CG,CG 的延长线交 BA 的延
高频考向探究
拓考向
2.[2018·保定定兴三模改编] 如图 23-8,在矩形 ABCD
中,对角线 AC,BD 相交于点 O,点 E,F 分别是 AO,AD 中
点,若 AB=12,BC=16,则△ AEF 的周长为
A.12
B.16
C.18
D.20
[答案] C
[解析] ∵四边形 ABCD 是矩形,∴AD=BC
ABFE 是菱形.
高频考向探究
探究三 正方形的性质与判定6年1次单独考,5次涉及
例 3 [2018·聊城] 如图 23-13,正方形 ABCD 中,E 是 BC 上的一点,连接 AE,过点 B 作 BH⊥AE,垂足为点 H,延长
BH 交 CD 于点 F,连接 AF.
(1)求证:AE=BF;
(2)若正方形边长是 5,BE=2,求 AF 的长.
B.当 E,F,G,H 是各条线段的中点,且 AC⊥BD 时,四边形 EFGH 为矩形
C.当 E,F,G,H 是各条线段的中点,且 AB=CD 时,四边形 EFGH 为菱形
D.当 E,F,G,H 不是各条线段的中点,四边形 EFGH 可以为平行四边形
图23-3
课前双基巩固
7.如图 23-4,在△ ABC 中,AB=AC,点 D 为 BC 的中点,AE 是∠FAC 的平分线,DE∥AB 交 AE 于 E,则四边形 ADCE
又∵∠ADC=90°,∴平行四边形 ADCE 是矩形.
图 23-4
高频考向探究
探究一 矩形的性质与判定6年1次单独考,3次涉及
例 1 [2018·青岛] 已知:如图 23-5,
ABCD,对角线 AC 与 BD 相
交于点 E,点 G 为 AD 的中点,连接 CG,CG 的延长线交 BA 的延
高频考向探究
拓考向
2.[2018·保定定兴三模改编] 如图 23-8,在矩形 ABCD
中,对角线 AC,BD 相交于点 O,点 E,F 分别是 AO,AD 中
点,若 AB=12,BC=16,则△ AEF 的周长为
A.12
B.16
C.18
D.20
[答案] C
[解析] ∵四边形 ABCD 是矩形,∴AD=BC
ABFE 是菱形.
高频考向探究
探究三 正方形的性质与判定6年1次单独考,5次涉及
例 3 [2018·聊城] 如图 23-13,正方形 ABCD 中,E 是 BC 上的一点,连接 AE,过点 B 作 BH⊥AE,垂足为点 H,延长
BH 交 CD 于点 F,连接 AF.
(1)求证:AE=BF;
(2)若正方形边长是 5,BE=2,求 AF 的长.
B.当 E,F,G,H 是各条线段的中点,且 AC⊥BD 时,四边形 EFGH 为矩形
C.当 E,F,G,H 是各条线段的中点,且 AB=CD 时,四边形 EFGH 为菱形
D.当 E,F,G,H 不是各条线段的中点,四边形 EFGH 可以为平行四边形
图23-3
课前双基巩固
7.如图 23-4,在△ ABC 中,AB=AC,点 D 为 BC 的中点,AE 是∠FAC 的平分线,DE∥AB 交 AE 于 E,则四边形 ADCE
中考数学总复习 第五单元 四边形 第 多边形与平行四边形数学课件
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么…”的形式)
(2)假命题:①四边形 ABCD 中,如果 AB∥CD,AD=BC,那么四边形 ABCD 是平行四边形.
②四边形 ABCD 中,对角线 AC 交 BD 于点 O,如果 AO=CO,AD=BC,那么四边形 ABCD
图20-6
解:(1)证明:∵EG∥BC,∴EF∥BD,∠ACB=∠AGE,∠AEG=∠ABC,∵AB=AC,∴∠ABC=∠ACB,
∴∠AEG=∠AGE.又 BE=BF,∴∠F=∠FEB=∠AEG=∠AGE,∴BF∥AC,∵ED∥AC,∴BF∥DE,
∴四边形 BDEF 为平行四边形.
第十九页,共二十九页。
高频考向探究
例 4 [2017·大庆] 如图 20-6,以 BC 为底边的等腰三角形 ABC,点 D,E,G 分别在 BC,AB,AC 上,且 EG∥BC,DE∥AC,
延长 GE 至点 F,使得 BF=BE.
(2)当∠C=45°,BD=2 时,求 D,F 两点间的距离.
图20-6
(2)如图,连接 FD,作 FH⊥DE,交 DE 的延长线于点 H,∵∠C=45°,∴∠BFE=∠BEF=45°,∴∠FBE=90°,
六
边形.
2.如图 20-8,在四边形 ABCD 中,AD=12,DO=OB=5,AC=26,∠ADB=90°,则 BC=
120
12
,四边形 ABCD 的面积=
∵∠DNC 是△ BND 的外角,∴∠NBD+∠NDB=∠DNC,
1
∵DN=NC=NB,∴∠DBN=∠BDN= ∠DNC=30°,∴∠BDC=90°.
2
∵tan∠DBC=
(2)假命题:①四边形 ABCD 中,如果 AB∥CD,AD=BC,那么四边形 ABCD 是平行四边形.
②四边形 ABCD 中,对角线 AC 交 BD 于点 O,如果 AO=CO,AD=BC,那么四边形 ABCD
图20-6
解:(1)证明:∵EG∥BC,∴EF∥BD,∠ACB=∠AGE,∠AEG=∠ABC,∵AB=AC,∴∠ABC=∠ACB,
∴∠AEG=∠AGE.又 BE=BF,∴∠F=∠FEB=∠AEG=∠AGE,∴BF∥AC,∵ED∥AC,∴BF∥DE,
∴四边形 BDEF 为平行四边形.
第十九页,共二十九页。
高频考向探究
例 4 [2017·大庆] 如图 20-6,以 BC 为底边的等腰三角形 ABC,点 D,E,G 分别在 BC,AB,AC 上,且 EG∥BC,DE∥AC,
延长 GE 至点 F,使得 BF=BE.
(2)当∠C=45°,BD=2 时,求 D,F 两点间的距离.
图20-6
(2)如图,连接 FD,作 FH⊥DE,交 DE 的延长线于点 H,∵∠C=45°,∴∠BFE=∠BEF=45°,∴∠FBE=90°,
六
边形.
2.如图 20-8,在四边形 ABCD 中,AD=12,DO=OB=5,AC=26,∠ADB=90°,则 BC=
120
12
,四边形 ABCD 的面积=
∵∠DNC 是△ BND 的外角,∴∠NBD+∠NDB=∠DNC,
1
∵DN=NC=NB,∴∠DBN=∠BDN= ∠DNC=30°,∴∠BDC=90°.
2
∵tan∠DBC=
中考数学复习方案 第五单元 四边形 第23课时 多边形与平行四边形课件00
4.[2018·南京(nán jīnɡ)]如图23-3,五边形ABCDE [答案(dáàn)] 72
是正五边形,若l1∥l2,则∠1-∠2=
°.
[解析] 如图,过点B作BF∥l1.
∵五边形ABCDE是正五边形,
∴∠ABC=108°.
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠CBF=180°-∠1,∠ABF=∠2,
②当BE=6 cm时,AB=6 cm,BC=6+4=10(cm),
∴▱ABCD的周长为2(AB+BC)=2×(6+10)=32(cm).
综上所述,▱ABCD的周长为28 cm或32 cm.故选C.
第十三页,共三十二页。
7.[2018·
聊城]如果(rúguǒ)一个正方形被截
[答案] 540°或360°或180°
180°-120°=60°.
故选C.考向二 平行四边形的判定(pàndìng)和性质
例2 如图23-5①,在▱ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交(xiāngjiāo)
于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
EC交于点M,AF的延长线与DC的延长线交于点N.
(1)求证:AB=CN.
(2)若AB=2n,BE=2MF,试用含n的式子表示(biǎoshì)线段AN的长.
解:(1)证明(zhèngmíng):∵四边形ABCD是平行四边形,
∴AB∥DN,∴∠B=∠FCN,∠BAF=∠N.
∵F是BC的中点,
∴BF=CF,∴△BAF≌△CNF,
的正多边形也是中心对称图形;
(2)正n边形有⑨ n
(-)·°
中考数学总复习 第五单元 四边形 第 多边形与平行四边形数学课件
如图②,四边形 ABCD 中,AO=CO,AD=BC,但四边形 ABCD 不是平行四边形.
图 20-4
高频考向探究
[方法模型] 证明四边形是平行四边形时,常需找“边”相等或平行.找“边”相等或平行的常见方法如下:
(1)找边相等:①平行四边形的对边相等、对角线互相平分;②三角形全等;③线段和差(有公共部分).
长为 6 cm
.
图 20-10
当堂效果检测
5.如图 20-11,在▱ABCD 中,EF∥BC,GH∥AB,EF,GH 的交点 P 在对角线 BD 上,图中面积相等的平行四边形有(
图 20-11
A.0 对
B.1 对
C.2 对
D.3 对
)
当堂效果检测
[答案] D
[解析] ∵四边形 ABCD 是平行四边形,∴S△ ABD=S△ CBD.
∠ = ∠,
∴CD+AD=9,∠OAE=∠OCF,在△ AEO 和△ CFO 中, = ,
∴△ AEO≌△CFO(ASA),
∠ = ∠,
∴OE=OF=1.5,AE=CF,
则四边形 EFCD 的周长=ED+CD+CF+EF=(DE+CF)+CD+EF=AD+CD+EF=9+3=12.
故选 C.
高频考向探究
探究三 平行四边形的判定
例 3 如图 20-4,四边形 ABCD 中,对角线 AC 与 BD 相交于点 O,在①AB∥CD;②AO=CO;③AD=BC 中任意选
取两个作为条件,以“四边形 ABCD 是平行四边形”作为结论构成命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例.
图 20-4
高频考向探究
[方法模型] 证明四边形是平行四边形时,常需找“边”相等或平行.找“边”相等或平行的常见方法如下:
(1)找边相等:①平行四边形的对边相等、对角线互相平分;②三角形全等;③线段和差(有公共部分).
长为 6 cm
.
图 20-10
当堂效果检测
5.如图 20-11,在▱ABCD 中,EF∥BC,GH∥AB,EF,GH 的交点 P 在对角线 BD 上,图中面积相等的平行四边形有(
图 20-11
A.0 对
B.1 对
C.2 对
D.3 对
)
当堂效果检测
[答案] D
[解析] ∵四边形 ABCD 是平行四边形,∴S△ ABD=S△ CBD.
∠ = ∠,
∴CD+AD=9,∠OAE=∠OCF,在△ AEO 和△ CFO 中, = ,
∴△ AEO≌△CFO(ASA),
∠ = ∠,
∴OE=OF=1.5,AE=CF,
则四边形 EFCD 的周长=ED+CD+CF+EF=(DE+CF)+CD+EF=AD+CD+EF=9+3=12.
故选 C.
高频考向探究
探究三 平行四边形的判定
例 3 如图 20-4,四边形 ABCD 中,对角线 AC 与 BD 相交于点 O,在①AB∥CD;②AO=CO;③AD=BC 中任意选
取两个作为条件,以“四边形 ABCD 是平行四边形”作为结论构成命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 易知一个小三角形的面积是大三角形面积的 , 9 S阴影 1 2 1 3 . 所以 S等边三角形ABC 9 3
(三)
河北中考题型突破
3.(2016河北一模)如图,鹏鹏从点P出发,沿直线前进
10米后向右转α,接着沿直线前进10米,再向右转α, …,照这样走下去,他第一次回到出发地点P时,一 共走了100米,则α的度数 为________ 36° .
返回
(二)
河北中考考点梳理
考点2
正多边形的性质
相等 ,各角______ 相等 的多边形叫做 定 在平面内,各边______ 义 正多边形 n2 (1)正n边形的每一个内角为____________ 180。 ;每一个 n 360。 外角为_________ n 性 (2)正(2n+1)边形是轴对称图形,对称轴有______ (2n+1) 质 条;正2n边形既是轴对称图形,又是中心对称 2n 条 图形,对称轴有________
命题是假命题.举反例法是判断一个命题是假命题
的常用方法.
平行四边形 B.对角线互相垂直的平行四边形是矩形 C.对角线互相垂直的梯形是等腰梯形 D.对角线相等的菱形是正方形
(三)
河北中考题型突破
2.(2016唐山模拟)下列命题错误的是(
C )
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数 D.两点之间,线段最短
(三)
返回
(三)
河北中考题型突破
题组一 多边形的相关计算
1.(2016长沙)六边形的内角和是( A.540° C.900°
B )
B.720° D.360°
(三)
河北中考题型突破
2.(2016唐山二模)如图,正六边形DEFGHI的顶点分别 S阴影 在等边三角形ABC各边上,则 =( C ) S等边三角形ABC 1 1 A. B. 3 2 2 3 C. D. 3 2
方法点拨
1.已知多边形的内角和α求边数n, 可用多边形内角和公式α=(n-2)· 180°求解;
2.已知正多边形的一个外角α求边数n,可用
n=
360
求解.
返回
(三)
河北中考题型突破
题组二 命题与证明
1. (2016北京海淀模拟)下列命题中,真命题是( D )
A.一组对边平行,另一组对边相等的四边形是
(三)
河北中考题型突破
∠BAC+∠ABC+∠ACB=180°. 求证: 证明: 过点C作CD∥AB,点E为BC的延长线上一点,如
答图①,
∵CD∥AB, ∴∠1=∠A,∠2=∠B. ∵∠ACB+∠1+∠2=180°, ∴∠BAC+∠ABC+∠ACB=180°.
(三)
河北中考题型突破
(2)如答图②,已知:△ABC中,AB=AC,AD是BC 边上的中线, ∠BAD=∠CAD. 求证: ∵AD是BC边上的中线, 证明:
第五单元
四边形
第23课时
多边形和命题
河北 6 年中考真题 河北中考考点梳理 河北中考题型突破
第一部分
教材知识梳理
河北中考考点梳理
考点1 多边形的性
考点2 正多边形的
考点3 命题
质
性质
温馨提示:点击文字链接进入
第一部分
教材知识梳理
河北中考题型突破
题组一 多边形的相 关计算
题组二 命题与证明
温馨提示:点击文字链接进入
(一)
河北6年中考真题
河北6年中考真题
24
(一)
河北6年中考真题
6
返回
(二)
河北பைடு நூலகம்考考点梳理
考点1
多边形的性质
内角和 定理 外角和
(n-2)×180° n边形的内角和为________________
定理 对角线
n边形的外角和为__________ 360°
过n(n>3)边形一个顶点可引(n-3)条对 n n 3 角线,n边形共有条 对角线 2
易知所走路线为一个正十边形.因为正十边形的 外角和为360°,且每个外角均相等, 所以α=360°÷10=36°.
(三)
河北中考题型突破
4.(2015北京)如图是由射线AB,BC,CD,DE,EA 组成的平面图形,则∠1+∠2+∠3+∠4+∠5=
________ 360° .
(三)
河北中考题型突破
河北中考题型突破
3.(2016邯郸一模)下列命题中逆命题是真命题的是( D ) A.对顶角相等
B.若两个角都是45°,那么这两个角相等
C.全等三角形的对应角相等 D.两直线平行,同位角相等
(三)
河北中考题型突破
4.(2016宁波)能说明命题“对于任何实数a,|a|>-a” 是假命题的一个反例可以是( A ) 1 A.a=-2 B.a= C.a=1 3
返回
(二)
河北中考考点梳理
考点3
命题
1.命题:判断一件事情的语句叫做命题.命题分为题
设和结论两部分.题设是已知事项,结论是由已知
事项推出的事项. 2.真命题和假命题:如果题设成立,那么结论一定成 立,这样的命题叫做真命题;如果题设成立时,不 能保证结论一定成立,这样的命题叫做假命题. 3.互逆命题:在两个命题中,如果第一个命题的题设 是另一个命题的结论,而第一个命题的结论是另一 个命题的题设,那么这两个命题叫做互逆命题.
D.a= 2
当a=-2时,|a|=|-2|=2,-a=-(-2)=2, |a|=-a,该命题结论不成立.
(三)
河北中考题型突破
5.(2016邯郸一模)(1)证明三角形的内角和是180°;
(2)已知命题:等腰三角形底边上的中线和顶角的平
分线重合,证明这个命题,并写出它的逆命题, 逆命题成立吗? 解:(1)已知:△ABC,如答图①.
AB AC , 在△ABD和△ACD中, AD AD , BD CD , ∴△ABD≌△ACD(SSS), ∴∠BAD=∠CAD.
∴BD=CD.
它的逆命题是:一条边上的中线和这条边的对角的 平分线重合的三角形是等腰三角形,成立.
(三)
河北中考题型突破
技巧点拨
要证明一个命题是真命题,需利用基本事实、 定义、定理、已知条件等进行推理,而要证明一个 命题是假命题,只需举出一个反例,即可说明这个
