拟可加模糊测度随机变量
模式识别复习题分解

《模式识别》试题库一、基本概念题1.1 模式识别的三大核心问题是:、、。
1.2、模式分布为团状时,选用聚类算法较好。
1.3 欧式距离具有。
马式距离具有。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性1.4 描述模式相似的测度有:。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度1.5 利用两类方法处理多类问题的技术途径有:(1);(2);(3)。
其中最常用的是第个技术途径。
1.6 判别函数的正负和数值大小在分类中的意义是:,。
1.7 感知器算法。
(1)只适用于线性可分的情况;(2)线性可分、不可分都适用。
1.8 积累位势函数法的判别界面一般为。
(1)线性界面;(2)非线性界面。
1.9 基于距离的类别可分性判据有:。
(1)1[]w BTr S S-(2)BWSS(3)BW BSS S+1.10 作为统计判别问题的模式分类,在()情况下,可使用聂曼-皮尔逊判决准则。
1.11 确定性模式非线形分类的势函数法中,位势函数K(x,x k)与积累位势函数K(x)的关系为()。
1.12 用作确定性模式非线形分类的势函数法,通常,两个n维向量x和x k的函数K(x,x k)若同时满足下列三个条件,都可作为势函数。
①();②( ); ③ K(x,x k )是光滑函数,且是x 和x k 之间距离的单调下降函数。
1.13 散度J ij 越大,说明ωi 类模式与ωj 类模式的分布( )。
当ωi 类模式与ωj 类模式的分布相同时,J ij =( )。
1.14 若用Parzen 窗法估计模式的类概率密度函数,窗口尺寸h1过小可能产生的问题是( ),h1过大可能产生的问题是( )。
1.15 信息熵可以作为一种可分性判据的原因是: 。
1.16作为统计判别问题的模式分类,在( )条件下,最小损失判决规则与最小错误判决规则是等价的。
1.17 随机变量l(x )=p( x |ω1)/p( x |ω2),l( x )又称似然比,则E {l( x )|ω2}=( )。
广义Sugeno模糊积分的次线性性

( )若 A , A 2 ,BE 且 B= n
=
( ) 0 ( ; A )
( )若 { c ,且 A t ,j 3 A} A ( T ( A ) );
() 4 若 { , A 且存在 自然数 A }: c A ,
模 糊积 分定 义 ,依 据拟加 法和拟 乘 法定 义及运 算性 质 , 究 了这种 广 义 Sgn 糊积 分 的次 可加 性 乃 至 研 ueo模
次线性 性 , 而进 一 步丰 富 了模 糊积 分的理论 。 从
关健 词 :模 糊积 发 ;广义 Sgn 模 糊积分 ;诱 导算 子 ; ueo 拟加 法 ;拟乘 法 ; K一拟 可加模 糊 测度
凡 使 ( ) <+。 0 A 。 ( , ( A) ( . A) 则 称为 一拟可 加模 糊测 度 , 相应 三元组 , ) 称为 K一拟可加模 糊 测度空 间 。 定 义 224 设 :0, .- ] [ +∞ ) [ , 一 0 +∞) 严 是 格 增加 的连续 函数 , 满足 :1 K( )= , 1 且 ( ) 0 0 K( )= 1;2 i x ( )l K( )=+。 则 称 为 R m 。, =[ , 0 +∞ )
( )口 ( 0c = ( 6 0 ( c ; 3 0 6 ) 0 ) 口 ) ( )a 4 00=a O= ,0 l= ; ,a 0 a
∞ ,∽ n ( = ,A , 有 ( )Ⅱ g ∥ ∈ 则 上 0 Ⅳ ) V ,
第 1期
李艳 红 :广 义 S gn u eo模糊 积分 的次线性 性
・ 1・ 8
由此定义 , V ,b ,d [ , +∞) 不 对 ,c ∈ 0 a ,
K-拟可加模糊测度空间上的广义Sugeno模糊积分

K- 可 加 模 糊 测 度 空 间 上 的 广 义 S gn 拟 u e o模 糊 积 分
李艳红 王 贵君。 ,
(.辽 东 学 院 师 范 学 院 ,辽 宁 丹东 1 8 0 ; .天 津 师 范 大学 数 学 科 学 学 院 , 津 30 8 ) 1 10 0 2 天 0 3 7
摘 要 : K 拟 可 加模 糊 测度 空 间上 应 用 已建 立 的 广 义 S g n 在 一 u e o模 糊 积 分模 型 , 对一 类非 负可 积 函 数 讨 论 了这 种 针
Tin i 0 3 7 a jn 3 0 8 ,Chn ) ia
Ge eaie u e o fzy itg aso q a i d iv u z a ues a e o ra fZ ein iest S in e n rl d S g n uz n er l n K- u s a dt e fzy mes r p c .J u n lo h j g Unv ri z - i a y( ce c
Sug no f z y i e a s e u z ntgr l .
K 算子和 t 子 , 义 了拟 加 法 、 算 定 拟乘 法 及 其 运算 ,
0 引 言
自从 1 7 9 4年 日本学 者 S E UG N0_ 首次提 出模 1 糊测度 与模糊积 分 概念 以来 , 糊 测 度论 这 一新 理 模 论得 到 了 巨大 的发 展. 9 7年 , UGE l 针对 模 18 S NOl 2 糊积分 不满足普 通 可加 性 这 一特 点 提 出 了拟加 法 、 拟乘法 的概念 , 并初 步建 立 了拟 可加 模糊 测 度 与积 分的理 论框架 , 这为 研究 非 可加 的模 糊 积分 理论 开
浅谈模糊集测度与概率

2 概率与模糊概率空间 概率是满足具有 性质
的一切 性质。
的 测度, 是一种正 规测度, 它具有 测度
定义 4: 定义在 s 模糊事 件域 上的 一个是单 值集合函 数 概率, 如 果它 满足:
成为
(1)
是 上的模 糊集测 度;
(2) 规范性:
定义 5: 设 是经典随 机试验 的样 本空间 , 如果 是 经典随 机试 验的一个模糊样本 空间, 为由 生成的模糊 事件域, 是定义在 上的
1 96 5 年美国 控制论 专家 Za de h 提出 模糊集的 概念, 这标志 着在众 多领域有重要 应用的新学科— —模糊数学的诞生, 从 而导致了模糊测 度 的产生 。最近 几年 来从事 这方 面研究 的学者 不少 , 并取得 了很多 有意 义的结 果。由 于模 糊测度 通常不 具有 可加性 , 难以完 全建 立相当 于经 典测度论中的 理论体系, 必须根据不 同问题的需要对 模糊测度本身附 加 某些条件 。为此, 国内外许 多学者作 了大量的 尝试, 得 到了一些有 意义 的结果, 但主要 的讨论时 对模糊测 度附加了 较强的次 可加性 或满足律, 它们 甚至 是通 过模 糊可加 性后 得到 的, 具有 一定 的局 限性 。
概率 , 则称 为
模 糊事 件的 概率 空间或 模糊 事件 的概 率场 。
性质 1: 设
为模 糊事件 的概率空 间, 则
( 1) 非负性: 对任意
;
(2) 规范性:
( 3) 可加性 : 如 果对于 中任 意不交 列
:
, 有:
推 论 1: 设 是 一个模 糊集 合的可 加类, 如 果
为可加Βιβλιοθήκη 。的, 则对 任意 的:
1 模糊集测度 定 义 1 : 设 是 任意 一个 模糊集 合类 。
【国家自然科学基金】_可加性_基金支持热词逐年推荐_【万方软件创新助手】_20140731
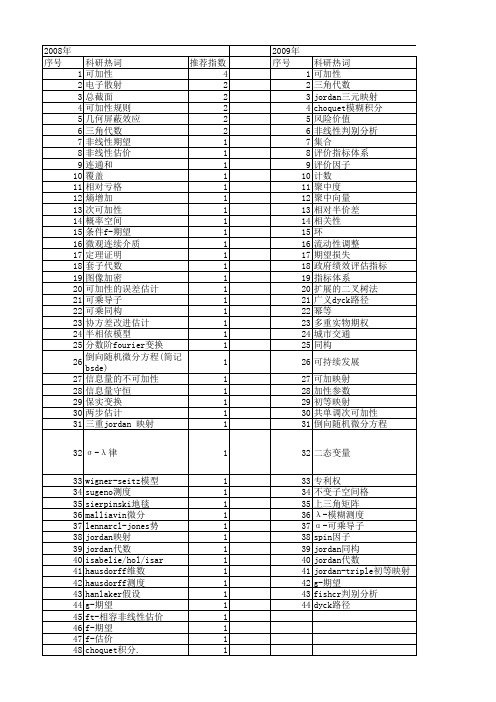
科研热词 可加性 决策 g-期望 鲁棒非脆弱控制 高斯白噪声 风险因子 项目群 非可加性测度 零可加 防空兵作战能力 间接损失 递归对策 误差抑制 自伴算子 聚合算子 综合评价 线性矩阵不等式 穷竭性 离散模糊时滞系统 直接损失 电压暂降 独立性风险 次可加性 模糊测度 模糊合作对策 核心 条件期望 条件g-期望 条件f-期望 最速可下降方向 最大熵准则 时变系统 旋转 数值分析 敏感设备 拟凸规划 拟凸函数 惯性导航 微分方程 广义可加性 对称算子 实测对比 失效度 失效可能性 多属性评价 噪声调频信号 可配置 可能性分布函数 可加性的误差 可乘jordan导子 区间概率 区间值集函数
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77
加权偏离度 共单调次可加性 共单调次可加 共单调可加性 倒向随机微分方程 伪双零渐近可加 伪上(下)自连续 伪一致上(下)自连续 云重心评判法 云理论 不交变差 下次微分 三重jordan映射 var t分布 montecarlo模拟 lq/h_∞控制 k-拟可加模糊测度 k-拟可加模糊数值积分 jordan代数 jensen不等式 g-估价 fpga f-期望 choquet期望
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
科研热词 推荐指数 可加性 4 电子散射 2 总截面 2 可加性规则 2 几何屏蔽效应 2 三角代数 2 非线性期望 1 非线性估价 1 连通和 1 覆盖 1 相对亏格 1 熵增加 1 次可加性 1 概率空间 1 条件f-期望 1 微观连续介质 1 定理证明 1 套子代数 1 图像加密 1 可加性的误差估计 1 可乘导子 1 可乘同构 1 协方差改进估计 1 半相依模型 1 分数阶fourier变换 1 倒向随机微分方程(简记bsde) 1 信息量的不可加性 1 信息量守恒 1 保实变换 1 两步估计 1 三重jordan 映射 1 σ -λ 律 1 wigner-seitz模型 1 sugeno测度 1 sierpinski地毯 1 malliavin微分 1 lennarcl-jones势 1 jordan映射 1 jordan代数 1 isabelie/hol/isar 1 hausdorff维数 1 hausdorff测度 1 hanlaker假设 1 g-期望 1 ft-相容非线性估价 1 f-期望 1 f-估价 1 choquet积分. 1 3-流形 1
教案_模糊数学概述

模糊数学概述任何事物都具有质和量两个侧面。
在分析和解决问题时,我们既可以考察对象的性质、属性等质的方面,也可以对对象的数量关系与空间位置进行分析。
数学就是研究现实世界中量的关系和空间形式的学科。
现实世界中,客观现象在质的表现上具有确定性和不确定性,而不确定性又分为随机性和模糊性。
这种属性反映在量的方面,自然导致研究量的数学学科要按照如下三种划分来分别刻画客观现象:⎪⎩⎪⎨⎧⎩⎨⎧模糊数学研究的领域—模糊性的量随机数学研究的领域—随机性的量不确定性的量精确数学研究的领域—确定性的量量因而,与精确数学和随机数学一样,模糊数学创立并发展为一门独立的数学学科,也是科学技术发展和社会实践需求的历史必然。
模糊数学是从量上来研究和处理模糊现象的一个数学分支,它以“模糊集合论”为基础。
模糊数学提供了一种处理不肯定性和不精确性问题的新方法,是描述模糊信息的有力工具,其应用范围已遍及自然科学和社会科学的几乎所有的领域。
由于模糊性数学发展的主流在于它的应用,因此人们也常称之为“模糊系统理论”、“模糊集与系统理论”或“模糊理论”。
1.模糊数学的产生现代数学是建立在集合论基础之上的。
集合论的重要意义就在于它能将数学的抽象能力延伸到人类认识过程的深处:用集合来描述概念,用集合的关系和运算表达判断和推理,从而将一切现实的理论系统都纳入集合描述的数学框架中。
毫无疑问,以经典集合论为基础的精确数学和随机数学在描述自然界多种客观现象的内在规律中,获得了显著的效果。
但是,和随机现象一样,在自然界和人们的日常生活中普遍存在着大量的模糊现象,如多云,阴天,小雨,大雨,贫困,温饱等。
由于经典集合论只能把自己的表现力限制在那些有明确外延的现象和概念上,它要求元素对集合的隶属关系必须是明确的,决不能模棱两可,因而对于那些经典集合无法反映的外延不分明的概念,以前人们都是尽量回避它们。
然而,随着现代科技的发展,我们所面对的系统日益复杂,模糊性总是伴随着复杂性出现;此外人文、社会学科及其它“软科学”的数学化、定量化趋向,也把模糊性的数学处理问题推向中心地位;更重要的是,计算机科学、控制理论、系统科学的迅速发展,要求电脑要像人脑那样具备模糊逻辑思维和形象思维的功能。
关于K-拟可加模糊积分的几点注记
关于K-拟可加模糊积分的几点注记
彭维玲;孙刚;王贵君
【期刊名称】《模糊系统与数学》
【年(卷),期】2003(17)4
【摘要】在 K-拟可加模糊积分定义及积分转换定理的基础上 ,证明这种模糊积分恰好构成 K-拟可加模糊测度 ,并依据积分转换定理讨论这种 K-拟可加模糊积分的一些补充性质。
【总页数】6页(P88-93)
【关键词】K-拟可加模糊积分;积分转换定理;K-拟可加模糊测度;诱导算子
【作者】彭维玲;孙刚;王贵君
【作者单位】通化师范学院数学系;天津师范大学数学科学学院
【正文语种】中文
【中图分类】O177.6;O159
【相关文献】
1.k-拟可加模糊积分的一致自连续性 [J], 李宏伟
2.K-拟可加模糊测度空间上的广义Sugeno模糊积分 [J], 李艳红;王贵君
3.k-拟可加模糊积分的一些补充性质 [J], 李宏伟
4.K-拟可加集值模糊积分的扩展性质 [J], 李艳红
5.K-拟可加模糊值积分的双零渐近可加与穷竭性 [J], 于姗姗;李艳红;王贵君
因版权原因,仅展示原文概要,查看原文内容请购买。
模糊测度和模糊积分及在分类技术中的应用
模糊测度和模糊积分是一种新兴的数学技术,它们可以用来衡量和分析不确定性和模糊性。
它们可以用来解决复杂的问题,如模糊控制、模糊优化、模糊决策等。
模糊测度和模糊积分在分类技术中也有着重要的应用。
模糊测度是一种用来衡量不确定性和模糊性的技术,它可以用来衡量一个变量的不确定性和模糊性。
它可以用来衡量一个变量的不确定性和模糊性,从而帮助我们更好地理解和处理不确定性和模糊性。
模糊测度可以用来衡量一个变量的不确定性和模糊性,从而帮助我们更好地理解和处理不确定性和模糊性。
模糊积分是一种用来衡量不确定性和模糊性的技术,它可以用来衡量一个变量的不确定性和模糊性。
它可以用来衡量一个变量的不确定性和模糊性,从而帮助我们更好地理解和处理不确定性和模糊性。
模糊积分可以用来衡量一个变量的不确定性和模糊性,从而帮助我们更好地理解和处理不确定性和模糊性。
模糊测度和模糊积分在分类技术中也有着重要的应用。
模糊测度和模糊积分可以用来衡量一个变量的不确定性和模糊性,从而帮助我们更好地理解和处理不确定性和模糊性。
它们可以用来改进分类技术,提高分类的准确性和精确性。
此外,模糊测度和模糊积分还可以用来改进分类技术,提高分类的准确性和精确性。
总之,模糊测度和模糊积分是一种新兴的数学技术,它们可以用来衡量和分析不确定性和模糊性。
它们可以用来解决复杂的问题,如模糊控制、模糊优化、模糊决策等。
此外,模
糊测度和模糊积分在分类技术中也有着重要的应用,可以用来改进分类技术,提高分类的准确性和精确性。
因此,模糊测度和模糊积分在分类技术中有着重要的应用前景。
第三章 模糊认知图
第三章模糊认知图3.1认知图因果知识通常涉及许多相互作用的事物及其关系,由于缺乏有力的分析工具,因此,对这类知识的处理显得比较困难。
在这种情况下,一些其它技术包括定性推理技术就被应用到因果知识的处理中。
认知图就是这种定性推理技术的一种。
认知图是一个新兴的研究领域,它是一种计算智能,提供了一个有效的软计算工具来支持基于先验知识的自适应行为。
对它的研究涉及到模糊数学、模糊推理、不确定性理论及神经网络等诸多学科。
认知图的显著特点就是可利用系统的先验知识、并对复杂系统的子系统具有简单的可加性,能表示出用树结构、Bayes网络及Markov模型等很难表示的具有反馈的动态因果系统。
在认知图中很容易鸟瞰系统中各事物间如何相互作用,每个事物与那些事物具有因果关系。
认知图通常由概念(concept)与概念间的关系(relations of concepts)组成。
概念(用节点表示)可以表示系统的动作、原因、结果、目的、感情、倾向及趋势等,它反映系统的属性、性能与品质。
概念间的关系表示概念间的因果关系(用带箭头的弧表示,箭头的方向表示因果联系的方向)。
3.2认知图的发展简史认知图首先由Tloman于1948年在 Cognitive Maps in Rats and Men一文中提出的,其最初目的是想为心理学建立一个模型,此后认知图便被应用到其他方向和领域中。
人们把认知图描述为有向图,认为认知图是由一些弧连接起来节点的集合,但不同的学者对弧与节点赋予不同的含义。
1955年Kelly依据个人构造理论(Personal construct theory)提出了认知图,概念间的关系是三值的,即利用“+”、“-"表示概念间不同方向因果关系的影响效果,“O”表示概念间不具有因果关系。
1976年Axelord在 structure of Decision –The Cognitive Maps of Political Elites 中提出的认知图比Kelly的更接近于动态系统。
模糊测度与积分及不确定性建模
模糊测度与积分及不确定性建模现代科学与工程领域中的许多问题都存在着不确定性,即使利用概率论也不能完全解决。
为了应对这种不确定性,人们引入了模糊概念,使用模糊测度和积分来进行不确定性建模。
本文将从模糊测度的定义及性质入手,探讨模糊积分的概念和计算方法,并进一步讨论如何运用模糊测度与积分建立不确定性模型。
一、模糊测度的定义及性质模糊测度是描述模糊集合上的不确定性的一种数学工具,常用于处理无法准确刻画的概念。
模糊测度的定义基于不精确性和不确定性的量化。
一个模糊测度是一个从模糊集合的幂集到实数集的映射,它满足以下性质:1. 非负性:对于任意的模糊集合A,模糊测度μ(A)大于等于0。
2. 规范性:空集的模糊测度为0。
3. 可加性:对于任意两个不相交的模糊集合A和B,它们的模糊测度之和等于它们的并集的模糊测度。
通过定义和性质,模糊测度可以提供关于不确定性的量化和度量,为不确定性建模提供了数学基础。
二、模糊积分的概念和计算方法模糊积分是模糊测度的一种扩展,它用于描述模糊集合上的模糊量的积分运算。
与传统的积分不同,模糊积分允许模糊集合在积分区间上的取值为模糊的。
1. 上积分:对于一个模糊集合A和一个定义在A上的函数f,上积分的定义如下:∫[A] f(x) dμ = sup {∫[A] φ(x) dμ | φ(x) ≤ f(x), φ(x)是可测函数}其中,φ(x)是定义在A上的可测函数。
2. 下积分:对于一个模糊集合A和一个定义在A上的函数f,下积分的定义如下:∫[A] f(x) dμ = inf {∫[A] φ(x) dμ | f(x) ≤ φ(x), φ(x)是可测函数}通过上积分和下积分,我们可以得到模糊集合上的模糊量的积分结果,从而实现对不确定性的建模和处理。
三、不确定性建模中的应用模糊测度与积分在不确定性建模中具有广泛的应用。
以下是几个典型的应用场景:1. 决策分析:在决策分析中,人们常常需要处理各种类型的不确定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
龙源期刊网
拟可加模糊测度随机变量
作者:杜二玲范毅君
来源:《新课程·教育学术》2009年第14期
摘要:本文依据K-拟可加模糊测度的相关知识,讨论K-拟可加模糊测度随机变量和K-拟可加模糊测度随机变量的分布函数。
定义K-拟可加模糊测度随机变量的数学期望,证明K-拟可加模糊测度空间上的马尔可夫不等式。
关键词:K-拟可加模糊测度随机变量数学期望
众所周知,模糊测度与模糊积分不满足一般的可加性,而在实际应用中存在着大量的非可加集函数。
考虑到非可加集函数的存在性,1987年日本著名学者Sugeno[1]提出并建立了拟可加模糊测度和积分,在此基础上文[2]对给定的K算子和t算子具体定义了扩张加法和扩张乘法的运算,并建立tK积分和Kt积分。
文[3]在结合文[1]和文[2]的基础上,取算子K=t得到了K-拟可加
模糊积分及其积分转换定理。
文[4]中对此进行了进一步的讨论。
文[5]证明了K-拟可加模糊积分是一种K-拟可加模糊测度,研究了这种K-拟可加模糊积分的可数可加性和绝对连续性等。
本文是在已有这些理论的基础上,讨论了K-拟可加模糊测度随机变量,定义了它的分布函数和数学期望并给出了它们的一些性质,证明了K-拟可加模糊测度空间上的马尔可夫不等式。
从而丰富了K-拟可加模糊测度的理论,拓展了K-拟可加模糊测度理论的应用范围,为进一步研究K-拟可加模糊测度提供了理论依据。
设X是任一非空经典集合,为X上的子集构成的σ-代数,(X,F)表示可测空间。
本文以下涉
及的可测与可积函数f,均是指在Lebesgue意义下的可测与可积函数,不再特殊指出。
1.拟可加模糊测度随机变量。
