2.第二单元 方程(组)与不等式(组)
中考数学复习 第二单元 方程(组)与不等式(组)第06课时 一元二次方程及其应用课件

基
础
知
识
巩
固
高
频
考
向
探
究
(续表)
应用类型
等量关系
面积问题
AB+BC+CD=a
S阴影=⑨ (a-2x)(b-2x)
S阴影=⑩(a-x)(b-x)
第八页,共三十四页。
S阴影= ⑪
-
·x
基
础
知
识
巩
固
高
频
考
向
探
究
对点演练
题组一 必会题
1.若关于x的方程(fāngchéng)(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是 (
耗),窗框的上部是等腰直角三角形,下部是两个全等的矩形,窗框的总面积为 3 m2
(材料的厚度忽略不计).若设等腰直角三角形的斜边长为 x m,下列方程符合题意的
A.16(1+2x)=25
B.25(1-2x)=16
)
[答案] D
[解析]一种药品原价每盒25元,两次降价的百分
率都为x,所以第一次降价后的价格用代数式表
示为25(1-x),第二次降价后的价格用代数
式表示为25(1-x)·(1-x)=25(1-x)2,根据题意可
列方程为25(1-x)2=16,故选D.
C.16(1+x)2=25
D.25(1-x)2=16
第二十六页,共三十四页。
基
础
知
识
巩
固
高
频
考
向
探
究
角度( jiǎodù)2 图形面积问题
例4 [2018·安徽名校模拟] 如图6-2,某街道办事处把一块矩形空地进行绿化.已知该矩形空地
【中考数学夺分大模块复习权威课件】-第2模块《方程(组)与不等式(组)》名师大串讲

第5讲
一次方程(组)
┃考点自主梳理与热身反馈 ┃ 考点1 一元一次方程及其解法
2x- 1 x+ 1 1.把方程 3x+ = 3- 去分母正确的是 (A ) 3 2 A. 18x+ 2(2x- 1)= 18- 3(x+ 1) B. 3x+ (2x- 1)= 3-(x+ 1) C. 18x+(2x- 1)= 18- (x+ 1) D. 3x+ 2(2x- 1)= 3- 3(x+ 1) 2.已知关于 x 的方程 4x- 3m= 2 的解是 x= m,则 m 的值 是 ________ . 2
第5讲┃ 一次方程(组)
考点2
二元一次方程组及其解法 D )
3x+ 4y= 2( 1), 1.代入法解方程组 比较合理的变形是( 2x- y= 5( 2),
2-4y A.由(1)得 x= 3 5+y C.由(2)得 x= 2
2-3x B.由 (1)得 y= 4 D.由 (2)得 y= 2x-5
第5讲┃ 一次方程(组)
3x- 2y= 7, 2.二元一次方程组 的解是 x+ 2y= 5 x= 3, A. y= 2 x= 1, B. y= 2 x= 4, C. y= 2 x= 3, D. y= 1
( D )
第5讲┃ 一次方程(组)
第5讲┃ 一次方程(组)
[中考点金] 根据定义、公式等找等量关系列方程( 组)是解题 的关键.
第5讲┃ 一次方程(组)
变式题 若整式 12- 3(9-y)与 5(y- 4)的值相等,则 y 5 =________. 2
第5讲┃ 一次方程(组)
探究二 建立方程(组)模型解决实际问题 例 2 九年级某班的一个综合实验活动小组去 A, B 两个车 站调查前年和去年“春运”期间的客流量情况, 如图 5-2 是调 查后小明与其他两位同学进行交流的情景,根据他们的对话, 请你分别求出 A, B 两个车站去年“春运”期间的客流量.
中考数学复习 一元一次不等式(组)及应用

“≠”连接而成的式子.
2.解集:一般地,一个含有未知数的不等式的所有
的解,组成这个不等式的解集.
如果a>b,那么a±c>b±c
3.性质如果a>b,c>0,那么ac>bc或ac>bc
如果a>b,c<0,那么ac
①_<_bc或ac
②_<_bc
第1部分 第二单元 方程(组)与不等式(组)
二、一元一次不等式 一元一次不等式
第二单元 方程(组)与不等式(组)
课时 8 一元一次不等式(组)及应用
CONTENTS
目 录
课前自测 知识梳理 知识过关
第1部分 第二单元 方程(组)与不等式(组)
课前自测
1.已知a>b,则下列不等式中不正确的是( C )
A.4a>4b
B.a+4>b+4
C.-4a>-4b
D.a-4>b-4
第1部分 第二单元 方程(组)与不等式(组)
第1部分 第二单元 方程(组)与不等式(组)
广东中考
1.(2013广东)已知实数a,b,若a>b,则下列结论 正确的是( D )
A.a-5<b-5 B.2+a<2+b C.a3<b3 D.3a>3b
第1部分 第二单元 方程(组)与不等式(组)
2.(2018广东)不等式3x-1≥x+3的解集是( D )
(1)求商场销售A,B两种型号计算器的销售价格分别 是多少元?(利润=销售价格-进货价格)
(2)商场准备用不多于2 500元的资金购进A,B两种 型号计算器共70台,问最少需要购进A型号的计算器多 少台?
第1部分 第二单元 方程(组)与不等式(组)
解:(1)设 A 种型号计算器的销售价格是 x 元,B 种
二元一次方程(组)和不等式(组)的应用

二元一次方程(组)和不等式(组)的应用1、端午节是我国传统的节日,人们素有吃粽子的习俗。
某商场在端午节来临之际,用3000元购进A、B两种粽子1100个,购买A种粽子与购买B种粽子的费用相同,已知A种粽子的单价是B种粽子的单价的1.2倍。
(1)求A、B两种粽子的单价各是多少?(2)若计划用不超过7000元的资金再次购进A、B两种粽子共260 0个,已知A、B 两种粽子的进价不变,求A种粽子最多能购进多少个?2、某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品,这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:老板:如果你在多买一个,就可以打八五折,花费比现在还省17元。
小明:那就多买一个吧,谢谢!(1)结合两人的对话内容,求小明原计划购买文具袋多少个?(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过400元,其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,那么小明最多可购买钢笔多少支?3、在端午节来临之际,某商店订购了A型和B型两种粽子,A型粽子28元/千克,B型粽子24元/千克,若B型粽子的总量比A型粽子的2倍少20千克,购进两种粽子公用了2560元,求两种型号粽子各多少千克?4、刘阿姨到超市购买大米,第一次按原价购买,用了105元,几天后,遇上这种大米8折出售,她用了140元又买了一些,两次一共购买了40 kg,这种大米的原价是多少?5、随着中国传统几日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折销售,乙品牌粽子打七五折销售,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需要660元,打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元。
(1)打折前甲乙两种品牌粽子每盒分别为多少元?(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?6、某商场购进甲乙两种商品,甲种商品公用了2000元,乙种商品公用了2400元。
专题(二) 方程、不等式的解法

(2)当 k=1 时,原方程为 x2+3x+1=0. ∵x1,x2 是该方程的两个实数根, ∴由根与系数的关系可知 x1+x2=-3,x1x2=1. ∴x21+x22=(x1+x2)2-2x1x2=(-3)2-2×1=7.
3.解不等式:2x-1>3x2-1,并把它的解集在数轴上表示出来.
解:去分母,得 4x-2>3x-1. 解得 x>1. 这个不等式的解集在数轴上表示如下:
4.解不等式组:25xx-≥-1>9-3(x,x+1),并把它的解集在数轴上表示出来. 解:解不等式 2x≥-9-x,得 x≥-3. 解不等式 5x-1>3(x+1),得 x>2. 则不等式组的解集为 x>2. 将解集表示在数轴上如下:
8.已知关于 x 的方程(x-3)(x-2)-p2=0. (1)求证:无论 p 取何值时,方程总有两个不相等的实数根; (2)设方程的两个实数根分别为 x1,x2,且满足 x21+x22=3x1x2,求实数 p 的值.解:(1)证明:∵(x-3)(x-2)-p2=0,
∴x2-5x+6-p2=0. ∴Δ=(-5)2-4×1×(6-p2)=25-24+4p2=1+4p2. ∵无论 p 取何值时,总有 4p2≥0, ∴1+4p2>0. ∴无论 p 取何值时,方程总有两个不相等的实数根.
2x+y=4,① (3)x-y=-1;② 解:①+②,得 2x+y+x-y=4-1.解得 x=1. 把 x=1 代入①,得 2+y=4.解得 y=2. ∴原方程组的解是xy= =12,.
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
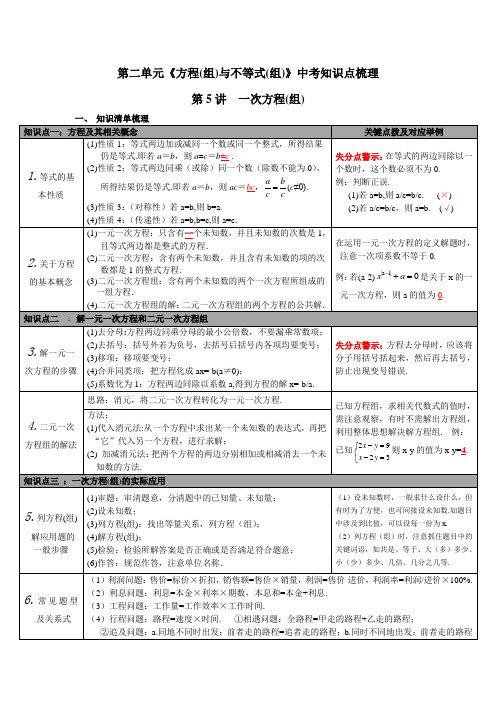
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
(北京)中考数学复习第二单元方程(组)与不等式(组)课时训练一次方程(组)

课时训练(五) 一次方程(组)(限时:40分钟)|夯实基础|1. [2019 •房山二模]方程组--2的解为(2.若2a 3x b y 与-a 2y b x+1是同类项,则( )A -2B.C -2]我国古代数学著作《孙子算经》中有一道题:“今有木 ,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条 ,绳子剩余4. 5尺,将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”设绳子长 x 尺,木条长y 尺,根据题意所列方程组正确的B.1-21D-1 125. [2019 •怀柔二模]为打造世界级原始创新战略高地的综合性国家科学中心 经从怀柔区延伸到密云区,怀柔科学城在两区的占地面积共100. 9平方千米,其中科学城在怀柔区的占地面积比在密云区占地面积的 2倍还多3. 4平方千米,如果设科学城在怀柔区的占地面积为 x 平方千米,在密云区的占地面积是 y 平方千米,则计算科学城在怀柔区和密云区的占地面积各是多少平方千米6. [201 •海淀期末]京张高铁是 2022年冬奥会的重要交通基础设施 ,考虑到不同路段的特殊情况 ,将根据不 同的运行区间设置不同的时速 .其中,北站到清河段全长 11千米,分为地下清华园隧道和地上区间两部分,运B .C. D.-23.数学文化[2019 •通州一模4. [2019 •门头沟二模]团体购买某公园门票,票价如下表:览公园,则共需支付门票费为 1290元;如果两个部门合在一起作为一个团体 ,同一时间购票游览公园,则需支付门票费为990元.那么该公司这两个部门的人数之差为A 20B. 35C. 30D. 40,经过延伸扩建的怀柔科学城,已,依题意可列方程组行速度分别设计为80千米/时和120千米/时.按此运行速度,地下隧道运行时间比地上大约多 2分钟 小时,求清华园隧道全长为多少千米 •设清华园隧道全长为 x 千米,依题意,可列方程为7. 数学文化[2019 •房山一模]《九章算术》是中国传统数学最重要的著作 ,奠定了中国传统数学的基本框架 , 其中方程术是重要的数学成就 •书中有一个方程问题:今有醇酒一斗,直钱五十;行酒一斗,直钱一十,今将钱三 十,得酒二斗,问醇、行酒各得几何?意思是:今有美酒一斗的价格是 50钱,普通酒一斗的价格是 10钱,现在买 两种酒2斗共付30钱,问买美酒、普通酒各多少 ?设买美酒x 斗,买普通酒y 斗,则可列方程组为 __________. 8. [2019 •平谷一模]甲、乙二人分别从相距 20 km 的A ,B 两地出发,相向而行•如图K& 1是小华绘制的甲、乙 二人运动两次的情形,设甲的速度是x km/h ,乙的速度是y km/h ,根据题意所列的方程组是甲走Odh第.次胆竺整進翌丝迺归图 K5-1注1: “指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日)“平 日”为世园会会期除“指定日”外的其他日期;注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票 ;注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为 996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有 _____________ 人.10. [201 •朝阳一模]保护和管理好湿地,对于维护一个城市生态平衡具有十分重要的意义 .2018年计划恢复湿地和计划新增湿地的面积共 2200公顷,其中计划恢复湿地面积比计划新增湿地面积的 2倍多400公顷.求计划恢复湿地和计划新增湿地的面积 .甲走lh第二次相距】I km例如,某户家庭年使用自来水200 m3,按此标准应缴纳:180 5+(200 -180) 7=1040(元);某户家庭年使用自来水300 m3,按此标准应缴纳:180 X 5+(260 -180) X 7+(300 -260) X 9=1820(元).. . 3 . . 3 (1)小刚家2016年共使用自来水170 m ,应缴纳_______________ 元;小刚家2017年共使用自来水260 m ,应缴纳元•⑵小强家2017年使用自来水共缴纳1180元,他家2017年共使用了多少自来水?|拓展提升| 12.在2019年的《最强大脑》节目中,有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图K52是一个最简单的二阶幻圆的模型,要求:内、外两个圆周上的四个数字之和相等;外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字从左到右依次为 _____________ .411图K5-213. [201 •朝阳期末]如图K53,在3X 3的方阵图中,填写了一些数、式子和汉字示一个数),若处于每一横行、每一竖列为 _______ .,以及两条斜对角线上的3个数之和都相等(其中每个式子或汉字都表,则这个方阵图中x的值□□E□H□□S图K5-31. A2. D3. B4. C [解析]设两个部门人数分别为 a , b. •/ 990不能被13整除,•••两个部门人数之和:a+b > 1 . ••• 1290不能被13整除,•••两个部门人数不能同时都少于 51人.•/ 1290不能被11整除,•两个部门人数不能同时在51〜100范围内.(1) 若 1 < a+b w 100 贝U 11(a+b )=990,得:a+b=90 ① 不妨设1w a < 0贝U 1 w b < 100由共需支付门票费为 1290元可知,13 a+11b=1290.②1 0由①②得: n 不符合题意.-0(2) 若 a+b>100,则 9( a+b ) =990,得 a+b=110.③ 不妨设1w a w 0贝y 1 w b < 100由共需支付门票费为 1290元可知,13 a+11b=1290.④由③④得:故两个部门的人数之差为 70- 40=30(人), 故选:C . 9. 3 [解析]设大家庭中有x 人买普通票,有y 人买优惠票,根据题意,10. 解:设计划新增湿地 x 公顷,则计划恢复湿地(2 x+400)公顷. 依题意,得 x+2x+400=2200. 解得x=600. 2x+400=1600.答:计划恢复湿地1600公顷,计划新增湿地600公顷. 11. 解:(1)850;1460⑵ 设小强家2017年共使用了 x m 3自来水.【参考答案】120120 0 9910 0解得5.100 9 211- _1 720~07. 2 10 8.2 20 11 20180X5V1180V1460,贝U 180X 5+7(x- 180) =1180.解得x=220.答:小强家2017年共使用了220 m3自来水.2 1 212.2,9 [解析]设外圆周上的数字为x,内圆周上的数字为y,依题意得21 ' 2解得9故答案为2,9.13.- 5。
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第四节 一元一次不等式(组)及其应用

有 3 个整数解,则 a 的取值范围为
( A)
A.1<a≤2
B.1<a<2
C.1≤a<2
D.1≤a≤2
6 . (2019 · 鄂 州 第 12 题 3 分 ) 若 关 于 x , y 的 二 元 一 次 方 程 组
x-3y=4m+3,
x+5y=5
的解满足 x+y≤0,则 m
的取值范围是__mm≤≤--22__.
③学校购买篮球和足球共 40 个.
(1)
若④购买篮球的个数不少于足球个数的23,则最少可购买篮球
116 6
个;
【分层分析】(1)设购买篮球 x 个,则由题干③可得购买足球((440 0--x)
个,由题干④可列不等式为
2 xx≥≥3((4400--xx)),解此不等式得
x) xx≥≥1166.
(2)若⑤购买篮球的费用不超过购买足球的费用,则最多可购买篮球115
(2)若此不等式组的解集为-4≤x<1,则 a 的值为--22; 【分层分析】(2)由题意得1a.-25168=0--m4 m,即 a=--22;
重难点 2:一元一次不等式的应用
(一题多设问)某校为举行体育比赛活动,准备购买若干个足球和篮
球作为奖品,已知①篮球的单价为 100 元/个,②足球的单价为 60 元/个,
第四节 一元一次不等式 (组)及其应用
【考情分析】湖北近 3 年主要考查:1.一元一次不等式(组)的解法及解集 表示,考查形式有:①求不等式(组)的解集;②求不等式(组)的解集并在 数轴上表示;③求不等式组的整数解;④确定不等式组中字母参数的取 值范围.2.一元一次不等式的应用,考查形式有:①利用不等式判断哪种 方案合算;②与方程(组)、函数结合确定方案问题,设题背景有购买问题、 销售费用问题,以解答题为主
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题链接
第二单元
方程(组)与不等式(组)
考点3
一元二次方程的应用
1.列一元二次方程解应用题的步骤和列一元一次方 程(组)解应用题步骤一样,即审、设、列、解、验、 答六步. 2.列一元二次方程解应用题中,经济类和面积类问 题是常考内容. (1)增长率等量关系:
增长量 A.增长率 = 基础量
返回考点
第二单元
方程(组)与不等式(组)
解:(1)设境外投资合作项目个数为x个,省外境 内投资合作项目为y个, x y 80 , 根据题意得 8x6 y 360 解得
x133 . y 215
(2)133×6+215×7.5=2410.5(亿元). 答:(1)境外投资合作项目为133个,省外境内投 资合作项目为215个.(2)东道主湖南省共引进资 金2410.5亿元.
x1 x2 x12 x22 = x2 x1 x1 x2
9 3 ( x1 x2 ) 2 2 x1x2 4 7 . 3 x1x2 2 2 返回考点
第二单元
方程(组)与不等式(组)
【归纳总结】解决关于一元二次方程的代数式 求值问题时,常用到根与系数的关系.常见的 变形形式有:
4x 3 y 1 2 y 4 x 1
返回考点
第二单元
方程(组)与不等式(组)
考点3 一次方程(组)的实际应用(高频考点)
1.列方程(组)解实际问题的步骤: (1)审:即审清题意,分清题中的已知量、未 知量; (2)设:即设关键未知数; (3)列:即找出适当等量关系,列方程(组); (4)解:即解方程(组); (5)验:即检验所解答案是否正确或是否符合 题意; (6)答:即规范作答,注意单位名称.
(4) x1 x2 ( x1 x2 ) 2 ( x1 x2 ) 2 4 x1 x2 .
返回考点
第二单元
方程(组)与不等式(组)
变式题2(’13荆州)已知关于
x的方程
kx (3k 1) x 2(k 1) 0.
2
(1)求证:无论k为何实数,方程总有实数根; (2)若此方程有两个实数根且 x1 x2 2,求k 的值. 【思路分析】(1)确定判别式的范围即可得出 结论;(2)根据根与系数的关系表示出 x1 x2 , x1 x2 , 继而根据题意可得出方程,解出即可.
返回考点
第二单元
方程(组)与不等式(组)
变式题1(’12岳阳)若关于x的一元二次方 程有实数根,则 kx2 (2k 1) x (k 1) 0 1 k 且k 0 8 k的取值范围是_____________ .
【解析】根据一元二次方程有实根,则需满足 k 0 ,由此可 两个条件,即 2 (2k 1)
a( x m)( x n) 0 的方程,用因式分解法求 x1 m, x2 n
(b2 4ac 0)
公式法
b b2 4ac x 2a 求根公式:x ③
若
配方法
ax2 bx c 0 不易于分解因式,可考虑配方为 2 a( x h) k , 再直接开方求解,配方法的关键是先将二
两个不相等的实数根. 2 (2)b 4ac ⑤ 两个相等的实数根. 2 b (3) 4ac ⑥ 有实数根.
0
一元二次方程有 一元二次方程没
例题链接
0
第二单元
方程(组)与不等式(组)
2.一元二次方程根与系数关系
设方程 ax bx c 0(a 0) 的两根分别为 x1 , x2 , 则 c b x1 x2 _______, x1 x2 ________. a a 如若 x1 , x2 , 是一元二次方程的 x2 x 2 0 两根,则 1 2 x1 x2 1, x1 x2 2. 1 1
类型一 类型二 类型三 类型四 一元二次方程的解法 一元二次方程根的判别式 一元二次方程根与系数的关系 一元二次方程的实际应用
第二单元
方程(组)与不等式(组)
考点1
一元二次方程及其解法
1.一元二次方程及相关概念 (1)如果一个方程通过移项可以使右边为0, 而左边是只含有① 1 个未知数的② 2 次多 项式,这样的方程叫做一元二次方程. 2 (2)一元二次方程的一般形式是 ax bx c 0 (a,b,c是常数且a ≠0),其中a,b,c分别叫 作二次项系数,一次项系数,常数项.
返回考点
第二单元
方程(组)与不等式(组)
(1)证明:①当 k 0 时,方程是一元一次 方程,有实数根; ②当 k 0 时,方程是一元二次方程,
b 4ac (3k 1) 4k (2k 1) (k 1) 0,
2 2 2
∴无论k为何实数,方程总有实数根. (2)解:∵此方程有两个实数根 x1 , x2 ,
第二单元
方程(组)与不等式(组)
变式题2(’12长沙)以“开放崛起,绿色发展” 为主题的第七届“中博会”已于2012年5月20日 在湖南长沙圆满落幕,作为东道主的湖南省一共 签订了境外与省外境内投资合作项目共348个, 其中境外投资合作项目个数的2倍比省外境内投 资合作项目个数多51个. (1)求湖南省签订的境外.省外境内的投资合 作项目分别有多少个? (2)若境外、省外境内投资合作项目平均每个 项目引进资金分别为6亿元,7.5亿元,求在这次 “中博会”中,东道主湖南省共引进资金多少亿 元?
图①
图②
图③
返回目录
第二单元
方程(组)与不等式(组)
类型一
一元二次方程的解法
2
x 4 x 5 0. 例1 解方程: 解:x2 4x 5 0, ( x 1)( x 5) 0, 则 x 1 0, 或 x 5 0, 所以 x1 1, x2 5. 【点评与拓展】解一元二次方程有四种方法,一般 地,当方程左边是一个完全平方形式,右边是零时, 考虑直接开平方法;当方程左边多项式可因式分解, 右边为零,或等号两边含有未知数的公共因式时, 可考虑用因式分解法;当方程既不易用直接开方法, 又不易用因式分解时,可选用公式法,配方法一般 不选取,除非有特殊说明时再应用.
第二单元
方程(组)与不等式(组)
常考类型剖析
类型一 类型二 二元一次方程组的解法 一次方程(组)的实际应用
第二单元
方程(组)与不等式(组)
考点2
二元一次方程(组)及其解法
1.二元一次方程 含有⑨ 两 个未知数,并且含未知数 的每一项都是⑩ 一次 的方程. 2.二元一次方程组 把两个含有相同未知数的二元一次方 程(或者一个二元一次方程,一个一 元一次方程)联立起来组成的方程 组.
返回目录
第二单元
方程(组)与不等式(组)
类型一
二元一次方程组的解法
例1(’13成都)解方程组:
返回考点
第二单元
方程(组)与不等式(组)
变式题1(’11永州)解方程组:
x y 3 5 x 3( x y) 1
• 23.(2011年长沙)某工程队承包了某标段全长1755 米的过江隧道施工任务,甲、乙两个班组分别从 东、西两端同时掘进.已知甲组比乙组平均每天 多掘进0.6米,经过5天施工,两组共掘进了45 米. • (1)求甲、乙两个班组平均每天各掘进多少米? • (2)为加快工程进度,通过改进施工技术,在剩 余的工程中,甲组平均每天能比原来多掘进0.2 米,乙组平均每天能比原来多掘进0.3米.按此 旄工进度,能够比原来少用多少天完成任务?
返回考点
第二单元
方程(组)与不等式(组)
类型三
一元二次方程根与系数的关系
2 2 x 3x 3 0 x 、 x 例3(’13攀枝花) 设 1 2 是方程
7 x1 x2 的值为_____. 的两个实数根,则 2 x2 x1
2 x 、 x 【解析】由 1 2 是方程 2 x 3x 3 0 的两个实数 3 3 根,由根与系数的关系知: x1 x2 = , x1 x2 = , 2 2
例题链接
次项系数化为1,再给方程两边加上一次项系数一半的平方
第二单元
方程(组)与不等式(组)
考点2 一元二次方程根的判别 式及根与系数关系
1.一元二次方程根的判别式
2 ax bx c ( 0 a 0) 关于 x 的一元二次方程 2 b 的根的判别式为 4ac. (1)b 2 4ac ④ 0 一元二次方程有
返回目录
第二单元
方程(组)与不等式(组)
2.一元二次方程的解法
直接开 平方法 因式分 解法 形如 ( x m) n(n 0) 的方程,可直接开方求解.则
2
一般形式 ax 2 bx c ( 0 a 0)
x1,2 n m
可化为 解.则
返回目录
例:某服装店用6000元购进A,B两种新式服 装,按标价售出后可获得毛利润3800元( 毛利润=售价﹣进价),这两种服装的进价 、标价如表所示: 价格 A型 B型 进价(元/件) 60 100 标价(元/件) 100 160 (1)这两种服装各购进的件数; (2)如果A中服装按标价的8折出售,B中 服装按标价的7折出售,那么这批服装全部 售完后,服装店比按标价出售少收入多少 元?
返回考点
第二单元
方程(组)与不等式(组)
第2课时
一元次二次方程及其应用
中考考点清单
考点1
一元二次方程及其解法
考点2 一元二次方程根的判别式及根 与系数关系 考点3 一元二次方程的应用
返回目录
