随机数据处理方法第三版课后答案(王清河著)中国石油大学出版社
随机信号分析(第3版)习题及答案

1. 2. 3. 4. 5.6.有四批零件,第一批有2000个零件,其中5%是次品。
第二批有500个零件,其中40%是次品。
第三批和第四批各有1000个零件,次品约占10%。
我们随机地选择一个批次,并随机地取出一个零件。
(1) 问所选零件为次品的概率是多少?(2) 发现次品后,它来自第二批的概率是多少?解:(1)用i B 表示第i 批的所有零件组成的事件,用D 表示所有次品零件组成的事件。
()()()()123414P B P B P B P B ====()()()()12341002000.050.420005001001000.10.110001000P D B P D B P D B P D B ========()11110.050.40.10.10.16254444P D =⨯+⨯+⨯+⨯=(2)发现次品后,它来自第二批的概率为,()()()()2220.250.40.6150.1625P B P D B P B D P D ⨯===7. 8.9. 设随机试验X 的分布律为求X 的概率密度和分布函数,并给出图形。
解:()()()()0.210.520.33f x x x xδδδ=-+-+-()()()()0.210.520.33F x u x u x u x =-+-+-10.11. 设随机变量X 的概率密度函数为()xf x ae -=,求:(1)系数a ;(2)其分布函数。
解:(1)由()1f x dx ∞-∞=⎰()()2xxx f x dx ae dx ae dx e dx a ∞∞∞---∞-∞-∞==+=⎰⎰⎰⎰所以12a =(2)()1()2xxtF x f t dt e dt --∞-∞==⎰⎰所以X 的分布函数为()1,0211,02xx e x F x e x -⎧<⎪⎪=⎨⎪-≥⎪⎩12.13.14.X Y求:(1)X 与Y 的联合分布函数与密度函数;(2)X 与Y 的边缘分布律;(3)Z XY =的分布律;(4)X 与Y 的相关系数。
随机信号分析(第3版)课后习题解答

随机信号分析(第3版)课后习题解答《随机信号分析》课程(32学时)—— 2007年教学内容建议1 概率论基础 1.12 随机信号2.1 两条样本函数为:0)(0=t X 、wt t X cos 21)(1=;1)0,(=x f X 、2)4,(=w x f X π;)(0-)2,(x wx f X δπ= 2.2 3103532)2,(=++=X E 、)()()(5-313-312-31)2,(x x x x F X εεε++= 2.3 )()(1-2121)21,(x x x F X εε+=、)()(2-21121)1,(x x x F X εε++=;)()()()(2-,1411,1412-,411,41)1,21,,(21x x x x x x x x x x F X -++-+++=εεεε2.4 略2.5 )()(1-1.09.0)5,(x x x F X εε+=;)()(y x y x y x F ,11.0,9.0)0025.0,0,,(-+=εε;0因为其概率为0.9;1的概率为1(样本函数),它是可预测的,就是样本函数。
2.6 略 2.7 略 2.8 )()(121121),(-++=x x n x f X δδ、0121)1(21)(=?+-?=n X E 、{})()]()([)]()()][()([),(2121221121n n n X n X E n m n X n m n X En n Cov X X -==--=δ;不可预测2.9 (2.19)10103523)()(),(2111=?==t t t t Cov σσρ、所以(X,Y )满足10103;5,2;2,2的高斯分布。
其概率密度函数为:-+--?--?-=-+--?----=5)2(5)2)(2(32)2(5exp215)2(10)2)(2(1010322)2()10/91(21exp 21),(2222y y x x y y x x y x f XY ππ;特征函数为:++-+=)6)(5)(2(21)22(exp ),(21222121v v v v v v j y x XY φ3 平稳性与功率谱密度3.1 kk k u t t u u f-=)4exp(2*21),,;,,(211π ;因为k 阶概率密度函数与绝对时间无关,所以为严格平稳过程。
统计学(第三版课后习题答案
18.29(元);原因:尽管两个企业的单位成本相同,但单位
成本较低的产品在乙企业的产量中所占比重较大,因此拉低了
总平均成本。
2.11 =426.67(万元);(万元)。
2.12 (1)(2)两位调查人员所得到的平均身高和标准差应该差不
多相同,因为均值和标准差的大小基本上不受样本大小的影
响。
(3)具有较大样本的调查人员有更大的机会取到最高或最低者,因
错误。
6.5 (1)检验统计量,在大样本情形下近似服从标准正态分布;
Hah 和网速是无形的
1:各章练习题答案
2.1 (1) 属于顺序数据。
(2)频数分布表如下:
服务质量等级评价的频数分布
服务质 家庭数 频率%
量等级 (频率)
A
14
14
B
21
21
C
32
32
D
18
18
E
15
15
合计 100
100
(3)条形图(略)
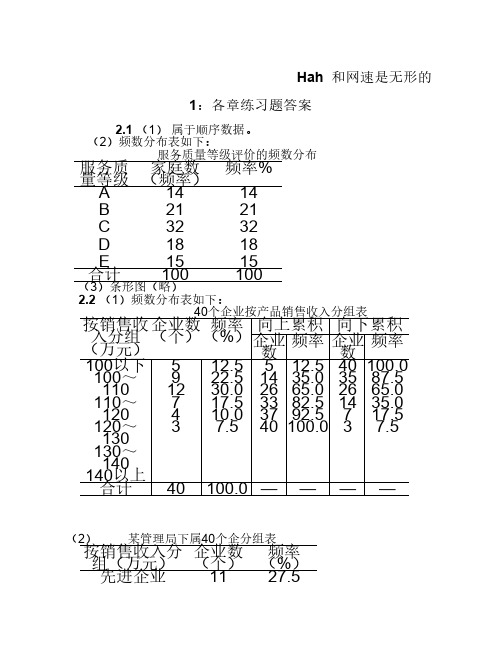
2.2 (1)频数分布表如下:
40个企业按产品销售收入分组表
幼儿组身高的离散系数:;
由于幼儿组身高的离散系数大于成年组身高的离散系数,说明幼儿
组身高的离散程度相对较大。
2.15 下表给出了一些主要描述统计量,请读者自己分析。
方法
方法
方法
A
B
C
平均 165.6 平均 128.73 平均 125.53
中位
中位
中位
数 165 数 129 数 126
众数 164 众数 128 众数 126
为样本越大,变化的范围就可能越大。
2.13 (1)女生的体重差异大,因为女生其中的离散系数为0.1大于
统计学(第三版课后习题答案

即有X ~N(10,9.995)。相应的概率为: P(X ≤10.5)=0.51995,P(X≤20.5)=0.853262。
可见误差比较大(这是由于P太小,二项分布偏斜太严重)。 【注】由于二项分布是离散型分布,而正态分布是连续性分布,所 以,用正态分布来近似计算二项分布的概率时,通常在二项分布的变量
直方图(略)。
2.4 (1)排序略。
(2)频数分布表如下:
100只灯泡使用寿命非频数分布
按使用寿命分 灯泡个 频率
组(小时) 数 (%)
(只)
650~660
2
2
660~670
5
5
670~680
6
6
680~690
14
14
690~700
26
26
700~710
18
18
710~720
13
13
720~730
10
求概率为:P(X ≤10)=0.58304。 (2)当被保险人死亡数超过20人时,保险公司就要亏本。所求概率 为: P(X>20)=1-P(X≤20)=1-0.99842=0.00158 (3)支付保险金额的均值=50000×E(X) =50000×20000×0.0005(元)=50(万元) 支付保险金额的标准差=50000×σ(X) =50000×(20000×0.0005×0.9995)1/2=158074(元)
即:,K/30≥1.64485,故K≥49.3456。 3.12设X =同一时刻需用咨询服务的商品种数,由题意有X~B(6,0.2)
(1)X的最可能值为:X0=[(n+1)p]=[7×0.2]=1 (取整 数) (2)
随机过程第三版课后答案

随机过程第三版课后答案【篇一:随机过程习题答案】们的均值分别为mx和my,它们的自相关函数分别为rx(?)和ry(?)。
(1)求z(t)=x(t)y(t)的自相关函数;(2)求z(t)=x(t)+y(t)的自相关函数。
答案:(1)rz(?)?e?z(t??)z(t)??e?x(t??)y(t??)x(t)y(t)?利用x(t)和y(t)独立的性质:rz(?)?e?x(t??)x(t)?e?y(t??)y(t)???rx(?)ry(?)(2)rz(?)?e?z(t??)z(t)??e??x(t??)?y(t??)???x(t)?y(t)?? ?e?x(t??)x (t)?x(t??)y(t)?y(t??)x(t)?y(t??)y(t)?仍然利用x(t)和y(t)互相独立的性质:rz(?)?rx(?)?2mxmy?ry(?)2、一个rc低通滤波电路如下图所示。
假定输入是均值为0、双边功率谱密度函数为n0/2的高斯白噪声。
(1)求输出信号的自相关函数和功率谱密度函数;(2)求输出信号的一维概率密度函数。
电流:i(t)电压:y(t)答案:(1)该系统的系统函数为h(s)?y(s)1? x(s)1?rcs则频率响应为h(j?)?11?jrc?n02而输入信号x(t)的功率谱密度函数为px(j?)?该系统是一个线性移不变系统,所以输出y(t)的功率谱密度函数为:py(j?)?px(j?)h(j?)?2n0/21?rc?2对py(j?)求傅里叶反变换,就得到输出的自相关函数:1ry(?)?2?????py(j?)ej??1d??2?n0/2j?????1?rc?2ed??(2)线性系统输入为高斯随机过程,则输出也一定是高斯的。
因此,为了求输出的一维概率密度函数,仅需知道输出随机过程的均值和方差即可。
均值:已知输入均值mx=0,则输出均值my=mxh(0)=02方差:ry(0)?var(y)?my因为均值为0,所以方差var(y)?ry(0)?一维pdf:略12?n0/2???1?rc2?2d??3、理想带通滤波器的中心频率为fc、带宽为b,其在通带的频率增益为1。
随机数据处理方法 第三版 课后答案(王清河 著) 中国石油大学出版社

(2) P( A3 | A) = 0.4 。 19.某专门化医院平均接待 K 型病患者 50%,L 型病患者 30%,M 型病患 者 20%,而治愈率分别为 7/10、8/10、9/10。今有一患者已治愈,问此患者是 K 型病的概率是多少?
提示与答案:依题意,这是一全概率公式及贝叶斯公式的应用问的事件是互逆的。
2.如果 x 表示一个沿着数轴随机运动的质点位置,试说明下列事件的包含、
互不相容等关系:
A = {x | x ≤ 20}
B = {x | x > 3}
C = {x | x < 9}
D = {x | x < −5} E = {x | x ≥ 9}
解:(1)包含关系: D ⊂ C ⊂ A 、 E ⊂ B 。
P( AB) = P( A ∩ B ) = P( A ∪ B) = 1 − P( A ∪ B)
=1 − 1 − P(B) + P( AB) 3
从而得 2 − P(B) = 0 ,即 3 P(B) = 2 3
7.一个袋中有 5 个红球 2 个白球,从中任取一球,看过颜色后就放回袋中, 然后再从袋中任取一球。求:(1)第一次和第二次都取到红球的概率;
球,也可能是黑球),并且也只有这两种可能。因此若把这两种可能看成两个事
件,这两个事件的和事件便构成了一个必然事件。
若设 A 表示:“由甲袋取出的球是白球”; B 表示:“由甲袋取出的球是黑 球”; C 表示:“从乙袋取出的球是白球”。则 P(C) = 5 /12 。
18.设有一箱同类产品是由三家工厂生产的,其中 1 是第一家工厂生产的, 2
17.有两个口袋,甲袋中盛有 2 个白球 1 个黑球;乙袋中盛有 1 个白球 2 个黑球。由甲袋任取一球放入乙袋,再从乙袋中取出一球,求取到白球的概率。
中国石油和化学工业优秀教材奖一等奖试验设计与数据处理第三版课后答案

中国石油和化学工业优秀教材奖一等奖试验设计与数据处理第三版课后答案一、单选题1.从互联网产生大数据的角度来看,大数据具有的特征是() [单选题] *A.“4V”特征:大量(Volume)、多样(Variety)、低价值密度(Value)、高速(Velocity)(正确答案)B.样本渐趋于总体,精确让位于模糊,相关性重于因果C.分布式存储,分布式并行计算D.没有特征2.下列可以用于分析数据趋势的是() [单选题] *A.饼图B.折线图(正确答案)C.动态热力图D.词云图3.数据分析的方法不包括() [单选题] *A线性分析(正确答案)B.关联分析C.聚类分析D.数据分类4.下列关于大数据的特征,说法正确的是()。
[单选题] *A.数据价值密度高B.数据类型少C.数据基本无变化D.数据体量巨大(正确答案)5.数据特征探索的主要任务是对数据进行预处理,以下不属于该过程的是()。
[单选题] *A.数据清洗B.异常数据处理C.数据缺失处理D.数据分类处理(正确答案)6.海军军官通过对前人航海日志的分析,绘制了新的航海路线图,标明了大风与洋流可能发生的地点。
这体现了大数据分析理念中的() [单选题] *A.在数据基础上倾向于全体数据而不是抽样数据B.在分析方法上更注重相关分析而不是因果分析(正确答案)C.在分析效果上更追究效率而不是绝对精确D.在数据规模上强调相对数据而不是绝对数据7.大数据时代已经在悄悄地改变我们的日常生活,也使人们日常生活更为便捷,如移动支付、网络约车出行、网络购物、网络预约挂号等。
以下不属于大数据分析的是()。
[单选题] *A.特征探索B.关联分析C.聚类与分类D.建模分析(正确答案)8.电子警察采用拍照的方式来约束车辆的行为,其拍照的过程属于()。
[单选题] *A.数据分析B.数据采集(正确答案)C.数据分类D.数据可视化表达9.某超市曾经研究销售数据,发现买商品A的人购买商品B的概率很大,这种属于数据的()。
概率论与数理统计 第三版课后答案

∴
4 6 12 3
15.已知在 10 只晶体管中有 2 只次品,在其中取两次,每次任取一只,作不放回 抽样。求下列事件的概率。
(1)两只都是正品;(2)两只都是次品;(3)一只是正品,一只是次品; (4)第二次取出的是次品。 解 设以 Ai(i=1,2)表示事件“第 i 次取出的是正品“,因为不放回抽样,故
(2) 不成立,因为 AB A B AB 。
(3) 成立, B A, B AB,又AB B, B AB 。
(4) 成立。 (5) 不成立,因左边包含事件 C,右边不包含事件 C,所以不成立。 (6) 成立。因若 BC≠φ,则因 CA,必有 BCAB,所以 AB≠φ与已知矛盾,
C51C82 C52 C140
13 0.619 21
11.将 3 鸡蛋随机地打入 5 个杯子中去,求杯子中鸡蛋的最大个数分别为 1,2,3 的概 率。
解 依题意知样本点总数为 53 个。
以 Ai(i=1, 2, 3)表示事件“杯子中鸡蛋的最大个数为 i”,则 A1 表示每杯最多放一只鸡
蛋,共有 A53 种放法,故
(2) ( A B)(A B ) A AB BA BB , 因为 AB BA A A ,
BB 且 C C ,所以 (A B)(A B ) A 。
(3)( A B)(A B )(A B) A( A B) AB AB 。 5.设 A,B,C 是三
1 P( AB) P(BC) 0, P( AC) 1 ,
事件,且 P(A)=P(B)= P(C)= 4 ,
8 求 A,
B,C 至少有一个发生的概率。 解 ∵ABCAB ∴0∠P(ABC)∠P(AB)=0,故 P(ABC)=0 ∴所求概率为
