球与各种几何体切、接问题专题(一))
立体几何中球的内切和外接问题(完美版)
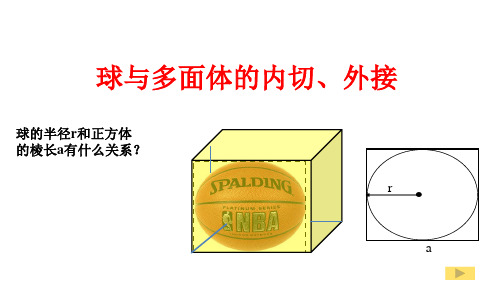
则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
ห้องสมุดไป่ตู้
切(如图).求:
(1)这个正三棱锥的表面积; (2)这个正三棱锥内切球的表面积与体积.
考点一 考点二 考点三
4
举一反三-突破提升
-30-
解:(1)底面正三角形中心到一边的距离为1 × 3×2 6 = 2,则正棱锥
32
侧面的斜高为 12 + ( 2)2 = 3.
∴S 侧=3×12×2 6 × 3=9 2.
,五个顶点都在同一个球面上,
P
设外接球半径为 R,在△OO1A 中有
D
解得 . ∴ .
O1
O C
A B
6
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2,
SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
B、体积为 3
D、外接球的表面积为 16
3
1正视图
1
3 1 侧视图
俯视图
点 A、B、C、D 均在同一球面上,其中
是正三角形,
AD 平面 ABC,AD=2AB=6,则该球的体积为 ( )
(A)
(B)
(C)
(D)
平面四边形 ABCD中, AB AD CD1, BD 2, BD CD ,
球与几何体的切接问题

r3=392π3r3.故圆锥SD与其外接球的体积比为 3323ππrr33=392.故选A. 93
题型二 几何体的内切球
例3 (1)半径为R的球的外切圆柱(球与圆柱的侧面、两底面 都相切)的表面积为__6_π_R_2___,体积为__2_π_R_3___.
状元笔记
柱体的外接球问题,其解题关键在于确定球心在多面体中的 位置,找到球的半径或直径与多面体相关元素之间的关系,结合 原有多面体的特征求出球的半径,然后再利用球的表面积和体积 公式进行正确计算.常见的方法是将多面体还原到正方体或长方 体中再去求解.
思考题 1 (1)已知各顶点都在一个球面上的正四棱柱
(2)已知直三棱柱 ABC-A1B1C1 的 6 个顶点都在球 O 的球面 上,若 AB=3,AC=4,AB⊥AC,AA1=12,则球 O 半径为( C )
3 17 A. 2
B.2 10
C.123
D.3 10
【解析】 由球心 O 作平面 ABC 的垂线,设垂足为 BC 的中点 M.
又 AM=12BC=52,OM=12AA1=6,
【解析】 本题考查几何体的外接球的表面积.因为四个
面都是直角三角形,且AB⊥平面BCD,所以CD⊥BC或
CD⊥BD,不妨设CD⊥BC,由鳖臑ABCD的体积为
2 3
,得
1 3
S△
BCD·AB=
1 3
×
1 2
×1×BC×2=
2 3
,则BC=2,BD=
BC2+CD2
= 5.
将鳖臑ABCD补成直三棱柱如图,取BD的中点
∵球心 O 到四个顶点的距离相等,均等于该正三棱锥外接球 的半径 R,
高中数学立体几何专题·球的切接问题

二.温故知新
同学们,请看下面球与正方体的三种组合体,你能从中得到什 么结论呢? D D
1 A1
A
B O
C
C1
B1 球外切正方体(切面) 球外切正方体(切棱)
球内接正方体
结论:
1.正方体的外接球的球心是体对角线的交点,半径是体对角线的一半 2.正方体的内切球的球心是体对角线的交点,半径是棱长的一半 3.与正方体的棱都相切的球的球心是体对角线的交点,半径是面对角线长的一半
球的“接”与“切”:
• 两个几何体相(内)切:一个几何体的各个面与另一 个几何体的各面相切 • 两个几何体相接:一个几何体的所有顶点都在另一个 几何体的表面上 • 解决“接切”问题的关键是画出正确的截面,把空 间“接切”转化为平面“接切”问题
球与正方体的“切”“接”问题
探究一: 若正方体的棱长为a,则 ⑴正方体的内切球直径= ⑵正方体的外接球直径= ⑶与正方体所有棱相切的球直径=
练习 1、求棱长为a的正四面体的外接球、 棱切球、内切球的体积之比。
2、正三棱锥的高为1,底面边长为2 6 ,
内有一个球与它的四个面都相切.求:
(1)外接球的表面积和体积; (2)内切球的表面积与体积.
解:(1)如图所示,底面正三角形的中心F到一边的距离为
1 3 FD= 2 6= 2, 2 2 则正三棱锥侧面的斜高PD= 1
球与正方体的“接切”问题
1.一个正方体的顶点都在球面上,它的 棱长是4cm,求这个球的体积. 2.长方体的共顶点的三个侧面面积分别 为 3,5, 乙球内切于该正方体的各条棱, 丙球外接于该正方体,则三球表 面面积之比为( ) A. 1:2:3 B.1: 2: 3 C. 1: 4: 9
1 3 2 径分别为: 2 a、2 a、2 a.
立体几何中球与几何体的切接问题

立体几何中球与几何体的切接问题(精讲+精练)一、外接球如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.二、内切球球的内切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作.当球与多面体的各个面相切时,注意球心到各面的距离相等即球的半径,求球的半径时,可用球心与多面体的各顶点连接,球的半径为分成的小棱锥的高,用体积法来求球的半径.【常用结论】①外接球模型一:墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a2+b2+c2.),秒杀公式:R2=a2+b2+c24.可求出球的半径从而解决问题.有以下四种类型:②外接球模型二:三棱锥的三组对棱长分别相等模型,一般用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长,即(长方体的长、宽、高分别为a、b、c).秒杀公式:R2=x2+y2+z28 (三棱锥的三组对棱长分别为x、y、z).可求出球的半径从而解决问题.A BCDA1B1C1D1类型ⅠA BCDA1B1C1D1类型ⅡA BCDA1B1C1D1类型ⅢA BCDA1B1C1D1例外型2R=③外接球模型三:直棱柱的外接球、圆柱的外接球模型,用找球心法(多面体的外接球的球心是过多面体的两个面的外心且分别垂直这两个面的直线的交点.一般情况下只作出一个面的垂线,然后设出球心用算术方法或代数方法即可解决问题.有时也作出两条垂线,交点即为球心.)解决.以直三棱柱为例,模型如下图,由对称性可知球心O 的位置是△ABC 的外心O 1与△A 1B 1C 1的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=,.④外接球模型四:垂面模型是有一条侧棱垂直底面的棱锥模型,可补为直棱柱内接于球,由对称性可知球心O 的位置是△CBD的外心O 1△AB 2D 2的外心O 2连线的中点,算出小圆O 1的半径AO 1=r ,OO 1=,. ⑤外接球模型五:有一侧面垂直底面的棱锥型,常见的是两个互相垂直的面都是特殊三角形且平面ABC ⊥平面BCD ,如类型Ⅰ,△ABC 与△BCD 都是直角三角形,类型Ⅱ,△ABC 是等边三角形,△BCD 是直角三角形,类型Ⅲ,△ABC 与△BCD 都是等边三角形,解决方法是分别过△ABC 与△BCD 的外心作该三角形所在平面的垂线,交点O 即为球心.类型Ⅳ,△ABC 与△BCD 都一般三角形,解决方法是过△BCD 的外心O 1作该三角形所在平面的垂线,用代数方法即可解决问题.设三棱锥A -BCD 的高为h ,外接球的半径为R ,球心为O .△BCD 的外心为O 1,O 1到BD 的距离为d ,O 与O 1的距离为m ,则Error!解得R .可用秒杀公式:R 2=r 12+r 22-l 24(其中r 1、r 2为两个面的外接圆的半径,l 为两个面的交线的长)AB C D A 1B 1C 1D 12h 2224h R r ∴=+O 1C 1AA 1B 1O B CRrh2hO 22h 2224h R r ∴=+r h C DB R A O 1O2h r hC D BR A O 1O2h O 2D 2B 2⑥外接球模型六:圆锥、顶点在底面的射影是底面外心的棱锥.秒杀公式:R =h 2+r 22h(其中h 为几何体的高,r 为几何体的底面半径或底面外接圆的圆心)⑦内切球思路:以三棱锥P -ABC 为例,求其内切球的半径.方法:等体积法,三棱锥P-ABC 体积等于内切球球心与四个面构成的四个三棱锥的体积之和;第一步:先求出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -PAB +V O -PAC +V O -PBC ⇒V P -ABC =13S △ABC ·r +13S △PAB ·r +13S △PAC ·r +13S △PBC ·r =13(S △ABC +S △PAB +S △PAC +S △PBC )·r ; 第三步:解出r =3V P -ABC SO -ABC +S O -PAB +S O -PAC +S O -PBC =3V S 表.【典例1】(2023·浙江·高三校联考期中)正四面体的所有顶点都在同一个表面积是36π的球面上,则该正四面体的棱长是 .类型Ⅰ类型Ⅱ类型ⅢABCDO 1O R rm h -m R dd 类型Ⅳ因为正四面体内接于球,则相应的一个正方体内接球,设正方体为则正四面体为,设球的半径为R ,则, 解得,所以则正方体的棱长为,【典例2】(2023·河南·开封高中校考模拟预测)已知四面体ABCD 中,,ABCD 外接球的体积为()A .B CD .则故11A CB D -2436R ππ=3R =16AC =23AB CD ==AC BD ==AD BC ==45π22222220,29,41,a b b c a c ⎧+=⎪+=⎨⎪+=⎩22a b R +=【典例3】(2023·黑龙江齐齐哈尔·高三齐齐哈尔市第八中学校校考阶段练习)设直三棱柱的所有顶点都在一个表面积是的球面上,且,则此直三棱柱的表面积是( ) A .B .C .D .【典例4】(2023·安徽宣城·高三统考期末)在三棱锥中,△ABC 是边长为3的等边三角形,侧棱PA ⊥平面ABC ,且,则三棱锥的外接球表面积为 .【答案】【解析】根据已知,底面是边长为3的等边三角形,平面, 可得此三棱锥外接球,即以为底面以为高的正三棱柱的外接球.111ABC A B C -40π1,120AB AC AA BAC ∠===16+8+8+16+-P ABC 4PA =-P ABC 28πABC PA ⊥ABC ABC PA的中点,的外接圆半径为所以球的半径为所以四面体外接球的表面积为故答案为:.【典例5】(2023·四川乐山·高三期末)已知正边长为1,将绕旋转至,使得平面平面,则三棱锥的外接球表面积为.取BC 中点G ,连接AG,DG ,则分别取与的外心的球心,由ABC r AN =R OA ==-P ABC 28πABC ABC BC DBC △ABC ⊥BCD D ABC -ABC DBC A BCD -AB AC DB DC BC =====2213122AG DG ⎛⎫∴==-=⎪⎝⎭【典例6】(2023·山东滨州·高三校考期中)已知正四棱锥的底面边长为侧棱长为6,则该四棱锥的外接球的体积为.,显然正四棱锥令,则在中,所以该四棱锥的外接球体积为【典例7】(2023·高三课时练习)边长为的正四面体内切球的体积为()A B C.DP ABCD-221133PO PA AO=-=PO AO R==1|33OO=1Rt AO O△22R AOA O==1π6设正四面体的内切球半径为由等体积法可得因此,该正四面体的内切球的体积为【题型训练1-刷真题】一、单选题322144243A BCDB ACE V V --⎛⎫=-=-⨯ ⎪ ⎪⎝⎭ABCD (21123A BCD V r S -==2.(2022·全国·统考高考真题)已知球上,则当该四棱锥的体积最大时,其高为(A .B .【答案】C【分析】方法一:先证明当四棱锥的顶点1312,底面所在圆的半径为[方法一]:导数法设正四棱锥的底面边长为,高为则,所以,所以正四棱锥的体积2a 2222l a h =+2232(3a =+26h l =2222a l h =-13V Sh =二、填空题【点睛】方法点睛:多面体与球切、接问题的求解方法(1)涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题求解;(2)若球面上四点P 、A 、B 、C 构成的三条线段PA 、PB 、PC 两两垂直,且PA =a ,PB =b ,PC =c ,一般把有关元素“补形”成为一个球内接长方体,根据4R2=a2+b2+c2求解;(3)正方体的内切球的直径为正方体的棱长;(4)球和正方体的棱相切时,球的直径为正方体的面对角线长;(5)利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.【题型训练2-刷模拟】一、单选题)故选:B3.(2023·全国·高三专题练习)在直三棱柱直三棱柱的外接球的体积为( )A .B . 【答案】C【分析】将直三棱柱放入长方体中,借助长方体的外接球求解8π316π34.(2023秋·四川眉山的球面上,则该圆柱的体积为(A .【答案】C【分析】设圆柱的底面半径为 A .B .【答案】B π12π外接球球心位置,求出外接球半径,即可求得答案 因为由于平面平面故平面,又M 为的外心,⊥22AB BC AC ===ACD ⊥ABC BM ⊥ACD DM ADC △的外接球,结合直三棱柱的性质求外接圆半径接球, 设四面体的外接球的球心为,半径为,,则, 的外接球表面积为.AEF A BCD -O R 132AB ==22217R O O r =+=24π28πR =8.(2023·四川成都·校联考二模)在三棱锥平面,若三棱锥A .【答案】B【分析】根据三棱锥中线面关系可先确定球心【详解】 的中点为,连接,因为,又因为平面平面,平面PAC ⊥ABC 231O 1PO AC ⊥112AO AC ==221(26)PA AO =-=PAC ⊥ABC是边长为 10.(2023春·四川绵阳底面是正方形,( )A .【答案】CABCD 89π【详解】 的边长为,在等边三角形平面,∴平面是等边三角形,则,设四棱锥外接球的半径为,为正方形为四棱锥P -ABCD 外接球球心,则易知ABCD 2x PAB ⊥ABCD PE ⊥PAB 3PE x =()211233633ABCD S PE x x ⋅⋅=⨯⨯=R 1O故选:C12.(2023秋·陕西西安·高三校联考开学考试)已知在三棱锥平面,则三棱锥A.B.⊂ABC-P ABC π4【点睛】求解几何体外接球有关的问题,关键点在于找到球心的位置,然后计算出外接球的半径接法和补形法,直接法是根据几何体的结构来找到球心;补形法是补形成直棱柱、长方体(正方体)等几何体,并根据这些几何体的结构找到球心并求得半径13.(2023秋·湖南衡阳·高三衡阳市田家炳实验中学校考阶段练习)球,.若由,则,即又,故,仅当BCD BD CD ⊥BD =24π9πR =32R =1BD =22BD CD ++4CD AC ⋅≤AC所以,四面体外接球即为长方体外接球,则半径由题意,四面体的四个侧面均为全等三角形,形内角,的外接球的直径,要想体积最设,则,,所以当时,,则有三棱锥所以. 故选:A16.(2023·河南·统考三模)如图,该几何体为两个底面半径为的体积为V 1,它的内切球的体积为V A . B .AB x =PA x =6BC x =-PC 2x =min 26PC =3min 4π86π3V R ==2:3的内切圆的半径即为该几何体内切球的半径,求出半径,再根据球的体积公17.(2023·福建宁德·校考模拟预测)将一个半径为半径为()A.C.313+ () 2313-【点睛】关键点点睛:此题考查圆锥的内切球问题,解题的关键是表示出圆锥的体积,化简后利用导数求出其最大值,从而可确定出圆的大小,考查空间想象能力和计算能力,属于较难题18.(2023·全国·高三专题练习)已知四棱锥A . C . 【答案】B所以故其内切圆表面积为故选:B .19.(2023·全国·高三专题练习)若一个正三棱柱存在外接球与内切球,则它的外接球与内切球体积之比为(823)π-(863)π-1133P ABCD ABCD V S PH S -=⋅=表面积24π(8r =-将直三棱柱补成如图所示的长方体,则外接球的直径即为该长方体的体对角线,故外接球的半径为故外接球的的表面积为. 故选:D.21.(2023春·贵州·高三校联考期中)已知正三棱锥221232+29π故选:A.22.(2023·全国·高三专题练习)已知圆台则该圆台的体积为( )A .B .【答案】B72π3143设上底面半径易知,作,垂足为1O B r =1BC O B r ==AC 2BD O A ⊥故选:A【点睛】解决与球有关的内切或外接的问题时,解题的关键是确定球心的位置.对于外切的问题要注意球心到各个面的距离相等且都为球半径;对于球的内接几何体的问题,注意球心到各个顶点的距离相等,解题时要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形,利用勾股定理求得球的半径.24.(2023秋·浙江丽水·高三浙江省丽水中学校联考期末)将菱形体积最大时,它的内切球和外接球表面积之比为(26323R +B ACD -因为,所以当平面平面时,平面平面,所以此时四面体的高最大为因为,所以BA BC =BO ⊥BAC ⊥DAC BO ⊂BAC BO B ACD -DA DC =二、填空题故答案为:26.(2023秋·四川眉山,则该三棱柱的外接球的表面积为【答案】又由三棱柱的高为,则球心因此球半径R 满足:所以外接球的表面积故答案为:4π2360π322R r d =+24πS R ==60π【点睛】求解正棱锥有关问题,要把握住正棱锥的性质,如底面是正多边形,定点在底面的射影是底面的中心等等.求解几何体外接球有关问题,目是求球的表面积还是求体积28.(2023·河南·统考模拟预测)在菱形ABC16【点睛】方法点睛:求空间多面体的外接球半径的常用方法:①补形法:侧面为直角三角形,或正四面体,或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;利用球的性质:几何体中在不同面均对直角的棱必然是球大圆直径,也即球的直径;定义法:到各个顶点距离均相等的点为外接球的球心,借助有特殊性底面的外接圆圆心,找其垂线,则 由,以为坐标原点, 设内切圆半径,易知由等面积可得,解得设四面体外接球球心为所以易知在平面射影为4,3AB BC ==AB ⊥B ,BA BC ABC r 12S lr =PABC O 'ABC31.(2023春·江西南昌·高三南昌市八一中学校考阶段练习)底面,,若【答案】32.(2023·四川绵阳·绵阳南山中学实验学校校考模拟预测)在边长为段,的中点,连接ABCD AC BD O = 163π-AB BC DE【答案】【分析】由题意可知两两垂直,所以将三棱锥就是三棱锥的外接球的直径,求出体对角线的长,则可求出外接球的表面积【详解】由题意可知两两垂直,且 33.(2023秋·河南周口这个圆台的体积为 【答案】【分析】根据圆台与球的性质结合圆台的表面积、体积公式计算即可6π,,OD OE OF ,,OD OE OF OD =1423π故答案为: 34.(2023·全国·高三专题练习)【答案】【分析】作出内切球的轴截面,再根据几何关系求解即可 设该内切球的球心为所以,由已知得所以,在中,142π38πO OE OF OB ===2,BD DF ==AOF AO【答案】 【分析】根据题意利用余弦定理求得方体的六个面的对角线,利用等体积法求出内切球半径,运算求解即可 设长方体从同一个顶点出发的三条棱长分别为则,解得又因为三棱锥是长方体切掉四个角的余下部分,23π222222749a b a c b c ⎧+=⎪+=⎨⎪+=⎩a b c ⎧⎪⎨⎪⎩A BCD -'因为菱形的四条边相等,对角线互相垂直中,面与面的面积是确定的,所以要使三棱锥表面积最大,则需要面最大即可,而且;,当时,取得最大值 因为,,所以由余弦定理知所以,易得. =ABC -ADC ABC DCB DAB S S = sin DCB DC BC ∠⋅⋅π2DCB ∠=DBC S △2DB =32EB ED ==22sin 3DED '∠=63DD '=设,高,则,在Rt 中,所以正四棱锥的体积,故当调递减,2AB a =PO h =2OD a =MOD 13V Sh =2282(4)V h h h h '=-+=--。
10道经典球的接切问题及详解[1]
![10道经典球的接切问题及详解[1]](https://img.taocdn.com/s3/m/25fffc6e0b1c59eef8c7b4da.png)
例5.自半径为 的球面上一点 ,引球的三条两两垂直的弦 ,求 的值.
分析:此题欲计算所求值,应首先把它们放在一个封闭的图形内进行计算,所以应引导学生构造熟悉的几何体并与球有密切的关系,便于将球的条件与之相联.
解:以 为从一个顶点出发的三条棱,将三棱锥 补成一个长方体,则另外四个顶点必在球面上,故长方体是球的内接长方体,则长方体的对角线长是球的直径.
A. B. C. D.
答案:A.球心如何确定?主要依据是球的界面性质:过截面圆心与截面垂直的直线必过球心.球心在过BC中点的平面BCD的垂线上,且在过BD中点M的平面ABD的垂线上,两面垂直,所以两垂线交点为N,于是半径可定,体积易算,如图
另外:如果注意到CD⊥AD,AD⊥AB,联想到长方体中的棱的特征,不难有补体的想法,如图——
由条件可抓住 是正四面体, 、 、 、 为球上四点,则球心在正四面体中心,设 ,则截面 与球心的距离 ,过点 、 、 的截面圆半径 ,所以 得 .
典型例题2——球面距离
例2过球面上两点作球的大圆,可能的个数是( ).
A.有且只有一个B.一个或无穷多个C.无数个D.以上均不正确
分析:对球面上两点及球心这三点的位置关系进行讨论.当三点不共线时,可以作一个大圆;当三点共线时,可作无数个大圆,故选B.
5.已知球的直径SC=4,A,B是该球球面上的两点,AB= , ,则棱锥S-ABC的体积为(2011辽宁高科理科12)
(A) (B) (C) (D)1
答案:C.
提示:对体进行分割,由A作AN⊥SC于N,连接BN,以截面为底求体积.如图——
2011-12-3wht解析
6.将4个半径为1的球装入正四面体型容器内,则此容器的最小高度为.(2011届马瑞瑶问题)
几何体与球的切接问题

几何体与球的切接问题纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一,高考命题小题综合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力。
【核心考点回顾】表面积柱体 2S ch S =+直棱柱底2(S c l S c ''=+斜棱柱底为直截面周长)2222()S r rl r r l πππ=+=+圆锥椎体 12S nah S '=+正棱锥底 2()S r rl r r l πππ=+=+圆锥球24S R π=体积柱体 V Sh =柱椎体 13V Sh =锥球343V R π=2.求空间几何体体积的常用方法(1)公式法:直接根据相关的体积公式计算。
(2)等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等。
(3)割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体。
3.常见几何体与球有关的切、接问题: (1)设正方体的棱长为a ,球的半径为R ,①若球为正方体的外接球,正方体的八个顶点在同一个球面上; 正方体中心与球心重合;则2R =3a ;②若球为正方体的内切球,正方体的六个面都与一个球都相切, 正方体中心与球心重合;则2R =a ;Sh③若球与正方体的各棱相切,则2R =2a .(2)长方体的共顶点的三条棱长分别为a ,b ,c ,外接球的半径为R ,则2R =a 2+b 2+c 2. 用长方体的对角线的公式,求出长方体的对角线长,即为外接球的直径, 从而得到外接球的半径;解决途径是作出截面图,在轴截面中建立关系。
常用结论有:长(正)方体的外接球直径是长(正)方体的体对角线。
(3)正四面体外接球:正四面体四个顶点都在一个球面上,正四面体的中心与球心重合; 数据关系:设正四面体的棱长为,高为;球的半径为,这时有;(4)正三棱锥的内切球:球与正三棱锥四个面相切,球心到四个面距离相等,都为球半径.这样求球的半径可转化为球球心到三棱锥面的距离,可采用等体积法解决, 即:四个小三棱锥的体积和为正三棱锥的体积,31⋅⋅=内切表正三棱锥R S V 。
(完整版)空间几何体与球的切接问题

空间几何体与球的切、接问题1.体积为 8 的正方体的极点都在同一球面上,则该球的表面积为()B.323种类一:三条棱两两垂直可转变为长方体(正方体)2.在三棱锥P ABC中,PA平面ABC , AC BC , AC BC 1, PA3则三棱锥外接球的体积为3.已知球 O 上四点 A、B、C、D,DA平面ABC,AB BC, DA AB BC a ,则球 O 的体积等于圆柱的外接球ORBC2设柱体的高为l ,底面外接圆的半径为r,则有R r2l24.直三棱柱 ABC- A1B1C1的 6 个极点都在球 O 的球面上”,若 AB=3,AC=4,AB⊥AC,AA1= 12,则球 O 的半径为种类二:有一条侧棱垂直于底面可转变为直棱柱5.已知三棱锥 P-ABC 中,三角形 ABC 为等边三角形,且 PA=8,PB=PC= 13 ,AB=3 ,则其外接球的体积为6.在三棱锥 P ABC 中, PA平面ABC , AC1, BC 2, PA 6,ACB 120 ,求三棱锥的外接球的表面积。
圆锥的外接球O O1A设椎体的高为 h, 底面外接圆的半径为 r, 则有R r 22 h R7.正四棱锥的极点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为()A. 81D.27448.在三棱锥 A-BCD中 ACD 与 BCD 都是边长为 2 的正三角形,且平面 ACD 平面BCD,求三棱锥外接球的体积练习 1、在四周体P ABC 中,PC平面ABC,AB=AC=1,BC=2 ,PC= 3 .则该四周体外接球的表面积为.练习 2、正三角形 ABC的边长为 2,将它沿高 AD翻折,使点 B 与点 C 间的距离为2 ,此时四周体ABCD外接球表面积为____________练习 3.已知三棱锥 S-ABC的全部极点都在球 O 的球面上, SC是球 O 的直径。
若平面 SCA⊥平面 SCB,SA=AC,SB=BC,三棱锥 S-ABC的体积为 9,则球 O 的表面积为 ________。
立体几何中球的内切和外接问题(完美版)
2 3 A. 3
B. 3 3
3 3 C. 2
正方体 ABCD A1 B1C1 D1 的棱长为 2 , MN 是它的内切球的一条弦 (我们把球面上任意两点之间的线段称为球的弦) , P 为正方体表面上 的动点,当弦 MN 的长度最大时, PM PN 的取值范围是 .
,∴ , ,∴
,
, .
∴外接球的半径为
,∴球的表面积等于
解析:球内接多面体,利用圆内接多边形的性质求出小 圆半径,通常用到余弦定理求余弦值,通过余弦值再利 c 用正弦定理得到小圆半径 sin C 2r ,从而解决问题。
5
A.
正棱锥的外接球的球心是在其高上
,侧棱 PA 与底面 )
例 5 在三棱锥 P-ABC 中,PA=PB=PC=
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2, SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
B.
C.1
D.
S
O
,即 .
C M B
A
7
,
解: 因为 所以 在 且
若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
D
1 r S全 3 2 2 3 r 3
E
r
6 2 S球 85 2 6
1 1 V多面体 S 全 r V S全 内切球 多 面 体3
3
r内 切 球
变式训练:一个正方体内接于一个球,过球心作一截面,如图所示,则截 面的可能图形是( )
考点三 4
组合体的表面积与体积
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球与各种几何体切、接问题近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见。
首先明确定义1 :若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2 :若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球•一、球与柱体的切接规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题•1、球与正方体(1)正方体的内切球,如图1。
位置关系:正方体的六个面都与一个球都相切,正方体中心与球心重合;数据关系:设正方体的棱长为a ,球的半径为r ,这时有2r =a。
(2)正方体的棱切球,如图2。
位置关系:正方体的十二条棱与球面相切,正方体中心与球心重合; 数据关系:设正方体的棱长为 a ,球的半径为r,这时有2^ 2a 。
(3) 正方体的外接球,如图 3。
位置关系:正方体的八个顶点在同一个球面上;正方体中心 与球心重合;= V EF C —直线En 冠得的绽段为球的截面圆船直径27J=√2。
点评;本题考查球与正启悴ft⅛撷的问题,;「闭球的Iffi 性质,转化成⅛⅛求球的截面IS 直径.2、球与长方体例2自半径为R 的球面上一点 M ,引球的三条两两垂直的弦 MA, MB , MC ,求MA 2 MB 2 MC 2 的值.数据关系:设正方体的棱长为a ,球的半径为r ,这时有2r = ∙ 3a.AI I!>013 √例1 棱长为1的正方体ABCD-AB 1C 1D 1的8个顶点都在球O 的表面上,E , F 分别是棱AA ,DD I 的中点,则直线EF 被球O 截得的线段长为( A .辽思路分析:由题意推出,球为正方体的外接球 •平面AA I DD I 截面所得圆面的半径AD 1 上,得知直线EF 被球O 截得的线段就是球的截面圆的直径2【解析】由题意可知,球为正方体的外接琰尸面.Li "丄载面所得圆面的半径5'二【解析】,3∕C ⅜A 一个顶点出发的三条協 將三棱笹M —ABC 补咸一个长方氷 则另外四个 顶点莎在球面上,故长方体是球的內接长方体,则长方体的⅛⅛i ⅛长是球的直径./. —Ur + 3Z52+J∕c—^(2J ?)2点评匕此题突出构造法的演用,姬渗透利用今割补劭的方法解决立体几何中体积计算••结论:长方体的外接球直径是长方体的对角线。
例3 (全国卷I 高考题)已知各顶点都在一个球面上的正四棱柱高为 4,体积为16,则这个球的表面积为()•A 。
16二 B. 20二 C 。
24二 D 。
32:思路分析:正四棱柱也是长方体•由长方体的体积16及高4可以求出长方体的底面边长为 2,可得长方体的长、宽、高分别为2, 2,4,长方体内接于球,它的体对角线正好为球的直径【解析】正四棱柱也是长方体口由长方体的対只16^73 4可以匸出长方体的底面辺长为2,因此,长方体 的长、宽、高分别为Z 2, 4。
因为长方体内接于球,所页”勺体对角线正好为球的直径•长方体体对角线 长为2√6•故球的表面积为24π •故选C.点评*本题考查球与长⅛⅛的间题,于打扶方体的性质・转化成为求其体对角线。
3、球与正棱柱(1) 结论1 :正棱柱的外接球的球心是上下底面中心的连线的中点。
(2) 结论2 :直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
一个六棱柱的h ⅛⅛½止六边形,其测棱雅直F 底面. 斷鮭梭幽顶点都在同i 球面匕11験棱柱的体积碍4打已知备顶点都亦同个球而上IHiIiPM 棱柱的高为虬 体积为⑷•则这牛球(1⅛⅛ι⅛ι⅛⅛. 24;TΛ-「[三棱柱 ABC 一 A i Zr I C l 中∙ AB = 4, AC = ⅛J = . AA λ = 4,160JT~T~⅛:InJril K 为—则这个坤的休积为财直 滋柱ABC - 4 Zr l C l 的外接球的表面积球与锥体的切接规则的锥体,如正四面体、正棱锥、特殊的一些棱锥等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱锥的棱和高产生联系,然后考查几何体的体积或者表面积等相关问题。
1、正四面体与球的切接问题(1) 正四面体的内切球,如图4.位置关系:正四面体的四个面都与一个球相切,正四面体的中心与球心重合;数据关系:设正四面体的棱长为 a ,高为h ;球的半径为R ,这时有【解析】如图正四面体A —BCD的中心为0,即内切球球心,内切球半径R即为0到正四面体各面的距离.∙.∙ AB = a, .∙.正四面体的高h=严a,又V A-BCD = 4V O—BCD, ()∙°∙ R=1h3 4=陰12(2)正四面体的外接球,位置关系:正四面体的四个顶点都在一个球面上,正四面体的中心与球心重合;数据关系:设正四面体的棱长为a ,高为h ;球的半径为R ,这时有4R = 3^-⅛a ;(可用结论:正四面体的高线与底面的交点是△ ABC 勺中心且其高线通过球心,这是 构造直角三角形解题的依据•此题关键是确定外接球的球心的位置,突破这一点3此问题便迎刃而解,正四面体外接球的半径是正四面体高的*内切球的半径是正1四面体高的4∙(3)正四面体的棱切球,位置关系:正四面体的六条棱与球面相切,正四面体的中心与球心重合;数据关系:设正四面体的棱长为 a ,高为h ;球的半径为 R ,这时有4R = 。
3h = S 2a, h - a 。
3正四面体高h 减去内切球的半径得到) 例5求棱长为1的正四面体外接球的半径。
设SO i 是正四面体S - ABC 的高,外接球的球心 0在SO i 上,设外接球半径为 R , AO i =则在△ ABC 中,用解直角三角形知识得 r =F ,3从而 SO i = SA 2- Aθ1= - '1 —1在Rt △ AOO 1中,由勾股定理得 R 2=-R )2 + (中)2,解得R =46已知正四面体A—BCD的棱长対G求它的外接球半径、內切球半径、棱切球半径” 解]由正四面陳的对隸性与球的对粽性知球心在正四面体的高上*设外接球半径为J?,如图(O为外接球球心,G^ΛBCD的重心)+所l⅛AG = —<J A C^L~CG L=解得R=區*例7设正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比。
思路分析:此题求解的第一个关键是搞清两个球的半径与正四面体的关系,第二个关键是两个球的半径之间的关系,依靠体积分割的方法来解决的。
【解析】如图,正四面⅛ABCD的中心J U, λPZι)的中50—则第一个域半径为正四面体的中心到各面的距离,第二个球的半径为正四面体白「到炉:加距离.^OO =rτOA= A S正四靳ft的一"面的面积严’—依题意得U^L)=^S(R ^r) t又4 亠4卩亠口二;GIS二R十$= 4尸即A =弘*Fςςrj内切球的表面积_丄万:_ 1內切球的体积_亍”_ 1 所以外接球的表面积^存肓•升接球的师:二二匚亍一/ZK点评:正四面慵与球的接切问题,可通过线面关系证出,內切球和外接球的两个球心是重合的,为正四面体高的四等分点, 幫定有内切球的半径y=—h(h为正四面体的高),且外接球的半径R=3r.Y S紳=孕T¥RMuG中,OC:= 0G」+CGs WR23 4 12棱切球半径为OE = J E E+o& =(4)为什么正四面体外接球和内切球心是同一个点?分析如图I I因为正四面体ΛΛABCDftJ外接球的球心O到点B,C t j∕∖∖D的距离相等,所以O在平面BCD /:\\内的射影O-到点B t UD的距离也B《一列相等.又因为在正四面体ABCD中/ VBCD是正三角形,所以O l是CV BCD的中心。
进而在正四面体罡]ABCD中,有Aa L平面BCD,所以球心0在高线AQ上;同理:球心0也在其它面的高线上. 又正四面体ABCD中各面上的高都相等•所以,由OA = OB = OC = OD,得[点0到正四面体各面的距离相等,所以点0也是正四面体ABeD的内切球的球心。
这样,正四面体的内切球的球心与外接球的球心重合。
记正四面体ABeD的高为h,则r÷R = h =今乱因此■只要求出!’和R中的一个■便可求出另一个*2. 其它棱锥与球的切接问题(1)球与正棱锥的组合,常见的有两类,一是球为三棱锥的外接球,此时三棱锥的各个顶点在球面上,根据截面图的特点,可以构造直角三角形进行求解•二是球为正棱锥的内切球,例如正三棱锥的内切球,球与正三棱锥四个面相切,球心到四个面的距离相等,都为球半径R •这样求球的半径可转化为球球心到三棱锥面的距离,故可采用等体积法解决,即四个小三棱锥的体积和为正三棱锥的体积.(2)球与一些特殊的棱锥进行组合,一定要抓住棱锥的几何性质,可综合利用截面法、补形法等进行求解。
结论1 :正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论2:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法。
途径1 :正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体。
途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体。
途径4 :若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体。
例8正三棱锥的高为1,底面边长为2,6,正三棱锥内有一个球与其四个面相切。
求球的表面积与体积.思路分析:此题求解的关键是搞清球的半径与正三棱锥的高及底面边长的关系,由等体积法V P —ABC =VO -PAB V O —PAC +V O _PBC +V。
」BC ,【解析】如國球0是正三棱锥P—ABC的内切玖O到兀二粧锥四个而的距冉都是球的半径虑尸H是正三棱維的高,1。
E是BCil)屮鬲H^LAE±,丄扭C的边。
,。
.⅛Ξ=-×2√6 = √2 。
PE =运6可左得到Sda二S*= S曲=^C PE =3√2 - S/ = f (2√6)2= MIK—1由等体积法,b运仪+Z亦+2运A —x6^xl = iχ3Λ∕2xJξx3 + ^x6√3x^⅛: Λ=-⅛^ = √6-2,3 3 3 2y[3 + 3二‰ =4衣:=丄巩质—2): =8(5-L^).τ.…T;=;总=i,τ(√6—2)∖点评;球心是決走球的位直关键泉本題和用球心钊正三巒口个面的距离相等且为球半径R来求出乩以球心的位置特点来抓球的基本墾,这是解决球有关间题常用的方法。
