关于麦克斯韦方程组的建立
【精品】第八讲：麦克斯韦方程组、电磁场的边界条件
第八讲：麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程，掌握它的基本性质；2、了解边界上场不连续的原因，能导出电磁场的边值关系；3、掌握电磁场方程微分形式和边界形式的联系与区别。
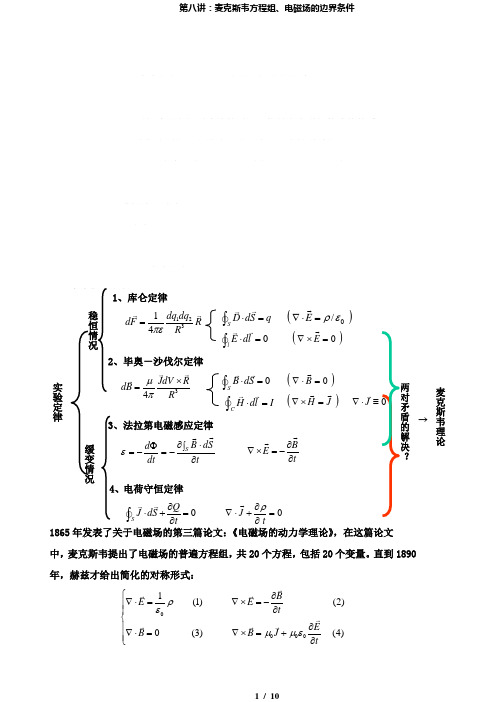
重点：1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点：电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组（Maxwell ’sEquations ）一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文：《电磁场的动力学理论》，在这篇论文中，麦克斯韦提出了电磁场的普遍方程组，共20个方程，包括20个变量。
直到1890 年，赫兹才给出简化的对称形式：00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥－沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组，其中（2）（4）含有对时间的偏导数，对应 运动方程，（1）（3）为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程，表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调，且与电荷守恒定律协调。
如（2）式和（3）式一致：由（2）式有：()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ，考虑到静磁时0=⋅∇B,所以取0=C 。
麦克斯韦方程
麦克斯韦方程组是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一套偏微分方程。
它们描述了电场、磁场、电荷密度和电流密度之间的关系。
它包含四个方程:电荷如何产生电场的高斯定理;不存在的磁单极子的高斯定律;电流与变化的电场如何产生磁场的麦克斯韦安培定律以及变化的磁场如何产生电场的法拉第电磁感应定律。
从麦克斯韦方程中，我们可以推断出光波是电磁波。
麦克斯韦方程和洛伦兹力方程构成了经典电磁学的完整组合。
1865年，麦克斯韦建立了由20个方程和20个变量组成的原始方程
麦克斯韦方程组是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一套偏微分方程。
它们描述了电场、磁场、电荷密度和电流密度之间的关系。
它包含四个方程:电荷如何产生电场的高斯定理;不存在的磁单极子的高斯定律;电流与变化的电场如何产生磁场的麦克斯韦安培定律以及变化的磁场如何产生电场的法拉第电磁感应定律。
详细介绍
麦克斯韦方程是英国物理学家麦克斯韦在19世纪建立的描述电场和磁场的四个基本方程。
麦克斯韦方程
麦克斯韦方程
微分形式的方程通常称为麦克斯韦方程。
在麦克斯韦方程组中，电场和磁场是一个整体。
方程组系统而完整地推广了电磁场的基本规律，预测了电磁波的存在。
核心理念
麦克斯韦的旋涡电场和位移电流假说的核心思想是:变化的磁场激发旋涡电场，变化的电场激发旋涡磁场;电场和磁场不是彼此孤立的，而是相互联系，相互激发，形成统一的电磁场(这也是电磁波的形成原理)。
麦克斯韦进一步整合了电场和磁场的所有定律，建立了完整的电磁场理论体系。
电磁理论体系的核心是麦克斯韦方程组。
麦克斯韦方程组
麦克斯韦方程组维基百科，自由的百科全书麦克斯韦方程组（Maxwell's equations）是英国物理学家詹姆斯·麦克斯韦在19世纪建立的一组偏微分方程，描述电场、磁场与电荷密度、电流密度之间的关系。
它含有的四个方程分别为：电荷是如何产生电场的高斯定理；论述了磁单极子的不存在的高斯磁定律；电流和变化的电场是怎样产生磁场的麦克斯韦-安培定律，以及变化的磁场是如何产生电场的法拉第电磁感应定律。
从麦克斯韦方程组，可以推论出光波是电磁波。
麦克斯韦方程组和洛伦兹力方程共同形成了经典电磁学的完整组合。
1865年，麦克斯韦建立了最初形式的方程，由20个等式和20个变量组成。
他在1873年尝试用四元数来表达，但未成功。
当代使用的数学表达式是由奥利弗·赫维赛德和约西亚·吉布斯于1884年使用矢量分析的形式重新表达的。
概论麦克斯韦方程组乃是由四个方程共同组成的。
它们分别为▪高斯定律描述电场是怎样由电荷生成的。
更详细地说，通过任意闭合表面的电通量与这闭合表面内的电荷之间的关系。
▪高斯磁定律表明，通过任意闭合表面的磁通量等于零，或者，磁场是一个螺线矢量场。
换句话说，类比于电荷的磁荷，又称为磁单极子，实际并不存在于宇宙。
▪法拉第电磁感应定律描述含时磁场怎样生成电场。
许多发电机的运作原理是法拉第电磁感应定律里的电磁感应效应：机械地旋转一块条形磁铁来生成一个含时磁场，紧接着生成一个电场于附近的导线。
▪麦克斯韦-安培定律阐明，磁场可以用两种方法生成：一种是靠电流（原本的安培定律），另一种是靠含时电场（麦克斯韦修正项目）。
这个定律意味着一个含时磁场可以生成含时电场，而含时电场又可以生成含时磁场。
这样，理论上允许电磁波的存在，传播于空间。
▪一般表述在这段落里，所有方程都采用国际单位制。
若改采其它单位制，经典力学的方程形式不会改变；但是，麦克斯韦方程组的形式会稍微改变，大致形式仍旧相同，只有不同的常数会出现于方程的某些位置。
浅谈麦克斯韦方程组的建立及启示
浅谈麦克斯韦方程组的建立及启示学号：1006020426 班级：通信四班姓名：王绥进摘要：麦克斯韦是继法拉第之后，集电磁学大成的伟大物理学家。
在前人工作的基础上，他对电磁学的研究进行了全面的总结，并提出了感生电场和位移电流的假设，建立了完整的电磁理论体系，为科学史的发展添上了浓墨重彩的一笔，他的物理研究方法及自身人格魅力也对后世产生了深远影响。
关键词：麦克斯韦方程组科学意义电磁理论特点正文：（一）麦克斯韦方程组简述1.积分形式这是1873年前后，麦克斯韦提出的表述电磁场普遍规律的四个方程.其中：（1）描述了电场的性质。
在一般情况下，电场可以是库仑电场也可以是变化磁场激发的感应电场，而感应电场是涡旋场，它的电位移线是闭合的，对封闭曲面的通量无贡献。
（2）描述了磁场的性质。
磁场可以由传导电流激发，也可以由变化电场的位移电流所激发，它们的磁场都是涡旋场，磁感应线都是闭合线，对封闭曲面的通量无贡献。
（3）描述了变化的磁场激发电场的规律。
（4）描述了变化的电场激发磁场的规律。
2.微分形式在电磁场的实际应用中，经常要知道空间逐点的电磁场量和电荷、电流之间的关系。
从数学形式上，就是将麦克斯韦方程组的积分形式化为微分形式。
（二）建立过程1845年，关于电磁现象的三个最基本的实验定律：库仑定律（1785年），安培—毕奥—萨伐尔定律（1820年），法拉第定律（1831-1845年）已被总结出来，法拉第的“电力线”和“磁力线”概念已发展成“电磁场概念”。
场概念的产生，也有麦克斯韦的一份功劳，这是当时物理学中一个伟大的创举，因为正是场概念的出现，使当时许多物理学家得以从牛顿“超距观念”的束缚中摆脱出来，普遍地接受了电磁作用和引力作用都是“近距作用”的思想。
1855年至1865年，麦克斯韦在全面地审视了库仑定律、安培—毕奥—萨伐尔定律和法拉第定律的基础上，把数学分析方法带进了电磁学的研究领域，由此导致麦克斯韦电磁理论的诞生.（三）麦克斯韦方程组建立的意义麦克斯韦将当时已发现的电磁场基本规律归纳为4个方程，分别以微分形式描述电场性质、磁场性质，揭示了变化的电场与磁场的关系、变化的磁场与电场的关系。
麦克斯韦方程组推导过程
麦克斯韦方程组是电磁学中描述电场和磁场的基本方程组，由詹姆斯·克拉克·麦克斯韦在19世纪中期推导出来。
这个方程组总共包含四个方程，分别是高斯定律、高斯磁定律、法拉第电磁感应定律和安培环路定律。
下面是麦克斯韦方程组的推导过程：1.高斯定律（电场的高斯定理）：高斯定律描述了电场的源和汇，即电荷和电场的关系。
我们从库仑定律出发，该定律描述了电荷之间的相互作用。
设一个正电荷Q位于原点，电场E为其造成的电场强度。
现在我们考虑一个半径为r的闭合球面S，它将原点包围。
根据高斯定律，电场通过球面的总通量等于包围在球心的电荷量的比例。
即，Φ(E) = ∮(E·dA) = (1/ε₀) * Q其中，Φ(E)表示电场E通过球面S的通量，∮(E·dA)表示电场E 的面积积分，ε₀是真空中的电介质常数（电容率）。
2.高斯磁定律：高斯磁定律指出，不存在孤立的磁荷（单极磁荷）。
这意味着磁场线总是形成闭合回路，没有类似电荷的单一起点或终点。
因此，对于任何闭合曲面S，磁场B通过曲面的通量为零。
即，Φ(B) = ∮(B·dA) = 0其中，Φ(B)表示磁场B通过曲面S的通量，∮(B·dA)表示磁场B的面积积分。
3.法拉第电磁感应定律：法拉第电磁感应定律描述了磁场随时间变化时，电场的感应效应。
考虑一个线圈或导体回路，它的边界为曲面S。
当磁场B通过这个曲面的通量随时间变化时，将会在回路内部产生电动势（电压）。
该电动势大小与通量变化率成正比。
法拉第电磁感应定律的数学表达式为：∮(E·dl) = -(dΦ(B)/dt)其中，∮(E·dl)表示沿着闭合回路的电场E的线积分，dl表示回路的微小线段，-(dΦ(B)/dt)表示磁场B通过曲面S的通量随时间的变化率。
4.安培环路定律：安培环路定律描述了电流通过闭合回路时，磁场的环绕效应。
假设我们有一个闭合回路C，其中有电流I通过。
麦克斯韦方程组
麦克斯韦方程是建立在库伦定律、安培定律、法 拉第电磁感应定律这几个实验定律的基础之上的。
一、法拉第电磁感应定律
1、研究对象 变化磁场产生电场。
2、研究内容
闭合线圈中的感应电动势与通过该线圈内部的磁
通量变化率成正比，
2024/3/14
dm dt
d dt
B ds
S
1
麦克斯韦方程组
电202荷4/3密/14度和电流密度。
9
麦克斯韦方程组
电场方程
E E荷 E感
E荷 / 0 +
E荷 0
E感
E感
0
B t
E
E
/ 0
B
t
E荷 有源场，又称纵场。
E感 有旋场，又称横场。
二20者24/均3/1对4 电荷有力的作用
磁场方程
B B流 B感
B流 0
③
对②式两边取散度，
(
E)
(
B)
t
③
2024/3/14
Case B
E
B
/0
0J
0 0
E t
① ④
对④式两边取散度，
左边： ( B) 0
右边：0
J
0 0
t
(
E)
电荷守恒定律
①
11
麦克斯韦方程组
2、方程的重要意义
揭示了电磁场内在运动规律，不仅
和
J
可以激发电磁
场，而且变化的电场和磁场也可以相互激发。
④
8
麦克斯韦方程组
E dS
1
dV
S
0 V
①
积 分 形
l
麦克斯韦方程的一种建立方法
麦克斯韦方程的一种建立方法本文选自物理时空获得授权发布英国物理学家麦克斯韦（james clerk maxwell，1831-1879）是经典电磁学的集大成者。
麦克斯韦于1873年出版的《电磁通论》，是一部最重要的电磁学经典著作。
在科学史上，牛顿把天上和地上的运动规律统一起来，实现了第一次大综合。
麦克斯韦把电、磁, 光统一起来，实现了第二次大综合，因此麦克斯韦被普遍认为是最有影响力的十九世纪物理学家。
在许多教科书中，麦克斯韦方程组的微分形式采用如下形式。
它由四个方程组成。
第四个方程右边的第二项是位移电流，是麦克斯韦理论上加上去的。
其他公式都是实验得出的经验公式。
可惜麦克斯韦英年早逝。
麦克斯韦受到后人的高度赞扬，但在他去世之前，麦克斯韦方程组并没有得到科学界的重视。
今年我注意到一篇好文章：“麦克斯韦方程进化发展史”。
是美国的james c. rautio。
文章中提到一些有价值的信息。
在19世纪70年代的欧洲，人们仍然坚持牛顿的传统物理学概念。
他们认为麦克斯韦理论对物质世界的新描述违背了传统，因此在德国和其他欧洲中心地区没有立足之地，甚至被视为一种奇怪的理论。
当时只有玻尔兹曼和亥姆霍兹支持电磁理论的研究。
赫兹后来成了亥姆霍兹的学生。
在老师的影响下，赫兹对电磁学进行了深入的研究。
经过反复实验，赫兹发明了一个无线电环，并用这个无线电环做了一系列实验。
终于在1888年，他发现了人们怀疑并期待已久的电磁波。
赫兹的实验发表后，在全世界科学界引起了轰动。
法拉第开创、麦克斯韦总结的电磁理论在这一点上取得了决定性的胜利。
麦克斯韦方程在他生前没有得到科学界的关注的另外一个原因，是由于麦克斯韦在他的《电磁通论》中，其理论的描述复杂得令人吃惊。
麦克斯韦最初提出的电磁理论公式包含了二十个方程。
所以当时英国科学界的泰斗根本不相信会有位移电流这样的东西存在。
麦克斯韦相信真空中有一种介质——或称之为以太——的存在。
他认为，以太充斥于所有空间，电磁行为是由于在这种以太中压缩、拉伸和运动所导致的结果。
建立麦克斯韦方程组的两种方法
L r
=
q( v ·
) A + q v ×(
+ q v ×( ×A) , E= -
A t
-
grad#, B=
×A 。
×A ) -
qgr ad #,
d dt
(
p
+
q
A)=
q(
v·
)A
对 E 取旋度,
×E = - t ×A -
×gr ad#,
×E= -
B t
。
对 B 取散度, ·B = ·( ×A ) = 0, ·B= 0。
s′系和 s 系的电荷密度变换满足 ′= !。
由于 x ′= x xx′+
t
tt′= !
x+
!
u c2
t , y ′=
y , z ′=
z, 有
′·rr′′3 = x ′rx′′3 + y ′ry′′3 +
z ′rz′′3 =
(!
x+
!
u c2
t ) rx′′3 +
y ry′′3 +
z ′rz′3 = 
阐述麦克斯韦方程组的建立及其物理意义
麦克斯韦方程组是一组被詹姆斯·克拉克·麦克斯韦提出的方程，用于描述电磁场的运动规律。
麦克斯韦方程组由四个方程组成，分别是高斯定律、法拉第电磁感应定律、安培环路定律和法拉第电磁感应修正定律。
麦克斯韦方程组的建立经历了一系列的实验和理论推导过程。
最早的实验是库仑对电荷间作用力的研究，他发现电荷之间的相互作用遵循库仑定律。
接着，奥斯特对磁感应强度与电流的关系进行了研究，提出了奥斯特定律。
法拉第进一步研究了电磁感应现象，发现了法拉第电磁感应定律和法拉第电磁感应修正定律。
麦克斯韦根据这些实验结果，结合电场和磁场的相互关系，推导出了麦克斯韦方程组。
其中，高斯定律描述了电场和电荷之间的关系，法拉第电磁感应定律描述了磁场和电场的变化之间的关系，安培环路定律描述了电流和磁场之间的关系，法拉第电磁感应修正定律修正了安培环路定律中的不足。
麦克斯韦方程组的物理意义十分重大。
它揭示了电磁场的运动规律，对于电磁波、电磁感应等现象的解释起到了关键作用。
麦克斯韦方程组统一了电场和磁场的描述，揭示了它们之间的密切联系，提出了电磁场的概念。
根据麦克斯韦方程组，我们可以推导出电磁波的存在和传播，解释了光的本质和性质。
此外，麦克斯韦方程组也为电磁感应的研究提供了理论基础，解释了电磁感应现象的产生和变化规律。
总之，麦克斯韦方程组的建立及其物理意义使我们更深入地理解
了电磁场的本质和运动规律，对于电磁学的发展起到了重要的推动作用。
麦克斯韦方程组实验的设计方案
参考文献
罗开春
电磁学
Griffiths D J
Introduction to Electrodynamics
Maxwell J C
Feynman R P
A Treatise on Electricity and Magnetism
The Feynman Lectures on Physics
结束语
电压数据
连接电压表进行测量 记录电压的大小和波动情 况
数据记录
确保数据记录准确无误 备份数据以防丢失
数据处理
数据处理是麦克斯韦 方程组实验中至关重 要的一步，通过对采 集到的数据进行处理， 可以分析得出实验结 果并与理论进行对比。 在数据处理过程中， 需要注意数据的准确 性和可靠性，以确保 得出的结论具有科学 依据。
利用麦克斯韦方程组进行电磁波传输技术的 研究和应用
02 天体物理学
运用麦克斯韦方程组探索宇宙中的电磁现象 和规律
03 通信工程
基于麦克斯韦方程组的理论，发展通信工程 技术
● 05
第五章 麦克斯韦方程组实验 总结
实验心得
01 仔细测量
确保实验数据准确性
02 多次重复实验
验证实验结果的可靠性
03 注意安全
● 06
第6章 麦克斯韦方程组实验 参考文献
参考书目
罗开春
电磁学
Griffiths D J
Introduction to Electrodynamics
Maxwell J C
Feynman R P
A Treatise on Electricity and Magnetism
The Feynman Lectures on Physics
建立麦克斯韦方程组的一种新方法
建立麦克斯韦方程组的一种新方法
张学清
【期刊名称】《大理学院学报：综合版》
【年(卷),期】1994(000)001
【摘要】《大学物理》1984年2期刊有陈熙谋等的《建立麦克斯韦方程组的其他途径》一文。
文中讨论了由库仑定律和洛化兹变换建立麦氏方程组的方法。
但文中的(20)和(21)两式的得到不太自然,其中的E和B只有在求出它们的散度和旋度后,经与麦克斯韦方程组进行比较才能说明它们分别是S系中的电场和磁场。
若我们事先不知麦氏方程组,那么上述两式中的E和B就不知其意义,故该文所述的方法有一定欠缺。
受该文的启发,作者想到了一种直接从电磁场的变换和库仑定律来建立麦克斯韦方程组的方法,该法在推导中不需与麦氏方程进行比较,且推导用的静电场并不限定为点电荷的静电场。
【总页数】4页(P50-53)
【作者】张学清
【作者单位】
【正文语种】中文
【中图分类】O441
【相关文献】
1.导出麦克斯韦方程组的一种新方法 [J], 黄文涛;吴含荣
2.建立时间戳识别模型的一种新方法 [J], 姚文杰; 艾旭升; 栾咏红; 李良
3.一种PCR检测耐甲氧西林金黄色葡萄球菌株新方法的建立 [J], 邢楣; 符林琳
4.建立一种医疗器械材料体外激活血小板的新方法 [J], 杨文润;莫晓彦;杨立峰;许建霞;郑保婷;祝冰倩;南方;潘贤珮
5.一种快速检测有效氯含量新方法的建立 [J], 马新华;李双;李晓丽;高志贤
因版权原因，仅展示原文概要，查看原文内容请购买。
建立惯性力场中的麦克斯韦方程组
第七节建立惯性力场中的麦克斯韦方程组和惯性力场的量子化建立惯性力场中的麦克斯韦方程组十分困难。
根据等效原理，先把引力场麦克斯韦方程组中的引力场加速度g换成惯性力场加速度a -就可以了。
下面我们按照数学物理方法分析思路先证明惯性力场就是电量电场，从而将麦克斯韦方程组推广到惯性力场；在进一步证明惯性力就是引力，扩大等效原理的适用范围。
一、证明惯性力就是电量电场力惯性力就是电量电场力，惯性力场就是电量电场。
根据统一思维，假定万有引力（B ）、电磁作用力（A ）、弱相互作用力（C ）、强相互作用力（D ）、惯性力（E ）在2400年统一，得物理学统一方程：E k D k C k B k A 4321====其中4321k k k k 、、、是比例系数。
摘取上式中：E k A 4=，可以轻松的证明万有引力就是惯性力。
摘取E k B k A 41==，可以证明万有引力和惯性力两者都是电量电场力。
由于万有引力和惯性力两者都是电量电场力，所以我们可以名正言顺的将麦克斯韦方程组推广到惯性力和万有引力。
并且引力场中的麦克斯韦方程组同样适用于惯性力场。
二、等效原理本质是等同原理等效原理指出惯性系中的万有引力与非惯性系中的惯性力是等效的，它的认识还是比较片面的。
我借花献佛再推广一步，认为惯性系中的万有引力与非惯性系中的惯性力是完全相同的作用力，两者都是电量电场力。
所以等效原理完全成立，等效原理可以认为是等同原理的一个特例。
有等同原理可知，任何形式的万有引力可以找出与之匹配的惯性力，最简单的就是静止天体的在某处产生的引力加速度与匀加速直线运动产生的加速度大小相等，方向相反，万有引力与惯性力等效。
较复杂一点的就是匀角速度转动的天体在某处产生的引力加速度，此时天体产生的引力加速度不在完全指向天体的球心，而是偏离天体中心指向天体旋转的一侧，加速度越大，偏离的越明显。
这相当于一个做匀加速直线运动的物体同时受到一个与物体运动方向垂直的大小恒定的加速度，此时物体做变加速度曲线运动（很复杂），此时物体产生的惯性力与匀角速度转动的天体相同。
麦克斯韦对麦克斯韦方程的贡献
麦克斯韦对麦克斯韦方程的贡献詹姆斯·克拉克·麦克斯韦（James Clerk Maxwell，1831-1879）是19世纪最伟大的科学家之一，他对电磁学的研究和贡献促成了现代物理学的发展。
麦克斯韦通过数学建立了电磁场的理论，提出了著名的麦克斯韦方程组，为电磁波的存在和传播提供了解释，并对电磁学做出了深刻的贡献。
麦克斯韦方程是描述电磁现象的一组偏微分方程组，通过这些方程可以定量描述电场和磁场的变化和相互作用。
麦克斯韦对电磁学的关键贡献主要体现在以下几个方面：1. 麦克斯韦方程的建立：麦克斯韦通过对电场和磁场的数学描述，提出了四个基本的偏微分方程，分别是高斯定律、法拉第电磁感应定律、法拉第电磁感应定律的修正以及安培环路定律。
这四个方程统一了电场和磁场的描述，使电磁现象能够用数学语言精确地描述和预测。
2. 麦克斯韦方程的预测：通过对麦克斯韦方程的数学求解，麦克斯韦预测了电磁波的存在和传播。
他发现，在满足一定条件的电场和磁场的情况下，电磁波可以自由传播，且传播速度等于光速。
这一发现为光的本质提供了解释，并且奠定了电磁波理论基础。
3. 电磁波的理论与实验验证：为了验证自己提出的电磁波理论，麦克斯韦进行了一系列的实验。
他设计了一种实验装置，利用变压器和电容器产生高频电场和磁场，并通过电磁波的辐射验证了他的理论预测。
这一系列实验证实了电磁波的存在并证明了麦克斯韦方程的正确性。
4. 归纳并完善了对电磁现象的数学描述：麦克斯韦基于丰富的实验和观察经验，提炼出一些普遍的规律，将电磁现象归纳为对电场和磁场的数学描述。
他的电磁学理论不仅仅是一套描述电磁现象的方程组，还能够在广泛的物理学和工程学领域应用，成为了现代科学的基础。
总之，麦克斯韦对于电磁学的贡献是巨大的。
他通过建立麦克斯韦方程、预测和实验证明了电磁波的存在和传播，并且提供了对电磁现象的深刻数学描述。
麦克斯韦对现代物理学和电磁学的影响长远而深远，为后世的科学家提供了宝贵的思想和方法。
麦克斯韦方程组的建立过程
麦克斯韦方程组的建立过程一、引言麦克斯韦方程组是描述电磁现象的基本方程，它由英国物理学家詹姆斯·克拉克·麦克斯韦于19世纪中叶提出。
在电磁学和无线电通信等领域都有广泛应用。
本文将介绍麦克斯韦方程组的建立过程。
二、电场和磁场的概念在介绍麦克斯韦方程组之前，我们需要先了解电场和磁场的概念。
1. 电场电场是指空间中存在着电荷所产生的力场。
当一个点电荷Q在空间中时，它会对周围空间产生一个力场E，该力场是由这个点电荷对周围空间中任何一个点带来的作用力所构成。
2. 磁场磁场是指空间中存在着磁体所产生的力场。
当一个带有电流I的导体在空间中时，它会对周围空间产生一个力场B，该力场是由这个导体对周围空间中任何一个点带来的作用力所构成。
三、法拉第定律和安培定律法拉第定律和安培定律是麦克斯韦方程组的基础。
1. 法拉第定律法拉第定律是描述电磁感应现象的基本定律。
当一个导体内部有磁通量变化时，它会在导体内部产生感应电动势。
该定律的数学表达式为：ε=-dΦ/dt，其中ε表示感应电动势，Φ表示磁通量，t表示时间。
2. 安培定律安培定律是描述电流和磁场之间相互作用的基本定律。
当一个导体内部有电流I时，它会在周围空间产生一个磁场B。
该定律的数学表达式为：B=μ0(I/2πr)，其中B表示磁场强度，μ0表示真空中的磁导率，r 表示距离。
四、麦克斯韦方程组的建立麦克斯韦方程组是由四个方程组成的。
这四个方程分别是高斯定理、法拉第定律、安培环路定理和法拉第旋转电场定理。
1. 高斯定理高斯定理描述了电荷与电场之间的关系。
该定理表明：对于任意一个闭合曲面S，通过该曲面的电场通量等于该曲面内部的电荷量除以真空中的介电常数。
数学表达式为：∮E·dS=Q/ε0，其中E表示电场强度，S表示曲面，Q表示该曲面内部的电荷量，ε0表示真空中的介电常数。
2. 法拉第定律法拉第定律描述了磁通量与感应电动势之间的关系。
该定律表明：当一个导体内部有磁通量变化时，它会在导体内部产生感应电动势。
经典电磁场理论的建立和发展及其重要意义
经典电磁场理论的建立和发展及其重要意义电子13班肖青秀2110501112电磁场理论的产生是物理学史上划时代的里程碑之一，电磁场理论体系的核心是麦克斯韦方程组，麦克斯韦全面总结电磁学研究的全部成果，建立完整的电磁场理论体系，完成物理学的又一次大综合，他的理论成果为现代无线电电子工业奠定理论基础。
1 经典电磁场理论体系完整的电磁场理论包括：1）麦克斯韦方程组：它是在库仑定律、毕奥-萨法尔定律、法拉第电磁感应定律以及麦克斯韦提出位移电流假说的基础上建立起来的。
它反映了电磁场的运动规律。
变化的电场和磁场可以互相激发而在空间独立存在。
由此，麦克斯韦预言了电磁波的存在，并预言了光是一种电磁波。
不随时间变化，则为静态场。
若电磁场的若电磁场很慢，则为拟稳场，说明市电在小尺度上可以用直流电路的计算方法。
麦克斯韦方程组的建立是物理系史上的第三次大综合。
2）洛伦兹力密度公式：它反映了电荷、电流受到的电磁场的作用力。
3）电荷守恒定律：它反映了自然界中关于电荷守恒的一个基本规律。
4）介质的电磁性质方程：它反映了物质在电磁场的作用下的性质，还反映了介质的结构。
以上四点构成了完整的电磁场理论。
经典电磁场理论体系的核心是麦克斯韦方程组。
在方程组中，电场和磁场相互联系、相互激发组成一个统一的电磁场。
麦克斯韦方程组的积分形式：其中：1）式描述了电场的性质，即电场的高斯定理。
2）式描述了磁场的性质，即磁场的高斯定理。
3）式描述了变化的磁场激发感生电场的规律。
4）式描述了变化的电场激发磁场的规律。
此外，还要加上电磁场量和表征介质电磁特性的量之间的关系：麦克斯韦方程组概括了电磁场的基本性质和规律，构成完整的经典电磁场理论体系，它不仅是整个宏观电磁理论的基础，而且也是许多现代电磁技术的理论基础。
麦克斯韦的电磁理论充分体现了物理概念创新、逻辑体系严密、数学形式简单优美、电场与磁场以及时间与空间的明显对称等明显的特点。
2 经典电磁场理论建立的过程以麦克斯韦方程组为核心的经典电磁理论，是由伟大的英国科学家麦克斯韦提出的，但在该理论建立的过程中凝结着无数各国科学工作者的科研成果，探究经典电磁场理论建立的过程及指导思想对科学探索研究仍然具有重要作用。
麦克斯韦方程组 本构
麦克斯韦方程组本构
麦克斯韦方程组是描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程，由英国物理学家詹姆斯·克拉克·麦克斯韦在19世纪建立。
它由四个方程组成：描述电荷如何产生电场的高斯定律、论述磁单极子不存在的高斯磁定律、描述电流和时变电场怎样产生磁场的麦克斯韦-安培定律、描述时变磁场如何产生电场的法拉第感应定律。
麦克斯韦方程组和洛伦兹力方程是经典电磁学的基础方程。
而本构关系主要涉及物质的本构参数，如弹性模量、泊松比等，这些参数决定了物质在受力后如何发生形变。
对于电磁场问题，需要用到电磁本构关系，如介电常数、磁导率、电导率等参数。
这些本构参数可以反映物质在电磁场作用下的行为特性。
麦克斯韦方程组和本构关系在各自领域中都有广泛的应用，是解决各种工程和科学问题的重要工具。
如需了解更多信息，建议查阅相关资料或咨询专业人士。
电磁感应的发展历程电磁感应的重要里程碑
电磁感应的发展历程电磁感应的重要里程碑电磁感应的发展历程：电磁感应的重要里程碑电磁感应是指当磁场变化时，产生感应电动势的现象。
它是电磁学的一个重要分支，对于现代科技和社会的发展起到了至关重要的作用。
本文将围绕电磁感应的发展历程，介绍几个重要里程碑。
1. 法拉第发现电磁感应电磁感应的历史可以追溯到19世纪初，当时英国科学家迈克尔·法拉第进行了一系列的实验。
1831年，他发现当一个导体线圈在磁场中移动时，会产生电流。
这一重大发现被称为法拉第电磁感应现象，为电磁感应的研究奠定了基础。
2. 麦克斯韦方程组的建立19世纪中期，苏格兰物理学家詹姆斯·克拉克·麦克斯韦提出了麦克斯韦方程组，系统地描述了电磁现象的规律。
麦克斯韦方程组归纳了电场和磁场之间的关系，对电磁感应的研究起到了重要的推动作用。
3. 电磁感应在发电中的应用电磁感应的重要意义之一就是其在发电领域的应用。
1873年，法国物理学家迪伦发明了第一个有效的发电机。
他利用电磁感应的原理，将导体线圈通过磁场转动，从而产生了稳定的电流。
这一发明大大促进了电力工业的发展，丰富了人们的能源选择。
4. 电磁感应推动电磁波的研究电磁感应与电磁波之间的关系也是电磁学发展的里程碑之一。
19世纪末，德国物理学家海因里希·赫兹通过实验证明了电磁波的存在和传播。
他使用了电磁感应的原理，通过产生和接收电磁波，验证了麦克斯韦方程组中的预言。
这一研究成果奠定了无线通信和无线电广播的基础。
5. 磁动势定律的提出磁动势定律是电磁感应的重要理论基础之一。
1873年，法国物理学家亨利·阿伦发现了磁动势定律。
他的实验表明，闭合线圈中的电动势与磁场中磁通量变化的速率成正比。
磁动势定律为电磁感应现象提供了定量描述的方法，促进了该领域的深入研究。
6. 可变磁通量的应用可变磁通量是一项重要的电磁感应应用技术。
通过改变线圈中磁场的强度或方向，可以控制感应电动势的大小和方向。
麦克斯韦方程组建立的逻辑过程
麦克斯韦方程组建立的逻辑过程李 翔,陈燕黎(信阳职业技术学院,河南信阳464000)摘 要:用逻辑学的观点分析和总结了麦克斯韦方程组建立的逻辑推理过程,即归纳推理确立电磁感应的本质,类比推理引入位移电流假说,假言推理预言电磁波的存在。
说明逻辑学是自然科学的形成和发展所必不可少的工具。
关键词:逻辑推理;麦克斯韦方程组;建立中图分类号: 文献标识码:A 文章编号:1008-4916(2005)03-0105-02The logical process ofM axwell equation suit .s foundationLI X iang ,C H E N Yan-li(X i nyang Vocati onal and Techn i ca lCo ll ege ,X i nyang 464000,Ch i na)A bstract :T h i s article ana l yzed and su mm arized t he l og ic i n ference process ofM axw e ll equa ti on su it .s foundation .T hat is epagoge establi shed t he nature o f e lectro m agnetis m reaction ,analog i s m i m ported the hypothesis of displace m ent e lectr i c cu rrent ,hypothesi s i nference pred i cted the ex istence of e lectro m agne tic ware ,fro m a ll of t he above ,i t i s true t hat log i cis an i ndispensable t oo l of the for m and deve l op m en t of natura l sc i ence .K ey words :log i c i n f e rence ;M axw e ll equa ti on suits ;establi sh麦克斯韦方程组的建立使宏观的电磁理论达到了十分完善的地步,它确立了电荷、电流与电场、磁场之间的普遍联系,揭示了电磁场的基本属性,并预示了电磁波的存在,建立了光的电磁理论,从而把光现象同电磁现象统一起来。
电磁理论麦克斯韦方程组的建立与静电力常量的确定
电磁理论麦克斯方程组的建立与静电力常量的确定静电力常量的数值究竟是谁给出的？人教版高中物理选修3-1讲到，在库仑那个年代，无法精确测量物体的电荷量，甚至连电荷量的单位都没有。
课本上接着讲了利用相同金属球分电荷的方法。
下面还有一个注释说，库仑最初的实验是用带电木髓球进行的，并非金属球。
库仑定律那个表达式，是库仑作为假设提出的。
库仑定律表达式中的比例系数的数值和量纲取决于库仑定律表达式中其他物理量的单位。
静电单位制中，比例系数就是个无量纲数1，无需测量。
具体请看任何一本电磁学书里关于电磁学单位制的介绍。
这里主要谈谈国际单位制中的静电力常量。
国际单位制是二十世纪才制定出的，所以静电力常量的数值肯定不是库仑给出的。
那么这个数值的给出者究竟是谁呢？史料中似乎难以寻觅，说明此人很低调。
让我们回顾一下麦克斯韦方程组，看看那个常量究竟是怎么回事，还有就是，它的数值究竟是怎么给出的。
在麦克斯韦建立起以他的名字命名的方程组以前，人们对电磁现象已经有了较好的认识。
对于稳恒情形，人们已经认识到所谓库仑定律和毕奥-萨伐尔定律；非稳恒情形时，则有所谓法拉第电磁感应定律。
库仑定律指出，静电情形时，F=kq1q2／r^2，k为比例系数。
引入电场强度E后，由库仑定律，得到一个微分关系式，▽•E =4πkρ，其中ρ是电荷密度。
▽•E表示E的散度。
上述微分方程中的4π是怎么出来的，请参阅任何一本电动力学或者数学物理方法书籍。
为了使微分方程的形式显得简洁一些，人们令4πk=1／ε0，即k=1／（4πε0）。
显然，如果给出ε0，k也就随之确定了。
这样上述微分方程就成为，▽•E=ρ／ε0稳恒情形下，关于磁感应强度B的毕奥-萨伐尔定律中，也有一个比例系数k’。
出于同样的考虑，令k’=μ0／﹙4π﹚。
注意，μ0在分母上。
把比例系数k，k’写成那样的形式，只是为了使后面的微分方程及相应结论具有简洁的形式，没有什么更特别的原因。
这样，毕奥-萨伐尔定律就写成其中I是电流强度，r是位矢，戴尖帽子的那个r，表示位矢对应的单位矢量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本科毕业论文题目：关于麦克斯韦方程组的建立目录1.引言 (1)2.麦克斯韦电磁场理论的建立 (1)3.麦克斯韦方程组 (2)3.1涡旋电场假说，位移电流假说 (2)3.2麦克斯韦方程组的简易推导 (3)3.3麦克斯韦方程组的微分形式 (5)4.建立麦克斯韦方程组的其他途径 (6)4.1根据能量原理和近距作用原理建立麦克斯韦方程组 (6)4.2根据库仑定律和洛论磁力变换建立麦克斯韦方程组 (11)5.麦克斯韦方程组的物理意义 (15)6.结束语 (15)7.参考文献 (16)8.致谢............................................. 错误!未定义书签。
关于麦克斯韦方程组的建立摘要：本文中阐述麦克斯韦电磁场理论的历史发展及运用涡旋电场和位移电流的概念，推导出麦克斯韦方程组的基本形式，并麦克斯韦方程组较深刻的进行讨论，推导出符合在任意时变电磁场的麦克斯韦方程组。
关键词：麦克斯韦方程组；电磁场；涡旋电场；位移电流1.引言麦克斯韦电磁场理论是十九世纪物理学中最伟大的成就之一，是继牛顿力学之后物理学史上又一次划时代的伟大贡献。
麦克斯韦全面总结了电磁学研究的成果。
并在此基础上提出了“涡旋电场”和“位移电流”的假说，建立了完整的电磁理论体系，不仅科学地预言了电磁波的存在。
而且揭示了光、电、磁现象的内在联系及统一性，完成了物理学的又一次大综合。
他的理论成果为现代无线电电子工业奠定了理论基础，麦克斯韦方程组不仅揭示了电磁场的运动规律。
更揭示了电磁场可以独立于电荷之外单独存在，这样就加深了我们对电磁场物质性的认识。
2.麦克斯韦电磁场理论的建立麦克斯韦首先从论述力线着手，初步建立起电与磁之间的数学关系。
1855年，他发表了第一篇电磁学论文《论法拉第的力线》。
在这篇论文中，用数学语言表述了法拉第的电紧张态和力线概念，引进了感生电场概念，推导出了感生电场与变化磁场的关系。
1862年他发表了第二篇论文《论物理力线》，不但进一步发展了法拉第的思想，扩充到磁场变化产生电场，而且得到了新的结果：电场变化产生磁场。
由此预言了电磁波的存在，并证明了这种波的速度等于光速，揭示了光的电磁本质。
这篇文章包括了麦克斯韦电磁理论研究的主要成果。
1864年他的第三篇论文《磁场的动力学理》，从几个基本实验事实出发，运用场论的观点，引进了位移电流概念，按照电磁学的基本原理(高斯定理、电荷守恒定律)推导出全电流定理，最后建立起电磁场的基本方程。
麦克斯韦在总结库仑、高斯、欧姆、安培、毕奥、萨伐尔、法拉第等前人的一系列发现和实验成果的基础上。
结合自己提出的涡旋电场和位移电流的概念，建立了第一个完整的电磁理论体系。
这个重要的研究结果以论文的形式发表在1865年的英国皇家学会的会报上。
论文中列出了最初形式的方程组，由20个等式和20个变量组成，包括麦克斯韦方程组的分量形式。
3.麦克斯韦方程组3.1涡旋电场假说，位移电流假说一个闭合回路固定在变化的磁场中，则穿过闭合回路的磁通量就要发生变化。
根据法拉第电磁感应定律，闭合回路中要产生感应电动势。
因而在闭合回路中，必定存在一种非静电性电场。
麦克斯韦对这种情况的电磁感应现象作出如下假设：任何变化的磁场在它周围空间里都要产生一种非静电性的电场，叫做感生电场，感生电场的场强用符号E 表示。
感生电场与静电场有相同处也有不同处。
它们相同处就是对场中的电荷都施以力的作用。
而不同处是：（1） 激发的原因不同，静电场是由静电荷激发的，而感生电场则是由变化磁场所激发：（2）静电场的电场线起源于正电荷，终止于负电荷，静电场是势场，而感生电场的电场线则是闭合的，其方向与变化涡旋电场的存在，才在闭合回路中产生感生电动势，其大小等于把单位正电荷沿任意闭合回路移动一周时，感生电场i E 所作的功，表示为：m i l d E Edl dt Φ=-=⎰ 式(3-1)应当指出：法拉第建立的电磁感应定律，只适用于由导体构成的回路，而根据麦克斯韦关于感生电场的假设，电磁感应定律有更深刻的意义，即不管有无导体构成闭合回路，也不管回路是在真空中还是在介质中，式(1)都是适用的。
如果有闭合的导体回路放人该感生电场中，感生电场就迫使导体中自由电荷作宏观运动，从而显示出感生电流；如果导体回路不存在，只不过没有感生电流而已，但感生电场还是存在的。
从式(3-1)还可看出：感生电场i E 的环流一般不为零，所以感生电场是涡旋场(又叫涡旋电场)。
位移电流概念是麦克斯韦在建立电磁场理论过程中提出的重要假设。
它表明，磁砀不仅可以由电流产生，变化的电场也可以产生磁场。
位移电流和有旋电场的概念从两个方面深刻而完整地揭示了电场和磁场之间的内在联系和相互依存，即电磁场是统一的不可分割的整体。
传导电流和位移电流都能产生磁场，两种磁场都能对其中的电流或运动电荷施加磁力，两种磁场的性质也相同，即都是有旋无源的。
但是，两种磁场也有区别，除了产生原因不同外，由于位移电流(确切地说是位移电流中由电场变化引起的真空位移电流部分)并不表示电荷在空间的运动，所以它与传导电流不同，没有热效应和化学效应，只有磁效应。
空间的总磁场是传导电流和位移电流产生的磁场之和，是无源有旋的矢量场，其磁力线闭合。
位移电流假设的提出，消除了把安培环路定理从恒定情形推广到变化情形时遇到的矛盾和困难，使麦克斯韦得以建立完备的电磁场方程组。
麦克斯韦方程组关于电磁波等理论预言实验的证实，不仅具有深刻的理论意义和巨大的应用价值，也证明了位移电流假设的正确性。
3.2麦克斯韦方程组的简易推导⑴. 麦克斯韦方程组的积分形式在电磁学中我们知道，一个点电荷q 发出的电通量总是正比于q ，与附近有没有其他电荷存在无关。
由库仑定律可以推出关于电通量的高斯定理： 0s q E dS ε=⎰⎰ 式(3-2)因静电场的电场线分布没有旋涡状结构，因而可推导静电场是无旋的。
1831年法拉第发现当磁场发生变化时，附近闭合线圈中的感应电动势与通过该线圈内部的磁通量变化率成正比，可表示为：S dB dS dt ε=-⎰⎰ 式(3-3)感应电动势是电场强度沿闭合回路的线积分，因此电磁应定律可写为：l S d dl B dS dt E =-⎰⎰⎰ 式(3-4)若回路L 是空间中的一条固定回路，则式(3-4)中对t 的全微分可代为偏微分：l B dl s dS dt∂E =-⎰⎰⎰ 式(3-5) 下面研究电流和磁场的相互作用。
实验指出，一个电流元 dl I 在磁场中所受的力可以表为：dF Idl B =⨯ 式(3-6)恒定电流激发磁场的规律由毕奥一萨伐尔定律给出。
设(')J x 为源点'x 上的电流密度，r 为'x 由到场点x 的距离，则场点上的磁感应强度为： 03(')()'4J x r B x dv r μπ⨯=⎰ 式(3-7) 式（3-7）中0μ为真空磁导率，积分遍及电流分布区域。
细导线上恒定电流激发磁场的毕奥一萨伐尔定律写为：3()4Idl r B x rμπ⨯=⎰ 式(3-8) 根据安培环路定律，对于连续电流分布j ，在计算磁场沿回路L 的环量时，只需考虑通过以L 为边界的曲面的电流，在S 以外流过的电流没有贡献。
因此，环路定律表为：0L s B dl j dS μ=⎰⎰⎰ 式(3-9) 上面研究了变化磁场激发电场，由麦克斯韦位移电流假设的结论变化电场激发磁场可推广得： 00()L s E B dl j dS tμε∂=+∂⎰⎰⎰ 式(3-10) 由电磁学的知识，我们知道由电流激发的磁感应线总是闭和曲线，因此，磁感应强度B 是无源场，表示B 无源性的积分形式是B 对任何闭和曲面的总通量为零，即利用磁场高斯定理得：0s B dS =⎰⎰ 式(3-11)由上得出麦克斯韦方程组的积分形式：0000()s l s s L s q dS B dl dS dt B dS E B dl j dS t εμεE =∂E =-=∂=+∂⎰⎰⎰⎰⎰⎰⎰⎰⎰ 式(3-12) 3.3麦克斯韦方程组的微分形式由麦克斯韦方程组的积分形式和数学公式：0()()s V L V A dS A dVA dl A dS ==∇=∇⨯⎰⎰⎰⎰⎰ 式(3-13)推导出微分形式如下： 00000E B E t B EB j t ρεμμε∇=∂∇⨯=-∂∇=∂∇⨯=+∂ 式(3-14)值得注意的是，在使用积分形式时，当有介质时需要补充三个描述介质性质的方程式，对于各向同性介质来说，有：00r r D EB H j Eεεμμσ=== 式(3-15)式（3-15） 中 r ε、r μ和σ分别是介质的相对介电常数，相对磁导率和电导率 j E σ=是欧姆定律的微分形式。
4.建立麦克斯韦方程组的其他途径在本文前面，已经详尽的介绍了麦克斯韦建立的电磁场方程组的历史过程。
在麦克斯韦之后，有些物理学家着手研究从别的途径建立麦克斯韦方程组的可能性。
他们所取得的成果，揭示了有关基本物理规律之间的深刻内在联系，同时也有利于加深对麦克斯韦方程组的理解。
下面讨论建立麦克斯韦方程组的另外两种方法。
它们是：⑴根据能量原理和近距作用原理建立麦克斯韦方程组；⑵根据库伦定律和洛仑兹变换建立麦克斯韦方程组；这两种建立麦克斯韦方程组的方法虽然并未揭示新的关系，而且推演较为复杂，但是，通过有关的讨论，可以使我们对麦克斯韦方程组与能源、近距作用原理、相对论的洛仑兹变换等基本物理规律之间的深刻内在联系和相互制约关系有具体的了解，这是大有好处的。
4.1 根据能量原理和近距作用原理建立麦克斯韦方程组能量守恒原理是自然界普遍遵循的一条基本原理。
通常在电动力学中，根据麦克斯韦方程组和洛仑兹力公式，可以推导出电磁场的能量密度和能流密度的具体表达式，从而说明电磁现象也同样遵从能量守恒原理。
然而，也可以从近距作用原理出发，认为电磁场本身具有能量和能流，进而根据能量原理建立麦克斯韦方程组。
由于试验电荷所受的电场力还与试验电荷的电量有关，因此，要确定电场强度的大小还需要作进一步的规定。
与通常规定试验电荷具有单位电量（正电荷）的办法不同，我们可以根据电场具有一定的能量来确定电场强度的大小。
由于电场对置于其中的电荷有作用力，能够使电荷运动，根据近距作用原理，电荷运动获得的能量必定来自电场，这也就说明电场具有一定的能量。
单位体积内的电场能量叫做电能密度，表示为e w。
显然，当电场为零时，电能密度应为零；另外，电能密度应该总是正的。
于是，我们可以把电能密度e w和与之相关的电场强度的大小E联系起来，用前者来定义后者，规定两者的关系即电能密度的表示式为：212e w E ε= 式(4-1) 式中E 是电场强度的大小，ε为比例系数，ε的数值取决于空间介质的性质以及测量单位的选择。