2018-2019学年度辽宁省沈阳市东北育才高三年级第五次模拟考试试卷与答案
2018-2019学年度辽宁省沈阳市东北育才高三年级第五次模拟考试试卷与答案

{正文}2018-2019学年度辽宁省沈阳市东北育才高三年级第五次模拟考试英语试卷第一部分听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Which ball game does Jack play best?A.Volleyball.B.Ping-pong.C.Tennis.2.How long did the game last?A.About two hours.B.About two hours and a half.C.About three hours.3.What does the woman mean?A.She likes doing morning exercises.B.She can’t get up early.C.She dislikes doing such exercises.4.H ow are Tom’s skills?A.Excellent.B.Just so-so.C.Very bad.5.What do you know about the woman?A.She likes volleyball.B.She doesn’t like basketball.C.She likes sports, too.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6.What kind of books is Mr. Black’s mother interested in?A.Romantic love stories.B.Funny stories.C.Books about Roman history.7.How old is Mr. Black’s mother?A.90.B.91.C.89.8.How long can one keep the books before he has to renew it?A.One month.B.Half a month.C.One week.听第7段材料,回答第9至11题。
【高三物理试题精选】2018届高三理综第五次模拟考试卷(东北育才学校含答案和解释)

2018届高三理综第五次模拟考试卷(东北育才学校含答案
和解释)
)n(Al3+)=72时,
2Al3+ + 7OH-=Al(OH)3↓+ AlO2- + 2H2O
B.CuCl2溶液与NaHS溶液反应,当n(CuCl2)n(NaHS)=12时
Cu2++2HS-=CuS↓+H2S↑
C.Cl2与FeBr2溶液反应,当n(Cl2)n(FeBr2)=11时,2Fe2+ + 4Br- +3Cl2=2 Fe3+ + 2Br2 + 6Cl-
D.Fe与稀硝酸反应,当n(Fe)n(HNO3)=12时,
3 Fe +2NO3- +8H+=3Fe2+ +2NO↑+4H2O
9 下列装置应用于实验室制NO并回收硝酸铜的实验,能达到实验目的是()
A. B.
用装置制取NO 用装置收集NO
C. D.
用装置分离炭粉和硝酸铜溶液用装置蒸干硝酸铜溶液制Cu(NO3)2 3H2O
10.短周期元素W、X、Y和Z的原子序数依次增大。
元素W是形成化合物数量众多,且分布极广的元素,X原子的最外层电子数是其电子层数的3倍,元素Y是地壳中含量最丰富的金属元素,Z元素的单质易溶于WZ2中。
下列说法错误的是()
A.元素X、Y与Z的原子半径大小Y Z X
B.元素W、Z的氯化物中,化学键类型相同,且各原子均满足8电子
C.元素X与元素Y形成的化合物是一种较好的耐火材料
D.元素X可与元素Z可组成3种二价阴离子
11.下列项目判断,结论正确的是。
辽宁省沈阳市东北育才学校2019届高三第五次模拟语文试题(解析版)

2018—2019学年度高三年级第五次模拟考试语文科试卷阅读下面的文字,完成各题。
日本、印度茶业虽然在制度的构建主体、组织形式等方面呈现出不同,但有着根本的共同之处,即实现全体茶业参与者的利益均衡而非仅仅一部分茶业参与者的既得利益,构建有利于整个茶业发展的有效秩序,即他们的整个社会能够建立一个完整有效的生产、销售、组织制度体系,这是其成功的关键。
反观中国情形,正如1891年湖北盐茶牙厘局针对华茶为何衰落进行的调查所指出的那样:华茶在生产、收集以及加工过程中,都普遍存在着资金短缺的问题,而资金短缺的部分原因是体制的松散结构。
这种结构不仅导致了产品质量的下降,而且还由于茶叶运抵汉口出售之前要换好几手,层层加码使其价格抬升,其标价就比其竞争对手高得多。
总之,数百年来在国内贸易中运行得很好的由收集代理人与中间人组成的精致的网络,一旦面对新的体制外竞争形势,却被证明是笨拙的、无能为力的了。
为什么中国不能构建印度、日本等国有效的茶业制度呢?在近代中国,特别是在晚清和北洋政府时期,政府干预经济的能力相当弱,也不可能为市场的运作提供具体的规则,同时由于单个企业力量是有限的,那么市场交易规则的构建主体由谁来承担?杜恂诚教授认为:“商会和同业公会责无旁贷地肩负起市场操作层面的创建和完善制度秩序的责任。
”如果我们将问题的视角放大到中外贸易领域,市场制度的构建不仅需要商会和同业公会肩负其责,而且我们也不能忽略洋商的作用。
问题在于,他们构建的制度对利益各方有着怎样的“好处”,以及对经济有着怎样的效果,更值得我们关注。
在中国近代,对外贸易方面和其他行业,国家被排除在制定规范各方之制度的权威之外。
中国茶叶对外贸易情况就是如此。
19世纪70年代后,中国茶业垄断货源、主导国际市场茶叶价格的优势不复存在,加之贸易不能直营,故在争夺茶叶贸易主导权方面,洋行、买办与茶栈三者之间进行了相互博弈,在此过程中,中国原有的贸易网络与洋行进行了自然的结合。
辽宁省沈阳市东北育才学校2019届高三第五次模拟数学(理)试题 Word版含答案
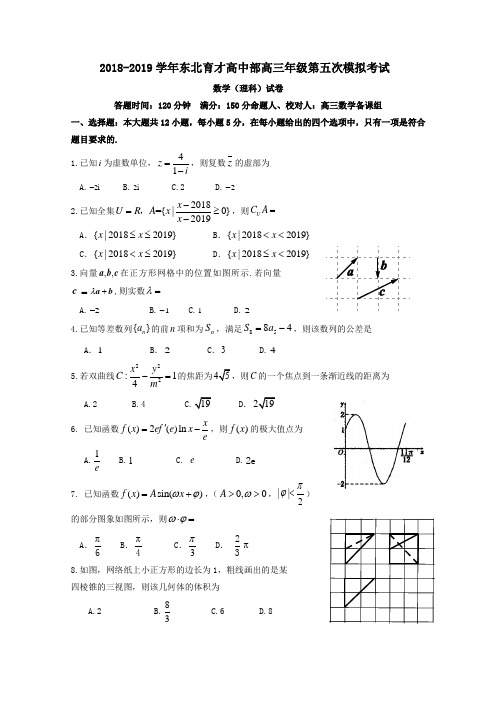
2018-2019学年东北育才高中部高三年级第五次模拟考试数学(理科)试卷答题时间:120分钟 满分:150分命题人、校对人:高三数学备课组一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,41z i=-,则复数z 的虚部为 A.2i - B.2i C.2 D.2- 2.已知全集2018={|0}2019x U R A x x -=≥-,,则U C A =A .{|20182019}x x ≤≤B .{|20182019}x x <<C .{|20182019}x x <≤D .{|20182019}x x ≤<3.向量,,a b c 在正方形网格中的位置如图所示.若向量c =λ+a b ,则实数=λA.2-B.1-C.1D.24.已知等差数列{}n a 的前n 项和为n S ,满足8584S a =-,则该数列的公差是 A .1B .2C .3D.45.若双曲线222:14x y C m-=的焦距为C 的一个焦点到一条渐近线的距离为.6. 已知函数()2()ln xf x ef e x e'=-,则()f x 的极大值点为 A.1eB.1C. eD.2e 7. 已知函数()sin()=+f x A x ωϕ,(0,0>>A ω,||2<πϕ) 的部分图象如图所示,则⋅=ωϕA .6π B .4π C .3πD . 23π 8.如图,网络纸上小正方形的边长为1,粗线画出的是某 四棱锥的三视图,则该几何体的体积为A.2B.83C.6D.89.某地区高考改革,实行“321++”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有 A.8种 B.12种 C.16种 D .20种 10.在右图算法框图中,若dx x a ⎰-=3)12(,程序运行的结果S 为二项式5)2(x +的展开式中3x 的系数 的9倍,那么判断框中应填入的关于k 的判断条件是 A.3k < B .3>kC .2<kD .2>k11.将半径为3,圆心角为23π的扇形围成一个圆锥,则该圆锥的内切球的表面积为 A.πB.2πC.3πD.4π12.已知函数()()133()log 2log 4=--+f x x x ,如下命题:①函数()f x 的定义域是[]4,2-; ②函数(1)f x -是偶函数; ③函数()f x 在区间[)1,2-上是减函数;④函数()f x 的值域为(,2]-∞-. 其中正确命题的个数是A.4B. 3C. 2D. 1 二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若实数,x y 满足约束条件41014x y y x y --≥⎧⎪≥⎨⎪+≤⎩则yz x =的最小值是________.14.如图所示,半径为1的圆O 是正方形MNPQ 的内切圆,将一颗豆子随机地扔到正方形MNPQ 内,用A 表示事件“豆子落在圆O 内”, B 表示事件“ 豆子落在扇形OEF (阴影部分)内”,则(|)=P B A . 15.设n S 是等比数列{}n a 的前n 项和,若51013S S =,则52010S S S += . 16.抛物线22y px =的焦点为F ,设1222(,),(,)A x y B x y是抛物线上的两个动点,若12||3x x p AB ++=,则AFB ∠的最大值为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本题满分12分)在ABC ∆中,角C B A 、、的对边分别为c b a 、、,且03sin 2sin 322=-+A A. (Ⅰ)求角A 的大小; (Ⅱ)若ABC ∆面积为3,且外接圆半径3=R ,求ABC ∆的周长.18. (本题满分12分)2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在[2585],之间,根据统计结果,做出频率分布直方图如下: (Ⅰ)求这100位作者年龄的样本平均数x 和样本方差2s (同一组数据用该区间的中点值 作代表);(Ⅱ)由频率分布直方图可以认为,作者年龄X 服从正态分布2(,)N μσ,其中μ近似为样本平均数x ,2σ近似为样本方差2s .(i )利用该正态分布,求(6073.4)P X <<;(ii )央视媒体平台从年龄在[4555],和[6575],的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间[4555],的人数是Y ,求变量Y 的分布列和数学期望.附:4.13180≈,若2~(,)X N μσ,则()0.683P X μσμσ-<<+=,(22)0.954P X μσμσ-<<+=19.(本小题满分12分)已知椭圆C :22221(0)x y a b a b +=>>的左、右焦点分别为12,F F ,离心率为2,直线l :2y x =与椭圆交于,M N ,四边形12MF NF的面积为3. (Ⅰ)求C 的方程;(Ⅱ)作与l 平行的直线与椭圆交于,A B 两点,且线段AB 的中点为P ,若12,PF PF 的斜率分别为12,k k ,求12k k +的取值范围.20.(本小题满分12分)如图,四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 是平行四边形,45ABC ∠=︒,2AD AP ==,AB DP ==,E 是CD 中点,点F 在线段PB 上.(Ⅰ)证明:AD PC ⊥;(Ⅱ)若PF uu u r=,PB λuu r [0,1]λ∈,求实数λ使直线EF 与平面PDC 所成角和直线EF 与平面ABCD 所成角相等.21.(本小题满分12分)已知函数()ln ,f x x ax a a R =-+∈. (Ⅰ)讨论()f x 的单调性; (Ⅱ)若21()()(1)2g x f x x =+-有三个不同的零点,求a 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程(本小题满分10分)已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的非负半轴重合.若曲线C的极坐标方程为6cos 2sin =+ρθθ,直线l的参数方程为12⎧=-⎪⎨=⎪⎩x y (t 为参数).(Ⅰ)求曲线C 的直角坐标方程与直线l 的普通方程;(Ⅱ)设点(1,2)Q ,直线l 与曲线C 交于、A B 两点,求|QA |·|QB |的值.23.选修4-5:不等式选讲(本小题满分10分) 已知函数()|1||2|f x x x =-++. (Ⅰ)求不等式()13f x <的解集;(Ⅱ)若()f x 的最小值为k ,且211(0)k mn m n+=>,证明:16m n +≥.2018-2019学年东北育才高中部高三年级第五次模拟考试 数学(理科)答案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.D2.C3.D4.A5.B6.D7.C8.A9.C 10.A 11.B 12.D 二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 13 14. 14 15. 11816. 2π3三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(Ⅰ)解:Q 03sin 2sin 322=-+A A∴03sin 2cos 132=-+-⨯A A,即0cos 3sin =-A A …………2分 3tan =∴A…………4分又π<<A 03π=∴A …………6分 (Ⅱ) Q 2sin a R A =…………7分33sin 32sin 2===∴πA R a…………8分 Q ABC ∆面积为33sin 21=∴A bc 得4=bc …………9分∵a 2=b 2+c 2﹣2bccosA , ∴b 2+c 2﹣bc=9, …………10分 ∴(b+c )2=9+3cb=9+12=21,∴b+c=21 ………11分∴周长a+b+c=3+21. …………12分18.(Ⅰ)这100位作者年龄的样本平均数x 和样本方差2s 分别为 300.05400.1500.15600.35700.2800.1560x =⨯+⨯+⨯+⨯+⨯+⨯=…2分222222(30)0.05(20)0.1(10)0.1500.35100.2200.15180s =-⨯+-⨯+-⨯⨯+⨯+⨯+⨯=…4分 (Ⅱ)(i )由(1)知,)18060(~,N X ,从而1(6073.4)(6013.46013.4)0.34152P X P X <<=-<<+=; …7分(ii )根据分层抽样的原理,可知这7人中年龄在[4555],内有3人,在[6575],内有4人,故Y 可能的取值为0,1,2,3 354)0(373403===C C C Y P ,3518)1(372413===C C C Y P ,3512)2(371423===C C C Y P 351)3(370433===C C C Y P 所以Y 的分布列为…11分所以Y 的数学期望为4181219()0123353535357E Y =⨯+⨯+⨯+⨯= …12分 19.(Ⅰ)解:由222221y x x y a b=⎧⎪⎨+=⎪⎩可得2222244a b y a b =+ 2ce a ==,222212a b e a -==,a c b∴== ………2分 23c =33=1b a =⎧⎪⎨=⎪⎩2212x y += ………5分 (Ⅱ)设直线AB 的方程为2(0)y x m m =+≠由22212y x mx y =+⎧⎪⎨+=⎪⎩,得2298220x mx m ++-= 226436(22)0m m ∆=-->,得29m <,()()3,00,3m ∴∈- ………7分设112200(,),(,),(,)A x y B x y P x y ,则21212822,99m x x m x x -+=-=0004,299mx m y x m =-=+=200001222000281118116y y x y m k k x x x m +=+==+---288116m=-(0m ≠) ………10分 ()128,0,7k k ⎛⎫∴+∈-∞-+∞ ⎪⎝⎭………12分20. (Ⅰ)解:PAD △中222PA AD PD +=,∴90PAD ∠=︒∴AD PA ⊥; ………1分 连AC ,ABC △中2222cos 4AC AB BC AB BC ABC =+-⋅∠= ………2分 ∴222AC BC AB +=∴AC BC ⊥,∴AD AC ⊥ ………4分 又PAAC A =∴AD ⊥平面PAC ∴AD PC ⊥ ………5分(Ⅱ)由(1):P A A D⊥,又侧面PAD ⊥底面ABCD 于AD ,∴PD ⊥底面ABCD ,∴以A 为原点,DA 延长线、AC 、AP 分别为x 、y 、z 轴建系; ………6分∴(000)A ,,,(220)B ,,,(020)C ,,,(200)D -,,,(110)E -,,,(002)P ,, ∴(022)PC =-,,,(202)PD =--,,,(222)PB =-,,, ………7分 设PFPBλ=,([01]λ∈,),则(222)PF λλλ=-,, (2222)F λλλ-+,,,(212122),,=+--+EF λλλ ………8分设平面PCD 的一个法向量()m x y z =,,,则00m PC m PD ⎧⋅=⎪⎨⋅=⎪⎩,可得(111)m =--,,又平面ABCD 的一个法向量(001)n =,, ………10分由题:cos cos EF m EF n =,,,即223EFEFλ-=解得:λ ………12分 21. (Ⅰ) 解:由已知()f x 的定乂域为(0,)+∞,又1'()=-f x a x, 当0≤a 时,'()0>f x 恒成立; 当0a >时,令'()0>f x 得10<<x a ;令'()0<f x 得1>x a. 综上所述,当0≤a 时,()f x 在(0,)+∞上为增函数; 当0a >时,()f x 在1(0,)a 上为增函数,在1(,)+∞a上为减函数. ………4分 (Ⅱ)由题意21g()(1)ln ,(0)2=-+-+>x x x ax a x ,则1g'()1=+--x x a x, 当1a ≤时,∵g'()0≥x ,∴g()x 在(0,)+∞上为增函数,不符合题意. ………6分当1a >时,2(1)1g'()x a x x x-++=,令2()(1)1x x a x ϕ=-++,则2(1)4(3)(1)0a a a ∆=+-=+->. 令()0x ϕ=的两根分别为12,x x 且12x x <, 则∵121x x =,∴1201<<<x x当1(0,)x x ∈时,()0x ϕ>,'()0g x ∴>,∴g()x 在1(0,)x 上为增函数, 当12()x x x ∈,时,()0x ϕ<,'()0g x ∴<,∴g()x 在12(,)x x 上为减函数, 当2(,)x x ∈+∞时,()0x ϕ>,'()0g x ∴>,∴ g()x 在2(,)x +∞上为增函数, ∵(1)0g =,∴g()x 在12(,)x x 上只有一个零点 1,且12g()0,g()0x x >< ………8分1111()()()()222221()(1)ln 2a a a a g ee e ae a -+-+-+-+∴=-+-+111()())22222111(11)ln (1)()222a a a e ea e a a -+-+-+<-++=--++( 11()()221(2)02a a e e -+-+=-<, 1()201a e-+<<Q ,又当1[,1)x x ∈时,()0g x >,1()210a ex -+∴<<∴g()x 在1(0,)x 上必有一个零点. ………10分又21(22)(21)ln(22)(22)2g a a a a a a +=+++-++ 211(21)(22)022a a a >+-+=>221a +>Q ,又当2(1,)x x ∈时,()0g x <,222a x ∴+>∴g()x 在2(,)x +∞上必有一个零点.综上所述,故a 的取值范围为(1,)+∞ ………12分 23.(Ⅰ)由ρ=6cos θ+2sin θ,得ρ2=6ρcos θ+2ρsin θ, 所以x 2+y 2=6x +2y ,即曲线C 的直角坐标方程为x 2+y 2-6x -2y =0.由⎩⎨⎧x =1-2t y =2+2t,消去参数t , 得直线l 的普通方程为x +y -3=0. ………5分 (Ⅱ)由(Ⅰ)知直线l 的参数方程可化为⎩⎪⎨⎪⎧x =1-22t ′y =2+22t ′(t ′为参数), ………7分代入曲线C 的直角坐标方程x 2+y 2-6x -2y =0得t ′2+32t ′-5=0. ………9分由韦达定理,得t ′1t ′2=-5,则|QA |·|QB |=|t ′1t ′2|=5. ………10分 23.(Ⅰ)由()13f x <,得|1||2|13x x -++<,则12113x x >⎧⎨+<⎩或21313x -≤≤⎧⎨<⎩或22113x x <-⎧⎨--<⎩,解得:76x -<<,故不等式()13f x <的解集为(7,6)-. ………5分 (2)证明:因为()|1||2|f x x x =-++|1(2)|3x x ≥--+=, 所以3k =,因为21191(0)k mn m n m n+=+=>,所以0,0m n >>, 199()()(10)1016n m m n m n m n m n +=++=++≥+= 当且仅当9n mm n =,即4,12m n ==时取等号,故16m n +≥. ………10分。
辽宁省沈阳市东北育才学校2019届高三第五次模拟考试理综试题(Word版含答案)解析)

2018-2019学年度东北育才高中部第五次模拟考试理科综合科试卷1.本卷分第Ⅰ卷和第Ⅱ卷两部分。
满分300分,考试时间150分钟。
2.答题前考生务必用0.5毫米黑色墨水签字笔填写好自己的姓名、班级、考号等信息3.作答时,请将答案正确填写在答题卡上。
第一卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;第Ⅱ卷请用直径0.5毫米的黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效...........................。
4.以下数据可供解题时参考:有关元素的相对原子质量是:H :1 C:12 N:14 O:16 F:19 Na:23 Mg:24 S:32 Cl:35.5 K:39 Mn:55 Fe:56 Se: 79 Cu:64 I :127第Ⅰ卷一、选择题(本题包括13小题,每小题6分。
在每小题给出的四个选项中,只有一项符合题目要求) 1.美国加州大学戴维斯分校的教授Jason DeJong研究发现了一种被称为巴氏芽孢杆菌的细菌,这种细菌能使方解石(碳酸钙)沉积在沙砾周围,从而将它们胶合固定在一起。
研究人员还发现如果向松散液态的沙砾中注射培养的细菌、附加营养和氧气,这些松散液态的沙砾就能转化为固态。
固态的沙砾有助于稳固地球从而达到预防地震的目的。
下列有关巴氏芽孢杆菌的叙述,正确的是()A.巴氏芽孢杆菌有核膜B.巴氏芽孢杆菌的细胞呼吸类型为厌氧型C.巴氏芽孢杆菌的遗传信息储存在DNA中D.巴氏芽孢杆菌无细胞器,但能进行有氧呼吸2.图表示人体内干细胞的增殖分化。
下列有关叙述正确的是()A.干细胞与白细胞的基因型不同,但合成的mRNA和蛋白质的种类相同B.血小板和红细胞内遗传信息的流动方向是C .图示所有的细胞中,干细胞具有细胞周期,而且其分裂能力较强D .白细胞能够穿过血管壁去吞噬病菌,这是因为细胞膜的选择透过性3.果蝇是XY 型性别决定的二倍体生物。
【全国百强校】辽宁省沈阳市东北育才学校2019届高三第五次模拟数学(文)试题(原卷版)

2018-2019学年度东北育才高中部高三年级第五次模拟考试数学(文科)试卷一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,B=,则()A. B. C. D.2.若复数满足(i为虚数单位),则复数在复平面内对应的点位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.已知平面向量,且,则实数的值为()A. B. C. D.4.在等差数列中,为其前项和,若,则()A. 60B. 75C. 90D. 1055.若以为公比的等比数列满足,则数列的首项为()A. B. C. D.6.设点在不等式组表示的平面区域上,则的最小值为()A. B. C. D.7.若函数与存在相同的零点,则的值为()A. 4或B. 4或C. 5或D. 6或8.若将函数的图像向左平移个单位长度,则平移后图像的一个对称中心可以为()A. B. C. D.9.如图,是双曲线的左、右焦点,过的直线与双曲线交于两点,若,则双曲线的离心率为()A. B. C. D.10.如图,网格纸上小正方形的边长为,粗实线画出的是某几何体的三视图,则该几何体的表面积为()A. B.C. D.11.“”是“是函数的极小值点”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件12.已知函数,若正实数满,则的最小值是()A. 1B.C. 9D. 18二.填空题:本大题共4小题.13.若函数,则_________.14.某校为了解学生学习的情况,采用分层抽样的方法从高一人、高二人、高三人中,抽取人进行问卷调查.已知高一被抽取的人数为,那么高三被抽取的人数为_______.15.某互联网公司借助手机微信平台推广自己的产品,对今年前5个月的微信推广费用与利润额(单位:百万元)进于了初步统计,得到下列表格中的数据:经计算,月微信推广费用与月利润额满足线性回归方程,则的值为______.16.若点M是棱长为的正方体的内切球O的球面上的动点,点N为棱上的一点,且,,则动点M的轨迹的长度为______.三:解答题。
2019届辽宁省沈阳市东北育才学校高三第五次模拟理科综合试题 word版
2018-2019学年度东北育才高中部第五次模拟考试理科综合科试卷命题人、校对人:高三理综合备课组1.本卷分第Ⅰ卷和第Ⅱ卷两部分。
满分300分,考试时间150分钟。
2.答题前考生务必用0.5毫米黑色墨水签字笔填写好自己的姓名、班级、考号等信息。
3.作答时,请将答案正确填写在答题卡上。
第一卷每小题选出答案后,用2B铅笔把答题卡上对应题目答案标号涂黑;第Ⅱ卷请用直径0.5毫米的黑色墨水签字笔在答题卡上各题答题区域内作答,超出答题区域......书写的答案无效,在试题卷、草稿纸上作答无效.....................。
4.以下数据可供解题时参考:有关元素的相对原子质量是:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 K-39 Ca-40 Fe-56 Mn-55 Cu-64 Zn-65 Ag-108第Ⅰ卷一、选择题(本题包括13小题,每小题6分。
在每小题给出的四个选项中,只有一项符合题目要求)1.下图所示为来自同一人体的4种细胞,下列叙述正确的是()A.因为来自同一人体,所以各细胞中的DNA含量相同B.因为各细胞中携带的基因不同, 所以形态、功能不同C.虽然各细胞大小不同,但细胞中含量最多的化合物相同D.虽然各细胞的生理功能不同,但吸收葡萄糖的方式相同2.微小核糖核酸(miRNA),是科学家在真核生物中发现的一类内源性的具有调控功能的非编码RNA,不同的miRNA在个体发育的不同阶段产生,且miRNA能通过与靶mRNA结合或引起靶mRNA的降解进而影响基因的表达。
下列有关miRNA的叙述错误的是()A. miRNA的产生与细胞的分化无关B. miRNA在真核细胞中不能编码蛋白质C. miRNA通过碱基互补配对识别靶mRNAD. miRNA可影响基因的表达过程的翻译阶段3.下列相关实验中涉及“分离”的叙述正确的是()A.噬菌体侵染细菌的实验中,离心的目的是使噬菌体的DNA和蛋白质分离B.植物细胞质壁分离实验中,滴加蔗糖溶液的目的是使原生质层与细胞壁分离C.植物根尖细胞有丝分裂实验中,可以观察到姐妹染色单体彼此分离的过程D.观察DNA和RNA在细胞中分布实验中,盐酸可以使染色质中的RNA与蛋白质分离4.下图为二倍体雄性田鼠(2n=54)体内某细胞正常分裂时相关物质或结构数量变化曲线的一部分,下列分析不正确的是()A.若该图表示有丝分裂染色体组数目的变化,则a=2,且数量为2a时,同源染色体分离B.若该图表示有丝分裂染色体数目的变化,则a=54,且数量为2a时着丝点数目是108C.若该图表示减数分裂每条染色体上DNA分子数目的变化,则a=1,数量为2a时可以发生基因重组D.若该图表示减数分裂核DNA分子数目的变化,则数量为a时细胞内没有同源染色体5. 某雌雄同花植物花色有红色和白色两种,受一对等位基因控制。
辽宁沈阳东北育才中学2018-2019学年度上学期高中学段高三联合考试物理答案
2018—2019学年度上学期高中学段高三联合考试高三年级物理科答案一、选择题⒈B ⒉A ⒊C ⒋A ⒌B ⒍D ⒎D ⒏D ⒐ABD ⒑ACD ⒒AC ⒓AD二、实验题⒔⑴B (3分) ⑵m A x 0=m A x 1+m B x 2(3分)⒕⑴AB(3分) ⑵ 222d g s t(3分) ⑶减小挡光片宽度;增大开始时弹簧的压缩量等(3分) 三、计算题⒖(10分)【答案】⑴v m =40 m/s ⑵F =2 500 N ⑶W 2=5×104 J 解:⑴自由落体过程:212m gh v = ……………………………………………………(2分)得v m =40 m/s ……………………………………………………………………(1分)⑵减速下落过程中, 22220m a h v -=- ……………………………………………(1分) 解得a 2=40 m/s 2根据牛顿第二定律 F -mg =ma 2…………………………………………………(1分) 解得F =2 500 N …………………………………………………………………(1分) 根据牛顿第三定律,小明对系统作用力的大小F 为2 500 N …………………(1分) ⑶人:全过程,动能定理W+mg (h 1+h 2)=0………………………………………………………………(2分)解得W=-mg (h 1+h 2)=-5×104J ……………………………………………………(1分) ⒗(12分)【答案】⑴3 m/s ⑵2 150 N ⑶1.25 m解:⑴运动员离开平台后从A 至B 的过程中,在竖直方向有:22y v gh = ①………(1分)在B 点有:0tan 2y v v θ=②………………………………………………………(1分) 由①②得:v 0=3 m/s ③ …………………………………………………………(1分) ⑵运动员在圆弧轨道最低点时,由牛顿第二定律可得2v N mg m R-=④……………(1分) 由动能定理得22011(1cos )222mg h R mv mv θ⎡⎤+-=-⎢⎥⎣⎦⑤………………………………(2分) 取立③④⑤解得N =2 150 N .………………………………………………………(1分) ⑶运动员从A 至D 过程有201sin cos 0222mgh mgL mgL mv θθμ--=-⑥……………………………………(3分) 由③⑥解得:L =1.25 m ⑦……………………………………………………………(2分)⒘(15分)【答案】⑴ ⑵2l ⑶①174mgl ②()134mg l L +;max C v = 解:⑴设物块到达B 点的速度为v B ,对物块从A 到B 由动能定理得: ()2192B mg l mv μ= ①…………………………………………………(1分)解得B v = ②………………………………………………………(1分)所以物块一直加速,运动到B 点时的速度大小 B v =…………………(1分) ⑵对物块与滑板:物块滑动至与滑板共速过程,设共同速度为v ,由动量守恒有mv B =(M +m )v ③………………………………………………………………(1分) 设物块相对于滑板滑动的距离为s 1,由能量守恒得()2211122B mgs mv M m v μ=-+ ④……………………………………………(1分) 联立解得s 1=6l <6.5l ⑤ …………………………………………………………(1分) 即达到共同速度v 时,物块不会脱离滑板滑下.对滑板由动能定理得 212mgL Mv μ= ⑥………………………………………(1分) 解得L =2l …………………………………………………………………………(1分) ⑶讨论:①当2l ≤L ≤5l 时,滑块与滑板先共速,后一起匀速运动至滑板与C 相碰,碰后滑块在滑板上继续做减速运动到右端,设此时的速度为v C1,对物块由动能定得:2211162222C B l mg l l mv mv μ⎛⎫-++=- ⎪⎝⎭⑨……………………………………(1分)解得1C v ……………………………………………………………………(1分) 所以克服摩擦力所做的功176224f l W mg l l mgl μ⎛⎫=++= ⎪⎝⎭…………………………(1分) ②当l ≤L<2l 时,滑板一直到碰到挡板C 前,两者均没有共速,此后滑块在滑板上继续减速到右端,设此时的速度为v C2,对物块:在滑板上滑动全过,程由动能定理得()222116.522C B mg l L mv mv μ-+=- ⑦ ……………………………(1分)解得20C v ………………………………………………………(1分) 所以克服摩擦力所做的功()()6.5134f mg W mg l L l L μ=+=+ ………………(1分)综上,当L =l 时,v C 最大,max C v = …………………………………………(1分)。
2018届辽宁省沈阳市东北育才学校高三第五次模拟考试 理科数学试题及答案
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知全集U 为实数集R ,集合{}|02A x x =<<,集合{}|lg 0B x x =>,则图中阴影部分表 示的集合为 ( )A.{|01}x x <≤B.{|02}x x <<C.{|1}x x <D.∅ (2)已知i 是虚数单位,若12(,)ii a b a bi-=+∈+R ,则复数a bi +在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限(3)已知向量(3,1),(1,2)a b =-=- ,则向量a 与b 夹角,a b <>等于( ) A .34π B .23π C .3π D .4π(4)过抛物线28y x =-的焦点作一条直线与抛物线相交于B A ,两点,它们到直线1x =的距离之和等于8,则这样的直线( )A.有且仅有一条B.有且仅有两条C.有无穷多条D.不存在(5)为了了解我校今年新入学的高一A 班学生的体重情况,将所得的 数据整理后,画出了频率分布直方图(如右图),已知高一A 班学生人数为48人,图中从左到右的前3个小组的频率之比为1∶2∶3,则第2小组的频数为( )A.16B.14C.12D.11(6)已知命题p:函数()1xf x x =-的图象的对称中心坐标为(1,1);命题q :若函数()g x 在区间[],a b 上是增函数,则有()()()()()b ag a b a g x dx g b b a -<<-⎰成立.下列命题为真命题的是( )A.p q ∧B.p q ⌝∧C.p q ∧⌝D.p q ⌝∧⌝(7)若[]x 表示不超过x 的最大整数,执行如图所示的程序框图, 则输出的S 值为 ( )A.4B.5C.7D.9(8)已知点(,)P x y 是双曲线:C 22(0)x y a a -=>右支上动点,双曲线C 的过点P 的切线分别交两条渐近线于点,A B ,则OAB 的面积是( )A.随x 的增大而增大B. 随x 的增大而减小C. 2aD. a(9)设等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,且满足(4)n n nT n S =+,则89a b 的值为( ) A. 1317 B. 89 C.57 D. 813(10)设函数2log |1|(1)() 2 (1)x x f x x -≠⎧=⎨=⎩,若关于x 的方程2()()0(,)f x bf x c b c R ++=∈恰有5个不同的实数解(1,2,3,4,5)i x i =,则51()i i f x =∑的值为( )A.8B.5C.4D.2(11)已知四棱柱1111ABCD A B C D -中,侧棱1AA ABCD ⊥底面,12AA =,底面ABCD 的边长均大于2,且45DAB ∠= ,点P 在底面ABCD 内运动且在,AB AD 上的射影分别为M ,N ,若2PA =,则三棱锥1P D MN -体积的最大值为( )A.1B.11)3C.1(23-D.1(23+(12) 定义在()02π,上的函数()f x ,()f x '是它的导函数,且恒有()()tan f x f x x '<⋅成立,则()A()()43ππB .()()12sin16f f π< C()()64f ππ>D()()63f ππ<第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.(13)如图,已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的最长的棱长为________(cm).(14)数列{}n a 的首项为2,数列{}n b 为等比数列且563b b =,则11a 的值为______.(15)若b a ,是两个非零向量,且]1,33[|,|||||∈+==λλb a b a ,则b 与b a -(16) 已知0a >且1a ≠,则使方程222log ()log ()aa x ak x a -=-有解时的k 的取值范围为______.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.(17)(本小题满分12分)在△ABC 中,A 、B 、C 的对边为a 、b 、c ,且2sin sin sin sin sin sin A C A B B C =+. (Ⅰ)求角B 的最大值;(Ⅱ)设向量sin ,1)22BB =+-a,(2cos 2B =b ,求a b 的取值范围.(18)(本小题满分12分)如图,在四棱锥P ABCD -中,侧面PAB ⊥底面ABCD ,且90PAB ABC ∠=∠= ,//AD BC ,2PA AB BC AD ===,E 是PC 的中点. (Ⅰ)求证:DE ⊥平面PBC ;(Ⅱ)求二面角A PD E --的余弦值.(19)(本小题满分12分)为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与. 志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物. 每位志愿者根据自身实际情况,只参与其中的某一项工作. 相关统计数据如下表所示:CD(Ⅰ)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?(Ⅱ)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用X 表示所选志愿者中的女生人数,写出随机变量X 的分布列及数学期望.(20)(本小题满分12分)已知双曲线C :2212y x -=的左、右两个顶点分别为A 、B .曲线M是以A 、B 两点为短轴端点,离心率为2的椭圆.设点P 在第一象限且在曲线C 上,直线AP 与椭圆M 相交于另一点T .(Ⅰ)设点P 、T 的横坐标分别为1x 、2x ,证明:121x x =;(Ⅱ)设TAB ∆与POB ∆(其中O 为坐标原点)的面积分别为1S 与2S ,且PA PB ≤9uu r uu rg ,求12S S ⋅ 的最大值.(21)(本小题满分12分)已知函数()2ln ()f x mx m x m =--∈R . (I )讨论()f x 的单调性;(II )若()0f x ≥恒成立,证明:当120x x <<时,21211()()11()2f x f x x x x ⎛⎫->-- ⎪⎝⎭(22)(本小题满分10分)选修4-1:几何证明选讲 如图,已知四边形ABCD 内接于圆O ,过B 作圆O 的切线交AD 的延长线于E ,若BD 是CBE ∠的平分线.证明: (Ⅰ)AD 是BAC ∠的平分线;(Ⅱ)AB BE AE CD ⋅=⋅.(23)(本小题满分10分)选修4-4:坐标系与参数方程设在平面上取定一个极坐标系,以极轴作为直角坐标系的x 轴的正半轴,以2πθ=的射线作为y 轴的正半轴,以极点为坐标原点,长度单位不变,建立直角坐标系,已知曲线C 的直角坐标方程为222x y +=,直线l 的参数方程12x ty t=-⎧⎨=⎩(t 为参数). (Ⅰ)写出直线l 的普通方程与曲线C 的极坐标方程;(Ⅱ)设平面上伸缩变换的坐标表达式为2X x Y y ==⎧⎨⎩,求C 在此变换下得到曲线C '的方程,并求曲线C '内接矩形的最大面积.(24)(本小题满分10分)选修4-5:不等式选讲已知函数()|1||1|f x x x =-++,不等式()4f x ≥的解集为M . (Ⅰ)求M ;(Ⅱ)当,a b M ∈时,证明:2|||1|2a a bb+≥+则21222033(0)95C P X C ===1112822048(1)95C C P X C ===2822014(2)95C P X C === ……………9分∴X 的分布列为 ……………10分由(Ⅰ)知, 211x x =.设21t x =,则14t <≤,221212S S t t ⋅=+-.因此21211()()11()2f x f x x x x ⎛⎫->-- ⎪⎝⎭ ……………………12分当1x <-时,由24x -≥,得2x ≤-; 当11x -≤≤时,由()24f x =<得()4f x ≥无解; 当1x >时,由24x ≥,得2x ≥; 所以{}|22M x x x =≤-≥或. …………………………5分(Ⅱ)当,a b M ∈时,即224,4a b ≥≥ 因为22222222224(4)(4)()(1)10244a a a a a b b b b b b --+-+=+--=≥ 所以222()(1)2aab b +≥+ ,因此2|||1|2aab b +≥+ …………………………10分。
2019届沈阳市东北育才学校高三第五次模拟考试英语试卷及答案
2019届沈阳市东北育才学校高三五模考试英语试卷第一部分听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Which ball game does Jack play best?A. Volleyball.B. Ping-pong.C. Tennis.2. How long did the game last?A. About two hours.B. About two hours and a half.C. About three hours.3. What does the woman mean?A. She likes doing morning exercises.B. She can’t get up early.C. She dislikes doing such exercises.4. How are Tom’s skills?A. Excellent.B. Just so-so.C. Very bad.5. What do you know about the woman?A. She likes volleyball.B. She doesn’t like basketball.C. She likes sports, too.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. What kind of books is Mr. Black’s mother interested in?A. Romantic love stories.B. Funny - 1 - / 19。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{正文}2018-2019学年度辽宁省沈阳市东北育才高三年级第五次模拟考试数学(理科)试卷答题时间:120分钟 满分:150分一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i 为虚数单位,41z i=-,则复数z 的虚部为 A .2i -B .2iC .2D .2-2.已知全集⎭⎬⎫⎩⎨⎧≥--==020192018,x x xA R U ,则U C A = A .{|20182019}x x ≤≤B .{|20182019}x x <<C .{|20182019}x x <≤D .{|20182019}x x ≤<3.向量,,a b c 在正方形网格中的位置如图所示.若向量c =λ+a b ,则实数=λA .2-B .1-C .1D .24.已知等差数列{}n a 的前n 项和为n S ,满足8584S a =-,则该数列的公差是A .1B .2C .3D .45.若双曲线222:14x y C m-=的焦距为45C 的一个焦点到一条渐近线的距离为A .2B .4C 19.2196.已知函数()2()ln xf x ef e x e'=-,则()f x 的极大值点为 A .1eB .1C .eD .2e7.已知函数()sin()=+f x A x ωϕ,(0,0>>A ω,||2<πϕ)的部分图象如图所示,则⋅=ωϕA .6π B .4π C .3πD .23π 8.如图,网络纸上小正方形的边长为1,粗线画出的是某四棱锥的三视图,则该几何体的体积为A .2B .83C .6D .8 9.某地区高考改革,实行“3+2+1”模式,即“3”指语文、数学、外语三门必考科目,“1”指在物理、历史两门科目中必选一门,“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科,则一名学生的不同选科组合有A .8种B .12种C .16种D .20种10.在下图算法框图中,若dx x a ⎰-=30)12(,程序运行的结果S 为二项式5)2(x +的展开式中3x 的系数的9倍,那么判断框中应填入的关于k 的判断条件是A .3k <B .3>kC .2<kD .2>k11.将半径为3,圆心角为23π的扇形围成一个圆锥,则该圆锥的内切球的表面积为A .πB .2πC .3πD .4π12.已知函数()()133()log 2log 4=--+f x x x ,如下命题①函数()f x 的定义域是[]4,2-;②函数(1)f x -是偶函数;③函数()f x 在区间[)1,2-上是减函数;④函数()f x 的值域为(,2]-∞-. 其中正确命题的个数是A .4B .3C .2D .1 二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若实数,x y 满足约束条件41014x y y x y --≥⎧⎪≥⎨⎪+≤⎩则yz x =的最小值是________.14.如图所示,半径为1的圆O 是正方形MNPQ 的内切圆,将一颗豆子随机地扔到正方形MNPQ 内,用A 表示事件“豆子落在圆O 内”, B 表示事件“ 豆子落在扇形OEF (阴影部分)内”,则(|)=P B A .15.设n S 是等比数列{}n a 的前n 项和,若51013S S =,则52010S S S += . 16.抛物线22y px =的焦点为F ,设1222(,),(,)A x y B x y 是抛物线上的两个动点,若1223||3x x p AB ++=,则AFB ∠的最大值为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本题满分12分)在ABC ∆中,角C B A 、、的对边分别为c b a 、、,且03sin 2sin 322=-+A A. (Ⅰ)求角A 的大小;(Ⅱ)若ABC ∆面积为3,且外接圆半径3=R ,求ABC ∆的周长. 18.(本题满分12分)2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在[2585],之间,根据统计结果,做出频率分布直方图如下:(Ⅰ)求这100位作者年龄的样本平均数x 和样本方差2s (同一组数据用该区间的中点值作代表);(Ⅱ)由频率分布直方图可以认为,作者年龄X 服从正态分布2(,)N μσ,其中μ近似为样本平均数x ,2σ近似为样本方差2s . (i )利用该正态分布,求(6073.4)P X <<;(ii )央视媒体平台从年龄在[4555],和[6575],的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间[4555],的人数是Y ,求变量Y 的分布列和数学期望.附:4.13180≈,若2~(,)X N μσ,则()0.683P X μσμσ-<<+=,(22)0.954P X μσμσ-<<+=19.(本小题满分12分)已知椭圆C :22221(0)x y a b a b +=>>的左、右焦点分别为12,F F ,离心率为22,直线l :2y x =与椭圆交于,M N ,四边形12MF NF 的面积为423. (Ⅰ)求C 的方程;(Ⅱ)作与l 平行的直线与椭圆交于,A B 两点,且线段AB 的中点为P ,若12,PF PF的斜率分别为12,k k ,求12k k +的取值范围.20.(本小题满分12分)如图,四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 是平行四边形,45ABC ∠=︒,2AD AP ==,22AB DP ==E 是CD 中点,点F 在线段PB 上.(Ⅰ)证明:AD PC ⊥;(Ⅱ)若[0,1]λ∈,求实数λ使直线EF 与平面PDC 所成角和直线EF 与平面ABCD 所成角相等.21.(本小题满分12分)已知函数()ln ,f x x ax a a R =-+∈. (Ⅰ)讨论()f x 的单调性; (Ⅱ)若21()()(1)2g x f x x =+-有三个不同的零点,求a 的取值范围. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程(本小题满分10分)已知极坐标系的极点与直角坐标系的原点重合,极轴与x 轴的非负半轴重合.若曲线C 的极坐标方程为6cos 2sin =+ρθθ,直线l 的参数方程为1222⎧=⎪⎨=⎪⎩x ty t(t 为参数).(Ⅰ)求曲线C 的直角坐标方程与直线l 的普通方程;(Ⅱ)设点(1,2)Q ,直线l 与曲线C 交于、A B 两点,求|QA|·|QB|的值.23.选修4-5:不等式选讲(本小题满分10分) 已知函数()|1||2|f x x x =-++. (Ⅰ)求不等式()13f x <的解集;(Ⅱ)若()f x 的最小值为k ,且211(0)k mn m n+=>,证明:16m n +≥.{答案}2018-2019学年度辽宁省沈阳市东北育才高三年级第五次模拟考试数学(理科)参考答案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.D 2.C 3.D 4.A 5.B 6.D 7.C 8.A 9.C 10.A 11.B 12.D 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.13 14.14 15.11816.2π3 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(Ⅰ)解:03sin2sin 322=-+A A∴03sin 2cos 132=-+-⨯A A,即0cos 3sin =-A A …………2分 3tan =∴A …………4分又π<<A 03π=∴A …………6分(Ⅱ)2sin a R A =…………7分33sin 32sin 2===∴πA R a…………8分 ABC ∆面积为33sin21=∴A bc 得4=bc …………9分∵a 2=b 2+c 2﹣2bccosA , ∴b 2+c 2﹣bc=9, …………10分 ∴(b+c )2=9+3cb=9+12=21,∴b+c=21 ………11分 ∴周长a+b+c=3+21. …………12分18.(Ⅰ)这100位作者年龄的样本平均数x 和样本方差2s 分别为 300.05400.1500.15600.35700.2800.1560x =⨯+⨯+⨯+⨯+⨯+⨯=…2分222222(30)0.05(20)0.1(10)0.1500.35100.2200.15180s =-⨯+-⨯+-⨯⨯+⨯+⨯+⨯=…4分(Ⅱ)(i )由(1)知,)18060(~,N X ,从而1(6073.4)(6013.46013.4)0.34152P X P X <<=-<<+=;…7分(ii )根据分层抽样的原理,可知这7人中年龄在[4555],内有3人,在[6575],内有4人,故Y 可能的取值为0,1,2,3354)0(373403===C C C Y P ,3518)1(372413===C C C Y P , 3512)2(371423===C C C Y P 351)3(37433===C C C Y P 所以Y 的分布列为…11分所以Y 的数学期望为4181219()0123353535357E Y =⨯+⨯+⨯+⨯= …12分 19.(Ⅰ)解:由222221y xx ya b=⎧⎪⎨+=⎪⎩可得2222244a b y a b =+c e a ==,222212a b e a -==,ac b ∴== ………2分 23c =33=1b a =⎧⎪⎨=⎪⎩2212x y += ………5分 (Ⅱ)设直线AB 的方程为2(0)y x m m =+≠由22212y x mx y =+⎧⎪⎨+=⎪⎩,得2298220x mx m ++-= 226436(22)0m m ∆=-->,得29m <,()()3,00,3m ∴∈- ………7分设112200(,),(,),(,)A x y B x y P x y ,则21212822,99m x x m x x -+=-=0004,299mx m y x m =-=+=200001222000281118116y y x y m k k x x x m +=+==+---288116m=-(0m ≠) ………10分 ()128,0,7k k ⎛⎫∴+∈-∞-+∞ ⎪⎝⎭………12分20.(Ⅰ)解:PAD △中222PA AD PD +=,∴90PAD ∠=︒∴AD PA ⊥; ………1分 连AC ,ABC △中2222cos 4AC AB BC AB BC ABC =+-⋅∠= ………2分 ∴222AC BC AB +=∴AC BC ⊥,∴AD AC ⊥ ………4分 又PA AC A =∴AD ⊥平面PAC ∴AD PC ⊥ ………5分(Ⅱ)由(1):PA AD ⊥,又侧面PAD ⊥底面ABCD 于AD ,∴PD ⊥底面ABCD ,∴以A 为原点,DA 延长线、AC 、AP 分别为x 、y 、z 轴建系; ………6分∴(000)A ,,,(220)B ,,,(020)C ,,,(200)D -,,,(110)E -,,,(002)P ,,∴(022)PC =-,,,(202)PD =--,,,(222)PB =-,,, ………7分设PFPBλ=,([01]λ∈,),则(222)PF λλλ=-,, (2222)F λλλ-+,,,(212122),,=+--+EF λλλ ………8分设平面PCD 的一个法向量()m x y z =,,,则00m PC m PD ⎧⋅=⎪⎨⋅=⎪⎩,可得(111)m =--,,又平面ABCD 的一个法向量(001)n =,, ………10分由题:cos cos EF m EF n =,,,即223EFEFλ-=解得:λ ………12分 21.(Ⅰ)解:由已知()f x 的定乂域为(0,)+∞,又1'()=-f x a x,当0≤a 时,'()0>f x 恒成立; 当0a >时,令'()0>f x 得10<<x a ;令'()0<f x 得1>x a. 综上所述,当0≤a 时,()f x 在(0,)+∞上为增函数;当0a >时,()f x 在1(0,)a 上为增函数,在1(,)+∞a上为减函数. ………4分 (Ⅱ)由题意21g()(1)ln ,(0)2=-+-+>x x x ax a x ,则1g'()1=+--x x a x, 当1a ≤时,∵g'()0≥x ,∴g()x 在(0,)+∞上为增函数,不符合题意. ………6分当1a >时,2(1)1g'()x a x x x-++=,令2()(1)1x x a x ϕ=-++,则2(1)4(3)(1)0a a a ∆=+-=+->. 令()0x ϕ=的两根分别为12,x x 且12x x <, 则∵121x x =,∴1201<<<x x当1(0,)x x ∈时,()0x ϕ>,'()0g x ∴>,∴g()x 在1(0,)x 上为增函数, 当12()x x x ∈,时,()0x ϕ<,'()0g x ∴<,∴g()x 在12(,)x x 上为减函数, 当2(,)x x ∈+∞时,()0x ϕ>,'()0g x ∴>,∴g()x 在2(,)x +∞上为增函数,∵(1)0g =,∴g()x 在12(,)x x 上只有一个零点 1,且12g()0,g()0x x >< ………8分1111()()()()222221()(1)ln 2a a a a g ee e ae a -+-+-+-+∴=-+-+111()())22222111(11)ln (1)()222a a a e ea e a a -+-+-+<-++=--++( 11()()221(2)02a a e e -+-+=-<, 1()201a e-+<<,又当1[,1)x x ∈时,()0g x >,1()210a ex -+∴<<∴g()x 在1(0,)x 上必有一个零点. ………10分又21(22)(21)ln(22)(22)2g a a a a a a +=+++-++211(21)(22)022a a a >+-+=> 221a +>,又当2(1,)x x ∈时,()0g x <,222a x ∴+>∴g()x 在2(,)x +∞上必有一个零点.综上所述,故a 的取值范围为(1,)+∞ ………12分22.(Ⅰ)由ρ=6cos θ+2sin θ,得ρ2=6ρcos θ+2ρsin θ,所以x 2+y 2=6x +2y ,即曲线C 的直角坐标方程为x 2+y 2-6x -2y =0.由⎩⎨⎧x =1-2t y =2+2t,消去参数t , 得直线l 的普通方程为x +y -3=0. ………5分(Ⅱ)由(Ⅰ)知直线l 的参数方程可化为⎩⎨⎧x =1-22t′y =2+22t′(t ′为参数), ………7分 代入曲线C 的直角坐标方程x 2+y 2-6x -2y =0得t′2+32t′-5=0. ………9分 由韦达定理,得t′1t ′2=-5,则|QA|·|QB|=|t′1t ′2|=5. ………10分23.(Ⅰ)由()13f x <,得|1||2|13x x -++<,则12113x x >⎧⎨+<⎩或21313x -≤≤⎧⎨<⎩或22113x x <-⎧⎨--<⎩,解得:76x -<<,故不等式()13f x <的解集为(7,6)-. ………5分(2)证明:因为()|1||2|f x x x =-++|1(2)|3x x ≥--+=,所以3k =, 因为21191(0)k mn m n m n+=+=>,所以0,0m n >>, 199()()(10)1016n m m n m n m n m n +=++=++≥+= 当且仅当9n m m n =,即4,12m n ==时取等号,故16m n +≥. ………10分。
