第十二章习题答案new

合集下载

高等数学(上册)第12章(1)习题答案_吴赣昌_人民大学出版社_高数_

高等数学(上册)第12章(1)习题答案_吴赣昌_人民大学出版社_高数_第十二章微分方程内容概要§12.1微分方程的基本概念内容概要课后习题全解1．指出下列微分方程的阶数：知识点：微分方程阶的定义★（1）某(y)24yy3某y0；解：出现的未知函数y的最高阶导数的阶数为1，∴方程的阶数为1。

注：通常会有同学误解成未知函数y的幂或y的导数的幂。

例：（错解）方程的阶数为2。

((y))★（2）2某y2y某2y0；解：出现的未知函数y的最高阶导数的阶数为2，∴方程的阶数为2。

★（3）某y5y2某y0；解：出现的未知函数y的最高阶导数的阶数为3，∴方程的阶数为3。

★（4）(7某6y)d某(某y)dy0。

(n)思路：先化成形如F(某,y,y,,y解：化简得)0的形式，可根据题意选某或y作为因变量。

dy6y7某，出现的未知函数y的最高阶导数的阶数为1，∴方程的阶数为1。

d某某y2指出下列各题中的函数是否为所给微分方程的解：知识点：微分方程的解的定义思路：将所给函数及其相应阶导数代入方程验证方程是否成立。

★（1）某y2y，y5某2；2解：将y10某，y5某代入原方程得左边所以某10某25某22y右边，y5某2是所给微分方程的解。

y2y0,yC1co某C2in某；解：yC1in某C2co某，将y2C1co某2C2in某，yC1co某C2in某，代入原方程得：左边所以★（3）y2y2C1co某2C2in某2(C1co某C2in某)右边，yC1co某C2in某是所给微分方程的解。

y22yy20,yC1某C2某2；某某2解：将yC1某C2某，yC12C2某，y2C2，代入原方程得：2C14C2某2(C1某C2某2)22y左边=yy22C20右边2某某某某所以yC1某C2某2是所给微分方程的解。

y(12)y12y0yC1e1某C2e2某；1某解：将yC1eC2e2某，yC11e1某C22e2某，yC112e1某C222e2某，代入原方程得：左边y(12)y12y22C11e1某C22e2某(12)(C11e1某C22e2某)12(C1e1某C2e2某) 0所以右边，yC1e1某C2e2某是所给微分方程的解。

(典型题)人教版八年级上册数学第十二章全等三角形含答案

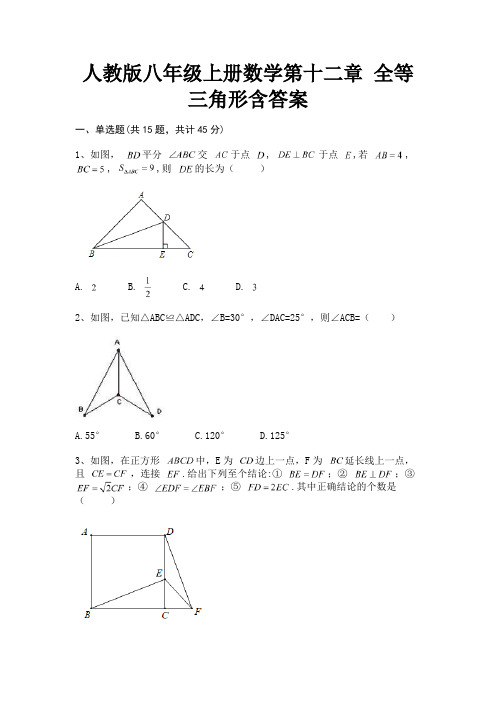
人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、如图，平分交于点, 于点,若,, ,则的长为（）A. B. C. D.2、如图，已知△ABC≌△ADC，∠B=30°，∠DAC=25°，则∠ACB=（）A.55°B.60°C.120°D.125°3、如图，在正方形中，E为边上一点，F为延长线上一点，且，连接.给出下列至个结论:① ；② ；③ ；④ ；⑤ .其中正确结论的个数是（）A. B. C. D.4、如图，在△AOB中，∠OAB＝∠AOB＝15°，OB＝8，OC平分∠AOB，点P在射线OC上，点Q为边OA上一动点，则PA+PQ的最小值是（）A.3B.4C.4D.35、如图所示，某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是( )A.带①去B.带②去C.带③去D.①②③都带去6、请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据图形全等的知识，说明画出∠A′O′B′=∠AOB的依据是（）A.SSSB.SASC.ASAD.AAS7、如图，AB=AD，添加下面的一个条件后．仍无法判定△ABC≌△ADC的是 ( )A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°8、如图，在已知的△ABC中，按以下步骤作图：①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于点M、N；②作直线MN交AB于点D，连接CD，若CD=AD，∠B=20°，则下列结论中错误的是（）A.∠CAD=40°B.∠ACD=70°C.点D为△ABC的外心 D.∠ACB=90°9、下列叙述中：①任意一个三角形的三条高至少有一条在此三角形内部；②以a，b，c为边(a，b，c都大于0，且a+b>c)可以构成一个三角形；③一个三角形内角之比为3:2:1，此三角形为直角三角形；④有两个角和一条边对应相等的两个三角形全等；是真命题的有（）个A.1B.2C.3D.410、如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是( )A.线段CD的中点B.CD与∠AOB的平分线的交点C.CD与过点O作的CD的垂线的交点D.以上均不对11、如图，中，于D，于E，AD交BE于点F，若，则等于A. B. C. D.12、如图，已知：∠1=∠2，要证明△ABC≌△ADE，还需补充的条件是（）A.AB＝AD，AC＝AEB.AB＝AD，BC＝DEC.AC＝AE，BC＝DED.以上都不对13、如图，一块三角形玻璃不小心摔碎成如图三片，只需带上其中的一片，玻璃店的师傅就能重新配一块与原来相同的三角形玻璃，你知道应带碎玻璃．（）A.③B.②C.①D.都不行14、规定：四条边对应相等，四个角对应相等的两个四边形全等．某学习小组在研究后发现判定两个四边形全等需要五组对应条件，于是把五组条件进行分类研究，并且针对二条边和三个角对应相等类型进行研究提出以下几种可能：① AB=A1B1， AD=A1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1；② AB=A1B1，AD=A1D1，∠A=∠A1，∠B=∠B1，∠D=∠D1；③ AB=A1B1， AD=A1D1，∠B=∠B1，∠C=∠C1，∠D=∠D1；④ AB=A1B1， CD=C1D1，∠A=∠A1，∠B=∠B1，∠C=∠C1．其中能判定四边形ABCD和四边形A1B1C1D1全等有（）个A.1B.2C.3D.415、如图，已知，添加下列条件后，仍无法判定△ ≌△的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图：△ABE≌△ACD，AB=10cm，∠A=60°，∠B=30°，则AD=________cm，∠ADC=________．17、如图，在Rt△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，任意长为半径画弧，两弧交于点O，作射线AO交BC于点D，若CD＝2，P为AB上一动点，则PD的最小值为________.18、已知△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC=________19、如图，已知∠1=∠2，请添加一个条件________使得△AOC≌△BOC．20、如图，将一张矩形纸片ABCD沿对角线BD折叠，点C的对应点为，再将所折得的图形沿EF折叠，使得点D和点A重合若，，则折痕EF的长为________．21、如图，已知△ABC≌△DCB，若∠ABC＝50°，∠ACB＝40°，则∠D＝________．22、如图，四边形ABCD是正方形，边长为4，点G在边BC上运动，DE⊥AG于E，BF∥DE交AG于点F，在运动过程中存在BF+EF的最小值，则这个最小值是________．23、如图，锐角三角形ABC和锐角三角形A'B'C'中，AD、A'D'分别是边BC、B'C'上的高，且AB＝A'B'，AD＝A'D'.要使△ABC≌△A'B'C'，则应补充条件：________（填写一个即可）24、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA＝3，OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE＝FP，则P点坐标为________．25、如图，将边长都为2 cm的正方形按如图所示摆放，点A1、A2、…、An分别是正方形的中心，则2014个这样的正方形重叠部分的面积和为________．三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、已知，，，，证明：.28、如图，CD是线段AB的垂直平分线，则∠CAD= ∠CBD．请说明理由:解:∵CD是线段AB的垂直平分线，∴AC=▲ ，▲ =BD．.在△ACD和△BCD中，. ▲ =BC，AD= ▲，CD=CD，∴△ACD≌▲ ( ) .∴∠CAD=∠CBD（）29、如图，已知AB⊥AC，AB=AC，DE过点A，且CD⊥DE，BE⊥DE，垂足分别为点D，E，试说明DE=DC+BE．30、已知：如图,△ABC中,点D、E分别为BC、AC边中点,连接AD,连接DE,过A 点作AF∥BC,交DE的延长线于F.连接CF,（1）求证：四边形ADCF是平行四边形；（2）对△ABC添加一个条件 ,使得四边形ADCF是矩形,并进行证明；（3）在（2）的基础上对△ABC再添加一个条件 ,使得四边形ADCF是正方形,不必证明.参考答案一、单选题(共15题，共计45分)1、A2、D3、C4、C5、C6、A7、C8、A9、C10、B11、A12、C13、A14、C15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、30、。

第十二章习题答案new

1、分析电子衍射与X 衍射有何异同？答：相同点：① 都是以满足布拉格方程作为产生衍射的必要条件。

② 两种衍射技术所得到的衍射花样在几何特征上大致相似。

不同点：① 电子波的波长比x 射线短的多，在同样满足布拉格条件时，它的衍射角很小，约为10-2rad 。

而X 射线产生衍射时，其衍射角最大可接近2。

② 在进行电子衍射操作时采用薄晶样品，增加了倒易阵点和爱瓦尔德球相交截的机会，使衍射条件变宽。

③ 因为电子波的波长短，采用爱瓦尔德球图解时，反射球的半径很大，在衍射角θ较小的范围内反射球的球面可以近似地看成是一个平面，从而也可以认为电子衍射产生的衍射斑点大致分布在一个二维倒易截面内。

④ 原子对电子的散射能力远高于它对x 射线的散射能力，故电子衍射束的强度较大，摄取衍射花样时曝光时间仅需数秒钟。

2、倒易点阵与正点阵之间关系如何？倒易点阵与晶体的电子衍射斑点之间有何对应关系？答：倒易点阵是与正点阵相对应的量纲为长度倒数的一个三维空间点阵，通过倒易点阵可以把晶体的电子衍射斑点直接解释成晶体相对应晶面的衍射结果，可以认为电子衍射斑点就是与晶体相对应的倒易点阵某一截面上阵点排列的像。

关系：① 倒易矢量g hkl 垂直于正点阵中对应的（hkl ）晶面，或平行于它的法向N hkl② 倒易点阵中的一个点代表正点阵中的一组晶面③ 倒易矢量的长度等于点阵中的相应晶面间距的倒数，即g hkl =1/d hkl④ 对正交点阵有a *//a ，b *//b ，c *//c ，a *=1/a ，b *=1/b ，c *=1/c 。

⑤ 只有在立方点阵中，晶面法向和同指数的晶向是重合的，即倒易矢量g hkl 是与相应指数的晶向[hkl]平行⑥ 某一倒易基矢量垂直于正交点阵中和自己异名的二基矢所成平面。

3、用爱瓦尔德图解法证明布拉格定律。

证：如图，以入射X 射线的波长λ的倒数为半径作一球（厄瓦尔德球），将试样放在球心O 处，入射线经试样与球相交于O*；以O*为倒易原点，若任一倒易点G 落在厄瓦尔德球面上，则G 对应的晶面满足衍射条件产生衍射。

八年级物理第十二章简单机械课后习题答案

第十二章简单机械课后习题新编《12.1杠杆》1.各式各样的剪刀都是一对对的杠杆。

在图中，哪些是省力杠杆，哪些是费力杠杆？要剪断铁片，应该使用哪种剪刀？剪纸时应该使用哪种剪刀？修剪树枝时应使用哪种剪刀？为什么？AC 是省力杠杆；B 是费力杠杆；要剪铁应使用A ；要剪纸应使用B ；要修剪树枝应使用C 。

2.在图中分别画出钳子、自行车手闸这两个杠杆（图中深色部分）工作时的支点、动力和动力臂、阻力和阻力臂。

3.图为指甲剪刀的示意图，它有几个杠杆？分别是省力杠杆，还是费力杠杆？有三个杠杆。

如图ABC 的动力臂大于阻力臂，是省力杠杆；OBD 、OED 的动力臂小于阻力臂，是费力杠杆；4.搬运砖头的独轮车，车厢和砖头所受的总重力G =1000N ，独轮车的有关尺寸如图所示。

推车时，人手向上的力F 应为多大？FL 1=GL 2F ×1m=1000N×0.3mF =300N《12.2滑轮》1.物体重1000N ，如果用一个定滑轮提起它，需要用多大的力？如果用一个动滑轮提起它，又要用多大的力（不计摩擦及滑轮自重）？ F 定=G=1000NF 1 L 1 L 2 F 2 F 2 L 2 F 1 L 1F 动=21G=21×1000N=500N2.仔细观察自行车，看看它上面有几种简单机械，分别说明它们各起到了什么作用。

车把：轮轴——变形杠杆——省力踏板：轮轴——变形杠杆——省力前闸、后闸：——杠杆——省力后轮：轮轴——变形杠杆——费力3.解释如图的科学漫画。

一个人要拉起比他体重大的物体，用定滑轮行吗？应该怎么办？不行。

应该使滑轮组。

4.利用如图甲所示的滑轮组提起一个重为2000N 的物体，不计摩擦及滑轮自重，绳子的拉力F 等于多少？如果要用这个滑轮组达到更加省力的效果，绳子应该怎样绕？请在图乙中画出绳子的绕法，并计算此时拉力的大小.F =41G=41×2000N=500NF =51G=51×2000N=400N 《12.3机械效率》 1.有没有机械效率为100%机械？为什么？举例说明，通过什么途径可以提高机械效率。

高等数学第12章课后习题答案(科学出版社).

习题 12.11. 判断下列方程是几阶微分方程:;)1(2y x dxdy +=;042)2(2=+-⎪⎭⎫⎝⎛x dx dy dx dy x;052)3(322=+⎪⎭⎫⎝⎛-xy dx dy dx y d x 2334(4)2()1xy x y x y x '''++=+.解 (1)是一阶线性微分方程; (2)是一阶非线性微分方程; (3)是二阶非线性微分方程; (4)是二阶非线性微分方程.2. 指出下列各题中的函数是否为所给微分方程的解：（1）2xy y '=，25y x =；（2）0y y ''+=，3sin 4cos y x x =-；（3）20y y y '''-+=，2e x y x =；（4）2()0xy x y yy ''''++=，y x =．解 (1)是; (2)是; (3)不是; (4)不是二阶非线性微分方程.3. 验证函数x C x y sin )(2+=(C 为任意常数)是方程0sin 2cot =--x x x y dxdy的通解, 并求满足初始条件0|2==πx y 的特解.解要验证一个函数是否是方程的通解，只要将函数代入方程，看是否恒等，再看函数式中所含的独立的任意常数的个数是否与方程的阶数相同.将x C x y sin )(2+=求一阶导数,得dxdy,cos )(sin 22x C x x x ++= 把y 和dxdy代入方程左边得 x x x y dxdysin 2cot --x x x x C x x C x x x sin 2cot sin )(cos )(sin 222-+-++=.0≡ 因方程两边恒等,且y 中含有一个任意常数,故x C x y sin )(2+=是题设方程的通解. 将初始条件02==πx y 代入通解x C x y sin )(2+=中，得C +=402π .42π-=C 从而所求特解为 .s i n422x x y ⎪⎪⎭⎫⎝⎛-=π 4．写出由下列条件确定的曲线所满足的微分方程.(1) 一曲线通过原点，并且它在(,)x y 处的切线斜率等于2x y +; (2) 一曲线通过点(2,3)，它在两坐标轴间的任一切线段均被切点所平分.解：由题意，2y x y '=+，00x y==解：设该曲线的方程为()y f x =，(,)x y 为其上任意一点，该点处的切线斜率为y '，过该点的切线方程为()Y y y X x '-=-。

沪教新版七年级上册《第12章_因式分解》2024年同步练习卷+答案解析

沪教新版七年级上册《第12章因式分解》2024年同步练习卷一、选择题：本题共5小题，每小题3分，共15分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列各式从左到右的变形中，是因式分解的为()A. B.C. D.2.如果一个多项式因式分解的结果是，那么这个多项式是()A. B. C. D.3.下列各式中，是完全平方式的是()A. B. C. D.4.把多项式分解因式的结果是()A. B.C. D.5.已知a，b，c是的三边长，且，则的形状为()A.钝角三角形B.等边三角形C.直角三角形D.等腰直角三角形二、单选题：本题共1小题，每小题5分，共5分。

在每小题给出的选项中，只有一项是符合题目要求的。

6.若能在整数范围内因式分解，则k可取的整数值有()A.2个B.3个C.4个D.6个三、填空题：本题共14小题，每小题3分，共42分。

7.多项式中各项的公因式是______.8.分解因式：______.9.分解因式：______.10.如果多项式，那么m的值为______.11.如果，且，则n的值是______.12.已知，，则______.13.已知，则的值是__________.14.若长方形的面积是，且其中一边长为，则长方形的另一边长是______.15.已知正方形的面积是，利用分解因式写出表示该正方形的边长的代数式______.16.已知，，则的值为______.17.分解因式，甲看错了a值，分解的结果是，乙看错了b值，分解的结果是，那么分解因式正确的结果应该是______.18.已知是一个完全平方式，则______.19.已知，则______.20.如果二次三项式为整数在整数范围内可分解因式，那么a的取值可以是______.四、解答题：本题共10小题，共80分。

解答应写出文字说明，证明过程或演算步骤。

21.本小题8分分解因式：22.本小题8分分解因式：计算：23.本小题8分分解因式：24.本小题8分分解因式：25.本小题8分分解因式：26.本小题8分因式分解：27.本小题8分因式分解：；已知：x、y为正整数，、且，求x、y的值.28.本小题8分阅读下面解题过程：分解因式：解：然后按照上述解题思路，完成下列因式分解：29.本小题8分利用乘法分配律可知：______；______.由整式乘法与因式分解的关系，我们又可以得到因式分解中的另两个公式：______；______.请利用新的公式对下列各题进行因式分解.；30.本小题8分先阅读下面例题的解法，然后解答后面的问题.例：若多项式分解因式的结果中有因式，求实数m的值.解：设为整式，若，则或由得左式为零，所以是方程的解，所以，所以问题：若多项式分解因式的结果中有因式，则实数p是多少？答案和解析1.【答案】C【解析】解：A、是整式的乘法运算，故选项错误；B、右边不是整式乘积的形式，故选项错误；C、，正确；D、右边不是整式乘积的形式，故选项错误．故选：根据因式分解的定义作答．因式分解是把一个多项式化成几个整式的积的形式，熟练地掌握因式分解的定义是解题关键．2.【答案】B【解析】解：故选：根据平方差公式得，进而解决此题．本题主要考查平方差公式以及因式分解的定义，熟练掌握平方差公式以及因式分解的定义是解决本题的关键．3.【答案】A【解析】解：，属于完全平方式；B.不属于完全平方式；C.不属于完全平方式；D.不属于完全平方式；故选：完全平方式分两种，一种是完全平方和公式，就是两个整式的和括号外的平方；另一种是完全平方差公式，就是两个整式的差括号外的平方．此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．4.【答案】C【解析】解：原式故选：先分两组，前面一组利用完全平方公式分解，然后利用平方差公式因式分解即可．本题考查了因式分解-分组分解：分组分解法一般是针对四项或四项以上多项式的因式分解，分组有两个目的，一是分组后能出现公因式，二是分组后能应用公式．5.【答案】B【解析】解：，，，即，，，，，的形状为等边三角形．故选：欲判断三角形的形状，不妨试着从边的关系出发，求出a、b、c之间的关系；给等式两边同时乘以2，再利用完全平方公式进行配方，可得到；接下来根据非负数的性质可得答案．考查学生综合运用数学知识的能力．此题是一道把等边三角形的判定、因式分解和非负数的性质结合求解的综合题．6.【答案】D【解析】【分析】本题主要考查因式分解的意义和十字相乘法分解因式，对常数项的不同分解是解本题的关键，属于拔高题．根据十字相乘法的分解方法和特点可知：k的值应该是20的两个因数的和，从而得出k的值．【解答】解：，，，，，，则k的值可能为：，，，，，，故整数k可以取的值有6个，故选：7.【答案】【解析】解：，所以多项式中各项的公因式是故答案为：先变形得出，再找出多项式的公因式即可．本题考查了公因式，能熟记找公因式的方法①系数找各项系数的最大公因数，②相同字母找最低次幂是解此题的关键．8.【答案】【解析】解：，故答案为：先提公因式，再利用平方差公式继续分解即可解答．本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式．9.【答案】【解析】解：，，故答案为：先提取公因式，再对余下的多项式利用完全平方公式继续分解．本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．10.【答案】【解析】解：，故答案为：把等式右边利用完全平方公式展开，然后根据对应项系数相等解答．本题考查了公式法分解因式，熟记完全平方公式的公式结构是解题的关键．11.【答案】【解析】解：，，，，故答案为：先根据两平方项确定出这两个数，即可确定n的值．本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．12.【答案】【解析】解：，即，且①，②，①+②，得：，解得，故答案为：由，即得出，结合，将两式相加消去b即可得．本题主要考查分式的加减法，解题的关键是掌握平方差公式和等式的性质．13.【答案】7【解析】解：，，故答案为：把已知条件两边分别平方，然后整理即可求解．完全平方公式：本题主要考查了完全平方公式，利用公式把已知条件两边平方是解题的关键．14.【答案】【解析】解：矩形的长为，故答案为：由题意得矩形的长为，然后利用多项式除以单项式的法则即可求出结果．本题考查多项式除以单项式运算．多项式除以单项式，先把多项式的每一项都分别除以这个单项式，然后再把所得的商相加．15.【答案】【解析】解：，正方形的边长的代数式是因为正方形的面积是，可以分解为，又有正方形的面积等于边长的平方可得，正方形的边长的代数式是此题考查对完全平方公式再实际中的应用，应熟练识记完全平方公式：16.【答案】4【解析】解：原式，当，时，原式故答案是：首先对所求的式子提公因式，然后利用完全平方公式分解，最后把，代入求值．本题考查了分解因式，提取公因式后利用完全平方公式进行二次分解，注意分解要彻底．17.【答案】【解析】解：分解因式，甲看错了a值，分解的结果是，，，乙看错了b值，分解的结果是，，，故答案为：根据已知分解因式，甲看错了a值，分解的结果是，可得出b的值，再根据乙看错了b值，分解的结果是，可求出a的值，进而因式分解即可．此题主要考查了因式分解的意义，根据已知分别得出a，b的值是解决问题的关键．18.【答案】或2【解析】解：由于，则，或故答案为：或这里首末两项是x和5这两个数的平方，那么中间一项为加上或减去x和5的积的2倍，故，再解k即可．此题主要考查了完全平方公式的应用，两数的平方和，再加上或减去它们积的2倍，就构成了一个完全平方式．注意积的2倍的符号，避免漏解．19.【答案】6【解析】解：已知等式变形得：，，，，，，，，解得：，，，则故答案为：已知等式左边14分为，结合后利用完全平方公式化简，再利用非负数的性质求出x，y与z的值，代入原式计算即可求出值．此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．20.【答案】或【解析】解：8可以分解为和，当8可以分解为时，根据十字相乘因式分解，，则；8可以分解为时，根据十字相乘因式分解，，则；故答案是或根据因式分解十字相乘，将8分解为和，再按照十字相乘进行因式分解即可．本题考查的是因式分解，用十字相乘的方法时，要注意数字的符号不能出现差错．21.【答案】解：【解析】将前两项分组后两项分组，进而提取公因式再利用平方差公式分解因式．此题主要考查了分组分解法因式分解，正确进行分组是解题关键．22.【答案】解：；【解析】先进行变形，再运用提公因式法进行因式分解；先运用平方差公式进行运算，再计算单项式乘以多项式．此题考查了整式乘法和因式分解的能力，关键是能准确运用对应法则和方法进行求解．23.【答案】解：【解析】先分组，分成，再运用完全平方公式分解．本题考查了因式分解．分解因式的一般步骤是：一提公因式，二套用公式，三分组，解本题的关键在于运用分组分解法进行因式分解，注意因式分解要彻底，一定要分解到每个因式都不能再分解为止．24.【答案】解：【解析】先将拆分为，再分组，利用完全平方公式及平方差公式求解即可．本题考查了分组分解法，分组分解法一般是针对四项或四项以上多项式的因式分解，分组有两个目的，一是分组后能出现公因式，二是分组后能应用公式．25.【答案】解：【解析】先利用完全平方公式和多项式乘以多项式展开，重新组合即可得出结论．此题主要考查了因式分解，完全平方公式，多项式乘以多项式，重新分组是解本题的关键．26.【答案】解：原式【解析】根据完全平方公式，可得答案．本题考查了因式分解，利用了完全平方公式分解因式．27.【答案】解：；，，，、y为正整数，，与也是整数，，，或，【解析】根据分组分解法分解因式即可；根据结论整体代入即可得到结论．本题考查了因式分解-分组分解法，熟练掌握分解因式的方法解题的关键．28.【答案】解：【解析】直接利用例题进行补项，进而分解因式得出答案．此题主要考查了分组分解法分解因式，正确补项是解题关键．29.【答案】【解析】解：；；；；；；故答案为：，，；根据多项式乘多项式的法则计算即可，再根据推导的公式进行因式分解．本题考查了因式分解和多项式乘多项式的逆向应用能力30.【答案】解：设为整式，若，则或由得左式为零，所以是方程的解，所以，所以【解析】仿照题例，先设，再求一次方程的值，代入计算得结果．本题考查了解一元一次方程、高次方程，理解题例，掌握题例的步骤是解决本题的关键．。

高等数学(经济类)课后习题及答案第十二章微分方程答案

习题12—1（A ）1. 指出下列各微分方程的阶数：（1）y y x 3='；（2）0d 2d )(3=--y x x x y ；（3）y y x y x '='+''+2)2(；（4）22()yy y y ''''''=-；（5）(5)(3)242cos y yy y x ''+-+=；（6）232d d 2d d P P tt t t+=；（7）0222)4(=+'-''+'''-y y y y y；答案：（1）一阶；（2）一阶；（3）二阶；（4）三阶；（5）五阶；（6）二阶；（7）四阶. 2. 验证下列各函数是否为所给微分方程的解. 如果是解，请指出是通解，还是特解？（1）函数3y x =，微分方程y y x 3='；（2）函数sin 3y C x =，微分方程90y y ''+=；（3）由C x y xy =++22确定的函数)(x y y =，微分方程(1)()0y dx x y dy +++=；（4）函数xy λe =（其中λ是给定的实数），微分方程0=+'''y y ．解：（1）因为23y x '=，左式233=xy x x y '==⋅=右式，所以函数3y x =是微分方程y y x 3='解．又因为函数3y x =不包含任意常数，所以是特解．（2）因为9sin39y C x y ''=-=-，即90y y ''+=，所以函数sin 3y C x =是微分方程90y y ''+=解，但是由于sin 3y C x =中只有一个任意常数，又因为微分方程是二阶的，所以sin 3y C x =既不是微分方程90y y ''+=的通解，也不是特解，只是解．（3）等式C x y xy =++22两边同时对x 求导，有d d 10d d y y y x y x x+++=，整理得(1)()0y dx x y dy +++=，所以由C x y xy =++22确定的函数)(x y y =是(1)()0y dx x y dy +++=的解，又C x y xy =++22中含有一个任意常数，而(1)()0y dx x y dy +++=是一阶微分方程，所以Cx y xy =++22是(1)()0y dx x y dy +++=通解．（4）因为x y λe =，则有3e xy λλ'''=，所以33ee (1)e xx x y y λλλλλ'''+=+=+．当1λ=-时，3(1)e 0x y y λλ'''+=+=，则x y λe =是微分方程0=+'''y y 的解，并且是特解；当1λ≠-时，3(1)e0xy y λλ'''+=+≠，则x y λe =不是微分方程0=+'''y y 的解．3. 若函数e xy α=是微分方程0y y ''''-=的解，求的α值．解：由e x y α=得，e x y αα'=，3e xy αα'''=，将它们代入微分方程0y y ''''-=，得32e e (1)=0x x x y y e ααααααα''''-=-=-，所以1α=-，0或1．4．验证下列所给的各函数是微分方程的通解，并求满足初始条件的特解.（1）函数21y Cx =+，微分方程22xy y '=-，初始条件(1)2y =；（2）函数22x y C +=，微分方程0yy x '+=，初始条件1)1(=y ；（3）函数12()xy C C x e =+，微分方程20y y y '''-+=，初始条件(0)0y =，(0)1y '=.解：（1）因为2y Cx '=，所以222(1)222xy x Cx Cx y '=⋅=+-=-．又2Cx y =中含有一个任意常数，22xy y '=-是一阶微分方程，所以函数21y Cx =+是微分方程22xy y '=-的通解．由(1)2y =，可得1C =，所以微分方程22xy y '=-满足初始条件(1)2y =的特解是2+1y x =．（2）对隐函数22x y C +=的两边求关于x 的导数，得220x yy '+=，即0yy x '+=．又22x y C +=中含有一个任意常数，0yy x '+=是一阶微分方程，所以隐函数22x y C +=是微分方程0yy x '+=的通解．由1)1(=y ，可得2C =，所以微分方程0yy x '+=满足初始条件1)1(=y 的特解是222x y +=．（3）因为212()e x y C C C x '=++，212(2)e xy C C C x ''=++，所以2y y y '''-+21221212(2222)e 0x C C C x C C C x C C x =++---++=．又因为函数12()x y C C x e =+中含有两个独立的任意常数，而20y y y '''-+=是二阶微分方程，所以12()xy C C x e =+是微分方程20y y y '''-+=的通解．由初始条件(0)0y =，(0)1y '=，有12101C C C =⎧⎨+=⎩，，得01=C ，12=C ，所以微分方程20y y y '''-+=满足初始条件(0)0y =，(0)1y '=的特解是e xy x =．习题12—1（B ）1．给定微分方程21y x '=+，（1）求过点(1,3)的积分曲线方程；（2）求出与直线13+=x y 相切的积分曲线方程．解：易验证2y x x C =++是微分方程21y x '=+的通解．（1）由曲线2y x x C =++过点(1,3)，有311C =++，得1C =，所求积分曲线为21y x x =++．（2）若曲线2y x x C =++与直线13+=x y 相切，则有213x +=（斜率相等），得1x =．当1=x 时，4=y ，所以切点为(1,4)，将其代入2y x x C =++，有411C =++，得2C =，所求曲线为22y x x =++．2．将积分方程2()()sin cos xf t dt xf x x x x π=--⎰（其中)(x f 是连续函数）转化为微分方程，给出初始条件，并求函数)(x f ．解：将2()()sin cos xf t dt xf x x x x π=--⎰两边同时对x 求导，有()()()sin cos sin f x f x xf x x x x x '=+--+，即()cos f x x '=，这就是所求的微分方程，容易得到其通解为()cos sin f x xdx x C ==+⎰．将2x π=代入到原方程2()()sin cos x f t dt xf x x x x π=--⎰中，有0()12f π=-，得初始条件为()12f π=，所以有11C =+，得0C =，所求函数为()sin f x x =．习题12—2（A ）1. 求下列可分离变量的微分方程的通解：（1）32yy x '=；（2）e yy x -'=；（3）y '=；（4）2(3)0ydx x x dy +-=．解：（1）分离变量32d 4d y y x x =，两边积分32d 4d y y x x =⎰⎰，整理得通解为24y x C =+．（2）分离变量e d d yy x x =，两边积分e d d y y x x =⎰⎰，整理得通解为21e 2y x C =+，或写作2ln()2x y C =+．（3）分离变量d y y =，两边积分d y y =⎰，整理得通解为1ln y C =，进而原方程通解为：y Ce =（4）分离变量有2d d 3y x y x x =--，整理得d 111()d 33y x y x x=---，两边积分d 111()d 33y x y x x ==---⎰⎰，整理得通解为11ln (ln 3ln )d 3y x x x C =---+，进而原方程通解为：3(3)x y Cx -=．2. 求下列齐次方程的通解：（1）2xy x y '=+；（2）(2)x y y y '-=；（3）22()d d 0x y x xy y -+=；（4）d (1ln)d 0yx y y x x-+=．解：（1）将方程改写为2y y x '=+，令u xy=，则x u x u x y y d d d d +=='，于是原方程化为d 2d u u xu x +=+，即2d d x u x =，积分得2ln ln u x C =+，即2ln yCx x=，所以原方程通解为2ln y x Cx =．（2）将方程改写为2d d -=y x y x ，令v yx =则y vy v y x d d d d +=，于是原方程化为2d d -=+v y v yv ，即y y v d 2d -=，积分得C y v ln ln 2+-=，即2ln yCy x =，所以原方程通解为2lny Cy x =．（3）将方程改写为d d y y x x x y =-，令u xy=，则x u x u x y d d d d +=，于是原方程化为d 1d u u x u x u +=-，即d d xu u x=-，积分得2ln 22u C x =-+，即222ln y C x x =-，所以原方程通解为2y 2x =2(ln )C x -．（4）将方程改写为(1ln )dy y y dx x x =+，令y u x =，则xu x u x y y d d d d +=='，于是原方程化为(1ln )du u xu u dx +=+，即ln du dxu u x=，积分得1ln ln ln u x C =+，即ln u Cx =（其中1)C C e =±，所以原方程通解为lnyCx x=，或写作e Cx y x =． 3. 求下列一阶线性微分方程的通解：（1）2y xy x '-=；（2）d 2e d x yy x+=；（3）sin cos e x y y x -'+=；（4）2(2cos )d (+1)d 0xy x x x y -+=．解：（1）法一：相应齐次方程为0y xy '-=，即d d y x x y =，积分得211ln 2y x C =+，即22e x y C =（其中1)C C e =±．令22()ex y u x =，代入原方程，有222222ee e2x x x u xu xu x '+-=，即222ex u x -'=，得2222()2ed 2e x x u x x x C --==-+⎰，所以原方程通解为222222(2e )e e 2x x x y C C -=-+=-．法二：()P x x =-、()2Q x x =，方程通解为 ()d ()d [()e d ]e P x xP x x y Q x x C -⎰⎰=+⎰d d (2e d )e x x x xx x C -⎰⎰=+⎰2222(2ed )e x x x x C -=+⎰2222(2e)e x x C -=-+22e 2x C =-．（2）()1P x =、()2e xQ x =，方程通解为 ()d ()d d d [()e d ]e (2e e d )e P x xP x x x xx y Q x x C x C --⎰⎰⎰⎰=+=+⎰⎰22(2e d )e (e )e e e x x x x x x x C C C ---=+=+=+⎰．（3）()cos P x x =、sin ()exQ x -=，方程通解为()d ()d cos d cos d sin [()e d ]e (e e d )e P x xP x x x x x x x y Q x x C x C ---⎰⎰⎰⎰=+=+⎰⎰sin sin (d )e ()e x x x C x C --=+=+⎰．（4）方程化为222cos 11x x y y x x '+=++，则有22()1x P x x =+、2cos ()1xQ x x =+，方程通解为 2222d d ()d ()d 112cos [()e d ]e (e d )e 1xxxx P x xP x xx x x y Q x x C x C x --++⎰⎰⎰⎰=+=++⎰⎰221sin (cos d )+1+1x Cx x C x x +=+=⎰． 4．求下微分方程满足所给初始条件的特解：（1）d 1d 2y x x y -=，(3)1y =；（2）sec y xy x y x '+=，2)1(π=y ；（3）2e xy y x '-=，(0)2y =；（4）ln ln xy x y x '+=，(e)1y =．解：（1）这是可分离变量方程，分离变量为2d (1)d y y x x =-，积分得22(1)2x y C -=-+，即方程通解为22(1)2x y C -+=．由(3)1y =，有3C =，方程特解为22(1)32x y -+=．（2）这是齐次方程secy y y x x '+=，令u xy=，则x u xu x y d d d d +=，于是原方程化为d sec d u u xu u x ++=，即d cos d xu u x=-，积分得1sin ln u x C =-+，即方程的通解为sin eyxx C =（其中1)C C e =±．由2)1(π=y ，可得1C e=，所以方程特解为sin 1e yx x -=．（3）这是一阶线性方程，2()1()e xP x Q x x =-=、，因此，方程通解为d d 2(e e d )e (e d )e [(1)e )]e x xx x x x x y x x C x x C x C -⎰⎰=+=+=-+⎰⎰．由(0)2y =，有21C =-+，得3=C ，方程特解为xx x y 2e )1(2e 3-+=．（4）原方程可化为11ln y y x x x '+=，这是一阶线性方程，1()ln P x x x =、1()Q x x=，方程通解为11d d 2ln ln 1111[e d ]e (ln )ln 2ln 2ln x x x x x xC y x C x C x x x x-⎰⎰=+=+=+⎰．由(e)1y =，有1121C =+，得12C =，所以方程特解为11(ln )2ln y x x =+．习题12—2（B ）1．求下列伯努利微分方程的通解：（1）yx xy y =-'；（2）2xy y y =-'．解：（1）1-=n ，令21y y z n==-（21=-n ），则原方程化为x n xz n x z )1()1(d d -=--，即x xz xz22d d =-，该方程通解为 222222d 2d (2e d )e (2e d )e (e )e e 1x x x xx x x x x z x x C x x C C C ---⎰⎰=+=+=-=-⎰⎰．所以，原方程通解为1e 22-=x C y ．（2）2=n ，令yyz n11==-（11-=-n ），则原方程化为x n z n x z )1()1(d d -=--，即x z xz-=+d d ，该方程通解为 1e e )e e (e )d e (e )d e (d d +-=+-=-=⎰+⎰-=----⎰⎰x C x C x x C C x x z x x x x x x xx ．所以，原方程通解为1e 1+-=-x C yx ． 2．用适当的变量代换求下列微分方程的通解：（1）22x y x y +=+'；（2）1+-='y x y ；（3）)ln (ln y x y y y x +=+'；（4）xy x y y xy 22tan 2+='．解：（1）令u x y =+2，则x u x x y d d 2d d =+，于是u x u=d d ，分离变量有x uu d d =，积分得C x u +=2，原方程通解为C x x y +=+22．（2）令1x y u -+=，则x u x y d d d d 1=-，于是u x u =-d d 1，即u xu-=1d d ，分离变量得x u u u u d )1(d -=-，或x u u d d )111(2-=-+，积分得x C u u -=-+)1ln (2，所以原方程通解为x C y x y x -=+--++-)11ln 1(2．（3）令u xy =，则x u x y xy d d d d =+，于是u x u x u ln d d =，分离变量得xxu u u d ln d =，积分得Cx u ln ln ln =，即Cx u e =，所以原方程通解为Cxxy e 1=．（4）u x y =2，即xu y =2，则x u x u y y d d 2+='，原方程化为u x xu xu x xu tan d d 2+=+，分离变量有xxu u d d cot =，该方程通解为Cx u ln sin ln =，即Cx u =sin ，所以原方程通解为Cx xy =2sin ．3．求微分方程(0(0)ydx x dy y -=>的通解．解：将方程改写为222)(1d d yxy x y y x x y x ++=++=这是以)(y x x =为未知函数的齐次方程，为此令yv x =，则y v y v y x d d d d +=，于是方程化为21d d v yvy +=，分离变量有yyv v d 1d 2=+，积分得C y v v ln ln )1ln(2+=++，即Cy v v =++21，进而原方程通解为Cx Cy 211+=． 4．求微分方程2d d yx yx y +=的通解．解：方程改写为y y x y x +=d d ，即y yxy x =-d d ，这是一阶线性微分方程，通解为 2d d )d ()d e(ey Cy y C y y y C x yy yy+=+=⎰+⎰=⎰⎰-．５．设函数)(x f 连续，且不恒为零，若⎰⎰+=120d )(2d )()(t t tf t t f x f x ，求函数)(x f ．解：方程两边同时对x 求导，有)()(x f x f ='，分离变量有x ffd d =，得通解为x C x fe )(=．记a t t tf =⎰12d )(，则a t t f x f x2d )()(0+=⎰，令0=x ，得初始条件a f 2)0(=．用0=x 代入到x C x f e )(=之中，有a C 2=，所以x a x f e 2)(=．由)e 21e (2)d e e(2d e 4d )(102221021221022102t t t t a t t a t t at t tf a -=-===⎰⎰⎰)1e ()e 21e (22210222+=-=a a t ，得1e 12+=a ，所以1e e 2)(2+=x x f ．６．设连续函数)(x f 满足1)(d )()(12-=+⎰x f t tt f t f x ，求函数)(x f ．解：方程1)(d )()(12-=+⎰x f t t t f t f x 两边同时对x 求导，有)()()(2x f xx f x f '=+，令)(x f y =，则方程可以改写为y x y y x +=2d d ，即y yxy x =-d d ，这是一阶线性微分方程，通解为 )()d ()d e(ed d y C y y C y y y C x yy yy+=+=⎰+⎰=⎰⎰-．用1=x 代入到方程1)(d )()(12-=+⎰x f t tt f t f x 之中，得初始条件1)1(=f ，于是11+=C ，故0=C ，于是2y x =，即所以函数为x x f =)(（注：根据初始条件1)1(=f ，所以不能取x x f -=)(）．习题12—3（A ）1. 求下列各微分方程的通解：（1）2+1y x ''=；（2）2cos e x y x '''=+；（3）20y xy '''-=；（4）2e xy y '''-=；（5）201y y y'''+=-．解：（1）2311(1)3y x dx x x C '=+=++⎰， 342112111()d 3122y x x C x x x C x C =++=+++⎰．（2）2211(cos e )d sin e 22x xy x x x C ''=+=++⎰， 2211211(sin e 2)d cos e 224x x y x C x x C x C '=++=-+++⎰， 2121(cos e 2)d 4x y x C x C x =-+++⎰221231sin e 8x x C x C x C =-++++．（3）方程不显含y ，令)(x p y ='，则p y '=''，于是d 20d pxp x-=，分离变量为d 2d p x x p =，积分得2ln p x C =+，即213p C x =（其中13)C C e =±，于是原方程降阶为213y C x '=，原方程通解为23121d 3C x C x x C y +==⎰．（4）方程不显含y ，令)(x p y ='，则p y '=''，于是2e xp p '-=，这是一阶线性微分方程，其通解为d d 2111(e e d )e (e d )e (e )e x x x x x x xp x C x C C -⎰⎰=+=+=+⎰⎰，于是原方程降阶为21e e x x y C '=+，所以原方程的通解为221121(e e )d e e 2x x xx y C x C C =+=++⎰．（5）方程不显含x ，令()y q y '=，则y qq '''=，于是2d 0d 1q q q y y +=-，即d 0d 1q q y y+=-，这是可分离变量的方程，先分离变量d d 1q y q y=--，再两边积分，并整理可得1(1)q C y =-．所以1d (1)d yC y x=-，解得12e 1C x y C =+，这就是原方程的通解． 2. 求下列各微分方程满足初始条件的特解：（1）311y x '''=+，(1)1y =，(1)1y '=，1(1)2y ''=；（2）2y y x '''-=，(0)1y =，(0)0y '=；（3）2eyy ''=，(0)0y =，(0)1y '=．解：（1）13211(1)d 2y x x C x x ''=+=-++⎰，由1(1)2y ''=，得10C =，所以212y x x''=-+； 222111()d 222y x x x C x x '=-+=++⎰，由(1)1y '=，得02=C ，所以21122y x x '=+； 2331111()d ln 2226y x x x x C x =+=++⎰，由1)1(=y ，得356C =，所以方程满足初始条件的特解为3115ln 266y x x =++．（2）方程不显含y ，令)(x p y ='，则p y '=''，原方程化为2p p x '-=，此方程通解为d d 1111(2e d )e (2e d )e (2e 2e )e e 22x xx x x x x x p x x C x x C C x C x ----⎰⎰=+=+=--=--⎰⎰，即1e 22xy C x '=--，由(0)0y '=，得12C =，从而2(e 1)x y x '=--，此方程通解为222(e 1)d 2e 2x x y x x x x C =--=--+⎰，由(0)1y =，得21C =-，所以方程满足初始条件的特解为22e 21x y x x =---．（3）方程不显含x ，令()y q y '=，则y qq '''=，于是2e y qq '=，分离变量有2d e d yq q y =，积分得221e yp C =+，即y '=由1)0(='y ，可知道0>'y ，所以y '=再由(0)0y =，(0)1y '=，得01=C ，所以e y y '=．分离变量有e d d yy x -=，积分得2e y x C --=+，由0)0(=y ，得21C =-，于是e 1y x --=-，化简为ln (1)y x =--，这就是方程满足初始条件的特解．习题12—3（B ）1. 求下列各微分方程的通解：（1）()e n ax b yx =+（a ，b 为常数）；（2）0ln=''-''xy y y x ；（3）2)(y y '=''．解：（1）由于1e d e axax x a =⎰，11d 1t t x x x t +=+⎰，故原方程的通解为 1121211e [()(1)(1)]axb n n n n n n y b n b n b x C x C x C x C a-+---=+++-++++++．（２）方程不显含y ，令)(x p y ='，则p y '=''，于是x p p p x ln='，即xpx p p ln ='，这是齐次方程，令u x p =，则x u x u x p p d d d d +=='，原方程化为u u xux u ln d d =+，分离变量有x x u u u d )1(ln d =-，积分得x C u 1ln )1ln(ln =-，即11e +==x C u xp ，原方程降阶为11e +='x C x y ，原方程通解为⎰⎰+++-==x x C x x y x C x C x C )d e e (1d e 11111112111)1(e 11C C x C x C +-=+．（３）方程既不显含y ，也不显含x ．（方法1）令)(x p y ='，则p y '=''，则2p p ='，分离变量有x ppd d 2=，积分得11C x p -=-，即xC p -=11，原方程降阶为x C y -='11，所以原方程的通解为)ln(d 121x C C x C xy --=-=⎰．（方法2）令()y q y '=，则y qq '''=，于是2d d q qq y =，分离变量有2d d q q q y=，积分得2ln q y C =-，即原方程降阶为2e d d C y xy-=，分离变量为x y y C d d e 2=-，积分得12e C x y C -=--，化简为)ln(12x C C y --=，这就是原方程的通解．2. 求下列各微分方程满足初始条件的特解：（1）2)(1y y '+=''，(0)1y =，(0)0y '=；（2）3()y y y ''''=+，(0)0y =，(0)1y '=；（3）)(22y y y y '-'=''，(0)1y =，(0)2y '=．解：（1）按不显含y 的方程求解，（注：本题按不显含x 方程求解困难）．令)(x p y ='，则p y '=''，于是21p p +='，分离变量有x ppd 1d 2=+，积分得1arctan C x p +=，即1arctan C x y +='，由(0)0y '=，得01=C ，于是x y tan ='，积分得2tan d ln cos y x x C x ==-⎰，由(0)1y =，得12=C ，所以方程满足初始条件的特解为1ln cos y x =-．（2）令()y q y '=，则y qq '''=，得3d d qqq q y=+，因为0q =不满足初始条件(0)1y '=，所以0q ≠，分离变量有2d d 1qy q =+，积分得1arctan q y C =-，即1tan ()y q y C '==-．由初始条件(0)0y =，(0)1y '=，有11tan (0C =+），得14C π=，故tan ()4y y π'=-．分离变量d d tan ()4y x y π=-，积分并整理得2sin ()e 4xy C π-=．再由初始条件(0)0y =，得22C =-arcsin 24x y =+π．（3）这是不含x 的二阶可降阶微分方程，令()y q y '=，则y qq '''=，则方程化为22()yqq q q '=-．因为0q =不满足初始条件2)0(='y ，所以0q ≠，分离变量有d d 21q yq y=-，积分得21ln(1)ln q C y -=，解得211y q C y '==+．由初始条件(0)1y =，(0)2y '=，有121+=C ，得11=C ，故12+='y y ，分离变量有x y y d 1d 2=+，积分得1arctan C x y +=，再由初始条件1)0(=y ，得42π=C ，所以原方程满足初始条件的特解为4arctan π+=x y ，即xxx y tan 1tan 1)4tan(-+=+=π．习题12—4（A ）1．指出下列各对函数在其定义区间内的线性相关性：（1）3x 与2x ；（2）e x 与e xx ；（3）e x-与2ex-；（4）x e 与5e x；（5）sin x 与x 2sin ；（6）x x cos sin 与x 2sin ；（7）e sec x x 与e tan xx ；（8）x ln 与ln x μ（0μ>）．解：（1）因为233x xx =不恒为常数，所以3x 与2x 在区间)(∞+-∞，内线性无关．（2）因为e ex x x x =不恒为常数，所以e x与e x x 在区间)(∞+-∞，内线性无关．（3）因为2e e e x xx ---=不恒为常数，所以e x -与2e x -在区间)(∞+-∞，内线性无关．（4）因为5e 5ex x =恒为常数，所以xe 与5e x 在区间)(∞+-∞，内线性相关．（5）因为sin 22cos sin xx x=不恒为常数，所以sin x 与x 2sin 在区间)(∞+-∞，内线性无关．（6）因为sin 22sin cos xx x=恒为常数，所以x x cos sin 与x 2sin 在区间)(∞+-∞，内线性相关．（7）因为e tan sin e sec x x xx x=不恒为常数，所以e sec x x 与e tan x x 在区间)(∞+-∞，内线性无关．（8）因为ln 0ln x xμμ=>恒为常数，所以x ln 与ln x μ在区间)0(∞+，内线性相关． 2．验证函数21e x y =，22e xy x =是微分方程440y y y '''-+=的两个线性无关的解，并写出该方程的通解．解：因为21e xy =，所以22112e =4e x xy y '''=，，因此 222111444e 8e 4e 0xx x y y y '''-+=-+=，所以21e xy =是440y y y '''-+=的解；同理，22e xy x =是440y y y '''-+=的解．又因为2221e exx y x x y ==不恒为常数，所以函数21e x y =，22e x y x =是微分方程440y y y '''-+=的两个线性无关的解．因此二阶线性齐次微分方程440y y y '''-+=通解为2112212()e x y C y C y C C x =+=+．3．通过观察给出微分方程0y y ''+=的两个线性无关的特解，并写出该方程的通解．解：0y y ''+=是二阶线性齐次微分方程，改写为y y ''=-，二阶导数与自身呈相反数的函数有1sin y x =，2cos y x =，它们是0y y ''+=的两个解，又21cos cot sin y x x y x==不恒为常数，于是1sin y x =，2cos y x =线性无关，所以方程0y y ''+=的通解为12sin cos y C x C x =+．4．写出下列各二阶常系数线性齐次微分方程的通解：（1）320y y y '''-+=；（2）10250y y y '''-+=；（3）2100y y y '''-+=；（4）02d d 22=-x tx．解：（1）特征方程为2320r r -+=，即(1)(2)0r r --=，特征根为11=r 、22r =（不相等实根），所以方程320y y y '''-+=的通解是212e e x x y C C =+．（２）特征方程为210250r r -+=，即2(5)0r -=，特征根为125r r ==（两个相等实根），所以方程10250y y y '''-+=的通解是512()e xy C C x =+．（3）特征方程为22100r r -+=，由二次代数方程求根公式，得特征根为21322b y i a -===±（一对共轭复根），所以方程2100y y y '''-+=的通解是12(cos3sin 3)e xy C x C x =+．（4）特征方程为022=-r ，特征根为21=r 、22-=r （不同实根），所以方程02d d 22=-x tx的通解是ttC C x 2221e e -+=（注意t 是自变量，x 是因变量）．5．求下列各微分方程满足初始条件的特解：（1）22d d 340d d y yy t t+-=，(0)2y =，(0)3y '=-；（2）20y y y '''-+=，(0)1y =，(0)2y '=；（3）450y y y '''-+=，(0)1y =，(0)0y '=．解：（1）特征方程为2340r r +-=，即(1)(4)0r r -+=，特征根为11=r 、24r =-，所以方程22d d 340d d y yy t t +-=的通解是412e e t t y C C -=+，且412e 4e t t dy C C dt-=-．由初始条件(0)2y =，(0)3y '=-，有1212243C C C C +=⎧⎨-=-⎩，，得1211C C =⎧⎨=⎩，，所以方程满足初始条件(0)2y =，(0)3y '=-的特解是4e e t ty -=+．（2）特征方程为2210r r -+=，即2(1)0r -=，特征根为121r r ==，所以方程20y y y '''-+=的通解是12()e x y C C x =+，且212()e x y C C C x '=++．由初始条件(0)1y =，(0)2y '=，有12112C C C =⎧⎨+=⎩，，得1211C C =⎧⎨=⎩，，所以方程满足初始条件(0)1y =，(0)1y '=-的特解是(1)e x y x =+．（3）特征方程为2450r r -+=，由二次代数方程求根公式，得特征根为2r i ==±，所以方程450y y y '''-+=的通解是212(cos sin )e x y C x C x =+，且21221[(2)cos (2)sin ]e xy C C x C C x '=++-．由初始条件(0)1y =，(0)0y '=，有112120C C C =⎧⎨+=⎩，，得1212C C =⎧⎨=-⎩，，所以方程满足初始条件(0)1y =，(0)0y '=的特解是2(cos 2sin )e xy x x =-． 6．求下列各二阶常系数线性非齐次微分方程的通解：（1）x y y +=+''1；（2）xy y y -=+'+''e 22；（3）223y y y x x '''+-=+-；（4）xx y y e 4=-''.解：（1）相应齐次方程为0=+''y y ，特征方程012=+r ，特征根为i r i r -==21、，相应齐次方程通解为x C x C Y sin cos 21+=．这里x x f +=1)(，01==λ、n 不是特征根，因此设b ax y +=*，将其代入到原方程之中，有x b ax +=+1，比较系数得11==b a 、，于是原方程的一个特解为x y +=1*．原方程的通解为x x C x C y Y y +++=+=1sin cos 21*．（2）相应齐次方程为02=+'+''y y y ，特征方程0122=++r r ，即0)1(2=+r ，特征根为121-==r r ，相应齐次方程通解为xx C C Y -+=e )(21．这里xx f -=e 2)(，10-==λ、n 是二重特征根，因此设x x ax a x y --=⋅=e e 22*，将其代入到原方程之中，化简有22=a ，得1=a ，于是原方程的一个特解为xx y -=e 2*，原方程的通解为212()exx y C C x x e --=++．（3）相应齐次方程为02=-'+''y y y ，特征方程0122=-+r r ，即0)1)(12(=+-r r ，特征根为2/1121=-=r r 、，相应齐次方程通解为2/21e e x x C C Y +=-．这里2()3f x x x =+-，02==λ、n 不是特征根，因此设c bx ax y ++=2*，代入到原方程之中，有224(2)()3a ax b ax bx c x x ++-++=+-，比较系数有12143a a b a b c -=-⎧⎪-=⎨⎪+-=⎩，，，得112a b c ===、、，于是原方程的一个特解为*22y x x =++．所以，原方程的通解为*/2212e e 2x x y Y y C C x x -=+=++++．（4）相应齐次方程为0=-''y y ，特征方程012=-r ，特征根为1121-==r r 、，相应齐次方程通解为xx C C Y -+=e e 21．这里xx x f e 4)(=，x x P n 4)(=，11==λ、n 是单重特征根，因此设x x bx ax b ax x y e )(e )(2*+=+=，将其代入到原方程之中，化简有x b ax a 4)2(22=++，比较系数得11-==b a 、，于是原方程的一个特解为x x x y e )(2*-=，所以原方程的通解为*y Y y +=x x x x x C C e )(e e 221-++=-．7．求下列各二阶常系数线性非齐次微分方程满足初始条件的特解：（1）261y y x '''-=-，(0)1y =，(0)3y '=；（2）xy y e 54=+''，(0)0y =，(0)1y '=；解：（1）相应齐次方程为20y y '''-=，特征方程220r r -=，特征根为10r =、22r =，相应齐次方程通解为212e xY C C =+．这里()61f x x =-，1n =、0λ=是单重特征根，因此设*2()y x ax b ax bx =+=+，代入到原方程之中，有42261ax a b x -+-=-，得32a =-，1b =-，于是原方程的一个特解为*232y x x =--．所以，原方程的通解为*22123e 2x y Y y C C x x =+=+--． 222e 31x y C x '=--，由初始条件(0)1y =，(0)3y '=，有1221213C C C +=⎧⎨-=⎩，，得11C =-、22C =，所以方程261y y x '''-=-满足初始条件(0)1y =，(0)3y '=的特解为2232e 12x y x x =---．（2）相应齐次方程为04=+''y y ，特征方程042=+r ，特征根为i r i r 2221-==、，相应齐次方程通解为x C x C Y 2sin 2cos 21+=．这里x x f e 5)(=，10==λ、n 不是特征根，因此设xa y e *=，代入到原方程之中，有x x x a a e 5e 4e =+，得1=a 于是原方程的一个特解为xy e *=．所以，原方程的通解为xx C x C y Y y e 2sin 2cos 21*++=+=．122sin 22cos 2e x y C x C x '=-++，由初始条件(0)0y =，(0)1y '=，有1210211C C +=⎧⎨+=⎩，，得11C =-、20C =，所以方程xy y e 54=+''满足初始条件(0)0y =，(0)1y '=的特解为e cos x y x =-．8. 求常系数线性非齐次微分方程2e xy +y =x+'''的通解.解：相应齐次方程为0='+''y y ，特征方程02=+r r ，特征根为1021-==r r 、，相应齐次方程通解为x12Y C C e -=+．这里x x x f e 2)(+=，将其分为)()()(21x f x f x f +=，x x f 2)(1=、xx f e )(2=．对x y y 2='+''，这里01==λ、n 是单重特征根，因此设bx ax b ax x y +=+=2*1)(，代入到x y y 2='+''之中，有x b ax a 2)2(2=++，比较系数得21-==b a 、，于是方程x y y 2='+''的一个特解为x x y 22*1-=；对xy y e ='+''，不难观察得一个特解2/e *2xy =．于是，原方程的一个特解为2/e 22*2*1*xx x y y y +-=+=．所以，原方程的通解为*y Y y +=2/e 2e221x xx x C C +-++=-．.习题12—4（B ）1．若)(1x y ϕ=，)(2x y ϕ=是二阶线性非齐次微分方程)()()(x f y x Q y x P y =+'+''的两个解，证明)()(12x x y ϕϕ-=是相应线性齐次微分方程0)()(=+'+''y x Q y x P y 的解．证：因为)()(12x x y ϕϕ-=，所以212121()()[()()]()[()()]()[()()]y P x y Q x y x x P x x x Q x x x φφφφφφ'''++''''''=-+-+-)]()()()()([)]()()()()([111222x x Q x x P x x x Q x x P x ϕϕϕϕϕϕ+'+''-+'+''= ()()0f x f x =-=．所以)()(12x x y ϕϕ-=是相应线性齐次微分方程0)()(=+'+''y x Q y x P y 的解．2．已知函数x x x x y 21e e )(+=，x x x x y -+=e e )(2，xx x x x y -++=e e e )(23都是微分方程)()()(x f y x Q y x P y =+'+''的解，写出该方程的通解．解：)()()(x f y x Q y x P y =+'+''是二阶非齐次线性微分方程，由函数xx x x y 21e e )(+=，x x x x y -+=e e )(2，x x x x x y -++=e e e )(23都是它的解，根据上题，则x x y y y y 22313e e =-=--、是相应齐次线性微分方程0)()(=+'+''y x Q y x P y 的两个解，而它们之比不恒等于常数，于是它们是线性无关的解，所以0)()(=+'+''y x Q y x P y 的通解为212x xY C e C e -=+，根据二阶非齐次线性微分方程解的结构，得方程)()()(x f y x Q y x P y =+'+''的通解是 22112C e e x x x x y Y y C e e x -=+=+++．3．若二阶常系数线性齐次微分方程的两个特解是2/21e ,e x x y y ==，写出该微分微分方程及其通解．解：由二阶常系数线性齐次微分方程的两个特解是2/21e ,e x x y y ==，则该二阶常系数线性齐次微分方程的特征根是21121==r r 、，于是特征方程是0)21)(1(=--r r ，即01322=+-r r ，所以微分方程为032=+'-''y y y ，通解为2/21e C e x x C y +=．4．若二阶常系数线性齐次微分方程有一个特解xx y 21e -=，写出该微分微分方程及其通解．解：由二阶常系数线性齐次微分方程有一个特解xx y 21e -=，则该二阶常系数线性齐次微分方程有一个特征根2-=r ，并且是二重根，于是特征方程是0)2(2=+r ，即0442=++r r ，所以微分方程为044=+'+''y y y ，通解为xx C y 221)e C (-+=．5．求下列各常系数线性非齐次微分方程的通解：（1）x x y y cos 4=+''；（2）xy y -=''+''e ．解：（1）相应齐次方程为0=+''y y ，特征方程为012=+r ，特征根为i r i r -==21、，应齐次方程通解为x C x C Y sin cos 21+=．这里x x x f cos 4)(=，最高多项式次数1=n ，i i =+βα是单重特征根，为此设*22[()cos +()sin ]=()cos +()sin y x ax b x cx d x ax bx x cx dx x =++++，代入到原方程之中，有x x x c b ax x d a cx cos 4sin )224(cos )224(=+--+++，比较系数有⎪⎪⎩⎪⎪⎨⎧=-=-=+=，，，，022*******b c a d a c 得，⎪⎪⎩⎪⎪⎨⎧====，，，，0110d c b a 于是原方程的一个特解为x x x x y sin cos 2*+=．所以，原方程的通解是x x x x x C x C y sin cos sin cos 221+++=．（2）相应齐次方程为0=''+'''y y ，特征方程为023=+r r ，特征根为、021==r r ，13-=r 应齐次方程通解为x C x C C Y -++=e 321．对原方程xy y -=''+''e ，这里10-==λ，n 是单重特征根，为此设xax y -=e *，代入到原方程之中，有x x x x a x a ---=-+-e e )2(e)3(，即x x a --=e e ，得1=a ，于是原方程x y y -=''+''e 的一个特解为x x y -=e *．所以，原方程的通解是*y Y y +=xx x C x C C --+++=e e 321．6．求下列各二阶常系数线性非齐次微分方程满足初始条件的特解：（1）x y y sin =+''，(0)1y =，(0)0y '=；（2）x y y xcos e 5='-''，(0)0y =，(0)2y '=．解：（1）相应齐次方程为0=+''y y ，特征方程为012=+r ，特征根为i r i r -==21、，应齐次方程通解为x C x C Y sin cos 21+=．对原方程x y y sin =+''，这里多项式最高次数i i n =+=βα，0是单重特征根，为此设x bx x ax y sin cos *+=，代入到原方程之中，有x x b x a sin cos 2sin 2=+-，比较系数有0212==-b a 、，得021=-=b a 、，于是原方程的一个特解为x x y cos 2*-=．所以，原方程的通解是x xx C x C y Y y cos 2sin cos 21*-+=+=． x xx C x C y sin 2cos )21(sin 21+-+-='，由初始条件(0)1y =，(0)0y '=，得21121==C C 、，所以方程满足初始条件的特解为x x x y sin 21cos )21(+-=．（2）相应齐次方程为0='-''y y ，特征方程为02=-r r ，特征根为1021==r r 、，应齐次方程通解为xC C Y e 21+=．对原方程x y y xcos e 5='-''，这里多项式最高次数i i n +=+=10βα，不是特征根，为此设*(cos sin )x y e a x b x =+，代入到原方程之中，有]sin )2(cos )2[(e x b a x a b x--+-x x cos e 5=，比较系数有⎩⎨⎧=--=-，，0252b a a b 得⎩⎨⎧=-=，，21b a 于是原方程的一个特解为)cos sin 2(e *x x y x -=，原方程的通解是)cos sin 2(e e 21*x x C C y Y y x x -++=+=．)cos sin 3(e e 2x x C y xx++='，由初始条件(0)0y =，(0)2y '=，有⎩⎨⎧=+=-+，，2101221C C C 得1021==C C 、，所以原方程满足初始条件的特解是x x x y e )cos sin 21(-+=．7．若连续函数()y f x =满足0()e ()()d xxf x t x f t t =+-⎰，求()y f x =的表达式．解：0()e ()d ()d xx xf x tf t t x f t t =+-⎰⎰，0()e ()d xxf x f t t '=-⎰，()e ()x f x f x ''=-，于是函数()y f x =满足微分方程e x f f ''+=，初始条件是(0)(0)1f f '==．e xf f ''+=是二阶常系数线性非齐次微分方程，相应齐次方程是0f f ''+=，特征方程为012=+r ，特征根为i r i r -==21、，应齐次方程通解为12cos sin Y C x C x =+．对原方程e xf f ''+=，这里10==λ，n 不是特征根，为此设*e xf a =，代入到原方程之中，得21=a ，于是原方程的一个特解为*1e 2x f =．所以，原方程的通解是*121()cos sin e 2xf x Y f C x C x =+=++．因为121()sin cos e 2xf x C x C x '=-++，由初始条件(0)(0)1f f '==，有12112112C C ⎧+=⎪⎪⎨⎪+=⎪⎩，，得2121==C C ，所以所求函数是1()(cos sin e )2xf x x x =++．8. 证明：若()f x 满足方程()(1)f x f x '=-，则必满足方程()()0f x f x ''+=，并求方程()(1)f x f x '=-的解．解：先证()f x 必满足方程()()0f x f x ''+=．由于()(1)f x f x '=-，则求导可得()(1)(1)[1(1)]()f x f x f x f x '''=--=---=-，故证明了()f x 必满足方程()()0f x f x ''+=．下面求解方程()(1)f x f x '=-．由于方程()()0f x f x ''+=的通解为12()cos sin f x C x C x =+，且()(1)f x f x '=-，所以1212sin cos cos(1)sin (1)C x C x C x C x -+=-+-，令0x =可得212cos1sin1C C C =+，则112cos1(1sin1)1sin1cos1C C C +==-，从而方程()(1)f x f x '=-的解为11sin1()(cos sin )cos1f x C x x +=+．习题12—5（A ）1. 设在冷库中存储的某种新鲜水果500吨，放置一段时间之后开始腐烂，腐烂率是未腐烂数量的0.001倍，设腐烂的数量为y 吨，则显然它是时间t 的函数，求此函数的表达式．解：由题意知0.001(500)dyy dt=⨯-，分离变量得，0.001500dydt y=-，两边积分，并整理得0.001500e t y C -=-（C 为任意常数），再结合(0)0y =，容易求出500C =，所以水果腐烂数量与时间的函数关系式为0.001500(1e )t y -=-．2. 已知某商品的需求量Q （单位：kg ）对价格P （单位：元）的弹性为ln 2EQP EP=-，且当0P =时，需求量600Q =Kg. （1）求该商品对价格的需求函数()Q P ；（2）求当价格1P =元时，市场对该商品的需求量；（3）当+P →∞时，需求量是否趋于稳定？解：（1）由已知条件知，ln 2EQ P dQP EP Q dP=⋅=-，分离变量得ln 2dQdP Q=-，所以有()2P Q P C -=（C 为任意常数）．再由(0)600Q =得，600C =，所以()6002P Q P -=⨯．（2）由（1）可知，当1P =元时，1(1)6002300Q -=⨯=（kg ）．（3）由()6002PQ P -=⨯可知，当+P →∞时，0Q →，即随着商品价格的无限增大，。

[VIP专享]大学物理第12章课后习题

Qq 4πε0r 2
E2 r
r＞R2 时，
q 4πε0r 2
int level(BinTreeNodlesevt}r*Beutsl,icnBt(rtrTuiontrcaoTetgtert,_eyapNnpetg)oy;oeN_pddinoeeodtd;fde*esreafc*ttrphsB*au{l)ti;cilrn/duh/tT;ciB/lr/tdo1eiTt;u1ea//NcnrNgoto_loiu(fdn(dtnbe*oetpivdlt{(roe(e}TbidpEititrcfrl(ero!-pbmu>tintrTvritgaey-l(>hlpbulteeie,rtrf=xdt)e,=apr{xkextta,)rt;ru{;k,kr)sd+n;tra+;u1t;ac}0txyBpieTNxv},ooidi{ndet&m*lkac)hi}nil(de)}l;s/e/ js+tr}+uj;cBf+BtoB.+Bid.r.L(;+adikTe+taanN=;t[agojB]e[tdkh=l.se+L+eA1e*+]nr.i;dfc=g(d.-[d;{aiB]1a/it;f/a.;t(dkaA[}ia[]>.kBtdB<}=a];aii.T[BLjt+;aNke.+d[Loni;-]aed-g>t)netahg,B[jt*]+h.)wBd+]{avhi;T=otilareiAedi[n(Be.i{dtm;.<Laive=etAoarngi.0[dLgie],e;jt2Ch=n(o{Sg-0ut9q1h,n/kAL])/t)/iL/[;2s1/e1AtA…aABBmf"…,.S(h+Bq"mniLT6m+irsnet8]e&mhBTen),amidn+dtn&a2Ot*acx(7o10u)n+t)0x{11*ixf=0( nT+o1)d*{ex2i_1f c(+(o!uT2/xn/-*10>tx+l2+cxh=1il;+dnx)o&2/d/h&e=tt_(pn!c:To0o//-duw>1enrw*_c2t/wchx-oi0.1ldu;xon)/)1c*t;cinx6o42.1ucleonfmtt+d/+5ap;t-a5//r7iLg9Cihs4ot8lNuet5nmof9ttdreLp4iegme.=h*ap3tMfAmBol(a[aTrTlit]ex(-;(><i2)nAlccetl[ha0i]}ise=l=ds1,0}A…Tc;[yoine2pu<-nT6ein=-yH>12tp)(]Te;v;enn[Co1-A-ti1o3m1d[u]nA)pHin-[/;in(tv-kL21]ene;]1reyais=A+)nef=[+(t-nm(k1Ta])eAT-p){y>nyA;r-p%c2eh…1iAld3e[2,1]3c,2e1oi20Vn0(u3e=bt×n4i{)n3t1a5)B0);,5b20A}{7,B(2ce[2a150,(l0)ds0cn(a20e,a)]×ie[13j1)1cnr2,a17Af2e0A4,i58g2jtB]b1u(B03}(a5r4,21[En)]06a1B;=07A51([}{0]b937S<A/3)56/HaL([06C0c,sT1b3)]uo[A.>81A0c5u,493]cBn<B0.]=taC5H[L8(0,A1De(4g]k/,Aa5>2EBef0,[)Fy,<]*4C[G)G]b[=2B1,,DHk)g+[]e>,I1AEJy,/[<(,81%C1c]-[8,a5bD1)]C>3C]B,D1<[D1]2Bd62,GFc3E>=41A,V5</1I5EdH475,Gf1231>01+0*J5,91<420G4+0e*30G241,7W1d+*787>13P031,4*9<1L74=41f=0+,515a24953>**/546,17<5+15=0g37413,2*0c5572>/4+517,5<6451*g524,0d+3>956,*5<0315f9+2,3e5W12>14P,12*<3L157g+=56,52f13053>105*693}64*1,{73+80217+9596510*77046873+1*71249264+*9503182+79012*176208590=*2092+8123169831731237*793}W2+531P352L5*0313173+s3T3125158*,21T2052=5,2…915W063…303P5,LTS Tini k1i(2i={a1b,2c,d…e…fg}S0)1,1k10in1i011k11k10n+1kk1Pn21>r+0ikm…00…11+1k0s1=0n11+n21K…ru…snkas1l ns,s=nk,nk a11a121a02K1)aru2s2kaa=2l203*:9(a1i+03/1jA2-03aB(3a131+Aa12=3B+42[…0+]3A…+a3aij1+n3inn149-+iH10-41au+jnfi84+fnm4+16a5B8n+58F1544):52=5706305306.986,2T76:0150,D811:00148110683171,F10ST6:06D413S024H515,1H12:007412101402H*1291u60+22f{f7m4*63a2+n58307*71836+21102*72306+722774*0674128+493}*()4+86*312=513219 5:13/5671(130+7822+6261+p03a1+341352+401143,41)p0=83,21a.8425,913,,p66331:121,0A1a24B13G,,CP4pJ9AD3KG21EHD12AFDaJ3GBH,EPaDHKBApGIBM3J2HEKIF1AJMCKCAEFCMFIIM

大学物理第十二章课后习题答案

第四篇气体动理论热力学基础求解气体动理论和热力学问题的基本思路和方法热运动包含气体动理论和热力学基础两部分．气体动理论从物质的微观结构出发，运用统计方法研究气体的热现象，通过寻求宏观量与微观量之间的关系，阐明气体的一些宏观性质和规律．而热力学基础是从宏观角度通过实验现象研究热运动规律．在求解这两章习题时要注意它们处理问题方法的差异．气体动理论主要研究对象是理想气体，求解这部分习题主要围绕以下三个方面：(1) 理想气体物态方程和能量均分定理的应用；(2) 麦克斯韦速率分布率的应用；(3)有关分子碰撞平均自由程和平均碰撞频率．热力学基础方面的习题则是围绕第一定律对理想气体的四个特殊过程(三个等值过程和一个绝热过程)和循环过程的应用，以及计算热力学过程的熵变，并用熵增定理判别过程的方向．1．近似计算的应用一般气体在温度不太低、压强不太大时，可近似当作理想气体，故理想气体也是一个理想模型．气体动理论是以理想气体为模型建立起来的，因此，气体动理论所述的定律、定理和公式只能在一定条件下使用．我们在求解气体动理论中有关问题时必须明确这一点．然而，这种从理想模型得出的结果在理论和实践上是有意义的．例如理想气体的内能公式以及由此得出的理想气体的摩尔定容热容2/m V,iR C =和摩尔定压热容()2/2m P,R i C +=都是近似公式，它们与在通常温度下的实验值相差不大，因此，除了在低温情况下以外，它们还都是可以使用的．在实际工作时如果要求精度较高，摩尔定容热容和摩尔定压热容应采用实验值．本书习题中有少数题给出了在某种条件下m V,C 和m P,C 的实验值就是这个道理．如习题中不给出实验值，可以采用近似的理论公式计算．2．热力学第一定律解题过程及注意事项热力学第一定律E W Q Δ+=，其中功⎰=21d V V V ρW ，内能增量T R i M m E Δ2Δ⋅=．本章习题主要是第一定律对理想气体的四个特殊过程(等体、等压、等温、绝热)以及由它们组成的循环过程的应用．解题的主要过程：(1) 明确研究对象是什么气体(单原子还是双原子)，气体的质量或物质的量是多少？ (２) 弄清系统经历的是些什么过程，并掌握这些过程的特征．(３) 画出各过程相应的p －V 图．应当知道准确作出热力学过程的p －V 图，可以给出一个比较清晰的物理图像．(４) 根据各过程的方程和状态方程确定各状态的参量，由各过程的特点和热力学第一定律就可计算出理想气体在各过程中的功、内能增量和吸放热了．在计算中要注意Q 和W 的正、负取法．3．关于内能的计算理想气体的内能是温度的单值函数，是状态量，与过程无关，而功和热量是过程量，在两个确定的初、末状态之间经历不同的过程，功和热量一般是不一样的，但内能的变化是相同的，且均等于()12m V,ΔT T C Mm E -=．因此，对理想气体来说，不论其经历什么过程都可用上述公式计算内能的增量．同样，我们在计算某一系统熵变的时候，由于熵是状态量，以无论在始、末状态之间系统经历了什么过程，始、末两个状态间的熵变是相同的．所以，要计算始末两状态之间经历的不可逆过程的熵变，就可通过计算两状态之间可逆过程熵变来求得，就是这个道理．4．麦克斯韦速率分布律的应用和分子碰撞的有关讨论深刻理解麦克斯韦速率分布律的物理意义，掌握速率分布函数f (v )和三种统计速率公式及物理意义是求解这部分习题的关键．三种速率为M RT /2P =v ，M RT π/8=v ，M RT /32=v ．注意它们的共同点都正比于M T /，而在物理意义上和用途上又有区别．P v 用于讨论分子速率分布图．v 用于讨论分子的碰撞；2v 用于讨论分子的平均平动动能．解题中只要抓住这些特点就比较方便．根据教学基本要求，有关分子碰撞内容的习题求解比较简单，往往只要记住平均碰撞频率公式v n d Z 22=和平均自由程n d Z λ2π2/1/==v ，甚至只要知道n Z ⋅∝v ，n /1∝λ及M T /∝v 这种比值关系就可求解许多有关习题．第十二章气体动理论12 －1 处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同，分子的平均平动动能也相同，则它们( )(A) 温度，压强均不相同 (B) 温度相同，但氦气压强大于氮气的压强(C) 温度，压强都相同 (D) 温度相同，但氦气压强小于氮气的压强分析与解理想气体分子的平均平动动能23k /kT =ε，仅与温度有关．因此当氦气和氮气的平均平动动能相同时，温度也相同．又由物态方程nkT p =，当两者分子数密度n 相同时，它们压强也相同．故选(C)．12 －2 三个容器A 、B 、C 中装有同种理想气体，其分子数密度n 相同，方均根速率之比()()()4:2:1::2/12C 2/12B 2/12A =v v v ，则其压强之比C B A ::p p p 为( )(A) 1∶2∶4 (B) 1∶4∶8(C) 1∶4∶16 (D) 4∶2∶1分析与解分子的方均根速率为M RT /3=2v ，因此对同种理想气体有3212C 2B 2A ::::T T T =v v v ，又由物态方程nkT ρ，当三个容器中分子数密度n 相同时，得16:4:1::::321321==T T T p p p .故选(C)． 12 －3 在一个体积不变的容器中，储有一定量的某种理想气体，温度为0T 时，气体分子的平均速率为0v ，分子平均碰撞次数为0Z ，平均自由程为0λ ，当气体温度升高为04T 时，气体分子的平均速率v 、平均碰撞频率Z 和平均自由程λ分别为( ) (A) 004,4,4λλZ Z ===0v v (B) 0022λλ===,,Z Z 0v v (C) 00422λλ===,,Z Z 0v v (D) 0042λλ===,,Z Z 0v v 分析与解理想气体分子的平均速率M RT π/8=v ，温度由0T 升至04T ，则平均速率变为0v 2；又平均碰撞频率v n d Z 2π2=，由于容器体积不变，即分子数密度n 不变，则平均碰撞频率变为0Z 2；而平均自由程n d λ2π2/1=，n 不变，则珔λ也不变．因此正确答案为(B)．12 －4 已知n 为单位体积的分子数，()v f 为麦克斯韦速率分布函数，则()v v d nf 表示( )(A) 速率v 附近，ｄv 区间内的分子数(B) 单位体积内速率在v v v d +~区间内的分子数(C) 速率v 附近，ｄv 区间内分子数占总分子数的比率(D) 单位时间内碰到单位器壁上，速率在v v v d ~+ 区间内的分子数分析与解麦克斯韦速率分布函数()()v v d /d N N f =，而v /N n =，则有()V N nf /d d =v v ．即表示单位体积内速率在v v v d ~+ 区间内的分子数．正确答案为(B)．12 －5 一打足气的自行车内胎，在C 07o1.=t 时，轮胎中空气的压强为Pa 100451⨯=.p ，则当温度变为C 037o2.=t 时，轮胎内空气的压强2p 2p 为多少？(设内胎容积不变)分析胎内空气可视为一定量的理想气体，其始末状态均为平衡态，由于气体的体积不变，由理想气体物态方程RT Mm pV =可知，压强p 与温度T 成正比．由此即可求出末态的压强．解由分析可知，当K 15310037152732...=+=T ，轮胎内空气压强为Pa 1043451122⨯==./T p T p可见当温度升高时，轮胎内气体压强变大，因此，夏季外出时自行车的车胎不宜充气太足，以免爆胎．12 －6 有一个体积为35m 1001⨯.的空气泡由水面下m 050.深的湖底处(温度为C 4o )升到湖面上来．若湖面的温度为C 017o.，求气泡到达湖面的体积．(取大气压强为Pa 10013150⨯=.p ) 分析将气泡看成是一定量的理想气体，它位于湖底和上升至湖面代表两个不同的平衡状态．利用理想气体物态方程即可求解本题．位于湖底时，气泡内的压强可用公式gh p p ρ+=0求出，其中ρ为水的密度( 常取33m kg 1001⋅⨯=.ρ)．解设气泡在湖底和湖面的状态参量分别为(p 1 ，V 1 ，T 1 )和(p 2 ,V 2 ，T 2 )．由分析知湖底处压强为gh ρp gh ρp p +=+=021，利用理想气体的物态方程222111T V p T V p = 可得空气泡到达湖面的体积为()3510120121212m 1011.6//-⨯=+==T p V T gh ρp T p V T p V12 －7 氧气瓶的容积为32m 1023-⨯.，其中氧气的压强为Pa 10317⨯.，氧气厂规定压强降到Pa 10016⨯.时，就应重新充气，以免经常洗瓶．某小型吹玻璃车间，平均每天用去3m 400.压强为Pa 100115⨯.的氧气，问一瓶氧气能用多少天？ (设使用过程中温度不变)分析由于使用条件的限制，瓶中氧气不可能完全被使用．为此，可通过两条不同的思路进行分析和求解：(1) 从氧气质量的角度来分析．利用理想气体物态方程RT Mm pV =可以分别计算出每天使用氧气的质量3m 和可供使用的氧气总质量(即原瓶中氧气的总质量1m 和需充气时瓶中剩余氧气的质量2m 之差)，从而可求得使用天数()321m m m n /-=．(2) 从容积角度来分析．利用等温膨胀条件将原瓶中氧气由初态(Pa 1030171⨯=.p , 321m 1023-⨯=.V )膨胀到需充气条件下的终态(Pa 1000162⨯=.p ，2V 待求)，比较可得2p 状态下实际使用掉的氧气的体积为12V V -．同样将每天使用的氧气由初态(Pa 1001153⨯=.p ，33m 400.=V )等温压缩到压强为p 2的终态，并算出此时的体积V′2 ，由此可得使用天数应为()212V V V n '-=/．解1 根据分析有RT V Mp m RT V Mp m RT V Mp m /;/;/333222111===则一瓶氧气可用天数()()5.9//33121321===-=V p V p p m m m n解2 根据分析中所述，由理想气体物态方程得等温膨胀后瓶内氧气在压强为Pa 1000162⨯=.p 时的体积为 2112p V p V /=每天用去相同状态的氧气容积2332p V p V /='则瓶内氧气可用天数为()()5.9//33121212=-='-=V p V p p V V V n12 －8 设想太阳是由氢原子组成的理想气体，其密度可当作是均匀的．若此理想气体的压强为Pa 1035114⨯.．试估计太阳的温度．(已知氢原子的质量Pa 1067127H -⨯=.m ，太阳半径kg 1067127H -⨯=.m ，太阳质量kg 1099130S ⨯=.m )分析本题可直接运用物态方程nkT p =进行计算．解氢原子的数密度可表示为()⎥⎦⎤⎢⎣⎡⋅==3S H S H S π34//R m m V m m n S 根据题给条件，由nkT p = 可得太阳的温度为()K 1016.13/π4/7S 3S H ⨯===k m R pm nk p T说明实际上太阳结构并非本题中所设想的理想化模型，因此，计算所得的太阳温度与实际的温度相差较大．估算太阳(或星体)表面温度的几种较实用的方法在教材第十五章有所介绍．12 －9 一容器内储有氧气，其压强为Pa 100115⨯.，温度为27 ℃，求：(1)气体分子的数密度；(2) 氧气的密度；(3) 分子的平均平动动能；(4) 分子间的平均距离．(设分子间均匀等距排列)分析在题中压强和温度的条件下，氧气可视为理想气体．因此，可由理想气体的物态方程、密度的定义以及分子的平均平动动能与温度的关系等求解．又因可将分子看成是均匀等距排列的，故每个分子占有的体积为30d V =，由数密度的含意可知n V /10=，d 即可求出．解 (1) 单位体积分子数325m 10442⨯==./kT p n(2) 氧气的密度-3m kg 301⋅===.//RT pM V m ρ(3) 氧气分子的平均平动动能J 102162321k -⨯==./kT ε(4) 氧气分子的平均距离m 10453193-⨯==./n d通过对本题的求解，我们可以对通常状态下理想气体的分子数密度、平均平动动能、分子间平均距离等物理量的数量级有所了解．12 －10 2.0×10－2 kg 氢气装在4.0×10-3 m 3 的容器内，当容器内的压强为3.90×105Pa 时，氢气分子的平均平动动能为多大？分析理想气体的温度是由分子的平均平动动能决定的，即23k /kT =ε．因此，根据题中给出的条件，通过物态方程pV ＝m/MRT ，求出容器内氢气的温度即可得k ε．解由分析知氢气的温度mRMPV T =，则氢气分子的平均平动动能为 ()8932323k ./===mR pVMk kT ε12 －11 温度为0 ℃和100 ℃时理想气体分子的平均平动动能各为多少？欲使分子的平均平动动能等于1eV ，气体的温度需多高？解分子在0℃和100 ℃时平均平动动能分别为J 10655232111-⨯==./kT εJ 10727232122-⨯==./kT ε由于1eV ＝1.6×10－19 J ，因此，分子具有1eV 平均平动动能时，气体温度为K 10737323k ⨯==./k T ε这个温度约为7.5 ×103 ℃．12 －12 某些恒星的温度可达到约1.0 ×108K ，这是发生聚变反应(也称热核反应)所需的温度.通常在此温度下恒星可视为由质子组成.求：(1) 质子的平均动能是多少？ (2) 质子的方均根速率为多大？分析将组成恒星的大量质子视为理想气体，质子可作为质点，其自由度 i ＝3，因此，质子的平均动能就等于平均平动动能.此外，由平均平动动能与温度的关系2/32/2kT m =v ，可得方均根速率2v .解 (1) 由分析可得质子的平均动能为 J 1007.22/32/3152k -⨯===kT m εv(2) 质子的方均根速率为1-62s m 1058.132⋅⨯==mkT v 12 －13 试求温度为300.0 K 和2.7 K(星际空间温度)的氢分子的平均速率、方均根速率及最概然速率.分析分清平均速率v 、方均根速率2v 及最概然速率p v 的物理意义，并利用三种速率相应的公式即可求解.解氢气的摩尔质量M ＝2 ×10－3kg·mol －1 ，气体温度T 1 ＝300.0K ，则有 1-31s m 1078.18⋅⨯==M πRT v 1-312s m 1093.13⋅⨯==M RT v 1-31p s m 1058.12⋅⨯==MRT v 气体温度T 2＝2.7K 时，有 1-31s m 1069.18⋅⨯==M πRT v 1-322s m 1083.13⋅⨯==MRT v1-31p s m 1050.12⋅⨯==MRT v 12 －14 如图所示，Ⅰ、Ⅱ两条曲线分别是氢气和氧气在同一温度下的麦克斯韦分子速率分布曲线.试由图中数据求：(1)氢气分子和氧气分子的最概然速率；(2) 两种气体所处的温度；(3) 若图中Ⅰ、Ⅱ分别表示氢气在不同温度下的麦克斯韦分子速率分布曲线.则哪条曲线的气体温度较高？分析由MRT 1p 2=v 可知，在相同温度下，由于不同气体的摩尔质量不同，它们的最概然速率v p 也就不同.因22O H M M <，故氢气比氧气的v p 要大，由此可判定图中曲线Ⅱ所标v p ＝2.0 ×103 m·s －1 应是对应于氢气分子的最概然速率.从而可求出该曲线所对应的温度.又因曲线Ⅰ、Ⅱ所处的温度相同，故曲线Ⅰ中氧气的最概然速率也可按上式求得.同样，由M RT2p =v 可知，如果是同种气体，当温度不同时，最概然速率v p 也不同.温度越高，v p 越大.而曲线Ⅱ对应的v p 较大，因而代表气体温度较高状态.解 (1) 由分析知氢气分子的最概然速率为()13H p s m 100.222H 2-⋅⨯==M RT v利用M O2 /M H2 ＝16 可得氧气分子最概然速率为()()12H p O p s m 100.54/22-⋅⨯==v v (2) 由M RT2p =v 得气体温度K 1081.42/22p⨯==R M T v (3) Ⅱ代表气体温度较高状态.12 －15 日冕的温度为2.0 ×106K ，所喷出的电子气可视为理想气体.试求其中电子的方均根速率和热运动平均动能.解方均根速率16e2s m 105.93-⋅⨯==m kT v 平均动能J 10142317k -⨯==./kT ε 12 －16 在容积为2.0 ×10－3m 3 的容器中，有内能为6.75 ×102J 的刚性双原子分子某理想气体.(1) 求气体的压强；(2) 设分子总数为5.4×1022 个，求分子的平均平动动能及气体的温度.分析 (1) 一定量理想气体的内能RT i M m E 2=，对刚性双原子分子而言，i ＝5.由上述内能公式和理想气体物态方程pV ＝mM RT 可解出气体的压强.(2)求得压强后，再依据题给数据可求得分子数密度，则由公式p ＝nkT 可求气体温度.气体分子的平均平动动能可由23k /kT ε=求出.解 (1) 由RT i M m E 2=和pV ＝mM RT 可得气体压强 ()Pa 1035125⨯==./iV E p(2) 分子数密度n ＝N/V ，则该气体的温度()()Pa 106235⨯===.//nk pV nk p T气体分子的平均平动动能为J 104972321k -⨯==./kT ε12 －17温度相同的氢气和氧气，若氢气分子的平均平动动能为6.21×10－21J ，试求(1) 氧气分子的平均平动动能及温度；(2) 氧气分子的最概然速率. 分析 (1) 理想气体分子的平均平动动能23k /kT ε=，是温度的单值函数，与气体种类无关.因此，氧气和氢气在相同温度下具有相同的平均平动动能，从而可以求出氧气的温度.(2) 知道温度后再由最概然速率公式M RT 2p =v 即可求解v p . 解 (1) 由分析知氧气分子的平均平动动能为J 102162321k -⨯==./kT ε，则氧气的温度为：K 30032k ==k εT /(2) 氧气的摩尔质量M ＝3.2 ×10－2 kg·mol －1 ，则有 12p s m 1095.32-⋅⨯==M RTv12 －18 声波在理想气体中传播的速率正比于气体分子的方均根速率.问声波通过氧气的速率与通过氢气的速率之比为多少？设这两种气体都是理想气体并具有相同的温度.分析由题意声波速率u 与气体分子的方均根速率成正比，即2v ∝u ；而在一定温度下，气体分子的方均根速率M /12∝v ，式中M 为气体的摩尔质量.因此，在一定温度下声波速率M u /1∝.解依据分析可设声速M A u /1=，式中A 为比例常量.则声波通过氧气与氢气的速率之比为2502222O H O H .==M M u u12 －19 已知质点离开地球引力作用所需的逃逸速率为gr v 2=，其中r 为地球半径.(1) 若使氢气分子和氧气分子的平均速率分别与逃逸速率相等，它们各自应有多高的温度；(2) 说明大气层中为什么氢气比氧气要少.(取r ＝6.40 ×106 m)分析气体分子热运动的平均速率MπRT 8=v ，对于摩尔质量M 不同的气体分子，为使v 等于逃逸速率v ，所需的温度是不同的；如果环境温度相同，则摩尔质量M 较小的就容易达到逃逸速率.解 (1) 由题意逃逸速率gr 2=v ，而分子热运动的平均速率M πRT 8=v .当v v = 时，有RMrg πT 4= 由于氢气的摩尔质量13H mol kg 10022--⋅⨯=.M ，氧气的摩尔质量12O mol kg 10232--⋅⨯=.M ，则它们达到逃逸速率时所需的温度分别为K 10891K,101815O 4H 22⨯=⨯=..T T(2) 根据上述分析，当温度相同时，氢气的平均速率比氧气的要大(约为4倍)，因此达到逃逸速率的氢气分子比氧气分子多.按大爆炸理论，宇宙在形成过程中经历了一个极高温过程.在地球形成的初期，虽然温度已大大降低，但温度值还是很高.因而，在气体分子产生过程中就开始有分子逃逸地球，其中氢气分子比氧气分子更易逃逸.另外，虽然目前的大气层温度不可能达到上述计算结果中逃逸速率所需的温度，但由麦克斯韦分子速率分布曲线可知，在任一温度下，总有一些气体分子的运动速率大于逃逸速率.从分布曲线也可知道在相同温度下氢气分子能达到逃逸速率的可能性大于氧气分子.故大气层中氢气比氧气要少.12 －20 容积为1m 3 的容器储有1mol 氧气，以v ＝10m·s －1 的速度运动，设容器突然停止，其中氧气的80％的机械运动动能转化为气体分子热运动动能.试求气体的温度及压强各升高了多少.分析容器作匀速直线运动时，容器内分子除了相对容器作杂乱无章的热运动外，还和容器一起作定向运动.其定向运动动能(即机械能)为m v 2/2.按照题意，当容器突然停止后，80％定向运动动能转为系统的内能.对一定量理想气体内能是温度的单值函数，则有关系式：()T R M m mv E Δ25%80Δ2⋅=⋅=成立，从而可求ΔT .再利用理想气体物态方程，可求压强的增量. 解由分析知T R M m m E Δ252/8.0Δ2⋅==v ，其中m 为容器内氧气质量.又氧气的摩尔质量为12m ol kg 1023--⋅⨯=.M ，解得ΔT ＝6.16 ×10－2 K当容器体积不变时，由pV ＝mRT/M 得Pa 51.0ΔΔ==T VR M m p 12 －21 有N 个质量均为m 的同种气体分子，它们的速率分布如图所示.(1) 说明曲线与横坐标所包围的面积的含义；(2) 由N 和0v 求a 值；(3) 求在速率0v /2到30v /2 间隔内的分子数；(4) 求分子的平均平动动能.分析处理与气体分子速率分布曲线有关的问题时，关键要理解分布函数()v f 的物理意义. ()v v d /d N N f =，题中纵坐标()v v d /d N Nf =，即处于速率v 附近单位速率区间内的分子数.同时要掌握()v f 的归一化条件，即()1d 0=⎰∞v v f .在此基础上，根据分布函数并运用数学方法(如函数求平均值或极值等)，即可求解本题.解 (1) 由于分子所允许的速率在0 到20v 的范围内，由归一化条件可知图中曲线下的面积()1d 0=⎰∞v v f 即曲线下面积表示系统分子总数N .(2 ) 从图中可知，在0 到0v 区间内，()0/v v v a Nf ；而在0 到20v 区间，()αNf =v .则利用归一化条件有v v v v v ⎰⎰+=000200d d v v a a N (3) 速率在0v /2到30v /2间隔内的分子数为12/7d d Δ2/300000N a a N =+=⎰⎰v v v v v v v (4) 分子速率平方的平均值按定义为()v v f v v v d /d 02022⎰⎰∞∞==N N 故分子的平均平动动能为20220302K 3631d d 2121000v v v v v v v v v v m N a N a m m ε=⎥⎦⎤⎢⎣⎡+==⎰⎰ 12 －22 试用麦克斯韦分子速率分布定律导出方均根速率和最概然速率. 分析麦克斯韦分子速率分布函数为()⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=kT m kT m f 2exp π2π4222/3v v v 采用数学中对连续函数求自变量平均值的方法，求解分子速率平方的平均值，即⎰⎰=N Nd d 22v v ，从而得出方均根速率.由于分布函数较复杂，在积分过程中需作适当的数学代换.另外，最概然速率是指麦克斯韦分子速率分布函数极大值所对应的速率，因而可采用求函数极值的方法求得.解 (1) 根据分析可得分子的方均根速率为2/1242/302/1022d 2exp π2π4/d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎰⎰∞v v v v v kT m kT m N N N令222/x kT m =v ，则有 2/12/12/104273.13d 2π42⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡=⎰∞-m RT m kT x e x m kT x v(2) 令()0d d =v v f ，即 02exp 222exp 2π2π42222/3=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛kT m kT m kT m T k m v v v v v 得 2/12/141.12⎪⎭⎫ ⎝⎛≈⎪⎭⎫ ⎝⎛==m RT m kT P v v12 －23 导体中自由电子的运动可看作类似于气体分子的运动(故称电子气).设导体中共有N 个自由电子，其中电子的最大速率为v Ｆ (称为费米速率).电子在速率v v v d ~+之间的概率为()()⎪⎩⎪⎨⎧>>>=v v v v v v 0,0 d π4d F 2A N A N N (1)画出分布函数图；(2) 用N 、v Ｆ定出常数A ；(3) 证明电子气中电子的平均动能53F /εε=，其中22F F /mv =ε.分析理解速率分布函数的物理意义，就不难求解本题.速率分布函数()vv d d 1N N f =，表示在v 附近单位速率区间的粒子数占总粒子数的百分比.它应满足归一化条件()()⎰⎰=∞F 00d d v v v v v f f ，因此根据题给条件可得()v v ~f 的函数关系，由此可作出解析图和求出A .在()v v ~f 函数关系确定的情况下，由()v v v v d 22f ⎰=可以求出v2 ，从而求出2/2v m ε=. 解 (1) 由题设可知，电子的速率分布函数()()()⎪⎩⎪⎨⎧>>>=F F 2 00 π4v v v v v v N A f ，其分布函数图如图所示. (2) 利用分析中所述归一化条件，有1d π4F02=⎰v v v NA 得 3F π4/3v N A = (3) ()53d N 4ππd 2F 20022F v v v v v v v v ===⎰⎰∞f 5/32/F 2εm ε==v12 －24 一飞机在地面时，机舱中的压力计指示为Pa 100115⨯.，到高空后压强降为Pa 101184⨯..设大气的温度均为27.0 ℃.问此时飞机距地面的高度为多少？(设空气的摩尔质量为2.89 ×10－2 kg·mol －1 )分析当温度不变时，大气压强随高度的变化主要是因为分子数密度的改变而造成.气体分子在重力场中的分布满足玻耳兹曼分布.利用地球表面附近气压公式()kT mgh p p /ex p 0-=，即可求得飞机的高度h .式中p 0 是地面的大气压强.解飞机高度为 ()()m 1093.1/ln /ln 300⨯===p p MgRT p p mg kT h 12 －25 在压强为Pa 1001.15⨯下，氮气分子的平均自由程为6.0×10－6cm,当温度不变时，在多大压强下，其平均自由程为1.0mm 。

人教版八年级上册数学第十二章全等三角形含答案

人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、在正方形ABCD中，E、F分别为BC、CD边上的两个动点，∠EAF＝45°，下列几个结论中：①EF＝BE＋DF；②MN2＝BM2＋DN2；③FA平分∠DFE；④连接MF，则△AMF为等腰直角三角形；⑤∠AMN＝∠AFE. 其中一定成立的结论有（）A.2个B.3个C.4个D.5个2、已知AD是△ABC的边BC上的中线，AB=12，AC=8，则边BC及中线AD的取值范围是（）A. B. C.D.3、如图：EA∥DF，AE=DF，要使△AEC≌△DBF，则只要（）A.AB=CDB.EC=BFC.∠A=∠DD.AB=BC4、如图，为等边三角形，是边上一点，在上取一点，使，在边上取一点，使，则的度数为（）A. B. C. D.5、如图，在菱形ABCD中，∠BAD＝100°，AB的垂直平分线交AC于点F，点E 为垂足，连接DF，则∠CDF＝（）A.50°B.40°C.30°D.15°6、AD是△ABC中∠BAC的平分线，DE⊥AB于点E，DF⊥AC交AC于点F．S△=7，DE=2，AB=4，则AC长是（）ABCA.4B.3C.6D.27、如图，△ABC和△DEF中，AB=DE，∠B=∠DEF，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（）A.AC=DFB.AC∥DFC.∠A=∠DD.∠ACB=∠F8、两个直角三角形全等的条件是（）A.一个锐角对应相等B.一条边对应相等C.两条直角边对应相等 D.两个角对应相等9、如图，∠ABC＝∠ABD，还应补充一个条件，才能推出△ABC≌△ABD.补充下列其中一个条件后，不一定能推出△ABC≌△ABD的是（）A.BC＝BDB.AC＝ADC.∠ACB＝∠ADBD.∠CAB＝∠DAB10、如图，在Rt△ABC中，∠ACB=90°，分别以AB、AC为腰向外作等腰直角三角形△ABD和△ACE，连结DE，CA的延长线交DE于点F,则与线段AF相等的是( )A. ACB. ABC. BCD. AB11、如图，是的角平分线，，垂足为E，，，，则长为（）A. B. C. D.12、如图，在Rt△ABC中，∠ACB＝90°，AE为△ABC的角平分线，且ED⊥AB，若AC＝6，BC＝8，则BD的长（）A.2B.3C.4D.513、如果△ABC的三边长分别为3，5，7，△DEF的三边长分别为3，3x－2，2x －1，若这两个三角形全等，则x等于（）A. B.3 C.4 D.514、下列说法正确的是（）A.全等三角形是指形状相同的两个三角形B.全等三角形的周长和面积分别相等C.全等三角形是指面积相等的两个三角形D.所有的等边三角形都是全等三角形15、下列命题中正确的命题有（）个①两个全等的三角形一定关于某直线对称；②等腰三角形的高、中线、角平分线互相重合；③等腰三角形的对称轴是顶角的平分线④顶角和底边对应相等的两个等腰三角形全等；A. B. C. D.二、填空题(共10题，共计30分)16、如图，在△ABC中，∠ABC＝45°，AC＝9cm，F是高AD和BE的交点，则BF的长是________.17、如图，已知≌，点B，E，C，F在同一条直线上，若，则=________．18、如图，∠C＝∠D＝90º，添加一个条件：________ (写出一个条件即可)，可使 Rt△ABC 与Rt△ABD 全等．19、如图，△ABC，点E是AB上一点，D是BC的中点，连接ED并延长至点F，使DF=DE，连接CF，则线段BE与线段CF的关系为________．20、如图（1）～（12）中全等的图形是________ 和________ ；________ 和________ ；________ 和________；________ 和________ ；________和________ ；________ 和________ ；（填图形的序号）21、如图，D为等边△ABC中边BC的中点，在边DA的延长线上取一点E，以CE 为边、在CE的左下方作等边△CEF，连结AF.若AB＝4，AF＝，则CF的值为________.22、如图，△ABC是等边三角形，AE＝CD，AD、BE相交于点P，BQ⊥DA于Q，PQ＝3，EP＝1，则DA的长是________.23、如图，在平面直角坐标系中，经过点A的双曲线同时经过点B，且点A在点B的左侧，点A的横坐标为，∠AOB=∠OBA=45°，则的值为________.24、如图，点P是的平分线上一点，PB AB与B，且PA=5cm，AC=12cm，则的面积是________ .25、如图， AB = 4cm ， AC = BD = 3cm . ∠CAB = ∠DBA ，点 P 在线段 AB 上以1cm / s 的速度由点 A 向点 B 运动，同时，点Q 在线段 BD 上由点 B 向点 D 运动.设运动时间为t(s) ，则当点Q 的运动速度为________cm / s 时， DACP 与DBPQ 全等.三、解答题(共5题，共计25分)26、如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC27、如图，在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：DF=BE．28、如图，AB∥CD，AB=CD，点E、F在AD上，且AE=DF．求证：△ABE≌△DCF．29、提出问题：如图1，将三角板放在正方形ABCD上，使三角板的直角顶点P 在对角线AC上，一条直角边经过点B，另一条直角边交边DC于点E，求证：PB=PE分析问题：学生甲：如图1，过点P作PM⊥BC，PN⊥CD，垂足分别为M，N通过证明两三角形全等，进而证明两条线段相等．学生乙：连接DP，如图2，很容易证明PD=PB，然后再通过“等角对等边”证明PE=PD，就可以证明PB=PE了．解决问题：请你选择上述一种方法给予证明．问题延伸：如图3，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交DC的延长线于点E，PB=PE还成立吗？若成立，请证明；若不成立，请说明理由．30、写出命题：“等腰三角形两腰上的高相等”的逆命题，并证明其逆命题是真命题.（要求写出已知、求证和证明过程）.参考答案一、单选题(共15题，共计45分)1、D2、A3、A4、C5、C6、B7、A8、C9、B10、C11、B12、C13、B14、B15、A二、填空题(共10题，共计30分)16、17、18、19、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、。

高等数学课后习题及参考答案(第十二章)

高等数学课后习题及参考答案（第十二章）习题12-1 1试说出下列各微分方程的阶数(1)x (y ')2-2yy '+x =0 解一阶 (2)x 2y '-xy '+y =0 解一阶 (3)xy '''+2y '+x 2y =0解三阶(4)(7x -6y )dx +(x +y )dy =0解一阶(5)022=++C Qdt dQ RdtQ d L解二阶(6)θρθρ2sin =+d d解一阶 2 指出下列各题中的函数是否为所给微分方程的解(1)xy '=2y y =5x 2解 y '=10x因为xy '=10x 2=2(5x 2)=2y 所以y =5x 2是所给微分方程的解(2)y '+y =0y =3sin x -4cos x解 y '=3cos x +4sin x因为y '+y =3cos x +4sin x +3sin x -4cos x =7sin x -cos x ≠0所以y =3sin x -4cos x 不是所给微分方程的解(3)y ''-2y '+y =0 y =x 2e x解 y '=2xe x +x 2e xy ''=2e x +2xe x +2xe x +x 2e x =2e x +4xe x +x 2e x因为y ''-2y '+y =2e x +4xe x +x 2e x -2(2xe x +x 2e x )+x 2e x =2e x ≠0所以y =x 2e x 不是所给微分方程的解(4)y ''-(1+2)y '+12y =0xx e C e C y 2121λλ+= 解 x x e C e C y 212211λλλλ+=' xx e C e C y 21222211λλλλ+=''因为y y y 2121)(λλλλ+'+-'')())((2121212121221121222211x x x x x x e C e C e C e C e C e C λλλλλλλλλλλλλλ++++-+= =0所以x x e C e C y 2121λλ+=是所给微分方程的解3 在下列各题中验证所给二元方程所确定的函数为所给微分方程的解(1)(x -2y )y '=2x -yx 2-xy +y 2=C解将x 2-xy +y 2=C 的两边对x 求导得 2x -y -xy '+2y y '=0即 (x -2y )y '=2x -y所以由x 2-xy +y 2=C 所确定的函数是所给微分方程的解(2)(xy -x )y ''+xy '2+yy '-2y '=0 y =ln(xy )解将y =ln(xy )的两边对x 求导得y y x y '+='11 即x xy yy -='再次求导得)(1)()()1()(2222y y y y y x x xy x xy y y y x x xy y x y y x xy y y '+'-'-⋅-=-+-'-=--'+--'=''注意到由y y x y '+='11可得1-'='y x y yx 所以)2(1])1([12y y y y x x xy y y y y y x x xy y '+'-'-⋅-='+'-'-'-⋅-=''从而 (xy -x )y ''+xy '2+yy '-2y '=0即由y =ln(xy )所确定的函数是所给微分方程的解4 在下列各题中确定函数关系式中所含的参数使函数满足所给的初始条件 (1)x 2-y 2=Cy |x =0=5解由y |x =0=0得02-52=C C =-25 故x 2-y 2=-25(2)y =(C 1+C 2x )e 2x y |x =0=0y '|x =0=1解 y '=C 2e 2x +2(C 1+C 2x )e 2x由y |x =0=0y '|x =0=1得⎩⎨⎧=+=1121C C C解之得C 1=0 C 2=1故y =xe 2x(3)y =C 1sin(x -C 2) y |x ==1 y '|x ==0解 y '=C 1cos(x -C 2) 由y |x ==1y '|x ==0得⎩⎨⎧=-=-0)cos(1)sin(2121C C C C ππ 即⎩⎨⎧=-=0cos 1sin 2121C C C C解之得C 1=1 22π=C 故)2sin(π-=x y 即y =-cos x5写出由下列条件确定的曲线所满足的微分方程(1)曲线在点(x y )处的切线的斜率等于该点横坐标的平方解设曲线为y =y (x ) 则曲线上点(xy )处的切线斜率为y '由条件y '=x 2 这便是所求微分方程(2)曲线上点P (xy )处的法线与x 轴的交点为Q 且线段PQ 被y 轴平分解设曲线为y =y (x ) 则曲线上点P (xy )处的法线斜率为y '-1 由条件第PQ 中点的横坐标为0 所以Q 点的坐标为(-x0) 从而有y x x y '-=+-10即yy '+2x =0 6用微分方程表示一物理命题某种气体的气压P 对于温度T 的变化率与气压成正比所温度的平方成反比解 2T P k dT dP = 其中k 为比例系数习题12-21 求下列微分方程的通解 (1)xy '-y ln y =0 解分离变量得dx xdy y y 1ln 1=两边积分得⎰⎰=dx xdy y y 1ln 1即 ln(ln y )=ln x +ln C , 故通解为y =e Cx .(2)3x 2+5x -5y '=0 解分离变量得5dy =(3x 2+5x )dx 两边积分得⎰⎰+=dxx x dy )53(52即 123255C x x y ++=故通解为C x x y ++=232151 其中151C C =为任意常数(3)2211y y x -='-解分离变量得2211x dx y dy-=-两边积分得⎰⎰-=-2211x dx y dy即 arcsin y =arcsin x +C故通解为y =sin(arcsin x +C ) (4)y '-xy '=a (y 2+y ')解方程变形为(1-x -a )y '=ay 2分离变量得dx x a a dy y--=112两边积分得⎰⎰--=dx x a a dy y112即 1)1ln(1C x a a y----=-故通解为)1ln(1x a a C y --+= 其中C =aC 1为任意常数(5)sec 2x tan ydx +sec 2y tan xdy =0 解分离变量得dx xx y y y tan sec tan sec 22-=两边积分得⎰⎰-=dx xx y y y tan sec tan sec 22 即 ln(tan y )=-ln(tan x )+ln C故通解为tan x tan y =C(6)y x dxdy+=10解分离变量得10-y dy =10x dx 两边积分得⎰⎰=-dxdy x y 1010即 10ln 10ln 1010ln 10C x y +=-- 或 10-y =10x +C 故通解为y =-lg(C -10x )(7)(e x +y -e x )dx +(e x +y +e y )dy =0解方程变形为e y (e x +1)dy =e x (1-e y )dx分离变量得dxe e dy e e xx y y +=-11两边积分得⎰⎰+=-dx e e dy e e xx y y 11 即 -ln(e y )=ln(e x +1)-ln C 故通解为(e x +1)(e y -1)=C(8)cos x sin ydx +sin x cos ydy =0 解分离变量得dx xx dy y ysin cos sin cos -= 两边积分得⎰⎰-=dx xx dy y ysin cos sin cos 即 ln(sin y )=-ln(sin x )+ln C 故通解为sin x sin y =C(9)0)1(32=++x dxdyy解分离变量得(y +1)2dy =-x 3dx 两边积分得⎰⎰-=+dxx dy y 32)1(即 14341)1(31C x y +-=+故通解为4(y +1)3+3x 4=C (C =12C 1) (10)ydx +(x 2-4x )dy =0 解分离变量得dx xx dy y )411(4-+=两边积分得⎰⎰-+=dx xx dy y )411(4即 ln y 4=ln x -ln(4-x )+ln C 故通解为y 4(4-x )=Cx2 求下列微分方程满足所给初始条件的特解(1)y '=e 2x -y y |x =0=0 解分离变量得 e y dy =e 2x dx 两边积分得⎰⎰=dxe dy e x y 2即 C e e x y +=221或 )21ln(2C e y x +=由y |x =0=0得0)21ln(=+C 21=C所以特解)2121ln(2+=x e y(2)cos x sin ydy =cos y sin xdx 4|0π==x y解分离变量得 tan y dy =tan x dx 两边积分得⎰⎰=xdxydy tan tan即 -ln(cos y )=-ln(cos x )-ln C 或 cos y =C cos x 由4|0π==x y 得CC ==0cos 4cos π 21=C所以特解为x y cos cos 2=(3)y 'sin x =y ln yey x ==2π解分离变量得dx xdy y y sin 1ln 1=两边积分得⎰⎰=dx x dy y y sin 1ln 1即 Cx y ln )2ln(tan )ln(ln +=或2tan x C e y =由e y x ==2π得4tan πC e e = C =1所以特解为2tan x e y =(4)cos ydx +(1+e -x )sin ydy =0 4|0π==x y解分离变量得dx e e dy y y xx +=-1cos sin两边积分得⎰⎰+=-dx e e dy y y xx 1cos sin即 ln|cos y |=ln(e x +1)+ln |C |或 cos y =C (e x +1)由4|0π==x y 得)1(4cos 4+=ππe C 42=C 所以特解为)1(42cos +=x e y(5)xdy +2ydx =0 y |x =2=1 解分离变量得 dx xdy y 21-=两边积分得⎰⎰-=dx xdy y 21即 ln y =-2ln x +ln C 或 y =Cx -2由y |x =2=1得C ⋅2-2=1 C =4 所以特解为24xy =3. 有一盛满了水的圆锥形漏漏斗, 高为10cm , 顶角为60︒, 漏斗下面有面积为0. 5cm 2的孔, 求水面高度变化的规律及流完所需的时间.解设t 时该已流出的水的体积为V , 高度为x 则由水力学有 x dtdV )9802(5.062.0⨯⨯⨯=, 即dt x dV )9802(5.062.0⨯⨯⨯=. 又因为330tan x x r =︒=,故 dx x dx r V 223ππ-=-=,从而 dx x dt x 23)9802(5.062.0π-=⨯⨯⨯,即 dx x dt 2398025.062.03⨯⨯⨯=π,因此 C x t +⨯⨯⨯-=2598025.062.032π.又因为当t =0时, x =10, 所以251098025.062.053⨯⨯⨯⨯=πC ,故水从小孔流出的规律为645.90305.0)10(98025.062.0532252525+-=-⨯⨯⨯⨯=x x t π.令x =0, 得水流完所需时间约为10s .4. 质量为1g (克)的质点受外力作用作直线运动, 这外力和时间成正比, 和质点运动的速度成反比. 在t =10s 时, 速度等于50cm/s , 外力为4g cm/s 2, 问从运动开始经过了一分钟后的速度是多少？解已知v t k F =, 并且法t =10s 时, v =50cm/s , F =4g cm/s 2, 故50104k =, 从而k =20, 因此vt F 20=.又由牛顿定律, F =ma , 即vt dt dv 201=⋅, 故v dv =20t d t . 这就是速度与时间应满足的微分方程. 解之得C t v +=221021, 即C t v 2202+=.由初始条件有C +⨯=⨯2210105021, C =250. 因此500202+=t v .当t =60s 时, cm/s 3.26950060202=+⨯=v .5. 镭的衰变有如下的规律: 镭的衰变速度与它的现存量R 成正比. 由经验材料得知, 镭经过1600年后, 只余原始量R 0的一半. 试求镭的量R 与时间t 的函数关系.解由题设知,R dt dR λ-=, 即dt RdR λ-=,两边积分得ln R =-λt +C 1, 从而 )( 1C t e C Ce R ==-λ.因为当t =0时, R =R 0, 故R 0=Ce 0=C , 即R =R 0e -λt .又由于当t =1600时, 021R R =, 故λ16000021-=e R R , 从而16002ln =λ.因此t te R e R R 000433.0010002ln 0--==.6. 一曲线通过点(2, 3), 它在两坐标轴间的任一切线线段均被切点所平分, 求这曲线方程.解设切点为P (x , y ), 则切线在x 轴, y 轴的截距分别为2x , 2y , 切线斜率为x yx y -=--2002,故曲线满足微分方程:xy dx dy -=, 即dx x dy y 11-=,从而 ln y +ln x =ln C , xy =C .因为曲线经过点(2, 3), 所以C =2⨯3=6, 曲线方程为xy =6.7. 小船从河边点O 处出发驶向对岸(两岸为平行直线). 设船速为a , 船行方向始终与河岸垂直, 又设河宽为h , 河中任一点处的水流速度与该点到两岸距离的乘积成正比(比例系数为k ). 求小船的航行路线.解建立坐标系如图. 设t 时刻船的位置为(x , y ), 此时水速为)(y h ky dtdx v -==, 故dx =ky (h -y )dt . 又由已知, y =at , 代入上式得 dx =kat (h -at )dt , 积分得C t ka kaht x +-=3223121.由初始条件x |t =0=0, 得C =0, 故3223121t ka kaht x -=.因此船运动路线的函数方程为⎪⎩⎪⎨⎧=-=ayy t ka kaht x 3223121, 从而一般方程为)312(32y y h a k x -=.习题12-31 求下列齐次方程的通解 (1)022=---'x y y y x解原方程变为1)(2--=xy x y dx dy令xyu =则原方程化为12-+=+u u dxdu x u 即dxx du u 1112=-两边积分得C x u u ln ln )1ln(2+=-+ 即Cx u u =-+12将xyu =代入上式得原方程的通解 Cx xyx y =-+1)(2 即222Cx x y y =-+(2)xy y dx dy xln =解原方程变为xyx y dx dy ln =令xy u =则原方程化为u u dxdu x u ln =+ 即dx x du u u 1)1(ln 1=-两边积分得ln(ln u -1)=ln x +ln C 即u =e Cx +1将xyu =代入上式得原方程的通解y =xe Cx +1(3)(x 2+y 2)dx -xydy =0 解这是齐次方程令xy u =即y =xu 则原方程化为(x 2+x 2u 2)dx -x 2u (udx +xdu )=0即dxxudu 1=两边积分得u 2=ln x 2+C将xyu =代入上式得原方程的通解y 2=x 2(ln x 2+C )(4)(x 3+y 3)dx -3xy 2dy =0解这是齐次方程令x yu = 即y =xu则原方程化为(x 3+x 3u 3)dx -3x 3u 2(udx +xdu )=0即dx x du u u 121332=-两边积分得C x u ln ln )21ln(213+=-- 即2312x Cu -= 将xyu =代入上式得原方程的通解x 3-2y 3=Cx(5)0ch 3)ch 3sh 2(=-+dy xyx dx x y y x y x解原方程变为xyx y dx dy +=th 32令xyu = 则原方程化为u u dx du x u +=+th 32 即dx xdu u u 2sh ch 3=两边积分得3ln(sh u )=2ln x +ln C 即sh 3u =Cx 2将xyu =代入上式得原方程的通解22sh Cx xy=(6)0)1(2)21(=-++dy yx e dx e y xy x解原方程变为yx y xe e yx dydx 21)1(2+-=令yx u = 则原方程化为uu e e u dy du y u 21)1(2+-=+ 即uue e u dy du y 212++-=分离变量得dyy du eu e u u1221-=++两边积分得ln(u +2e u )=-ln y +ln C 即y (u +2e u )=C将y x u =代入上式得原方程的通解Ce yx y y x=+)2(即C ye x yx=+22 求下列齐次方程满足所给初始条件的特解 (1)(y 2-3x 2)dy +2xydx =0 y |x =0=1解这是齐次方程令xyu =, 即y =xu 则原方程化为(x 2u 2-3x 2)(udx +xdu )+2x 2udx =0即 dx x du u u u 1332=-- 或dx xdu u u u 1)11113(=-+++-两边积分得-3ln |u |+ln|u +1|+ln|u -1|=ln|x |+ln|C | 即u 2-1=Cxu 3将xyu =代入上式得原方程的通解y 2-x 2=Cy 3由y |x =0=1得C =1 故所求特解为y 2-x 2=y 3(2)xyy x y +=' y |x =1=2解令xyu =, 则原方程化为 u u dx du x u +=+1 即dx xudu 1=两边积分得C x u +=ln 212将xyu =代入上式得原方程的通解y 2=2x 2(ln x +C )由y |x =1=2得C =2 故所求特解为y 2=2x 2(ln x +2)(3)(x 2+2xy -y 2)dx +(y 2+2xy -x 2)dy =0 y |x =1=1解这是齐次方程令xyu =, 即y =xu 则原方程化为(x 2+2x 2u -x 2u 2)dx +(x 2u 2+2x 2u -x 2)(udx +xdu )=0即 dxx du u u u u u 1112232-=+++-+或 dx xdu u u u 1)1211(2=+-+ 两边积分得ln|u +1|-ln(u 2+1)=ln|x |+ln|C | 即u +1=Cx (u 2+1)将xyu =代入上式得原方程的通解x +y =C (x 2+y 2)由y |x =1=1得C =1 故所求特解为x +y =(x 2+y 2)3设有连结点O (00)和A (11)的一段向上凸的曲线弧A O对于A O上任一点P (xy ) 曲线弧P O与直线段OP 所围图形的面积为x 2 求曲线弧A O的方程解设曲线弧A O的方程为y =y (x ) 由题意得20)(21)(x x xy dx x y x=-⎰两边求导得x x y x x y x y 2)(21)(21)(='--即 4-='x yy令xy u = 则有4-=+u dx du x u 即dx xdu u 41-=两边积分得u =-4ln x +C将xyu =代入上式得方程的通解y =-4x ln x +Cx 由于A (1 1)在曲线上即y (1)=1 因而C =1 从则所求方程为y =-4x ln x +x习题12-41. 求下列微分方程的通解:(1)x e y dxdy-=+;解 )()()(C x e C dx e e e C dx e e e y x x x x dxx dx +=+⋅=+⎰⋅⎰=-----⎰⎰.(2)xy '+y =x 2+3x +2;解原方程变为x x y x y 231++=+'.])23([11C dx e xx e y dx x dxx +⎰⋅++⎰=⎰- ])23([1])23([12C dx x x xC xdx x x x +++=+++=⎰⎰xC x x C x x x x +++=+++=22331)22331(1223.(3)y '+y cos x =e -sin x ;解 )(cos sin cos C dx e e e y xdxx dx +⎰⋅⎰=⎰--)()(sin sin sin sin C x e C dx e e e x x x x +=+⋅=---⎰.(4)y '+y tan x =sin 2x ;解 )2sin (tan tan C dx e x e y xdx xdx +⎰⋅⎰=⎰- )2sin (cos ln cos ln C dx e x e x x +⋅=⎰- ⎰+⋅=)cos 1cos sin 2(cos C dx xx x x=cos x (-2cos x +C )=C cos x -2cos 2x . (5)(x 2-1)y '+2xy -cos x =0;解原方程变形为1cos 1222-=-+'x x y x x y .)1cos (1221222C dx e x x e y dx x xdx x x +⎰⋅-⎰=⎰--- )(sin 11])1(1cos[112222C x x C dx x x x x +-=+-⋅--=⎰. (6)23=+ρθρd d ;解 )2(33C d e e d d +⎰⋅⎰=⎰-θρθθ)2(33C d e e +=⎰-θθθ θθθ33332)32(--+=+=Ce C e e .(7)x xy dxdy42=+;解 )4(22C dx e x e y xdxxdx +⎰⋅⎰=⎰-)4(22C dx e x e x x +⋅=⎰- 2222)2(x x x Ce C e e --+=+=. (8)y ln ydx +(x -ln y )dy =0;解原方程变形为y x y y dy dx 1ln 1=+.)1(ln 1ln 1C dy e ye x dy y y dyy y +⎰⋅⎰=⎰-)ln 1(ln 1C ydy yy +⋅=⎰yC y C y y ln ln 21)ln 21(ln 12+=+=.(9)3)2(2)2(-+=-x y dxdyx ; 解原方程变形为2)2(221-=--x y x dx dy.])2(2[21221C dx e x e y dxx dx x +⎰⋅-⎰=⎰---⎰+-⋅--=]21)2(2)[2(2C dx x x x=(x -2)[(x -2)2+C ]=(x -2)3+C (x -2).(10)02)6(2=+-y dxdyx y .解原方程变形为y x y dy dx 213-=-.])21([33C dy e y e x dy y dy y +⎰⋅-⎰=⎰- )121(33C dy yy y +⋅-=⎰32321)21(Cy y C y y +=+=.2. 求下列微分方程满足所给初始条件的特解:(1)x x y dx dysec tan =-, y |x =0=0;解 )sec (tan tan C dx e x e y xdxxdx+⎰⋅⎰=⎰-)(cos 1)cos sec (cos 1C x xC xdx x x +=+⋅=⎰. 由y |x =0=0, 得C =0, 故所求特解为y =x sec x .(2)x x x ydx dy sin =+, y |x =π=1;解)sin (11C dx e xx e y dx x dx x +⎰⋅⎰=⎰-)cos (1)sin (1C x xC xdx x x x +-=+⋅=⎰.由y |x =π=1, 得C =π-1, 故所求特解为)cos 1(1x x y --=π.(3)x e x y dx dycos 5cot =+, 4|2-==πx y ; 解 )5(cot cos cot C dx e e e y xdx x xdx +⎰⋅⎰=⎰-)5(sin 1)sin 5(sin 1cos cos C e xC xdx e x x x +-=+⋅=⎰. 由4|2-==πx y , 得C =1, 故所求特解为)15(sin 1cos +-=x e x y .(4)83=+y dxdy, y |x =0=2; 解 )8(33C dx e e y dxdx +⎰⋅⎰=⎰-x x x x x Ce C e e C dx e e 3333338)38()8(---+=+=+=⎰.由y |x =0=2, 得32-=C , 故所求特解为)4(323x e y --=.(5)13232=-+y x x dx dy , y |x =1=0. 解)1(32323232C dx e e y dxx x dx x x +⎰⋅⎰=⎰---)21()1(22221131313C e e x C dx e x e x x x x x +=+=--⎰. 由y |x =1=0, 得eC 21-=, 故所求特解为)1(211132--=x e x y .3. 求一曲线的方程, 这曲线通过原点, 并且它在点(x , y )处的切线斜率等于2x +y .解由题意知y '=2x +y , 并且y |x =0=0. 由通解公式得)2()2(C dx xe e C dx xe e y x x dxdx +=+⎰⎰=⎰⎰--=e x (-2xe -x -2e -x +C )=Ce x -2x -2.由y |x =0=0, 得C =2, 故所求曲线的方程为y =2(e x -x -1).4. 设有一质量为m 的质点作直线运动, 从速度等于零的时刻起, 有一个与运动方向一至、大小与时间成正比(比例系数为k 1)的力作用于它, 此外还受一与速度成正比(比例系数为k 2)的阻力作用. 求质点运动的速度与时间的函数关系.解由牛顿定律F =ma , 得v k t k dtdv m 21-=, 即t m kv m k dt dv 12=+.由通解公式得 )()(222211C dt e t m k e C dt e t m k ev t m kt m k dt mk dt m k +⋅=+⎰⋅⎰=⎰⎰--)(22222121C e k m k te k k et m kt mk tmk +-=-. 由题意, 当t =0时v =0, 于是得221k mk C =. 因此 )(22122121222k m k e k m k te k k ev t m k t m k t m k +-=-即 )1(222121t m ke k mk t k k v ---=.5. 设有一个由电阻R =10Ω、电感L =2h(亨)和电源电压E =20sin5t V (伏)串联组成的电路. 开关K 合上后, 电路中有电源通过. 求电流i 与时间t 的函数关系. 解由回路电压定律知01025sin 20=--i dt di t , 即t i dtdi 5sin 105=+.由通解公式得t dtdt Ce t t C dt e t e i 5555cos 5sin )5sin 10(--+-=+⎰⋅⎰=⎰.因为当t =0时i =0, 所以C =1. 因此)45sin(25cos 5sin 55π-+=+-=--t e e t t i t t (A).6. 设曲dy x x xf dx x yf L])(2[)(2-+⎰在右半平面(x >0)内与路径无关, 其中f (x )可导, 且f (1)=1, 求f (x ).解因为当x >0时, 所给积分与路径无关, 所以 ])(2[)]([2x x xf xx yf y -∂∂=∂∂,即 f (x )=2f (x )+2xf '(x )-2x , 或 1)(21)(=+'x f x x f .因此xC x C dx x x C dx e e x f dx x dxx +=+=+⎰⋅⎰=⎰⎰-32)(1)1()(2121. 由f (1)=1可得31=C , 故x x x f 3132)(+=.7. 求下列伯努利方程的通解:(1))sin (cos 2x x y y dxdy-=+;解原方程可变形为x x ydx dy y sin cos 112-=+, 即x x y dx y d cos sin )(11-=---. ])cos sin ([1C dx e x x e y dxdx +⎰⋅-⎰=--⎰x Ce C dx e x x e x x x sin ])sin (cos [-=+-=⎰-, 原方程的通解为x Ce yx sin 1-=.(2)23xy xy dxdy=-; 解原方程可变形为 x y x dxdy y =-1312, 即x xy dx y d -=+--113)(. ])([331C dx e x e y xdxxdx +⎰⋅-⎰=⎰--)(222323C dx xe e x x +-=⎰-31)31(222232323-=+-=--x x x Ce C e e , 原方程的通解为311223-=-x Ce y . (3)4)21(3131y x y dx dy -=+; 解原方程可变形为 )21(31131134x y dx dy y -=+, 即12)(33-=---x y dx y d . ])12([3C dx e x e y dxdx +⎰⋅-⎰=--⎰x x x Ce x C dx e x e +--=+-=⎰-12])12([, 原方程的通解为1213--=x Ce yx .(4)5xy y dxdy=-; 解原方程可变形为 x ydx dy y =-4511, 即x y dx y d 44)(44-=+--. ])4([444C dx e x e y dxdx +⎰⋅-⎰=⎰--)4(44C dx xe e x +-=⎰- x Ce x 441-++-=,原方程的通解为x Ce x y 44411-++-=.(5)xdy -[y +xy 3(1+ln x )]dx =0. 解原方程可变形为)ln 1(11123x y x dx dy y +=⋅-⋅, 即)ln 1(22)(22x y x dx y d +-=+--.])ln 1(2[222C dx e x e ydx x dx x +⎰⋅+-⎰=⎰-- ])ln 1(2[122C dx x x x++-=⎰ x x x x C 94ln 322--=, 原方程的通解为x x x x C y 94ln 32122--=. 8. 验证形如yf (xy )dx +xg (xy )dy =0的微分方程, 可经变量代换v =xy 化为可分离变量的方程, 并求其通解. 解原方程可变形为)()(xy xg xy yf dx dy -=. 在代换v =xy 下原方程化为)()(22v g x v vf x v dx dv x -=-, 即dx xdu v f v g v v g 1)]()([)(=-, 积分得 C x du v f v g v v g +=-⎰ln )]()([)(, 对上式求出积分后, 将v =xy 代回, 即得通解.9. 用适当的变量代换将下列方程化为可分离变量的方程, 然后求出通解:(1)2)(y x dxdy+=;解令u =x +y , 则原方程化为 21u dx du =-, 即21udu dx +=.两边积分得x =arctan u +C .将u =x +y 代入上式得原方程的通解x =arctan(x +y )+C , 即y =-x +tan(x -C ).(2)11+-=yx dx dy;解令u =x -y , 则原方程化为111+=-udx du , 即dx =-udu .两边积分得1221C u x +-=.将u =x +y 代入上式得原方程的通解12)(21C y x x +--=, 即(x -y )2=-2x +C (C =2C 1).(3)xy '+y =y (ln x +ln y );解令u =xy , 则原方程化为u x u x u x u dx du x x ln )1(2=+-, 即du uu dx x ln 11=.两边积分得ln x +ln C =lnln u , 即u =e Cx . 将u =xy 代入上式得原方程的通解 xy =e Cx , 即Cx e xy 1=.(4)y '=y 2+2(sin x -1)y +sin 2x -2sin x -cos x +1; 解原方程变形为y '=(y +sin x -1)2-cos x . 令u =y +sin x -1, 则原方程化为 x u x dx du cos cos 2-=-, 即dx du u =21. 两边积分得C x u+=-1.将u =y +sin x -1代入上式得原方程的通解C x x y +=-+-1sin 1, 即Cx x y +--=1sin 1.(5)y (xy +1)dx +x (1+xy +x 2y 2)dy =0 . 解原方程变形为)1()1(22y x xy x xy y dx dy +++-=. 令u =xy , 则原方程化为)1()1(1222u u x u u x u dx du x +++-=-, 即)1(1223u u x u dx du x ++=. 分离变量得du uu u dx x )111(123++=. 两边积分得u uu C x ln 121ln 21+--=+.将u =xy 代入上式得原方程的通解xy xy y x C x ln 121ln 221+--=+, 即 2x 2y 2ln y -2xy -1=Cx 2y 2(C =2C 1).习题12-5 1判别下列方程中哪些是全微分方程并求全微分方程的通解(1)(3x 2+6xy 2)dx +(6x 2y +4y 2)dy =0解这里P =3x 2+6xy 2 Q =6x 2y +4y 2因为x Qxy y P ∂∂==∂∂12所以此方程是全微分方程其通解为Cdy y y x dx x yx=++⎰⎰02202)46(3即 Cy y x x =++3223343(2)(a 2-2xy -y 2)dx -(x +y )2dy =0解这里P =a 2-2xy -y 2Q =-(x +y )2 因为x Qy x y P ∂∂=--=∂∂22所以此方程是全微分方程其通解为Cdy y x dx a yx=+-⎰⎰0202)(即 a 2x -x 2y -xy 2=C(3)e y dx +(xe y -2y )dy =0解这里P =e y Q =xe y -2y因为x Qe y P y ∂∂==∂∂所以此方程是全微分方程其通解为Cdy y xe dx e yy x =-+⎰⎰000)2(即 xe y -y 2=C(4)(x cos y +cos x )y '-y sin x +sin y =0解原方程变形为(x cos y +cos x )dy -(y sin x +sin y )dx =0这里P =-(y sin x +sin y ) Q =x cos y +cos x因为x Qx y y P ∂∂=-=∂∂sin cos所以此方程是全微分方程其通解为Cdy x y x dx yx=++⎰⎰00)cos cos (0即 x sin y +y cos x =C 解(5)(x 2-y )dx -xdy =0 解这里P =x 2-yQ =-x 因为xQy P ∂∂=-=∂∂1所以此方程是全微分方程其通解为Cxdy dx x yx=-⎰⎰002即 C xy x =-331(6)y (x -2y )dx -x 2dy =0解这里P =y (x -2y ) Q =-x 2 因为yx y P 4-=∂∂ x x Q 2-=∂∂所以此方程不是全微分方程 (7)(1+e 2)d+2e 2d=0解这里P =1+e 2 Q =2e 2因为x Qe y P ∂∂==∂∂θ22所以此方程是全微分方程其通解为Cd e d =+⎰⎰θθρθρρ02022即(e 2+1)=C(8)(x 2+y 2)dx +xydy =0解这里P =x 2+y 2 Q =xy 因为y y P 2=∂∂ y x Q=∂∂所以此方程不是全微分方程2利用观察法求出下列方程的积分因子并求其通解(1)(x +y )(dx -dy )=dx +dy解方程两边同时乘以yx +1得yx dydx dy dx ++=- 即d (x -y )=d ln(x +y )所以y x +1为原方程的一个积分因子并且原方程的通解为x -y =ln(x +y )+C(2)ydx -xdy +y 2xdx =0解方程两边同时乘以21y 得02=+-xdx yxdyydx 即0)2()(2=+x d y x d所以21y为原方程的一个积分因子并且原方程的通解为C x y x =+22(3)y 2(x -3y )dx +(1-3y 2x )dy =0解原方程变形为xy 2dx -3y 3dx +dy -3x 2dy =0两边同时乘以21y并整理得)33(2=+-+xdy ydx ydyxdx 即0)(3)1()2(2=--xy d yd x d所以21y为原方程的一个积分因子并且原方程的通解为C xy yx =--3122 (4)xdx +ydy =(x 2+y 2)dx解方程两边同时乘以221y x +得 022=-++dx y x ydyxdx 即0)]ln(21[22=-+dx y x d所以221y x +为原方程的一个积分因子并且原方程的通解为x 2+y 2=Ce 2x(5)(x -y 2)dx +2xydy =0 解原方程变形为 xdx -y 2dx +2xydy =0两边同时乘以21x得0222=-+x dx y xydy x dx 即0)()(ln 2=+x y d x d 所以21x为原方程的一个积分因子并且原方程的通解为C xy x =+2ln 即x ln x +y 2=Cx(6)2ydx -3xy 2dx -xdy =0 解方程两边同时乘以x 得 2xydx -x 2dy -3x 2y 2dx =0 即yd (x 2)-x 2dy -3x 2y 2dx =0再除以y 2得03)(2222=--dx x ydyx x yd 即0)(32=-x y x d所以2yx 为原方程的一个积分因子并且原方程的通解为032=-x yx3 验证)]()([1xy g xy f xy -是微分方程yf (xy )dx +xg (xy )dy =0的积分因子并求下列方程的通解解方程两边乘以)]()([1xy g xy f xy -得0])()([)]()([1=+-dy xy xg dx xy yf xy g xy f xy 这里)]()([)(xy g xy f x xy f P -= )]()([)(xy g xy f y xy g Q -=因为x Qxy g xy f xy g xy f xy g xy f y P ∂∂=-'-'=∂∂2)]()([)()()()( 所以)]()([1xy g xy f xy -是原方程的一个积分因子(1)y (x 2y 2+2)dx +x (2-2x 2y 2)dy =0解这里f (xy )=x 2y 2+2 g (xy )=2-2x 2y 2所以3331)]()([1y x xy g xy f xy =- 是方程的一个积分因子方程两边同乘以3331y x 得全微分方程 032323222232=-++dy y x y x dx y x x其通解为Cdy y x y x dx x x y x=-++⎰⎰132221323232即 Cy x y x =-+-)11ln (ln 31222或2212yx e Cy x =(2)y (2xy +1)dx +x (1+2xy -x 3y 3)dy =0解这里f (x y )=2x y +1 g (x y )=1+2x y -x 3 y 3 , 所以441)]()([1yx xy g xy f xy =- 是方程的一个积分因子方程两边同乘以441yx 得全微分方程2112433334=-+++dy y x y x xy dx y x xy其通解为 C dy y x y x xy dx x x y x =-+++⎰⎰14333142112即 C y y x y x =++||ln 31133224用积分因子法解下列一阶线性方程(1)xy '+2y =4ln x解原方程变为xxy x y ln 42=+' 其积分因子为22)(x e x dxx =⎰=μ在方程x x y x y ln 42=+'的两边乘以x 2得x 2y '+2xy =4x ln x 即(x 2y )'=4x ln x两边积分得C x x x xdx x y x +-==⎰222ln 2ln 4原方程的通解为21ln 2x Cx y +-=(2)y '-tan x ⋅y =x解积分因子为x e x xdxcos )(tan =⎰=-μ在方程的两边乘以cos x 得 cos x ⋅y '-sin x ⋅y =x cos x 即(cos x ⋅y )'=x cos x两边积分得C x x x xdx x y x ++==⋅⎰cos sin cos cos方程的通解为xCx x y cos 1tan ++=习题12-61 求下列各微分方程的通解 (1)y ''=x +sin x解 12cos 21)sin (C x x dx x x y +-=+='⎰21312sin 61)cos 21(C x C x x dx C x x y ++-=+-=⎰原方程的通解为213sin 61C x C x x y ++-=(2)y '''=xe x解 12C e xe dx xe y x x x +-==''⎰21122)2(C x C e xe dx C e xe y x x x x ++-=+-='⎰3221213)22(C x C x C e xe dx C x C e xe y x x x x +++-=++-=⎰原方程的通解为32213C x C x C e xe y x x +++-=(3)211xy +=''解 12arctan 11C x dx xy +=+='⎰x C dx xx x x dx C x y 1211arctan )(arctan ++-=+=⎰⎰212)1ln(21arctan C x C x x x +++-=原方程的通解为2121ln arctan C x C x x x y +++-=(4)y ''=1+y '2解令p =y ' 则原方程化为p '=1+p 2 即dx dp p=+211两边积分得arctan p =x +C 1 即y '=p =tan(x +C 1) 211|)cos(|ln )tan(C C x dx C x y ++-=+=⎰原方程的通解为21|)cos(|ln C C x y ++-=(5)y ''=y '+x解令p =y ' 则原方程化为 p '-p =x由一阶线性非齐次方程的通解公式得1)()(111--=+=+⎰⋅⎰=⎰⎰--x e C C dx xe e C dx e x e p x x x dxdx即 y '=C 1e x -x -1于是 221121)1(C x x e C dx x e C y x x +--=--=⎰原方程的通解为22121C x x e C y x +--=(6)xy ''+y '=0解令p =y ' 则原方程化为 x p '+p =0 即01=+'p xp由一阶线性齐次方程的通解公式得xC e C e C p xdxx 1ln 111==⎰=--即 x C y 1=' 于是 211ln C x C dx xCy +==⎰原方程的通解为 y =C 1ln x +C 2(7)yy ''+'=y '2 解令p =y ' 则dydppdx dy dy dp y =⋅='' 原方程化为 21p dydpyp=+ 即dy y dp p p 112=-两边积分得||ln ||ln |1|ln 2112C y p +=- 即22121y C p ±-当|y '|=|p |>1时方程变为 2211y C y +±=' 即dxdy y C ±=+21)(11两边积分得arcsh(C 1y )=±C 1x +C 2 即原方程的通解为)(sh 1121x C C C y ±=当|y '|=|p |<1时方程变为2211y C y -±=' 即dxdy y C ±=-21)(11两边积分得arcsin(C 1y )=±C 1x +C 2 即原方程的通解为)(sin 1121x C C C y ±=(8)y 3y ''-1=0 解令p =y ' 则dydp py ='' 原方程化为013=-dydppy 即pdp =y -3dy两边积分得122212121C y p +-=- 即p 2=-y -2+C 1故 21--±='y C y 即dx dy yC ±=--211两边积分得)(12121C x C y C +±=-即原方程的通解为 C 1y 2=(C 1x +C 2)2(9)y y 1=''解令p =y ' 则dydp py ='' 原方程化为y dy dp p1= 即dyypdp 1=两边积分得122221C y p += 即1244C y p += 故 12C y y +±=' 即dx dy C y ±=+11两边积分得原方程的通 211231]2)(32[C C y C C y x ++-+±=(10)y ''=y '3+y ' 解令p =y '则dydppy ='' 原方程化为 p p dy dp p +=3 即0)]1([2=+-p dydpp由p =0得y =C 这是原方程的一个解由0)1(2=+-p dydp得arctan p =y -C 1 即y '=p =tan(y -C 1)从而 )sin(ln )tan(1112C y dy C y C x -=-=+⎰ 故原方程的通解为12arcsin C e y C x +=+2 求下列各微分方程满足所给初始条件的特解(1)y 3 y ''+1=0 y |x =1=1 y '|x =1=0解令p =y ', 则dy dpp y ='', 原方程化为013=+dy dppy , 即dy ypdp 31-=, 两边积分得1221C yp +=, 即y y C y 211+±='.由y |x =1=1, y '|x =1=0得C 1=-1, 从而y y y 21-±=',分离变量得 dx dy yy=-±21, 两边积分得221C x y +=-± 即22)(1C x y +-±=由y |x =1=1得C 2=-1, 2)1(1--=x y 从而原方程的通解为22x x y -=.(2)y ''-ay '2=0 y |x =0=0 y '|x =0=-1解令p =y ', 则原方程化为02=-ap dxdp即adxdp p=21两边积分得11C ax p+=- 即11C ax y +-='由y '|x =0=-1得C 1=111+-='ax y 两边积分得2)1ln(1C ax a y ++-=由y |x =0=0得C 2=0故所求特解为)1ln(1+-=ax ay(3)y '''=e ax y |x =1=y '|x =1=y ''|x =1=0 解 11C e adx e y ax ax +==''⎰由y ''|x =1=0得a e aC 11-=2211)11(C x e a e a dx e a e a y a ax a ax +-=-='⎰由y '|x =1=0得a a e ae a C 2211-=dx e a e a x e a e a y a a a ax )1111(22⎰-+-= 322311211C x e a x e a x e a e a a a a ax +-+-= 由y |x =1=0得a a a a e a e a e a e a C 32312111-+-= 故所求特解为 322232)22()1(2a a a e a x a e a x e a e y a a a ax ----+-=(4)y ''=e 2y y |x =0=y '|x =0=0解令p =y ', 则dydpp y ='', 原方程化为y e dydpp 2= 即pdp =e 2y dy积分得p 2=e 2y +C 1即12C e y y +±='由y |x =0=y '|x =0=0得C 1=-1 故12-±='y e y 从而dx dy e y±=-112 积分得-arcsin e -y =±x +C 2 由y |x =0=0得22π-=C 故x x e y cos )2sin(=-=-π从而所求特解为y =-lncos x (5)yy 3='' y |x =0=1y '|x =0=2解令p =y ', 则dydppy ='', 原方程化为 y dydpp 3= 即dy y pdp 3=两边积分得12322221C y p += 即1232C y y +±=' 由y |x =0=1 y '|x =0=2得C 1=0432y y =' 从而dxdy y 243=-两边积分得24124C x y += 即42)4121(C x y +=由y |x =0=1得C 2=4故原方程的特解为4)121(+=x y(6)y ''+y '2=1 y |x =0=0 y '|x =0=0解令p =y ', 则dy dpp y ='', 原方程化为12=+p dydpp 即2222=+p dydp于是 1)2(211222+=+⎰⋅⎰=--⎰y dydy e C C dy e e p即 121+±='-y e C y由y |x =0=0 y '|x =0=0得C 1=-1ye y 21--±='故dx dy ey ±=--211两边积分得22)1ln(C x e e y y +±=-+由y |x =0=0得C 2=0xe e y y ±=-+)1ln(2从而得原方程的特解y =lnch x3 试求y ''=x 的经过点M (01)且在此点与直线121+=x y 相切的积分曲线解 1221C x y +='21361C x C x y ++=由题意得y |x =0=121|0='=x y由21|0='=x y 得211=C 再由y |x =0=1得C 2=1 因此所求曲线为121613++=x x y4 设有一质量为m 的物体在空中由静止开始下落如果空气阻力为R =c 2v 2(其中c 为常数 v 为物体运动的速度) 试求物体下落的距离s 与时间t 的函数关系解以t =0对应的物体位置为原点垂直向下的直线为s 正轴建立坐标系由题设得⎪⎩⎪⎨⎧==-===0| |0022t t v s v c mg dt dv m将方程分离变量得 dt vc mg mdv =-22两边积分得 1||ln C kt mgcv mgcv +=-+(其中m g c k 2=) 由v |t =0=0得C 1=0ktmgcv mg cv =-+||ln 即ktem gcv m g cv =-+。

高数第十二章习题答案

2 2
y 2 x 2 0 （ y y 2 x 2 Cx 2 ）
2
2. x y x xy y
（ y x tan(ln x C ) ）
3.
( xy y ) cos 2
y
y 1 2y y x0 sin C ln x 2 （ x 2 ） x x
3 x2
D. 是特解
4. y 3 xy, y Ce 2 A. 是解
（ C ） C. 是通解 D. 是特解
B. 不是解
四、求下列可分离变量的微分方程解： 1. ( xy x)dx ( y x y )dy 0 （ y 1 C ( x 1) ）
2 2 2 2
2. y e
2
（ D ） C. 是通解 D. 是特解
B. 不是解
2. y y 0, y 3sin x 4 cos x （ B ） A. 是解 B. 不是解
2 x
C. 是通解（ B ） C. 是通解
D. 是特解
3. y 2 y y 0, y x e A. 是解 B. 不是解
2
二、指出下列微分方程的阶，同时指出它是线性的，还是非线性的： 1. x( y) 2 yy x 1 （一n x
2
（二阶线性微分方程）
1 y2 dy 3. dx 1 x 2 （一阶非线性微分方程）
4. (7 x 3 y ) dx ( x y ) dy 0 （一阶非线性微分方程）三、指出下列各题中的函数是否为所给微分方程的解，如果是解，是通解，还是特解？ 1. xy 2 y, y 5 x A. 是解
x y
5. (e
e x )dx (e x y e y )dy 0 （ (e x 1)(e y 1) C ）

高鸿业《宏观经济学》课后习题答案第十二章--习题答案

第十二章国民收入核算1.宏观经济学和微观经济学有什么联系和区别？为什么有些经济活动从微观看是合理的,有效的,而从宏观看却是不合理的,无效的？解答：两者之间的区别在于：<1>研究的对象不同.微观经济学研究组成整体经济的单个经济主体的最优化行为,而宏观经济学研究一国整体经济的运行规律和宏观经济政策.<2>解决的问题不同.微观经济学要解决资源配置问题,而宏观经济学要解决资源利用问题.<3>中心理论不同.微观经济学的中心理论是价格理论,所有的分析都是围绕价格机制的运行展开的,而宏观经济学的中心理论是国民收入<产出>理论,所有的分析都是围绕国民收入<产出>的决定展开的.<4>研究方法不同.微观经济学采用的是个量分析方法,而宏观经济学采用的是总量分析方法.两者之间的联系主要表现在：<1>相互补充.经济学研究的目的是实现社会经济福利的最大化.为此,既要实现资源的最优配置,又要实现资源的充分利用.微观经济学是在假设资源得到充分利用的前提下研究资源如何实现最优配置的问题,而宏观经济学是在假设资源已经实现最优配置的前提下研究如何充分利用这些资源.它们共同构成经济学的基本框架.<2>微观经济学和宏观经济学都以实证分析作为主要的分析和研究方法.<3>微观经济学是宏观经济学的基础.当代宏观经济学越来越重视微观基础的研究,即将宏观经济分析建立在微观经济主体行为分析的基础上.由于微观经济学和宏观经济学分析问题的角度不同,分析方法也不同,因此有些经济活动从微观看是合理的、有效的,而从宏观看是不合理的、无效的.例如,在经济生活中,某个厂商降低工资,从该企业的角度看,成本低了,市场竞争力强了,但是如果所有厂商都降低工资,则上面降低工资的那个厂商的竞争力就不会增强,而且职工整体工资收入降低以后,整个社会的消费以与有效需求也会降低.同样,一个人或者一个家庭实行节约,可以增加家庭财富,但是如果大家都节约,社会需求就会降低,生产和就业就会受到影响.2.举例说明最终产品和中间产品的区别不是根据产品的物质属性而是根据产品是否进入最终使用者手中.解答：在国民收入核算中,一件产品究竟是中间产品还是最终产品,不能根据产品的物质属性来加以区别,而只能根据产品是否进入最终使用者手中这一点来加以区别.例如,我们不能根据产品的物质属性来判断面粉和面包究竟是最终产品还是中间产品.看起来,面粉一定是中间产品,面包一定是最终产品.其实不然.如果面粉为面包厂所购买,则面粉是中间产品,如果面粉为家庭主妇所购买,则是最终产品.同样,如果面包由面包商店卖给消费者,则此面包是最终产品,但如果面包由生产厂出售给面包商店,则它还属于中间产品.3.举例说明经济中流量和存量的联系和区别,财富和收入是流量还是存量？解答：存量指某一时点上存在的某种经济变量的数值,其大小没有时间维度,而流量是指一定时期内发生的某种经济变量的数值,其大小有时间维度；但是二者也有联系,流量来自存量,又归于存量,存量由流量累积而成.拿财富与收入来说,财富是存量,收入是流量.4.为什么人们从公司债券中得到的利息应计入GDP,而从政府公债中得到的利息不计入GDP？解答：购买公司债券实际上是借钱给公司用,公司将从人们手中借到的钱用作生产经营,比方说购买机器设备,这样这笔钱就提供了生产性服务,可被认为创造了价值,因而公司债券的利息可看作是资本这一要素提供生产性服务的报酬或收入,因此要计入GDP.可是政府的公债利息被看作是转移支付,因为政府借的债不一定用于生产经营,而往往是用于弥补财政赤字.政府公债利息常常被看作是用从纳税人身上取得的收入来加以支付的,因而习惯上被看作是转移支付.5.为什么人们购买债券和股票从个人来说可算是投资,但在经济学上不算是投资？解答：经济学上所讲的投资是增加或替换资本资产的支出,即建造新厂房、购买新机器设备等行为,而人们购买债券和股票只是一种证券交易活动,并不是实际的生产经营活动.人们购买债券或股票,是一种产权转移活动,因而不属于经济学意义的投资活动,也不能计入GDP.公司从人们手里取得了出售债券或股票的货币资金再去购买厂房或机器设备,才算投资活动.6.为什么政府给公务员发工资要计入GDP,而给灾区或困难人群发的救济金不计入GDP？解答：政府给公务员发工资要计入GDP是因为公务员提供了为社会工作的服务,政府给他们的工资就是购买他们的服务,因此属于政府购买,而政府给灾区或困难人群发的救济金不计入GDP,并不是因为灾区或困难人群提供了服务,创造了收入,相反,是因为他们发生了经济困难,丧失了生活来源才给予其救济的,因此这部分救济金属于政府转移支付.政府转移支付只是简单地通过税收<包括社会保险税>把收入从一个人或一个组织手中转移到另一个人或另一个组织手中,并没有相应的货物或劳务的交换发生.所以政府转移支付和政府购买虽都属政府支出,但前者不计入GDP而后者计入GDP.7.为什么企业向政府缴纳的间接税<如营业税>也计入GDP？解答：间接税虽由出售产品的厂商缴纳,但它是加到产品价格上作为产品价格的构成部分由购买者负担的.间接税虽然不形成要素所有者收入,而是政府的收入,但毕竟是购买商品的家庭或厂商的支出,因此,为了使支出法计得的GDP 和收入法计得的GDP相一致,必须把间接税加到收入方面计入GDP.举例说,某人购买一件上衣支出100美元,这100美元以支出形式计入GDP.实际上,若这件上衣价格中含有5美元的营业税和3美元的折旧,则作为要素收入的只有92美元.因而,从收入法计算GDP时,应把这5美元和3美元一起加到92美元中作为收入计入GDP.8.下列项目是否计入GDP,为什么？<1>政府转移支付；<2>购买一辆用过的卡车；<3>购买普通股票；<4>购买一块地产.解答：<1>政府转移支付不计入GDP,因为政府转移支付只是简单地通过税收<包括社会保险税>把收入从一个人或一个组织手中转移到另一个人或另一个组织手中,并没有相应的货物或劳务的交换发生.例如,政府给残疾人发放救济金,并不是因为残疾人创造了收入；相反,是因为他丧失了创造收入的能力从而失去了生活来源才给予其救济的.<2>购买用过的卡车不计入GDP,因为卡车生产时已经计入GDP了,当然买卖这辆卡车的交易手续费是计入GDP的.<3>买卖股票的价值不计入GDP,例如我买卖了一万元某股票,这仅是财产权的转移,并不是价值的生产.<4>购买一块地产也只是财产权的转移,因而也不计入GDP.9.在统计中,社会保险税增加对GDP、NDP、NI、PI和DPI这五个总量中哪个总量有影响？为什么？解答：社会保险税实质上是企业和职工为得到社会保障而支付的保险金,它由政府有关部门<一般是社会保险局>按一定比率以税收的形式征收.社会保险税是从国民收入中扣除的,因此,社会保险税的增加并不影响GDP、NDP和NI,但影响个人收入PI.社会保险税增加会减少个人收入,从而也从某种意义上会影响个人可支配收入.然而,应当认为社会保险税的增加并不直接影响个人可支配收入,因为一旦个人收入确定以后,只有个人所得税的变动才会影响个人可支配收入DPI.10.如果甲乙两国合并成一个国家,对GDP总和会有什么影响<假定两国产出不变>？解答：如果甲乙两国合并成一个国家,对GDP总和会有影响.因为甲乙两国未合并成一个国家时,双方可能有贸易往来,但这种贸易只会影响甲国或乙国的GDP,对两国GDP总和不会有影响.举例说,甲国向乙国出口10台机器,价值10万美元,乙国向甲国出口800套服装,价值8万美元,从甲国看,计入GDP的有净出口2万美元,从乙国看,计入GDP的有净出口－2万美元；从两国GDP总和看,计入GDP的价值为零.如果这两国并成一个国家,两国贸易就变成两地区间的贸易.甲地区出售给乙地区10台机器,从收入看,甲地区增加10万美元；从支出看,乙地区增加10万美元.相反,乙地区出售给甲地区800套服装,从收入看,乙地区增加8万美元；从支出看,甲地区增加8万美元.由于甲乙两地属于同一个国家,因此,该国共收入18万美元,而投资加消费的支出也是18万美元,因此,无论从收入还是从支出看,计入GDP的价值都是18万美元.11.假设某国某年发生了以下活动：<a>一银矿公司支付7.5万美元工资给矿工开采了50千克银卖给一银器制造商,售价10万美元；<b>银器制造商支付5万美元工资给工人加工一批项链卖给消费者,售价40万美元.<1>用最终产品生产法计算GDP.<2>每个生产阶段生产了多少价值？用增值法计算GDP.<3>在生产活动中赚得的工资和利润各共为多少？用收入法计算GDP.解答：<1>项链为最终产品,价值40万美元.<2>开矿阶段生产10万美元,银器制造阶段生产30万美元,即40万美元－10万美元＝30万美元,两个阶段共增值40万美元.<3>在生产活动中,所获工资共计7.5＋5＝12.5<万美元>在生产活动中,所获利润共计<10－7.5>＋<30－5>＝27.5<万美元>用收入法计得的GDP为12.5＋27.5＝40<万美元>可见,用最终产品法、增值法和收入法计得的GDP是相同的.12.一经济社会生产三种产品：书本、面包和菜豆.它们在1998年和1999年的产量和价<2>1999年名义GDP；<3>以1998年为基期,1998年和1999年的实际GDP是多少,这两年实际GDP变化多少百分比？<4>以1999年为基期,1998年和1999年的实际GDP是多少,这两年实际GDP变化多少百分比？<5>"GDP的变化取决于我们用哪一年的价格作衡量实际GDP的基期的价格.〞这句话对否？<6>用1998年作为基期,计算1998年和1999年的GDP折算指数.解答：<1>1998年名义GDP＝100×10＋200×1＋500×0.5＝1450<美元>.<2>1999年名义GDP＝110×10＋200×1.5＋450×1＝1850<美元>.<3>以1998年为基期,1998年实际GDP＝1450美元,1999年实际GDP＝110×10＋200×1＋450×0.5＝1525<美元>,这两年实际GDP变化百分比＝<1525－1450>/1450≈5.17%.<4>以1999年为基期,1999年实际GDP＝1850<美元>,1998年的实际GDP＝100×10＋200×1.5＋500×1＝1800<美元>,这两年实际GDP变化百分比＝<1850－1800>/1800≈2.78%.<5>GDP的变化由两个因素造成：一是所生产的物品和劳务数量的变动,二是物品和劳务价格的变动."GDP的变化取决于我们以哪一年的价格作衡量实际GDP的基期的价格〞这句话只说出了后一个因素,所以是不完整的.<6>用1998年作为基期,1998年GDP折算指数＝名义GDP/实际GDP＝1450/1450＝100%,1999年GDP折算指数＝1850/1525＝121.3%.13.假定一国有下列国民收入统计资料：单位：亿美元试计算：<1>国内生产净值；<2>净出口；<3>政府税收减去转移支付后的收入；<4>个人可支配收入；<5>个人储蓄.解答：<1>国内生产净值＝国内生产总值－资本消耗补偿,而资本消耗补偿即折旧等于总投资减净投资后的余额,即500＝800－300,因此国内生产净值＝4800－500＝4300<亿美元>.<2>从GDP＝c＋i＋g＋nx中可知nx＝GDP－c－i－g,因此,净出口nx＝4800－3000－800－960＝40<亿美元>.<3>用BS代表政府预算盈余,T代表净税收即政府税收减去转移支付后的收入,则有BS ＝T－g,从而有T＝BS＋g＝30＋960＝990<亿美元>.<4>个人可支配收入本来是个人收入减去个人所得税后的余额,本题条件中没有说明间接税、公司利润、社会保险税等因素,因此,可从国民生产净值中直接得到个人可支配收入,即y d＝NNP－T＝4300－990＝3310<亿美元>.<5>个人储蓄S＝y d－c＝3310－3000＝310<亿美元>.14.假定国内生产总值是5000,个人可支配收入是4100,政府预算赤字是200,消费是3800,贸易赤字是100<单位都是亿元>.试计算：<1>储蓄；<2>投资；<3>政府支出.解答：<1>用s代表储蓄<即私人储蓄s p>,用y d代表个人可支配收入,则s＝y d－c＝4100－3800＝300<亿元><2>用i代表投资,用s p、s g、s r分别代表私人部门、政府部门和国外部门的储蓄,则s g＝t －g＝BS,在这里,t代表政府税收收入,g代表政府支出,BS代表预算盈余,在本题中,s g＝BS＝－200.s r表示外国部门的储蓄,即外国的出口减去进口,对本国来说,则是进口减出口,在本题中为100,因此投资为i＝s p＋s g＋s r＝300＋<－200>＋100＝200<亿元><3>从GDP＝c＋i＋g＋<x－m>中可知,政府支出g＝5000－3800－200－<－100>＝1100<亿元>15.储蓄—投资恒等式为什么不意味着计划的储蓄恒等于计划的投资？解答：在国民收入核算体系中存在的储蓄—投资恒等式完全是根据储蓄和投资的定义得出的.根据定义,国内生产总值总等于消费加投资,国民总收入则等于消费加储蓄,国内生产总值又总等于国民总收入,这样才有了储蓄恒等于投资的关系.这种恒等关系就是两部门经济的总供给<C＋S>和总需求<C＋I>的恒等关系.只要遵循储蓄和投资的这些定义,储蓄和投资就一定相等,而不管经济是否充分就业或存在通货膨胀,即是否均衡.但这一恒等式并不意味着人们意愿的或者说事前计划的储蓄总会等于企业想要的投资.在实际经济生活中,储蓄和投资的主体与动机都不一样,这就会引起计划投资和计划储蓄的不一致,形成总需求和总供给不平衡,引起经济扩X和收缩.分析宏观经济均衡时所讲的投资要等于储蓄,是指只有计划投资等于计划储蓄时,才能形成经济的均衡状态.这和国民收入核算中实际发生的投资总等于实际发生的储蓄这种恒等关系并不是一回事.。

西方经济学原理第十二章课后思考题答案

9、答：在国民收入核算体系中，存在的储蓄---投资恒等、在国民收入核算体系中，存在的储蓄投资恒等式完全是根据储蓄和投资的定义得出的。根据定义，式完全是根据储蓄和投资的定义得出的。根据定义，国内生产总值总等于消费加投资，内生产总值总等于消费加投资，国民总收入则等于消费加储蓄，国内生产总值又总等于国民总收入，加储蓄，国内生产总值又总等于国民总收入，这样才有了储蓄恒等于投资的关系。了储蓄恒等于投资的关系。这种恒等关系就是两部门经济的总供给（济的总供给（C + S）和总需求（C + I）的恒等关系。）和总需求（）的恒等关系。只要遵守储蓄和投资的这些定义，储蓄和投资一定相等，只要遵守储蓄和投资的这些定义，储蓄和投资一定相等，而不管经济是否充分就业或通货膨胀，既是否均衡。而不管经济是否充分就业或通货膨胀，既是否均衡。但这一恒等式并不意味着人们意愿的或者说事前计划的储蓄总会企业想要有的投资。在实际经济生活中，蓄总会企业想要有的投资。在实际经济生活中，储蓄和投资的主体及动机都不一样，投资的主体及动机都不一样，这就会引起计划投资和计划储蓄的不一致，形成总需求和总供给的不平衡，划储蓄的不一致，形成总需求和总供给的不平衡，引起经济扩张和收缩。经济扩张和收缩。分析宏观经济均衡时所讲的投资要等于储蓄，是指只有计划投资等于计划储蓄时，于储蓄，是指只有计划投资等于计划储蓄时，才能形成经济的均衡状态。经济的均衡状态。这和国民收入核算中的实际发生的储蓄这种恒等关系并不是一回事。蓄这种恒等关系并不是一回事。
3、解答：、解答：如果甲乙两国合并成一个国家，总和不会有影响。如果甲乙两国合并成一个国家，对GDP总和不会有影响。总和不会有影响因为甲乙两国未合并成一个国家时，因为甲乙两国未合并成一个国家时，双方可能有贸易往但这种贸易只会影响甲国或乙国的GDP，对两国来，但这种贸易只会影响甲国或乙国的， GDP总和不会有影响。如：甲国向乙国出口价值万美总和不会有影响。甲国向乙国出口价值10万美总和不会有影响乙国向甲国出口价值8万美元对甲来说，万美元，元，乙国向甲国出口价值万美元，对甲来说，计入 GDP中的净出口为万美元，计入乙的中的净出口为2万美元中的净出口为万美元，计入乙的GDP中的净出口中的净出口万美元，总和为零。为—2万美元，两国万美元两国GDP总和为零。若两国并成一个国总和为零从收入看，甲的收入为10万美元乙的收入为8；万美元，家，从收入看，甲的收入为万美元，乙的收入为；从支出看，甲的支出为8万美元乙的支出为10万美元万美元，万美元，支出看，甲的支出为万美元，乙的支出为万美元，所以无论用收入法还是支出法，都是18万美元以无论用收入法还是支出法，GDP都是万美元。都是万美元。

人教版八年级上册数学第十二章全等三角形含答案

人教版八年级上册数学第十二章全等三角形含答案一、单选题(共15题，共计45分)1、某地为了发展旅游业，要在三条公路围成的一块平地上修建一个度假村，使度假村到三条公路的距离相等，这个度假村的选址地点共有（）处．A.1B.2C.3D.42、如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC，垂足为D、E，F分别是CD，AD上的点，且CE＝AF。

如果∠AED＝62°，那么∠DBF的度数为( )A.62°B.38°C.28°D.26°3、如图，线段AD与BC交于点O ，且AC=BD ， AD=BC ，则下面的结论中不正确的是( )A.△ABC≌△BADB.∠CAB=∠DBAC.OB=OCD.∠C=∠D4、如图，菱形ABCD的边AD⊥EF，垂足为点E，点H是菱形ABCD的对称中心.若FC= ，EF= DE，则菱形ABCD的边长为（）A. B.3 C.4 D.55、用两个完全相同的直角三角形拼下列图形：(1)平行四边形，(2)矩形，(3)菱形，(4)正方形，(5)等腰三角形，(6)等边三角形，一定可以拼成的图形是（）A.(1)(4)(5);B.(2)(5)(6);C.(1)(2)(3);D.(1)(2)(5).6、如图，∠AOP=∠BOP，PD⊥OB，PC⊥OA，则下列结论正确的是( )A.PD=PCB.PD≠PCC.有时相等，有时不等D.PD＞PC7、如图，△AOC≌△BOD，∠A和∠B，∠C和∠D是对应角，下列几组边中是对应边的是（）A.AC与BDB.AO与ODC.OC与OBD.OC与BD8、如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM．下列结论：①DF=DN；③AE=CN；③△DMN是等腰三角形；④∠BMD=45°，其中正确的结论个数是（）A.1个B.2个C.3个D.4个9、如图，已知AB=DC，AD=BC，E、F在DB上两点且BF=DE，若∠AED=80°，∠ADB=30°，则∠BFC=（）A.150°B.40°C.80°D.90°10、如图，在Rt△ABC的斜边BC上截取CD=CA，过点D作DE⊥BC，交AB于E，则下列结论一定正确的是（）A.AE=BEB.DB=DEC.AE=BDD.∠BCE=∠ACE11、如图，在△ABC中，∠ACB＝90°，CH⊥AB，垂足为点H，AD平分∠BAC，与CH相交于点D，过点D作DE∥BC，与边AB相交于点E，那么下列结论中一定正确的是（）A.DA=DEB.AC=ECC.AH＝EHD.CD＝ED12、如图，，且，则的度数为（）A. B. C. D.13、在中，已知，AD是的角平分线，于点E.若的面积为S，则的面积为（）A. B. C. D.14、如图，在正方形中，，点，分别在、上，，，相交于点，若图中阴影部分的面积与正方形的面积之比为，则的周长为（）A. B. C. D.15、如图，三条公路两两相交，现计划修建一个油库，要求油库到这三条公路的距离相等，那么选择油库的位置有（）处．A.1B.2C.3D.4二、填空题(共10题，共计30分)16、如图，OC平分∠AOB，D为OC上一点，DE⊥OB于E，若DE＝7，则D到OA 的距离为________．17、如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为________18、下面四个命题：①面积相等的两个直角三角形全等；②两边及其中一边上的中线分别相等的两个三角形全等；③斜边和斜边上的中线分别相等的两个直角三角形全等；④两角及第三个角的平分线分别相等的两个三角形全等.其中正确的命题为________.19、如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若＝，则＝________用含k的代数式表示）．20、如图，已知等边三角形的边长为，点为平面内一动点，且，将点绕点按逆时针方向转转，得到点，连接，则的最大值________.21、在△ABC中，AC＝5，中线AD＝4，则边AB的取值范围是________.22、等腰三角形ABC中，顶角A为40°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、分析电子衍射与X 衍射有何异同？答：相同点：① 都是以满足布拉格方程作为产生衍射的必要条件。

② 两种衍射技术所得到的衍射花样在几何特征上大致相似。

不同点：① 电子波的波长比x 射线短的多，在同样满足布拉格条件时，它的衍射角很小，约为10-2rad 。

而X 射线产生衍射时，其衍射角最大可接近2。

② 在进行电子衍射操作时采用薄晶样品，增加了倒易阵点和爱瓦尔德球相交截的机会，使衍射条件变宽。

④ 原子对电子的散射能力远高于它对x 射线的散射能力，故电子衍射束的强度较大，摄取衍射花样时曝光时间仅需数秒钟。

3、用爱瓦尔德图解法证明布拉格定律。

令入射方向矢量为k （k = 1/λ），衍射方向矢量为k ，，衍射矢量为g 。

则有g = 2ksin θ。

∵g=1/d ；k=1/λ，∴2dsin θ=λ。

即厄瓦尔德球图解与布拉格方程等价。

4、画出fcc、bcc晶体的倒易点阵，并标出基本适量a*，b*，c*。

5、何为零层倒易面和晶带定理？说明同一晶带中各晶面及其倒易矢量与晶带轴之间的关系。

答：在倒易点阵中，通过倒易原点O*且与某一晶带轴[uvw]垂直的二维平面称为零层倒易面。

因为零层倒易面上的倒易面上的各倒易矢量都和晶带轴r=[uvw]垂直，故有g.r=0即hu+kv+lw=0这就是晶带定理。

6、为何对称入射时，即只有倒易点阵原点在爱瓦尔德球面上，也能得到除中心斑点以外的一系列衍射斑点？答：如果倒易点是几何点，那么对称入射时就没有倒易点落在厄瓦尔德球上。

但是，由于电镜样品是薄样品，倒易点拉长成倒易杆。

倒易杆与厄瓦尔德球相交可以产生衍射。

8、举例说明如何用选区衍射的方法来确定新相的惯习面及母相与新相的位向关系。

答：例如分析钢淬火时，马氏体在奥氏体的一定结晶面上形成的，此面为惯习面，它在相变过程中应该保持不变形与不转动。

由于马氏体相变时原子规则地发生位移,使新相(马氏体)和母相之间始终保持一定的位向关系。

在铁基合金中由面心立方母相γ变为体心立方(正方)马氏体M时具有著名的K-S关系：{111}γ∥{011}M,<01ī>γ∥<ī11>M和西山关系：{111}γ∥{110}M，<211>γ∥<110>M。

惯性面的取向分析：利用透射电镜测定惯性面的指数，其根据是选区衍射花样与选区内组织形貌的微区对应性。

这里特介绍一种最基本、较简便的方法。

该方法的基本要点为：使用双倾台或旋转台倾转样品，使惯性面平行于入射束方向，在此位向下获得的衍射花样中将出现该惯性面的衍射斑点。

把这个位向下拍照的形貌像和相应的选区衍射花样对照，经磁转角校正后，即可确定惯性面的指数。

其具体操作步骤如下：1) 利用双倾台倾转样品，使惯性面处于与入射束平行的方向。

2) 拍照包含有惯性面的形貌像，以及该视场的选区电子衍射花样。

3) 标定选区电子衍射花样，经磁转角校正后（即确保TEM方式下和SAED方式下，没有磁转角差异），将惯性面在形貌像中的迹线（TEM图像的得边界线）画在衍射花样中。

4) 由透射斑点作迹线的垂线，该垂线所通过的衍射斑点的指数即为惯性面的指数。

例如：镍基合金中的片状—Ni3Nb相常沿着基体(面心立方结构)的某些特定平面生长。

当片状相表面相对入射束倾斜一定角度时，在形貌像中片状相的投影宽度较大(见图实4—1a)；如果倾斜样品使片状相表面逐渐趋近平行于入射束，其在形貌像中的投影宽度将不断减小；当入射束方向与片状相表面平行时，片状相在形貌像中显示最小的宽度(图实4—1b)。

图实4—1c是入射电子束与片状相表面平行时拍照的基体衍射花样。

由图实4—1c所示的衍射花样的标定结果，可以确定片状相的生长惯习面为基体的(111)面。

通常习惯用基体的晶面表示第二相的惯习面。

母相与新相的位向分析：利用两相合成的电子衍射花样的标定结果，可以直接确定两相间的取向关系。

具体的分析方法是，在衍射花样中找出两相平行的倒易矢量，即两相的这两个衍射斑点的连线通过透射斑点，其所对应的晶面互相平行，由此可获得两相间一对晶面的平行关系；另外，由两相衍射花样的晶带轴方向互相平行，可以得到两相间一对晶向的平行关系。

由图实4—3a给出的两相合成电子衍射花样的标定结果可确定两相的取向关系：(200)M∥(002)，[011]M∥。

例如根据书上P176的衍射斑点的结果，可知马氏体的晶带轴是[001],奥氏体的晶带轴是[011]。

马氏体和奥氏体的位向关系： 9、说明多晶、单晶及非晶衍射花样的特征及形成原理。

答：多晶体的电子衍射花样是一系列不同半径的同心圆环单晶衍射花样是由排列得十分整齐的许多斑点所组成的非晶态物质的衍射花样只有一个漫散中心斑点单晶花样是一个零层二维倒易截面，其倒易点规则排列，具有明显对称性，且处于二维网络的格点上。

因此表达花样对称性的基本单元为平行四边形。

单晶电子衍射花样就是(uvw)*0零层倒易截面的放大像。

多晶试样可以看成是由许多取向任意的小单晶组成的。

故可设想让一个小单晶的倒易点阵绕原点旋转，同一反射面hkl 的各等价倒易点（即（hkl ）平面族中各平面）将分布在以1/d hkl 为半径的球面上，而不同的反射面，其等价倒易点将分布在半径不同的同心球面上，这些球面与反射球面相截，得到一系列同心园环，从反射球心向各园环连线，投影到屏上，就是多晶电子衍射图。

非晶的原子表现为近程有序，长程无序；原子的分布在非常小的范围内有一定的序。

由于单个原子团或多面体中原子具有近邻关系反映到倒空间也具有对应原子近邻距离的一个或两个倒易球面，反射球面与它们相交得到的轨迹都是一个或两个半径恒定并且以倒易点阵原点为中心同心圆环。

一、填空题1、电子衍射和X 射线衍射的不同之处在于入射波长不同、试样尺寸形状不同，以及样品对电子和X 射线的散射能力不同。

2、电子衍射产生的复杂衍射花样是高阶劳厄斑、超结构斑点、二次衍射、孪晶斑点和菊池花样。

3、偏离矢量S 的最大值对应倒易杆的长度，它反映的是θ角偏离布拉格方程的程度。

4、单晶体衍射花样标定中最重要的一步是确定晶体结构。

5、二次衍射可以使密排六方、金刚石结构的花样中在本该消光的位置产生衍射花样，但体心立方和面心立方结构的花样中不会产生多余衍射。

6、倒易矢量的方向是对应正空间晶面的法线；倒易矢量的长度等于对应晶面间距的倒数。

7、只要倒易阵点落在厄瓦尔德球面上，就表示该晶面满足布拉格条件，能产生衍射。

()()[][]⎭⎬⎫M M A 001//011011//111A二、名词解释1、偏离矢量s ：倒易杆中心至与爱瓦尔德球面交截点的距离可用矢量s 表示，s 就是偏离矢量。

2、晶带定律：凡是属于[uvw]晶带的晶面，它的晶面指数(hkl)都必须符合hu+kv+lw=0，通常把这种关系式称为晶带定律。

3、相机常数：定义 K=Lλ，称相机常数，其中L 为镜筒长度，λ为电子波长。

三、选择题1、单晶体电子衍射花样是（ A ）。

A. 规则的平行四边形斑点；B. 同心圆环；C. 晕环；D.不规则斑点。

2、薄片状晶体的倒易点形状是（ C ）。

A. 尺寸很小的倒易点；B. 尺寸很大的球；C. 有一定长度的倒易杆；D. 倒易圆盘。

3、当偏离矢量S<0时，倒易点是在厄瓦尔德球的（ A ）。

A. 球面外；B. 球面上；C. 球面内；D. B+C 。

4、能帮助消除180º不唯一性的复杂衍射花样是（ A ）。

A. 高阶劳厄斑；B. 超结构斑点；C. 二次衍射斑；D. 孪晶斑点。

5、菊池线可以帮助（ D ）。

A. 估计样品的厚度；B. 确定180º不唯一性；C. 鉴别有序固溶体；D. 精确测定晶体取向。

6、如果单晶体衍射花样是正六边形，那么晶体结构是（ D ）。

A. 六方结构；B. 立方结构；C. 四方结构；D. A 或B 。

7、有一倒易矢量为*+*+*=*c b a g 22，与它对应的正空间晶面是（ C ）。

A. （210）；B. （220）；C. （221）；D. （110）；。

四、是非题1、多晶衍射环和粉末德拜衍射花样一样，随着环直径增大，衍射晶面指数也由低到高。

（√）2、单晶衍射花样中的所有斑点同属于一个晶带。

（×）3、偏离矢量S=0时，衍射斑点最亮。

这是因为S=0时是精确满足布拉格方程，所以衍射强度最大。

（ √ ）4、对于未知晶体结构，仅凭一张衍射花样是不能确定其晶体结构的。

还要从不同位向拍摄多幅衍射花样，并根据材料成分、加工历史等或结合其它方法综合判断晶体结构。

（√）5、电子衍射和X 射线衍射一样必须严格符合布拉格方程。

（×）6、倒易矢量能唯一地代表对应的正空间晶面。

（√ ）五、问答题1、试推导电子衍射的基本公式，并指出L λ的物理意义。

解：图为电子衍射花样形成原理图。

其中样品放在爱瓦尔德球的球心O 处。

当入射电子束和样品内某一组晶面（h k l ）相遇，并满足布拉格方程时，在K ˊ方向产生衍射束，其中图中O ˊ、G ˊ点分别为入射束与衍射束在底片上产生的透射斑点（中心斑点）和衍射斑点。

hkl g （矢量）是衍射晶面的倒易矢量，其端点O *，G 位于爱瓦尔德球面上，投影G ˊ通过转换进入正空间。

∵电子束发散角很小，约2º-3º，∴可认为△OO *G ∽△OO ˊG ˊ，那么矢量hkl g 与矢量k 垂直∴有R/L=hkl g /k又∵有hkl g =1/hkl d k=1/λ∴R=L λ/hkl d = L λhkl g …………………⑴又∵近似有矢量R ∥矢量hkl g∴上式亦可以写成R = L λg ……………⑵式⑴⑵就是电子衍射的基本公式式中L λ称为电子衍射的相机常数（L 为相机长度）。

第十二章习题答案new

高等数学(上册)第12章(1)习题答案_吴赣昌_人民大学出版社_高数_

(典型题)人教版八年级上册数学第十二章 全等三角形含答案

第十二章习题答案new

八年级物理第十二章 简单机械课后习题答案

高等数学第12章课后习题答案(科学出版社).

沪教新版七年级上册《第12章_因式分解》2024年同步练习卷+答案解析

高等数学(经济类)课后习题及答案第十二章 微分方程答案

[VIP专享]大学物理第12章课后习题

大学物理第十二章课后习题答案

人教版八年级上册数学第十二章 全等三角形含答案

高等数学课后习题及参考答案(第十二章)

高数第十二章习题答案

高鸿业《宏观经济学》课后习题答案第十二章--习题答案

西方经济学原理第十二章课后思考题答案

人教版八年级上册数学第十二章 全等三角形 含答案

(典型题)人教版八年级上册数学第十二章全等三角形含答案

八年级物理第十二章简单机械课后习题答案

高等数学(经济类)课后习题及答案第十二章微分方程答案

人教版八年级上册数学第十二章全等三角形含答案

人教版八年级上册数学第十二章全等三角形含答案