轮系的计算
轮系的传动比计算

构件
原来的转速 转化轮系中的转速
1
n1
n1H=n1-nH
2
n2
n2H=n2-nH
3
n3
n3H=n3-nH
H
nH
nHH=nH-nH=0
转化轮系中,轮1、3间的传动比可以按定轴齿轮系传动比求解:
iH
13
n1H
n
H 3
n1 nH n3 nH
Z2Z3 Z1Z2
Z3 Z1
新能源汽车技术教学资源库
新能源汽车技术教学资源库
定轴轮系:行星架的转速为0。
n2
2
2
2
n3
23
O2
O2
O2
H
H
H
H
nH
O3
O1
OH
O3 O1
OH
O3 O1
OH
1
1
1
1
n1
3
3
3
F=2
差动轮系
F=1
行星轮系
F=1
定轴轮系
2.周转轮系的传动比计算
新能源汽车技术教学资源库
新能源汽车技术教学资源库
用“反转法”,给整个轮系加上一个(-nH),各构件间的相对 运动不变。
(2)空间定轴轮系的传动比计算
新能源汽车技术教学资源库
解:由公式
i16
n1 n6
z2 z3 z4 z5 z6 z1z2 z3 z4 z5
z2 z4 z5 z6 z1z2 z4 z5
因为齿轮1转动方向向下,所以齿轮6的转动方向向左。
三、周转轮系的传动比计算
新能源汽车技术教学资源库
1.周转轮系的组成
(1)对于圆柱齿轮组成的定轴轮系确定传动比正负的方法: a.外啮合的次数; b.画箭头。
轮系的传动比计算

轮系的传动比计算1源自新能源汽车技术教学资源库一、轮系的传动比
轮系中首末两轮的转速之比称为轮系的传动比,用iab表
示。
iab na / nb
轮系的传动比计算,包括计算传动比的大小和确定转向两 个内容。
新能源汽车技术教学资源库
二、定轴轮系的传动比计算
z5 n4 i45 n5 z4
z 2 z3 z 5 n1 3 z 2 z 3 z 4 z5 i15 (1) n5 z1 z2 z3 z4 z1 z 2 z3
新能源汽车技术教学资源库
轮系传动比的一般表达式:
n表示外啮合的次数。
n主 n 各从动轮齿数的乘积 i ( 1 ) n从 各主动轮齿数的乘积
新能源汽车技术教学资源库
例4-7
图示轮系中,已知各轮齿数z1=20,z2=40,z2’=20,z3=30,
解: (1)分解轮系 定轴轮系:轮1,2 周转轮系:轮2’,3 ,H,4 (2)分别计算各轮系传动比 定轴轮系传动比:
z4=80。计算传动比i1H。
i12
(3)联立以上两式,得
n1 z2 2 n2 z1
齿轮4既是从动轮,又是主动轮,其存在不影响传动比,但改
变了外啮合的次数,称为过桥齿轮或惰轮。
(1)对于圆柱齿轮组成的定轴轮系确定传动比正负的方法: a.外啮合的次数; b.画箭头。 (2)当轮系中包含圆锥齿轮、蜗杆蜗轮时,传动比的计算仍用上 式计算,但各轮的转向必须画箭头确定。 a.当首末两轮轴线平行时,仍用正负表示两轮之间的关系。 b.当首末两轮轴线不平行时,不能用正负表示,只能依次画箭
解得
iH1 10000
新能源汽车技术教学资源库
第5章 轮系

例5 如图所示为电动卷扬机的传动装置,已知各轮齿 数,求i15 。
r
5
r
4 2 1 2
3
B
解:这一混合轮系可划分为由齿轮1、2、2’、3和转臂 H组成
的差动轮系,由齿轮5、4、3’组成的定轴轮系。而此定轴轮 系将差动轮系的中心轮3和转臂H(5)联系起来。 齿轮1、2、2’、3和H组成的差动轮系的传动比为
定轴轮系
I
1 2 4
3
2
3 V
5
定轴轮系
周转轮系
如图,齿轮2-2’的轴线 O2是绕齿轮1的固定轴线O1转
3
1
O3
动的。轴线不动的齿轮称为
中心轮,如图中齿轮1和3; 其轴线转动的齿轮称为行星 轮,如图中齿轮2和2';作为 行星轮轴线的构件称为系杆, 如图中的转柄H。通过在整个 轮系上加上一个与系杆旋转 方向相反、大小相同的角速 度,可以把周转轮系转化成 定轴轮系。
已知:z1=100,z2=101,
z2 =100,z3=99。
求传动比
i
H1?
1 H 1 101 99 i 1 1 i1H 0 H H 100 100
H 13
i1H
101 99 1 1 100 100 10000
H 1 iH1 10000 1 i1H
z 2 z3 z 4 z5 i15 (1) ' ' z1 z 2 z3 z 4
3
I
1 2 4
3
所以
25 132 28 10.5 22 20 20 n1 1450 n5 138.1 rpm i 10.5
2
3 V
5
转向与轮1相同。
机械设计基础第五章轮系

2. 根据周转轮系的组合方式,利用周转轮系传动比计算公式求
03
出周转轮系的传动比。
实例分析与计算
1
3. 将定轴轮系和周转轮系的传动比相乘,得到复 合轮系的传动比。
2
4. 根据输入转速和复合轮系的传动比,求出输出 转速。
3
计算结果:通过实例分析和计算,得到了复合轮 系的输出转速。
05 轮系应用与实例分析
仿真结果输出
将仿真结果以图形、数据等形式输出,以便 进行后续的分析和处理。
实验与仿真结果对比分析
01
数据对比
将实验数据和仿真数据进行对比 ,分析两者之间的差异和一致性 。
结果分析
02
03
优化设计
根据对比结果,分析轮系设计的 合理性和可行性,找出可能存在 的问题和改进方向。
针对分析结果,对轮系设计进行 优化和改进,提高轮系的性能和 稳定性。
04 复合轮系传动比计算
复合轮系构成及特点
构成
由定轴轮系和周转轮系(或几个周转轮系)组合而成,称为复合轮系。
特点
复合轮系的传动比较复杂,其传动比的计算需结合定轴轮系和周转轮系的传动比计算公式进行。
复合轮系传动比计算公式
对于由定轴轮系和周转轮系组成的复合轮系,其传动比计算 公式为:i=n1/nK=(Z2×Z4×…×Zk)/(Z1×Z3×…×Zk-1)×(1)m,其中n1为输入转速,nK为输出转速,Z为各齿轮齿数 ,m为从输入轴到输出轴外啮合齿轮的对数。
火车车轮与轨道
通过轮系保证火车在铁轨 上的平稳运行和导向作用 。
船舶推进器
利用轮系将主机的动力传 递给螺旋桨,推动船舶前 进。
军事装备中轮系应用举例
坦克传动系统
采用轮系实现坦克发动机的动力 输出与行走机构的连接,确保坦 克在各种地形条件下的机动性。
定轴轮系传动比的计算

§5-6 定轴轮系传动比的计算一、轮系的基本概念●轮系:由一系列相互啮合的齿轮组成的传动系统;●轮系的分类:定轴轮系:所有齿轮轴线的位置固定不动;周转轮系:至少有一个齿轮的轴线不固定;●定轴轮系的分类:平面定轴轮系:轴线平行;空间定轴轮系:不一定平行;●轮系的传动比:轮系中首、末两轮的角速度(或转速)之比,包括两轮的角速比的大小和转向关系。
传动比的大小:当首轮用“1”、末轮用“k”表示时,其传动比的大小为: i1k=ω1/ωk=n1/n k传动比的方向:首末两轮的转向关系。
相互啮合的两个齿轮的转向关系:二、平面定轴轮系传动比的计算特点:●轮系由圆柱齿轮组成,轴线互相平行;●传动比有正负之分: 首末两轮转向相同为“+”,相反为“-”。
1、传动比大小设Ⅰ为输入轴,Ⅴ为输出轴;各轮的齿数用Z来表示;角速度用ω表示;首先计算各对齿轮的传动比:所以:结论:定轴轮系的传动比等于各对齿轮传动比的连乘积,其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比;2、传动比方向在计算传动比时,应计入传动比的符号:首末两轮转向相同为“+”,相反为“-”。
(1)公式法式中:m为外啮合圆柱齿轮的对数举例:(2)箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向,转向相同为“+”,相反为“-”。
举例:122112zzi==ωω32223332zizωωωω'''===33434443zizωωωω'''===455445zzi==ωω11211)1(--==kkmkk zzzziωω三、空间定轴轮系的传动比特点:●轮系中包含有空间齿轮(如锥齿轮、蜗轮蜗杆、螺旋齿轮等); ●首末两轮的轴线不一定平行。
1 传动比的大小2 传动比的方向注意:只能采用箭头标注法,不能采用(-1)m 法判断。
分两种情况讨论:情况1:首、末两轮轴线平行传动比计算式前应加“+”、“-”号,表示两轮的转向关系。
行星轮系自由度

行星轮系自由度一、行星轮系简介行星轮系是一种常见的传动装置,由行星齿轮和太阳齿轮组成。
其具有许多独特的特点,其中之一就是自由度。
本文将详细探讨行星轮系的自由度问题。
1.1 行星轮系的构造行星轮系由一根轴和多个行星轮组成。
太阳齿轮位于行星轮系的中心,而行星轮则绕太阳齿轮旋转。
行星轮还与一个轮系(通常是外部环)相连,形成一个闭合的系统。
1.2 行星轮系的工作原理在行星轮系中,太阳齿轮是动力输入端,行星齿轮则是输出端。
当太阳齿轮旋转时,通过行星轮的转动,将动力传递到轮系上的外部环。
这种传动方式具有很高的效率和扭矩转动比。
二、行星轮系的自由度2.1 自由度的定义自由度是指系统可变动的自由度量。
在行星轮系中,自由度的定义与节点数和约束条件有关。
行星轮系的自由度可以用以下公式表示:自由度 = 节点数 - 约束条件在行星轮系中,节点数等于齿轮数+1,约束条件等于行星轮个数。
2.2 行星轮系的自由度计算方法行星轮系的自由度计算可以通过以下步骤完成:步骤1:确定齿轮数和行星轮个数。
步骤2:根据步骤1中的数据,计算节点数。
步骤3:根据行星轮个数,计算约束条件。
步骤4:应用自由度计算公式,得出行星轮系的自由度。
2.3 行星轮系的自由度举例例如,一个包含3个齿轮和2个行星轮的行星轮系,其计算过程如下:步骤1:齿轮数 = 3,行星轮个数 = 2步骤2:节点数 = 齿轮数 + 1 = 3 + 1 = 4步骤3:约束条件 = 行星轮个数 = 2步骤4:自由度 = 节点数 - 约束条件 = 4 - 2 = 2因此,该行星轮系的自由度为2。
三、行星轮系的自由度对传动性能的影响行星轮系的自由度对传动性能有着重要的影响。
自由度越大,系统的灵活性和可变性就越高,但也可能导致传动精度的下降。
下面将详细探讨自由度对传动性能的影响。
3.1 自由度与传动精度的关系自由度越大,行星轮系的误差累积越容易。
因为行星轮系的每个行星轮都可以自由运动,其位置误差会随着传动的进行而逐渐累积。
第十章-轮系

z2 z1
17 27
n1=3000rpm nH=920rpm 得n2 = 2383.5rpm
注意:空间轮系的方向只能用箭头画,但 在公式中一定要反映出正负号来!!
例题2
i13H
n1H n3H
n1 nH n3 nH
z2z3 z1z2'
3080 2.4 20 50
若 n1=50rpm
利用公式计算时应注意:
(1)公式只适用于齿轮1、齿轮k和 系杆H三构件的轴线平行或重合的情况, 齿数比前的“+”、“”号由转化轮系按定 轴轮系方法确定。
i1H3
1 H 3 H
z3 z1
i1H2
1 2
H H
(2) ω1、ωk、ωH均为代数值,代入公式计算时要带上相应 的“+”、“”号,当规定某一构件转向为“+”时,则转向与
最后 i14 = n1/n4= i13 X i34 =-10.13X( -1.67)=16.9
也可: i1H = i15 =n1/n5 = 43.9 i54 =n5/n4 =z4/z5 = 30/78=0.385
最后 i14 = n1/n4= i15 X i54 =43.9X 0.385=16.9
例题:在图示双螺旋桨飞机的减速器中,已知
1、轮系中各轮几何轴线均互相平行
i1N
1 N
n1 nN
(1)k
所有从动轮齿数乘积 所有主动轮齿数乘积
k 为外啮合次数! 若计算结果为“+”,表明首、末 两轮的转向相同;反之,则转向相反。
规定:
外啮合:二轮转向相反,用负号“-”表示;
内啮合:二轮转向相同,用正号“+”表示。
2、轮系中所有各齿轮的几何轴线不都平行,但首、末 两轮的轴线互相平行
定轴轮系传动比的计算
4)iGKH ≠iGK iGKH —为转化轮系中G、K两轮的转速之比,其大小及正负号按定轴轮系传动比
的计算方法确定;
iGK —为行星轮系中由G、 K两轮的转速之比,其大小及正负号须按上式计算后
方能确定。
4.确定转化轮系的传动比符号 1)转化轮系中,所有齿轮的轴线均平行,直接按(-1)m表示转化
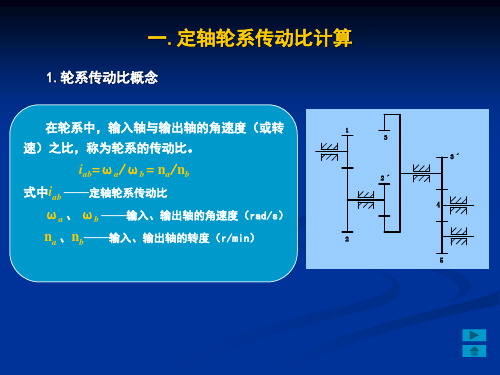
一.定轴轮系传动比计算
1.轮系传动比概念
在轮系中,输入轴与输出轴的角速度(或转 速)之比,称为轮系的传动比。
iab=ωa/ωb = na/nb 式中iab ——定轴轮系传动比
ωa 、 ωb ——输入、输出轴的角速度(rad/s) na 、nb——输入、输出轴的转度(r/min)
1 3 2ˊ
2
3ˊ 4 5
轮系传动比符号,m—表示转化轮系中外啮合齿对数。
2)对于锥齿轮行星轮系,首末两轮轴线平行,应对各对齿逐对标出转向, 若首、末两轮转向相同,转化轮系传动比为正,反之为负。
行星轮系
锥齿轮行星轮 系
例14-3 如图所示的行星轮系中,各齿轮的齿数为Z1=27、Z2=17 、 Z3=61,转速n1=6000r/min,转向见图。求传动比i1H及nH
2 H
n1 1 3
例14-4 如图所示的锥齿轮行星轮系中,各齿轮的齿数为Z1=20、 Z2=30、Z2ˊ=50 、Z3=80,已知转速n1=100r/min。试求行星架的转速nH
2' 2
3 H
1
例14-5 如图所示大传动比行星轮系中,各齿轮的齿数为Z1=100、 Z2=101、Z3=100 、Z4=99。试求iH1
1
3
4ˊ
2ˊ 4
5
8
2
