三角形高阶
《三角形的内角和外角》课件

根据题目给出的两个角度,可以确定第三个角度的大小,再根据正弦定理计算出各边长, 最后根据余弦定理得出答案
总结
此题考察了三角形内角和定理及正余弦定理的应用,需要学员们有一定的数学思维和计算 能力。
06
教学反思与展望
教学的收获与不足
• 收获 • 学生掌握了三角形内角和定理及其推论,并能够运用这些定理解决一些实际问题。 • 学生通过实践操作,增强了动手能力和探究能力,激发了对数学的兴趣。 • 教师的教学水平得到了提高,对三角形内角和定理及其推论有了更深入的认识和理解。 • 不足 • 部分学生对于一些重要的概念和定理的理解还不够深刻,需要进一步加强。 • 在实践操作环节中,有些学生没有认真参与,需要教师加强指导和督促。
解答分析
首先根据题意画出图形,根据已知条件角A等于角B,可得出两条 边相等,进而证明出三角形ABC是等腰三角形。
总结
此题考察了等腰三角形判定定理的运用,同时培养学员分析问题 的能力,逐步提高学员的几何推理能力。
高阶习题分析与解答
高阶习题3
已知三角形ABC中,角A等于30度,角B等于45度,求三角形ABC三个内角的大小。
教学背景
知识背景
学生在小学阶段已经对三角形有了一定的了解,知道一些基 本的几何概念和测量方法。在初中阶段,学生开始学习更复 杂的几何知识,本课程作为衔接课程,旨在帮助学生更好地 适应这一转变。
教学难点
如何引导学生通过实践、探究和应用来深入理解三角形的内 角和外角的概念,并解决实际问题。
教学目标
1 2 3
三角形内角和等于外角和
$\angle A + \angle B + \angle C = \angle A + \angle B + \angle C$
行列式的计算方法

0
0
01
0
xn 0 0
1
0
00
= 1 x12 x22
n
= 1 xi2 i 1
1
xn2
今天给同学们介绍的是计算行列式最常用的几种 方法,行列式类型有很多,在具体的求解过程中要 根据行列式本身的结构特点选取恰当的方法。
bvTJLDoXLxEk9x$n-9WJ vBvj Wo9BSKYUR56rHZ+ E$+Tsr 2SDI0yby3ODsz8cji Uc!ol5dZ2P09anv4Ljf4xwOLsH0nl0E!Vo8B(4U)a$gRM5c IRTNeMR55* vP&i5&$d*cKedJYs$IyLZK!!Tby(qQ0jeJHJqEj%IS6oRaTj Nez+ DI8z#K8yN8H DrE3Pe*8gYQ)D5(KZ 5TJ421*3lbVqI1R*cnsJilsj)U AEpd- D kWPZ&AzuXf+ xOmCa9ZJ Xxdm8WNqa)QBWLK)-&R 5phwU b-ztUil E(SK8xhWxkHDD% K(csj v$AYjp#gn9o*uQVXJgrM(ocR mbhhG9KOkS72yfIEvQwQeJgN m&M0M5J 4X1mx-
加边法最大的特点就是要找每行或每列相同的因子,那么升阶之后,就 可利用行列式的性质把绝大多数元素化为0, 这样就达到简化计算的效果例 求行列式的值源自x12 1 Dn x2x1
x1x2 x22 1
xn x1 xn x2
x1xn x2 xn
xn2 1
解 行列式第1列有共同元素 x1 ,第2列有共同元素 x,2…,第 n 列有 共同元素 xn .根据这些特点给原行列式加边得
2024年人教版高二数学复习知识点总结

2024年人教版高二数学复习知识点总结第一章函数与方程1.1 函数与映射函数的定义、函数的性质、函数的四则运算、复合函数、反函数映射的定义、映射的性质、一一映射、单射、满射1.2 一元二次函数及其应用一元二次函数的定义、一元二次函数的图像、一元二次函数的性质、一元二次函数的解析式、一元二次函数的图像与解析式的关系、一元二次函数的最值、一元二次函数的应用1.3 不等式不等式的定义、解不等式、不等式的性质、不等式的运算、一元一次不等式、一元二次不等式1.4 线性规划线性规划的定义、线性规划中的常见问题、线性规划的解法、线性规划的应用第二章三角函数与解三角形2.1 三角函数三角函数的定义、三角函数的性质、三角函数的图像、三角函数的周期、三角函数的关系式2.2 平面向量平面向量的定义、平面向量的运算、平面向量的线性运算、平面向量的数量积、平面向量的夹角、平面向量的投影、平面向量的正交2.3 解三角形解直角三角形、解一般三角形、解等腰三角形、解等边三角形、解特殊三角形、解复合三角形第三章数列与数项级数3.1 数列的概念数列的定义、数列的性质、数列的通项、数列的分类、数列的极限3.2 数列的通项公式等差数列、等比数列、等差数列与等比数列的关系、通项公式的推导方法、通项公式的应用3.3 数列的求和部分和、数列的前n项和、无穷数列的求和、等差数列的求和、等比数列的求和、部分和公式的应用3.4 级数级数的定义、级数的性质、无穷级数的收敛性、级数的求和、级数的应用第四章导数与导数应用4.1 导数的基本概念导数的定义、导数的性质、导数的基本运算、导数与函数的图像关系4.2 导数的应用函数的单调性、函数的极值、函数的曲线与切线、函数的凹凸性、函数的拐点、函数的极限与导数4.3 高阶导数和隐函数高阶导数的定义、高阶导数的求法、高阶导数的性质、隐函数的导数、隐函数的高阶导数第五章积分与积分应用5.1 不定积分不定积分的定义、不定积分的性质、不定积分的基本公式、不定积分的线性运算5.2 定积分定积分的定义、定积分的性质、定积分的线性运算、定积分的几何意义、定积分的求法5.3 微分方程微分方程的定义、微分方程的解、一阶微分方程、二阶微分方程、线性微分方程、微分方程的应用5.4 积分应用反常积分、曲线长度、曲线面积、体积、几何应用、物理应用以上是____年人教版高二数学的复习知识点总结,共计____字。
圆锥曲线中的阿基米德三角形(高阶拓展)(学生版)--高中数学
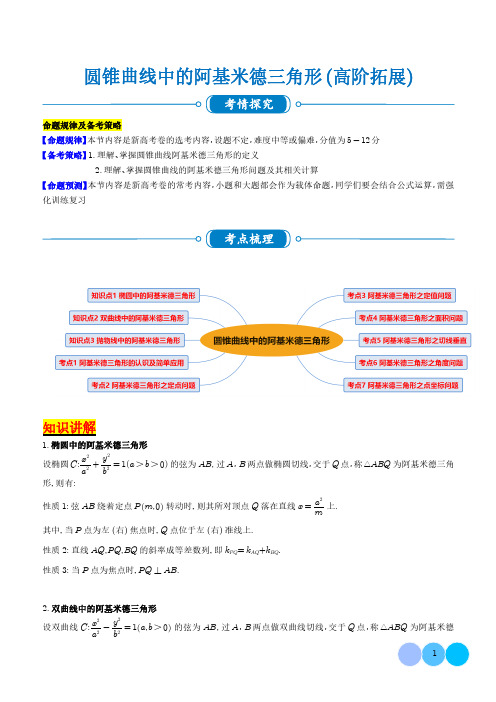
圆锥曲线中的阿基米德三角形(高阶拓展)考情探究命题规律及备考策略【命题规律】本节内容是新高考卷的选考内容,设题不定,难度中等或偏难,分值为5-12分【备考策略】1.理解、掌握圆锥曲线阿基米德三角形的定义2.理解、掌握圆锥曲线的阿基米德三角形问题及其相关计算【命题预测】本节内容是新高考卷的常考内容,小题和大题都会作为载体命题,同学们要会结合公式运算,需强化训练复习考点梳理知识讲解1.椭圆中的阿基米德三角形设椭圆C :x 2a 2+y 2b2=1a >b >0 的弦为AB ,过A ,B 两点做椭圆切线,交于Q 点,称△ABQ 为阿基米德三角形, 则有:性质1:弦AB 绕着定点P m ,0 转动时, 则其所对顶点Q 落在直线x =a 2m 上.其中, 当P 点为左(右)焦点时, Q 点位于左(右)准线上.性质2:直线AQ ,PQ ,BQ 的斜率成等差数列, 即k PQ =k AQ +k BQ .性质3:当P 点为焦点时, PQ ⊥AB .2.双曲线中的阿基米德三角形设双曲线C :x 2a 2-y 2b2=1a ,b >0 的弦为AB ,过A ,B 两点做双曲线切线,交于Q 点,称△ABQ 为阿基米德三角形, 则有:性质1:弦AB绕者定点P m,0转动时, 则其所对顶点Q落在直线x=a2m上.其中, 当P点为左(右)焦点时, Q点位于左(右)准线上.性质2:直线AQ,PQ,BQ的斜率成等差数列, 即k PQ=k AQ+k BQ.性质3:当P点为焦点时, PQ⊥AB.3.抛物线中的阿基米德三角形抛物线的弦为AB,过A,B两点做抛物线切线,交于Q点,称△ABQ为阿基米德三角形, 则有:(1)阿基米德三角形底边上的中线平行于抛物线的轴(2)若阿基米德三角形的底边即弦AB过抛物线内的定点C, 则另一顶点Q的轨迹为一条直线(3)若直线l与抛物线没有公共点,以l上的点为顶点的阿基米德三角形的底边过定点(若直线l方程为:ax+by+c=0, 则定点的坐标为C ca ,-bpa.(4)底边为a的阿基米德三角形的面积最大值为a3 8p.(5)若阿基米德三角形的底边过焦点, 顶点Q的轨迹为准线, 且阿基米德三角形的面积最小值为p2(6)在阿基米德三角形中, ∠QFA=∠QFB(7)AF⋅BF=QF2.(8)抛物线上任取一点I(不与A,B重合), 过I作抛物线切线交QA,QB于S,T,连接AI,BI, 则△ABI的面积是△QST面积的2倍考点一、阿基米德三角形的认识及简单应用1(2022·全国·高三专题练习)过抛物线y2=2px p>0的焦点F作抛物线的弦,与抛物线交于A,B两点,分别过A,B两点作抛物线的切线l1,l2相交于点P,△PAB又常被称作阿基米德三角形.△PAB的面积S的最小值为()A.p23B.p22C.p2D.2p22(2023·甘肃·高三校考阶段练习)抛物线上任意两点A,B处的切线交于点P,称△PAB为“阿基米德三角形”,当线段AB经过抛物线的焦点F时,△PAB具有以下特征:①P点必在抛物线的准线上;②PF⊥AB.若经过抛物线y2=4x的焦点的一条弦为AB,“阿基米德三角形”为△PAB,且点P的纵坐标为4,则直线AB的方程为()A.x-2y-1=0B.2x+y-2=0C.x+2y-1=0D.2x-y-2=03(2023·全国·高三专题练习)阿基米德(Archimedes,公元前287年-公元前212年),出生于古希腊西西里岛叙拉古(今意大利西西里岛上),伟大的古希腊数学家、物理学家,与高斯、牛顿并称为世界三大数学家.有一类三角形叫做阿基米德三角形(过抛物线的弦与过弦端点的两切线所围成的三角形),他利用“通近法”得到抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23(即右图中阴影部分面积等于△PAB面积的23).若抛物线方程为y2=2px(p>0),且直线x=p2与抛物线围成封闭图形的面积为6,则p=()A.1B.2C.32D.34(2023·新疆克拉玛依·克拉玛依市高级中学校考模拟预测)我们把圆锥曲线的弦AB与过弦的端点A,B处的两条切线所围成的三角形△PAB(P为两切线的交点)叫做“阿基米德三角形”.抛物线有一类特殊的“阿基米德三角形”,当线段AB经过抛物线的焦点F时,△PAB具有以下性质:①P点必在抛物线的准线上;②PA⊥PB;③PF⊥AB.已知直线l:y=k x-1与抛物线y2=4x交于A,B点,若AB=8,则抛物线的“阿基米德三角形”△PAB的面积为()A.82B.42C.22D.25(2022秋·广东茂名·高三统考)阿基米德(公元前287年~公元前212年)是古希腊伟大的物理学家,数学家和天文学家,并享有“数学之神”的称号.他研究抛物线的求积法,得出了著名的阿基米德定理.在该定理中,抛物线的弦与过弦的端点的两切线所围成的三角形被称为“阿基米德三角形”.若抛物线上任意两点A,B处的切线交于点P,则△PAB为“阿基米德三角形”,且当线段AB经过抛物线的焦点F时,△PAB具有以下特征:(1)P点必在抛物线的准线上;(2)PA⊥PB;(3)PF⊥AB.若经过抛物线y2=8x 的焦点的一条弦为AB,“阿基米德三角形”为△PAB,且点P在直线x-y+6=0上,则直线AB的方程为()A.x-y-2=0B.x-2y-2=0C.x+y-2=0D.x+2y-2=06(2022·全国·高三专题练习)我们把圆锥曲线的弦AB与过弦的端点A,B处的两条切线所围成的三角形△PAB (P 为两切线的交点)叫做“阿基米德三角形”,抛物线有一类特殊的“阿基米德三角形”,当线段AB 经过抛物线的焦点F 时,△PAB 具有以下性质:①P 点必在抛物线的准线上;②PA ⊥PB ;③PF ⊥AB .已知直线l :y =k (x -1)与抛物线C :y 2=4x 交于A ,B 点,若AB =8,记此时抛物线C 的“阿基米德三角形”为△PAB ,则P 点为()A.-1,±2B.-1,2C.-1,-2D.-1,±17(2022·全国·高三专题练习)阿基米德(公元前287年-公元前212年)是古希腊伟大的物理学家、数学家、天文学家,不仅在物理学方面贡献巨大,还享有“数学之神”的称号.抛物线上任意两点A ,B 处的切线交于点P ,称三角形PAB 为“阿基米德三角形”.已知抛物线C :x 2=8y 的焦点为F ,过A ,B 两点的直线的方程为3x -3y +6=0,关于“阿基米德三角形”△PAB ,下列结论不正确的是()A.AB =323B.PA ⊥PBC.PF ⊥ABD.点P 的坐标为3,-28(2023·全国·高三专题练习)阿基米德(公元前287年~公元前212年)是古希腊伟大的物理学家、数学家和天文学家.他研究抛物线的求积法得出著名的阿基米德定理,并享有“数学之神”的称号.抛物线的弦与过弦的端点的两条切线所围成的三角形被称为阿基米德三角形.如图,△PAB 为阿基米德三角形.抛物线x 2=2py (p >0)上有两个不同的点A x 1,y 1 ,B x 2,y 2 ,以A ,B 为切点的抛物线的切线PA ,PB 相交于P .给出如下结论,其中正确的为()(1)若弦AB 过焦点,则△ABP 为直角三角形且∠APB =90°;(2)点P 的坐标是x 1+x 22,x 1x22;(3)△PAB 的边AB 所在的直线方程为x 1+x 2 x -2py -x 1x 2=0;(4)△PAB 的边AB 上的中线与y 轴平行(或重合).A.(2)(3)(4)B.(1)(2)C.(1)(2)(3)D.(1)(3)(4)考点二、阿基米德三角形之定点问题9(2023秋·江西上饶·高三统考期末)(多选)若M 1,0 ,N 4,0 ,点Q 满足QN =2QM,记点Q 的轨迹为曲线C ,直线l :x +y -4=0,P 为l 上的动点,过点P 作曲线C 的两条切线PA ,PB ,切点为A ,B ,则下列说法中正确的是()A.PQ 的最小值为22-2B.直线AB 恒过定点1,1C.PA ⋅PB的最小值为0D.当PO ⋅AB 最小时,直线AB 的方程为x +y -1=010(2023·全国·高三专题练习)在平面直角坐标系xOy 中,M 为直线y =x -3上的动点,过点M 作抛物线C :x 2=2y 的两条切线MA ,MB ,切点分别为A ,B ,N 为AB 的中点.(1)证明MN ⊥x 轴;(2)直线AB 是否恒过定点?若是,求出这个定点的坐标;若不是,请说明理由.11(2021·北京·高三专题练习)抛物线C :x 2=2py (p >0),Q 为直线y =-p2上的动点,过点Q 作抛物线C 的两条切线,切点分别为M ,N .(1)证明:直线MN 过定点;(2)若以G 0,5p2为圆心的圆与直线MN 相切,且切点为线段MN 的中点,求该圆的面积.12(2023·湖南岳阳·高三校考)已知曲线C :y =x 22,D 为直线y =-12上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点;(2)若以E 0,52为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程.13(2023秋·山东临沂·高三校考期末)已知M -2,0 ,N -1,0 ,动点Q 满足QM QN=2,动点Q 的轨迹为曲线C .(1)求曲线C 的方程;(2)若点P 是直线y =12x -2上的动点,过点P 作曲线C 的两条切线PC ,PD ,切点为C ,D ,则直线CD 是否过定点?若经过定点,求出定点的坐标;若不经过定点,请说明理由.14(2023·辽宁大连·高三校考阶段练习)在平面直角坐标系中,已知两个定点A (0,4),B (0,1),动点P 满足|PA |=2|PB |,设动点P 的轨迹为曲线E .(1)求曲线E 的方程;(2)若直线l :y =kx -4与曲线E 交于不同的两点C ,D ,且∠OCD =30°(O 为坐标原点),求直线l 的斜率;(3)若点Q 是直线l :x -y -4=0上的动点,过Q 作曲线E 的两条切线QM ,QN ,切点为M ,N ,探究:直线MN 是否过定点.15(2023秋·山西太原·高三校考期末)已知点A 0,-1 ,B 0,1 ,动点P 满足PB AB =PA ⋅BA.记点P 的轨迹为曲线C .(1)求C 的方程;(2)设D 为直线y =-2上的动点,过D 作C 的两条切线,切点分别是E ,F .证明:直线EF 过定点.16(2023·全国·高三专题练习)设点P 为直线y =x -3上的动点,过点P 作抛物线x 2=2y 的两条切线,切点为A ,B .(1)证明:直线AB 过定点;(2)若以线段AB 为直径的圆过坐标原点O ,求点P 的坐标和圆的方程.考点三、阿基米德三角形之定值问题17(2023·河南郑州·高三校考期末)如图,已知抛物线C :y 2=2px (p >0)上的点到焦点的距离的最小值为1,过点P -4,0 作抛物线C 的两条切线,切点分别为A ,B ,D 为线段PA 上的动点,过点D 作抛物线的切线,切点为E (异于点A ,B ),且直线DE 交线段PB 于点H .(1)求抛物线C 的方程;(2)证明:AD +BH 为定值.18(2023·全国·高三专题练习)已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点(1,0),椭圆Γ1的离心率为12,抛物线Γ2的顶点为原点.(1)求椭圆Γ1和抛物线Γ2的方程;(2)设点P 为抛物线Γ2准线上的任意一点,过点P 作抛物线Γ2的两条切线PA ,PB ,其中A ,B 为切点.设直线PA ,PB 的斜率分别为k 1,k 2,求证:k 1k 2为定值.考点四、阿基米德三角形之面积问题19(2023·全国·高三专题练习)已知抛物线C :x 2=2py (p >0)的焦点到原点的距离等于直线l :x -4y -4=0的斜率.(1)求抛物线C的方程及准线方程;(2)点P是直线l上的动点,过点P作抛物线C的两条切线,切点分别为A,B,求△PAB面积的最小值.20(2023·全国·高三专题练习)已知点A(0,2),动点M到点A的距离比动点M到直线y=-1的距离大1,动点M的轨迹为曲线C.(1)求曲线C的方程;(2)Q为直线y=-1上的动点,过Q作曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值21(2023·全国·高三专题练习)已知抛物线C的方程为x2=4y,点P是抛物线C的准线上的任意一点,过点P作抛物线C的两条切线,切点分别为A,B,点M是AB的中点.(1)求证:切线PA和PB互相垂直;(2)求证:直线PM与y轴平行;(3)求△PAB面积的最小值.考点五、阿基米德三角形之切线垂直22(2023·全国·高三专题练习)抛物级x2=2py(p>0)的焦点F到直线y=-p2的距离为2.(1)求抛物线的方程;(2)设直线y=kx+1交抛物线于A x1,y1,B x2,y2两点,分别过A,B两点作抛物线的两条切线,两切线的交点为P,求证:PF⊥AB .23(2023·全国·高三专题练习)已知抛物线C的方程为x2=4y,过点P作抛物线C的两条切线,切点分别为A,B.(1)若点P坐标为0,-1,求切线PA,PB的方程;(2)若点P是抛物线C的准线上的任意一点,求证:切线PA和PB互相垂直.考点六、阿基米德三角形之角度问题24(2023·全国·高三专题练习)已知F ,F 分别是椭圆C 1:17x 2+16y 2=17的上、下焦点,直线l 1过点F 且垂直于椭圆长轴,动直线l 2垂直l 1于点G ,线段GF 的垂直平分线交l 2于点H ,点H 的轨迹为C 2.(1)求轨迹C 2的方程;(2)若动点P 在直线l :x -y -2=0上运动,且过点P 作轨迹C 2的两条切线PA 、PB ,切点为A 、B ,试猜想∠PFA 与∠PFB 的大小关系,并证明你的结论的正确性.25(江西·高考真题)设抛物线C :y =x 2的焦点为F ,动点P 在直线l :x -y -2=0上运动,过P 作抛物线C 的两条切线PA 、PB ,且与抛物线C 分别相切于A 、B 两点.(1)求△APB 的重心G 的轨迹方程.(2)证明∠PFA =∠PFB .考点七、阿基米德三角形之点坐标问题26(2023·全国·高三专题练习)已知动点P 到直线y =-8的距离比到点0,1 的距离大7.(1)求动点P 的轨迹方程;(2)记动点P 的轨迹为曲线C ,点M 在直线l 1:y =-1上运动,过点M 作曲线C 的两条切线,切点分别为A ,B ,点N 是平面内一定点,线段MA ,NA ,NB ,MB 的中点依次为E ,F ,G ,H ,若当M 点运动时,四边形EFGH 总为矩形,求定点N 的坐标.27(2023春·广东茂名·高三校考阶段练习)已知平面内动点P x ,y ,P 到定点F 6,0 的距离与P 到定直线l :x =463的距离之比为32,(1)记动点P 的轨迹为曲线C ,求C 的标准方程.(2)已知点M 是圆x 2+y 2=10上任意一点,过点M 作做曲线C 的两条切线,切点分别是A ,B ,求△MAB 面积的最大值,并确定此时点M 的坐标.注:椭圆:x 2a 2+y 2b 2=1a >b >0 上任意一点P x 0,y 0 处的切线方程是:x 0x a 2+y 0y b2=1.28(2023秋·湖北武汉·高三华中师大一附中校考期末)已知抛物线C 的顶点为坐标原点O ,焦点F 在x 轴的正半轴,点Q m ,2 抛物线上,且Q 到抛物线的准线的距离为2.(1)求抛物线C 的方程;(2)动点P 在抛物线的准线上,过点P 作拋物线C 的两条切线分别交y 轴于A ,B 两点,当△PAB 面积为2时,求点P的坐标.好题冲关【能力提升】1(2022·陕西·校联考模拟预测)抛物线上任意两点A、B处的切线交于点P,称△PAB为“阿基米德三角形”.当线段AB经过抛物线焦点F时,△PAB具有以下特征:①P点必在抛物线的准线上;②△PAB 为直角三角形,且PA⊥PB;③PF⊥AB.若经过抛物线y2=4x焦点的一条弦为AB,阿基米德三角形为△PAB,且点P的纵坐标为4,则直线AB的方程为()A.x-2y-1=0B.2x+y-2=0C.x+2y-1=0D.2x-y-2=02(2023·全国·高三专题练习)抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形,在数学发展的历史长河中,它不断地闪炼出真理的光辉,这个两千多年的古老图形,蕴藏着很多性质.已知抛物线y2=4x,过焦点的弦AB的两个端点的切线相交于点M,则下列说法正确的是()A.M点必在直线x=-2上,且以AB为直径的圆过M点B.M点必在直线x=-1上,但以AB为直径的圆不过M点C.M点必在直线x=-2上,但以AB为直径的圆不过M点D.M点必在直线x=-1上,且以AB为直径的圆过M点3(2022·全国·高三专题练习)圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形,过抛物线焦点F作抛物线的弦,与抛物线交于A,B两点,分别过A,B两点作抛物线的切线l1,l2相交于点P,那么阿基米德三角形PAB满足以下特性:①点P必在抛物线的准线上;②△PAB为直角三角形,且∠APB为直角;③PF⊥AB,已知P为抛物线y2=x的准线上一点,则阿基米德三角形PAB面积的最小值为()A.12B.14C.2D.14(2023·青海西宁·统考二模)抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形.阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的斜率之积为定值.设抛物线y2=2px(p>0),弦AB过焦点,△ABQ为阿基米德三角形,则△ABQ的面积的最小值为()A.p22B.p2C.2p2D.4p25(2023·宁夏银川·六盘山高级中学校考三模)已知动点P到直线y=-54的距离比到定点0,14的距离大1.(1)求动点P的轨迹C的方程.(2)若M为直线y=x-2上一动点,过点M作曲线C的两条切线MA,MB,切点为A,B,N为AB的中点.①求证:MN⊥x轴;②直线AB是否恒过一定点?若是,求出这个定点的坐标;若不是,请说明理由.6(2022·全国·高三专题练习)在直角坐标系xOy中,已知抛物线C:y2=2px p>0,点M32,y是抛物线C 上的一点,点M 到焦点的距离为2.(1)求抛物线C 的方程;(2)点P x 0,y 0 为圆E :x +2 2+y 2=1上的任意一点,过点Р作抛物线C 的两条切线PA ,PB ,切点分别为A ,B ,求点О到直线AB 距离的最大值.7(2023·全国·高三专题练习)如图已知P -2,t 是直线x =-2上的动点,过点P 作抛物线y 2=4x 的两条切线,切点分别为A ,B ,与y 轴分别交于C ,D .(1)求证:直线AB 过定点,并求出该定点;(2)设直线AB 与x 轴相交于点Q ,记A ,B 两点到直线PQ 的距离分别为d 1,d 2;求当ABd 1+d 2取最大值时△PCD 的面积.8(2023·全国·高三专题练习)已知点A (-4,4)、B (4,4),直线AM 与BM 相交于点M ,且直线AM 的斜率与直线BM 的斜率之差为-2,点M 的轨迹为曲线C .(1)求曲线C 的轨迹方程;(2)Q 为直线y =-1上的动点,过Q 作曲线C 的切线,切点分别为D 、E ,求△QDE 的面积S 的最小值.9(2023·全国·高三专题练习)已知抛物线C 的方程为x 2=2py p >0 ,点A x ,32是抛物线上的一点,且到抛物线焦点的距离为2.(1)求抛物线的方程;(2)点Q 为直线y =-12上的动点,过点Q 作抛物线C 的两条切线,切点分别为D ,E ,求△QDE 面积的最小值.10(2022春·安徽滁州·高二校考开学考试)已知抛物线C :y 2=2px p >0 上的任意一点到焦点的距离比到y 轴的距离大12.11(1)求抛物线C 的方程;(2)过抛物线外一点P m ,n 作抛物线的两条切线,切点分别为A ,B ,若三角形ABP 的重心G 在定直线l :y =32x 上,求三角形ABP 面积的最大值.【真题感知】11(全国·统考高考真题)已知曲线C :y =x 22,D 为直线y =-12上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点:(2)若以E 0,52为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.12(辽宁·高考真题)如图,抛物线C 1:x 2=4y ,C 2:x 2=-2py p >0 .点M x 0,y 0 在抛物线C 2上,过M 作C 1的切线,切点为A ,B M 为原点O 时,A ,B 重合于O .当x 0=1-2时,切线MA 的斜率为-12.(I )求p 的值;(II )当M 在C 2上运动时,求线段AB 中点N 的轨迹方程(A,B 重合于O 时,中点为O)。
有限元三角形单元

有限元三角形单元
有限元三角形单元是有限元分析中常用的基本构件,用于建立复杂结构的数学模型,以进行工程分析。
这些三角形单元是用来离散化连续问题的,将其转换为有限元模型,以便计算机可以进行数值求解。
在有限元分析中,三角形单元有不同类型,其中常见的包括:
1. 线性三角形单元:
- 由三个节点组成的简单三角形单元。
- 三角形的三条边都是直线。
- 这种单元的形状函数是线性的,适用于简单的结构和问题。
2. 二阶和高阶三角形单元:
- 包括更多节点以提高精度的三角形单元。
- 二阶三角形单元具有额外的中间节点,使得形状函数更复杂,从而提高了精度。
- 高阶三角形单元同样通过增加节点来提高精度,但也增加了计算复杂度。
这些三角形单元被用于建立有限元模型,将结构或物体分割成小的几何形状,每个形状都有对应的节点和单元连接关系。
通过这些节点之间的位移和边界条件来建立结构的数学模型,从而进行力学、热力学等各种工程分析。
选择适当类型和精度的三角形单元对于准确地模拟实际问题非常重要,因为它们直接影响到模型的计算精度和效率。
奥数知识点-图形计数

巧数图形例1、数出下图中共有多少条线段。
分析与解:对于基础图形,用最小线段为单位,按序递增。
单拼:3(段),双拼:2(段),三拼:1(段)通过以上的计数方法可以发现:开小火车的方式解决。
最小线段(基础线段)的数量为火车头火车头为基础线段数3段:3+2+1=6(段){或者,线段个数=基础线段数×端点÷2(高阶)基础线段要求:手拉手,肩并肩对于相交的线段,分别计算各个方向,然后加总例2、数出下页左上图中锐角的个数。
分析与解:对于基础图形,可以使用开小火车的方式解决。
最小线段的数量为火车头。
/或者,角的个数=最小角个数×(最小角个数+1)÷2又,角的个数=射线的个数×(射线个数-1)÷2例3、下列各图形中,三角形的个数各是多少分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车头。
所以,三角形个数=底边线段个数(每个底边基础线段构成一个基础三角形)或者,三角形的个数=最小三角形个数×(最小三角形个数+1)÷2(高阶)¥以上的内容基本是单层规整图形:数线段(数角,数三角形),解决方法:开小火车!对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的数量。
例4、下列图形中各有多少个三角形分析与解:方法(1)使用分层计数法:图(1)~图(2)上层:4+3+2+1=10(个)上层:4+3+2+1=10(个)下层: 0(个);中层:0(个)上下层:4+3+2+1=10(个)下层:0(个)[ 上中层:4+3+2+1=10(个)中下层:0(个)—上中下层:4+3+2+1=10总数:10+0+10=20(个)总数:—10+10+10=30(个)方法(2)公式法:第一层三角形的总数×层数公式法:第一层三角形的总数×层数图(1)图(2)第一层:4+3+2+1=10(个)4+3+2+1=10(个),第一层:层数: 2(层)层数: 3(层)总数:10×2=20(个)¥总数:10×3=30(个)例5、下列图形中各有多少个三角形分层法:;上层:4+3+2+1=10(个)下层: 4(个)(吹泡泡法)上下层:。
行列式的计算方法

引言 (1)一、行列式的定义及性质 (2)(一)行列式的定义及相关公式 (2)(二)n级行列式的性质: (4)二、行列式的计算 (6)(一)行列式的基本计算方法 (6)1、定义法: (6)2、三角形法: (7)3、降阶法: (12)4、换元法: (14)5、递推法: (15)6、数学归纳法: (16)7、目标行列式法: (18)(二)行列式的辅助计算方法 (19)1、加边法: (19)2、析因子法: (21)3、连加法: (21)4、拆项法: (22)5、乘积法: (23)结束语 (24)参考文献: (26)行列式的计算方法摘要行列式是线性代数理论中极其重要的组成部分,是高等数学的一个基本的概念。
行列式产生于解线性方程组中,并且也是最早应用于解线性方程组中,并且在其他学科分支都有广泛的应用,可以说它是数学、物理学以及工科许多课程的重要学习工具.行列式也为解决实际问题带来了许多方便。
本文针对行列式这一数学工具,进行系统讨论,从不同的角度理解了行列式的定义,重点证明了行列式性质,介绍一些展开定理,总结了行列式的几种计算方法,如定义法、三角形法、降阶法、换元法、递推法、数学归纳法及目标行列式法.辅助方法有:加边法、析因子法、乘积法、连加法、拆项法等,并结合例题说明行列式计算的技巧性和灵活性。
关键词行列式,计算方法,线性方程组。
The Calculation of DeterminantLiuHui(College of Mathematics and Physics Bohai University Liaoning Jinzhou 121000 China)Abstract The determinant is the extremely important constituent in the linear algebra theory, it is a basic concept of higher mathematics。
过程性变式,促进学生高阶思维发展——过程性变式设计理念下的“三角形”单元复习教学探索

.J•纟衣学下半月.数学◊沈强[6\过程性变式,漫丿促进学生高阶思维发展过程性变式设计理念F的“三角形”单元复习教学探索变式教学是一种广泛使用的教学方式。
在数学课堂教学中,有两种本质不同的变式类型:概念性变式和过程性变式。
概念性变式是指通过改变概念呈现方式,来帮助学生识别概念的本质特征,并体会其内涵的策略。
过程性变式是指创建变式问题或情境,让学生进行探究,找到问题的解决方案,以此让学生逐步或从多种途径学会建立不同概念之间的联系⑴。
本文试图从学生的认知视角,探讨在几何复习课中使用过程性变式来促进学生高阶思维的发展。
=、研究设i十1.参与者与背景。
分析的这一课是人教版教材四年级下册“三角形”单元的复习课。
执教者是已任教小学数学17年的高级教师。
参与研究的核心成员中,有三位是浙江省特级教师,其中两位是正高级教师,其他的是名师工作站的成员。
2.数据收集。
每次研讨和试教后,教师简要阐述自己的教学计划和实施情况,核心成员进行点评,其他成员对问题进行评议和交流,提出后案一期修改建议和方向。
收集到的资料包括教学设计、课堂实录、学生观察表、会议记录单等。
例3.教学计划说明。
教学计划中明确了本节课可的主要教学目标:第一,通过任务驱动帮助学生=梳理本单元的知识内容,加深对三角形特征的认二识,巩固知识并提高技能。
第二,通过设计变式问剧题,尝试用想象和推理来处理任务,培养学生的空间观念,提高推理能力。
本节课包括三个主要阶段:第一阶段,情境变式(基本三角形的构建)。
教师出示问题:从7根小棒(18、10、8、6、6、6、2,长度单位为厘米)中选3根,能围成几个不同的三角形?要求学生根据三角形的三边关系,有序地将符合条件的三角形记录下来。
教师将答案按一定的顺序排列。
第二阶段,问题变式(复杂问题的解决)。
教师先出示基本问题:根据边的长短,判断分别是什么三角形(等腰、等边、不等边三角形)。
再出示变异问题:根据边的长短,将其按角分类(锐角、直角、钝角三角形)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元几何矩阵Be如下:
单元应力矩阵Se如下: 本构矩阵 D 对平面应力和平面应变略有不同:
E; 平面应力
E1
=
{ 1
E − μ2
;
平面应变
������;平面应力 ������1 = { ������ ; 平面应变
1 − ������ 单位刚度矩阵Ke如下: Ke = ∫ BeT DBe������V
… …
N4 0
0 N4
]
δe
=
Neδe
图 6:5 节点单元
N1 = L1 N2 = L2(1 − 3L3) N3 = 3(1 − 3L2) N4 = 2L2L3 在有限元分析中,经常会碰到一些比较 特殊的 几何 区域, 需要较 高的计 算精 度, 例如凹角、台阶和孔洞等突变区域;有多种材料连接的区域;边界条件比较复杂 的区域;需要特别关注的区域。这些区域有可能只在一个方向或很小的范围对精度 要求高,这时,这一类 4 节点三角形单元和 5 节点单元就可以很好的满足这一要 求。 3 评价基于 ANSYS: Ansys 中选择三角形plane182 单元和三角形plane183 单元,分别代表三角 形三节点单元和六节点单元,用来分别对简支梁的受力情况进行计算:
开卷试题二
一 类 三 角形高次元的 设想、实现与评价
1、 设 想 :
作为一种较为普及的有限元单元,三角形单元非常适合与求解二维问题。并且能够
处理二维边界问题,此外它的形函数相对便于构建。
线性三角形单元在有限元分析中有着计算简单,计算量小,几何适应性好,单元易分割等
优点。特别是当对包含锐角的、几何形状复杂的二维模型进行网格划分时,往往会采用三
这些单元有着下面几个共同特点:有中节点的边是高阶的,没有中节点的边是
线性的,若所有中节点都不存在则该单元退化成为线性单元。这样的节点分布可以
满足部分边的精度要求又可以减少单元整体的自由度。
以图 5 中的 4 节点三角形单元为 Nhomakorabea,其位移差值和形函数为:
ue
=
{UV}
=
[N01
0 N1
N2 0 0 N2
5%
E183 80
5.29944 5.8753 5.625 6%
4%
表2
从上表中可以看出,PLANE182单元(线性三角形单元)当单元总数增大使得拉
应力和压应力的计算精度逐渐增大,在单元总数均大于40的情况下,二次六节点计算出来
的误差在5%左右,而线性三角形单元所计算的误差超过了60%,当其单元总数达到80
,
该单元应变、应力随坐标完全呈线性变化,属于高精度单元。 单元位移模式和形函数可以通过三角形单元的面积坐标来描述。
图 2 面积坐标
如图 2 所示,所示,三角形任意一点 P 的面积坐标为(������������,������������,������������), 定义为������������ =
图 12 长度方向 20 份高度方向 2 份
图 13 长度为 40 份高度为 2 份 当采用 PLANE183 单元时计算结果如下:
图 14 单元密度为 15
图 17 单元密度为 7.5 现在回到模型上(见图 9): 应为按照平面问题处理,所以在求解集中力点处的挠度可以使用位移法。
UY = F4������×2������×12×2×4������×23,其中I = bh3
采用线性三角形单元PLANE182的压力云图如下:
图 18 单元总数为 40 的压力分布云图 图 19 单元总数为 80 压力分布云图
图 20 单元总数为 160 的压力云图 图 21 单元总数为 800 时的压力云图
采用高阶三角形单元 PLANE182 的压力云图如下: 图 22 单元总数为 40 的压力分布云图 图 23 单元总数为 80 的压力分布云图
Ve
将单元几何矩阵Be和本构矩阵 D 代入上式,可得单元刚度矩阵Ke的表达式如下:
通过上述理论推导,我们得到了三角形二阶单元的位移模式,并分析了其完备性 和协调性给出了形函数,几何矩阵,应力矩 阵和单 元刚度 的具 体表达 式。 2.2 三角形 10 节点(三角形的每条边上插入 2 个两个节点,另加一个形心) 其位移模式为:
位移模式为:
图 1 三角形(2 阶)6 节点单元
很显然该模式为完全二次多项式,能够较好地模拟刚体位移和常应变,因此其满足完备性 条件。此外由于该位移模式决定了单元边界上位移呈二次抛物线分布,相邻单元公共边界 上有三个公共节点,保证了相邻单元在边界上位移的连续性,因而是协调元,单元满足收 敛条件。其应变可以写为:
但是,高次三角形单元仍有一些问题没有解决,如高次三角形形函数的普遍性还不理 想,不能用原有的线性三角形单元的形函数的方法来推导,和一元函数的插值方法不相 同,故有线性三角形到高次三角形单元的转化是一个具有挑战的问题。因此这里主要讨论 和构造二次三角形单元。
2、 三 角 形二阶单 元和三阶单元 2.1 三角形 6 节点(在三边中点处分别插入一个节点)
33%
800
0.004996
0.0050242
1%
PLANE183
40
80
0.005245 0.005307
0.0050242
4%
0.0050242
6%
表1 同样是单元数为40,线性三角形单元的误差达到了50%,而PLANE183 的二次六节点插值三 角形单元的 误差只有4%,可以看出PLANE182 的三角形单元即线性三角形单元的精度要差 很多,而PLANE182 要想将精度控制在5%之内,要将单元数量增加至800.而PLANE183 即二 次六节点二次插值三角形单元计算出位移的相对误差随着网格数量的增加 没有明显变化, 而且有增大的趋势,所以6 节点三角形单元不需要将单元数量设置大来获得高精度。
0时期拉应力的误差仍然在15%,压应力的误差控制到了5%左右,可见二次六节点三角
形单元的计算精度要明显的高于线性三角形单元。
图 4 三角形 6 阶(10 节点)单元
其面积坐标的形式函数为:
ue
=
{UV}
=
[N01
0 N2 N1 0
0 N2
… …
N10 0
0 N10
]
δe
=
Neδe
1 Ni = 2 (3Li − 1)(3Li − 2)Li, i = 1,2,3
9 N4 = 2 L1 L2(3L1 − 1)
9 N5 = 2 L1 L2(3L2 − 1)
������������ = (2������������ − 1)������������ ,������ = 1,2,3 ������4 = 4������1������2 ������5 = 4������2������3 ������6 = 4������3������1
单元节点位移向两以及单元节点载荷向量定义如下:
10 节点三角形的位移模式是完全三次多项式,因此该模式 满足完备性条件。每条边上都是三次函数。同时每条边都有 4 个节点,可以确定一个三次函数,因此该单元的位移模式 也满足协调性条件。
三角形三阶 10 节点单元的位移模式和形函数和 6 节点 三角形不同,但几何矩阵,应力矩阵和单元刚度矩阵的推导 方法与之前一样。
EI
12
解得: UY=0.0050223mm
纵向位移方面,采用 PLANE182 和 PLANE183 单元的对比如下
单元类型
单元总数
竖直方向位移 理论解
相对误差
PLANE182 40 80
0.002481 0.003131
0.0050242
51%
0.0050242
38%
160
0.003362
0.0050242
图 7 建立模型
首先建立高度为20mm长度为 150mm的 梁模型 ,厚度 设置为 1,杨式 模量设 置 为2.1e5MPa。泊松比设置 为0. 3, 该梁两 端简支 中间受 垂直向 下的力 10N。
然后对模型划分网格,长度方向上的单 元先后 设置 为15, 7. 5, 3. 75将高度 方向 上的单元设置为10以下是网格划分情况:
图 8 长度方向分为 10 份高度方向分为 2 份
图 9 长度方向 20 份高度方向 2 份
图 10 长度方向 40 份高度方向 20 份 添加约束
在座节点添加 XY 方向的位移约束,由节点只添加 Y 方向上的约束,并在重点加载 10N 的集中力。 当采用 PLANE182 单元时计算结果如下:
图 11 长度方向 10 份高度 2 份
a)
a)
PLAN 40
1.56219 1.59952 5.625 72%
72%
E182 80
2.08817 2.15279 5.625 63%
62%
160 2.32886 2.37878 5.625 59%
58%
800 4.78208 5.28041 5.625 15%
6%
PLAN 40
5.2703 5.32207 5.625 6%
������������������,������������
=
������������,������
������
������
=
������������。面积坐标与直角坐标的转换关 系如下 :
������
图 3 节点编号 三角形二阶单元的节点顺序如图3 所示,节点1,2,3 逆时针排列,节点4,5,6 分别位于 12 边,23 边,31 边的中点。利用面积坐标,形函数可写为:
角形单元,而且其简单的拓扑性质使得研制网格生成器变得相对容易。但是,由于其位移差
值函数是线性的,这就不可避免的产生一些缺点。线性三角形单元的差值函数为:
