能量守恒定律 刚体的定轴转动
合集下载
刚体的定轴转动
第一节 刚体运动的描述
图5- 4 刚体的角量描述
第二节 刚体的定轴转动定律
一、 力对转轴的力矩
对于刚体的定轴转动而言，若 作用在刚体上p点的力F在转动平面 内，力的作用点p相对于转轴的位 矢为r，力臂为d，则力F对转轴的 力矩为
M=r×F 其中，力矩的大小M=Frsin θ 如图5-5所示.
图5- 5 力在转动平面内
第一节 刚体运动的描述
图5- 1 刚体的平动
第一节 刚体运动的描述
2. 刚体的转动
刚体在运动过程中，如果其上所有的点都绕同一条直线做圆 周运动，那么这种运动称为转动，这条直线称为转轴.如果转轴的 位置或方向随时间变化，那么这种转动称为非定轴转动；如果转 轴的位置或方向是固定不动的，那么这种转动称为定轴转动.
第一节 刚体运动的描述
一、 刚体的平动和转动
1. 刚体的平动
刚体在运动过程中,如果其上任意两点间所连的直线始终保持平 行,那么这种运动称为刚体的平动.例如,汽缸中活塞的运动、车床上 车刀的运动、升降机运动等,都属于平动.显然,刚体做平动时,刚体上 任意一条直线在刚体平动过程中始终保持平行,如图5-1所示.直线上 所有的点应有完全相同的位移、速度和加速度.在平动过程中,刚体上 所有点的运动是完全相同的，它们都具有相同的位移、速度和加速 度.因此，可以用刚体上任意一点的运动来代表整个刚体的平动.前面 质点运动的描述和质点力学的规律，实际上是刚体的平动规律.
第一节 刚体运动的描述
一般物体在外力作用下，其形状和大小都要发生变 化.但如果在外力作用下，物体的形状和大小保持不变， 即物体内任意两点之间的距离不因外力而改变，这样的物 体称为刚体.刚体可以看成由无数个连续分布的质点组成 的质点系，每个质点称为刚体的一个质量元，这样刚体的 每个质量元都服从质点力学规律.不同于质点，刚体这个 特殊的质点系的力学规律有自己特殊的表现形式.
守恒定律与刚体定轴转动精品课件
▶
引力势能：Ep
=
−
Gm1 r
m2
▶
弹性势能：
1 2
k
(x
−
x0 )2
质心：⃗rC
=
∑∑i immi⃗ri i ，或 ⃗rC
=
∫ ∫⃗rdm
dm
质心运动定理：F⃗ 外 = m⃗aC
克尼希定理：Ek = ECk M + EC
质点的角动量：⃗L = ⃗r × ⃗p = m⃗r × ⃗v
角动量定理：M⃗
=
一质量为 m 的滑块以初速度 v0 沿切线方向进入屏障的一端，
⃗v
如图所示。设滑块与屏障间的摩擦系数为 µ。证明：当滑块从
屏障的另一端滑出时，摩擦力所做的功为
O
Wf
=
1 2
mv20(e−2µπ
− 1)。
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
. .. . . ..
2 / 33
功、动能、角动量定理
基本概念
功：质点在力 F⃗ 的作用下有位移 d⃗r，
该力做的功 dW = F⃗ ·d⃗r = Fdr cos θ,
∫B WAB = F⃗ ·d⃗r
A
动能（运动状态速率
v
的函数）：
1 2
mv2
（质点动能）
动能定理
▶ 质点的动能定理： WAB = EkB − EkA
. . . .... .... .... . . . . .... .... .... . .
. .. . . .. 10 / 33
讨论题
2. 判断在下列几种情况中机械能是否守恒： (1) 当物体在空气中下落时，以物体和地球为系统 (2) 当地球表面物体匀速上升时，以物体与地球为系统（不计空气阻力） (3) 子弹水平地射入放在光滑水平桌面上的木块内，以子弹和木块为系统 (4) 当一球沿光滑的固定斜面向下滑动时，以小球和地球为系统
(完整版)刚体转动守恒定律
速度0＝0，下摆到竖直位置时的角速度为 ，按 力矩的功和转动动能增量的关系式得
定轴转动的动能定理
mg l 1 J 2
22
由此得 mgl
J
因 J 1 ml 2 代入上式得 3g
3
J
所以细棒在竖直位置时，端点A和中心点C的速度
分别为
vA l 3gl
vC
l
2
1 2
3gl
刚体的平面平行运动
c.若系统内既有平动也有转动现象 发生，若对某一定轴的合外力矩为 零,则系统对该轴的角动量守恒。
定轴转动刚体的角动量守恒定律
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
dv d2 x a dt dt2
P mv F
EK
1 mv2 2
m
dA Fdx Fdt
刚体的定轴转动
d
dt
d
dt
Mz
dLz dt
t2 Mdt t1
L2 L1
dL
L2
L1
角动量定理的微分形式：
t2 t1
M
d
t
J
J0
t2 M d t为t t2 t1时间内力矩M 对给定轴的冲量矩
t1
。
2. 定轴转动刚体的角动量守恒定律
角动量守恒定律：若一个系统一段时间内
所受合外力矩M 恒为零，则此系统的总角 动量L 为一恒量。
解 先对细棒OA所受的力
作一分析；重力G 作用在 O
棒的中心点C，方向竖直向
下；轴和棒之间没有摩擦
力，轴对棒作用的支承力N
垂直于棒和轴的接触面且
通过O点，在棒的下摆过
G
程中，此力的方向和大小
4-7 刚体定轴转动的势能和机械能守恒
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
刚体作为特殊的质点系，满足质点系的功能原理 和当条件成立时满足机械能守恒
刚体重力势能：
Δ mi
C×
hc hi
刚体重力势能等于质量集中于质 心， Ep=0 质心的重力势能。
第四章 刚体的转动
1
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
讨论
子细 弹绳 击质 入量 沙不 袋计
1 3mva 2 2 mva ( ml ma ) 2 2 3 m'l 3ma
第四章 刚体的转动
5
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
射入竿后，以子弹、细 杆和地球为系统：
外力： F
F
o
'
30
a
m dWF M F d 0 v in 非保守内力：刚体内力 W刚体 0
W
ex
W 0
in nc
第四章 刚体的转动
6
E E0
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
选初始位置为势能零点
o
30
1 1 ( ml 2 ma 2 ) 2 2 3
o
a
m v
'
l o mga (1 cos30 ) m g (1 cos 30 ) 2
dAF 0
N
M d 0 d 0 dAN N
第四章
刚体的转动
m1 g
9
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
FN
考虑过程：m2位移（下降）dh
4-7
刚体定轴转动的势能和机械能守恒
刚体作为特殊的质点系，满足质点系的功能原理 和当条件成立时满足机械能守恒
刚体重力势能：
Δ mi
C×
hc hi
刚体重力势能等于质量集中于质 心， Ep=0 质心的重力势能。
第四章 刚体的转动
1
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
讨论
子细 弹绳 击质 入量 沙不 袋计
1 3mva 2 2 mva ( ml ma ) 2 2 3 m'l 3ma
第四章 刚体的转动
5
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
射入竿后，以子弹、细 杆和地球为系统：
外力： F
F
o
'
30
a
m dWF M F d 0 v in 非保守内力：刚体内力 W刚体 0
W
ex
W 0
in nc
第四章 刚体的转动
6
E E0
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
选初始位置为势能零点
o
30
1 1 ( ml 2 ma 2 ) 2 2 3
o
a
m v
'
l o mga (1 cos30 ) m g (1 cos 30 ) 2
dAF 0
N
M d 0 d 0 dAN N
第四章
刚体的转动
m1 g
9
大学 物理学
4-7
刚体定轴转动的势能和机械能守恒
FN
考虑过程：m2位移（下降）dh
刚体定轴转动角动量守恒定律
角动量守恒； 机械能不守恒 .
机械能不守恒 .
第四章 刚体力学
角动量守恒； 机械能守恒 .
2
大学 物理
4-4 刚体定轴转动的角动量守恒定律
例：细棒m1，l静止放在摩擦系数为的水平桌上，可绕O旋转， 1 2 J m1l ., 小球以v1垂直击另一端，并以v2反向弹回。 3 求：（）碰后棒角速度；（）开始转动到停止所需 1 2 时间。 O 解： (1)碰撞过程中，角动量守 恒（向外为转轴正向）
生活中的例子：芭蕾舞 、滑冰、跳水
第四章 刚体力学
1
大学 物理
4-4 刚体定轴转动的角动量守恒定律 讨论 子 弹 击 入 杆 圆 锥 摆
子细 弹绳 击质 入量 沙不 袋计
o
o
Hale Waihona Puke o T'
v
m
v
p
o
v
R
以子弹和沙袋为系统 动量守恒；
以子弹和杆为系统 动量不守恒； 角动量守恒；
圆锥摆系统 动量不守恒；
m2v1l m2v2l J
3m2 (v1 v2 ) m1l
(2)对棒，用角动量定理（ 设摩擦力矩 r ) M v1
l
m2
m1
v2
1 M r dt 0 J m1l 2 0 3
t
第四章
刚体力学
3
大学 物理
t
4-4 刚体定轴转动的角动量守恒定律
1 M r dt 0 J m1l 2 0 3
4-4 刚体定轴转动的角动量守恒定律
例 长为 l 的均质细直杆OA，一端悬于O点铅直下垂，如图 所示。一单摆也悬于O点，摆线长也为l，摆球质量为m。现将 单摆拉到水平位置后由静止释放，摆球在 A 处与直杆作完全 弹性碰撞后恰好静止。试求：⑴ 细直杆的质量m0；⑵ 碰撞后 细直杆摆动的最大角度。（忽略一切阻力）
刚体的能量定轴转动的动能定理
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。
求： 当杆过铅直位置时的角速度：
N
YZ
XO
r
mg
刚体定轴转动的势能和机械能守恒_1446
m1l 2
12m2u
(m1 3m2 )l
u(m1 3m2)
m1 3m2
4.7 刚体定轴转动的势能和机械能守恒
4.7-4一长为l，质量为m1的棒可绕O点在竖直 平面内自由转动．一质量为m2，速度为v的子 弹射入棒内不复出，射入点距O点为a．若棒
偏转过的最大角度为60°，问子弹的初速度
联立解得 v Jg(m2a0.5m1l)
m2a
4.7 刚体定轴转动的势能和机械能守恒
水平面内绕通过其中心的竖直定轴转动，开
始细棒静止．质量为m2的小球，以水平速度 u与棒的端点作弹性碰撞．求：碰后小球弹
回的速度及棒的角速度
m2
解:不考虑摩擦力矩的作用,
O
u
弹性碰撞前后: 角动量守恒 m2u2l Jm22l 机械能守恒 12m2u212J212m22
m1 l
J
1 2
运动过程中只有保守内力做功，刚体 系统的机械能仍然守恒。
4.7 刚体定轴转动的势能和机械能守恒
4.7-1如图所示，一匀质细杆，质量为m1， 长为L，可绕通过其一端的水平光滑轴O在
铅直面内转动，另一端连接一质量为m2的小
球．现将杆抬至水平，静止后释放，求杆
摆至铅直位置时杆的角速度
解：杆摆下过程机械能守恒
刚体定轴转 动的势能和 机械能守恒
4.7 刚体定轴转动的势能和机械能守恒
刚体在重力、弹性力等保守力作用 下转动,刚体定轴转动的势能为：
E p m igh i( m ih i)gii刚体质心高度
m ihi
h c i m i
得 Ep mghc
i
刚体与地球系统的重力势能，等于刚体 的质量集中于质心时系统所具有的势能。
《大学物理》3.4刚体定轴转动的角动量定理 角动量守恒定律
我国第一颗人造地球卫星沿椭圆轨道绕地球运动， 例：我国第一颗人造地球卫星沿椭圆轨道绕地球运动，地心为该椭圆 的一个焦点。 的一个焦点。已知地球半径 R ，卫星的近地点到地面距离 l ，卫星的远 地点到地面距离 l 。若卫星在近地点速率为 v1 ，求它在远地点速率 v2 。
1 2
卫星在运动过程中，所受力主要是万有引力， 解：卫星在运动过程中，所受力主要是万有引力，其它力忽 略不计，故卫星在运动过程中对地心角动量守恒。 略不计，故卫星在运动过程中对地心角动量守恒。 m
0
r
A
θ = 90
0
mv
质点作圆周运动的角动量
θ
L = rmv = mr ω
2
2.2刚体的角动量 刚体的角动量 刚体对 oz轴的角动量为
z
ω
v
2
i
L = ∑ m r ω = (∑ m r )ω
2 i i i i
o
r
i
m
i
∑ m r 刚体绕 oz 轴的转动惯量
2 i i
L = Jω
L = Jω
刚体对转轴的角动量等于其转动惯量与角速度乘积。 刚体对转轴的角动量等于其转动惯量与角速度乘积。
1 m v 0 a = ( ML2 + ma 2 )ω 3
子弹射入后一起摆动的过程只有重力做功，故系统机 械能守恒。
1 1 L 2 2 2 ( ML + ma )ω = mga (1 cos60°) + Mg (1 cos60°) 2 3 2
ω=
3(2ma + ML)g 2(3ma 2 + ML2 )
二、角动量定理和角动量守恒定理
1× mv 对时间求导 = r × (mv ) + × mv dt dt dt dr d dL ∵ = v , F = (mv ) M = dt dt dt dL 质点所受合外力矩等于质 ∴ = r × F + v × mv dt 点角动量对时间的变化率
刚体的定轴转动
角动量守恒定律
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
30
例 质量很小长度为l 的均匀细杆, 可绕过其中心 O 并与 纸面垂直的轴在竖直平面内转动 . 当细杆静止于水平位 置时, 有一只小虫以速率 v0 垂直落在距点 O 为 l/4 处, 并背离点O 向细杆的端点 A 爬行. 设小虫与细杆的质量 均为m. 问: 欲使细杆以恒定的角速度转动, 小虫应以多 大速率向细杆端点爬行? 解: 碰撞前后系统角动量 守恒
rj
j
内力矩之和 0
mi ri
2
令
J mi ri
2
M ij M ji
第2章 运动定律与力学中的守恒定律
——刚体转动惯量
M J
2–6 J
刚体作定轴转动时，刚体的角加速度与它所受 合外力矩成正比，与刚体的转动惯量成反比。
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
35
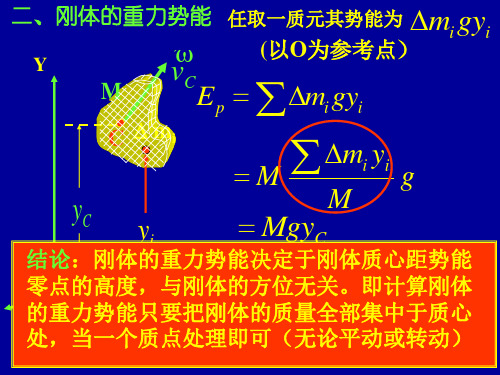
4、质量为m的不太大的整个刚体的重力势能
E P yg d m g y d m
Y y yc C
dm
mg
结论：
ydm
m
m gyc
O m X
一个不太大的刚体的重力势能 和它的全部质量集中在质心时所具 有的势能一样。
第2章 运动定律与力学中的守恒定律
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
4
转轴
转轴 Z
ri vi
O 转动平面
Δmi
Ｐ
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
5
3.刚体定轴转动的特点
• 各质点都作圆周运动；
54定轴转动刚体的角动量守恒定律
得：
l A
t = 2 m2 (v1 + v2 ) / µ m1 g
R/2
R
o
v
ω
8
（1） ） 2 2 1 1 R R 2 2 m ω 0 + MR ω 0 = − m ω mE + MR ω ME 2 2 2 2
ω
mE
= ω mM + ω ME
ω
mM
v =− R2
R/2
得 ω ME = (21Rω0 + 2v) / 21R （2）由 ）
o
ω1
= 70kg⋅ m2 J1 = J 0 + 2ml1 = 60+ 2×5×1 2 2 = 604kg⋅ m2 . J 2 = J 0 + 2ml2 = 60 + 2 × 5 × 0.2
2
2
由 J1ω1 = J 2ω 2 J1ω1 3 × 70 -1 = 得 ω2 = = 3.5s 60.4 J2 机械能不守恒， 机械能不守恒，因为人收臂时做功
R
o
v
ωME R = 0
得 v = −21Rω 0 / 2
ω
9
例6、质量为 m1、长为 l 的均匀细 、 杆,静止平放在滑动摩擦系数为 µ 的 静止平放在滑动摩擦系数为 水平桌面上,它可绕过其端点 水平桌面上 它可绕过其端点 o 且与 桌面垂直的固定光滑轴转动,另有一 桌面垂直的固定光滑轴转动 另有一 水平运动的质量为m 水平运动的质量为 2的小滑块 , 从 相碰撞,设 侧面垂直与杆的另一端 A 相碰撞 设 碰撞时间极短,已知小滑块在碰撞前 碰撞时间极短 已知小滑块在碰撞前 后的速度分别为 v1 和 v2 ,方向如图 方向如图 所示,求碰撞后从细杆开始转动到停 所示 求碰撞后从细杆开始转动到停 止转动过程所需时间,（ 止转动过程所需时间 （已知杆绕点 o 的转动惯量 J= ml2/ 3 )
l A
t = 2 m2 (v1 + v2 ) / µ m1 g
R/2
R
o
v
ω
8
（1） ） 2 2 1 1 R R 2 2 m ω 0 + MR ω 0 = − m ω mE + MR ω ME 2 2 2 2
ω
mE
= ω mM + ω ME
ω
mM
v =− R2
R/2
得 ω ME = (21Rω0 + 2v) / 21R （2）由 ）
o
ω1
= 70kg⋅ m2 J1 = J 0 + 2ml1 = 60+ 2×5×1 2 2 = 604kg⋅ m2 . J 2 = J 0 + 2ml2 = 60 + 2 × 5 × 0.2
2
2
由 J1ω1 = J 2ω 2 J1ω1 3 × 70 -1 = 得 ω2 = = 3.5s 60.4 J2 机械能不守恒， 机械能不守恒，因为人收臂时做功
R
o
v
ωME R = 0
得 v = −21Rω 0 / 2
ω
9
例6、质量为 m1、长为 l 的均匀细 、 杆,静止平放在滑动摩擦系数为 µ 的 静止平放在滑动摩擦系数为 水平桌面上,它可绕过其端点 水平桌面上 它可绕过其端点 o 且与 桌面垂直的固定光滑轴转动,另有一 桌面垂直的固定光滑轴转动 另有一 水平运动的质量为m 水平运动的质量为 2的小滑块 , 从 相碰撞,设 侧面垂直与杆的另一端 A 相碰撞 设 碰撞时间极短,已知小滑块在碰撞前 碰撞时间极短 已知小滑块在碰撞前 后的速度分别为 v1 和 v2 ,方向如图 方向如图 所示,求碰撞后从细杆开始转动到停 所示 求碰撞后从细杆开始转动到停 止转动过程所需时间,（ 止转动过程所需时间 （已知杆绕点 o 的转动惯量 J= ml2/ 3 )
§3-3定轴转动刚体的角动量守恒定律
v0
J
1 3
ml
2
解：系统的合外力矩为零,角动量守恒
mv 0 l mv 0 l 0 mvl mvl J
v l
代入上式
6v0 7l
太原理工大学物理系
例3 一个物体正在绕固定光滑轴自由转动时， A 它受热膨胀或遇冷收缩时，角速度不变
B 它受热时角速度变大，遇冷时角速度变小
பைடு நூலகம்
桌面高为h处以初速度V0落下，撞击弹簧后跳回到
高为h处时速度仍为V0，以小球为系统，则在这整 个过程中小球的 A 动能不守恒，动量不守恒B 动能守恒，动量守恒 C 机械能不守恒，动量守恒 D 机械能守恒，动量守
恒
太原理工大学物理系
例6 质量为m的小球，用轻绳AB、BC连接，如 图，剪断轻绳AB前后的瞬间，绳BC中的张力 比T：T’=
§3-3 定轴转动刚体的角动量守恒定律 由转动定律
M J
dL
dt 刚体所受的(对轴的)外力矩等于刚体(对轴的) 角动量的时间变化率。
或写作
t2 t1
M dt dL
对于一段时间过程有
M dt
t2 t1
d L L末 L初
太原理工大学物理系
三、定轴转动刚体的角动量守恒定律 如合外力矩等于零 L J 常 量 即转动过程中角动量(大小、方向)保持不变 角动量守恒定律比转动定律适用范围更广泛， 这里可以有
2 2
a
dv dt
d dt
d dt
d
2
dt
2
P mv
L J
F
dA Fdx F ma
刚体定轴转动的角动量定理和角动量守恒定律课件
转动惯量的特性
只与刚体的质量和各质点到转动轴 的距离有关，与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ，等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量，具有方向和大小；对 于定轴转动，角动量位于转轴上；角 动量是相对量，与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种，一种是基于牛顿第二定律和转动定理推导，另一种是通过分析系统的能 量变化来证明。通过这些证明方法，可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明，对于不受外力矩或所受外力矩的矢量和为零的系统，其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用，如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例，其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时，可以将其视为 刚体定轴转动，这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时，也是一个刚体定 轴转动的例子，其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时，可以通过改变身体的姿势来改变转动惯量，从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
只与刚体的质量和各质点到转动轴 的距离有关，与转动角速度的大小 无关。
02
角动量定理
角动量的定义与性质
角动量的定义
角动量是描述刚体转动状态的物理量 ，等于刚体的转动惯量乘以角速度。
角动量的性质
角动量是矢量，具有方向和大小；对 于定轴转动，角动量位于转轴上；角 动量是相对量，与参考系的选择有关 。
理解角动量守恒定律的证明方法是深入理解该定律的重要途径。
详细描述
证明角动量守恒定律的方法主要有两种，一种是基于牛顿第二定律和转动定理推导，另一种是通过分析系统的能 量变化来证明。通过这些证明方法，可以更深入地理解角动量守恒定律的物理意义和适用条件。
04
刚体定轴转动的实例 分析
刚体定轴转动的实例介绍
角动量守恒定律的内容及应用
总结词
掌握角动量守恒定律的内容及应用是解决实际问题的关键。
详细描述
角动量守恒定律表明，对于不受外力矩或所受外力矩的矢量和为零的系统，其总角动量保持不变。这 一原理在日常生活、工程技术和科学研究中有广泛的应用，如行星运动、陀螺仪、火箭飞行等。
角动量守恒定律的证明方法
总结词
陀螺仪
风扇
陀螺仪是一个典型的刚体定轴转动实 例，其工作原理就是角动量守恒定律 。
当风扇的扇叶旋转时，可以将其视为 刚体定轴转动，这个过程涉及到角动 量定理的应用。
自行车轮
自行车轮在转动时，也是一个刚体定 轴转动的例子，其转动惯量对于理解 角动量定理和角动量守恒定律非常有 帮助。
刚体定轴转动的角动量定理应用实例
舞蹈演员在进行旋转动作时，可以通过改变身体的姿势来改变转动惯量，从而控制旋转的 速度。
刚体定轴转动的角动量守恒定律应用实例
刚体定轴转动的角动量定理 角动量守恒定律
考虑到
t
12v0 dr g 7lg v cos t cos( t) dt 2 24v0 7l
例：圆盘（R，M），人（m）开始静止，人
走一周，求盘相对地转动的角度.
1 I 2 MR 2 2
解： 系统对转轴 角动量守恒
M=0
I11 () I 22 0
I1 mR
I
i i
i
const.
但角动量可在内部传递。
3 刚体定轴转动的角动量守恒定律 若M 讨论
守 恒条件:
0 ，则
L I 常量
M 0
若 I 不变， 不变；若 I 变， 也变，但 L I 不变. 内力矩不改变系统的角动量. 在冲击等问题中
M M L 常量
解：在走动过程中,人－盘系统 L=const. 设任意时刻，人对盘: ；盘对地: 则有 mR2 ( ) 1 MR 2 0 2
2m 2m M
2m dt dt 2m M
0
2m d 2m M
2
0
d
y FN
FT
O 图(a)
W
x
FNx ma c x
FT mg FNy ma c y
根据转动定理
2 7 FT R mg R mR 2 z 3 9
起动时
ac x 0
ac y
2 zR 3
a z R
67 FT mg 90
FNx 0
FNy
29 mg 90
2、子弹和棒的总动量在水方向上是否守恒？ 3、若将杆换成软绳系一质量为 M 的重物，在 水平方向上动量是否守恒？
t
12v0 dr g 7lg v cos t cos( t) dt 2 24v0 7l
例：圆盘（R，M），人（m）开始静止，人
走一周，求盘相对地转动的角度.
1 I 2 MR 2 2
解： 系统对转轴 角动量守恒
M=0
I11 () I 22 0
I1 mR
I
i i
i
const.
但角动量可在内部传递。
3 刚体定轴转动的角动量守恒定律 若M 讨论
守 恒条件:
0 ，则
L I 常量
M 0
若 I 不变， 不变；若 I 变， 也变，但 L I 不变. 内力矩不改变系统的角动量. 在冲击等问题中
M M L 常量
解：在走动过程中,人－盘系统 L=const. 设任意时刻，人对盘: ；盘对地: 则有 mR2 ( ) 1 MR 2 0 2
2m 2m M
2m dt dt 2m M
0
2m d 2m M
2
0
d
y FN
FT
O 图(a)
W
x
FNx ma c x
FT mg FNy ma c y
根据转动定理
2 7 FT R mg R mR 2 z 3 9
起动时
ac x 0
ac y
2 zR 3
a z R
67 FT mg 90
FNx 0
FNy
29 mg 90
2、子弹和棒的总动量在水方向上是否守恒？ 3、若将杆换成软绳系一质量为 M 的重物，在 水平方向上动量是否守恒？
刚体定轴转动角动量守恒定律解析
MR2
2
d
dt
R0
t
t
d dt
0
0
01
ut
(
2m
)
1 2
arctan[ M ]
0
2mu2t 2
MR2
dt
第四u章( 2Mm
1
刚) 2体力学
R
8 22
大学 物理
4-4 刚体定轴转动的角动量守恒定律
角动量守恒定律在工程技术上的应用
陀螺仪与导航
陀螺仪：能够绕其对称轴高速 旋转的厚重的对称刚体。
l 2
处)
解得
t
2 m2
v1 v2
m1g
O
关于摩擦力矩 在x处取dm，dm m1 dx
x l
l
dm
元摩擦力 df dmg
m1
元摩擦力矩 dMr df x dmg x
总摩擦力矩
M r
dMr
l m1 gxdx m1g l 2
0
l
l2
m1g
l 2
第四章 刚体力学
4
大学 物理
4-4 刚体定轴转动的角动量守恒定律
例 一长为l，质量为m0的杆可绕支点O自由转动。一质量为
m，速度为v的子弹射入距支点为a的棒内。若棒偏转角为
30°。问子弹的初速度为多少。
解： 射入过程角动量守恒：
o
mva
1 3
m0l
2
ma2
30°
la
转动过程机械能守恒：
v
1 1 23
m0l 2
ma2
2
mga1 cos30
m0 g
l 2
1 cos30
v 1 ma
g 2 6
2
d
dt
R0
t
t
d dt
0
0
01
ut
(
2m
)
1 2
arctan[ M ]
0
2mu2t 2
MR2
dt
第四u章( 2Mm
1
刚) 2体力学
R
8 22
大学 物理
4-4 刚体定轴转动的角动量守恒定律
角动量守恒定律在工程技术上的应用
陀螺仪与导航
陀螺仪：能够绕其对称轴高速 旋转的厚重的对称刚体。
l 2
处)
解得
t
2 m2
v1 v2
m1g
O
关于摩擦力矩 在x处取dm，dm m1 dx
x l
l
dm
元摩擦力 df dmg
m1
元摩擦力矩 dMr df x dmg x
总摩擦力矩
M r
dMr
l m1 gxdx m1g l 2
0
l
l2
m1g
l 2
第四章 刚体力学
4
大学 物理
4-4 刚体定轴转动的角动量守恒定律
例 一长为l，质量为m0的杆可绕支点O自由转动。一质量为
m，速度为v的子弹射入距支点为a的棒内。若棒偏转角为
30°。问子弹的初速度为多少。
解： 射入过程角动量守恒：
o
mva
1 3
m0l
2
ma2
30°
la
转动过程机械能守恒：
v
1 1 23
m0l 2
ma2
2
mga1 cos30
m0 g
l 2
1 cos30
v 1 ma
g 2 6
大学物理第3章 刚体定轴转动与角动量守恒
第3章 刚体定轴转动和角动量守恒定律在前几章质点运动中，我们忽略了物体自身大小和形状，将物体视为质点，用质点的运动代替了整个物体的运动。
但是在实际物体运动中，不仅物体在大小和形状千差，而且运动又有平动和转动之别。
这时我们需要另一个突出主要特征，忽视其次要因素，既具有大小又具有形状的理想模型——刚体。
在受力的作用时，其形状和体积都不发生任何变化的物体，称做刚体。
本章将介绍刚体所遵从的力学规律，重点讨论刚体的定轴转动这种简单的情况。
由于刚体转动的基本概念和原理与前几章质点运动的基本概念和原理相似，因此我们将刚体转动与质点运动对比学习一会事半功倍。
§3-1 刚体定轴转动1. 刚体运动的形式刚体的运动可以分为平动、转动及平动与转动的叠加。
平动的定义为，在刚体在运动过程中，刚体中任意两点的连线始终平行。
如图5-1所示。
由于平动时刚体内各点的运动情况都是一样的，因此描述刚体平动只需要描写刚体内一点的运动，也就是说刚体的平动只要用其中一个点的运动就可以代表它整体的运动。
转动的定义为，刚体运动时，刚体中所有质点都绕同一条直线作圆周运动，这条直线称为转轴。
转轴可以是固定的，也可以是变化的。
若转轴固定，称为刚体定轴转动。
若转轴不固定，运动比较复杂。
刚体的一般运动可以看作是平动和转动的叠加。
平动在前几章已经研究过，本章我们主要研究定轴转动。
2. 刚体的定轴转动研究刚体绕定轴转动时，选与转轴垂直的圆周轨道所在平面为转动平面。
由于描述各质元运动的角量，如角位移、角速度和角加速度都是一样的，因此描述刚体运动时用角量较为方便。
因为刚体上各质元的半径不同，所以各质元的速度和加速度不相等。
角速度和角加速度一般情况下是矢量，由于刚体定轴转动时角速度和角加速度的方向沿转轴方向，因此可用带有“+、-”的标量表示角速度和角加速度。
这种方法我们并不陌生，质点作直线运动时我们也是用带有“+、-”的标量表示速度和加速度。
角速度的大小为 dtd θω= （3-1） 它的方向规定为沿转轴的方向，其指向由右手螺旋法则确定。
4章(2)转动动能 机械能守恒定律
2
Lz J
刚体的角动量定理：
t2
t1
M d t L J 2 J1
四、刚体的角动量守恒定律：
由M 外 dL dt ：
M 外 0 时，L J 常矢量
若物体所受的合外力矩为零，或不受外力矩，物 体的角动量保持不变。
注意:
J
2
1 ( J ) 2 J
2
L
2
2J
注意：转动动能实质与平动动能相同，表达式不同。
一般刚体动能 ： E k E k 平 E k 转
2、力矩的功：
质点 外力 A F dr
位 移ds
1 2
mv
2
1 2
J
2
z
dr ds
刚体 外力矩 ？
2
1 4
l
v
2
o
l 4
J O J C Md
7 48
Ml
l
2) 碰前棒作平动，对O 点的角动量按质心处理。故有：
L o Mv l 4 1 4 Mlv
方向：
3 ) 设碰后的角速度为ω 。碰撞中外力矩为零，角动量守恒。
1 4 Mlv J
12 7l
v
方向：
• [例题6]太阳质量为m，自转周期为25.3天，若在演化过程中最
故冲头做功：
A 5 . 45 10 3 J A
三、刚体的机械能守恒定律: 1、刚体的重力势能: 刚体质量全部集中于质心时，相对于零势点所具有的势能。
E p mi ghi g mi hi mg
i i i
Lz J
刚体的角动量定理：
t2
t1
M d t L J 2 J1
四、刚体的角动量守恒定律：
由M 外 dL dt ：
M 外 0 时，L J 常矢量
若物体所受的合外力矩为零，或不受外力矩，物 体的角动量保持不变。
注意:
J
2
1 ( J ) 2 J
2
L
2
2J
注意：转动动能实质与平动动能相同，表达式不同。
一般刚体动能 ： E k E k 平 E k 转
2、力矩的功：
质点 外力 A F dr
位 移ds
1 2
mv
2
1 2
J
2
z
dr ds
刚体 外力矩 ？
2
1 4
l
v
2
o
l 4
J O J C Md
7 48
Ml
l
2) 碰前棒作平动，对O 点的角动量按质心处理。故有：
L o Mv l 4 1 4 Mlv
方向：
3 ) 设碰后的角速度为ω 。碰撞中外力矩为零，角动量守恒。
1 4 Mlv J
12 7l
v
方向：
• [例题6]太阳质量为m，自转周期为25.3天，若在演化过程中最
故冲头做功：
A 5 . 45 10 3 J A
三、刚体的机械能守恒定律: 1、刚体的重力势能: 刚体质量全部集中于质心时，相对于零势点所具有的势能。
E p mi ghi g mi hi mg
i i i
45 刚体定轴转动的角动量定理及角动量守恒
例1（图）质量很小长度为l 的均匀细杆，可 绕过其中心 O并与纸面垂直的轴在竖直平面 内转动．当细杆静止于水平位置时，有一只
小虫以速率 v0 垂直落在距点O为 l/4 处，并背
离点O 向细杆的端点A 爬行．设小虫与细杆 的质量均为m．问：欲使细杆以恒定的角速 度转动，小虫应以多大速率向细杆端点爬行?
例2 一杂技演员M由距水平跷板高为h 处 自由下落到跷板的一端A，并把跷板另一端 的演员N弹了起来．问演员N可弹起多高?
N
C
B l
M
h A
l/2
4.5刚体定轴转动的角动量定理及角动量守恒
设跷板是匀质的，长度为l，质量为m'，
跷板可绕中部支撑点C 在竖直平面内转动， 演员的质量均为m．假定演员M落在跷板上， 与跷板的碰撞是完全非弹性碰撞．
质元受的摩擦力矩为：
dM gxdm
细杆受的摩擦力矩为：
M l/2 dM 2 l/2 g xdx 1 mgl
l/2
0
4
已知 L0 J0 L 0
由角动量定理：
t
－ 0
得：
1 4
mgldt t l0
3g
0
J
0
dx
Ox
x
4.5刚体定轴转动的角动量定理及角动量守恒
解 碰撞前M落在 A点的速度 vM (2gh)1 2
碰撞后的瞬间，M、N具有相同的线速度
u l
2
4.5刚体定轴转动的角动量定理及角动量守恒
1：M、N和跷板组成的系统，角动量守恒
mvM
l 2
J
2mu
l 2
1 12
ml 2
第2章-能量守恒定律(刚体的定轴转动)
Fij
转动定律 M J 刚体定轴转动的角加速度与它所受的合 外力矩成正比，与刚体的转动惯量成反比.
第二章 守恒定律
14
物理 （工）
2-4
刚体的定轴转动
转动定律 M J
M 讨论 （1） J
d （2） M J J dt
（3）M 0， ω=常量
第二章 守恒定律
15
物理 （工）
in
>> M L 常量
ex
角动量守恒定律是自然界的一个基本定律.
第二章 守恒定律
26
物理 （工）
2-4
刚体的定轴转动
例题 一轻绳绕在有水平轴的定滑轮上， 滑轮质量为 m ，绳下端挂一物体，物体所受 重力为 G, 滑轮的角加速度为 β 1 ，若将物体 去掉而以与G相等的力 直接向下拉绳子，滑 β2 β1 R R 轮的角加速度β 2将 (A) 不变 (C) 变大 (D) 无法判断
物理 （工）
2-4
刚体的定轴转动
§2-4 刚体的定轴转动
第二章 守恒定律
物理 （工）
2-4
刚体的定轴转动
刚体：在外力作用下，形状和大小都不 发生变化的物体．(任意两质点间距离保持 不变的特殊质点组．) ⑴ 刚体是理想模型 说明： ⑵ 刚体模型是为简化问题引进的．
刚体的运动形式：平动、转动．
第二章 守恒定律
（3）刚体内作用力和反作用力的力矩 互相抵消．
M ij
rj
j
Fji
ij
O
M ji
d
iF ri
Mij M ji
第二章 守恒定律
11
物理 （工）
2-4
刚体的定轴转动
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 守恒定律
17
物理 （工）
2-4 刚体的定轴转动
➢ 转动定律应用 M J
说明
(1) M J , 与 M 方向相同．
(2) 为瞬时关系．
(3) 转动中M J与平动中F ma
地位相同．
第二章 守恒定律
18
物理 （工）
2-4 刚体的定轴转动
说明
刚体的转动惯量与以下三个因素有关：
第二章 守恒定律
14
物理 （工）
2-4 刚体的定轴转动
转动定律 M J 讨论 （1） M
J （2） M J J d
dt
（3）M 0， ω=常量
第二章 守恒定律
15
物理 （工）
三 转动惯量
2-4 刚体的定轴转动
J mjrj2 J r2dm j
➢ 转动惯量的单位：kg·m2
第二章 守恒定律
22
物理 （工）
2-4 刚体的定轴转动
2 刚体定轴转动的角动量定理
质M点i mi受ddLt合i 力d矩(dJMti()包括ddMt (iemx、iri
Miin
2)
)
对定轴转动的刚体
M
MMidex(Jdd)t
(
M i in
mi dL
矩等于角动量的增量．——定轴转动的角
动量定理
第二章 守恒定律
24
物理 （工）
2-4 刚体的定轴转动
3 刚体定轴转动的角动量守恒定律
若 M 0，则 L J =常量
如果物体所受的合外力矩等于零， 或者不受外力矩的作用，物体的角动量 保持不变．——角动量守恒定律
第二章 守恒定律
25
物理 （工）
2
物理 （工）
平动：刚体中所 有点的运动轨迹都保 持完全相同．
2-4 刚体的定轴转动
特点：各点运动
状态一样，如：v、a
等都相同．
刚体平动 质点运动
第二章 守恒定律
3
物理 （工）
2-4 刚体的定轴转动
转动：分定轴转动和非定轴转动
刚体的平面运动
第二章 守恒定律
4
物理 （工）
2-4 刚体的定轴转动
J R 2π r3dr π R4 所以 J 1 mR2
0
2
2
第二章 守恒定律
21
物理 （工）
2-4 刚体的定轴转动
二 刚体定轴转动的角动量定理
和角动量守恒定律
1 刚体定轴转动
的角动量
L
mi ri 2
i
(
miri2 )
L
i
J
z
O ri vi
mi
j
第二章 守恒定律
13
物理 （工）
2-4 刚体的定轴转动
Mej ( mjrj2 )α
j
定义转动惯量
J mjrj2 J r2dm j
z
O rj
Fej
m j
Fij
转动定律 M J
刚体定轴转动的角加速度与它所受的合 外力矩成正比，与刚体的转动惯量成反比.
2-4 刚体的定轴转动
讨论
➢ 守恒条件 M 0
若 J 不变，不变； 若 J 变， 也变，但 L J 不变.
➢ 内力矩不改变系统的角动量.
➢ 在冲击等问题中 M in >> M exL 常量
➢ 角动量守恒定律是自然界的一个基本定律.
第二章 守恒定律
26
物理 （工）
2-4 刚体的定轴转动
Ft
F
O
r m
Fn
第二章 守恒定律
12
物理 （工）
2-4 刚体的定轴转动
（2）刚体
质量元受外力
内力
Fij
Fej，
Mej Mij mjrj2
外力矩 内力矩
z
O rj
Fej
m j
Fij
Mej Mij mjrj2
j
j
Mij M ji Mij 0
0 ，合外力矩
ri
2)
d(J)
dt
dt dt
第二章 守恒定律
23
物理 （工）
2-4 刚体的定轴转动
对定轴转的刚体，受合外力矩M，从
t1到 t2内，角速度从ω1变为 ω2，积分可得：
t2
t1
Mdt
J2
J1
非刚体定轴转动的角动量定理
t2
t1
Mdt
J 22
J11
当转轴给定时，作用在物体上的冲量
第二章 守恒定律
20
物理 （工）
2-4 刚体的定轴转动
例2-14 一质量为 m 、半径为 R 的均匀圆盘，求通
过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 ，
r 在盘上取半径为 ，宽为 dr
的圆环
圆环质量 dm 2π rdr
O
RR
r
dr
圆环对轴的转动惯量
dJ r2dm 2π r3dr 而 m π R2
➢ J 的意义：转动惯性的量度 .
第二章 守恒定律
16
物理 （工）
2-4 刚体的定轴转动
➢ J 的计算方法
❖ 质量离散分布
J mjrj2 m1r12 m2r22 mjrj2
❖ 质量连续分布
J mjrj2 r2dm j
r2dV V
dm：质量元 dV ：体积元
角速度矢量 lim d
t 0
方向:
t dt
右手螺旋方向
第二章 守恒定律
6
物理 （工）
刚体定轴转动 (一维转动)的转动 方向可以用角速度 的正、负来表示.
角加速度 d
dt
2-4 刚体的定轴转动
z
>0
z
<0
第二章 守恒定律
7
物理 （工）
2-4 刚体的定轴转动
z的力矩 F
F
Fi 0,
i
F
Mi 0
i
z
F
M
Od
r
P*
F
Fi 0,
i
F
Mi 0
i
第二章 守恒定律
9
物理 （工）
2-4 刚体的定轴转动
讨论 （1）若力 F不在转动平面内，把力分
解为平行和垂直于转轴方向的两个分量
F
Fz
物理 （工）
2-4 刚体的定轴转动
§2-4 刚体的定轴转动
第二章 守恒定律
物理 （工）
2-4 刚体的定轴转动
刚体：在外力作用下，形状和大小都不 发生变化的物体．(任意两质点间距离保持 不变的特殊质点组．)
说明：⑴ 刚体是理想模型 ⑵ 刚体模型是为简化问题引进的．
刚体的运动形式：平动、转动．
第二章 守恒定律
F
其中 Fz对转轴的
力矩为零，故 F 对转
轴的力矩 Mzk
r
F
z
F
k
O rFz
F
M z rF sin
第二章 守恒定律
10
物理 （工）
2-4 刚体的定轴转动
（2）合力矩等于各分力 矩的矢量和 M M1 M2 M3
（3）刚体内作用力和反作用力的力矩 互相抵消．
定轴转动的特点
(1) 每一质点均作圆周运动，圆面为转动 平面；
(2) 任一质点运动 ,,均相同，但
v, a不同；
(3) 运动描述仅需一个角坐标．
第二章 守恒定律
8
物理 （工）
2-4 刚体的定轴转动
一 力矩
用来描述力对刚体
的转动作用．
M Frsin Fd
d: 力臂
FM对 转r轴
解 GR J2 2 GR J FT R J1 1 FT R J
又 G > FT
所以 2 > 1
答案：选（C）
R β1
FT FT’
G
第二章 守恒定律
R β2
G
28
物理 （工）
2-4 刚体的定轴转动
2012.10真题第2的体密度 有关． （2）与刚体的几何形状(及体密度 的分
布)有关．
（3）与转轴的位置有关．
第二章 守恒定律
19
物理 （工）
2-4 刚体的定轴转动
2010.10
一匀质圆盘对某轴的转动惯量J=50kg·m2， 若它受到对于该轴的合外力矩M=l00N·m， 则圆盘的角加速度 α=______________rad/s2.
刚体的一般运动可看作：
随质心的平动 + 绕质心的转动 的合成
第二章 守恒定律
5
物理 （工）
2-4 刚体的定轴转动
一 刚体转动的角速度和角加速度
角坐标 (t)
z
ω
沿逆时针方向转动 > 0 沿顺时针方向转动 < 0
r P’(t+dt)
.. O d P(t)
x
角位移 (t t) (t)
M ij
rj
j
O
d
ri
i
Fij
Fji
M ji
第二章 守恒定律
Mij M ji
11
物理 （工）
二 转动定律 （1）单个质点 m