大学物理(上册) 4.4刚体绕定轴转动的动能定理(7)
合集下载
4.4_力矩作功__刚体绕定轴转动的动能定理
3 g sin θ 1 2 ω = ( ) 2 l
第4章 刚体的定轴转动
2
4.4 力矩作功 刚体绕定轴转动的动能定理
力的空间累积效应 力矩的空间累积效应 4.4.1 力矩作功 力的功,动能 动能定理 力的功 动能,动能定理 动能 动能定理. 力矩的功,转动动能 动能定理. 转动动能,动能定理 力矩的功 转动动能 动能定理
v v dW = F ⋅ dr = Ft ds = Ft rdθ
o
30
o
a
m v v
'
1 1 2 ( m′l + ma 2 )ω 2 = 2 3 l mga (1 − cos 30°) + m′g (1 − cos 30°) 2
v = g (2 − 3 )(m′l + 2ma )(m′l + 3ma ) 6 ma
2 2
第4章 刚体的定轴转动
4.4 力矩作功 刚体绕定轴转动的动能定理
2
第4章 刚体的定轴转动
4.4 力矩作功 刚体绕定轴转动的动能定理
讨论 子细 弹绳 击质 入量 沙不 袋计
o
v v
子 弹 击 入 杆
o
圆 锥 摆
o
v θ T
'பைடு நூலகம்
m
v v
v p
o
v v
R
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统 动量守恒； 动量不守恒； 动量守恒； 动量不守恒； 动量不守恒； 动量不守恒； 角动量守恒； 角动量守恒； 角动量守恒； 角动量守恒； 角动量守恒； 角动量守恒； 机械能不 机械能不守恒 . 机械能守恒 . 机械能不守恒 . 机械能不
一根长为l、质量为m 例 一根长为 、质量为 的均匀细棒, 的均匀细棒 棒的一端可绕通过 O点并垂直于纸面的轴转动 棒 点并垂直于纸面的轴转动, 点并垂直于纸面的轴转动 的小球. 的另一端有质量为 m 的小球 开 始时, 棒静止地处于水平位置A. 始时 棒静止地处于水平位置 当棒转过 θ 角到达位置 B, 棒的 角速度为多少? 角速度为多少
大学物理4-4定轴转动的动能定理
表明：一个不太大的刚体的重力势能与它的质量集 中在质心时所具有的势能一样。
刚体在重力场中运动时重力作功为 即重力作功等于刚体重力势能的减少
定轴转动的动能定理
例 题 4-7 如 图 ， 冲 床 上 配 置 一 质 量 为 5000kg 的 飞 轮 ， r1=0.3m, r2=0.2m.今用转速为900rev/min的电动机借皮 带传动来驱动飞轮，已知电动机的传动轴直径为 d=10cm。（1）求飞轮的转动动能。
A M d M d 0 0
对于刚体的运动，因质
点间相对距离不变，故任何
一对内力作功为零。
O
F
d r
drP2.刚体定来自转动的动能定理根据刚体定轴转动定理 M J d
dt
则物体在 d时t 间内转过角位移 d 时 dt
外力矩所做元功为：
dA Md J d d Jd d Jd
dt
dt
总外力矩对刚体所作的功为：
解 先对细棒oA所受的力作 O
一分析；重力 G作用在棒的
中心点C，方向竖直向下； 轴和棒之间没有摩擦力，轴
对棒作用力 通N过o点，在
棒的下摆过程中，此力的方 向和大小是随时改变的。
C
G
v
A
A
定轴转动的动能定理
在棒的下摆过程中，支撑力 不N做功。
棒从水平位置摆到竖直位置过程中，重力所作的 功是
A mgl / 2
60
这样飞轮的转动动能是
Ek
1 2
J2
1 2
325
2 3.14 150 60
2
40055J
（2）在冲断钢片过程中，冲力F所作的功为
A Fd 9.80 104 0.5 103 J
刚体的能量定轴转动的动能定理
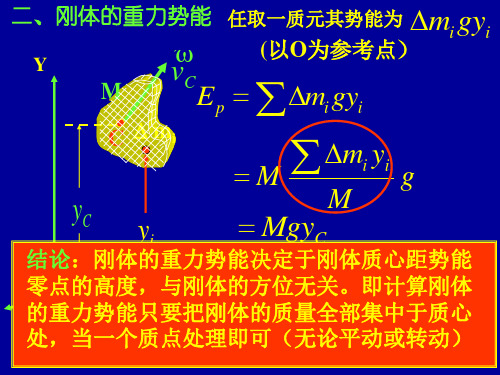
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。
求： 当杆过铅直位置时的角速度：
N
YZ
XO
r
mg
大学物理 第四章 刚体的转动 4-4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
6
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
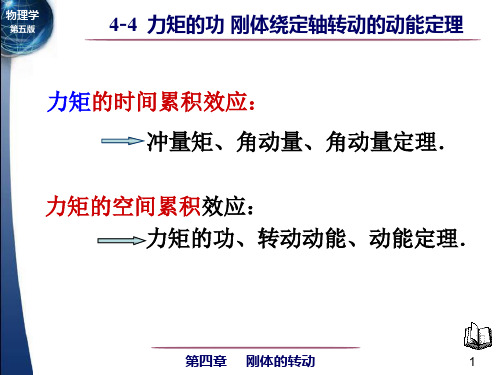
W =∫
外力的功
θ2
θ1
1 1 2 2 M d θ = Jω 2 − Jω 1 2 2
刚体动能的改变 质点系的动能 定理在刚体中 的具体表现
刚体作为特殊的质点系， 刚体作为特殊的质点系， 满足质点系的动能定理： 满足质点系的动能定理：
方向： 方向：
dM
刚体的转动
14
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
2 µ mg 2 dM = r dr 2 R
整个唱片所受的摩 擦力矩为
R
v df
o
r
dl dr
M = ∫ dM
方向： 方向：
dM
M
2 µmg M = 2 R
∫
R
0
2 r dr = µRmg 3
2
刚体的转动
第四章
非保守内力： 非保守内力：刚体内力 W
m v v
in 刚体
=0
∴W
ex
+W
in nc
=0
18
E = E0
第四章 刚体的转动
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
o
选初始位置为势能零点
30
o
a
1 1 2 2 2 ( m′l + ma )ω = 2 3
o
m v v
'
l ′g (1 − cos 30o ) mga(1 − cos 30 ) + m 2
v dr φ
o
刚体的转动
6
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
W =∫
外力的功
θ2
θ1
1 1 2 2 M d θ = Jω 2 − Jω 1 2 2
刚体动能的改变 质点系的动能 定理在刚体中 的具体表现
刚体作为特殊的质点系， 刚体作为特殊的质点系， 满足质点系的动能定理： 满足质点系的动能定理：
方向： 方向：
dM
刚体的转动
14
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
2 µ mg 2 dM = r dr 2 R
整个唱片所受的摩 擦力矩为
R
v df
o
r
dl dr
M = ∫ dM
方向： 方向：
dM
M
2 µmg M = 2 R
∫
R
0
2 r dr = µRmg 3
2
刚体的转动
第四章
非保守内力： 非保守内力：刚体内力 W
m v v
in 刚体
=0
∴W
ex
+W
in nc
=0
18
E = E0
第四章 刚体的转动
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理 -
o
选初始位置为势能零点
30
o
a
1 1 2 2 2 ( m′l + ma )ω = 2 3
o
m v v
'
l ′g (1 − cos 30o ) mga(1 − cos 30 ) + m 2
v dr φ
o
刚体的转动
大学物理课件：刚体定轴转动
M f k 2
(1)
由刚体定轴转动定律得：
k2 J J d
(2)
dt
对上式分离变量并积分得：
0
k
J
t
dt
0
2 0
d 2
(3)
得到所需时间为： t J
(4)
k0
（2）由刚体定轴转动定律得：
k2 J J d d J d
(5)
dt d d
0
对上式分离变量并积分得： k
d
2
设 为两飞轮啮合后共同角速度：
J AA 33.3rad s1
JA JB
例题4.3.2 质量 M 、半径 R 的圆盘，绕过圆心 O
且垂直于盘面的水平光滑固定轴转动，已知其角速
惯量，故该量有关于刚体，还有关于转轴！ 2.由上述结果看出：
JO
1 3
ml 2
1 12
ml2 +m（ l ）2 2
JO
+m（ l ）2 2
4.2.3 平行轴定理
平行轴定理：质量为 m的刚体，如果
对其质心轴的转动惯量为 JC ，则对任
一与该轴平行，相距为 d 的转轴的转
动惯量为：
J O J C md 2
2.合力矩等于各分力矩的矢量和 ：
M M1 M2 M3
(2)
3.刚体内力矩互相抵消：
M ij M ji
注意：内力矩对刚体 动力学效应无贡献；
M ij
o
rj
d ri
i
j
Fji Fij
M ji
例题4.2.1 研磨专用动力卡盘是专门为精密研磨 机所设计，如图所示用于固定被加工工件，卡盘在 绕垂直通过盘心的轴转动时会与接触工件产生滑动 摩擦。试求卡盘转动时受到的摩擦力矩。设其质
刚体力学_功 动能定理
m
.
N
R
m1
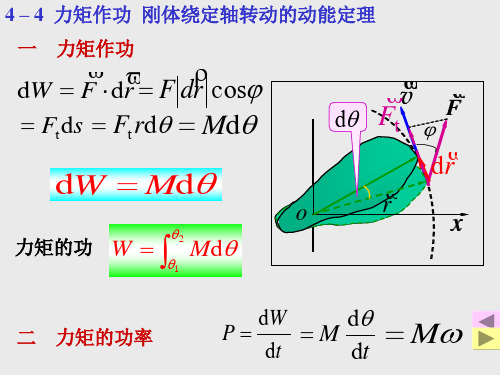
m2 解: 把m1、m2和m看作一系统 系统所受 m g 看作一系统,系统所受 看作一系统 1 m2 g 合外力有重力m 、 合外力有重力 1g、m2g,这两个力对轴 这两个力对轴 支撑力N通过转轴 的力矩分别为m 的力矩分别为 1gR、m2gR;支撑力 通过转轴 对轴的力 、 支撑力 通过转轴,对轴的力 矩为零.加上阻力矩 加上阻力矩M 系统所受合外力矩为 顺时针为正) 系统所受合外力矩为(顺时针为正 矩为零 加上阻力矩 f ,系统所受合外力矩为 顺时针为正 M=m2gR-m1gR-Mf 系统的总角动量为(顺时针为正 顺时针为正) 系统的角 m: Jω 系统的总角动量为 顺时针为正 动量包括 m1: Rm1v L=Jω+Rm1v+Rm2v m2: Rm2v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的圆盘， 例 一质量为 m' 、半径为 R 的圆盘，可绕一垂 圆盘上绕有轻绳， 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳， 问物体由静止下落高度 一端挂质量为m 一端挂质量为 的物体 . 问物体由静止下落高度 h 时， 其速度的大小为多少? 其速度的大小为多少 设绳的质量忽略不计 . v 对圆盘做功， 解1 拉力 FT 对圆盘做功，由刚体绕定轴转动的动 v 能定理可得， 能定理可得，拉力 FT 的力矩所作的功为
o
圆 锥 摆
o
v θ T
'
m
v v
v p
o
v v
R
以子弹和杆为系统 守恒； 动量不守恒； 守恒； 角动量 守恒； 机械能 不守恒 .
圆锥摆系统 守恒； 动量不守恒； 对 O'O 轴角动量 守恒； 守恒； 机械能 守恒 .
4-4 力矩作功 刚体绕定轴转动的动能定理
称为力矩的功。 力矩对转动物体作的功等于相应力矩和角位移的乘 积。
1) 如果力矩的大小和方向都不变，则
W
0
dW M d M0 Nhomakorabea
即恒力矩对绕定轴转动的刚体所作的功，等于力 矩的大小与转过的角度的乘积。 2) 如果作用在绕定轴转动的刚体上的力矩是变化的， 则 2 2 W dW Md
得: h 2hc 3h0
2
1 2
4
§4-4 力矩作功 刚体绕定轴转动的动能定理
在空间过程中力矩的作用效果和刚体运动之间的关系。 F 一、力矩作功 v
dW F dr F cos | dr |
在此过程中，力作的功：
O
d r
dr
P
F cosrd F cosr F cosr M
dW Md
1 2 定轴转动刚体的动能： EK J 2
即刚体绕定轴转动的转动动能等于刚体的转动惯量与角速 度二次方的乘积的一半。 1 2 质点的动能：
EK
2
mv
四、 刚体绕定轴转动的动能定理 将定轴转动的转动定律两边乘以d 再同时对 积分，有:
2
1
Md
2
1
d J d dt
O
m C
i
g ( mi hi ) m gh c
i
x
一个不太大的刚体的重力势能相当于它的全部质量都集
中在质心时所具有的势能。
六、机械能守恒 质点系的机械能守恒定律： 若外力和非保守性内力都不作功，即 in W ex 0 Wnc 0
E
i 1
n
ki
EPi Eki0 EPi0
1) 如果力矩的大小和方向都不变，则
W
0
dW M d M0 Nhomakorabea
即恒力矩对绕定轴转动的刚体所作的功，等于力 矩的大小与转过的角度的乘积。 2) 如果作用在绕定轴转动的刚体上的力矩是变化的， 则 2 2 W dW Md
得: h 2hc 3h0
2
1 2
4
§4-4 力矩作功 刚体绕定轴转动的动能定理
在空间过程中力矩的作用效果和刚体运动之间的关系。 F 一、力矩作功 v
dW F dr F cos | dr |
在此过程中，力作的功：
O
d r
dr
P
F cosrd F cosr F cosr M
dW Md
1 2 定轴转动刚体的动能： EK J 2
即刚体绕定轴转动的转动动能等于刚体的转动惯量与角速 度二次方的乘积的一半。 1 2 质点的动能：
EK
2
mv
四、 刚体绕定轴转动的动能定理 将定轴转动的转动定律两边乘以d 再同时对 积分，有:
2
1
Md
2
1
d J d dt
O
m C
i
g ( mi hi ) m gh c
i
x
一个不太大的刚体的重力势能相当于它的全部质量都集
中在质心时所具有的势能。
六、机械能守恒 质点系的机械能守恒定律： 若外力和非保守性内力都不作功，即 in W ex 0 Wnc 0
E
i 1
n
ki
EPi Eki0 EPi0
4-4 力矩的功 刚体绕定轴转动的动能定理
1 1 1 2 2 2 2 Eki = ∆mi vi = ∆mi ⋅ (riω ) = ∆mi ⋅ ri ⋅ ω 2 2 2
整个刚体绕定轴转动的动能： 整个刚体绕定轴转动的动能： 1 1 2 1 2 2 2 Ek = ∆ m i v i = (∑ ∆mi ri )ω = Jω 2 i 2 i 2
∑
刚体绕定轴转动的动能是由于刚体具有一定 的转动角速度ω而具有的能量 而具有的能量。 的转动角速度 而具有的能量。
J1 = ml J 2 = m′l
2
2
1 ′l 2 J3 = m 3
②从A到B过程系统机械能守恒（只有保守力做 过程系统机械能守恒（ ），取 点为重力势能零点 点为重力势能零点， 功），取A点为重力势能零点，则有 1 1 3 2 (J 2 + J 3 )ω0 + m′gl = m′g (2l ) + m′g l 2 2 2
第四章
刚体的转动
5
物理学
第五版
以子弹和杆为系统
o
子 弹 击 入 杆
动量不守恒； 动量不守恒； 角动量守恒； 角动量守恒；
v v
机械能不守恒． 机械能不守恒．
第四章
刚体的转动
6
物理学
第五版
o
圆 锥 摆
'
圆锥摆系统 动量不守恒； 动量不守恒；
R
v θ T
m
v p
o
v v
角动量守恒； 角动量守恒； 机械能守恒． 机械能守恒．
第五版
作业：4-30、4-31
第四章
刚体的转动
16
v m v = m + m ′v ′ 2
m
②从A到B过程系统机械能守恒，设m′在B处的 过程系统机械能守恒， 速度为v′h，取A点为重力势能零点，则有 点为重力势能零点， 点为重力势能零点 1 1 ′v′ = 2m′gl + m′v′ 2 m h 2 2 ③ m′能够越过B点作圆周运动的条件是
刚体定轴转动的动能定理
dm 积分遍及刚体体积V，
分几种情况：
dV , ( x, y, z )
1、刚体具有对称中心，对称中心就是质心；
2、若刚体无对称中心，但可以划分为几部分，而每一部 分都有对称中心，各部分的中心就是各部分的质心，这些质心 形成为分立的质点组，则刚体的质心就归结为这一质点组的质 心； 3、前二个条件都不具备，这时就必须求积分，计算刚体 的质心。
dri j r j ri rij (为什么?) dt dt r r ij j 2 2 d r j d ri i 2 2 即 v j v i , a j ai O ri dt dt
dr j
由于 i ，j 是任意两个质元，所以刚体上所有质元均有相同的速 度和加速度，各质元的运动轨迹的形状也相同。这里很自然想 到一个代表性的质元——质心。
二、刚体的转动
如果刚体上各质元都绕同一直线作圆周运动就称为刚体转 动，这条直线称为转轴，转轴固定于参考系的情况称为定轴转 动。例如机器上齿轮的运动，门窗等都是定轴转动。若转轴上 有一点静止于参考系，而转轴的方向在变动，这种转动称为定 点转动。例如玩具陀螺的转动就属于定点转动。
分析表明：刚体的任何复杂运动总可以分解为平动和转动（定 轴转动或定点转动）的叠加，例如车轮的滚动、螺帽的运动。 研究刚体绕定轴转动时，通常取任一垂直于定轴的平面作 为转动平面，如图所示，通过分析，转动平面内各个质点的运 动情况搞清楚了，整个刚体的运动情况就知道了。取任一质点 P，P在这一转动平面内绕O点作圆周运动，用矢径 r 与Ox 轴间
唯一确定。总之，为描述平面运动，必须给出
rB rB (t ) xB (t )i yB (t ) j, 或 xB xB (t ), yB yB (t )
4_4力矩的功 刚体绕定轴转动的动能定理
1
第四章 刚体的转动 4-4力矩作功 刚体绕 定轴转动的动能定理
§4-4 力矩的功 刚体绕定轴转动的动能定理
一 力矩作功
刚体转过 d ，力 F 作元功
dW F dr F cos ds
F cos rd Md
即：dW Md
o
（1）如果力矩的大小和方向都不变，则
d
v
F
2
r dr
x
W
五 机械能守恒定律
对于含有刚体的系统,如果在运动过程中只有保守内 力作功,则此系统的机械能守恒。
8
第四章 刚体的转动 4-4力矩作功 刚体绕 定轴转动的动能定理
讨论 下列三种情况中动量、角动量和机械能的守恒情况.
子细
o
弹绳
击质
入量 沙不
v
袋计
子o
弹 击 入 杆
v
o'
圆 锥
T
摆 m oR
p v
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统
杆转过 300 时重力矩所作的功；（3）当杆转到铅直位置时
系统的角速度和质点的线速度。
解：重力矩作功：
W 30 Md 0
30 3 mgl cos d
02
3 mgl sin 30 3 mgl
2
04
3 mgl 4 ml 2
2
3
9g
8l
（2） 解法1：利用功的定义求
重力矩：
M mg l cos mgl cos
F 0 外
M 0
动量守恒 F 外 0 角动量守恒 M外 0
动量不守恒 角动量守恒
外
有摩擦力
有摩擦力 机械能不守恒.
机械能不守恒.
第四章 刚体的转动 4-4力矩作功 刚体绕 定轴转动的动能定理
§4-4 力矩的功 刚体绕定轴转动的动能定理
一 力矩作功
刚体转过 d ，力 F 作元功
dW F dr F cos ds
F cos rd Md
即：dW Md
o
（1）如果力矩的大小和方向都不变，则
d
v
F
2
r dr
x
W
五 机械能守恒定律
对于含有刚体的系统,如果在运动过程中只有保守内 力作功,则此系统的机械能守恒。
8
第四章 刚体的转动 4-4力矩作功 刚体绕 定轴转动的动能定理
讨论 下列三种情况中动量、角动量和机械能的守恒情况.
子细
o
弹绳
击质
入量 沙不
v
袋计
子o
弹 击 入 杆
v
o'
圆 锥
T
摆 m oR
p v
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统
杆转过 300 时重力矩所作的功；（3）当杆转到铅直位置时
系统的角速度和质点的线速度。
解：重力矩作功：
W 30 Md 0
30 3 mgl cos d
02
3 mgl sin 30 3 mgl
2
04
3 mgl 4 ml 2
2
3
9g
8l
（2） 解法1：利用功的定义求
重力矩：
M mg l cos mgl cos
F 0 外
M 0
动量守恒 F 外 0 角动量守恒 M外 0
动量不守恒 角动量守恒
外
有摩擦力
有摩擦力 机械能不守恒.
机械能不守恒.
4.4刚体绕定轴转动的动能定理(7)
mv
3 4
l
1 3
M
l
2
m
3 4Hale Waihona Puke l2
解得棒开始运动时刚体系的角速度为：
mv
3 4
=8.88rads-1
1 3
M
9 16
m
l
（2）把木棒、子弹、地球视为刚体系统，由于子弹射
入木棒后，木棒的摆动过程只有重力作功，重力属
于保守内力，故系统的机械能守恒。选取初态木棒A
点和
l 2
处，分别为子弹、棒重力势能零势点，注意
到，初态仅有动能末态只有势能，由机械能守恒定
律得：
1
1
Ml 2
m
3
l
2
2
Mg
l
(1
cos
)
mg
3l
(1
cos
)
2 3
4
2
4
cos
1
2 3
M
9 8
m
l
2
0.074
94.3
(6)
刚体绕定轴转动动能定理：合外力矩对定轴转 动刚体所作的功，等于刚体转动动能的增量.
刚体绕定轴转动的机械能：
E
Ek
Ep
E
1 2
J2
Ep
(6)
例题4.4.1 长 l 0.4m、质量 M 1.0kg 的匀质木棒如 图所示，可绕水平轴O在铅直平面内转动，初态木棒
自然铅直悬垂，设质量为 m 8g的子弹以v 200m s1
3-4刚体绕定轴转动的动能定理
1 2 T h m v 根据 1 , 立即可以求得张力T1 1 2
1 2 1 T1 m1v 2 h
m1m 2 g m1 m 2
1 2
M
第3章 刚体力学
大学物理学 刘成林等编
1 2 根据 (m2 g T2 )h m2 v 或 T2 r T1 r J 2
可以立即算出张力T2
A M z 75 2.8 10 J 2.1 10 J
2
4
第3章 刚体力学 例 5：质量为 m1 的物体置于完全光滑的水平桌面 上 , 用一根不可伸长的细绳拉着 , 细绳跨过固定于 桌子边缘的定滑轮后，在下端悬挂一个质量为 m2 的 物体 , 如图所示。已知滑轮是一个质量为 M ,半径为r 的圆盘, 轴间的摩擦力忽略不计。求滑轮与 m1 之间 的绳子的张力 T1 、滑轮与 m2 之间的绳子的张力 T2 以 及物体运动的加速度 a 。
大学物理学 刘成林等编
N
闸瓦
解：为了求得飞轮从制 f 飞轮 动到停止所转过的角度 和摩擦力矩所作的功A, 必须先求得摩擦力、摩擦力矩 和飞轮的角加速度。
第3章 刚体力学 闸瓦对飞轮施加的摩擦力的大小等于摩擦系数与 正压力的乘积
大学物理学 刘成林等编
f N 0.50 500 N 2.5 10 N
i 1
n
2
代入动能公式中, 得到刚体转动动能的一般表达式
Ek
1 2 J 2
刚体转动动能与质点运动动能在表达形式上是 相似性的。
第3章 刚体力学 三、刚体定轴转动动能定理
大学物理学 刘成林等编
根据功能原理, 外力和非保守内力对系统作的 总功等于系统机械能的增量。对于刚体一切内力 所作的功都为零。对定轴转动的刚体 , 外力的功 即为外力矩所作的功; 系统的机械能为刚体的转 动动能。
刚体绕定轴转动的动能定理
v F Ft dr dr
x
W 2 Md
1
比较 W
F dr
第四章 刚体的转动
2
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
二 力矩的功率 P dW M d M
dt
比较
P
dt
F
v
三 转动动能
Ek i 12mi vi2
1 (
2i
miri2 ) 2
1 2
J 2
第四章 刚体的转动
所受的摩擦力为
df
mg
πR2 drdl
此力对点o的力矩为
rdf
mg
πR2
rdrdl
df
dl dr
or
R
第四章 刚体的转动
10
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
于是，在宽为dr的 圆环上，唱片所受的摩 擦力矩为
mg
dM πR2 rdr(2πr)
df
dl dr
or
R
2mg
R2
v m'
率为多少?
解 子弹、竿组成一系统，应用角动量守恒
mva
(1 ml 2 3
ma2 )，
3mva m'l 2 3ma2
第四章 刚体的转动
13
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
射入竿后，以子弹、细
杆和地球为系统，E =常量．
o 30
1 (1 ml 2 ma2 ) 2
23 mga(1 cos30o ) mg
l
a v m'
(1 cos30o )
2
解得：
刚体定轴转动的动能定理 ppt课件
dt 12
dt
考虑到 t
dr g cost 7lg cos(12 v0 t)ຫໍສະໝຸດ dt 224 v0
7l
上页 下页 返回 结束
第七章 刚体力学 作业： P256 7.4.2 7.5.1
上页 下页 返回 结束
O
上页 下页 返回 结束
第七章 刚体力学
[解](1)由机械能守恒得
m ghc
1 2
I 2
hc
1 2
l
I 1 ml2 3
联立得
3g
l
O Ep=0 C
v l 3gl
上页 下页 返回 结束
(2)根据质心运动定理
FN W mac
分量式
FNn
m
g
m
vc2 rc
mvM
l 2
I
2mu
l 2
1 ml 2
12
1 2
ml 2
解得
mvMl 2
ml 2 12 ml 2 2
6m(2gh)1 2 (m 6m)l
M
N
C
B
l
h A
l/2
上页 下页 返回 结束
第七章 刚体力学 演员N以u起跳，达到的高度，由机械能守恒：
h u 2 l 2 2 ( 3m )2 h
第七章 刚体力学
角动量守恒条件：
M 0
刚体所受的合外力矩为零
若I不变，ω不变； 若I变，ω也变，但 L I 不变.
内力矩不改变系统的角动量.
在冲击等问题中，因内力矩远大于外力矩 ，此时， 角动量守恒。
4-4 力矩的功 刚体绕定轴转动的动能定理
一 力矩作 功 dW FdrF tds
F trd
dWM d
o
Байду номын сангаас
力矩的功：
v F d Ftdr r
x
W 2 Md
比较
1
WFdr
第四章 刚体的转动
2
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
二 力矩的功率 PdWMdM
dt
比较
P dtF v
三 转动动能
Ek
i
12mivi2
1( 2i
Algebra 2/Trig
4-4 力矩的功 刚体绕定轴转动的动能定理
M acintosh P IC T im age form at
is not supported
8.6 Radical Expressions and Radical Functions Pages 520-527
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
12
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
射入竿后，以子弹、细
杆和地球为系统，E =常量．
o 30
1(1ml2m2a)2
23 mg(1a co3so 0)mgl
a
v m '
(1co3s0o)
2
解得：
v g (2 3 )m ( l 2 m )m ( a l2 3 m 2 )6 a m
miri2)21 2J2
第四章 刚体的转动
3
物理学
第五版
4-4 力矩的功 刚体绕定轴转动的动能定理
四 刚体绕定轴转动的动能定理
4-4 力矩作功 刚体绕定轴转动的动能定理
P2 M f 22 k23 k(2πn23 ) 68.0 W
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
理已知: n1 = 7rad/s, n2 = 10rad/s; Mf = k 2,
k = 2.74×10-4 N·m·rad-2·s2. 求（2）吊扇由静止匀加
0 FTRd R 0 FTd
1 2
J
2
1 2
J
2 0
FN
o
P'
FT
o
R m' m
, 0 和 、 0 分别
为圆盘终了和起始时的角
FT
m
h
坐标和角速度 .
P
m
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
0
理
FT Rd
R
0
FTd
1 J 2
2
1 J
2
v g(2 3)(ml 2ma)(ml2 3ma2 ) 6 ma
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
例理3 一根长为l、质量为m
的均匀细棒, 棒的一端可绕通过 o
O点并垂直于纸面的轴转动, 棒
m, l A
m
的另一端有质量为 m 的小球. 开
始时, 棒静止地处于水平位置A.
棒长为 l ，质量为 m ，开始时将棒置于水平状态，然后
由静止摆下，求棒摆到竖直的瞬间（1）棒的角速度；
（2）棒的转动动能；（3）质心的加速度（不计摩擦阻
力）。
解：（3）棒所受合力矩 M 0
O
由转动定律 M J 0 0
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
理已知: n1 = 7rad/s, n2 = 10rad/s; Mf = k 2,
k = 2.74×10-4 N·m·rad-2·s2. 求（2）吊扇由静止匀加
0 FTRd R 0 FTd
1 2
J
2
1 2
J
2 0
FN
o
P'
FT
o
R m' m
, 0 和 、 0 分别
为圆盘终了和起始时的角
FT
m
h
坐标和角速度 .
P
m
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
0
理
FT Rd
R
0
FTd
1 J 2
2
1 J
2
v g(2 3)(ml 2ma)(ml2 3ma2 ) 6 ma
第四章 刚体转动
4 – 4 力矩作功 刚体绕定轴转动的动能定
物理学教程 （第二版）
例理3 一根长为l、质量为m
的均匀细棒, 棒的一端可绕通过 o
O点并垂直于纸面的轴转动, 棒
m, l A
m
的另一端有质量为 m 的小球. 开
始时, 棒静止地处于水平位置A.
棒长为 l ，质量为 m ，开始时将棒置于水平状态，然后
由静止摆下，求棒摆到竖直的瞬间（1）棒的角速度；
（2）棒的转动动能；（3）质心的加速度（不计摩擦阻
力）。
解：（3）棒所受合力矩 M 0
O
由转动定律 M J 0 0
4-4定轴转动的动能定理
三.定轴转动的动能定理
根据定轴转动定理 则物体在
dt时间内转过角位移 dθ = ω dt 时
d M = (Jω) dt
外力矩所做元功为： 外力矩所做元功为：
d dθ dA = Mdθ = ( Jω)dθ = Jdω = Jωdω dt dt
θ2 ω2
总外力矩对刚体所作的功为： 总外力矩对刚体所作的功为：
§4-4 定轴转动的动能定理 一.力矩的功
1.定义：当刚体在外力矩作用下绕定轴转动而发 定义： 定义 生角位移时，就称力矩对刚体做功。 生角位移时，就称力矩对刚体做功。 由于刚体内任意两质点 的相对位移为零， 的相对位移为零，所以 内力不做功； 内力不做功；平行于转 轴的的外力也不做功； 轴的的外力也不做功； r 只有垂直于转轴的力 F 才做功(即在图示中的 才做功 即在图示中的 r 就是在平面内的力) F 就是在平面内的力 0
r r
0‘
dθ
r dr
r F
ϕ
P
r 作用下， 在外力 F 作用下，刚体有一角位移 dθ ，对应线位移 r，则 为 dr r 点作功： 力 F 对 P点作功： 点作功
r r d A = ϕ)
0
= F ds sin ϕ = Fr dθ sinϕ
r r
0‘
dθ
r dr
1 2 ∆mivi 2
v = ωr
i i
因此整个刚体的动能 1 1 2 EK = ∑ ∆mivi = 2 2
(∑∆m r )ω
2 i i
2
刚体的转动动能
式中∑∆miri 2是刚体对转轴的转动惯量 所以上式写为
J
，
1 2 EK = Jω 2
上式中的动能是刚体因转动而具有的动能，因 上式中的动能是刚体因转动而具有的动能， 此叫刚体的转动动能。 此叫刚体的转动动能。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1）设木棒铅垂、子弹未射入时为刚体 系初态，子弹射入棒开始运动时为刚体 系末态，由角动量守恒定律得：
3 mv l M l m l 4 3 4 3 1
2 2
解得棒开始运动时刚体系的角速度为：
mv 3 4 = 8 .8 8 ra d s
-1
9 1 m l M 16 3
4.4 刚体绕定轴转动的动能定理 4.4.1 力矩的功 1、力矩的功
d W F d r Ft d s Ft rd M d
d
Ft
r
v
F
dr
(1)
1 2
o
x
力矩的功：W
2、力矩的功率
P
M d
(2)
M
dW dt
M
d dt
(3)
4.4.2 刚体绕定轴的转动动能 1、刚体绕定轴的转动动能
2
2 cos 1 3
M
9 8
m
l g
2 M 3m
2
0 .0 7 4 9 4 .3
3、质点运动与刚体定轴转动的对比 教材P75表4.3 两类运动的对比：质点运动和刚体定轴转动的规 律在形式上相似，通过对比可以加深对刚体定轴 转动规律的理解，表4.3给出两种运动的对比。
刚体绕定轴转动的机械能：
E Ek Ep E 1 2 J
2
Ep
(6)
例题4.4.1 长 l 0 . 4 m 、质量 M 1 .0 k g 的匀质木棒如 图所示，可绕水平轴O在铅直平面内转动，初态木棒 1 m 8 g v 200 m s 自然铅直悬垂，设质量为 的子弹以 的速率从A点射入棒中并与棒一起运动。已知A、O 两点间距 3 l 4 ，试求：（1）棒开始运动时的 ； （2）棒的最大偏转角度。 解：分析 将子弹与木棒视为刚体系， 子弹射入木棒瞬间，系统所受重力及 轴对木棒的约束力均过转轴 O，因此 对转轴的合外力矩为零，故系统角动 量守恒。
（2）把木棒、子弹、地球视为刚体系统，由于子弹射 入木棒后，木棒的摆动过程只有重力作功，重力属 于保守内力，故系统的机械能守恒。选取初态木棒A 点和 l 2 处，分别为子弹、棒重力势能零势点，注意 到，初态仅有动能末态只有势能，由机械能守恒定 律得：
1 1 3 2 Ml m 2 3 4 l 3l 2 l M g (1 c o s ) m g (1 c o s ) 2 4
E
k
i
1 2
mБайду номын сангаасvi
2
2
1 2
(
i
m i ri )
2
1 2
J
2
(4)
2、刚体绕定轴转动的动能定理
W
1
2
M d
J d dt d
1
1
1
2
J d
(5)
W
1
2
M d
1 2
J
2 2
1 2
J 1
2
(6)
刚体绕定轴转动动能定理：合外力矩对定轴转 动刚体所作的功，等于刚体转动动能的增量.