大学物理 力矩的功 刚体绕定轴转动的动能定理

起始时的角速度 .
、 0分别为圆盘终了和
1 2 1 2 W J J 0 2 2
FN
o P '
FT
m
R
o
m'
FT
m
h
P
m
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
1 2 1 2 W J J 0 2 2
由质点动能定理
FT FT
7
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
解 (1) 如图取面 积元ds = drdl，该面元 所受的摩擦力为
df
df
mg
πR
2
o
r
dl dr
drdl
R
此力对点o的力矩为
rdf
mg
πR
2
rdrdl
8
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
(2) 由转动定律求 ，(唱片J=mR2/2)
10
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
讨论
子细 弹绳 击质 入量 沙不 袋计
o
v
子 弹 击 入 杆
o
圆 锥 摆
o
T
'
m
v
p
o
v
R
以子弹和沙袋为系统 以子弹和杆为系统 圆锥摆系统 动量守恒； 动量不守恒； 动量不守恒； 角动量守恒； 角动量守恒； 角动量守恒； 机械能不守恒 . 机械能不守恒 . 机械能守恒 .
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
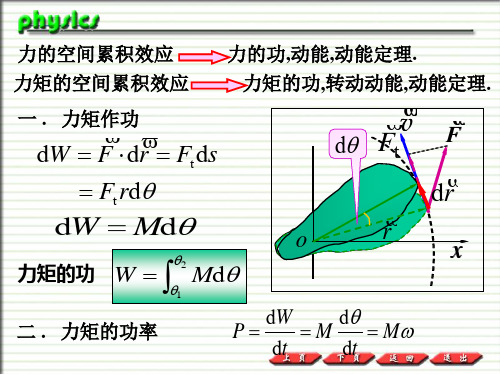
力的空间累积效应 力矩的空间累积效应
力的功,动能,动能定理. 力矩的功,转动动能,动能定理.
一
dW F dr Ft ds Ft rd
力矩作功
d
Ft
r
v
F
dr
dW Md
力矩的功 W

第四章 刚体的转动
例2 一长为 l , 质量为 m 的竿可绕支点O自由 转动 . 一质量为 m的子弹以一定速率射入竿内距支 点为 a 处，使竿的偏转角为30º 问子弹的初速率为 . 多少 ?
解 把子弹和竿看作一个系统 . 子弹射入竿的过程系统角动量守恒
o
30

1 2 2 mva ( ml ma ) 3
2 2
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
例1 留声机的转盘绕通过盘心垂直盘面的
轴以角速率 ω作匀速转动．放上唱片后，唱片将 在摩擦力作用下随转盘一起转动．设唱片的半径 为R，质量为m，它与转盘间的摩擦系数为 ，求： (1)唱片与转盘间的摩擦力矩； (2)唱片达到角速 度ω 时需要多长时间；(3)在这段时间内，转盘 的驱动力矩做了多少功？
于是，在宽为dr的 圆环上，唱片所受的摩 擦力矩为
df
9
πR R 2mg 2 r dr 2 R 2mg R 2 2 M r dr Rmg 2 R 0 3
2
dM
mg
o
r
dl dr
rdr (2πr )
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
M 4g （作匀加速转动） J 3R 3R 由 0 t 可求得 t 4 g 2 2 (3) 由 0 2 可得在 0 到 t 2 的时间内，转过的角度为 3 R 8g 1 驱动力矩做的功为 W M mR 2 2 4
2
1
o
Md
dW d P M M dt dt
x
二
力矩的功率
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
三
转动动能
1 1 2 1 2 2 2 Ek mi vi ( mi ri ) J 2 i 2 i 2
四 刚体绕定轴转动的动能定理
W Md
FN
1 1 2 2 mgh W mv mv 0 2 2
物体由静止开始下落
o P '
FT
m
FT
v0J mR 2 2
解得
v R
mgh v2 m 2m
m 2 gh (m' 2) m
4 – 4 力矩的功 刚体绕定轴转动的动能定理
1
2
2
1
2 d J d J d 1 dt
W
2
1
1 1 2 2 Md J 2 J1 2 2
合外力矩对绕定轴转动的刚体所作的功等于刚体 转动动能的增量 .
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
例1 一质量为 m' 、半径为 R 的圆盘，可绕一垂 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳， 一端挂质量为m 的物体 . 问物体在静止下落高度 h 时， 其速度的大小为多少? 设绳的质量忽略不计 . 解 拉力 FT 对圆盘做功，由刚体绕定轴转动的动 能定理可得，拉力 FT 的力矩所作的功为
a
v
m
'
4 – 4 力矩的功 刚体绕定轴转动的动能定理
第四章 刚体的转动
射入竿后，由动能定理.
o
30
'

1 1 2 2 2 0 ( ml ma ) 2 3
a m
v
l mga(1 cos30) mg (1 cos 30) 2
v g (2 3 )( ml 2ma )( ml 3ma ) 6 ma