圆周运动绳杆模型精讲
球—绳模型(学生版)--竖直面内三种圆周运动模型
竖直面内三种圆周运动模型精讲精练模型球-绳模型【知识点精讲】球-绳模型实例球与绳连接在竖直面内圆周运动球沿竖直面圆周内轨道运动图示最高点无支撑最高点无支撑最高点受力特征重力、弹力，弹力方向向下或等于零重力、弹力，弹力方向向下、等于零或向上受力示意图力学特征mg+F N=mv2r临界特征F N=0，v min=gr过最高点条件v≥gr速度和弹力关系讨论分析①恰好过最高点时，v=gr，mg=mv2r，F N=0，绳、轨道对球无弹力②能过最高点时，v≥gr，F N+mg=mv2r，绳、轨道对球产生弹力F N③不能过最高点时，v<gr，在到达最高点前小球已经脱离了圆轨道做斜抛运动【方法归纳】(1)定模型：首先判断是轻绳模型还是轻杆模型，两种模型物体过最高点的临界条件不同．(2)确定临界点：抓住球-绳模型中球恰好能过最高点时v=gR的临界条件．(3)研究状态：通常情况下竖直平面内的圆周运动只涉及最高点和最低点的运动情况．(4)受力分析：对物体在最高点或最低点时进行受力分析，根据牛顿第二定律列出方程：F合=F向．(5)过程分析：应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程．【针对性训练】1(2018•高考全国卷Ⅲ)如图，在竖直平面内，一半径为R的光滑圆弧轨道ABC和水平轨道P A在A 点相切。
BC为圆弧轨道的直径。
O为圆心，OA和OB之间的夹角为α，sinα=35，一质量为m的小球沿水平轨道向右运动，经A点沿圆弧轨道通过C点，落至水平轨道；在整个过程中，除受到重力及轨道作用力外，小球还一直受到一水平恒力的作用，已知小球在C点所受合力的方向指向圆心，且此时小球对轨道的压力恰好为零。
重力加速度大小为g。
求：(1)水平恒力的大小和小球到达C点时速度的大小；(2)小球到达A点时动量的大小；(3)小球从C点落至水平轨道所用的时间。
2(12分)(2020新高考冲刺仿真模拟)某兴趣小组设计了一个玩具轨道模型如图甲所示，将一质量为m=0.5kg的玩具小车(可以视为质点)放在P点，用弹簧装置将其从静止弹出(弹性势能完全转化为小车初始动能)，使其沿着半径为r=1.0m的光滑圆形竖直轨道OAO′运动，玩具小车与水平面PB的阻力为其自身重力的0.5倍(g取10m/s2)，PB=16.0m，O为PB中点．B点右侧是一个高h=1.25m，宽L= 2.0m的壕沟．求：(1)要使小车恰好能越过圆形轨道的最高点A，小车在O点受到轨道弹力的大小；(2)要求小车能安全越过A点，并从B点平抛后越过壕沟，则弹簧的弹性势能至少为多少？(3)若在弹性限度内，弹簧的最大弹性势能E pm=40J，以O点为坐标原点，OB为x轴，从O到B方向为正方向，在图乙坐标上画出小车能进入圆形轨道且不脱离轨道情况下，弹簧弹性势能E p与小车停止位置坐标x关系图．3(2024年5月四川宜宾质检)如图所示，在距地面上方h的光滑水平台面上，质量为m=4kg的物块左侧压缩一个轻质弹簧，弹簧与物块未拴接。
圆周运动绳杆模型
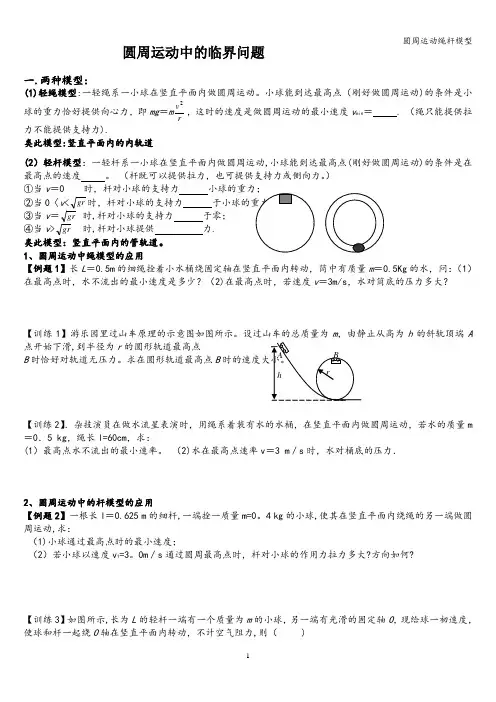
圆周运动绳杆模型1圆周运动中的临界问题一.两种模型:(1)轻绳模型:一轻绳系一小球在竖直平面内做圆周运动。
小球能到达最高点（刚好做圆周运动)的条件是小球的重力恰好提供向心力，即mg ＝m rv 2，这时的速度是做圆周运动的最小速度v min ＝ . （绳只能提供拉力不能提供支持力).类此模型:竖直平面内的内轨道(2）轻杆模型：一轻杆系一小球在竖直平面内做圆周运动,小球能到达最高点(刚好做圆周运动)的条件是在最高点的速度 。
（杆既可以提供拉力，也可提供支持力或侧向力。
） ①当v ＝0 时，杆对小球的支持力 小球的重力；②当0〈v <gr 时，杆对小球的支持力 于小球的重力；③当v ＝gr时,杆对小球的支持力 于零； ④当v >gr 时,杆对小球提供 力. 类此模型：竖直平面内的管轨道。
1、圆周运动中绳模型的应用【例题1】长L ＝0.5m 的细绳拴着小水桶绕固定轴在竖直平面内转动，筒中有质量m ＝0.5Kg 的水，问：（1）在最高点时，水不流出的最小速度是多少？（2)在最高点时，若速度v ＝3m/s ，水对筒底的压力多大？【训练1】游乐园里过山车原理的示意图如图所示。
设过山车的总质量为m ，由静止从高为h 的斜轨顶端A 点开始下滑,到半径为r 的圆形轨道最高点B 时恰好对轨道无压力。
求在圆形轨道最高点B【训练2】．杂技演员在做水流星表演时，用绳系着装有水的水桶，在竖直平面内做圆周运动，若水的质量m ＝0．5 kg ，绳长l=60cm ，求：(1）最高点水不流出的最小速率。
（2)水在最高点速率v ＝3 m ／s 时，水对桶底的压力．2、圆周运动中的杆模型的应用 【例题2】一根长l ＝0.625 m 的细杆,一端拴一质量m=0。
4 kg 的小球,使其在竖直平面内绕绳的另一端做圆周运动,求：（1)小球通过最高点时的最小速度；（2）若小球以速度v 1=3。
0m ／s 通过圆周最高点时，杆对小球的作用力拉力多大?方向如何?【训练3】如图所示,长为L 的轻杆一端有一个质量为m 的小球，另一端有光滑的固定轴O ，现给球一初速度，使球和杆一起绕O 轴在竖直平面内转动，不计空气阻力,则（ )2vR A 。
圆周运动绳杆模型
2．临界问题分析 物体在竖直平面内做的圆周运动是一种典型的变速曲线运 动， 该类运动常有临界问题， 并伴有“最大”“最小”“刚好” 等词语，现就两种模型分析比较如下：
解析：根据机械能守恒，设张成龙在最低点的速度为 v，最 高点最小速度为零，由最低点到最高点 1 2 则 mgh＝ mv ，h＝2l， 2 所以 v＝ 2gh＝2 gl＝8 m/s.
(2)在最高点张成龙处于静止状态，故对杠的压力等于重力 FN＝mg＝560 N，在最低点做圆周运动．设杠对张成龙的作用力 v2 v2 为 FN′，则 FN′－mg＝m l ，故 FN′＝mg＋m l ＝560 N＋ 82 56× N＝2800 N，由牛顿第三定律，张成龙对杆的作用力大 1.6 小为 2800 N.
由上述三式知 a0＝4g 设小球受盒子右侧面的作用力为 F，受上侧面的作用力为 FN，根据牛顿运动定律知 在水平方向上 F＝ma0 即 F＝4mg 即 FN＝－mg
在竖直方向上 FN＋mg＝0
因为 F 为正值、FN 为负值，由牛顿第三定律知小球对盒子 的右侧面和下侧面有作用力，大小分别为 4mg 和 mg.
【小球对盒子的右侧面和下侧面有
作用力，大小分别为 4mg 和 mg
在判断盒子对小球的作用力的大小和方向 时，可以首先做出假设，然后应用牛顿第二定律列式求解，最后 根据结果的符号判断力的真实方向．
在 2012 年第 30 届伦敦奥运会体操男团中国 队卫晟冠军． 如右图张成龙在单杆比赛中正完成一个单臂回环动 作，且恰好静止在最高点．设张成龙的重心离杠 1.60 米，体重 大约 56 公斤．忽略摩擦力，认为张成龙做的是圆周运动，试求： (1)张成龙在最低点应以多大的速度才能达到如图效果； (2)张成龙在最高、最低点时对杠的作用力．
圆周运动绳杆模型讲解学习
轻绳模型
轻杆模型
常见 类型
过最高 点的临 界条件
由mg＝mvr2 得v临＝ gr
由小球能运动即可得v临＝0
(1)当 v＝0 时，FN＝mg，
FN 为支持力，沿半径背
讨论 分析
(1)过最高点时， v≥ gr，FN＋mg＝ mvr2，绳、轨道对球 产生弹力 FN (2)不能过最高点 v< gr，在到达最高 点前小球已经脱离
(1)若要使盒子运动到最高点时与小球之间恰好无作用力， 则该同学拿着盒子做匀速圆周运动的周期为多少？
(2)若该同学拿着盒子以第(1)问中周期的12做匀速圆周运动， 则当盒子运动到如图所示(球心与 O 点位于同一水平面上)时，小 球对盒子的哪些面有作用力，作用力大小分别为多少？
【思维启迪】 mg＝mR(2Tπ0)2→周期 T0→T′＝T20→F′向＝ mR(T2′π )2→盒子对小球的作用力→小球对盒子的作用力
【尝试解答】 (1)设盒子的运动周期为 T0.因为在最高点时 盒子与小球之间刚好无作用力，因此小球仅受重力作用，由重力
提供向心力，根据牛顿第二定律得 mg＝mR(2Tπ0)2
解之得 T0＝2π
R g
(2)设此时盒子的运动周期为 T，则小球的向心加速度为 a0 ＝4Tπ22R
由第(1)问知 T0＝2π Rg且 T＝T20
一、模型建构：竖直平面内圆周运动的绳杆模型 1．模型概述 在竖直平面内做圆周运动的物体，按运动至轨道最高点时的 受力情况可分为两类．一是无支撑(如球与绳连接，沿内轨道的 “过山车”等)，称为“绳(环)约束模型”，二是有支撑(如球与 杆连接，在弯管内的运动等)，称为“杆(管道)约束模型”．
2．临界问题分析 物体在竖直平面内做的圆周运动是一种典型的变速曲线运 动，该类运动常有临界问题，并伴有“最大”“最小”“刚好” 等词语，现就两种模型分析比较如下：
绳模型和杆模型
（二）轻杆模型 A）特点： 小球在竖直平面内做圆周运动时，物体能被支持 B）临界条件 （1）能否到达最高点的临界条件: V=0
(2)拉力还是支持力的临界条件： C）讨论： F
1）当 V＞ rg 时，杆对小 球施加拉力，且速度越大， 拉力越大（此时杆子相当于 绳子） 2）当 0＜V＜ rg 时，杆对球施加支 持力，速度越大，支持里越小
表演“水流星” ，需要保证杯 子在圆周运动最高点的线速度不 得小于 gr v gr 即：
V rg
K
E G
例1．如图所示，质量为m的小球置于正方
体的光滑盒子中，盒子的边长略大于球的直径。 某同学拿着该盒子在竖直平面内做半径为R的 匀速圆周运动，已知重力加速度为g，问： 图5－7－6
要使盒子在最高点时盒子与小球之间恰好无作用力，
则该盒子做匀速圆周运动的周期为多少？
[思路点拨] 解答本题时应注意： 1小球在最高点的合力等于向心力。 2通过最高点的临界
[解析 ] 设此时盒子的运动周期为 T 0，因为在最高点时
盒子与小球之间恰好无作用力，因此小球仅受重力作用。 根据牛顿第二定律得
4 2 mg m 2 r T0
，
得
T0 2
r g
1）质量为m的小球在竖直平面内的圆轨道的内则运动， 经过最高点而不脱离轨道的临界速度为V，当小球以2V 的速度经过最高点时，对轨道的压力是多大？ 解析: v m 由临界速度得：mg= r ， 当小球的速度为2v时，
（2）当V2=4m/s时，杆受到的力大小，是拉力还 是压力？
A
B
3)如图：在A与B点，杆对球 的力是（ AD ） A）A处可能为拉力，B处为拉力 B）A处可能为拉力，B处为压力 C）A处可能为支持力，B处为压力 D）A处可能为支持力，B处为拉力
圆周运动绳杆模型
悬索桥的吊索通过绳杆模型将主梁与主缆连接，使主梁能够 悬挂在主缆上并保持平衡。
卫星轨道的设计与运行
人造卫星轨道
人造卫星的轨道通过绳杆模型与地球 连接，通过地球引力与绳杆模型的拉 力平衡，使卫星能够绕地球做圆周运 动。
月球探测器轨道
月球探测器的轨道通过绳杆模型与月 球连接，通过月球引力与绳杆模型的 拉力平衡，使探测器能够绕月球做圆 周运动。
05
绳杆模型在现实生活中的应用
游乐场的旋转设施
旋转木马
绳杆模型在旋转木马中起到支撑和传动的作用，通过绳索与木马连接，实现木马 的旋转运动。
摩天轮
摩天轮的旋转臂通过绳索与座舱连接，使座舱在旋转臂上做圆周运动，同时绳索 也起到安全保护的作用。
桥梁的拉索设计
斜拉桥
斜拉桥的拉索通过绳杆模型将主梁与桥墩连接，使主梁能够 承受载荷并保持稳定。
双摆运动
总结词
双摆运动是指两个单摆同时进行摆动，其运动轨迹为两个圆弧或椭圆弧的组合，适用于分析具有两个 固定圆心和摆长的双摆系统。
详细描述
双摆运动是两个单摆同时进行摆动的组合运动，其运动轨迹为两个圆弧或椭圆弧的组合。在双摆运动 中，两个单摆的摆线长度和初始角度都可以不同，但它们都受到重力的作用。在摆动过程中，双摆系 统的角速度、角加速度、回复力、动能和势能等物理量都随时间变化。
运动。
向心力的方向始终指向圆心，与 速度方向垂直。
绳杆模型中的离心力分析
离心力：当物体做圆周运动时， 若没有向心力作用，物体将沿 切线方向飞出。
在圆周运动绳杆模型中，离心 力与向心力大小相等、方向相 反。
离心力的大小与物体的质量、 速度和圆周半径有关。
04
圆周运动绳杆模型的实例分析
圆周运动中绳模型和杆模型的一般解析
圆周运动中绳模型和杆模型的一般解析一：绳模型：若已不可伸长的绳子长L ，其一端栓有一质量m 的小球（可看成质点）。
现使绳子拉着小球绕一点O 做匀速圆周运动，则（1）小球恰好通过最高点的速度v 。
(2)当能通过最高点时，绳子拉F 。
解：（1）小球恰能通过最高点的临界条件是绳子没有拉力， 则对小球研究，其只受重力mg 作用，故，由其做圆周运动得:L v m mg 2= 故 gL v =(2)由分析得，当小球到最高点时速度gL v v =>'时，则，mg Lmv F -=2' 而，当gL v v =<'时，那么小球重力mg 大于其所需向心力，因此小球做向心运动。
二：杆模型：若一硬质轻杆长L ，其一端有一质量m的小球（可看成质点）。
现使杆和小球绕一点O 做匀速圆周运动， 则 （1）小球恰好通过最高点的速度v 。
(2)当能通过最高点时，杆对小球的作用力F 。
解：（1）因为杆具有不可弯曲不可伸长的性质，所以小球在最高点，当速度为0时，恰好能通过。
（2）①由绳模型可知，当小球通过最高点速度gL v =时，恰好有绳子拉力为0，则同理可知，当杆拉小球到最高点时， 若小球速度gL v =时，小球所需向心力恰好等于重力mg ， 故，此时杆对小球没有作用力。
②当小球通过最高点时速度gL v >时，则小球所需向心力比重力mg 大，所以此时杆对小球表现为拉力，使小球不至于做离心运动故对小球有， L mv mg F 2=+③同理，当小球通过最高点时速度gL v <时，则小球所需向心力小于重力mg ，所以此时小球对杆有压力作用，有牛顿第三定律得，杆对小球表现为支持力作用，故对小球有， L mv F mg 2=-。
微课：绳杆模型圆周运动最高点分析(罗新勇)
苏州园区二中
罗新勇
2014.4
a
1
模型一：绳模型
用长为L的细绳拴着质量为m的小球，使小球在竖 直平面内做圆周运动，小球在最高点的速度为v .
试分析：绳的张力与速度的关系怎样？
v
L mg
F
o
分析：小球受重力和拉力 v2
F mg m L
v2 F m mg
(1) mg m v2 时， 即：v gL
L
杆对球的作用力向下
a
5
v L mg
F
o
Ｆ
v L mg
o
mgF mv2 L
F
v2 m
mg
L
(2)
mg
m v2 L
时，
即：v
gL
重力恰好提供向心力，杆没有作用力；
v2 (3) mg m L
时， 即：v
gL
杆对球的作用力向上
mgF mv2 L
F mgmv2 L
L
绳子对小球的力只能向下，即：
F0
a
2
v
L mg
F
o
得：
v2 m mg 0
L
v gL
取 v0 gL 叫临界速度。
(1) v v0 时， F0
绳中拉力为零，重力提供向心力；
(2) v v0
时，
v2 F m mg0
L
重力和拉力的合力提供向心力；
(3) v v0 时，
物体离开圆轨道做曲线运动；
a
3
拓展： 若物体沿竖直轨道内侧运动，在
最高点的情况与绳模型一致。
v
a
4
模型二：杆模型：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 (2)若该同学拿着盒子以第(1)问中周期的 做匀速圆周运动， 2 则当盒子运动到如图所示(球心与 O 点位于同一水平面上)时， 小 球对盒子的哪些面有作用力，作用力大小分别为多少？
T0 2π 2 【思维启迪】 mg＝mR( ) →周期 T0→T′＝ →F′向＝ T0 2 2π 2 mR( ) →盒子对小球的作用力→小球对盒子的作用力 T′
【尝试解答】 (1)设盒子的运动周期为 T0.因为在最高点时 盒子与小球之间刚好无作用力， 因此小球仅受重力作用， 由重力 2π 2 提供向心力，根据牛顿第二定律得 mg＝mR( ) T0 解之得 T0＝2π R g
(2)设此时盒子的运动周期为 T，则小球的向心加速度为 a0 4π2 ＝ 2R T 由第(1)问知 T0＝2π R T0 g 且 T＝ 2
由上述三式知 a0＝4g 设小球受盒子右侧面的作用力为 F，受上侧面的作用力为 FN，根据牛顿运动定律知 在水平方向上 F＝ma0 即 F＝4mg 即 FN＝－mg
在竖直方向上 FN＋mg＝0
因为 F 为正值、FN 为负值，由牛顿第三定律知小球对盒子 的右侧面和下侧面有作用力，大小分别为 4mg 和 mg.
解析：根据机械能守恒，设张成龙在最低点的速度为 v，最 高点最小速度为零，由最低点到最高点 1 2 则 mgh＝ mv ，h＝2l， 2 所以 v＝ 2gh＝2 gl＝8 m/s.
(2)在最高点张成龙处于静止状态，故对杠的压力等于重力 FN＝mg＝560 N，在最低点做圆周运动．设杠对张成龙的作用力 v2 v2 为 FN′，则 FN′－mg＝m l ，故 FN′＝mg＋m l ＝560 N＋ 82 56× N＝2800 N，由牛顿第三定律，张成龙对杆的作用力大 1.6 小为 2800 N.
一、模型建构：竖直平面内圆周运动的绳杆模型 1．模型概述 在竖直平面内做圆周运动的物体， 按运动至轨道最高点时的 受力情况可分为两类．一是无支撑 (如球与绳连接，沿内轨道的 “过山车”等)，称为“绳(环)约束模型”，二是有支撑(如球与 杆连接，在弯管内的运动等)，称为“杆(管道)约束模型”．
2．临界问题分析 物体在竖直平面内做的圆周运动是一种典型的变速曲线运 动， 该类运动常有临界问题， 并伴有“最大”“最小”“刚好” 等词语，现就两种模型分析比较如下：
【答案】 (1)2π
R gLeabharlann (2)小球对盒子的右侧面和下侧面有
作用力，大小分别为 4mg 和 mg
在判断盒子对小球的作用力的大小和方向 时，可以首先做出假设，然后应用牛顿第二定律列式求解，最后 根据结果的符号判断力的真实方向．
在 2012 年第 30 届伦敦奥运会体操男团中国 队卫晟冠军． 如右图张成龙在单杆比赛中正完成一个单臂回环动 作，且恰好静止在最高点．设张成龙的重心离杠 1.60 米，体重 大约 56 公斤．忽略摩擦力，认为张成龙做的是圆周运动，试求： (1)张成龙在最低点应以多大的速度才能达到如图效果； (2)张成龙在最高、最低点时对杠的作用力．
(2013· 长春模拟)如右图所示，质量为 m 的小球 置于方形的光滑盒子中， 盒子的边长略大于小球的直径. 某同学 拿着该盒子在竖直平面内以 O 点为圆心做半径为 R 的匀速圆周 运动，已知重力加速度为 g，空气阻力不计．求： (1)若要使盒子运动到最高点时与小球之间恰好无作用力， 则该同学拿着盒子做匀速圆周运动的周期为多少？
轻绳模型
轻杆模型
常见 类型
过最高 点的临 界条件
v2 由mg＝m r 得v临＝ gr
由小球能运动即可得v临＝0
(1)过最高点时， v≥ gr，FN＋mg＝ v2 m r ，绳、轨道对球 讨论 产生弹力 FN 分析 (2)不能过最高点 v< gr， 在到达最高 点前小球已经脱离 了圆轨道
(1)当 v＝0 时， FN＝mg， FN 为支持力， 沿半径背 离圆心 (2)当 0<v< gr时， －FN v2 支＋mg＝m r ，FN 背向 圆心，随 v 的增大而减 小 (3)当 v＝ gr时， FN＝0 (4)当 v> gr时， v2 FN 拉＋mg＝m r ，FN 指 向圆心并随 v 的增大而 增大
答案：(1)8 m/s (2)560 N 2800 N