’学而思‘ 秋 初一数学直播超常班 全国 试卷
2013秋季七年级数学超常
x 2 B 7. 关于 x 的一元二次方程 x x n 0 没有实数根，则抛物线 y x x n 的顶点在第___________象限． 1 1 1 1 4n 0 n 抛物线的顶点坐标为 , n 【分析】 4 2 4 1 1 1 ∵ n n 0 n 0 所以抛物线的顶点在第一象限 4 4 4
R x P O
R x
C2
C2
【分析】 ⑴ 用反证法.假设正 △PQR 的三顶点 P、Q、R 位于反比例函数的同一支上，不妨设为 c1 ，其坐标分 ( x2，y2 )、 ( x3，y3 ) ， 0 x1 x2 x3 ，则一定有 y1 y2 y3 0 ．于是： 别为 ( x1，y1 )、
2 2 13. 若方程 x 2a x 4a 3 0 有且只有一个实数根，求实数 a 的值．
【分析】
2 2 设函数 f x x 2a x 4a 3 ，则显然 f x 的图像关于 y 轴对称．
∵ f x 0 有且只有一个实数根，∴这个实数根只有可能为 0
所以函数 f x 的表达式为 y 2 x 1。 12. 作函数 y 3 x x 1 的图像，并根据图像求出函数的最小值．
【分析】
2 x 4 y 2 2 x 4
( x 3) (1 x 3) ，根据表达式作图像，如上，当 1 x 3 时，显然函数的最小值为2． ( x 1)
2 2 ⑴因为 f f x 1 f k x 1 b k k x 1 b b k x k kb b 4x 7 ； k 2 k 2 k2 4 所以 2 ；解得 或 ； b 1 b 3 k kb b 7 所以函数 f x 的表达式为 y 2 x 1 或 y 2 x 3 。
七年级“学而思杯”模拟试题及答案
“学而思杯”模拟题七年级数学试卷姓名： 考号： 年级： 学校： 考生须知：1、试卷分为填空题和解答题两部分，其中第Ⅰ卷为填空题，第Ⅱ卷为解答题。
2、试卷分值满分100+10分，考试时间100分钟，其中填空题60分，解答题40分，附加题10分，考试前请认真审题，看清题目，按要求认真作答。
一、填空题：（每小题4分，共15题，共计60分）１．已知3x <-，化简：|3|2|1|||x +-+= ．2．方程组||12,||6x y x y +=⎧⎨+=⎩的解的个数为 ．３.如图：直线l 上依次分布着A 、B 、C 、D 、E 、F 六点，以这六点为端点的所有线段的长度 之和为46厘米，以B 、C 、D 、E 四点为端点的所有线段的长度之和为11厘米，那么线段AF 的长度为______厘米．FEDCBAl4．拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉成了许多细的面条，如图所示：…这样捏合后第 次可拉出128根面条．5．直角边长分别为3cm 和4cm 的三角形内部有一点p ，已知p 点到三角形其中两条边的距离分别为3.2cm 和0.5cm ，那么该点到第三条边的距离为_______cm ．6．在568后面补上三个数字，组成一个六位数，使它能被3、4、5分别整除。
符合这些条件的六位数中，最小的一个是 ．7．求和：242424241231001111221331100100++++=++++++++ ．8．化简231(1)1()n x x x x x -⎡⎤+-+-++-=⎣⎦ ．9．A 、B 、C 三个微型机器人围绕一个圆形轨道高速运动，它们顺时针同时同地出发后，A 在2秒钟占追上B ，2.5秒钟时追上C 。
当C 追上B 时，C 和B 运动路程的比是32∶。
问第1分钟时，A 围绕这个圆形轨道运动了 圈？10．古时候有两位贩卖家畜的商人把他们共有的一群牛卖掉，每头牛卖得的钱数正好等于牛的头数.他们把所得的钱买回了一群大羊，每只大羊10元，剩下的钱正好搭配买了一只小羊.他们平分这些羊，结果第一人多得了一只大羊；第二人得到了那只小羊.为了公平，第一人应找补给第二人 元钱.11．某个小组有12名学生，将120张卡片分给这些学生，使得每个人拥有的卡片数各不相同并且不超过20张，那么这12个人中拥有卡片不多于10张的最多有______人．12．有一串数：2003-，1999-，1995-，1991-…，按一定的规律排列，那么这串数中前 个数的和最小．13．已知a 、b 都是整数，并且()5a b +是一个四位正整数，()7a b -也是一个四位正整数，那么22a b +=______．14．张老师购买一套住宅，有两种分期付款方式，一种是第一年付八万元，以后每年付款两万元；另一种是前一半时间每年付款两万八千元，后一半时间，每年付款两万两千元，两种付款方式中付款钱数和付款时间都相同.如一次性付款，可少付房款两万五千元.现在王老师一次性付款，要付房款 万元.15．如图，三角形ABC 的面积为a ,:2:1BD DC =，E 是AC 的中点，AD 与于点P ，那么四边形PDCE 的面积为_______________．(用含a二、解答题（每小题10分，共4题，共计40分）16．计算下列式子的值：222222129911005000220050009999005000++⋅⋅⋅+-+-+-+．17．某学校的初三年级的同学要从8名候选人中投票选举三好学生，规定每人必须从这8名候选人中任意选两名，那么至少有多少人参加投票，才能保证必有不少于5名同学投了相同两个候选人的票？18.如图所示，剪一块硬纸片可以做成一个多面体的纸模型（沿虚线折，沿实线粘）。
“学而思杯”初一奥数测试卷
以下是无忧考为大家整理的“学而思杯”初一奥数测试卷的文章，供大家学习参考！
Ⅰ卷 一、选择题：（本题共15小题，每小题4分，共60分） 1. 已知a是正数，且a 2. 已知x2 xy 3,xy y2 2,则2x2 xy 3y2 3. 观察按下列规则排成的一列数： 24 1，则a2 2等于_________. aa 1121231234123451，，，，，，，，，，，，，，，，……在上式 12432142315316 122中，从左起第m个数记为G(m)， 当G(m) 时,则m的值为________,这m个数的积 2010 为___________. 4. 若n满足(n 2004)2 (2005 n)2 1，则(n 2004)(2005 n)等于_____________. 5. 设x、y、z均为正实数，且满足 是_________. 6. 将一长方形切去一角后得一边长分别是13、19、20、25和31的五边形（顺序不一定按此）.则此五边形的面积为 __________.
1 z 2x 2y x yx 2y 2z y zy 2x 2z，则x、y三个数的大小关系、z zx7. 水果市场有甲、乙、丙三种水果，如果买甲2千克，乙1千 克，丙4千克，共付钱6元；如果买甲4千 克，乙2千克，丙2千克，共付钱4元；今要买甲4千克，乙2 千克，丙5千克，则共应付钱____________. 8. 已知p,q均为质数，且满足7p2 3q 79，则p ，q _________. 9. 若干名游客要乘坐汽车，要求每辆汽车坐的人数相等，如果每辆汽车乘坐30人，那么有一人未能上车； 如果少一辆汽车，那么，所有游客正好能平均分到各辆汽车上，已知每辆汽车最多容纳40人，则有游客 人. 10. 方程x 2y 3 x y 1 1的整数解的个数是 11. 如图，矩形ABCD中，点E,F,G,H分别在边AB，BC，CD，DA上， 点P在矩形ABCD内．若AB 4cm，BC 6cm，AE CG 3cm， BF DH 4cm，四边形AEPH的面积为5cm2，则四边形PFCG的面积 为_________cm2． 12. 设A 48 ( 13. 已知a b c 6,a2 b2 c2 12，则a2010 b2010 c2010 _____________. 14. 已知：m为非零实数，且x x 15. 对于一个自然数n，如果能找到自然数a(a＞0)和b(b＞0)，使n 1 a b ab,则称n为一个“十字相乘 数”，例如:4 1 1 1 1 1，则4是一个“十字相乘数”，在1～20这20个自然数中，“十字相乘数”共有_________个. 12 12111 )，则 A的整数部分是__________. 32 442 41002 4x2 1 m，则 __________.
2023 年第四届超常(数学)思维与创新能力测评 初一年级 数学真题
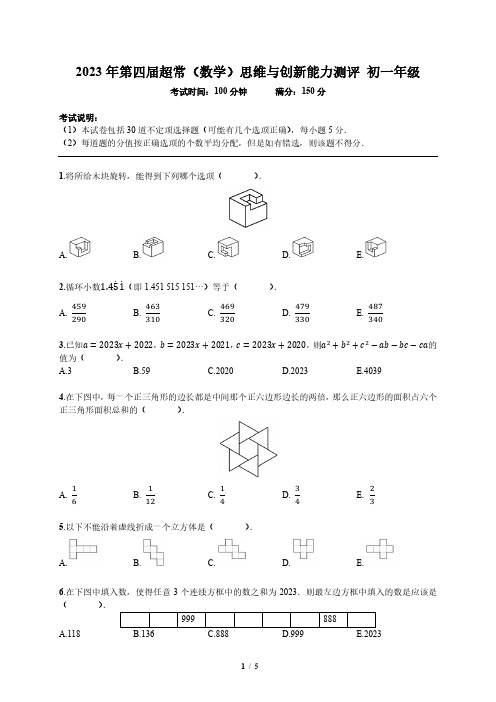
2023年第四届超常（数学）思维与创新能力测评 初一年级考试时间：100分钟满分：150分考试说明：（1）本试卷包括30道不定项选择题（可能有几个选项正确），每小题5分．（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分．1.将所给木块旋转，能得到下列哪个选项（）．A. B. C. D. E.2.循环小数1.451（即1.451 515 151…）等于（）． A. 459290B.463310C.469320D. 479330E.4873403.已知a =2023x +2022，b =2023x +2021，c =2023x +2020，则a 2+b 2+c 2−ab −bc −ca 的值为（ ）．A.3 B.59 C.2020 D.2023 E.40394.在下图中，每一个正三角形的边长都是中间那个正六边形边长的两倍，那么正六边形的面积占六个正三角形面积总和的（ ）．A.16B.112C.14D.34E.235.以下不能沿着虚线折成一个立方体是（）．A. B. C. D. E.6.在下图中填入数，使得任意3个连续方框中的数之和为2023．则最左边方框中填入的数是应该是（ ）．A.1187.已知202009=102000∙409∙2n，则n的值为（）．A.1991B.2000C.2009D.4018E.50008.如图，某城有一组十分奇怪的限速规定：在离城1km处有一个120km/h的标牌，在离城12km处有一个60km/h的标牌，在离城13km处有一个40km/h的标牌，在离城14km处有一个30km/h的标牌，在离城15km处有一个24km/h的标牌，在离城16km处有一个20km/h的标牌，如果你从120km/h的标牌处出发一直以限定时速行驶，那么需要（）才能到达该城．A.30sB.1min13.5sC.1min42sD.2min27sE.3min9.如图所示，三个正方形以顶点相连接在一起，图中已给出若干角的度数，则x的值是（）．A.41B.42C.43D.44E.4610.一辆自行车的链条在具有48个齿的前链齿轮上运行，通常经过具有18个齿的后轮轴的链齿轮．当后链齿轮每旋转一整圈时，踏板转过的角度是（）．A.135°B.360°C.960°D.120°E.6712°11.如图，一个立方体的八个角都被切去，形成一些三角形面．将该图形的所有24个角都用对角线连起来，这些对角线中穿过图形内部的共有（）条．A.84B.108C.120D.142E.24012.把一个三位数首位前和末位后添写上1，这样得到的五位数比原来的三位数增加14789．则原来三位数的三个数字之和是（）．A.10B.9C.8D.7E.613. Ⅰ号混合液由柠檬汁、油和醋以1:2:3的比例配成，Ⅱ号混合液由同样三种液体以3:4:5的比例配成，将两种混合液倒在一起后，新的混合液的比例不可能是（）．A.2:5:8B.4:5:6C.3:5:7D.5:6:7E.7:9:1114.如图所示的网球场中有（）个长方形．A.19B.29C.23D.30E.3115.已知|x−1|+|x−2|=1，则x的值（）．A.只能为1B.只能为2C．可能为任何实数 D.为满足1≤x≤2的一切实数E.以上都不对16.下图是一张城市的道路平面图，除了一条短对角线外，道路全是东西向或南北向的．由于一条路的修补而不可能从点X通过．从P到Q的所有可能走的路线中，有些路线是最短的．则这样的最短路线有（）条．A.4B.7C.9D.14E.1617.甲、乙一起工作，甲每工作1天休息2天，乙每工作1天休息3天．已知第一天他们都在工作，最后一天乙肯定在工作．甲、乙同时休息时间比同时工作时间多128天．则他们从第一天到最后一天经过了（）天．A.180B.308C.309D.312E.50018.要使关于x的方程ax−1=x+a无解，则a=（）．A.-1B.0C.1D.2E.以上都不对19.小刚和月月搭乘某航空公司的飞机从A地飞往B地，但因为他们的行李超出了航空公司规定的重量，所以要求他们支付附加费．航空公司收费方法是对超出规定的重量每千克收取相同的费用．小刚付了60元，月月付了100元．他们一共有52kg的行李，如果小刚自己带着两人的全部行李走，他将必须付340元．每人最多可带（不需要付附加费的）行李（）kg．A.20B.15C.12D.18E.3020.一个4×4的反幻方是指将数1~16填入4×4方格表内，使得每行、每列、每条对角线上的数之和，经排序后恰好形成十个连续的正整数．如图是一个尚未完成的反幻方，则星号“*”所在方格内应填入（）．A.1B.2C.15D.16E.以上都不对21.某学校新建5个教室，平均每班减少6人．如果再建5个教室，那么平均每班又减少4人．假设学生总数保持不变，这个学校可能有（）名学生．A.560B.600C.650D.720E.80022.在一个2023边形（可以是凹多边形）的内角中，锐角至多有（）个．A.2023B.672C.944D.1345E.134923.在一列数1，2，3，…，10000中，有（）个数恰好包含两个相邻的数字9．例如：993，1992和9929就是这样的数，而9295或1999则不是．A.270B.271C.280D.123E.26124.从1970年起小红开始收集日历且以后每年都这样做，直到以后每一年至少可用一本已经收集到的日历来代用时为止．则必须收集日历的最后年份是（）年．A.1983B.1984C.1997D.2023E.以上都不对25.100个正整数之和为101101，则它们的最大公约数的最大可能值是（）．A.101B.1100C.1001D.2002E.1001026.如图所示，你有一些白色的1×12×1瓦片．当用这些瓦片以紧贴邻边的方式来覆盖一个3×1的矩形时，共可以设计出4种颜色方案（WWW，BWW，WBW，WWB）．那么如果用这些瓦片来覆盖一个10×1的矩形，将可以设计出（）种颜色方案．A.47B.89C.155D.286E.30027.已知A，B，C，D，E，F，G，H，I是9个互不相同的非零数字，满足：A除以B余C，D除以E余F，G除以H余I，那么ABC+DEF+GHI的结果是（）．A.1368B.1458C.1188D.2547E.195328.令s为真分数，即s<t，且为最简分数．若t的值为2到9，s，t为正整数，则符合条件的不同的真t分数有（）．A.26B.27C.28D.30E.3629.有27个同样大小的小正方体，每个小正方体的六个面上写着一个相同的数，且恰为1~27，用这27个小正方体拼成如图所示的大正方体．请根据如图所示的数据以及下面所给出的条件推断，从六个方向都看不见的小正方体的面上所写的数是（）．①数9，13和16在同一条直线上．②数22在9和6之间．③17紧挨着5和13，但与9不相邻．④14紧挨着24和27．⑤数20在14的上面．A.22B.20C.17D.9E.530.一个棱长为6的正方体被切割成若干个棱长为整数的小正方体，若这些小正方体的表面积之和是切割前的大正方体的表面积的10倍，则切割成的小正方体中，棱长为1的小正方体的个数可能为3（）．A.15B.24C.42D.56E.60。
2013年寒春学而思数学高端班次选拔考试 七年级试卷(联赛体系)
A． 3
B． 6
C．2
1 1 2 的值为（ ） 2 a b A．5 B．7 C．9 D．11. 7、如图 1， ABC, ADE 均为正三角形，若 EBD 35 ，则 BEC ( ) A. 95 B. 105 C. 115 D. 125
6、设 a2 1 3a ， b2 1 3b ，且 a b ，则代数式
C C E A B D A B
姓名：
密
D
一、选择题（每题 4 分，一共 40 分）
年级：
1、化简 3 5 13 48 的结果是（ ） ．
1 2
图1
图2
6 2
A． 2 B．
9、对 于 自 然 数 n ， 将 其 各 位 数 字 之 和 记 为 an ， 如 a2009 2 0 0 9 11 ， D．
12、已知 a 5 1 ，则 2a3 7a2 2a 12 的值等于_____________． 13、若 x
2 5 1
，且 a x , b x ，则 a3 b3 3ab _____________．
ab bc caቤተ መጻሕፍቲ ባይዱ k ，则 k ___________． bc ca ab
2013 年寒春学而思数学高端班次选拔考试
考号：
七年级试卷（联赛体系）
考生须知： 1、本次考试时间 13:40-15:10，共 90 分钟，满分 120 分； 2、请在试卷左侧认真填写考生信息; 3、考试成绩会在 1 月 3 日 e 度论坛公布。
2013 年学而思元旦高端班次班选拔考试数学试卷 8、如 图 2 ， 在 四 边 形 A B C D中 ， AC ∥ BD , AB BC, AB BC, AC AD , 则 CAD ( ) A. 22.5 B. 25 C. 30 D. 35
学而思初一竞赛班选拔考试数学试卷(内部资料)
⑴求 ；
⑵若有理数 满足 ，求满足条件的有序数对 ；
⑶求证：① ；② ；
⑷求 ．
A.和为 B.和为 C.互余D.互补
6.观察图中的数轴：
用字母 依次表示 对应的数，则 的大小关系是
A. B. C. D.
二、填空题（本题共32分，每小题4分）
7.计算： _____________．
8.已知方程 的解与方程 的解相同，则 _____________．
9.如图，线段 ， ， 是 的中点， 是 的中点，若 ，则 的长为_____________．
绝密★启用前
2015年学而思初一竞赛班选拔考试试卷
数学试卷
考试时间：2015年8月16日上午9:00～10:30
姓名_____________________学员编号________________________
考
生
须
知
1．本试卷共2页，三道大题，18道小题，满分100分。考试时间90分钟。
2．答题前，请考生务必用蓝、黑色字迹的圆珠笔、签字笔或钢笔在试卷和答题纸上准确填写姓名和学员编号。
3.已知 都是有理数，并且 ， ，则 与
A.互为相反数B.互为倒数C.互为负倒数D.相等
4.有四种说法：
⑴正数的平方不一定大于它本身；⑵正数的立方不一定大于它本身；
⑶负数的平方不一定大于它本身；⑷负数的立方不一定大于它本．
这四种说法中，不正确的说法的个数是
A. 0个B. 1个C. 2个D. 3个
5.如图， ，那么 与 之间的关系是
10.若方程组 的解满足 ，则 的取值范围是______________．
2024年学而思培优中考数学一模试卷+答案解析
2024年学而思培优中考数学一模试卷一、选择题：本题共10小题，每小题3分，共30分。
在每小题给出的选项中，只有一项是符合题目要求的。
1.已知实数，则实数a 的倒数为( )A. 2024B.C.D.2.下列图形中，属于轴对称图形的是( )A.B.C.D.3.近来，中国芯片技术获得重大突破，7nm 芯片已经量产，一举打破以美国为首的西方世界的技术封锁，已知，则用科学记数法表示为( )A.B.C.D.4.下列说法中不正确的是( )A. 数据4，9，5，7，5的平均数是6B. 任意画一个多边形，其外角和等于是必然事件C. 了解某市中学生50米跑的成绩，应采用抽样调查D. 某幼树在一定条件下移植成活的概率是，则种植10棵这种树，结果一定有9棵成活5.一副三角板如图所示摆放．若，则的度数是( )A. B. C. D.6.如图，在菱形ABCD 中，点E 是BC 的中点，以C 为圆心、CE 为半径作弧，交CD 于点F ，连接AE 、若，，则阴影部分的面积为( )A. B.C. D.7.从1、2、3、4四个数中随机选取两个不同的数，分别记为a、c，则关于x的一元二次方程有实数解的概率为( )A. B. C. D.8.的图象平移或翻折后经过坐标原点有以下4种方法：①向右平移1个单位长度；②向右平移3个单位长度，再向上平移4个单位长度；③向上平移1个单位长度；④沿x轴翻折，再向下平移1个单位长度.你认为小郑的4种方法中正确的个数有( )A. 4个B. 3个C. 2个D. 1个9.如图，在正五边形ABCDE中，若，则( )A. 2B.C.D.10.如图，在等腰中，，点P在以AB为直径的半圆上，M为PC的中点，当点P沿半圆从点A运动至点B时，点M运动的路径长是( )A.B.C.D.二、填空题：本题共5小题，每小题3分，共15分。
11.因式分解：______.12.一次函数满足，则它的图象必经过一定点，这定点的坐标是______13.如图菱形ABCD的边长为4，，将菱形沿EF折叠，顶点C恰好落在AB边的中点G处，则______.14.规定：表示a，b之间的一种运算．现有如下的运算法则：，例如：，，则______.15.如图，在中，，射线AB分别交y轴于点D，交双曲线于点B，C，连接OB，OC，当OB平分时，AO与AC满足，若的面积为4，则______.三、计算题：本大题共2小题，共12分。
学而思初一数学寒假班第7讲 阶段测试 教师版(培优梳理—目标中考高分班)
数学测试卷（培优梳理-目标中考高分班）一、选择题（每题3分，共30分，将答案填在下面的空格处） 1. 下列方程组中，不是二元一次方程组的是（ ）A ．3251x y x +=⎧⎨=⎩B ．267x y x y -=⎧⎨+=⎩C ．1019x x y =⎧⎨-=⎩D ．153x xy =⎧⎨=⎩2. 下列说法正确的是（ ）A. 2(1)-的平方根是1-B. 1-的平方根是1-C. 2-是8-的立方根D. 16的平方根是43. 下列运算正确的是（ ）A. 321a a -= B. 842x x x -=C.2- D. ()326328x y x y -=-4. 若方程组422x yx y a +=⎧⎨-=⎩中的x 是y 的2倍，则a 等于（ ）A ．9-B ．8C ．7-D ．6-5. 一个样本有20个数据：3531333537393538403936343537363234353634，，，，，，，，，，，，，，，，，，，，其中众数为（ ）A. 34B. 35C. 36D. 376. 为了从甲、乙、丙、丁四位同学中选派两位选手参加数学竞赛，老师对他们的五次数学测验成绩进行统计，得出他们的平均分均为85分，且、、、． 根据统计结果，派去参加竞赛的两位同学是（ ）A ．甲、乙B ．甲、丙C ．甲、丁D ．乙、丙7.等于（ ）A. 3.14π-B. 3.14π-C. 3.14π+D. (3.14)π-+8. 若关于x 、y 的二元一次方程组59x y kx y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解，则1002=甲s 1102=乙s 1202=丙s 902=丁sk 的值为（ ）A. 34-B. 34C. 43D. 43-9. 下面是某同学在一次测验中的计算摘录，其中正确的个数有（ ）① 236a a a ⋅=；② ()333ab a b -=-；③3332a a a +=； ④ ()2212366x x x -+=-；⑤()()212152n m x y x y +--⋅-=52120n m x y +--⑥()()()2x x y y x y x y ---=-A ．1个B ．3个C ．4个D ．5个10. 已知106a =，102b =，则210a b +的值为（ ）A ．8B ．36 C. 38． D ．72二、填空题（每题3分，共24分，将答案填在下面的空格处）11. 13的小数部分是 .12.21(2013)0x y ++-=，则y x = .13. 已知a 、b 、c 是三个有理数，且a 与b 的平均数是127，b 与c 的和的三分之一是78，c 与a 的和的四分之一是52，那么a ，b ，c 的平均数是 .14. 如果21x y =⎧⎨=⎩是方程75ax by bx cy +=⎧⎨+=⎩的解，则a 与c 的关系是 .15. 若21m n =+，则2244m mn n -+的值是 .16. 若1235x y z ++=，3217x y z ++=，则111x y z ++= .17. 已知3,1a b ==，则()()(2)a b a b b b +-+-= .18. 如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽边长分别是2和1的长方形．现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片 张才能用它们拼成一个新的正方形．三、解答题（每题4分，共16分）19. 已知2,3x y a a ==，求x y a +与2x y a -的值.20. 解方程组37528x y x y -=⎧⎨+=⎩21. 解方程组::3:4:5238x y z x y z =⎧⎨+-=-⎩22. 先化简再求值：()()()()222424x y x y x y y x xy +-+-++. 其中1x =，1y =-.四、解答题（每题6分，共30分）23. 已知21a -的平方根是3±，39a b +-的立方根是2，c 求2a b c++的算术平方根．24. k 为何值时，关于x y ，的方程组35223x y k x y k -=+⎧⎨-=⎩的解的和为20．25. m 取何整数值时，方程组2441x my x y +=⎧⎨+=⎩的解x y ，都是整数？26. 如图a 是一个长为2m 、宽为2n 的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图b 形状拼成一个正方形．⑴你认为图b 中的阴影部分的正方形的边长等于多少？⑵观察图b 你能写出下列三个代数式之间的等量关系吗？代数式：()()22,,m n m n mn +-. ⑶已知7,6m n mn +==，求()2m n -的值．27. 为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）. 已知A 、B 两组捐款户数的比为1 : 5.请结合以上信息解答下列问题.(1) a= ，本次调查样本的容量是 ； (2) 先求出C 组的户数，再补全“捐款户数分组统计图1”；(3) 若该社区有500户住户，请根据以上信息估计，全社区捐款不少于300元的户数是多少？组别 捐款额（x ）元 户数 A 1≤x <100 a B 100≤x <200 10 C 200≤x <300 D 300≤x <400 Ex ≥400捐款户数分组统计图1捐款户数分组统计图2五、 附加题（每题10分，共20分）28. 已知关于x 、y 的二元一次方程(1)(2)520a x a y a -+++-=，当a 每取一个值时，就有一个方程，而这些方程有一个公共解，求出这个公共解.29．古运河是扬州的母亲河，为打造古运河风光带，现有一段长为180米的河道整治任务由A 、B 两个工程队先后接力完成．A 工程队每天整治12米，B 工程队每天整治8米，共用时20天．⑴根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：甲：128x y x y ⎧+=⎪⎨+=⎪⎩乙：128x y x y⎧+=⎪⎨+=⎪⎩根据甲、乙两名同学所列的方程组，请你分别指出未知数x ，y 表示的意义，然后在方框中补全甲、乙两名同学所列的方程组： 甲：x 表示，y 表示； 乙：x 表示，y 表示；⑵求A 、B 两工程队分别整治河道多少米？（写出完整的解答过程）学而思学校 初一寒假 数学测试卷参考答案三、解答题：每题4分，共16分． 19. 6x y x y a a a +=⋅=()2243x y x y a a a -=÷=20.21x y =⎧⎨=-⎩ 21.6810x y z =⎧⎪=⎨⎪=⎩22. 原式22222448482x y x xy y xy xy =-+-+++2252x xy =+把1x =，1y =-代入原式527=+=．四、解答题：每小题6分，共30分． 23. 根据题意，可得219,398a a b -=+-=；故5,2a b ==； 可得c=7； 则216a b c ++=； 则16的算术平方根为4．24. 这是含有字母的二元一次方程组，求解此类题需将字母看作常数求解方程组的解，然后再根据题目条件求出字母的值． 解方程组35223x y k x y k -=+⎧⎨-=⎩得：264x k y k =-⎧⎨=-⎩又因为：20x y +=，即：31020k -=所以：10k =．25. 把m 作为已知数，解方程组得81828x m y m ⎧=-⎪⎪-⎨⎪=⎪-⎩∵x 是整数，∴8m -取8的约数1248±±±±，，，． ∵y 是整数，∴8m -取2的约数12±±，． 取它们的公共部分，812m -=±±，． 解得97106m =，，，．经检验97106m =，，，时，方程组的解都是整数．26. ⑴m n -．⑵()()224m n m n mn +=-+．⑶()()224494625m n m n mn -=+-=-⨯=．27.⑴2，50；⑵5040%20⨯=，C 组的户数为20 ，补图见图2． ⑶∵ 500(28%8%)180⨯+=，∴ 根据以上信息估计，全社区捐款不少 于300元的户数是180．五、附加题：每题10分，共20分28. 原方程变为(2)(25)0a x y x y +----=，由于公共解与a 无关，∴20250x y x y +-=⎧⎨--=⎩， ∴31x y =⎧⎨=-⎩29. （1）甲：20128180x y x y ⎧+=⎪⎨+=⎪⎩乙：18020128x y x y⎧+=⎪⎨+=⎪⎩捐款户数分组统计图1甲：x表示A工程队整治的天数，y表示B工程队整治的天数；乙：x表示A工程队整治的米数，y表示B工程队整治的米数；（2）按甲同学的思路解答：∴515 xy=⎧⎨=⎩1260,8120x y∴==即A工程队整治河道60米，B工程队整治河道120米.。
学而思初一数学秋季班第1讲.有理数与数轴.基础-提高班.教师版
1初一秋季·第1讲·基础-提高班·教师版长度单位实数5级 有理数综合运算实数4级 有理数与数轴 实数3级 有理数的混合运算 满分晋级阶梯漫画释义1有理数与数轴2初一秋季·第1讲·基础-提高班·教师版知识点切片（3个）2+1+1知识点目标有理数与数轴（2） 1、点表示数；2、比较大小 相反数与数轴（1） 1、相反数的几何意义 绝对值与数轴（1）1、绝对值的几何意义题型切片（6个）对应题目题型目标用数轴表示数 例1、练习1数轴上点、线段的移动 例2、例3、练习2 利用数轴比较大小例4、练习3 利用数轴性质建立方程求点对应的数 例5、练习4 数轴折叠 例6、练习5 周期问题与数轴例7、练习6数轴：规定了原点、正方向和单位长度的直线叫做数轴；原点、正方向、单位长度称为数轴的三要素，三者缺一不可.有理数与数轴的关系：一切有理数都可以用数轴上的点表示出来.在数轴上，右边的点所对应的数总比左边的点所对应的数大.正数都大于0，负数都小于0，正数大于一切负数. 注意：数轴上的点不都代表有理数，如π.相反数：只有符号不同的两个数，互称为相反数．特别地，0的相反数是0.数轴上，位于原点两侧且到原点距离相等的点表示的数互为相反数.绝对值：一个数a 的绝对值就是数轴上表示数a 的点与原点的距离．数a 的绝对值记作a ．正数的绝对值是它本身，0的绝对值是0，负数的绝对值是它的相反数．数轴上的点，对应的数绝对值越大，离原点越远.【例1】 ⑴在数轴上画出表示12.540252--，，，，各数的点，并按从小到大的顺序重新排列，用“<”连接起来.⑵如图，数轴上表示数2-的相反数的点是（ ）A ．点PB ．点QC ．点MD ．点N ⑶数轴的单位长度为1，点A ，B 表示的数的绝对值相等，那么点A 表示的数是（ ） A ．4- B ．2- C ．0 D ．4【解析】⑴分别将数的对应点在数轴上画出，如图，按数轴上从左到右的点对应从小到大的实数，得到 1420 2.552-<-<<< ⑵A .⑶B .【例2】 ⑴数轴上有一点A ，它表示的有理数是3-，将点A 向左移动3个单位得到点B ，再向右移动8个单位，得到点C ，则点B 表示的数是 ，点C 表示的数是 ．P Q M 52.50-2123初一秋季·第1讲·基础-提高班·教师版⑵在数轴上，坐标是整数的点称为“整点”．设数轴的单位长度是1厘米，若在这个数轴上随意画出一条长2013厘米的线段AB ，则线段AB 盖住的整点至少有 个， 至多有个．【解析】 ⑴由数轴的基本定义可知为62-+，.⑵2013；2014针对例2⑵的铺垫：1、⑴在数轴上，表示1999-和1999的两个点之间有 个整数（含1999-和1999）． ⑵在数轴上，表示1999.1-和1999.9的两个点之间有 个整数． 【解析】 ⑴3999；⑵ 3999．针对例2⑵的拓展：1、设数轴的单位长度是1厘米，若在这个数轴上随意画出一条长120132厘米的线段AB ，则线段AB 盖住的整点至少有 个，至多有 个．2、设数轴的单位长度是1厘米，若在这个数轴上随意画出一条长M （M 为正整数）厘米的线段AB ，则线段AB 盖住的整点至少有 个，至多有 个．3、设数轴的单位长度是1厘米，若在这个数轴上随意画出一条长M （1m M m <<+，m为正整数）厘米的线段AB ，则线段AB 盖住的整点至少有 个，至多有 个．【解析】 1、2013；2014. 2、M ，1M +.3、m ，1m +.【例3】 ⑴一个机器人从数轴原点出发，沿数轴正方向以每前进3步后退2步的程序运动，设该机器人每秒钟前进或后退1步，并且每步的距离为1个单位长，n x 表示第n 秒时机器人在数轴上的位置所对应的数. ①求3x 、5x 的值.②比较2013x 与2014x 的大小.⑵电子跳蚤在数轴上的某一点0K ，第一步由点0K 向左跳1个单位到点1K ，第二步由点1K 向右跳2个单位到点2K ，第三步由点2K 向左跳3个单位到点3K ，第四步由点3K 向右跳4个单位到点4K ，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点100K 所表示的数恰好是19.94．求电子跳蚤的初始位置点0K 所表示的数．【解析】⑴①33x =，51x =.②2013405x =，2014404x =，20132014x x <.⑵假设电子跳蚤的起点0K 为0x ，规定向左为负，向右为正，根据题意可得： 01234569910019.94x -+-+-+--+=L L ，030.06x =-．【例4】 ⑴有理数a b ，在数轴上的对应点如图，试比较a a b b a b a b --+-，，，，，的大小.4初一秋季·第1讲·基础-提高班·教师版⑵已知a b ，是不为0的有理数，且a a b b a b =-=>，，，那么用数轴上的点来表示a b ，，正确的应该是哪一个（）DCB A【解析】⑴根据a b ，在数轴上的位置可知，00a b <>，，且a 的绝对值比2b 的绝对值大，所以a b a a b b b a -<<+<-<<-.⑵ C ，根据题意，00a b <>，，且在数轴上a 的对应点与原点的距离较b 的对应点大.【例5】 ⑴如图，数轴上标出若干点，每相邻的两点相距一个单位长度，点A 、B 、C 、D 对应的数分别为整数a 、b 、c 、d ，且24d a -=．试问：数轴上的原点在哪一点上？A B C D MN⑵如图，数轴上标出若干个点，每相邻的两点相距1个单位，点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ．①若2a b c d +++=-，那么与数轴原点最接近的点是（ ）A ．A 点B ．B 点C ．C 点D ．D 点② 若7a b +=，那么与数轴原点最接近的点是（ ）A ．A 点B ．B 点C ．C 点D ．D 点⑶如图，在数轴上有若干个点，每相邻两个点之间的距离是一个单位长，有理数a 、b 、c 、d 所表示的点是这些点中的4个，且在数轴上的位置如图所示，已知343a b =-，求2c d +的值.dc b a【解析】⑴由数轴可知，3d a =+，代入24d a -=得324a a +-=，解得1a =-所以原点应在点B 处．⑵①C ．(3)(4)(7)2a a a a ++++++=-，4a =-，1b =-，0c =，3d =． ② A ．37a a ++=，4a a +=，∴0a >，2a =．⑶2-. 提示：2b a =+.【例6】 已知在纸面上有一数轴（如图），折叠纸面．1⑴ 若1表示的点与1-表示的点重合，则2-表示的点与数 表示的点重合： ⑵ 若1-表示的点与3表示的点重合，则5表示的点与数 表示的点重合；⑶ 若数轴上A 、B 两点之间的距离为c 个单位长度，点A 表示的有理数是a ，并且A 、A5初一秋季·第1讲·基础-提高班·教师版B 两点经折叠后重合，请写出此时折线与数轴的交点表示的有理数是多少？【解析】 ⑴ 2；⑵3-； ⑶此时折线与数轴的交点表示的有理数是12a c ±.【例7】如图所示，数轴被折成90︒，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3．先让圆周上数字2所对应的点与数轴上的数3所对应的点重合，数轴固定，圆紧贴数轴沿着数轴的正方向滚动，那么数轴上的数2013将与圆周上的数字 重合？98765431023【解析】201345031÷=L ，则与数字0重合． 针对例7的铺垫：4个单位长度，在圆的4等分点处 标上数字0，1，2，3．先让圆周上数字0所对应的点与数轴上的数1-所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数2012-将与圆周上的数字 重合．3210-5-4-3-2-1【解析】20124503÷=，则与数字0重合． 针对例7的拓展：1、如图所示，一数轴被折围成长为3，宽为2的长方形，圆的周长为4且圆上刻一指针，若1在数轴固定的情况下，圆紧贴数轴沿数轴正方向滚动，当圆与7接触的时候，指针的方向是（ ）DCBA76543210-12、如图，边长为1的等边三角形ABC 从图示的位置开始在数轴上顺时针无滑动地向右滚动，当三角形的一个顶点落在2013x =处时，三角形停止滚动. ①落在2013x =处的点是ABC △的哪个顶点？说明理由. ②在滚动过程中，点A 走过的路程是多少？…20131C B A6初一秋季·第1讲·基础-提高班·教师版3、把一数轴折成如图所示，第1段为1个单位长度，第2段为2个单位长度，第3段为3个单位长度，……，点O 处有一个圆，圆上刻一指针，开始指针朝东，圆周为4个单位长度，圆紧贴数轴沿着数轴的正方向滚动，当圆与点A 接触时，指针指向 （东、南、西、北），当圆与2009接触时，指针指向 （东、南、西、北）．O 北西南东-10【解析】1、C ．2、①顶点C ；②894π.3、在直的数轴上，线段41AO =，414101=⨯+，指针指向北；2009(14)2023--=，因为636420162⨯=，202320167-=，故2009在点O 的西边，202345053÷=+，指针指 向西．7初一秋季·第1讲·基础-提高班·教师版训练1.在下列各数：(2)--，2(2)--，2--，2(2)-，2(2)--中，负数的个数为 个． 【解析】 2.训练2. 若0a b +=，c 和d 互为倒数，m 的绝对值为2，求代数式22()a b m cd ++-的值 【解析】 3.训练3. 数轴上的一个点表示一个数，当这个点表示的是整数时，我们称它是整数点．如果有一条数轴的单位长度是1厘米时，有一条2米长的线段放在数轴上它可以盖住多少个整数点？ 【解析】 200或201.训练4. 如图所示，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3．先让圆周上数字0所对应的点与数轴上的数1-所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数2006-将与圆周上的数字 重合．【解析】 200645012÷=L ，则与数字2重合．3210-58初一秋季·第1讲·基础-提高班·教师版用数轴表示数【练习1】 一辆货车从超市出发，向东走了3km 到达小彬家，继续向前走了1.5km 到达小颖家，然后向西走了9.5km 到达小明家，最后回到超市⑴以超市为原点，向东作为正方向，用1个单位长度表示1km ，在数轴上表示出小明，小彬，小颖家的位置. ⑵小明家距离小彬家多远？ ⑶货车一共行驶了多少千米？ 【解析】⑴如图所示：小颖家小彬家超市小明家西东⑵小明距离小彬家8km⑶货车共行驶了3 1.59.5519km +++=. 数轴上的点、线段的移动【练习2】 ⑴在数轴上，点A 和点B 都在与154-对应的点上，若点A 以每秒3个单位长度的速度向右运动，点B 以每秒2个单位长度的速度向左运动，则7秒之后，点A 和点B 所处的位置对应的数是什么？这时线段AB 的长度是多少？⑵在数轴上表示整数的点称为整数点，某数轴的单位长度是1cm ，若在这个数轴上随意画出一条长2007cm 的线段AB ．被线段AB 盖住的整数有（ ）个．A ．2005或2006B ．2006或2007C ．2007或2008D ．2008或2009【解析】⑴点A 对应的数是694，点B 对应的数是714-，线段AB 的长度是35；⑵C.利用数轴比较大小 【练习3】 数a b c d ，，，所对应的点A B C D ，，，在数轴上的位置如图所示，那么a c +与b d +的大小关系为 .【解析】a c b d +<+.利用数轴性质建立方程求点对应的数【练习4】 如图，数轴上标出若干个点，每相邻两点相距1个单位，点A 、B 、C 、D 对应的整数a 、b 、c 、d ，且29b a -=，那么数轴的原点对应点是（ ）．A ．A 点B ．B 点C ．C 点D ．D 点【解析】C ．2(4)9b b --=，1b =-．9初一秋季·第1讲·基础-提高班·教师版数轴折叠【练习5】 已知在纸面上有一数轴（如图），折叠纸面．1⑴若1-表示的点与5表示的点重合，则7表示的点与数 表示的点重合； ⑵ 若数轴上A 、B 两点之间的距离为8个单位长度，点A 表示的有理数是10-，并且A 、B 两点经折叠后重合，请写出此时折线与数轴的交点表示的有理数是多少？【解析】⑴ 3-；⑵此时折线与数轴的交点表示的有理数是6-或14-.周期问题与数轴【练习6】 如图，圆的周长为3，在圆的三等分点处标上数字0、1、2. 圆从图示的位置向右滚动，那么数轴上的2013将与圆上哪个数字重合？120…201321﹣1【解析】1.数轴是谁最先发现的？勒内·笛卡儿1596年3月31日生于法国安德尔-卢瓦尔省的图赖讷（现笛卡尔，因笛卡儿得名），1650年2月11日逝世于瑞典斯德哥尔摩，是世界著名的法国哲学家、数学家、物理学家。
学而思数学试卷_七年级
一、选择题（每题3分，共30分）1. 下列哪个数是负数？A. -5B. 0C. 3D. -3.52. 下列哪个图形是正方形？A. 矩形B. 三角形C. 梯形D. 正五边形3. 下列哪个数是偶数？A. 13B. 16C. 21D. 254. 下列哪个数是质数？A. 4B. 6C. 8D. 95. 下列哪个等式成立？A. 2 + 3 = 5B. 3 × 4 = 12C. 5 - 2 = 3D. 6 ÷ 3 = 26. 下列哪个数是无限不循环小数？A. 0.333...B. 0.25C. 0.666...D. 0.1257. 下列哪个分数约分后等于2/3？A. 4/6B. 6/9C. 8/12D. 10/158. 下列哪个方程的解是x = 5？A. 2x + 3 = 13B. 3x - 4 = 11C. 4x + 5 = 19D. 5x - 6 = 179. 下列哪个几何体的体积最大？A. 正方体B. 长方体C. 球D. 圆柱10. 下列哪个图形的对称轴最多？A. 正方形B. 矩形C. 等腰三角形D. 平行四边形二、填空题（每题3分，共30分）11. 1的相反数是_________。
12. -2 + 5的差是_________。
13. 3 × 4 + 2的值是_________。
14. 下列数的平方根是负数的是_________。
15. 下列数的立方根是正数的是_________。
16. 下列分数中，分子大于分母的是_________。
17. 下列等式中，等号两边不相等的是_________。
18. 下列几何图形中，有无数条对称轴的是_________。
19. 下列数中，是等差数列的一项是_________。
20. 下列数中，是等比数列的一项是_________。
三、解答题（每题10分，共40分）21. 解下列方程：3x - 5 = 14。
22. 简化下列分数：12/16。
学而思综测7年级数学试卷
输入x
乘以3
加上5
取相反数
小于5
是 输出
否 第 13 题图 14. 在同一条直线上顺次有三点 A、B、C，AC 3AB 15cm ，M 为 BC 中点，射线 CB 上有一点 P， 若 P 点位置满足 AP : BP 2 : 3 ，则 MP _________．
15. 某生产车间的高级技工小刘每天可加工 15 个零件，现接到订单要加工一批零件，加工了全部零
须
目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案．
知
4. 答第Ⅱ卷（非选择题）时，答案用 0.5 毫米黑色笔迹签字笔书写在“答题卡”上．
除画图外，请不要用铅笔答题．
5. 考试结束，只收答题卡，试卷和草稿纸可以带回．
初中期末综合能力测评查分时间：2018 年 1 月 3 日上午 10：00．
2
姓名 准考证号
A
B
图1
密 封 线 内 不 要 答 题
※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※ ※※※※※※※
第 5 页共 8 页
M
N
A
B
H
图2
第 6 页共 8 页
24. （本题 12 分）已知 AOB ，以 O 为顶点作射线 OC，OC 顺时针旋转 得到射线 OD，且 ， 0 180 （涉及的角均为大于 0 且小于或等于180 的角）． ⑴ 如图 1，若 90 ， 30 ，若 COD 在 AOB 内部，OE 平分 BOC ，OF 平分 AOD ， 则 EOF ______； ⑵ 当 COD 旋转到图 2 所示位置时，OC 在直线 OB 上方，OD 在直线 OB 下方，仍有 OE 平 分 BOC ， OF 平分 AOD ，试用 和 表示 EOF ； ⑶ 在⑴的条件下，如图 3，若射线 OC 从 OA 出发以10 /秒的速度顺时针旋转，旋转过程中 OD 也随之转动，OQ 为 COD 的角平分线，当 OC 出发时，射线 OP 从 OA 出发往返于 AOB 内，速度为15 /秒，当 OD 和 OA 重合时所有运动停止，设 ts 时 OP 和 OQ 所在直线重合， 试求出所有满足条件的 t 的值．
学而思初中数学模拟试卷
1. 下列数中，有理数是（）A. √2B. πC. 0.101001…D. -√92. 若a，b，c是等差数列，且a+b+c=0，则b的值为（）A. 0B. -1C. 1D. 无法确定3. 已知二次函数y=ax^2+bx+c的图象开口向上，且顶点坐标为（-2，3），则a的值为（）A. 1B. -1C. 2D. -24. 在直角坐标系中，点A（2，3），B（-1，2），C（-3，-1），则△ABC的周长为（）A. 8B. 10C. 12D. 145. 若a，b，c是等比数列，且a+b+c=0，则b的值为（）A. 0B. -1C. 1D. 无法确定6. 在平面直角坐标系中，点P（2，-1）关于y轴的对称点为Q，则Q的坐标为（）A.（2，1）B.（-2，1）C.（-2，-1）D.（2，-1）7. 已知等差数列{an}的首项为1，公差为2，则第10项与第15项之和为（）A. 28B. 30C. 32D. 348. 在平面直角坐标系中，直线y=kx+b与x轴、y轴的交点分别为A、B，若OA=OB，则k的值为（）A. 1B. -1C. 0D. 无法确定9. 若x+y=3，xy=2，则x^2+y^2的值为（）A. 7B. 8C. 9D. 1010. 在等腰三角形ABC中，底边BC=6，腰AC=8，则底角A的度数为（）A. 30°B. 45°C. 60°D. 75°1. 下列各数中，绝对值最小的是（）A. -3B. -2C. -1D. 02. 若x^2-2x+1=0，则x的值为（）3. 已知等比数列{an}的首项为2，公比为3，则第5项与第8项的积为（）4. 在平面直角坐标系中，点P（3，4）关于原点的对称点为Q，则Q的坐标为（）5. 若x+y=5，xy=6，则x^2+y^2+2xy的值为（）6. 在平面直角坐标系中，直线y=kx+b与x轴、y轴的交点分别为A、B，若OA=OB，则k的值为（）7. 若a，b，c是等差数列，且a+b+c=0，则b的值为（）8. 已知等差数列{an}的首项为1，公差为2，则第10项与第15项之和为（）9. 在平面直角坐标系中，直线y=kx+b与x轴、y轴的交点分别为A、B，若OA=OB，则k的值为（）10. 在等腰三角形ABC中，底边BC=6，腰AC=8，则底角A的度数为（）三、解答题（每题10分，共30分）1. 已知等差数列{an}的首项为3，公差为2，求第10项与第15项之和。
2020 年超常(数学)思维与创新能力测评 (初一 初赛)含答案
2020年超常（数学）思维与创新能力测评（初一 初赛）姓名：_____________ 考试时间：90分钟 满分：120分考试说明（1）本试卷包括25道不定项选择题（可能有几个选项正确），其中第1〜10题各4分，第 11—20题各5分，第21〜25题各6分。
（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分。
1. 分数22222+1+1+1+1+21+21+22+1可以表示成m n的形式，m 和n 为互素正整数，则2m +n 的值为（ ）.A.15B.25C.35D.55E.752. 三个边长为2cm 的正方形如图所示，甲的中心在乙的一个顶点上，乙的中心在丙的一个顶点上，甲与丙不重叠，则甲、乙、丙一共覆盖的面积是（ ）cm 2A.6B.7C.8D.9E.103. 立方体的6个面如图所示用未干的油漆着色(其中前面、上面、右面如左图，其它三个面如右图). 如果按箭头方向把立方体翻转90°，那么这个立方体在纸上会留下的痕迹（包括初始位置）是（）.A. 1—1，2—2，3—3，4—4，5—5，6—6B. 1—1，2—3，3—5，4—2，5—4，6—6C. 1—1，2—3，3—6，4—10，5—7，6—1D. 1—3，2—5，3—6，4—10，5—7，6—1E. 1—3，2—4，3—5，4—6，5—10，6—114. 已知a=−2019×2019−2019 2018×2018+2018b=−2020×2020−2020 2019×2019+2019c=−2021×2021−2021 2020×2020+2020则abc等于（）.A.−1B.3C.−3D.1E.25. 已知a1，a2，a3，⋯，a2020，a2021均为正数. 且M=(a1+a2+a3+⋯+a2020)(a2+a3+⋯+a2021)N=(a1+a2+a3+⋯+a2021)(a2+a3+⋯+a2020)则M与N的大小关系为（）.A.M>NB.M≥NC.M<ND.M≤NE.M、N关系不确定6. 下列图中能够相互补充构成立方体的图形对是（）.A.1—8，2—11B.3—6，4—12C.5—16，7—14D.9—13，10—15E.1—9，3—77. 三角形内角平分线的交点称为三角形的内心，如图，D是△ABC的内心，E是△ABD的内心，F是△BDE的内心. 若∠BFE的度数为整数，则∠BFE不可能为（）度.A.100B.108C.112D.120E.1358. 算式可怕新冠×抗×抗×抗×抗=新冠不可怕每个汉字代表一个数字，不同的汉字代表不同的数字，那么，这个算式的结果“新冠不可怕”=（）.A.98765B.90762C.91056D.92056E.569209. 在一个正方形中，画有一些横线段、纵线段及斜线段，如图所示，则图中矩形（包括正方形）和三角形分别有（）个.A.265，267B.266，268C.268，266D.365，367E.366，36810. 由于贯彻“绿水青山就是金山银山”的号召，某地自然环境改善，水鸟数量持续增多，在一串湖泊的上空飞行着一群白天鹅，它们飞行经过每个湖泊时，都停下天鹅群的一半加上“半只”天鹅，剩下的天鹅群继续往前飞，最后所有的天鹅全部停在若干个湖中，则这群天鹅原来可能有（）只.A.63B.127C.255D.1023E.202111. 黑白方块排列，要从逆时针“↺”或顺时针“↻”旋转后的形状、数量、方位等找出其正确的排列情形. 以下选项符合上述规律的是（）.12. 一些小姑娘去采蘑菇，其中一人釆到6朵，其余的人每人都采到13朵. 第二次又有一些小姑娘（人数与第一次不同）出去釆蘑菇，其中一人采到5朵，其余的人每人都采到10朵. 已知两次采到的蘑菇数相同，并且蘑菇数大于100，但不超过200，如果不计顺序，两次去采蘑菇的人数为（）个.A.10B.12C.14D.16E.1813.COUNTEREXAMPLE TO EULER'S CONJECTURE ON SUMS OF LIKE POWERSBY L. J. LANDER AND T. R. PARKINCommunicated by J. D. Swift,June 27,1966A direct search on the CDC 6600 yielded275+845+1105+1335=1445as the smallest instance in which four fifth powers sum to a fifth power. This is a counterexample to a conjecture by Euler[1] that at least n n th powers are required to sum to an n th power，n>2.REFERENCE1. L. E. Dickson，History of the theory of numbers，Vol. ，Chelsen，New York，1952，p. 648.有人说这是史上最短的数学论文了，它推翻了伟大数学家欧拉的一个猜想. 几百年前，大数学家欧拉提出过一个猜想：至少n个n次方数加起来才能等于一个n次方数. 几百年后两个数学家找到了一个反例，推翻了这个猜想. 只需要4个5次方数加起来就能等于一个5次方数. 当然也许还有其他反例. 如果大家能找到也可以发表，从而青史留名.以1445=275+845+1105+1335为反例推翻了欧拉猜想，那么问题来了，277+847+1107+1337（）.A.小于1447−1B.等于1447−1C.等于1447D.等于1447+2E.大于1447+114. 如图所示是一个14边形（有14个边的多边形），它有5个锐角，对一个2 001边形，若它的任意两个边除了顶点处之外并不相交于内部，请问这个多边形最多可能有（）个锐角.A.1001B.667C.1334D.1335E.200115. 从村里往同一方向走出三个行人：第一个人出村后过2min第二个人出去，第二个人出村后过3min第三个人出去. 第三个行人出村后过了5min赶上了第二个行人，又过了2min他赶上了第一个行人. 第二个行人出村后过了（）min能赶上第一个行人.A.10B.14C.20D.28E.4016. 用重1g，3g，9g，27g，81g，243g和728g（注意：不是729g）的砝码各1个，在天平上分别称量重200g，500g，1000g的物体甲，乙，丙，可以准确称量的是（）.A.甲B.乙C.甲和乙D.甲，乙和丙E.无法确定17. 古代有位将军，他的军队缺乏训练，无法命令他的士兵排成整齐的队列报数.这位将军另打了个主意，他把他的士兵排成四路纵队，这样余下一人；然后再排成五路、七路、十一路和十七路纵队，分别余下一人、三人、一人和十一人. 一周后他与另一位将军交战，损失了一些人，也俘虏了一些人，人数的情况如下：这位将军在交战前有5281个士兵，则他在交战后还剩下（）个士兵.A.1000B.2851C.29031D.20202E.无法确定18. 立体组合与展开是一体的两面，只要了解组合之规则，同样可以施用于展开，反之亦然. 左下图是下列哪个立方体的展开面？（）19. x，y，z都是正整数，x<y<z，且xy+yz+xz=xyz，则x+y+z的值为（）.A.8B.9C.10D.11E.无法确定20. 鹏城杯足球赛共有4支队参赛，每两支球队比赛一场，每场胜队得3分，负队得0分，打平各得1分. 赛完各队得分分别为2分、3分、4分、5分，比赛结果前三名分别是甲、乙、丙. 则第四名负于（）.A.甲B.乙C.丙D.甲和乙E.甲或乙21. O是AB的中点，青蛙从A跳到B，称之为关于中心O作了一次“对称跳”，记为T(O).对任意给定的△ABC，一只青蛙从P0开始，T(A)至P1，然后T(B)至P2，再T(C)至P3；继续T(A)至P4，T(B)至P5，再T(C)至P6，…，以下正确的是（）.A. 青蛙将越跳越远.B .青蛙将最终跳入三角形内.C. P6与P0重合，即六次跳动回到原处.D. P12与P0重合，即十二次跳动回到原处.E. 是否跳回原地，与在三角形内还是三角形外无关.22. 李明和马丽参加一次猜数比赛. 李明被告知某三个正整数的和，马丽被告知这三个数的乘积. 李明对马丽说：“如果你的数比我的数大，我就能猜出这三个数.”马丽回答道：“可惜我的数比你的数小.”这三个数的和是（）.A.3B.4C.6D.10E.1223. 线段AK，BM，CN，DL把边长为1的正方形ABCD分成面积为S1，S2，S 3，S4的4个三角形和5个四边形，中间一个四边形的面积等于S，且S=S 1+S2+S3+S4（如图）. 则AL+BK+CM+DN=（）.A.1B.2C.3D.4E.无法确定24. 有20张卡片，黑、白各10张，分别写有数字0~9. 把它们像扑克牌那样洗过后，如下图那样排成两行. 排列规则如下：①从左至右按从小到大的顺序排列.②黑、白卡片数字相同时，黑卡片放在左边.则图中I、II、III、IV卡片上的数字可能是( ).A.3B.9C.6D.8E.725. 对于数列a1，a2，a3，⋯，已知|a1|=1，对于每一个k=1，2，⋯，|a k+1|=|a k+1|.（1）若n=2019，则|a1+a2+⋯+a n|最小可能值为x;（2）若n=2020，则|a1+a2+⋯+a n|最小可能值为y.则x+y=（）.A.2020B.100C.87D.44E.无法确定2020年超常（数学）思维与创新能力测评（初一初赛答案）姓名：_____________ 考试时间：90分钟满分：120分考试说明（1）本试卷包括25道不定项选择题（可能有几个选项正确），其中第1〜10题各4分，第 11—20题各5分，第21〜25题各6分。
学而思七年级期末试卷数学
一、选择题（每题3分，共30分）1. 下列数中，是质数的是（）A. 15B. 21C. 29D. 352. 如果一个数既是3的倍数又是5的倍数，那么这个数一定是（）A. 2的倍数B. 3和5的最小公倍数C. 15的倍数D. 以上都是3. 下列方程中，x=5是它的解的是（）A. 2x + 1 = 11B. 3x - 4 = 13C. 4x + 3 = 15D. 5x - 2 = 194. 一个长方形的长是8cm，宽是5cm，它的周长是（）A. 15cmB. 16cmC. 30cmD. 40cm5. 一个等腰三角形的底边长为10cm，腰长为8cm，那么这个三角形的面积是（）A. 32cm²B. 40cm²C. 48cm²D. 64cm²6. 下列函数中，是正比例函数的是（）A. y = 2x + 3B. y = 4xC. y = 3x²D. y = 5x - 27. 一个正方形的边长为6cm，它的对角线长是（）A. 6cmB. 8cmC. 10cmD. 12cm8. 在一次数学考试中，小明得了85分，比班级平均分高5分，那么班级的平均分是（）A. 80分B. 82分C. 85分D. 88分9. 下列数中，是负数的是（）A. -3B. 0C. 3D. 510. 一个梯形的上底长为4cm，下底长为6cm，高为3cm，那么这个梯形的面积是（）A. 12cm²B. 15cm²C. 18cm²D. 21cm²二、填空题（每题3分，共30分）11. 3的平方根是__________。
12. 下列数中，是偶数的是__________。
13. 一个数的倒数是它的__________。
14. 下列方程中，x=2是它的解的是__________。
15. 一个等腰三角形的底边长为8cm，腰长为6cm，那么这个三角形的面积是__________cm²。
学而思七年级期末数学试卷
一、选择题（每题5分，共25分）1. 下列数中，是整数的是（）A. -3.14B. 2.5C. -√2D. 02. 下列图形中，是轴对称图形的是（）A. 正方形B. 长方形C. 三角形D. 梯形3. 已知一个数的平方是25，那么这个数是（）A. ±5B. ±10C. ±15D. ±204. 在等腰三角形ABC中，AB=AC，如果AB=5cm，那么BC的长度是（）A. 5cmB. 10cmC. 15cmD. 20cm5. 已知一个数的平方根是2，那么这个数是（）A. 4B. -4C. ±4D. 0二、填空题（每题5分，共25分）6. 3的平方根是______，5的立方根是______。
7. 如果一个数的倒数是-2，那么这个数是______。
8. 下列数中，是负数的是______。
9. 下列图形中，是平行四边形的是______。
10. 一个等腰三角形的底边长是6cm，腰长是8cm，那么这个三角形的面积是______cm²。
三、解答题（共50分）11. （10分）计算下列各式的值：（1）(-3)² - 2 × (-5) + 4 × 2³（2）√(16) - √(25) + √(36)12. （10分）已知一个数的绝对值是5，写出这个数的所有可能值。
13. （10分）一个长方形的长是6cm，宽是4cm，求这个长方形的面积和周长。
14. （10分）在直角三角形ABC中，∠A=90°，AB=3cm，BC=4cm，求斜边AC的长度。
15. （10分）已知一个数的平方根是±3，写出这个数的所有可能值。
16. （10分）一个等腰三角形的底边长是8cm，腰长是10cm，求这个三角形的面积。
四、应用题（共15分）17. （5分）小明家离学校有1000米，他每分钟走80米，求小明从家到学校需要多少分钟？18. （5分）一个长方体的长、宽、高分别是5cm、3cm、4cm，求这个长方体的体积。
七年级下数学学而思试卷
试卷第1页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：________班级：________考号：________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………绝密★启用前七年级下册期中考试模拟卷（二）本次试卷题量大，适合作为考前复习使用考试时间：100分钟学校：___________姓名：___________班级：___________考号：___________题号一二三总分得分注意事项：答题前填写好自己的姓名、班级、考号等信息第Ⅰ卷（选择题）评卷人得分一．选择题（共6小题，每小题3分，共18分）1．已知，那么a=（）A．0B．0或1C．0或﹣1D．0，﹣1或12．下列说法正确的是（）A．9的平方根是3B．8的立方根是±2C．=x D．﹣一定是负数3．有一个如图的数值转换器，当输入64时，输出的是（）A．8B．2C．2D．34．已知，三个实数a，b，c在数轴上的点如图所示，|a﹣b|+|c﹣a|﹣|c+b|的值可能是（）A．2a B．2b C．2c D．﹣2a试卷第2页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………5．下列运算中，正确的是（）A ．B ．C ．D ．．6．下列选项正确的是（）A ．=±1B ．=﹣2C ．=﹣5D ．=1第Ⅱ卷（非选择题）评卷人得分二．填空题（共16小题，每小题2分，共32分）7．A 在数轴上表示的数为，则与点A 距离为的点表示的数是．8．分数（填“是”或“不是”）9．下列判断：①﹣0.3是0.09的平方根；②只有正数才有平方根；③﹣4是﹣16的平方根；④（）2的平方根是±．正确的是（写序号）．10．的绝对值是，倒数是．11．比较大小：．12．的平方根是，﹣的立方根是．13．若a 2=9，则a 3=．14．若|b ﹣1|与互为相反数，则（a +b ）2015=．15．如图，若∠BOC=42°，BO ⊥DE ，垂足为O ，则∠AOD=度．16．如图，直线a 、b 都与直线c 相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠1=∠4；④∠5+∠8=180°，其中能判断a ∥b 的条件是：．（把你认为正确的序号填在空格内）试卷第3页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：________班级：________考号：________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………17．如图：BE 平分∠ABC ，DE ∥BC ．如果∠2=22°，那么∠ADE=．18．如图，已知AB ∥CD ，∠B=20°，∠D=15°，则∠E +∠F=°．19．如图，已知AB ∥ED ，则∠B +∠C +∠D 的度数是．20．如图，已知点B 、F 、C 、E 在一条直线上，FB=CE ，AC=DF ，要使△ABC ≌△DEF 成立，请添加一个条件，这个条件可以是．21．如图，已知AB 与CD 相交于点O ，且AB=CD ，当满足时，AD=BC ．（只需填出一个条件）22．如图，已知点D ，E 是BC 上的三等分点，△ADE 是等边三角形，那么∠BAC 的度数为．试卷第4页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………评卷人得分三．解答题（共9小题）23．计算：×÷×﹣÷．24．计算：﹣2+（2）2．25．计算：+（﹣3）0．26．计算：．27．数轴上的点A 、B 、C 依次表示三个实数、π、．（1）如图，在数轴上描出点A 、B 、C 的大致位置；（2）求出A 、C 两点之间的距离．28．已知：如图，AB ⊥BD ，ED ⊥BD ，C 是BD 上的一点，AC ⊥CE ，AB=CD ，求证：BC=DE ．试卷第5页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：________班级：________考号：________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………29．已知：如图，AD 、BC 相交于点O ，OA=OD ，OB=OC ，点E 、F 在AD 上，且BE ∥CF ，求证：∠ABE=∠DCF ．30．如图，在四边形ABCD 中，AB ∥CD ，∠B=∠ADC ，点E 是BC 边上的一点，且AE=DC ．（1）求证：△ABC ≌△EAD ；（2）如果AB ⊥AC ，求证：∠BAE=2∠ACB ．试卷第6页，总6页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…………○…………内…………○…………装…………○…………订…………○…………线…………○…………31．如图，已知△ABC 以边AB 、AC 为边向形外作等边△ABD 和等边△ACE ，联结BE 、CD 相交于点G ．求证：（1）BE=CD ；（2）∠DGB=60°．模拟卷二1七年级下期中考试模拟卷（二）参考答案与试题解析一．选择题（共6小题）1．已知，那么a=（）A．0B．0或1C．0或﹣1D．0，﹣1或1【分析】由于已知，由此得到a 的算术平方根就是自己本身，根据“0的平方根是0，0的算术平方根也是0，1的算术平方根也是1”即可求解．【解答】解：∵=a，∴a=0或1．故选：B．2．下列说法正确的是（）A．9的平方根是3B．8的立方根是±2C．=xD．﹣一定是负数【分析】根据平方根和立方根的定义进行选择即可．【解答】解：A、9的平方根是±3，故A 不正确；B、8的立方根是2，故B 不正确；C、不能化简，故C 错误；D、﹣一定是负数，故D 正确；故选：D．3．有一个如图的数值转换器，当输入64时，输出的是（）A．8B．2C．2D．3【分析】根据框图得出输入x，得出，若是有理数，再次输入，若是无理数即可输出结果．【解答】解：当x=64时，第一次得出8，是有理数，再输入，第二次得出2，即可输出2，故选：B．4．已知，三个实数a，b，c 在数轴上的点如图所示，|a﹣b|+|c﹣a|﹣|c+b|的值可能是（）A．2a B．2b C．2c D．﹣2a模拟卷二。
七年级数学学而思试卷
一、选择题（每题3分，共30分）1. 下列数中，不是整数的是（）A. -3B. 0.5C. 5D. -22. 下列各数中，有最小正整数的是（）A. -3B. 0C. 3D. -53. 如果a=3，那么a²的值是（）A. 6B. 9C. 12D. 154. 下列各式中，正确的是（）A. 5 + 3 = 8B. 5 - 3 = 2C. 5 × 3 = 8D. 5 ÷ 3 = 15. 下列图形中，不是平行四边形的是（）A. 长方形B. 正方形C. 等腰梯形D. 菱形6. 下列各数中，是偶数的是（）A. 3B. 5C. 7D. 87. 下列各式中，正确的是（）A. 2a + 3 = 5B. 2a - 3 = 5C. 2a × 3 = 5D. 2a ÷ 3 = 58. 如果x=2，那么2x - 3的值是（）A. 1B. 2C. 3D. 49. 下列各数中，是质数的是（）A. 4B. 6C. 8D. 1110. 下列图形中，不是圆的是（）A. 圆B. 椭圆C. 正方形D. 矩形二、填空题（每题3分，共30分）11. 2的平方根是______。
12. 下列各数中，最小的负数是______。
13. 如果a=5，那么a³的值是______。
14. 下列各式中，正确的是______。
15. 下列图形中，是轴对称图形的是______。
16. 下列各数中，是合数的是______。
17. 如果x=3，那么3x + 2的值是______。
18. 下列各式中，正确的是______。
19. 下列图形中，是中心对称图形的是______。
20. 下列各数中，最大的整数是______。
三、解答题（每题10分，共40分）21. 简化下列各数：-5 + 3 - 2。
22. 求下列各式的值：2 × (-3) + 4。
23. 已知a=2，b=-3，求下列各式的值：(a + b) × 2。
学而思初一数学秋季班第1章+有理数的分类和相反数绝对值+提高
第一章有理数的分类和相反数绝对值本章进步目标★★★★☆☆Level 4通过对本节课的学习，你能够：1. 对有理数的认识与分类达到【初级理解】级别；2. 对数轴的认识与应用达到【初级应用】级别；3. 对相反数绝对值的认识与应用达到【高级理解】级别；VISIBLE PROGRESS SYSTEM进步可视化教学体系今天人们都能用正负数来表示两种相反意义的量．例如若以冰点的温度表示0℃，则开水的温度为+100℃，而零下10℃则记为-10℃．若以海平面为0点，则珠穆朗玛峰的高度约为+8844米，最深的马里亚纳海沟深约-11034米．在日常生活中，人们常用“+”表示收入，用“-”表示支出．可是在历史上，负数的引入却经历了漫长而曲折的道路．古人在实践活动中遇到了一些问题：如两人相互借用东西，对借出方和借入方来说，同一东西具有不同的意义；再如从同一地点，两人同时向相反方向行走，离开出发点的距离即使相同，但其表示的意义却不同．久而久之，古人意识到仅用数量表示一个事物是不全面的，似乎还应加上表示方向的符号．因此为了表示具有相反意义的量和解决被减数小于减数等问题，逐渐产生了负数．我国是世界上最早使用负数概念的国家．《九章算术》中已经开始使用负数，而且明确指出若“卖”是正，则“买”是负；“余钱”是正，则“不足钱”是负．刘徽注《九章算术》，定义正负数为“两算得失相反”，同时还规定了有理数的加、减法则，认为“正、负术曰：同名相益，异名相除．”这“同名”、“异名”即现在的“同号”、“异号”、“除”和“益”则是“减”和“加”，这些思想，西方要迟于中国八九百年才出现．印度在公元7世纪才采用负数，公元628年，印度的《婆罗摩修正体系》一书中，把负数解释为负债和损失．在西方，直到1484年，法国的舒开才给出了二次方程的一个负根．1544年，德国的史提菲把负数定义为比任何数都小的数．1545年，意大利的卡当著《大法》，成为欧洲第一部论述负数的著作．虽然负数早已出现在人们的计算过程中，但却迟迟得不到学术界的承认，直到17世纪，数学、力学、天文学获得广泛发展，使用负数可以大大简化计算，所以负数才正式进入了数学．特别是1637年，法国数学家笛卡尔发明了解析几何学，建立了坐标点，将平面点与负数、零、正数组成的实数对应起来，使负数得到了解释，从而加速了人们对负数的承认．但直到19世纪，德国数学家魏尔斯特拉斯等人为整数奠定了逻辑基础以后，负数才在现代数学中获得巩固的地位．第一关有理数的分类★★☆☆☆☆Level 2本关进步目标★★☆☆☆☆你能够熟记负数的相关概念；★★☆☆☆☆你能够对有理数进行分类。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
时，xk
=
xk−1
+
1
−
k 4([
− 4
1]
−
[
k
− 4
2
])(
取整数符
号 [a] 表示不超过实数 a 的最大整数，例如 [2.3]=2，[0.4] = 0)，则 x2017 =
．
三、解答题（共 8 题，前 6 题每题 6 分，后 2 题每题 8 分，共 52 分）
17.计算： 1 + 1 + 1 + · · · + 1 ．
21. 某电脑公司经销甲种型号电脑，今年三月份的电脑售价比去年同期每台降价 1000 元，如果卖出相同 数量的电脑，去年销售额为 10 万元，今年销售额只有 8 万元． （1）今年三月份甲种电脑每台售价多少元？ （2）为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为 3500 元，乙种电脑 每台进价为 3000 元，公司预计用不多于 5 万元且不少于 4.8 万元的资金购进这两种电脑共 15 台， 有几种进货方案？
1 × 6 6 × 11 11 × 16
51 × 56
18（. 1）解方程：x − 2x + 5 = 1 − 2x − 3 ．
6
3
（2）解方程组
x+y = 9① 3(x + y) + 2x = 33②
．
第 3 页 （共 6 页）
3x − 2y = 4 19.已知方程组 mx + ny = 7
1 [(a − b)2 + (b − c)2 + (a − c)2]，该等式从左到右的变形，不仅保持了结构的对称性，还体现了数 2 学的和谐、简洁美．
（1）若 a = 2011，b = 2012，c = 2013，你能很快求出 a2 + b2 + c2 − ab − bc − ac 的值吗？
（2）若 a − b = 3 ，b − c = 3 ，a2 + b2 + c2 = 1，求 ab + bc + ac 的值．
（2）若数轴上表示数 a 的点位于 −4 与 3 之间，求 |a − 3 |+| a + 4| 的值．
（3）当 a 取何值时，|a − 1 |+| a − 3 |+| a + 4| 的值最小，最小值是多少？请说明理由．
23. 利 用 我 们 学 过 的 知 识， 可 以 导 出 下 面 这 个 形 式 优 美 的 等 式：a2 + b2 + c2 − ab − bc − ac =
数 m 的个数为( )
A. 8
B. 6
C. 4
D. 3
第 1 页 （共 6 页）
7. 已知 a = 20162，b = 2015 × 2017，则( )
A. a = b
B. a > b
C. a < b
D. a ⩽ b
8.
x + y = a 若方程组 x − y = 4a
的解是二元一次方程 3x − 5y − 90 = 0 的一个解，则 a 的值是( )
5
5
第 5 页 （共 6 页）
24. 环岛是为了减少车辆行驶冲突，在多个交通路口交汇的地方设置的交通设施，多为圆形，它使车辆按 统一方向行驶，将冲突点转变为通行点，能有效地减少交通事故的发生，如图是该交通环岛的简化模 型 (因路段 FG 施工，禁止从路段 EF 行驶过来的车辆在环岛内通行，只能往环岛外行驶)，某时段内该 交通环岛的进出机动车辆数如图所示，图中箭头方向表示车辆的行驶方向． （1）求该时段内路段 AB 上的机动车辆数 x1． （2）求该时段内从 F 口驶出的机动车辆数 x2． （3）若 a = 10，b = 4，求该时段内路段 CD 上的机动车辆数 x3．
第 6 页 （共 6 页）
示为( )
A. 0.5 × 1011 千克 B. 50 × 109 千克
C. 5 × 109 千克
D. 5 × 1010 千克
3. 正确的算式是( ) A. (−1)2011 = −2011 B. 2(−3)2 = 36
C. −3 ÷ 1 × 2 = −3
D.
1
1 ÷ (− )
=
−1
2
22
4. 已知 a、b 两数在数轴上对应的点如图所示，下列结论正确的是( )
A. 点 C
B. 点 D
C. 点 A
D. 点 B
二、填空题（共 6 题，每题 3 分，共 18 分）
11.若多项式 3x2 + kx − 2x + 1(k 为常数) 中不含有 x 的一次项，则 k =
．
12. 设 a + b + c = 0，abc > 0，则 a + b + c 的值是
．
|a| |b| |c|
第 4 页 （共 6 页）
22. 结合数轴与绝对值的知识回答下列问题． （1）数轴上表示 4 和 1 的两点之间的距离是 3：：而 |4 − 1| = 3；表示 −3 和 2 两点之间的距离是 5： 而 | − 3 − 2| = 5；表示 −4 和 −7 两点之间的距离是 3，而 | − 4 − (−7) | = 3，一般地，数轴上表示 数 m 和数 n 的两点之间的距离等于 |m − n|．如果表示数 a 和 3 的两点之间的距离是 7，则可记为： |a − 3| = 7，那么 a =
A. 3
B. 2
C. 6
D. 7
9.
x − m < 0 若关于 x 的不等式 7 − 2x ⩽ 1
的整数解共有 4 个，则 m 的取值范围是( )
A. 6 < m < 7
B. 6 ⩽ m < 7
C. 6 ⩽ m ⩽ 7
D. 6 < m ⩽ 7
10.正方形 ABCD 在数轴上的位置如图所示，点 D、A 对应的数分别为 0 和 1，若正方形 ABCD 绕着顶点 顺时针方向在数轴上连续翻转，翻转 1 次后，点 B 所对应的数为 2；则翻转 2017 次后，数轴上数 2017 所对应的点是( )
13.如果规定符号“⊗”的意义为 a⊗b = ab ，则 2 ⊗ (−3) 的值是
．
a+b
14.已知 |m| = |2m − 3|，则 m = Nhomakorabea．
第 2 页 （共 6 页）
15.按照如图的程序计算，若输入 n 的值为 3 时，计算结果为
．
16. 在一列数
x1，x2，x3，…中，已知
x1
=
1，且当
k
⩾
2mx − 3ny = 19 与 5y − x = 3
有相同的解，求 m，n 的值．
20（. 1）因式分解：x2 − 6x − 16；
（2）因式分解：2x2 − 3xy + y2 + 8x − 5y + 6．
(
)(
)
（3）因式分解： x2 + 5x + 2 x2 + 5x + 3 − 12．
2017 秋-期中考试
初中数学·初一超常班（QG）
(考试时间：90 分钟 满分：100 分)
【注意】 本卷配有答题卡，请按照答题卡作答要求在答题卡上作答。
一、选择题（共 10 题，每题 3 分，共 30 分）
1.
1 −(− )
的相反数是( )
2
A. 2
B. 1
2
C. −2
D. − 1 2
2. 拒绝“餐桌浪费”刻不容缓，据统计全国每年浪费食物总量约 500 千万千克，这个数用科学记数法表
A. ab < 0
B. |a| > |b|
C. a + b > 0
D. b − a < 0
5. 如果代数式 3x2 − 4x 的值为 6，那么 6x2 − 8x − 9 的值为( )
A. 12
B. 3
C. 3
2
D. −3
6. 设二次三项式 x2 + mx + 6 可分解为两个一次因式的乘积，且各因式的系数都是整数，则满足条件的整