’学而思‘【2017-秋】初一数学直播超常班(全国)试卷

合集下载

学而思初一数学秋季班第2讲.有理数综合运算.尖子班.学生版

11初一秋季·第2讲·尖子班·学生版如何计算？实数7级实数初步实数6级绝对值实数5级有理数综合运算满分晋级阶梯漫画释义2有理数综合运算12 初一秋季·第2讲·尖子班·学生版知识点切片（4个） 7+2+1+1知识点目标有理数综合运算（7） 1、有理数加减法则；2、有理数加法的运算律；3、有理数减法法则；4、有理数乘法法则；5、有理数除法法则；6、有理数乘方；7、有理数混合运算的运算顺序裂项技巧（2） 1、分数裂项；2、整数裂项连锁约分（1） 1、连锁约分，简便运算整体思想（1）1、整体思想，化繁为简题型切片（6个）对应题目题型目标乘法分配律的应用例1、练习1 连续自然数的加减交替例2、练习1 有理数综合运算例3、练习2裂项例4、例5、练习3、练习4 连锁约分例6、练习5 整体思想例7、练习6有理数综合运算1．有理数加法法则：① 同号两数相加，取相同的符号，并把绝对值相加．② 绝对值不相等的异号两数相加，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值．③ 一个数同0相加，仍得这个数．2．有理数加法的运算律：①两个加数相加，交换加数的位置，和不变．a b b a +=+（加法交换律） ②三个数相加，先把前两个数相加，或者先把后两个数相加，和不变． ()()a b c a b c ++=++（加法结合律）.3．有理数减法法则：减去一个数，等于加上这个数的相反数，()a b a b -=+-.4. 有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘. 任何数同0相乘，都得0.5. 有理数除法法则：除以一个不等于0的数，等于乘以这个数的倒数.1a b a b÷=⋅，(0b ≠)两数相除，同号得正，异号得负，并把绝对值相除；0除以任何一个不等于0的数，都得0. 6. 有理数乘方知识导航知识、题型切片13初一秋季·第2讲·尖子班·学生版概念：求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂. 在n a 中，a 叫做底数，n 叫做指数.含义：n a 中，a 为底数，n 为指数，它表示a 的个数，n a 表示有n 个a 连续相乘. 特别注意:负数及分数的乘方，应把底数加上括号.7. 有理数混合运算的运算顺序： ① 先乘方，再乘除，最后加减； ② 同级运算，从左到右进行；③ 如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行.加减法为一级运算，乘除法为二级运算，乘方及开方（以后学）称为三级运算.同级运算，按从左到右的顺序进行；不同级运算，先算三级运算，然后二级，最后一级；如果有括号，先算括号里的，有多重括号时，先算小括号里的，再算中括号里的，最后算大括号里的.④ 在进行有理数运算时，先确定符号，再计算绝对值，有括号的先算括号里的数.【例1】计算：⑴735(1)(36)1246⎡⎤-+---⨯-⎢⎥⎣⎦⑵11171110()71110⨯⨯⨯++⑶111(0.25)(5)( 3.5)()2244-⨯-+⨯-+-⨯⑷371(8)32-⨯-乘法分配律的应用14 初一秋季·第2讲·尖子班·学生版⑸112571113623461236⎛⎫⎛⎫-÷+---+ ⎪ ⎪⎝⎭⎝⎭【例2】⑴填空：12344950-+-++-= ；123499100101-+-++-+= ； ⑵计算：()112341n n +-+-++-⨯.连续自然数加减交替问题15初一秋季·第2讲·尖子班·学生版【例3】计算：⑴()216123113284 2.5242523412⎛⎫-÷-⨯+++--⨯ ⎪⎝⎭⑵()22213111112190.75242222⎡⎤⎛⎫⎛⎫÷÷-+÷--⨯--⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦⑶()()3220132231313 1.20.33⎛⎫--⨯-÷--⨯÷ ⎪⎝⎭⑷()()231814511722851755⎡⎤⎛⎫⎛⎫-⨯-+-⨯----⨯-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦有理数综合运算16 初一秋季·第2讲·尖子班·学生版⑸()2323510.3534124111159650.52-÷⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⨯-÷-⨯-⨯ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦÷1.分数裂项技巧：⑴()11111n n n n =-++； ⑵()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭；⑶()()()()()1111122112n n n n n n n ⎡⎤=-⎢⎥+++++⎢⎥⎣⎦；⑷()()()()()1111222n n k n k k n n k n k n k ⎡⎤=-⎢⎥+++++⎢⎥⎣⎦.2.整数裂项技巧：⑴()()()()()()()()111121121133n n n n n n n n n n n n +=++--=++--+⎡⎤⎡⎤⎣⎦⎣⎦； ⑵()()()()()()()()()()()()1112123112311244n n n n n n n n n n n n n n n n ++=+++--=+++--++⎡⎤⎡⎤⎣⎦⎣⎦.3.连锁约分多个分数相乘通过约掉分子分母中的相同因数简便运算.思路导航分数裂项运算17初一秋季·第2讲·尖子班·学生版【例4】计算：⑴11111161111161621212626313136+++++⨯⨯⨯⨯⨯⨯； ⑵2310011(12)(12)(123)(1299)(12100)----⨯++++++++++.【例5】计算：⑴12233499100⨯+⨯+⨯++⨯；整数裂项运算18 初一秋季·第2讲·尖子班·学生版⑵1335579799⨯+⨯+⨯++⨯；⑶123234484950⨯⨯+⨯⨯++⨯⨯.【例6】计算：⑴11111111111111241035911⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++---- ⎪⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭连锁约分运算19初一秋季·第2讲·尖子班·学生版⑵11111111111113243546979998100⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+⨯+⨯+⨯+⨯⨯+⨯+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯⨯⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭【例7】 ⑴已知1111111112581120411101640+++++++=，111111112581120411101640---+--++的值为 .⑵计算：11111111111111232006232005232006232005⎛⎫⎛⎫⎛⎫⎛⎫+++⨯++++-++++⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭整体思想20 初一秋季·第2讲·尖子班·学生版学案1. 计算：1111111261220304256⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫--+-++--+--+ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦学案2. 计算：1111113243517191820+++++⨯⨯⨯⨯⨯学案3. 33221129234+==⨯⨯；33322112336344++==⨯⨯；33332211234100454+++==⨯⨯；……．⑴ 若n 为正整数，猜想3333123n ++++= ；⑵ 利用上题的结论来比较3333123100++++与()25000-的大小．学案4. 设三个互不相等的有理数，既可分别表示为1a b a +，，的形式，又可分别表示为0bba，，的形式，则20042001a b +=初一秋季·第2讲·尖子班·学生版乘法分配律的应用、连续自然数的加减交替【练习1】 ⑴ 计算：()()(){}()34|15|73-+---+-----⎡⎤⎣⎦；⑵ 计算：1111181232⎛⎫⎛⎫-÷-+- ⎪ ⎪⎝⎭⎝⎭；⑶ 计算： 135********++++-----.有理数综合运算【练习2】计算：4343(27)(2)(2)3⎡⎤⎛⎫-÷---⨯-+- ⎪⎢⎥⎝⎭⎣⎦裂项【练习3】计算：1111112612203042-----= ．【练习4】计算：2446688101012⨯+⨯+⨯+⨯+⨯.复习巩固连锁约分【练习5】计算：11111111 11111111 22334420132013⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+-+-+-⎪⎪⎪⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭整体思想【练习6】计算：()()()() 222222222222 123492350123502349+++++++-+++++++.初一秋季·第2讲·尖子班·学生版1+1=2吗？皮亚诺（Peano,Giuseppe ）意大利数学家。

学而思七年级期末数学试卷

一、选择题（每题5分，共25分）1. 下列选项中，不是同类项的是（）A. 3a^2bB. 2ab^2C. 5a^2b^2D. 4a^2b2. 下列方程中，无解的是（）A. 2x + 3 = 7B. 2x - 5 = 0C. 3x + 2 = 5D. 3x + 2 = 03. 下列不等式中，不正确的是（）A. 3x + 2 > 7B. 2x - 5 < 0C. 3x + 2 ≥ 7D. 2x - 5 ≥ 04. 下列选项中，不是正比例函数的是（）A. y = 2xB. y = 3x + 1C. y = 4x - 2D. y = 5x5. 下列选项中，不是反比例函数的是（）A. y = 2/xB. y = 3/xC. y = 4/xD. y = 5/x二、填空题（每题5分，共25分）6. 已知一元二次方程x^2 - 3x + 2 = 0，则方程的解为______。

7. 已知等差数列{an}的首项为2，公差为3，则第10项an = ______。

8. 已知平行四边形的对角线互相平分，且对角线长分别为8cm和6cm，则平行四边形的面积是______cm^2。

9. 已知一个长方体的长、宽、高分别为2cm、3cm、4cm，则长方体的体积是______cm^3。

10. 已知一个圆的半径为5cm，则圆的面积是______cm^2。

三、解答题（每题10分，共30分）11. 解方程：3x^2 - 5x + 2 = 0。

12. 求等差数列{an}的前10项和。

13. 已知一个等边三角形的边长为6cm，求该三角形的面积。

四、应用题（每题10分，共20分）14. 小明骑自行车从家到学校，以每小时15km的速度匀速行驶，若小明从家出发后40分钟到达学校，则小明家到学校的距离是多少千米？15. 小华在超市购买了一些苹果和香蕉，苹果的价格是每千克10元，香蕉的价格是每千克5元。

小华共花费了60元，且苹果的重量是香蕉的两倍。

七年级“学而思杯”模拟试题及答案

“学而思杯”模拟题七年级数学试卷姓名：考号：年级：学校：考生须知：1、试卷分为填空题和解答题两部分，其中第Ⅰ卷为填空题，第Ⅱ卷为解答题。

2、试卷分值满分100+10分，考试时间100分钟，其中填空题60分，解答题40分，附加题10分，考试前请认真审题，看清题目，按要求认真作答。

一、填空题：（每小题4分，共15题，共计60分）１．已知3x <-，化简：|3|2|1|||x +-+= ．2．方程组||12,||6x y x y +=⎧⎨+=⎩的解的个数为．３.如图：直线l 上依次分布着A 、B 、C 、D 、E 、F 六点，以这六点为端点的所有线段的长度之和为46厘米，以B 、C 、D 、E 四点为端点的所有线段的长度之和为11厘米，那么线段AF 的长度为______厘米．FEDCBAl4．拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉成了许多细的面条，如图所示：…这样捏合后第次可拉出128根面条．5．直角边长分别为3cm 和4cm 的三角形内部有一点p ，已知p 点到三角形其中两条边的距离分别为3.2cm 和0.5cm ，那么该点到第三条边的距离为_______cm ．6．在568后面补上三个数字，组成一个六位数，使它能被3、4、5分别整除。

符合这些条件的六位数中，最小的一个是．7．求和：242424241231001111221331100100++++=++++++++ ．8．化简231(1)1()n x x x x x -⎡⎤+-+-++-=⎣⎦ ．9．A 、B 、C 三个微型机器人围绕一个圆形轨道高速运动，它们顺时针同时同地出发后，A 在2秒钟占追上B ，2.5秒钟时追上C 。

当C 追上B 时，C 和B 运动路程的比是32∶。

问第1分钟时，A 围绕这个圆形轨道运动了圈？10．古时候有两位贩卖家畜的商人把他们共有的一群牛卖掉，每头牛卖得的钱数正好等于牛的头数.他们把所得的钱买回了一群大羊，每只大羊10元，剩下的钱正好搭配买了一只小羊.他们平分这些羊，结果第一人多得了一只大羊；第二人得到了那只小羊.为了公平，第一人应找补给第二人元钱.11．某个小组有12名学生，将120张卡片分给这些学生，使得每个人拥有的卡片数各不相同并且不超过20张，那么这12个人中拥有卡片不多于10张的最多有______人．12．有一串数：2003-，1999-，1995-，1991-…，按一定的规律排列，那么这串数中前个数的和最小．13．已知a 、b 都是整数，并且()5a b +是一个四位正整数，()7a b -也是一个四位正整数，那么22a b +=______．14．张老师购买一套住宅，有两种分期付款方式，一种是第一年付八万元，以后每年付款两万元；另一种是前一半时间每年付款两万八千元，后一半时间，每年付款两万两千元，两种付款方式中付款钱数和付款时间都相同.如一次性付款，可少付房款两万五千元.现在王老师一次性付款，要付房款万元.15．如图，三角形ABC 的面积为a ,:2:1BD DC =，E 是AC 的中点，AD 与于点P ，那么四边形PDCE 的面积为_______________．(用含a二、解答题（每小题10分，共4题，共计40分）16．计算下列式子的值：222222129911005000220050009999005000++⋅⋅⋅+-+-+-+．17．某学校的初三年级的同学要从8名候选人中投票选举三好学生，规定每人必须从这8名候选人中任意选两名，那么至少有多少人参加投票，才能保证必有不少于5名同学投了相同两个候选人的票？18.如图所示，剪一块硬纸片可以做成一个多面体的纸模型（沿虚线折，沿实线粘）。

2023 年第四届超常(数学)思维与创新能力测评初一年级数学真题

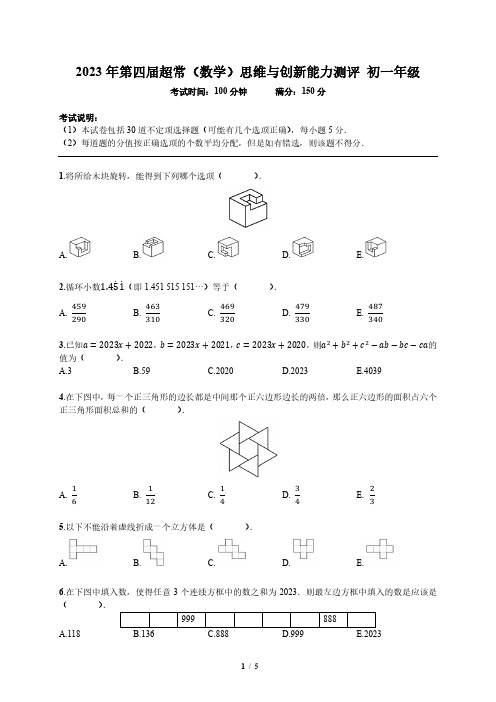
2023年第四届超常（数学）思维与创新能力测评初一年级考试时间：100分钟满分：150分考试说明：（1）本试卷包括30道不定项选择题（可能有几个选项正确），每小题5分．（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分．1.将所给木块旋转，能得到下列哪个选项（）．A. B. C. D. E.2.循环小数1.451（即1.451 515 151…）等于（）． A. 459290B.463310C.469320D. 479330E.4873403.已知a =2023x +2022，b =2023x +2021，c =2023x +2020，则a 2+b 2+c 2−ab −bc −ca 的值为（）．A.3 B.59 C.2020 D.2023 E.40394.在下图中，每一个正三角形的边长都是中间那个正六边形边长的两倍，那么正六边形的面积占六个正三角形面积总和的（）．A.16B.112C.14D.34E.235.以下不能沿着虚线折成一个立方体是（）．A. B. C. D. E.6.在下图中填入数，使得任意3个连续方框中的数之和为2023．则最左边方框中填入的数是应该是（）．A.1187.已知202009=102000∙409∙2n，则n的值为（）．A.1991B.2000C.2009D.4018E.50008.如图，某城有一组十分奇怪的限速规定：在离城1km处有一个120km/h的标牌，在离城12km处有一个60km/h的标牌，在离城13km处有一个40km/h的标牌，在离城14km处有一个30km/h的标牌，在离城15km处有一个24km/h的标牌，在离城16km处有一个20km/h的标牌，如果你从120km/h的标牌处出发一直以限定时速行驶，那么需要（）才能到达该城．A.30sB.1min13.5sC.1min42sD.2min27sE.3min9.如图所示，三个正方形以顶点相连接在一起，图中已给出若干角的度数，则x的值是（）．A.41B.42C.43D.44E.4610.一辆自行车的链条在具有48个齿的前链齿轮上运行，通常经过具有18个齿的后轮轴的链齿轮．当后链齿轮每旋转一整圈时，踏板转过的角度是（）．A.135°B.360°C.960°D.120°E.6712°11.如图，一个立方体的八个角都被切去，形成一些三角形面．将该图形的所有24个角都用对角线连起来，这些对角线中穿过图形内部的共有（）条．A.84B.108C.120D.142E.24012.把一个三位数首位前和末位后添写上1，这样得到的五位数比原来的三位数增加14789．则原来三位数的三个数字之和是（）．A.10B.9C.8D.7E.613. Ⅰ号混合液由柠檬汁、油和醋以1:2:3的比例配成，Ⅱ号混合液由同样三种液体以3:4:5的比例配成，将两种混合液倒在一起后，新的混合液的比例不可能是（）．A.2:5:8B.4:5:6C.3:5:7D.5:6:7E.7:9:1114.如图所示的网球场中有（）个长方形．A.19B.29C.23D.30E.3115.已知|x−1|+|x−2|=1，则x的值（）．A.只能为1B.只能为2C．可能为任何实数 D.为满足1≤x≤2的一切实数E.以上都不对16.下图是一张城市的道路平面图，除了一条短对角线外，道路全是东西向或南北向的．由于一条路的修补而不可能从点X通过．从P到Q的所有可能走的路线中，有些路线是最短的．则这样的最短路线有（）条．A.4B.7C.9D.14E.1617.甲、乙一起工作，甲每工作1天休息2天，乙每工作1天休息3天．已知第一天他们都在工作，最后一天乙肯定在工作．甲、乙同时休息时间比同时工作时间多128天．则他们从第一天到最后一天经过了（）天．A.180B.308C.309D.312E.50018.要使关于x的方程ax−1=x+a无解，则a=（）．A.-1B.0C.1D.2E.以上都不对19.小刚和月月搭乘某航空公司的飞机从A地飞往B地，但因为他们的行李超出了航空公司规定的重量，所以要求他们支付附加费．航空公司收费方法是对超出规定的重量每千克收取相同的费用．小刚付了60元，月月付了100元．他们一共有52kg的行李，如果小刚自己带着两人的全部行李走，他将必须付340元．每人最多可带（不需要付附加费的）行李（）kg．A.20B.15C.12D.18E.3020.一个4×4的反幻方是指将数1~16填入4×4方格表内，使得每行、每列、每条对角线上的数之和，经排序后恰好形成十个连续的正整数．如图是一个尚未完成的反幻方，则星号“*”所在方格内应填入（）．A.1B.2C.15D.16E.以上都不对21.某学校新建5个教室，平均每班减少6人．如果再建5个教室，那么平均每班又减少4人．假设学生总数保持不变，这个学校可能有（）名学生．A.560B.600C.650D.720E.80022.在一个2023边形（可以是凹多边形）的内角中，锐角至多有（）个．A.2023B.672C.944D.1345E.134923.在一列数1，2，3，…，10000中，有（）个数恰好包含两个相邻的数字9．例如：993，1992和9929就是这样的数，而9295或1999则不是．A.270B.271C.280D.123E.26124.从1970年起小红开始收集日历且以后每年都这样做，直到以后每一年至少可用一本已经收集到的日历来代用时为止．则必须收集日历的最后年份是（）年．A.1983B.1984C.1997D.2023E.以上都不对25.100个正整数之和为101101，则它们的最大公约数的最大可能值是（）．A.101B.1100C.1001D.2002E.1001026.如图所示，你有一些白色的1×12×1瓦片．当用这些瓦片以紧贴邻边的方式来覆盖一个3×1的矩形时，共可以设计出4种颜色方案（WWW，BWW，WBW，WWB）．那么如果用这些瓦片来覆盖一个10×1的矩形，将可以设计出（）种颜色方案．A.47B.89C.155D.286E.30027.已知A，B，C，D，E，F，G，H，I是9个互不相同的非零数字，满足：A除以B余C，D除以E余F，G除以H余I，那么ABC+DEF+GHI的结果是（）．A.1368B.1458C.1188D.2547E.195328.令s为真分数，即s<t，且为最简分数．若t的值为2到9，s，t为正整数，则符合条件的不同的真t分数有（）．A.26B.27C.28D.30E.3629.有27个同样大小的小正方体，每个小正方体的六个面上写着一个相同的数，且恰为1~27，用这27个小正方体拼成如图所示的大正方体．请根据如图所示的数据以及下面所给出的条件推断，从六个方向都看不见的小正方体的面上所写的数是（）．①数9，13和16在同一条直线上．②数22在9和6之间．③17紧挨着5和13，但与9不相邻．④14紧挨着24和27．⑤数20在14的上面．A.22B.20C.17D.9E.530.一个棱长为6的正方体被切割成若干个棱长为整数的小正方体，若这些小正方体的表面积之和是切割前的大正方体的表面积的10倍，则切割成的小正方体中，棱长为1的小正方体的个数可能为3（）．A.15B.24C.42D.56E.60。

学而思初中数学试卷答案

1. 下列哪个数是负数？A. -5B. 5C. 0D. -3.5答案：A2. 若a > b，那么下列哪个不等式一定成立？A. a + 2 > b + 2B. a - 2 > b - 2C. a / 2 > b / 2D. a 2 > b 2答案：A3. 下列哪个方程的解是x = 3？A. 2x + 1 = 7B. 3x - 2 = 7C. 4x + 1 = 7D. 5x - 2 = 7答案：B4. 若一个等腰三角形的底边长为8，腰长为10，那么该三角形的周长是多少？A. 24B. 26C. 28D. 305. 下列哪个图形是轴对称图形？A. 正方形B. 长方形C. 等腰三角形D. 平行四边形答案：A二、填空题（每题5分，共25分）6. 若a = 5，b = 3，则a - b = ________。

答案：27. 下列数列中，下一个数是_______。

1, 3, 5, 7, 9, ...答案：118. 下列分数中，分子与分母相差最大的是_______。

A. 1/2B. 2/3C. 3/4D. 4/5答案：C9. 下列哪个数的平方根是2？A. 4B. 9C. 16答案：A10. 若一个数的倒数是1/3，那么这个数是_______。

答案：3三、解答题（每题10分，共40分）11. 解方程：2x - 3 = 7答案：x = 512. 计算下列表达式的值：(5 + 3) 2 / (4 - 2)答案：913. 已知一个等腰三角形的底边长为10，腰长为8，求该三角形的面积。

答案：4014. 已知一个平行四边形的底边长为6，高为4，求该平行四边形的面积。

答案：24四、附加题（10分）15. 下列哪个数是质数？A. 15B. 21C. 23D. 27答案：C总结：本试卷涵盖了初中数学的基础知识，包括实数、方程、几何图形等。

通过解答这些问题，可以检验学生对数学知识的掌握程度。

希望同学们在今后的学习中继续努力，不断提高自己的数学水平。

奥数培优超常思维竞赛初一年级数学试卷及答案

超常思维竞赛数学初一年级考试时间：100 分钟满分 150 分1. 一个正三角形全涂上黑色，每次做一个变换，即把正黑三角形分成四个全等的小三角形，中间的小正三角形涂上白色(如图). 经过五次变换后，仍是黑色的部分占整个三角形的（）.A.(12)5B.(23)5C.(34)5D.(45)5E.132.在某种计算机语言(例如 APL)中，当一个代数式中没有圆括号时，式中的运算规定为从右到左逐一进行.例如，在这种语言中的a ×b −c ，就相当于在通常代数记号中的a(b −c) . 现在用这种语言书写了一个式子：a ÷b −c +d ，那么用通常代数记号表示时，它应是（）.A.ab −c +dB.ab −c −dC.d+c−b aD.ab−c+dE.ab−c−d3.冥王星有三颗卫星，卫星1绕冥王星一周为6天，卫星2绕冥王星一周为10天，卫星3绕冥王星一周为15天. 从图中所示的位置开始，三颗卫星最少需要（）天才能同时回到原来的位置.A.20B.30C.60D.100E.3604.如图所示，等腰△ABC 中，AB =AC ，△DEF 为内接正三角形，∠BFD =α，∠ADE =β，∠FEC =γ，则（）.A.β=α+γ2B.β=α−γ2C.α=β−γ2D.α=β+γ2E.以上都不对5.若(r +1r )2=3,则r 3+1r 3=( ). A.−1B.0C.1D.2E.36.一个裁缝在一棵树下遇见一只乌龟. 当乌龟是裁缝现在年龄时，裁缝只有其现在年龄的14. 当树是乌龟现在年龄时，乌龟只有其现在年龄的17. 若三者现在年龄之和为264岁，则乌龟的现在年龄为（）岁.A.55B.66C.77D.88E.997.循环小数0.328181818181⋯可以被等同表示为m n，m 与n 为互素正整数，则m +n 的值为( ) A.1000B.1461C.2021D.19181E.无法确定8.一个正方形的地面用同样大小的正方形瓷砖铺满，两条对角线上铺黑色的，其他地方铺白色的，如图所示. 如果铺满地面共用101块黑色的瓷砖，那么，铺满地面所用瓷砖的总块数是（）.A.121B.625C.676D.2500E.26019.在锐角△ABC 中，三个内角的度数都是质数，以下说法错误的有( ).A.只有一个，且为等腰三角形 B.至少有两个，且都为等腰三角形C.只有一个，但不是等腰三角形D.至少有一个，其中有非等腰三角形E.这样的三角形根本不存在10.有四个数，每次从中挑选三个数，求其平均数，再把第四个数加上.因为每次可留下一个不同的数不选，因此这样的操作有四种不同的方式. 已知得出的四个结果为7，21，23与29，则原来的四个数中最大的数是（）.A.18B.19C.20D.21E.以上都不对11.如图所示，在一个4×6的球台上，有两个小球P和Q. 若小球P依次经过球台边AB，BC，CD和DA反弹后，恰好击中小球Q. 则小球P击出时，瞄准应是AB边上的(图中A k(k=1，2，…，5)为AB边的六等分点)（）.A.A2B.A3C.A4D.A5E.其他点12. 音乐家勃拉姆斯曾经给一位名为Agade(阿加特)的歌唱家写过一首六重奏.如果字母I不为零，当如下加法算式成立时，S+I+N+G=（）.(相同的字母代表相同的数字，不同的字母代表不同的数字.)A.20B.21C.22D.24E.2613.如图所示，在各边都相等的五边形ABCDE中，∠ABC=2∠DBE，那么∠ABC=（）.A.45°B.60°C.75°D.90°E.以上都不对14.在英国的康沃尔语(Cornish)中，对于200以下的数字读法都是采取二十进制的. 如果十进制中的147在二十进制中的读音是“seyth ha seyth ugens”，而十进制中的49在二十进制中的读音是“naw ha dew ugens”，那么二十进制中读音是“dew ha naw ugens”的数指的是十进制中的（）.A.168B.180C.182D.186E.以上都不对15.△ABC的三个内角∠BAC，∠ABC，∠ACB的外角依次记为α，β，γ，若β=2∠ABC，α−γ=40°，则∠BAC=（）.A.30°B.40°C.45°D.60°E.以上都不对16.某次数学竞赛共有12道试题，答对者每题得8分；未作答者每题得3分；答错者每题得0分. 小威在此次竞赛中的得分是35分，则他在此次竞赛中最多答错（）道题.A.4B.5C.6D.7E.以上都不对17.A，B，C 在距离为dm的跑道上等速赛跑，到终点时，A超过B为20m，B超过C为10m，A超过C为28m，则d=（）m.A.100B.150C.200D.400E.以上都不对18.如图所示，一个线快用完了的绕线筒，由绕在它上面的细线沿着很平的表面拉动.它的内筒的直径是5cm，外轮的直径是10cm. 假设只有滚动而没有滑动，当细线的端点移动12cm时，绕线筒将移动（）cm.A.8B.10C.8πD.10πE.以上都不对19.1898年6月9日英国强迫清政府签约，将香港975.1平方公里土地租借给英国99年. 1997年7月1日香港回归祖国，中国人民终于洗刷了百年耻辱. 已知1997年7月1日是星期二，那么，1898年6月9日是星期（）.A.一B.二C.六D.日E.以上都不对20.分数3713可以写成形式2+1x+1y+1 z其中(x，y，z)=（）.A.（1，5，3）B.（1，5，4）C.（1，4，3）D.（2，2，3）E.以上都不对21. 已知一数列有58项，每项都具有p+n型，其中p代表小于或等于61的所有质数2， 3，5，…，61之积，而n依次取2，3，4，…，59之值，设N为此数列中出现质数的数目，则N=（）.A.0B.1C.2D.3E.422. 如图所示，在大房间的一面墙壁上，边长为15cm的正六边形A横排20片和以其一部分所形成的梯形B，三角形C，D，E，菱形F等六种瓷砖毫无空隙地排列在一起. 已知墙壁高3.3m，仔细观察各层瓷砖的排列特点，其中菱形F瓷砖需使用（）片.A.180B.190C.200D.210E.以上都不对23.如图所示，3条直线p，q，r中的每条直线把此图分成2个具有相同面积的区域，则X，Y的大小关系是（）.A.X>YB.X≥YC.X<YD.X≤YE.以上都不对24.矩形PQRS按下图的方式分成9个大小都不相同的正方形(注意这是示意图，未按比例画出).所有正方形的边长都等于单位长的整数倍，其中最小的是一个2×2的正方形. 次小的正方形的边长等于（）个单位长.A.1B.2C.3D.4E.以上都不对25.小明有2cm×1cm×1cm的砖块若干块，打算用它们来构造一个大的积木. 当小明拼到如图所示的形状时，已用尽了所有的砖块，则小明原来有（）块砖块.A.50B.52C.54D.56E.以上都不对26.如图所示，点M是△ABC两个内角平分线的交点，点N是△ABC两个外角平分线的交点，已知∠CMB∶∠CNB=3∶2，则∠CAB的度数是（）.A.30°B.35°C.40°D.45°E.以上都不对27.一只狗追一只兔子，狗跳6次的时间兔子只跳了5次，狗跳4次的距离和兔子跳7次的距离相等. 兔子跑出5.5千米后狗开始在后面追，则兔子再跑出（）千米的路程时被狗追上.A.4B.4.5C.5D.5.5E.以上都不对28.有九个分数的和为1，它们的分子都是1，其中的五个分数是13，17，19，111，133，又其余四个分数的分母个位数字均为5，则这些分数的分母分别是( )A.5，15，35，105B.5，25，35，135C.5，15，45，385D.5，25，105，385E.5，15，25，45，13529.凸四边形ABCD中，∠ADB=∠ABC=105°，∠DAB=∠DCB=45°，若A点到直线BD的距离为101，则线段CD的长度是（）.A.101B.151.5C.202D.303E.以上都不对30.平行四边形内的一点到四条边的距离分别是1，2，3，4，则这样的平行四边形面积的最小值为（）.A.21B.24C.25D.20E.以上都不对超常思维竞赛数学初一年级答案考试时间：100分钟满分150分。

学而思数学初中测试题1答案

初一年级第一学期期中测试题一答案第Ⅰ卷一选择题（每小题3分共30分）题号 1 2 3 4 5 6 7 8 9 10 答案ABBDDCBCBA二填空题（每小题3分共18分）题号 11 12 13 14 15 16答案-312658-5或-17781 第15题只写一个答案2分三解答题17 （1） ()()42025-÷+⨯-解：原式()510-+-= ----------4分（此步前后计算各2分） 15-= ----------6分（2） ()7221543-⨯+⎪⎭⎫⎝⎛-÷-解：原式()728154-⨯+⎪⎭⎫ ⎝⎛-÷-= ----------2分()()14404-+--= ----------4分（此步两个计算各1分） 30= ---------6分18 （1）5423--+a a解：原式5243-+-=a a ----------2分3--=a ----------6分（此步两个计算各2分）（2） ()()22532x x --+解：原式22562x x +-+= ----------4分（此步两个计算各2分） 56222-++=x x ----------5分 132+=x ----------6分 19 （1） x x 23163-=+解： 63123-=+x x ----------2分 255=x ----------4分 5=x ----------6分（2）174333x x -=+ 解： 433731+=-x x ----------2分 72=-x ----------4分 27-=x ----------6分或： 1279x x -=+----------2分7129x x -=+----------3分621x -=----------4分27-=x ----------6分 20 解：原式y x xy y x xy y x 22243322-+-+= ----------2分 xy xy y x y x y x 32432222++--= ----------3分 xy y x 552+-= ----------4分当1x =-，1y =时，原式()()1151152⨯-⨯+⨯-⨯-= ----------5分()55-+-= ----------7分10-= ----------8分21 解：（1）（标识正确一个点得1分，本小题共3分）（2）小明家与小刚家相距：()()千米734=-- ----------5分（3）这辆货车此次送货共耗油：()()升5.255.135.85.14=⨯+++ ----------7分答：小明家与小刚家相距7千米，这辆货车此次送货共耗油25.5升。

学而思初一数学寒假班第7讲阶段测试教师版(培优梳理—目标中考高分班)

数学测试卷（培优梳理-目标中考高分班）一、选择题（每题3分，共30分，将答案填在下面的空格处） 1. 下列方程组中，不是二元一次方程组的是（）A ．3251x y x +=⎧⎨=⎩B ．267x y x y -=⎧⎨+=⎩C ．1019x x y =⎧⎨-=⎩D ．153x xy =⎧⎨=⎩2. 下列说法正确的是（）A. 2(1)-的平方根是1-B. 1-的平方根是1-C. 2-是8-的立方根D. 16的平方根是43. 下列运算正确的是（）A. 321a a -= B. 842x x x -=C.2- D. ()326328x y x y -=-4. 若方程组422x yx y a +=⎧⎨-=⎩中的x 是y 的2倍，则a 等于（）A ．9-B ．8C ．7-D ．6-5. 一个样本有20个数据：3531333537393538403936343537363234353634，，，，，，，，，，，，，，，，，，，，其中众数为（）A. 34B. 35C. 36D. 376. 为了从甲、乙、丙、丁四位同学中选派两位选手参加数学竞赛，老师对他们的五次数学测验成绩进行统计，得出他们的平均分均为85分，且、、、．根据统计结果，派去参加竞赛的两位同学是（）A ．甲、乙B ．甲、丙C ．甲、丁D ．乙、丙7.等于（）A. 3.14π-B. 3.14π-C. 3.14π+D. (3.14)π-+8. 若关于x 、y 的二元一次方程组59x y kx y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解，则1002=甲s 1102=乙s 1202=丙s 902=丁sk 的值为（）A. 34-B. 34C. 43D. 43-9. 下面是某同学在一次测验中的计算摘录，其中正确的个数有（）① 236a a a ⋅=；② ()333ab a b -=-；③3332a a a +=； ④ ()2212366x x x -+=-；⑤()()212152n m x y x y +--⋅-=52120n m x y +--⑥()()()2x x y y x y x y ---=-A ．1个B ．3个C ．4个D ．5个10. 已知106a =，102b =，则210a b +的值为（）A ．8B ．36 C. 38． D ．72二、填空题（每题3分，共24分，将答案填在下面的空格处）11. 13的小数部分是 .12.21(2013)0x y ++-=，则y x = .13. 已知a 、b 、c 是三个有理数，且a 与b 的平均数是127，b 与c 的和的三分之一是78，c 与a 的和的四分之一是52，那么a ，b ，c 的平均数是 .14. 如果21x y =⎧⎨=⎩是方程75ax by bx cy +=⎧⎨+=⎩的解，则a 与c 的关系是 .15. 若21m n =+，则2244m mn n -+的值是 .16. 若1235x y z ++=，3217x y z ++=，则111x y z ++= .17. 已知3,1a b ==，则()()(2)a b a b b b +-+-= .18. 如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽边长分别是2和1的长方形．现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片张才能用它们拼成一个新的正方形．三、解答题（每题4分，共16分）19. 已知2,3x y a a ==，求x y a +与2x y a -的值.20. 解方程组37528x y x y -=⎧⎨+=⎩21. 解方程组::3:4:5238x y z x y z =⎧⎨+-=-⎩22. 先化简再求值：()()()()222424x y x y x y y x xy +-+-++. 其中1x =，1y =-.四、解答题（每题6分，共30分）23. 已知21a -的平方根是3±，39a b +-的立方根是2，c 求2a b c++的算术平方根．24. k 为何值时，关于x y ，的方程组35223x y k x y k -=+⎧⎨-=⎩的解的和为20．25. m 取何整数值时，方程组2441x my x y +=⎧⎨+=⎩的解x y ，都是整数？26. 如图a 是一个长为2m 、宽为2n 的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图b 形状拼成一个正方形．⑴你认为图b 中的阴影部分的正方形的边长等于多少？⑵观察图b 你能写出下列三个代数式之间的等量关系吗？代数式：()()22,,m n m n mn +-. ⑶已知7,6m n mn +==，求()2m n -的值．27. 为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）. 已知A 、B 两组捐款户数的比为1 : 5.请结合以上信息解答下列问题.(1) a= ，本次调查样本的容量是； (2) 先求出C 组的户数，再补全“捐款户数分组统计图1”；(3) 若该社区有500户住户，请根据以上信息估计，全社区捐款不少于300元的户数是多少？组别捐款额（x ）元户数 A 1≤x <100 a B 100≤x <200 10 C 200≤x <300 D 300≤x <400 Ex ≥400捐款户数分组统计图1捐款户数分组统计图2五、附加题（每题10分，共20分）28. 已知关于x 、y 的二元一次方程(1)(2)520a x a y a -+++-=，当a 每取一个值时，就有一个方程，而这些方程有一个公共解，求出这个公共解.29．古运河是扬州的母亲河，为打造古运河风光带，现有一段长为180米的河道整治任务由A 、B 两个工程队先后接力完成．A 工程队每天整治12米，B 工程队每天整治8米，共用时20天．⑴根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：甲：128x y x y ⎧+=⎪⎨+=⎪⎩乙：128x y x y⎧+=⎪⎨+=⎪⎩根据甲、乙两名同学所列的方程组，请你分别指出未知数x ，y 表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：甲：x 表示，y 表示；乙：x 表示，y 表示；⑵求A 、B 两工程队分别整治河道多少米？（写出完整的解答过程）学而思学校初一寒假数学测试卷参考答案三、解答题：每题4分，共16分． 19. 6x y x y a a a +=⋅=()2243x y x y a a a -=÷=20.21x y =⎧⎨=-⎩ 21.6810x y z =⎧⎪=⎨⎪=⎩22. 原式22222448482x y x xy y xy xy =-+-+++2252x xy =+把1x =，1y =-代入原式527=+=．四、解答题：每小题6分，共30分． 23. 根据题意，可得219,398a a b -=+-=；故5,2a b ==；可得c=7；则216a b c ++=；则16的算术平方根为4．24. 这是含有字母的二元一次方程组，求解此类题需将字母看作常数求解方程组的解，然后再根据题目条件求出字母的值．解方程组35223x y k x y k -=+⎧⎨-=⎩得：264x k y k =-⎧⎨=-⎩又因为：20x y +=，即：31020k -=所以：10k =．25. 把m 作为已知数，解方程组得81828x m y m ⎧=-⎪⎪-⎨⎪=⎪-⎩∵x 是整数，∴8m -取8的约数1248±±±±，，，． ∵y 是整数，∴8m -取2的约数12±±，．取它们的公共部分，812m -=±±，．解得97106m =，，，．经检验97106m =，，，时，方程组的解都是整数．26. ⑴m n -．⑵()()224m n m n mn +=-+．⑶()()224494625m n m n mn -=+-=-⨯=．27.⑴2，50；⑵5040%20⨯=，C 组的户数为20 ，补图见图2． ⑶∵ 500(28%8%)180⨯+=，∴ 根据以上信息估计，全社区捐款不少于300元的户数是180．五、附加题：每题10分，共20分28. 原方程变为(2)(25)0a x y x y +----=，由于公共解与a 无关，∴20250x y x y +-=⎧⎨--=⎩， ∴31x y =⎧⎨=-⎩29. （1）甲：20128180x y x y ⎧+=⎪⎨+=⎪⎩乙：18020128x y x y⎧+=⎪⎨+=⎪⎩捐款户数分组统计图1甲：x表示A工程队整治的天数，y表示B工程队整治的天数；乙：x表示A工程队整治的米数，y表示B工程队整治的米数；（2）按甲同学的思路解答：∴515 xy=⎧⎨=⎩1260,8120x y∴==即A工程队整治河道60米，B工程队整治河道120米.。

学而思试卷初中数学答案

一、选择题1. 下列哪个数是正数？（）A. -5B. 0C. 3D. -3答案：C解析：正数是指大于0的数，所以选项C是正确答案。

2. 一个等腰三角形的底边长为6cm，腰长为8cm，那么这个三角形的面积是多少平方厘米？（）A. 24B. 30C. 36D. 48答案：B解析：等腰三角形的面积可以用公式S = (底边长× 高) ÷ 2来计算。

首先，我们可以通过勾股定理求出高，即高为√(腰长^2 - (底边长÷ 2)^2) = √(8^2 - (6 ÷ 2)^2) = √(64 - 9) = √55。

所以，面积S = (6 × √55) ÷ 2 = 3√55 ≈ 30。

3. 下列哪个方程的解是x = 3？（）A. 2x + 1 = 7B. 3x - 2 = 7C. 4x + 3 = 11D. 5x - 4 = 11答案：A解析：将x = 3代入各个选项中的方程，发现只有选项A满足2x + 1 = 2×3 + 1 = 7。

4. 下列哪个图形的对称轴有两条？（）A. 等边三角形B. 等腰梯形C. 正方形D. 长方形答案：C解析：对称轴是指将图形对折后，两部分完全重合的直线。

等边三角形和等腰梯形都只有一条对称轴，而正方形有两条对称轴，分别是两条对角线。

5. 下列哪个分数约分后等于1/3？（）A. 2/6B. 3/9C. 4/12D. 5/15答案：A解析：将各个选项中的分数约分，发现只有选项A的2/6可以约分为1/3。

二、填空题1. 5 + 3 × 2 - 4 = （）答案：12解析：根据数学运算的优先级，先进行乘法运算，得到5 + 6 - 4，再进行加减运算，得到最终结果12。

2. 一个数的平方根是-2，那么这个数是（）答案：4解析：一个数的平方根是-2，那么这个数必须是负数，且其平方等于4，所以这个数是4。

3. 一个长方体的长、宽、高分别是3cm、4cm、5cm，那么这个长方体的体积是（）答案：60立方厘米解析：长方体的体积可以用公式V = 长× 宽× 高来计算，所以V = 3 × 4 × 5 = 60立方厘米。

学而思初一数学秋季班第5讲.找规律、程序运算和定义新运算.基础-提高班.教师版

1初一秋季·第5讲·基础-提高班·教师版生活水平提高了满分晋级阶梯漫画释义5找规律、程序运算和定义新运算代数式3级找规律、程序运算和定义新运算代数式2级整体思想求值代数式1级整式的概念及加减运算2初一秋季·第5讲·基础-提高班·教师版题型切片（六个）对应题目题型目标数列的规律例1；练习1 数表的规律例2；练习2 图形的规律例3；练习3 算式的规律例4；练习4 程序运算例5、例6：练习5 定义新运算例7；练习6找规律解题思维过程：从简单、局部或特殊情况入手，经过提炼、归纳和猜想，探索规律，获得结论.有时候还需要通过类比联想才能找到隐含条件.一般有下列几个类型：⑴一列数的规律：把握常见几类数的排列规律及每个数与排列序号n 之间的关系.⑵一列等式的规律：用含有字母的代数式总结规律，注意此代数式与序号n 之间的关系. ⑶图形（图表）规律：观察前几个图形，确定每个图形中图形的个数或图形总数与序号n 之间的关系.⑷图形变换的规律：找准循环周期内图形变换的特点，然后用图形变换总次数除以一个循环变换周期，进而观察商和余数.⑸数形结合的规律：观察前n 项（一般前3项）及利用题中的已知条件，归纳猜想一般性结论.常见的数列规律：⑴ 1，3，5，7，9，… ，21n -（n 为正整数）． ⑵ 2，4，6，8，10，…，2n （n 为正整数）． ⑶ 2，4，8，16，32，…，2n （n 为正整数）． ⑷ 2，5，10，17，26，…，21n +（n 为正整数）． ⑸0, 3, 8, 15， 24，…，21n - （n 为正整数）． ⑹ 2， 6， 12， 20，…， (1)n n +（n 为正整数）． ⑺x -，x +，x -，x +，x -，x +，…，(1)n x -（n 为正整数）．⑻x +，x -，x +，x -，x +，x -，…，1(1)n x +-（n 为正整数）． ⑼特殊数列：①斐波那契数列：1，1，2，3，5，8，13，…，从第三个数开始每一个数等于与它相邻的前两个数的和.②三角形数：1,3,6,10,15,21，…，(1)2n n +.【例1】 ⑴ 观察下列一组数：12，34，56，78，…，它们是按一定规律排列的．那么这一组数的第k 个数是．（k 为正整数）数列的规律思路导航题型切片3初一秋季·第5讲·基础-提高班·教师版⑵瑞士中学教师巴尔末成功地从光谱数据95，1612，2521，3632，…中得到巴尔末公式，从而打开了光谱奥妙的大门．请你按这种规律写出第八个数据是．⑶找规律，并按规律填上第五个数:357924816--，，，，，第n 个数为： . （n 为正整数）⑷有一列数12-，25，310-，417，…，那么第7个数是．第n 个数为 . （n 为正整数）（5）一组按规律排列的式子：2b a -，52b a ，83b a -，114b a，…（0ab ≠），其中第7个式子是，第n 个式子是 .（n 为正整数）【解析】 ⑴ 212k k -；（2） 10096， ⑶1132-，21(1)2n n n +-；⑷ 750-，2(1)1nn n -+ ；（5）207b a -，31(1)n n nb a --．【例2】 ⑴将杨辉三角中的每一个数都换成分数，得到一个如图所示的分数三角形，称为莱布尼茨三角形，若用有序数对(),m n 表示第m 行，从左到右第n 个数，如()4,3表示分数112.那么()9,2表示的分数是 . 1112211136311114121241111152030205（2）正整数按图的规律排列. 请写出第20行第21列的数字: ．数表的规律4初一秋季·第5讲·基础-提高班·教师版⑶按一定的规律排列成的数表如图所示.①当“X”型框中间数字为15时，框中五个数的和为 .当“X”型框中间数字为-57时，框中五个数的和为 .②如果设“X”型框中间的数为a ，请用含a 的代数式表示“X”型框中五个数的和； ③若将“X”型框上下左右移动，所框住的五个数之和能等于－285吗？若能，请求出这-13 -5 7 -9 11 -13 15 -17 19 -21 23 -25 27 -29 31 -33 35 -37 39 -41 43 -45 47 -49 51 -53 55 -57 59 -61 63 -65 67 -69 71 ………………【解析】 ⑴172⑵ 420；观察可得规律：第一行第二列的数：212=⨯；第二行第三列的数：623=⨯；第三行第四列的数：1234=⨯； ……第n 行第1n +列的数：(1)n n +故可得第20行第21列的数为：2021420⨯=.（3）①-45，171 ②-3a ③不能，中间数字应该为95，但是95却在最后一列第一行第二行第三行第四行第五行第一列第二列第三列第四列第五列 1 2 5 10 17 ... 4 3 6 11 18 ... 9 8 7 12 19 ... 16 15 14 13 20 (25)232221………5初一秋季·第5讲·基础-提高班·教师版【例3】 ⑴ 下图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，第3个图案由个基础图形组成，……，第n （n 是正整数）个图案由个基础图形组成．⑵观察下列图形：它们是按照一定规律排列的，依照此规律，第9个图形中共有个★，第n 个图形有个★.⑶ 图1是一个三角形，分别连接这个三角形三边的中点得到图2，再分别连接图2中间小三角形三边的中点，得到图3．图3图2图1① 图2有个三角形；图3有个三角形；② 按上面的方法继续下去，第n 个图形中有多少个三角形？⑷如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是．【解析】 ⑴ 10，31n +； ⑵；28,3n+1；⑶ ①5，9．② 43n -． ⑷(2)n n +或22n n +或2(1)1n +-；算式的规律图形的规律第1个图形第2个图形第3个图形第4个图形6初一秋季·第5讲·基础-提高班·教师版【例4】观察下列等式：①23a a +=；②65a a +=；③127a a+=；④209a a +=…；则根据此规律第6个等式为，第n 个等式为．【解析】 1342=+aa ； 122+=++n a n n a .一般的以计算机程序为背景的新型求值题，解这类题的关键是弄清计算机程序与数学表达式之间的关系．【例5】 ⑴ 如下图，输入23x =-，则输出值y 是．y=-x +4(x >1)y=x +4(x ≤1)输出 y输入 x⑵ 如下图所示是计算机程序计算，若开始输入1x =-，则最后输出的结果是 .YES NO输出结果<-5计算1+x -2x 2输入x 的值⑶ 如图所示的运算程序中，若开始输入的x 值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……，第2013次输出的结果为．x +3x 2x 为奇数x 为偶数输出输入x⑷ 按下面的程序计算，若开始输入的值x 为正整数，最后输出的结果为853，试求出满足条件的x 的所有值.程序运算思路导航7初一秋季·第5讲·基础-提高班·教师版>800输出结果是否将值赋给x ，再次运算计算4x +1的值输入x【解析】 ⑴5-；此程序为选择式，因91x =-≤，故4945y x =+=-+=-.⑵ 9-；经过第一次程序运算得2-，因为25->-，需要返回循环；经第二次运算得9-，因为95-<-，此程序结束，故输出结果为9-. ⑶ 6．（提示：利用循环，多进行几次运算．）⑷ 由题意：()85314213>0-÷=，()2131453>0-÷=，()531413>0-÷=，()13143>0-÷=，()1314>02-÷=∴只有213，53，13，3符合题意．（也可用方程思想理解：∵ x 为正整数， ∴ 415x +≥. 当41853x +=时，213x =. 当41213x +=时，53x =. 当4153x +=时，13x =. 当4113x +=时，3x =.综上所述，213x =或53x =或13x =或3x =）.【例6】阅读右面的框图并回答下列问题：（1）若A 为785，则E=_____________；（2）按框图流程，取不同的三位数A ，所得E 的值都相同吗？如果相同，请说明理由；如果不同，请求出E 的所有可能的值；（3）将框图中的第一步变为“任意写一个个位数字不为0的三位数A ，它的百位数字减去个位数字所得的差大于．．2．”，其余的步骤不变，请猜想E 的值是否为定值？并对你猜想的结论加以证明．【解析】 ⑴E =1089； ⑵ E 的值都相同．理由如下：设A =100a+10b +c 且a －c =2，则B =100c +10b + a ．∴C =A －B =(100a +10b +c )－(100c +10b + a )=99a －99c =99(a －c )=99×2=198． ∴D =891．∴E =C +D =198+891=1089． (3) E =1089．8初一秋季·第5讲·基础-提高班·教师版证法1：设A =100a +10b +c 且a －c >2，则B =100c +10b + a ．∴C =A －B =(100a +10b +c )－(100c +10b + a )=100(a －c )+(c －a )=100(a －c －1)+10×9+(10+c －a ) ． ∴D =100(10+c －a ) +10×9+ (a －c －1) ．∴E =C +D =[100(a －c －1)+10×9+(10+c －a )]+[ 100(10+c －a ) +10×9+ (a －c －1)]=1089．定义新运算⑴基本思路：严格按照新定义的运算规则，把已知的数代入，转化为加减乘除的运算，然后按照基本运算过程、运算律进行运算.⑵注意事项：①新的运算不一定符合运算律，特别注意运算顺序. ②每个新定义的运算符号只能在本题中使用.【例7】 ⑴现定义两种新运算∆∇、，对于任意两个整数a 、b ，都有：1a b a b ∆=+-， 1b a b a ∇=-.试求：(∆∆∇(34)21)的值.⑵ 用“×”定义新运算：对于任意a b ，，都有a ×b 2a b =-．例如，4×27479=-=，那么5×3= ；当m 为有理数时，m ×（1-×2）= ．⑶ 对于正整数a ，b ，c ，d ，规定a b ad bc c d=-，若1134bd <<，则b d += ．⑷ 定义：a 是不为1的有理数，我们把11a -称为a 的差倒数．．．．如：2的差倒数是1112=--，1-的差倒数是()11112=--．已知113a =-， ① 2a 是1a 的差倒数，则2a = ； ② 3a 是2a 的差倒数，则3a = ；③ 4a 是3a 的差倒数，则4a = ，…，依此类推，则2009a = ．【解析】 ⑴ 6；⑵ 22，21m +；⑶由题意得42bd -=，故2bd =，又b d ，为正整数，所以3b d +=.定义新运算思路导航9初一秋季·第5讲·基础-提高班·教师版⑷ ①34；② 4；③ 13-；34. 【点评】一个值得注意的问题是：定义一个新运算，这个新运算常常不满足加法、乘法所满足的运算律，因此在没有确定新运算是否具有这些性质之前，不能运用这些运算律来解题．【选讲题】【例8】（1）右图为手的示意图，在各个手指间标记字母A B C D ，，，．请你按图中箭头所指方向（即A B C D C B A B →→→→→→→C →→…的方式）从A 开始数连续的正整数1234，，，，…，当数到12时，对应的字母是_______；当字母C 第201次出现时，恰好数到的数是；当字母C 第21n +次出现时（n 为正整数），恰好数到的数是（用含n 的代数式表示）．【解析】 B ，603，63n + . （2）数1234,,,,a a a a 满足下列条件：10a =，211a a =-+ ,322a a =-+,433a a =-+,则2013a 的值为 .【解析】 1006(3)如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去：⑴ 填表：⑵ 如果剪了100次，共剪出多少个小正方形？ ⑶ 如果剪n 次，共剪出多少个小正方形？【解析】 ⑴ 如表．剪的次数1 23 4 5 正方形个数 47101316⑵ 如果剪了100次，共剪出11003301+⨯=个小正方形； ⑶ 如果剪n 次，共剪出13n +个小正方形.剪的次数1 2 3 4 5 正方形个数 4 710 初一秋季·第5讲·基础-提高班·教师版训练1. 下面是一组按规律排列的数：1，2，4，8，16，……，第2002个数应该是（）A ．20022B ．200221-C ．20012D ．以上答案均不对【解析】 C.训练2. 根据右图所示的程序计算变量y 的值，若输入自变量x 的值为32，则输出的结果是．（汇文中学期中）【解析】 72-.训练3. 读一读：式子“12345100++++++”表示1开始的100个连续自然数的和．由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“12345100++++++”表示为1001n n =∑，这里“∑”是求和符号．例如：1357999++++++，即从1开始的100以内的连续奇数的和，可表示为50121n n =-∑（）；又如333333333312345678910+++++++++可表示为1031n n =∑．通过对以上材料的阅读，请解答下列问题．⑴ 246810100++++++（即从2开始的100以内的连续偶数的和）用求和符号可表示为． ⑵ 计算5211n n =-=∑（）．（填写最后的计算结果）（北大附中期中）【解析】 ⑴ 5012n n =∑；⑵ 50,52222221(1(11(21(31(41(5150n n=-=-----=∑))+)+)+)+)训练4. 在某种特制的计算器有一个按键★★★，它代表运算2a b a b++-．例如：输入顺序 1，★★★，2-，ENTER=屏幕显示()1***2-2上述操作即是求()()12122+-+--的值，运算结果为2．回答下面的问题：y=-x -2(1<x ≤2)y=x 2(-1≤x ≤1)y=x -2(-2≤x <-1)输出y 的值输入x 的值11初一秋季·第5讲·基础-提高班·教师版⑴ 小明的输入顺序为5-，★★★，7，ENTER=，运算结果是．⑵ 小杰的输入顺序为100101，★★★，165-，ENTER=，★★★，1101-，ENTER=，★★★，6665-，ENTER=，★★★，101100，ENTER=，运算结果是．⑶ 若在20112012-，20102011-，20092010-，……，12-，0，12，……，20092010，20102011这些数中，任意选取两个作为a 、b 的值，进行★★★运算，则所有的运算结果中最大的值是．（一零一期中）【解析】 ⑴ 7⑵6665⑶ 2011201212 初一秋季·第5讲·基础-提高班·教师版数列的规律【练习1】 ⑴ 观察一列有规律的数：4，8，16，32，…，它的第2007个数是（）A ．20072B ．200721-C ．20082D ．20062⑵ 观察下列单项式，2x ，25x -，341017x x -，，……根据你发现的规律写出第5个式子是，第8个式子是，第n 个式子是．（n 为正整数）【解析】 ⑴ C ． ⑵ 582665x x -，，12(1)(1)n n n x +-+.数表的规律【练习2】下面是由自然数排成的数表，分为A ，B ，C 三列，按这个规律，1999在第列。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

k−1 k−2 ]−[ ])( 取整数符 4 4 ．
三、解答题（共 8 题，前 6 题每题 6 分，后 2 题每题 8 分，共 52 分）
17. 计算： 1 1 1 1 + + +···+ ． 1 × 6 6 × 11 11 × 16 51 × 56
18. （1）解方程：x −
2x − 3 2x + 5 = 1− ． 6 3
第 6 页（共 6 页）
（2）若数轴上表示数 a 的点位于 −4 与 3 之间，求 |a − 3 |+| a + 4| 的值．
（3）当 a 取何值时，|a − 1 |+| a − 3 |+| a + 4| 的值最小，最小值是多少？请说明理由．
23. 利用我们学过的知识，可以导出下面这个形式优美的等式：a2 + b2 + c2 − ab − bc − ac = 1 [(a − b)2 + (b − c)2 + (a − c)2 ]，该等式从左到右的变形，不仅保持了结构的对称性，还体现了数 2 学的和谐、简洁美．（1）若 a = 2011，b = 2012，c = 2013，你能很快求出 a2 + b2 + c2 − ab − bc − ac 的值吗？ 3 3 （2）若 a − b = ，b − c = ，a2 + b2 + c2 = 1，求 ab + bc + ac 的值． 5 5
x+y = 9① （2）解方程组． 3(x + y) + 2x = 33②
第 3 页（共 6 页）
19. 已知方程组
3x − 2y = 4 mx + ny = 7
与
2mx − 3ny = 19 5y − x = 3
有相同的解，求 m，n 的值．
20. （1）因式分解：x2 − 6x − 16；
第 5 页（共 6 页）
24. 环岛是为了减少车辆行驶冲突，在多个交通路口交汇的地方设置的交通设施，多为圆形，它使车按统一方向行驶，将冲突点转变为通行点，能有效地减少交通事故的发生，如图是该交通环岛的简化模型 (因路段 FG 施工，禁止从路段 EF 行驶过来的车辆在环岛内通行，只能往环岛外行驶)，某时段内该交通环岛的进出机动车辆数如图所示，图中箭头方向表示车辆的行驶方向．（1）求该时段内路段 AB 上的机动车辆数 x1 ．（2）求该时段内从 F 口驶出的机动车辆数 x2 ．（3）若 a = 10，b = 4，求该时段内路段 CD 上的机动车辆数 x3 ．
8. 若方程组 A. 3
的解是二元一次方程 3x − 5y − 90 = 0 的一个解，则 a 的值是( ) B. 2 C. 6 D. 7
9. 若关于 x 的不等式 A. 6 < m < 7
x − m < 0 7 − 2x ⩽ 1
的整数解共有 4 个，则 m 的取值范围是( ) C. 6 ⩽ m ⩽ 7 D. 6 < m ⩽ 7
2. 拒绝“餐桌浪费”刻不容缓，据统计全国每年浪费食物总量约 500 千万千克，这个数用科学记数法表示为( ) A. 0.5 × 1011 千克 B. 50 × 109 千克 C. 5 × 109 千克 D. 5 × 1010 千克
3. 正确的算式是( ) A. (−1)2011 = −2011 B. 2(−3)2 = 36 C. −3 ÷ 1 × 2 = −3 2 D. 1 1 ÷ (− ) = −1 2 2
2017 秋-期中考试初中数学·初一超常班（QG）
(考试时间：90 分钟满分：100 分)
【注意】本卷配有答题卡，请按照答题卡作答要求在答题卡上作答。
一、选择题（共 10 题，每题 3 分，共 30 分）
1. 1 −(− ) 的相反数是( ) 2 1 A. 2 B. 2
C. −2
D. −
1 2
C. 点 A
D. 点 B
二、填空题（共 6 题，每题 3 分，共 18 分）
11. 若多项式 3x2 + kx − 2x + 1(k 为常数) 中不含有 x 的一次项，则 k = ．
12. 设 a + b + c = 0，abc > 0，则
a b c + + 的值是 |a| |b| |c|
．
13. 如果规定符号“⊗”的意义为 a⊗b =
（2）因式分解：2x2 − 3xy + y2 + 8x − 5y + 6．
( )( ) （3）因式分解： x2 + 5x + 2 x2 + 5x + 3 − 12．
21. 某电脑公司经销甲种型号电脑，今年三月份的电脑售价比去年同期每台降价 1000 元，如果卖出相同数量的电脑，去年销售额为 10 万元，今年销售额只有 8 万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为 3500 元，乙种电脑每台进价为 3000 元，公司预计用不多于 5 万元且不少于 4.8 万元的资金购进这两种电脑共 15 台，有几种进货方案？
ab ，则 2 ⊗ (−3) 的值是 a+b
．
14. 已知 |m| = |2m − 3|，则 m =
．
第 2 页（共 6 页）
15. 按照如图的程序计算，若输入 n 的值为 3 时，计算结果为
．
16. 在一列数 x1 ，x2 ，x3 ，…中，已知 x1 = 1，且当 k ⩾ 2 时，xk = xk−1 + 1 − 4([ 号 [a] 表示不超过实数 a 的最大整数，例如 [2.3]=2，[0.4] = 0)，则 x2017 =
第 4 页（共 6 页）
22. 结合数轴与绝对值的知识回答下列问题．（1）数轴上表示 4 和 1 的两点之间的距离是 3：：而 |4 − 1| = 3；表示 −3 和 2 两点之间的距离是 5：而 | − 3 − 2| = 5；表示 −4 和 −7 两点之间的距离是 3，而 | − 4 − (−7) | = 3，一般地，数轴上表示数 m 和数 n 的两点之间的距离等于 |m − n|．如果表示数 a 和 3 的两点之间的距离是 7，则可记为： |a − 3| = 7，那么 a =
4. 已知 a、b 两数在数轴上对应的点如图所示，下列结论正确的是( )
A. ab < 0
B. |a| > |b|
C. a + b > 0
D. b − a < 0
5. 如果代数式 3x2 − 4x 的值为 6，那么 6x2 − 8x − 9 的值为( ) 3 A. 12 B. 3 C. 2
D. −3
6. 设二次三项式 x2 + mx + 6 可分解为两个一次因式的乘积，且各因式的系数都是整数，则满足条件的整数 m 的个数为( ) A. 8 B. 6 C. 4 D. 3
第 1 页（共 6 页）
7. 已知 a = 20162 ，b = 2015 × 2017，则( ) A. a = b x + y = a x − y = 4a B. a > b C. a < b D. a ⩽ b
B. 6 ⩽ m < 7
10. 正方形 ABCD 在数轴上的位置如图所示，点 D、A 对应的数分别为 0 和 1，若正方形 ABCD 绕着顶点顺时针方向在数轴上连续翻转，翻转 1 次后，点 B 所对应的数为 2；则翻转 2017 次后，数轴上数 2017 所对应的点是( )
A. 点 C
B. 点 D