第二章-平面体系的机动分析
第2章平面体系的机动分析

§2-2 平面几何不变体系的组成规律
例2-2 试分析图示体系的几何构造。
解 (1)分析图(a)中的体系 以刚片ⅠⅡⅢ为对象,由于三个瞬铰不共线,因此体系内部 为几何不变,且无多余约束。作为一个整体,体系对地面有三个 自由度。 (2)分析图(b)中的体系 同样方法进行分析,由于三个瞬铰共线,因此体系内部也是 瞬变的。
§2-2 平面几何不变体系的组成规律
1. 一个点与一个刚片 之间的连接方式 2. 两个刚片之间的连 接方式
规律1 一个刚片与一个点 用两根链杆相连,且三个铰不在 一直线上,则组成几何不变的整 体,且没有多余约束。
规律2 两个刚片用一个 铰和一根链杆相连,且三 个铰不在一直线上,则组 成几何不变的整体,且没 有多余约束。
试分析图示体系的几何构造
D
E
0 23
Ⅱ
013 基础 Ⅲ
Ⅰ
023
Ⅱ
B
Ⅰ
A
012
012
C
基础 Ⅲ
013
刚片Ⅰ、Ⅱ、Ⅲ由不共线的三 铰相连,所以体系为无多余约 束的几何不变体。
刚片Ⅰ、Ⅱ、Ⅲ由共线的三铰 相连,所以体系为无多余约束 的几何不变体。
分析图示铰结体系
以铰结三角形123为基础,增加一个二元体得结点4, 1234为几何不变体系;如此依次增加二元体,最后的体系 为几何不变体系,没有多余联系。 或:从结点10开始拆除二元体,依次拆除结点9,8, 7…,最后剩下铰结三角形123,它是几何不变的,故原体 系为几何不变体系,没有多余联系。
§2-2 平面几何不变体系的组成规律
装配过程有两种:
(1)从基础出发进行装配:取基础作为基本刚片,将周围某
个部件按基本装配格式固定在基本刚片上,形成一个扩
第二章 平面体系的机动分析

§2-3 几何不变体系的基本组成规则
1、三刚片规则 (基本规则)
三个刚片用不在同一直线上的三个单铰两两铰联,则组成的 体系是几何不变的,而且没有多余联系。 2、二元体规则 二元体:两根不在一直线上的链杆联结一个新结点的构造。 在一个体系上增加或拆除二元体,不会改变原有体系的几何 构造性质。 3、两刚片规则 两个刚片用一个铰和一根不通过此铰的链杆相联(或用三根不 全平行也不交于同一点的链杆相联),则为几何不变体系,而 且没有多余联系。
7
8
1 2 3
4 7 8
5
6
1 2 3 4
(教材题2-15)
5
6
常变
例4(教材例2-1):
1 2 3 4 5
解:
1、结点编号 2、列表分析
地基 杆件1-2
刚片一 杆件2-3
刚片二 杆件3-4
刚片三 杆件4-5
刚片四
3、结论 该体系为几何不变,且无多余联系。
14 13 15 16 8 9 6 4 1 2 10 11 12 7 5 13 8
14 15 16 9 6 4 1 2 10 11 12
1
2
8
9
刚片5-9
刚片二
刚片三
3、结论
地基
该体系为几何不变,且无多余联系。
Байду номын сангаас
4
3
例7:
解: 1、结点编号 2、列表分析
1 2 3
刚片1-2
地基
刚片一 +1-4-2 +1-3-2
刚片二
4
3、结论
该体系为几何不变,且有两个多 余联系。
1
2
4
李廉锟第四版《结构力学》第2章平面体系的机动分析习题+参考答案
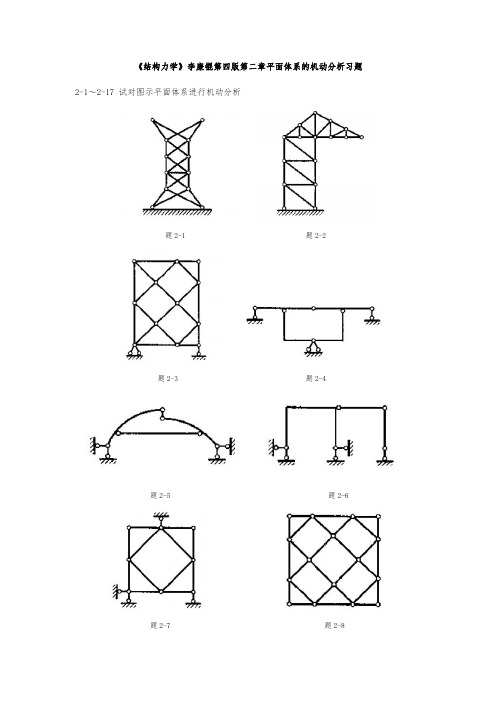
《结构力学》李廉锟第四版第二章平面体系的机动分析习题2-1~2-17试对图示平面体系进行机动分析题2-1题2-2题2-3题2-4题2-5题2-6题2-7题2-8题2-9(a、b处非结点)题2-10(k处非结点)题2-11题2-12题2-13题2-14题2-15(k处非结点)题2-16题2-172-18、2-19添加最少数目的链杆和支承链杆,使体系成为几何不变,而且无多余约束。
题2-18题2-19《结构力学》李廉锟第四版第二章平面体系的机动分析参考答案题2-1说明:自上往下依次拆除二元体,或者自下往上依次添加二元体,故体系为有一个多余约束的几何不变体系(多余约束:中间的横杆或者也可以看成支座上多了一根水平杆)。
题2-2说明:如图所示取刚片1和刚片2,采用二刚片规则(两刚片用一个铰和一根不通过此铰的链杆相联),为几何不变体系,而且没有多余联系。
刚片1由二元体组成,刚片2从大地向上组装二元体组成。
题2-3说明:先不考虑支座的三根链杆,考虑上部几何构造,去掉二元体简化分析,取如上图所示刚片1、刚片2和刚片3。
刚片1和刚片2通过一个实铰联结;刚片1和刚片3通过两根平行链杆联结,交于无穷远处;刚片2和刚片3通过两根平行链杆联结,交于无穷远处;三铰不共线,故上部无多余约束且几何不变。
最后上部与大地通过一个铰和一根不通过此铰的链杆相联,故整个体系为无多余约束的几何不变体系。
题2-4说明:如上图所示取刚片1、刚片2和刚片3,刚片1和刚片2交于铰12O ,刚片1和刚片3交于铰13O ,刚片2和刚片3交于铰23O ,三铰不共线,故原体系为无多余约束的几何不变体系。
题2-5说明:将大地等效成一根链杆,取如图所示刚片1和刚片2,显然两刚片通过三根链杆相联,且三根链杆既不相互平行也不相交于一点,故原体系为无多余约束的几何不变体系。
题2-6说明:先拆除二元体以简化分析,可知右部分为常变部分;左部分为有一个多余约束的几何不变体系,故体系为几何常变体系。
第二章:平面体系的机动分析(结构力学 李廉锟 第五版 配套)

y A' B' D Dy B Dx
x
A 0
自由度: 描述几何体系运动时,所需独立坐标的数目。 几何体系运动时,可以独立改变的坐标的数目。 几何可变体系自由度大于0 几何不变体系自由度等于0 平面内的点自由度为2 平面内的刚体自由度为3
联系(约束)
如果体系有了自由度,必须消除,消除的办法是增加约束。
W=3×7-(2×9)-3=0
平面杆件体系的自由度
若每个节点均为自由,则有2j个自由度,但连接节点的每根杆 件都起一个约束作用,则体系的计算自由度为
W=2j-b -r
j---刚片数; b---杆件数; r ---支座链杆数。
算例
j=4
b=4 r=3
j=8
b=12
r=4
W=2×4-4-3=1
W=2×8-12-4=0
在运动中改变位置。
虚铰特例 2杆平行等长,刚片位置改变,链杆仍平行但改变方 向,虚铰转到另一无穷远点(常变体系)
2杆平行不等长,刚片位置改变,链杆不再平行, 虚铰转到有限远点(瞬变体系)
基本组成规则
基本规则的应用
利用组成规律可以两种方式构造一般的结构:
(1)从基础出发构造
(2)从内部刚片出发构造
2.5 机动分析
1,3
.
.1,2
2,3
.
.
无多余约束的几何不变体系
几何瞬变体系
1,2
. .
1,3 2,3
. 2,3
几何瞬变体系
1,2 1,3
F
D C E
F
D C B E
A
A
B
F
D
C A
E
D
E
C
结构力学平面体系的机动分析

x, y , 1 , 6-2=4
2
x, y , 1 , 2 , 3 9-22=5
一单铰:两个联系, 两个链杆。
联结n个刚片的复铰: (n-1)个单铰。
• (3) 多余联系(约束) y
A • 在一个体系中增加一个约束,而体系的自 由度并不减少,则此约束称为多余约束。
B
C
D
x
• 自由度S=(各构件自由度总和)-(非多余约束数) • 计算自由度W=(各构件自由度总和)-(全部约束数)
2-2 平面体系的计算自由度
• 一:基本概念
(1)自由度:物体运动时可以独立变化的几何参数的数目,
也就是确定物体位置所需的独立坐标数目。
y x y x
y x y
x
• (2)一个联系(约束):凡减少一个自由度的装置。
1
x
2
1
y
ห้องสมุดไป่ตู้
2
x
1
y
3 2
1
,
2
3-1=2 一根链杆:一个 联系
F
E
G
C 刚片2 A 刚片1
D B
H
小结:
W>0
平面体系
机动分析
计算自由度
W=0 W<0 三刚片规则
简单组成规则
二元体规则
两刚片规则
对图示体系进行机动分析
3 H 1 2 3
(2)
A 1 3 D
B 2 E 3
(1)
C
3
F G
3
( 3)
自学:三刚片体系中虚铰在无穷远处的情况及零载法。
作业:教材第二章习题 1,2,5,6,8。
• 一 . 三刚片规则
第二章-平面体系几何组成分析

2-3 几何不变体系的基本组成规律 基本规则
2-4 瞬变体系
FNAB =FNAC =FN
2FN sina=FP
δ
FN =FP /(2 sina )
l2 2 l 2
2l
2-5 几何组成分析示例 几何组成分析目的
体系
几何不变 几何可变
无多余约束的几何不变体系 有多余约束的几何不变体系
瞬变体系 常变体系
2-2 平面体系的计算自由度 约束/联系
复刚结点
连接n个刚片的复刚结点, 相当于(n -1)个单刚结点, 能减少3(n -1)个自由度, 故相当于3(n -1)个约束。
2-2 平面体系的计算自由度 必要约束/多余约束
必要约束
多余约束
多余约束
必要约束
结论:只有必要约束才能对体系自由度有影响。
2-2 平面体系的计算自由度
2-5 几何组成分析示例 例题 I
B
A
C
DE
B
AⅠ
ⅡC
DE
Ⅲ
2-5 几何组成分析示例 例题 II
2-5 几何组成分析示例 例题 III
利用虚铰
等效链杆
2-5 几何组成分析示例 例题 VI
将刚片画成直杆
将
画成
2-5 几何组成分析示例 例题 V
主从结构
2-5 几何组成分析示例 例题 VI
C B A
第二章
平面体系的机动分析
Geometric Construction Analysis of Planar Systems
2-1 概述 机动分析前提假设
结构可变性分为: 物理可变形;几何可变性。
机动分析前提假设: 不考虑材料变形。
2-1 概述 体系的分类
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第2章 平面体系的机动分析【圣才出品】

相当于三刚片规则。同理,两刚片规则中链杆仍然可以看作一个刚片。因此三个基本组成
规则实质上只是同一个规则。
5.何谓瞬变体系?为什么土木工程中要避免采用瞬变和接近瞬变的体系? 答:(1)瞬变体系的定义 瞬变体系是指经微小位移后由几何可变转化为几何不变的体系,瞬变体系是一种几何 可变体系。 (2)在土木工程的实际中,由于材料变形,瞬变体系一经受力即偏离原有位置,而 内力通常也很大,甚至可能导致体系的破坏。同时,瞬变体系的位移只是理论上为无穷小, 实际上在很小的荷载作用下也会产生很大的位移。因此,土木工程中要பைடு நூலகம்免采用瞬变和接
二、平面体系的计算自由度 ★★★★★ 1.自由度和约束(见表 2-1-2)
表 2-1-2 自由度和约束
2.平面体系的计算自由度(见表 2-1-3) 表 2-1-3 平面体系的计算自由度
2 / 37
圣才电子书
十万种考研考证电子书、题库视频学习平 台
三、几何不变体系的基本组成规则(见表 2-1-4) ★★★★★ 表 2-1-4 几何不变体系的基本组成规则
9 / 37
圣才电子书
十万种考研考证电子书、题库视频学习平
台
近瞬变的体系,以保证结构的安全和正常使用。
6.试小结机动分析的一般步骤和技巧。 答:(1)机动分析的一般步骤 ①一般先考察体系的计算自由度。如果 W>0,已表明体系是几何可变的;如果 W≤0,进一步做组成分析。 ②运用几何组成的基本规则做几何组成分析。 (2)机动分析的一般技巧 ①对于较复杂的体系,宜先把能直接观察出的几何不变部分当作刚片。 ②以地基或刚片为基础按二元体或两刚片规则逐步扩大刚片范围。 ③拆除二元体使体系的组成简化,以便进一步用基本的组成规则去分析它们。
2第二章-结构力学平面体系的机动分析.

x
x
或由若干杆件组成的几何不变体系)。
A(x,y)
y x
2. 刚片的自由度——3 14:08
o
第二章 平面体系的机动分析
§2-2 平面体系的自由度计算
二、平面刚片系的自由度 1.平面刚片系的组成:
简单铰 ⑴各刚片间用铰相连 复铰 ⑵各刚片用一定的支杆 (sup portLink )与基础相连。
W 2j br
v w3 2j b3
第二章 平面体系的机动分析
§2-2 平面体系的自由度计算
例3 .
j=9 b=15 r=3
W 2j br 2 9 15 3 0
14:08
第二章 平面体系的机动分析
§2-2 平面体系的自由度计算
例4.
j=6 b=9 r=3
14:08
自由度:3m 约 束: 2h 约 束: r
体系自由度(计算): W 3m (2h r )
第二章 平面体系的机动分析
§2-2 平面体系的自由度计算
如果体系不与基础相连,即r=0时, 体系对基础有三个自由度,仅研究体 系本身的内部可变度V。 则知
W V 3
得:V
≤0 因此,体系几何不变的必要条件: 14:08
小
W>0, W=0,
结
缺少足够联系,体系几何可变。 具备成为几何不变体系所要求 的最少联系数目。
W<0, 体系具有多余联系。 W> 0
14:08
体系几何可变
W< 0
体系几何不变
本节课到此结 束再见!
14:08
第二章 平面体系的机动分析
结构力学
第二章 平面体系的机动分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四
杆
不
几何不变体系
全
平
行
§2-6 三刚片虚铰在无穷远处的讨论
四
杆
全
平 行
几何瞬变体系
§2-6 三刚片虚铰在无穷远处的讨论
四 杆 平 行 几何常变体系 等 长
§2-6 三刚片虚铰在无穷远处的讨论
三铰无穷远 如何?请大家 自行分析 !
§2-7 几何构造与静定性的关系
F FAx
FAy 如何求支 座反力?
Ⅱ
§2-3 几何不变体系的简单组成规则
2. 三刚片用位于同一直线上的三个铰相联, 组成瞬变体系。( 几何可变 )
不符合三刚片规则
A
C
B
C’
§2-3 几何不变体系的简单组成规则
地基、AC、BC为刚片; A、B、C为单铰
无多余联系的几何不变体
§2-3 几何不变体系的简单组成规则
二、 二元体规则
在刚片上增加一个二元体,是几何不变体系。
则体系自由度: W = 2j-(b+r)
§2-2 平面体系的计算自由度
例1:计算图示体系的自由度
AC CDB CE EF CF DF DG FG
1
1
3
2 3
有几个刚片?
有几个单铰?
有几个支座链杆?
W=3×8-(2 ×10+4)=0
§2-2 平面体系的计算自由度
例2:计算图示体系的自由度
1
2 按刚片计算
§2-5 机动分析示例
例2-1 对图示体系作几何组成分析。
方法一:从基础出发; 利用两刚片规则;
扩大刚片;
反复利用两刚片规则;
结论: 无多余联系的几何不变体.
方法二:加、减二元体
§2-5 机动分析示例
例2-2 对图示体系作几何组成分析。
瞬变体系
1. 去支座后再分析体系本身,为什么可以这样?
2.有二元体吗? 有
静定结构
FB
无多余 联系几何 不变。
§2-7 几何构造与静定性的关系
F FAx
FAy
FC
能否求全 部反力?
超静定结构
FB
有多余 联系几何 不变。
§2-7 几何构造与静定性的关系
小结:
几何不变体系 可作为结构
体系
无多余联系
静定结构
有多余联系
超静定结构
ቤተ መጻሕፍቲ ባይዱ
几何可变体系 常变 不可作结构 瞬变
结论与讨论
9根杆, 9个刚片
有几个单铰?
3
3
3根支座链杆 W=3 ×9-(2×12+3)=0
按铰结链杆计算
2
1
W=2 ×6-(9+3)=0
§2-2 平面体系的计算自由度
例3:计算图示体系的自由度
1①
2
②3
解: m 3, h 2, r 4
w 3m (2h r) 3 3 (2 2 4) 1
§2-2 平面体系的计算自由度
结构的组装顺序和受力分析次序密切相关。
正确区分静定、超静定,正确判定超静定结构的 多余约束数十分重要。
超静定结构可通过合理地减少多余约束使其变成静 定结构。
分析一个体系可变性时,应注意刚体形状可任意改 换。按照找大刚体(或刚片)、减二元体、去支座分 析内部可变性等,使体系得到最大限度简化后,再应 用三角形规则分析。
2.平面刚片系的组成
⑴各刚片间用铰相连复 简铰 单铰
连接方式 ⑵各刚片用一定的支杆
(sup portLink)与基础相连。
§2-2 平面体系的计算自由度
3.联系(constraint)
1根链杆为1个联系
联系(约束)--减少自由度的装置。 1个单铰为2个联系
(1(2) )链单杆铰
铰
x
α
β
n=3 平面内一y刚片 n=2
C
二元体: 在刚片上增加由
两根链杆连接而成的一
个新的铰结点,这个
“两杆一铰”体系,称
A
D
B
为二元体。
刚片1
§2-3 几何不变体系的简单组成规则
几何不变体系中,增加或减少二元体,仍为 几何不变体系。
§2-3 几何不变体系的简单组成规则
加减二二元元体体组简成化结分构析
§2-3 几何不变体系的简单组成规则
当计算自由度W >0 时,体系一定是可变的。但 W≤0仅是体系几何不变的必要条件。
几何不变体系
形状可几任何意可替变换 体系
§2-2 平面体系的计算自由度
一、平面体系的自由度 (degree of freedom of planar system)
1.自由度数--确定物体位置所需要的独立坐标数
体系运动时可独立改变的几何参数数目
平面内一刚片
平面内一点 n=2
n=3
x
y
§2-2 平面体系的计算自由度
F
G
D
E
如何变静定? 唯一吗?
§2-5 机动分析示例
A
C
E DD
E
如何才能不变? 可变吗? 有多余吗?
B
§2-6 三刚片虚铰在无穷远处的讨论 (a) 一铰无穷远情况
不平行
几何不变体系
§2-6 三刚片虚铰在无穷远处的讨论
平
行
几何常变体系
等
长
§2-6 三刚片虚铰在无穷远处的讨论 (b) 两铰无穷远情况
P
A
C
B
C1 不能平衡
微小位移后,不能继续位移
瞬变体系(instantaneously unstable system) --原为几何可变,经微小位移后即转化为
几何不变的体系。
§2-4 瞬变体系
瞬变体系 ——小荷载引起巨大内力(图1) ——工程结构不能用瞬变体系
几何可变体系: 瞬变 , 常变
• 例:(图2-17) 二刚片三链杆相联情况 • (a)三链杆交于一点; • (b)三链杆完全平行(不等长); • (c)三链杆完全平行(在刚片异侧) ; • (d)三链杆完全平行(等长)
单铰联后 n=4
1个自由刚片3个自由度 2个自由刚片有6个自由度
§2-2 平面体系的计算自由度
3.联系(constraint)
(1) 链杆; (3) 复铰
(2) 单铰;
复铰 等于多少个
单铰?
五个自由度:X A 、YA 、 θ1、θ2 、θ3
n个杆件组成的复铰, 相当于(n-1)个单铰。
§2-2 平面体系的计算自由度
第二章 平面体系的机动分析
§2-1 引言 §2-2 平面体系的计算自由度 §2-3 几何不变体系的简单组成规则 §2-4 瞬变体系 §2-5 机动分析示例 §2-6几何构造与静定性的关系
§2-1 引言
一、几何不变体系 (geometrically stable system):
一个杆系,在荷载作用下,若略去杆件本身的弹性变 形而能保持其几何形状和位置不变的体系。
如何减二元体?
§2-3 几何不变体系的简单组成规则
三、两刚片规则:
两个刚片用一个铰和一个不通过该铰的链杆连接, 组成几何不变体系。
铰
链杆
Ⅱ
§2-3 几何不变体系的简单组成规则
三、两刚片规则:两个刚片用三根不全平行也不交
于同一点的链杆相联,组成无多余联系的几何不
变体系。 实铰 虚铰
铰
O
C 刚片2 E
§2-5 机动分析示例
加、减二 元体
无多几何不变
§2-5 机动分析示例
例2-3 对图示体系作几何组成分析。
找出三个刚片 无多余联系的几何不变体
§2-5 机动分析示例
例2-4 对图示体系作几何组成分析。
找
刚
片、
找
虚
铰
Ⅰ
瞬变体系
Ⅱ Ⅲ
它可 变吗?
行吗?
行吗?
§2-5 机动分析示例
机动分析步骤总结:
P
几何不变 弹性变形
可称之为结构
§2-1 引言
二、几何可变体系(geometrically unstable system):
一个杆系,在荷载作用下,即使略去杆件本身的弹性变形, 它也不能保持其几何形状和位置,而发生机械运动的体系。
P
几何可变 只能称之为机构
§2-1 引言
三、杆系的机动分析:
机动分析就是判断一个杆系是否是几何不变体系,同时还 要研究几何不变体系的组成规律。又称:
1. 可首先通过自由度的计算,检查体系是否满足几何 不变的必要条件(W≤0)。对于较为简单的体系,一般都略 去自由度的计算,直接应用上述规则进行分折。
2. 在进行分折应时,宜先判别体系中有无二元体,如 有,则应先撤去,以使体系得到简化。
3. 如果体系仅通过三根既不完全平行,又不完全相交 的支座链杆与基础相联接的体系,则可直接分析体系内 部的几何组成。如果体系与基础相连的支座连杆数多于 三根,应把基础也看成刚片作整体分析。
§2-2 平面体系的计算自由度
W>0, 缺少足够联系,体系几何可变。 W=0, 具备成为几何不变体系所要求的最少
联系数目。 W<0, 体系具有多余联系。
W> 0
体系几何可变
W< 0
体系几何不变
因此,体系几何不变的必要条件:W≤0
如果体系不与基础相连,即r=0时,体系对 基础有三个自由度,仅研究体系本身的内部可 变度V。
§2-3 几何不变体系的简单组成规则
( Geometric construction analysis (Kinematics analysis))
一、三刚片规则 三个刚片用不在同一直线上的三个单铰两两相 连,所组成的平面体系几何不变。
§2-3 几何不变体系的简单组成规则
