分数除法例已知一个数的几分之几是多少求这个数
已知一个数的几分之几是多少-求这个数的教案

已知一个数的几分之几是多少-求这个数的教案(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--“已知一个数的几分之几是多少,求这个数”教案教学内容:“已知一个数的几分之几是多少,求这个数”的实际应用问题教学目标:1、结合具体情境,理解“已知一个数的几分之几是多少,求这个数”的应用题的结构特征,能够用方程或算术方法解答这类简单的实际问题。
2、借助线段图培养学生分析、解决问题的能力。
3、进一步渗透转化的数学思想。
教学重难点:重点:通过分析比较,找出分数乘、除法应用题的区别和联系,掌握解决问题的规律。
难点:运用分数除法解决实际问题。
教学准备:课件教学过程(一)复习师:同学们我们第一单元已经学过了分数乘法应用题,老师现在来考一考你们学得怎么样?师出示复习题1、找出题中的单位“1”,并写出数量关系式。
2、应用题:爸爸的体重是75千克,小明的体重是爸爸的。
小明的体重是多少千克?说明做此题要求:1.找出题中的单位“1”。
2.说出数量关系。
3.列式解答。
先让全班学生独立完成,然后抽一个学生到黑板板演,最后集体评讲。
师问:做分数乘法应用题的关键是什么?生异口同声的回答:找准单位“1”。
师:同学们真棒!找到了解答分数乘法应用题的钥匙了。
师:同学们已经学会了解答分数乘法应用题,你们想学解答分数除法应用题吗? 生:迫不及待的回答:想。
师:那么我们这一节课就来探讨一下:“已知一个数的几分之几是多少,求这个数”的应用题的解答方法好吗?生:大声地说: “好”!二、谈话引入新课1、小调查:你的体重大约是多少千克?保留整十数。
学生回答。
2、师:我们对自己的身体应该是再熟悉不过了, 我们的身体内有很多科学知识藏在里面呢,你们知道自己体内水分的含量吗同学们,你们知道在我们体内含量最多的物质是什么吗?生:水师:对!水是我们体内含量最多的物质,它对我们人体是至关重要的,是构成我们人体组织的主要成分。
六年级数学知识点:分数除法解决问题知识点

六年级数学知识点:分数除法解决问题知识点在六年级的数学学习中,分数除法解决问题是一个重要的知识点。
掌握这部分内容,对于同学们进一步理解数学运算、提高解题能力有着关键作用。
首先,我们来了解一下什么是分数除法。
分数除法是分数乘法的逆运算,就是已知两个因数的积与其中一个因数,求另一个因数的运算。
分数除法解决问题的类型多种多样,下面我们来逐一探讨。
一、已知一个数的几分之几是多少,求这个数这是分数除法解决问题中最常见的类型。
例如:小明看了一本书的\(\frac{2}{5}\),正好是 40 页,这本书一共有多少页?解题思路:我们把这本书的总页数看作单位“1”,已知总页数的\(\frac{2}{5}\)是 40 页,要求总页数,就用 40 除以\(\frac{2}{5}\)。
列式为:\(40÷\frac{2}{5}=40×\frac{5}{2}=100\)(页)在解决这类问题时,关键是要找准单位“1”,并且要明确已知量对应的分率,用已知量除以对应的分率,就可以求出单位“1”的量。
二、已知比一个数多(或少)几分之几的数是多少,求这个数比如:水果店运来的苹果比梨多\(\frac{1}{4}\),运来苹果125 千克,运来梨多少千克?解题思路:我们把梨的重量看作单位“1”,苹果比梨多\(\frac{1}{4}\),那么苹果的重量就是梨的\((1 +\frac{1}{4})\)。
列式为:\(125÷(1 +\frac{1}{4})= 125÷\frac{5}{4} =125×\frac{4}{5} = 100\)(千克)或者:水果店运来的苹果比梨少\(\frac{1}{5}\),运来苹果80 千克,运来梨多少千克?同样把梨的重量看作单位“1”,苹果比梨少\(\frac{1}{5}\),那么苹果的重量就是梨的\((1 \frac{1}{5})\)。
列式为:\(80÷(1 \frac{1}{5})= 80÷\frac{4}{5} = 80×\frac{5}{4} = 100\)(千克)解决这类问题,还是要先找准单位“1”,弄清楚已知量与单位“1”的关系,再列式计算。
已知一个数的几分之几是多少__求这个数分数除法解决问题例1

已知一个数的几分之几是多少,
求这个数的应用题
分数除法
解决问题(一)
单位“1”的量×分率=分率对应的量
找出下面题中的单位“1”,并写出数量关系式。
分数除法 解决问题
1 (1)白兔的只数占总只数的 3 。 ( 总只数 )× 1 =(白兔只数 ) 4 (2)甲数正好是乙数的 5 。 4 ( 乙 数 )× =( 甲 数 ) 5 5 (3)男生人数的 6 恰好和女生同样多。
5 (男生人数 )× =( 女生人数) 6
3
分数除法 解决问题
找单位“1”,并写出相应的等量关系。
4、一桶水,用去 3 。 4
把( 一桶水 (
)看作单位“1”。
一桶水 )× 3 =( 用去的数量 ) 4
复 习
3、走进生活、解决问题
7 爸爸体重75千克,小明的体重是爸爸的 15 。
分数除法 解决问题
小明的体重
解:设爸爸的体重是 x千克。
7 15 x 35 7 15 15 x 35 35 15 7 15 x 35 75 (kg) 7 答:爸爸的体重是75千克 x 75
算术方法: 35 7
分数除法 解决问题
已知一个数的几分之几是多少,求这个数 的应用题解法 单位“1”的量是未知 方程解法:的
单位“1”指的量×对应的分率=分率对应的量
Hale Waihona Puke 4分数除法 解决问题
2 成人体内水分的重量 我体内有28kg的水 3 4 儿童的体重 儿童体内水分的重量 分,可是我的体重 7 5 才是爸爸的 。 7 15 爸爸的体重 小明的体重 15 成人的体重
(1)小明的体重是多少千克? 你能根据问题,选择适当的条件编一道应用题吗?
“已知一个数的几分之几是多少,求这个数”教学反思

“已知一个数的几分之几是多少,求这个数”教学反思第一篇:“已知一个数的几分之几是多少,求这个数”教学反思“已知一个数的几分之几是多少,求这个数”教学反思分数除法应用题历来是六年级内容的重点和难点,每学到这部分内容,学生往往出错,不知道该乘还是该除。
今天我讲这部分内容,由分数乘法应用题入手,让学生直接把单位“1”变成要求的问题,然后根据数量关系找出等量关系,依据等量关系列方程解答,这样仍然是从乘法的角度思考问题,对学生来讲没有一点难度。
例如:一盒水彩笔有36枝,从盒中拿出4分之1,让学生提出问题(拿出多少枝?或还有多少枝?)这两个问题都是求一个数的几分之几是多少,所以用乘法计算。
现在改为“一盒水彩笔拿出4分之1,正好是9枝,这盒水彩笔共有多少枝?”引导学生先画线段图,再找等量关系,找到等量关系,用方程解答就轻而易举了。
时间长了之后,学生就会自然而然地知道为什么用除法列式(相当于已知两个因数的积和其中一个因数求另一个因数的运算)。
在教学中,我们应该从学生的角度思考,用什么方法能让学生更好的理解,更好的掌握。
第二篇:已知一个数的几分之几是多少求这个数解决问题(1)课题解决问题(1)课型新授课设计说明用分数除法解决“已知一个数的几分之几是多少,求这个数”的应用题教学是整个小学阶段应用题教学的难点之一,为了突破这个难点,教材鼓励学生用方程法解这类简单的分数除法问题。
本课时在教学设计上有如下几个特点:1.有效利用线段图,理清题中的数量关系。
因为题中的等量关系是列方程的依据,所以能否弄清题中的数量关系是正确列方程的关键。
借助线段图理解题意,不但生动、形象,而且题里存在的数量关系也令人一目了然。
2.适时引导,鼓励解法多样性。
对用除法解决问题的同学,借助画线段图帮助理清解题思路,鼓励学生用方程法和算术法两种方法解决此类问题。
学习目标1.使学生掌握解答“已知一个数的几分之几是多少,求这个数”的应用题的方法,能熟练地列方程解答这类应用题。
已知一个数的几分之几是多少,求这个数的应用题教学设计(含试卷)

已知一个数的几分之几是多少,求这个数的应用题教学设计已知一个数的几分之几是多少,求这个数的应用题教学设计教学目标:知识目标:使学生学会掌握“已知一个数的几分之几是多少,求这个数的应用题的解答方法,能熟练地列方程解答这类应用题。
能力目标:进一步培养学生自主探索问题解决的能力和分析、推理和判断等思维能力,提高解答应用题的能力。
情感目标:培养学生良好的分析能力和学习习惯。
教学重点:弄清单位“1”的量,会分析题中的数量关系,能用方程解答已知一个数的几分之几是多少,求这个数的应用题。
教学难点:分数除法应用题的特点及解题思路和解题方法。
教学过程:一、复习1、下面各题中应该把哪个量看作单位“1”?(1)棉田的面积占全村耕地面积的2/5 。
(2)小军的体重是爸爸体重的3/8。
(3)故事书的本数占图书总数的 1/3。
(4)汽车的速度相当于飞机速度的1/5 。
2、找出题中的等量关系。
(1)白兔的只数占总只数的1/3 。
(2)甲数正好是乙数的4/5。
(3)男生人数的5/6恰好和女生同样多。
3、根据提供的数学信息,思考问题并解决问题。
(1)根据测定,成人体内的水分约占体重的1/3,而儿童体内的水分约占体重的4/5 ,六年级学生小明的体重为30千克,他体内的水分有多少千克?(2)看看题目中所给的三个条件是否都用得上,并说说为什么。
(3)选择解决问题所需的条件,确定出单位“1”,并引导学生说出数量关系式。
小明的体重×4/5=体内水分的重量(4)列式计算。
板书:小明的体重×4/5=体内水分的重量30×4/5=24(千克)二、新授1、教学例1的第一个问题:小明的体重是多少千克?提供数学信息:根据测定,成人体内的水分约占体重的 1/3 ,而儿童体内的水分约占体重的 4/5 ,六年级学生小明体内的水分有28千克,他的体重是多少千克?(1)读题、理解题意,寻找相关的数学信息,并画出线段图来表示题意。
(2)引导学生结合线段图理解题意,分析题中的数量关系式,并写出等量关系式。
《已知一个数的几分之几是多少,求这个数》优秀教案
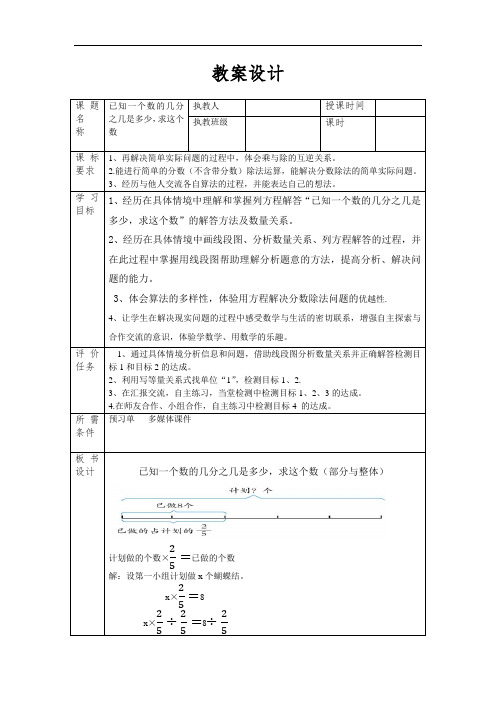
教案设计已知一个数的几分之几是多少,求这个数(部分与整体)计划做的个数×25=已做的个数 解:设第一小组计划做x 个蝴蝶结。
x ×25=8x ×25÷25=8÷25学习过程口算练习5 9×1= 1÷27= 45×10 =16÷23=4 7÷43=8×34= 3÷16=34÷3=一、回顾预习,课题出示谈话:昨天老师让预习新课,今天我们要学习什么内容?预设:用方程解决问题二、小组互学,重点明确1.出示情境信息与问题,让学生再熟悉一下。
第一小组计划做多少个蝴蝶结?2.出示交流提示:(1)师友交流预习成果,如果遇到解决不了的问题,小组内交流,并完成预习单。
(2)汇报展示时,学友先说,学师再进行补充。
三、合作探究,难点突破。
经过刚才大家的课前预习和小组交流,相信大家对这个问题一定有了很多的想法,哪组师友愿意来和大家一起分享一下你的预习成果。
1.找出题目中的单位“1”完成了本组计划的25,把计划做的个数看作单位“1”2.利用线段图,分析数量关系。
画线段图分析问题,我们在以前就用过,看看今天我们同学利用的怎么样?找学生板书画线段图的过程。
(教师要对不规范和不准确的地方及时的纠正。
)质疑:为什么画一条线段?(部分与整体的关系)3.分析线段图,找出等量关系。
根据线段图,你能找到题目中的等量关系吗?哪位同学愿意和大家交流一下。
学生汇报等量关系:4.利用等量关系,列方程求解并检验。
想一想在等量关系式中,谁是未知的?所以这个问题适合用什么方法来解决?明确:(1)用方程解决问题。
(2)将未知的单位“1”设为χ。
你准备设哪一个量,根据什么列方程?引导学生根据数量关系式,将未知的单位“1”设为χ,列方程来解决问题。
5.学生交流列方程的方法。
师:哪个小组汇报一下你们的解决问题方法?(投影展示学生作品)(1)交流分析的方法,展示画图法。
已知一个数的几分之几是多少__求这个数分数除法解决问题例1解剖

单位“1”指的量×对应的分率=分率对应的量
4
分数除法 解决问题
成人的体重 2 成人体内水分的重量 我体内有28kg的水
3
儿童的体重 4 儿童体内水分的重量 分,可是我的体重
5 爸爸的体重 7 小明的体重
才是爸爸的 7。
15
15
(1)小明的体重是多少千克? 你能根据问题,选择适当的条件编一道应用题吗?
一本书,小丽看了60页,正好占全书页 数的 3 。这本书还有多少页没有看?
4
分数除法 解决问题
3、清河村有棉田21公顷,占全 村耕地面积的3/7。全村耕地面 积是多少公顷? (先说出想的过程,再解答。)
分数除法 解决问题
1、小明体重24千克,是爸爸体重的 3 ,
爸爸体重是多少千克?
8
2、一个修路队修一条路,第一天修了全
分率对应的量÷分率=单位“1”的量
分数除法 解决问题
已知一个数的几分之几是多少,求这个数 的应用题解法
单位“1”的量是未知 的
1、读题,理解题意后,画线段图。 2、找出数量关系式:
单位“1”的量×分率=分率对应的量
3、列方程解答
分数除法 解决问题
全部图书数量 2 科普书数量 5
故事书数量 4 科普书数量 3
(1)小明体内有28kg的水分,而儿童体内分的数水除 分法 约解 决 问 题
占体重的 4 。小明的体重是多少千克? 5
水分28kg
小明的体重 4 小明体内水分的重量 5
水分约占体重的54 体重?kg
小明体内水分的重量 4 小明的体重 5
解:设小明的体重是 x千克。
4 x 28 5 x 28 4
分数除法 解决问题
一杯水喝去了80克,
用分数除法解决问题的过程和方法

用分数除法解决问题的过程和方法一、工程问题类。
1. 一项工程,甲队单独做需要10天完成,甲队的工作效率是多少?过程:把这项工程的工作量看作单位“1”,根据工作效率 = 工作量÷工作时间,甲队单独做需要10天完成,所以甲队的工作效率为1÷10=(1)/(10)。
解析:在工程问题中,通常将工作量设为单位“1”,工作效率就是单位时间内完成的工作量。
这里用工作量1除以甲队完成工作的时间10天,就得到甲队的工作效率(1)/(10)。
2. 一项工程,甲队单独做12天完成,乙队单独做15天完成。
甲队每天完成这项工程的几分之几?乙队每天完成这项工程的几分之几?过程:甲队:把工程总量看作单位“1”,甲队单独做12天完成,甲队每天完成1÷12 = (1)/(12)。
乙队:同理,乙队单独做15天完成,乙队每天完成1÷15=(1)/(15)。
解析:对于工程问题,用单位“1”除以工作时间就得到工作效率。
这里分别用1除以甲队的工作时间12天和乙队的工作时间15天,得到甲队和乙队每天完成工程的比例(1)/(12)和(1)/(15)。
3. 一项工程,甲队单独做8天完成,乙队单独做10天完成。
甲队的工作效率是乙队工作效率的多少倍?过程:甲队工作效率:1÷8=(1)/(8)乙队工作效率:1÷10=(1)/(10)倍数关系:(1)/(8)÷(1)/(10)=(1)/(8)×10=(5)/(4)解析:先分别求出甲队和乙队的工作效率,然后用甲队的工作效率除以乙队的工作效率,得到倍数关系。
在除法运算中,除以一个分数等于乘以它的倒数,所以(1)/(8)÷(1)/(10)=(1)/(8)×10=(5)/(4)。
二、已知一个数的几分之几是多少,求这个数类。
4. 已知一个数的(2)/(3)是10,求这个数。
过程:设这个数为x,根据题意可得(2)/(3)x = 10,则x=10÷(2)/(3)=10×(3)/(2) = 15。
