基本初等函数
13基本初等函数

PutianUniversity
§3. 初等函数
二、 初等函数
凡是由常数和基本初等函数经过有限次四则运算及 有限次的函数复合所构成并可用一个式子表示的函数, 称为初等函数.
例:
yloagxes
inx 1 x2 ,
y3xex 1x2
是初等函 而 D 数i, r函 ich y 数 lse g x 、 、 tn y [x]等
§3. 初等函数
一、基本初等函数 指数函数、对数函数、幂函数、三角函数、反三角函数、
双曲函数统称为基本初等函数。
1、指数函数 yax (a0 ,a1 ) y ex
y (1)x a
PutianUniversity
(0,1)
y ax (a1)
§3. 初等函数
2、对数函数 y lo a x( g a 0 ,a 1 )ylnx
(1,0)
PutianUniversity
yloagx
(a1)
y log1 x
a
§3. 初等函数
3、幂函数
yx y
y x2
1
(是常)数
yx y x
(1,1)
o1
x
y 1 x
PutianUniversity
§3. 初等函数
4、三角函数
正弦函数 ysin x
ysinx
PutianUniversity
§3. 初等函数
双曲 tax n 正 sh ix n 切 e x h e x co xs e xh e x
D:( , ) 奇函数, 有界函数,
PutianUniversity
§3. 初等函数
双曲函数常用公式
基本初等函数

基本初等函数包括以下几种:(1)常数函数y = c(c 为常数)(2)幂函数y = x^a(a 为非0 常数)(3)指数函数y = a^x(a>0, a≠1)(4)对数函数y =log(a) x(a>0, a≠1)(5)三角函数:主要有以下6 个:正弦函数y =sin x余弦函数y =cos x正切函数y =tan x余切函数y =cot x正割函数y =sec x余割函数y =csc x此外,还有正矢、余矢等罕用的三角函数。
(6)反三角函数:主要有以下6 个:反正弦函数y = arcsin x反余弦函数y = arccos x反正切函数y = arctan x反余切函数y = arccot x反正割函数y = arcsec x反余割函数y = arccsc x初等函数是由基本初等函数经过有限次的有理运算和复合而成的函数。
基本初等函数和初等函数在其定义区间内均为连续函数幂函数简介形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。
因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续统的极为深刻的知识。
特性对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:首先我们知道如果a=p/q,且p/q为既约分数(即p、q互质),q和p都是整数,则x^(p/q)=q 次根号下(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。
当指数a是负整数时,设a=-k,则y=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。
因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:排除了为0与负数两种可能,即对于x>0,则a可以是任意实数;排除了为0这种可能,即对于x<0或x>0的所有实数,q不能是偶数;排除了为负数这种可能,即对于x为大于或等于0的所有实数,a就不能是负数。
(整理)基本初等函数.

函数的概念1.函数的概念:设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f (x )和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数。
记作:y =f (x ),x ∈A 。
其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{f (x )| x ∈A }叫做函数的值域。
注意:(1)“y =f (x )”是函数符号,可以用任意的字母表示,如“y =g(x )”;(2)函数符号“y =f (x )”中的f (x )表示与x 对应的函数值,一个数,而不是f 乘x 。
2.构成函数的三要素:定义域、对应关系和值域 3.两个函数的相等:函数的定义含有三个要素,即定义域A 、值域C 和对应法则f 。
当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定。
因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数。
4.区间(1)区间的分类:开区间、闭区间、半开半闭区间;(2)无穷区间;(3)区间的数轴表示。
5.映射一般地,设A 、B 是两个非空的集合,如果按某一个确定的对应法则f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应f :A →B 为从集合A 到集合B 的一个映射。
记作“f :A →B ”。
映射和函数的区别:映射是两个集合之间的对应关系,集合A 所有元素在B 中有元素对应,集合B 中的元素在A 中不一定有对应的元素。
但是函数,自变量x 所有的值在因变量y 里面都有对应,而因变量y 的所有元素在自变量x 中也有对应; 6.分段函数若一个函数的定义域分成了若干个子区间,而每个子区间的解析式不同,这种函数又称分段函数; 7.复合函数若y =f (u),u=g(x ),x ∈(a ,b ),u ∈(m,n),那么y =f [g(x )]称为复合函数,u 称为中间变量,它的取值范围是g(x )的值域。
六大基本初等函数图像及其性质

六大基本初等函数图像及其性质六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 α1.2.幂函数的性质;21xy1)当α为正整数时,函数的定义域为区间为∈x,他们的图形都经过原点,并当α>1时在原点-∞(+∞,)处与x轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数;m时,n为偶数时函数的定义3)当α为正有理数n域为(0, +∞),n为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n图形于x轴相切,如果m<n,图形于y轴相切,且m为偶数时,还跟y轴对称;m,n均为奇数时,跟原点对称;5)当α为负有理数时,n为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1)当1>a 时函数为单调增,当10<<a 时函数为单调减;2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ; 1xa.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式); a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) nm n m a a a +=⋅ (2) n m n m a a a -=÷(3)()()mn nmnm aaa ==(4) ()n n nb a ab =b.根式的性质; (1)()a a nn= ; (2)当n为奇数时,a a nn =当n 为偶数时,f x xxx g ⎪⎫⎛=1)(⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a an m nm (2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 Nab=,那么数b 叫做以a 为底N 的对数,记作bN a=log,其中a 叫做对数的底数,N 叫做真数,式子N alog 叫做对数式。
六大基本初等函数图像及其性质
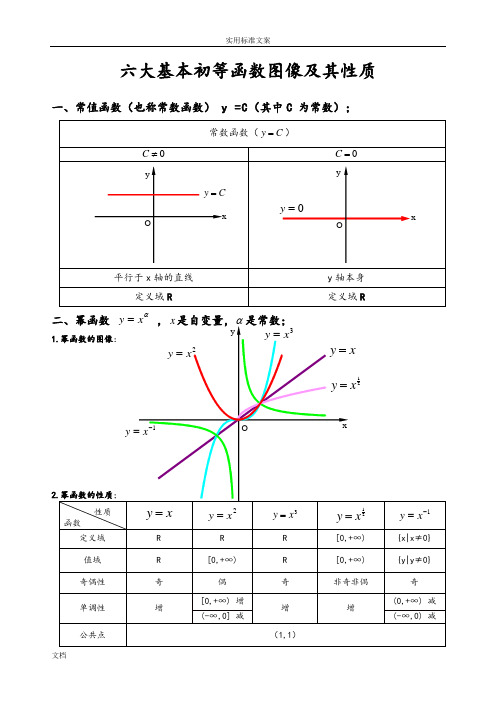
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xy Ox y =2x y =21xy =1-=xy 3x y = O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
基本初等函数知识总结

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数(y=C)(1)定义域: D(f)=(-∞,+∞)(2)值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0,C)在y轴上截距为C的直线(4 )图像:(5)周期性:常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T,f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义:形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数.(2)性质:在(0,+∞)内总有意义①当α>0时函数图像过点(0,0)和(1,1),在(0,+∞)内单调增加且无界②当α<0时函数图像过点(1,1),在(0,+∞)内单调减少且无界(3)图像:3.指数函数y=a^x(a>0且a≠1)(1)定义域:x∈R(2)值域:(0,+∞)(3)性质:①单调性:1.当0<a<1时,在(-∞,+∞)内单调减少 2.当a >1时,在(-∞,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(4)图像:①由指数函数y=a^x与直线x=1相交于点(1,a)可知:在y轴右侧,图像从下到上相应的底数由小变大。
②由指数函数y=a^x与直线x=-1相交于点(-1,1/a)可知:在y轴左侧,图像从下到上相应的底数由大变小。
③指数函数的底数与图像间的关系可概括的记忆为:在y轴右边“底大图高”;在y轴左边“底大图低” 如图:(5)运算法则:①②③④4.对数函数y=logax(a>0 且a≠1)(1)定义:如果a^x=N(a>0,且a ≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数一般地,函数y=logax(a>0,且a ≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数(2)定义域:(0,+∞),即x>0(3)值域:R(4)性质:①单调性:1.当0<a<1时,在(0,+∞)内单调减少 2.当a >1时,在(0,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(5)图像:【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式:5.三角函数⑴正弦函数y=sin x(1)定义:对边与斜边的比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ(K∈Z)时,Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:奇函数③对称性:对称中心是(Kπ,0),K ∈Z;对称轴是直线x=Kπ+π/2,K ∈Z④单调性:在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减⑤有界性:有界函数(6)图像:(2)余弦函数y=cos x(1)定义:邻边与斜边之比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ +π /2(K∈Z)时,Y取最大值1 2.当X=2Kπ +π (K∈Z)时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:偶函数③对称性:对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z④单调性:在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增⑤有界性:有界函数(6)图像:(3)正切函数y=tan x(1)定义:对边与邻边之比(2)定义域:{x∣x≠Kπ+π/2,K∈Z}(3)值域:R(4)最值:无最大值和最小值(5)性质:①周期性:最小正周期都是πT=π②奇偶性:奇函数③对称性:对称中心是(Kπ/2,0),K∈Z④单调性:在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增⑤有界性:无界函数(6)图像:(4)余切函数y=cot x(1)定义:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切。
六大基本初等函数图像及性质

六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点(1,1)xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0,+∞) 奇偶性 非奇非偶公共点过点(0,1),即0=x 时,1=y单调性在),(∞+∞-是增函数 在),(∞+∞-是减函数 1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
基本初等函数定义

基本初等函数定义
1基本初等函数定义
基本初等函数是数学中的一个概念,它也可以称为基本函数,Primary functions,或基础函数。
它被用来定义和描述许多不同的数学模型。
它的定义是:具有某种形式的函数,可以用对数、指数函数、三角函数或其他几何函数组合而成,用来分析某类特定问题。
基本初等函数主要有三种:偶函数、奇函数和其他函数。
偶函数是指在其定义域上,它的取值在坐标轴的对称轴上是对称的,例如二次函数、sinx函数和cosx函数。
奇函数的取值则保持对称,但对称轴不是坐标轴,而是原点,例如tanx函数和cotx函数。
最后,还有一些特殊的函数,例如圆函数、非偶函数和非奇函数,它们可以组合在一起构造特殊的数学模型。
基本初等函数不仅用于模型建构,还可以用来分析数学函数在定义域上的取值规律,以便预测它们在实际问题中的行为。
在几何学中,它常常用于描述和表示不同几何形状的性质,例如点、线、圆、矩形、多边形等。
此外,它还可以用于描述空间几何形状的性质,例如平面、球体等。
因此,基本初等函数在数学和几何学的应用是非常重要的,它们为我们理解数学和几何学中的复杂概念和问题提供了方便的工具和实用的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数
初等函数是由基本初等函数经过有限次的四则运算和复合运算所得到的函数。
基本初等函数和初等函数在其定义区间内均为连续函数。
不是初等函数的函数,称为非初等函数,如狄利克雷函数和黎曼函数。
有两种分类方法:数学分析有六种基本初等函数,高等数学只有五种。
基本初等函数包括以下几类:
(1)常数函数y=c(c为常数)
(2)幂函数y=x^a(a为常数)
(3)指数函数y=a^x(a>0,a≠1)
(4)对数函数y=log(a)x(a>0,a≠1,真数x>0)
(5)三角函数和反三角函数(如正弦函数:y=sinx反正弦函数:y=arcsinx等)
幂函数定义:一般来说,形状如y=xα(α具有理数的函数,即以底数为自变量,幂为变量,指数为常数的函数称为幂函数。
例如函数y=x0、y=x1、y=x2、y=x-1(注:y=x-1=1/xy=x0时x ≠0)等等都是幂函数。
一般形式如下:(α它是常数,可以是自然数、有理数,也可以是任复数。
指数函数定义:指数函数是数学中的一个重要函数。
应用于值e的函数写为exp(x)。
也可以等价写作ex,e是数学常数,是自然对数的底数,近似等于2.718281828,又称欧拉数。
一般形式如下:(a>0,a≠1)
对数函数定义:一般来说,函数y=logax(a>0,且a≠1)称为对数函数,即以幂(真数)为自变量,指数为因变量,底数为常量函数,称为对数函数。
x是自变量,函数定义域为(0、∞),即x>0.它实际上是指数函数的反函数,可以表示为x=ay。
因此,指数函数中对a的规定也适用于对数函数。
一般形式如下:(a>0,a≠1,x>0,特别当α=e时,记为y=lnx)
常见的三角函数主要有以下六种:
正弦函数:y=sinx
余弦函数:y=cosx
正切函数:y=tanx
余切函数:y=cotx
正割函数:y=secx
余割函数:y=cscx
此外,还有正矢、余矢等罕见的三角函数。
主要有六种反三角函数:
反正弦函数:y=arcsinx
反余弦函数:y=arccosx
反正切函数:y=arctanx
反余切函数:y=arccotx
反正切割函数:y=arcsecx
反余切函数:y=arccscx。
