函数的基本初等函数与复合函数
初等函数、简单函数、复合函数、初等函数的概念及关系

初等函数、简单函数、复合函数、初等函数的概念及
关系
1.初等函数:
初等函数是由基本初等函数经过有限次四则运算(加、减、乘、除)与有限次复合形成的函数。
基本初等函数包括以下几种类型:-常数函数:如f(x)=C,C是常数。
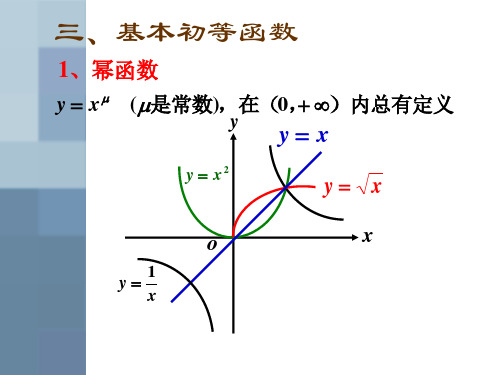
-幂函数:如f(x)=x^n,n为实数。
-指数函数:如f(x)=a^x,a>0且a≠1.
-对数函数:如f(x)=log_a(x),a>0且a≠1.
-三角函数:sin(x),cos(x),tan(x),cot(x),sec(x),csc(x)及其逆函数(反三角函数)。
2.简单函数:
简单函数通常是指构成复杂函数的基本单元,它们相对独立且形式较为简单。
在解决具体问题时,简单函数可能指的就是上述基本初等函数,或者是通过基本初等函数进行一次或几次基本运算(如加法、乘法等)得到的函数。
3.复合函数:
复合函数是两个或多个函数通过变量的代换相互结合而成的新
函数。
如果存在两个函数f和g,那么可以定义一个复合函数h(x)=f(g(x)),其中g的值域需包含在f的定义域内。
例如,`h(x)
=sin(2x)`就是一个复合函数,其中`g(x)=2x`作为外层函数的“内层”被嵌套到`f(u)=sin(u)`中。
关系上:
-所有的基本初等函数都是简单函数。
-简单函数经过组合(包括复合和四则运算)可以形成更复杂的初等函数。
-复合函数是构造初等函数过程中的一种重要手段,它可以将几个简单函数联接起来构建新的、具有更丰富特性的函数表达式。
1.3 复合函数和初等函数

练习题答案
[e , e 3 ] ; 一、1 、基本初等函数; 2 、 x2 3、 y e ; 4、 y sin u, u ln v , v 2 x ; 5 、[-1,1],[ 2k , 2k ],[ a ,1 a ] , 1 [a ,1 a ] 0 a 2 . 1 a 2 e , x 1 1, x 0 f [ g ( x )] 0 , x 0 三、 ; g[ f ( x )] 1, x 1 . 1, x 0 1 , x 1 e
三、分段函数
在自变量的不同变化范围中, 对应法则用不 同的式子来表示的函数,称为分段函数.
例如,
2 x 1, f ( x) 2 x 1,
y x2 1
x0 x0
y 2x 1
一般来说,分段函数不是初等函数,但也有例外 .
x, 例如 y x ,
复合而成.
练习:习题1.3 第2题
( 1)y u , u 1 x 2 (2)y eu , u x 1 3x (3)y sin u, u 2 (4)y u 2 , u cos v, v 3 x 1 (5)y ln u, u v , v 1 x (6) y arccos u, u 1 x 2
二、应用图形的“叠加 ”作函数 y x sin x 的图形 .
1,x 1 三、设 f ( x ) 0,x 1 ,g ( x ) e x , 1,x 1 求 f [ g( x )] ,g[ f ( x )] ,并作出它们的图形 .
四、火车站行李收费规定如下: 20 千克以下不计费, 20~50 千克每千克收费 0.20 元,超出 50 千克超 出部分每千克 0.30 元,试建立行李收费 f ( x ) (元 ) 于行李重量 x (千克) 之间的函数关系,并作出图 形.
1.5基本初等函数、初等函数、复合函数

1 cos 2 x 1 cos 2 x 2 sin x , cos x 2 2
2
《微积分》(第三版) 电子教案
首页
上一页
下一页
结束
6 反三角函数 三角函数都是周期函数,对于值域中的任何都有无 穷多个与之对应,故三角函数在其定义域内不存在 反函数.为了定义它们的反函数,必须限制自变量的 取值范围,使得该函数在这个范围内单调.
《微积分》(第三版) 电子教案
首页
上一页
下一页
结束
常用的三角函数公式:
(1)商的关系
sin x cos x 1 1 1 tan x , cot x ,sec x , csc x , tan x cos x sin x cos x sin x cot x
(2)平方关系
sin 2 x cos2 x 1,sec2 x 1 tan 2 x,csc2 x 1 cot 2 x
《微积分》(第三版) 电子教案
首页
上一页
下一页
结束
二、复合函数
设yf(u) ug(x) 如果将ug(x)代入f(u)中 得到的表达式 f[g(x)]是有意义的 则yf[g(x)]是一个以x为自变量 y为因变量 的新函数 称为由yf(u)和ug(x)复合而成的复合函数
《微积分》(第三版) 电子教案
《微积分》(第三版) 电子教案
首页
上一页
下一页
结束
6 反三角函数 常用的反三角函数有yarcsin x yarccos x yarctanx 函数值的确定
求arccos x 在[0, ]内确定一点 使cos x 则arccos x
1) 例如 求 arccos( 2 1 ) 2 因为 cos2 1 所以 arccos( 3 2 2 3
基本初等函数 复合函数 双曲函数 反双曲函数的定义

(一)函数的定义 (二)极限的概念
(三)连续的概念
基本初等函数
复合函数 初等函数
函 数 的定义
反函数 隐函数
函 数 的性质 单值与多值 奇偶性 单调性 有界性 周期性
双曲函数与 反双曲函数
反函数与直接 函数之间关系
Байду номын сангаас
1、函数的定义
定义 设 x 和 y 是两个变量,D 是一个给定的数 集.如果对于每个数 x D,变量 y 按照一定法 则总有确定的数值和它对应,则称 y 是 x 的函数, 记作 y f ( x ).
1
o
1
x
(5) 函数的周期性:
设函数 f(x) 的定义域为D,如果存在一个不为零的 数l,使得对于任一 x D,有 ( x l ) D .且 f(x+l)=f(x) 恒成立,则称f(x)为周期函数,l 称为 f(x) 的周期.(通 常说周期函数的周期是指其最小正周期).
T 1
y
1
y x [ x]
y
称f ( x )为偶函数; 称f ( x )为奇函数; y
y x
y x
3
o
o
x
偶函数
x
奇函数
(3) 函数的单调性:
设函数f(x)的定义域为D,区间I D,如果对于区间I上 任意两点 x1 x2,当 x1 x2时,恒有: 及 (1) f ( x1 ) f ( x2 ),则称函数 f (x) 在区间I上是单调增加的; 或(2) f ( x1 ) f ( x2 ), 则称函数 f (x)在区间I上是单调递减的; 单调增加和单调减少的函数统称为单调函数。 y
cosh x sinh x 1 ; sinh 2 x 2 sinh x cosh x ;
03.反函数_复合函数与初等函数

x3
也就是说:两个函数复合时, 也就是说:两个函数复合时,内层函数 与 外层函数 的 次序不可颠倒 !
(2) 两个以上函数,在可复合的条件下,可以进行有次序的多次 ) 两个以上函数,在可复合的条件下, 复合。例如: 复合。例如:
y = sin x, y = arctgx 与 y = x 2 + 1 按照先后次序可以复合 成:
§4.复合函数与初等函数 复合函数与初等函数 1. 复合函数概念 1)定义 给定函数 u = f ( x ),x ∈ D 和 y = g ( u ),u ∈ U . ) 假定 Z ( f ) ⊆ U .现在以前一函数的定义域 D 作为 新的定义域 , 现在以前一函数的定义域 如下: 并定义 新的对应规律 如下:对于任意的 x ∈ D , 先令唯一的 u = f ( x ) 与之相对应,因为这里 u ∈ Z ( f ) ⊆ U 与之相对应, 所以再可令唯一的 y = g ( u ) 与 x 最后相对应 , 即 : x → u → y . 这样定义出的 新函数 被称为原函数 u = f ( x ),x ∈ D 与 y = g ( u ),u ∈ U 的 复合函数,记为 : 复合函数, y = g ( f ( x ) ) ,x ∈ D . 我们称 u = f ( x ) ,x ∈ D 为内层函数 , y = g ( u ) ,u ∈ U 为 为中间变量。 外层函数 , u 为中间变量。 由于习惯记法 , 表示, 表示,因此我们也可说: 函数的自变量总用 x 表示,因变量总用 y 表示,因此我们也可说: 当 Z ( f ) ⊆ U 时 , y = f ( x ), x ∈ D 与 y = g ( x ), x ∈ U 可以 复合成 复合函数 : y = g ( f ( x ) ) ,x ∈ D .
第一章第4节 复合函数与初等函数

作 业
• 习题一的第16、17题(交) • 课外作业,习题一的1-20题中没做过的。
常见的经济函数
1、成本函数 某商品的成本是指生产一定数量的产品所需的全
部经济资源投入(劳力、原料、设备等)的价格或费用
总额,它由固定成本与可变成本组成. 平均成本是生产一定数量的产品,平均每单位产 品的成本. 在生产技术水平和生产要素的价格固定不变的条 件下,产品的成本与平均成本都是产量的函数. 成本函数 平均成本函数
3x 2 例如 函数 y ax bx c, y , 4x 6
2
x 1 x 2 x , x 0 而y x , y 1 x x2 xn e , x ≥ 0
5
y ln
( x 2 1) cos 2 x
等都是初等函数;
是非初等函数。 大部分分段函数不是初等函数。
例如 y arcsinu, u 2 x 2 ; y arcsin( 2 x 2 )
3、复合函数的中间变量可以不止一个,也就是可以由两个以上 的函数经过复合而成。
x 例如 y cot , 2
y u,
u cot v ,
v
x . 2
例 1:下列函数能否构成复合函数?若能,写出 y=f[g(x)],并求 其定义域: ( 1) y u ,
(2)幂函数:y=x (常数
x
x
)
a
(特别地,常用对数 y=lgx,自然对数 y=lnx) (5)三角函数:y=sinx, y=cosx, y=tanx, y=cotx, y=secx, y=cscx (6)反三角函数:y=arcsinx, y=arccosx, y=arctanx, y=arccotx,
基本初等函数公式及运算法则

基本初等函数公式及运算法则一、基本初等函数公式:1. 幂函数公式: $(a^m)^n=a^{mn}$;2. 对数函数公式: $\log_{a^n}b=\frac{1}{n}\log_ab$;3. 指数函数公式: $a^{\log_ab}=b$;4.三角函数公式:$\begin{aligned} (\sin x)^2+(\cos x)^2&=1\\ (\secx)^2&=1+(\tan x)^2 \\ (\csc x)^2&=1+(\cot x)^2 \end{aligned}$。
5.反三角函数公式:$\begin{aligned} \sin^{-1}x+\cos^{-1} x&=\frac{\pi}{2}\\\tan^{-1}x+\cot^{-1} x&=\frac{\pi}{2} \end{aligned}$。
6.双曲函数公式:$\begin{aligned} \cosh^2x-\sinh^2x&=1\\ \cos^2x+\sinh^2x&=1 \end{aligned}$。
二、基本初等函数运算法则:1.基本四则运算法则:加法、减法、乘法、除法;2. 复合函数法则:$(f\circ g)(x)=f(g(x))$;3. 取模运算法则:$(a+b)\bmod m=(a\bmod m+b\bmod m)\bmod m$;4. 取整函数法则:$\lfloor x+y\rfloor=\lfloorx\rfloor+\lfloor y\rfloor,\lceil x+y\rceil=\lceil x\rceil+\lceil y\rceil$;5.比较大小法则:对于正整数$a,b,c$,若。
$(1)\ a>b>0,c>0$,则$ac>bc$;$(2)\ a>b>0,c<0$,则$ac<bc$;$(3)\ a<b<0,c>0$,则$ac<bc$;$(4)\ a<b<0,c<0$,则$ac>bc$。
大一高数之函数
……
……
t 年后人口为p=9.6259×(1+12‰) t
即
p 9.6259 1.012t
到2005年底,即27年后, 我国人口为 p 9.6259 1.012 .
27
两边取常用对数, lg p lg 9.6259 27 lg1.012 4.9835 27 0.0051 5.1212, 查反对数表, p 13.22(亿).
即根据1978年的数据,可推算出2005年底 我国人口为13.22亿.
人口模型 : 设某地某年人口为p0,人口自然 增长率为r,那么t 年后的人口p为 p p0 (1 r ) .
t
马尔萨斯(malthus,英,1776 — 1834) 根据上述模型提出了他的人口理论,这一模 型只适用于生物种群的生存环境较为优雅宽 松的情况.当生物种群数量增长到一定值时, 恶化的生态环境将抑制种群数量的增长,进 而出现负增长,此时马尔萨斯人口模型就不 适用了.
A1 A(1 r )t ;
r 若每期结算m次,则每次利率为 , m t期内共结算mt次,t期后的本利和为
r mt Am A(1 ) . m 如果,即按照每个瞬间“即存即算” 来计算本利和,则归结为求极限
r mt lim A(1 ) m m
这个求极限问题将在第二章的应用中 介绍.
y cos x
正切函数
y tan x
π π 定义域 : ( kπ , kπ ), k Z; 值域( , ), 2 2 π π 以π 为周期, 在每个开区间( kπ , kπ )上 2 2 递增.
余切函数
y cot x
定义域 : kπ ,( k 1)π ), k Z;值域( , ), ( 以π 为周期, 在每个开区间( π ,( k 1)π ) k 上 递减.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的基本初等函数与复合函数函数作为数学中重要的概念,是数学研究的核心内容之一。
本文将
探讨函数的基本初等函数与复合函数,并介绍它们的定义、性质和应用。
1. 基本初等函数
基本初等函数是指一些常见的基本函数,包括常数函数、幂函数、
指数函数、对数函数、三角函数和反三角函数等。
每个基本初等函数
都有其独特的性质和特点。
1.1 常数函数
常数函数是指函数图像上所有的点都位于同一条水平线上,即对于
任意的x值,函数的取值都是一个常数。
常数函数的表达式为f(x) = C,其中C为常数。
1.2 幂函数
幂函数是指函数的定义域为全体实数,并且函数表达式为f(x) = x^a,其中a为实数指数。
幂函数的图像呈现出平滑的曲线,且取决于指数a
的不同而有不同的特征。
1.3 指数函数
指数函数是以常数e为底的幂函数,其定义域为全体实数。
指数函
数的表达式为f(x) = e^x,其中e约等于2.71828。
指数函数具有快速上
升的特点,是模型中常见的函数之一。
1.4 对数函数
对数函数是指以某个正实数为底的幂函数的反函数,其定义域为正实数集合。
对数函数的表达式为f(x) = log_a(x),其中a为底数。
对数函数具有递增且变化逐渐减缓的特点。
1.5 三角函数与反三角函数
三角函数包括正弦函数、余弦函数和正切函数等,其定义域为全体实数。
三角函数具有周期性和周期性平移的特点。
反三角函数是指三角函数的反函数,其定义域和值域视情况而定。
2. 复合函数
复合函数是指多个函数的组合形成的新的函数。
设有两个函数f(x)和g(x),则其复合函数为f(g(x))。
复合函数的性质取决于原函数之间的关系。
复合函数的定义要求满足两个函数的定义域和值域相互对应,且内层函数的值域必须是外层函数的定义域。
复合函数的运算法则是由内到外进行运算。
3. 应用
基本初等函数和复合函数在数学和实际问题中有着广泛的应用。
在数学上,基本初等函数是构建更复杂函数的基础,通过组合使用这些基本函数,可以推导出其他函数的性质和特点。
基本初等函数的研究为数学发展提供了坚实的基础。
在实际生活中,函数的应用非常广泛。
例如,指数函数可用于描述人口增长或物质衰变等自然现象;对数函数可用于解决与倍数关系相关的问题;三角函数可用于描述周期性变化的现象等等。
复合函数则可以帮助我们解决更为复杂的问题,例如经济学中的成本函数与收益函数的复合运用。
总结起来,基本初等函数与复合函数是数学中重要的概念和工具,具有广泛的应用领域。
通过深入了解其定义、性质和应用,我们可以更好地理解函数的本质和运用。
