高三数学-2018高考数学冲刺单选试题精选50道(代数部分
2018年江苏省高考冲刺压轴数学试卷(附答案)
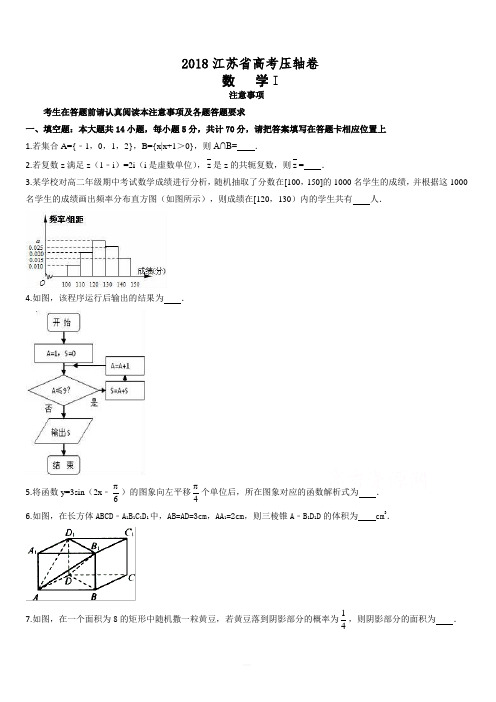
2018江苏省高考压轴卷数 学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求一、填空题:本大题共14小题,每小题5分,共计70分,请把答案填写在答题卡相应位置上 1.若集合A={﹣1,0,1,2},B={x|x+1>0},则A∩B= .2.若复数z 满足z (1﹣i )=2i (i 是虚数单位),z 是z 的共轭复数,则z = .3.某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有 人.4.如图,该程序运行后输出的结果为 .5.将函数y=3sin (2x ﹣6π)的图象向左平移4π个单位后,所在图象对应的函数解析式为 . 6.如图,在长方体ABCD ﹣A 1B 1C 1D 1中,AB=AD=3cm ,AA 1=2cm ,则三棱锥A ﹣B 1D 1D 的体积为 cm 3.7.如图,在一个面积为8的矩形中随机撒一粒黄豆,若黄豆落到阴影部分的概率为41,则阴影部分的面积为 .8.已知双曲线﹣=1(a>0,b>0)的左、右端点分别为A、B两点,点C(0, b),若线段AC的垂直平分线过点B,则双曲线的离心率为.9.设公比不为1的等比数列{a n}满足a1a2a3=﹣81,且a2,a4,a 3成等差数列,则数列{a n}的前4项和为.10.设定义在R上的偶函数f(x)在区间(﹣∞,0]上单调递减,若f(1﹣m)<f(m),则实数m的取值范围是.11.已知函数f(x)=,若a、b、c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是.12.如图,在△ABC中,已知AN=21AC,P是BN上一点,若AP=m AB+41AC,则实数m的值是.13.已知非零向量a,b满足|a|=|b|=|a+b|,则a与2a-b夹角的余弦值为.14.已知函数f(x)=⎩⎨⎧≥++-<1x,ax25x9x1x,xsin23,若函数f(x)的图象与直线y=x有三个不同的公共点,则实数a的取值集合为.15.如图,在三棱柱ABC A1B1C1中,AB AC,点E,F分别在棱BB1 ,CC1上(均异于端点),且∠ABE∠ACF,AE⊥BB1,AF⊥CC1.求证:(1)平面AEF⊥平面BB1C1C;(2)BC // 平面AEF.16.在△ABC中,角,,A B C的对边分别为,,a b c,且()2cos cosa b C c B-⋅=⋅.AA1B1C1BCFE(第16题)(1)求角C 的大小;(2)若2c =,△ABC 的面积为3,求该三角形的周长.17.已知中心在坐标原点的椭圆C ,F 1,F 2 分别为椭圆的左、右焦点,长轴长为6,离心率为(1)求椭圆C 的标准方程;(2)已知点P 在椭圆C 上,且PF 1=4,求点P 到右准线的距离.18.如图,四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为直角梯形,AD ∥BC ,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E ,F ,G 分别为BC ,PD ,PC 的中点. (1)求EF 与DG 所成角的余弦值;(2)若M 为EF 上一点,N 为DG 上一点,是否存在MN ,使得MN ⊥平面PBC ?若存在,求出点M ,N 的坐标;若不存在,请说明理由.19.设等比数列a 1,a 2,a 3,a 4的公比为q ,等差数列b 1,b 2,b 3,b 4的公差为d ,且10q d ≠≠,. 记i i i c a b =+(i1,2,3,4).(1)求证:数列123c c c ,,不是等差数列; (2)设11a =,2q =.若数列123c c c ,,是等比数列,求b 2关于d 的函数关系式及其定义域; (3)数列1234c c c c ,,,能否为等比数列?并说明理由. 20.(16分)已知f (x )=x 2+mx+1(m ∈R ),g (x )=e x .(1)当x ∈[0,2]时,F (x )=f (x )﹣g (x )为增函数,求实数m 的取值范围; (2)若m ∈(﹣1,0),设函数 G(x)=)x (g )x (f ,H(x)=﹣41x+45,求证:对任意x 1,x 2∈[1,1﹣m],G (x 1)<H (x 2)恒成立.数学II (附加题)注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页,均为非选择题(第21题 ~第23题)。
2018年高考数学三轮冲刺点对点试卷函数导数三角函数含

函数、导数、三角函数1.已知函数()21ln 2f x a x x =+,在其概念域内任取两个不等实数1x 、2x ,不等式()()12123f x a f x a x x +-+>-恒成立,那么实数a 的取值范围为A. [)2,+∞B. (],2-∞C. 9[,)4+∞ D. 90,4⎛⎤ ⎥⎝⎦ 【答案】A2.已知函数()()22log f x a x a =++(0a >)的最小值为8,那么( )A. ()5,6a ∈B. ()7,8a ∈C. ()8,9a ∈D. ()9,10a ∈【答案】A3.函数()111x f x n x+=-的大致图象为( ) A.B. C. D.【答案】D 4.假设曲线212y x e=与曲线ln y a x =在它们的公共点(),P s t 处具有公共切线,那么实数a =( ) A. 1 B. 12 C. 1- D. 2 【答案】A5.已知角α的极点与原点O 重合,始边与x 轴的正半轴重合,假设它的终边通过点()21P ,,那么tan 24πα⎛⎫+= ⎪⎝⎭A. -7B. 17-C. 17D. 7 【答案】A 6.已知函数2tan 3y x πω⎛⎫=+ ⎪⎝⎭的最小正周期为2π,将函数2sin (0)6y x πωω⎛⎫=+> ⎪⎝⎭的图象沿x 轴向右平移4π个单位,取得函数()y f x =的图象,那么函数()f x 在,44ππ⎡⎤-⎢⎥⎣⎦的值域为( ) A. 3,12⎡⎤-⎢⎥⎣⎦ B. 11,22⎡⎤-⎢⎥⎣⎦ C. []1,1- D. 11,2⎡⎤-⎢⎥⎣⎦【答案】D7.假设函数对任意的,总有()()10f mx f x -+>恒成立,那么x 的取值范围是( )A.B. C. D.【答案】A8.假设函数的图像如下图,那么实数的值可能为( )A.B. C. D.【答案】B9.假设函数的图象关于直线对称,那么的最小值为( ) A. B. 1/2 C. D. 【答案】C10.已知是概念在R 上的偶函数,当时,,假设,那么a 的取值范围为( )A. B. C. D.【答案】B11.已知函数()f x 是概念在()0,+∞的可导函数, ()f x '为其导函数,当0x >且1x ≠时, ()()201f x xf x x -'+>,假设曲线()y f x =在1x =处的切线的斜率为34-,那么()1f =( ) A. 0 B. 1 C.38 D. 15 【答案】C12.假设曲线2ln y x ax =+(a 为常数)不存在斜率为负数的切线,那么实数a 的取值范围是( ) A. 1,2⎛⎫-+∞ ⎪⎝⎭ B. 1,2⎡⎫-+∞⎪⎢⎣⎭ C. ()0,+∞ D. [)0,+∞ 【答案】D13.设函数()232(0)2f x x ax a =->与()2g x a lnx b =+有公共点,且在公共点处的切线方程相同,那么实数b 的最大值为( )A. 212eB. 212eC. 1eD. 232e- 【答案】A14.函数的最小值为 ( ) A. B. C. D.【答案】C15.假设函数的图象向左平移个单位,取得函数的图象,那么以下关于表达正确的选项是( )A.的最小正周期为 B. 在内单调递增 C. 的图象关于对称 D. 的图象关于对称 【答案】C16.已知当时,函数取得极大值,那么( ) A. 1/2 B. 2/3 C.D. 【答案】D17.已知函数()2ax f x x =- ,假设()43f x f x ⎛⎫+= ⎪⎝⎭,()()4f x f x b +-=,那么a ,b 的值依次为( ) A .3,3 B .-3,3 C .3,6 D .【答案】C18.在[]0,6上任取实数a ,()12f x x a=-在[]1,2上递减的概率为 ( ) A .16 B .13 C .12 D .23【答案】D 19. 已知函数()[)()232,0,32,,0x x f x x a a x ⎧∈+∞⎪=⎨+-+∈-∞⎪⎩在区间(),-∞+∞上是增函数,那么常数a 的取值范围是 ( )A .()1,2B .(][),12,-∞+∞ C .[]1,2 D .()(),12,-∞+∞ 【答案】C20.已知曲线2()ln(1)f x x a x =++在原点处的切线方程为y x =-,那么a =________.【答案】-121.已知函数1)(+-=mx e x f x 的图像为曲线C ,假设曲线C 存在与直线ex y =垂直的切线,那么实数m 的取值范围为( )A .),[+∞eB .),(+∞eC .),1(+∞eD .)1,(e-∞【答案】C 22.已知函数()0()210x e a x f x a R x x ⎧+≤=∈⎨->⎩,假设函数()f x 在R 上有两个零点,那么a 的取值范围是( ) A .(),1-∞- B .(),0-∞ C .()1,0- D .[)1,0-23. 已知函数x x x x f cos 56sin 5)(+-=,那么对任意实数)0(,≠+b a b a ,ba b f a f ++)()(的值 ( ) A.恒大于0 B.恒等于0 C.恒小于0 D.符号不确信【答案】A.24.若sin tan 2x x =,那么22sin tan x x -=( )A .2B .2-C .4D .4-【答案】D。
2018年全国各地高考数学模拟试题代数专题试题汇编(含答案解析)

2018年全国各地高考数学模拟试题代数部分解答题汇编(含答案解析)1.(2018•海南二模)设函数f(x)=|x+a|+2a.(1)若不等式f(x)≤1的解集为{x|﹣2≤x≤4},求a的值;(2)在(1)的条件下,若不等式f(x)≥k2﹣k﹣4恒成立,求k的取值范围.2.(2018•芗城区校级一模)某工厂统计资料显示,一种产品次品率p与日产量x(件)(x∈N,0<x≤100)之间的关系如表:已知生产一件正品盈利a元,生产一件次品损失元.(Ⅰ)试将该厂的日盈利额y(元)表示为日产里x(件)的函数;(Ⅱ)为获取最大盈利,该厂的日产里x应定为多少件?3.(2018•芗城区校级一模)设常数a>0,函数(Ⅰ)当时,求函数f(x)的极大值和极小值;(Ⅱ)若函数f(x)在其定义域内为增函数,求a的取值范围.4.(2018•兴庆区校级三模)设f(x)=|x﹣1|+2|x+1|的最小值为m.(1)求m的值;(2)设a、b∈R,a2+b2=m,求+的最小值.5.(2018•兰州模拟)已知向量,,函数.(1)求f(x)的最小正周期;(2)当时,f(x)的最小值为5,求m的值.6.(2018•麒麟区校级模拟)已知向量=(2,1),=(x,﹣2),⊥(+),则实数x的值是.7.(2018•鄂伦春自治旗二模)在等差数列{a n}中,a3n=6n﹣1.(1)求数列{a n}的通项公式;(2)设数列的前n项和为S n,证明:.8.(2018•房山区二模)已知等差数列{a n}满足a1+a2=10,a4﹣a3=2.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设等比数列{b n}满足b2=a3,b3=a7.问:b5与数列{a n}的第几项相等?9.(2018•海拉尔区校级二模)已知向量(x∈R),设函数f(x)=﹣1.(1)求函数f(x)的单调增区间;(2)已知△ABC的三个内角分别为A,B,C,若∠A为锐角且f(A)=2,B=,边AB=3,求边BC.10.(2018•蚌埠二模)已知等差数列{a n}满足a2=2,a1+a4=5.(I)求数列{a n}的通项公式;(II)若数列{b n}满足:b1=3,b2=6,{b n﹣a n}为等比数列,求数列{b n}的前n项和T n.11.(2018•凌源市模拟)已知数列{a n}的前n项和为S n满足S n=,且a1﹣1,2a2,a3+7成等差数列.(1)求数列{a n}的通项公式;(2)令b n=2log9a n(n∈N*),求数列的前n项和T n.12.(2018•淄博一模)已知{a n}是公差为3的等差数列,数列{b n}满足.(1)求数列{a n}的通项公式;(2)求数列{b n}的前n项和S n.13.(2018•潍坊二模)已知等比数列{a n}的前n项和为S n,a1=2,a n>0(n∈N*),S6+a6是S4+a4,S5+a5的等差中项.(1)求数列{a n}的通项公式;(2)设,数列的前n项和为T n,求T n.14.(2018•东莞市二模)已知等比数列{a n}与等差数列{b n},a1=b1=1,a1≠a2,a1,a2,b3成等差数列,b1,a2,b4成等比数列.(Ⅰ)求{a n},{b n}的通项公式;(Ⅱ)设S n,T n分别是数列{a n},{b n},的前n项和,若S n+T n>100,求n的最小值.15.(2018•石景山区一模)等差数列{a n}中,a2=4,其前n项和S n满足.(Ⅰ)求实数λ的值,并求数列{a n}的通项公式;(Ⅱ)若数列是首项为λ、公比为2λ的等比数列,求数列{b n}的前n 项的和T n.16.(2018•荆州区校级二模)已知数列{a n}是递增的等差数列,a2=3,若a1,a3﹣a1,a8+a1成等比数列.(1)求数列{a n}的通项公式;(2)若b n=,数列{b n}的前n项和S n,求S n.17.(2018•天津一模)某大型企业计划在A、B两市举行新产品推介会,受产品时效性和成本影响,新产品推介会总时间不能超过30天,且在A市时间不少于B市,推介会总费用不超过5万元.在A、B两市举行新产品推介会的费用分别为每天0.2万元和0.1万元,销售纯收益分别为每天3万元和2万元.分别用x,y表示该企业计划在A、B两市举行新产品推介会的天数.(Ⅰ)用x,y列出满足条件的数学关系式,并画出相应的平面区域;(Ⅱ)该企业如何分配在A、B两市做新产品推介会的天数,才能使企业获得的销售纯收益最大?最大销售纯收益是多少?18.(2018•济南一模)记S n为数列{a n}的前n项和,已知,n∈N*.(1)求数列{a n}的通项公式;(2)设,求数列{b n}的前n项和T n.19.(2018•浉河区校级二模)设f(x)=|x+1|﹣|2x﹣1|,(1)求不等式f(x)≤x+2的解集;(2)若不等式满足f(x)≤|x|(|a﹣1|+|a+1|)对任意实数x≠0恒成立,求实数a的取值范围.20.(2018•澧县校级一模)设函数的定义域为集合A,函数g (x)=﹣x2+2x+a(0≤x≤3,a∈R)的值域为集合B.(1)求的值;(2)若A∩B=∅,求实数a的取值范围.21.(2018•新昌县校级模拟)已知向量,函数(Ⅰ)求函数f(x)的最大值和单调递增区间;(Ⅱ)在△ABC中,角A,B,C所对边分别为a,b,c,满足b2=ac且,求值.22.(2018•成都模拟)已知公差不为零的等差数列{a n}中,a3=7,且a1,a4,a13成等比数列.(1)求数列{a n}的通项公式;(2)记数列的前n项和S n,求S n.23.(2018•益阳模拟)已知{a n}是各项均为正数的等差数列,且数列{}的前n项和为,n∈N*(1)求数列{a n}的通项公式;(2)若数列{a n}的前n项和为S n,数列{}的前n项和T n,求证T n.24.(2018•全国一模)已知数列{a n}的前n项和为.(1)求数列{a n}的通项公式;(2)设b n=log2a n,求.25.(2018•广西二模)已知公差不为0的等差数列{a n}的前n项和S n,S1+1,S3,S4成等差数列,且a1、a2,a5成等比数列.(1)求数列{a n}的通项公式;(2)若S4,S6,S n成等比数列,求n及此等比数列的公比.26.(2018•宿州三模)已知数列{a n}的前n项和为S n,数列{S n}的前n项和为T n,满足.(Ⅰ)证明数列{a n+2}是等比数列,并求出数列{a n}的通项公式;(Ⅱ)设b n=n•a n,求数列{b n}的前n项和K n.27.(2018•全国四模)已知等差数列{a n}的前n项和为S n,且S4﹣S2=7a1,S5=30.(1)求{a n}的通项公式a n;(2)设b n=,数列{b n}的前n项和T n<log2(m2﹣m)对任意n∈N*恒成立,求实数m的取值范围.28.(2018•黔东南州一模)各项均为正数的等比数列{a n}的前n项和为S n.已知a1=3,S3=39.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设数列{c n}满足,求数列{c n}的前n项和T n.29.(2018•深圳一模)设数列{a n}的前n项和为S n,a1=2,a n+1=2+S n,(n∈N*).(I)求数列{a n}的通项公式;(Ⅱ)设b n=log2(a n)2,求数列{}的前n项和T n30.(2018•上饶二模)已知数列{a n}的前n项和.(1)求数列{a n}的通项公式;(2)设b n=log2(a n﹣1),求.31.(2018•黑龙江模拟)已知数列{a n}中,a1=1,又数列{}(n∈N*)是公差为1的等差数列.(1)求数列{a n}的通项公式a n;(2)求数列{a n}的前n项和S n.32.(2018•重庆模拟)将函数f(x)=2sin(x﹣)+cosx在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{a n}(n∈N*)(1)求数列{a n}的通项公式;(2)设b n=,数列{b n}的前n项和为T n,求T n的表达式.33.(2018•葫芦岛二模)已知函数f(x)=(a,b∈R且a≠0,e为自然对数的底数).(1)若曲线f(x)在点(e,f(e))处的切线斜率为0,且f(x)有极小值,求实数a的取值范围;(2)当a=b=1时,证明:xf(x)+2<0.34.(2018•上饶二模)数列{a n}的前n项和为S n,且,数列{b n}为等差数列,且.(1)分别求数列{a n}和{b n}的通项公式;(2)求数列{a n b n}的前n项和T n.35.(2018•淄博二模)已知等比数列{a n}的前n项和为S n,数列是公差为1的等差数列,若a1=2b1,a4﹣a2=12,S4+2S2=3S3.(I)求数列{a n},{b n}的通项公式;(II)设c n=,T n为{c n}的前n项和,求T2n.36.(2018•河南一模)设正项等比数列{a n},a4=81,且a2,a3的等差中项为.(I)求数列{a n}的通项公式;(II)若b n=log3a2n﹣1,数列{b n}的前n项和为S n,数列,T n 为数列{c n}的前n项和,若T n<λn恒成立,求λ的取值范围.37.(2018•黔东南州二模)已知数列{a n}的前n项和为S n,且满足S n=(a n﹣1),n∈N*.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=log2a n,记数列{}的前n项和为T n.证明:T n.38.(2018•南平一模)已知等差数列{a n}满足a3=6,前7项和为S7=49.(1)求{a n}的通项公式;(2)设数列{b n}满足,求{b n}的前n项和T n.39.(2018•榆林二模)已知正项数列{a n}满足a1=1,a+a n=a﹣a n+1,数列{b n}的前n项和S n满足S n=n2+a n.(1)求数列{a n},{b n}的通项公式;(2)求数列{}的前n项和T n.40.(2018•湖南模拟)设S n是数列{a n}的前n项和,已知a1=1,S n=2﹣2a n+1.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设,求数列{b n}的前n项和T n.参考答案与试题解析1.【分析】(1)|x+a|+2a≤1即2a﹣1≤x+a≤1﹣2a,所以a﹣1≤x≤1﹣3a,根据﹣2≤x≤4即可求出a的值;(2)不等式f(x)≥k2﹣k﹣4恒成立即为,显然|x﹣1|﹣2的最小值为﹣2,最后即可解出k的范围.【解答】解:(1)因为|x+a|+2a≤1,所以|x+a|≤1﹣2a,所以2a﹣1≤x+a≤1﹣2a,所以a﹣1≤x≤1﹣3a.因为不等式f(x)≤1的解集为{x|﹣2≤x≤4},所以,解得a=﹣1.(2)由(1)得f(x)=|x﹣1|﹣2.要使不等式f(x)≥k2﹣k﹣4恒成立,只需,所以﹣2≥k2﹣k﹣4,即k2﹣k﹣2≤0.所以k的取值范围是[﹣1,2].【点评】本题考查了不等式恒成立的问题,将恒成立问题转化为求最值是解题关键,属于中档题.2.【分析】(Ⅰ)由生产一件正品盈利a元,生产一件次品损失元,可得y=ax•(1﹣)﹣•x•,化简可得所求函数式;(Ⅱ)令t=108﹣x,可得x=108﹣t,转化为t的函数,运用基本不等式,即可得到所求最大值,相应的x的值.【解答】解:(Ⅰ)生产一件正品盈利a元,生产一件次品损失元,可得y=ax•(1﹣)﹣•x•=•,x∈N,0<x≤100;(Ⅱ)令t=108﹣x,可得x=108﹣t,可得f(t)=a(108﹣t)•(1﹣)﹣﹣(108﹣t)•=﹣a(t+)+≤﹣a•2+=a.当且仅当t=12,即x=96时,上式取得等号,为获取最大盈利,该厂的日产里x应定为96件.【点评】本题考查函数在实际问题中的运用,考查基本不等式的运用:求最值,以及化简运算能力,属于中档题.3.【分析】(Ⅰ)求得f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,可得极值;(Ⅱ)若函数f(x)在其定义域内为增函数,可得f′(x)≥0在[0,+∞)恒成立,运用参数分离和可化为二次函数的最值求法,可得a的范围.【解答】解:(Ⅰ)当时,f(x)=﹣ln(x+)的导数为f′(x)=﹣==,当<x<时,f′(x)<0,f(x)递减;当x>或0<x<时,f′(x)>0,f(x)递增,可得f(x)的极大值为f()=;f(x)的极小值为f()=﹣ln3;(Ⅱ)若函数f(x)在其定义域内为增函数,可得f′(x)≥0在[0,+∞)恒成立,即为:﹣≥0在[0,+∞)恒成立,可得a≥﹣x+2的最大值,由﹣x+2=﹣(﹣1)2+1,可得x=1时,取得最大值1,则a≥1.【点评】本题考查导数的运用:求单调性和极值,考查参数分离和可化为二次函数的最值求法,以及运算能力,属于中档题.4.【分析】(1)利用零点取绝对值,即可求解最小值;(2)构造基本不等号式,利用乘以“1”法求解即可;【解答】解:(1)由f(x)=|x﹣1|+2|x+1|=根据图象可知f(x)最小值为m=2.(2)由a2+b2=2,可得a2+1+b2+1=4,∴那么:+=(+)()=(当且仅当4(a2+1)=b2+1时取等号)即+的最小值为.【点评】本题主要考查函数最值的求解,根据基本不等式的性质以及零点分段法是解决本题的关键.5.【分析】(1)根据向量的数量积公式和两角和的正弦公式可化简可得f(x)=,再根据周期的定义即可求出,(2)根据正弦函数的性质即可求出m的值.【解答】(1)由题意知:f(x)=cos(2x,sin2x)•(,1)==,所以f(x)的最小正周期为T=π.(2)由(1)知:,当时,.所以当时,f(x)的最小值为.又∵f(x)的最小值为5,∴,即.【点评】本题考查了向量的数量积和三角函数的化简和性质,考查了运算能力,属于基础题.6.【分析】利用平面向量运算法则先求出=(2+x,﹣1),再由⊥(+),能求出实数x的值.【解答】解:∵向量=(2,1),=(x,﹣2),∴=(2+x,﹣1),∵⊥(+),∴=2(2+x)+1×(﹣1)=0,解得x=﹣.∴实数x的值是﹣.【点评】本题考查实数值的求法,考查平面向量坐标运算法则、向量垂直的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.7.【分析】(1)由题意可得,解得即可,(2)根据等比数列的求和公式,即可证明【解答】解:(1)∵a3n=6n﹣1,∴a3=5,a6=11,∴,解得,∴a n=2n﹣1.证明:(2)∵=,∴.【点评】本题考查了等差数列的通项公式和等比数列的求和公式,属于基础题8.【分析】(Ⅰ)设公差为d的等差数列{a n},运用等差数列的通项公式,解方程可得首项和公差,即可得到所求;(Ⅱ)设公比为q的等比数列{b n},运用等比数列的通项公式可得公比和首项,即可得到所求b5,结合等差数列的通项公式,解方程即可得到所求值.【解答】解:(Ⅰ)设公差为d的等差数列{a n}满足a1+a2=10,a4﹣a3=2,可得2a1+d=10,d=2,解得a1=4,则a n=4+2(n﹣1)=2n+2;(Ⅱ)设公比为q的等比数列{b n}满足b2=a3,b3=a7,可得b2=8,b3=16,则公比q==2,b1=4,则b n=4•2n﹣1=2n+1,由2n+2=b5=26,解得n=31,则b5与数列{a n}的第31项相等.【点评】本题考查等差数列和等比数列的通项公式的运用,考查方程思想和运算能力,属于基础题.9.【分析】利用向量的数量积求出函数的解析式并化简三角函数式,利用三角函数的性质解得本题.【解答】解:由已知得到函数f(x)=﹣1=2cos2x+2sinxcosx﹣1=cos2x+sin2x=2cos(2x﹣);所以(1)函数f(x)的单调增区间是(2x﹣)∈[2kπ﹣π,2kπ],即x∈[kπ﹣,kπ+],k∈Z;(2)已知△ABC的三个内角分别为A,B,C,f(A)=2,则2cos(2A﹣)=2,因为∠A为锐角,所以A=,又B=,边AB=3,所以由正弦定理得,即,解得BC=.【点评】本题考查了向量的数量积公式、三角函数式的化简以及三角函数性质和解三角形,属于中档题.10.【分析】(Ⅰ)由题意可得,解得a1=d=1,即可求出通项公式,(Ⅱ)b1=3,b2=6,{b n﹣a n}为等比数列,求出b n=n+2n,再分组求和即可.【解答】解:(Ⅰ)等差数列{a n}满足a2=2,a1+a4=5,则,解得a1=d=1,∴a n=1+(n﹣1)=n,(Ⅱ)∵b1=3,b2=6,{b n﹣a n}为等比数列,设公比为q,∴b1﹣a1=3﹣1=2,b2﹣a2=6﹣2=4,∴q=2,∴b n﹣a n=2×2n﹣1=2n,∴b n=n+2n,∴数列{b n}的前n项和T n=(1+2+3+…+n)+(2+22+…++2n)=+=+2n+1﹣2.【点评】本题考查了等差数列和等比数列的通项公式和求和公式,考查了运算能力,属于基础题.11.【分析】(1)根据a n=S n﹣S n﹣1可得出{a n}的递推公式,于是{a n}为等比数列,根据a1﹣1,2a2,a3+7成等差数列解方程计算a1即可得出a n;(2)计算b n=,使用裂项法求和.【解答】解:(1)由得2S n=3a n﹣a1,由,做差得a n=3a n﹣1(n≥2),∴数列{a n}是公比为3的等比数列,又a1﹣1,2a2,a3+7成等差数列,4a2=a1+a3+6,即12a1=a1+9a1+6,解得a1=3,∴.(2)b n=2log93n=n,∴,∴.【点评】本题考查了等比数列的性质,裂项法求和,属于基础题.12.【分析】(1)根据等差数列的定义即可求出通项公式,(2)由数列的递推公式可得{b n}是首项为、公比为的等比数列,再根据等比数列的求和公式即可求出.【解答】解:(1)由已知a1b2=b1+b2且,得a1=4,∴{a n}是首项为4,公差为3的等差数列,通项公式为a n=4+(n﹣1)×3=3n+1;(2)由(1)知a n b n+1=nb n+b n+1,得:(3n+1)b n+1﹣b n+1=nb n,∴,因此{b n}是首项为、公比为的等比数列,则.【点评】本题考查了数列的递推公式公式判断等差数列或等比数列,考查了等比数列的求和公式,属于基础题.13.【分析】(1)根据S6+a6是S4+a4,S5+a5的等差中项建立关系,a1=2,即可求解数列{a n}的通项公式(2)设,将{a n}的通项公式带入化简可得{b n}的通项公式,利用裂项相消法前n项和为T n,【解答】解:(1)∵S6+a6是S4+a4,S5+a5的等差中项.∴2(S4+a4)=S4+a4+S5+a5化简得4a6=a4∵a1=2,{a n}是等比数列,设公比为q,则.∵a n>0(n∈N*),∴q>0∴q=∴数列{a n}的通项公式a n==;(2)由==2n﹣3.∴数列{b n}的通项公式b n=2n﹣3.那么:==()数列的前n项和为T n=(﹣1﹣1)+(1﹣)+()+……+()=﹣1﹣=.【点评】本题考查了等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于基础题.14.【分析】(Ⅰ)设数列{a n}的公比为q,数列{b n}的公差为d,d≠0,运用等比数列和等差数列中项的性质,可得d,q的方程组,解方程即可得到所求通项;(Ⅱ)运用等比数列和等差数列的求和公式,结合数列的单调性,即可得到所求n的最小值.【解答】解:(Ⅰ)设数列{a n}的公比为q,数列{b n}的公差为d,d≠0,a1,a2,b3成等差数列,b1,a2,b4成等比数列,可得a1+b3=2a2,a22=b1b4,则解得(舍)或,∴.(Ⅱ)由(Ⅰ)易知.由S n+T n>100,得,∵是单调递增数列,且,∴n的最小值为7.【点评】本题考查等比数列、等差数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于基础题.15.【分析】(I)利用a2=S2﹣S1=4+2λ﹣1﹣λ=4,求出λ=1,再利用数列中a n与S n关系求通项公式.(II)求出数列的通项公式,再得出数列{b n}的通项公式,最后根据通项公式形式选择相应方法求和.【解答】解:(I)因为a2=S2﹣S1=4+2λ﹣1﹣λ=4,解得λ=1∴当n≥2时,则=2n,当n=1时,也满足,所以a n=2n.(II)由已知数列是首项为1、公比为2的等比数列其通项公式为,且首项,故,=2n﹣1=,T n=(1+21+…+2n﹣1)…﹣[(1﹣)+()+…+()]=2n﹣1﹣.【点评】本题考查利用数列中a n与S n关系求通项公式.数列公式法、裂项法求和.考查转化、计算能力.16.【分析】(1)直接利用等差数列的性质求出数列的通项公式.(2)利用裂项相消法求出数列的和.【解答】解:(1)设{a n}的公差为d,d>0,由条件得,∴,∴a n=1+2(n﹣1)=2n﹣1.(2),∴S n=(1﹣+﹣+…+﹣)=.【点评】本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用.17.【分析】(Ⅰ)根据题意列出x、y满足的不等式组,画出不等式组表示的平面区域;(Ⅱ)根据图形找出最优解,计算目标函数的最大值即可.【解答】解:(Ⅰ)根据题意知,x,y满足的条件为,目标函数是z=3x+2y,画出不等式组表示的平面区域,如图所示;(Ⅱ)根据图形知,当目标函数过点M时,z取得最大值;由,解得M(20,10),即企业在A市推销20天,B市推销10天,才能使企业获得的销售纯收益最大,且最大销售纯收益是z=3×20+2×10=80(万元).【点评】本题考查了简单的线性规划实际应用问题,是基础题.18.【分析】(1)根据数列的,n∈N*.利用a n=S n﹣S n﹣1.求通项公式即可.(2)化简数列的通项公式,利用裂项消项法求解数列的和即可.【解答】解:(1)由,得当n=1时,a1=S1=3;当n≥2时,a n=S n﹣S n﹣1=2n2+n﹣[2(n﹣1)2+(n﹣1)]=4n﹣1.所以a n=4n﹣1.(2)==,所以=.【点评】本题主要考查数列通项公式和前n项和的求解,利用累加法和分组求和法是解决本题的关键.19.【分析】(1)利用x的范围去掉绝对值符号,然后求解不等式的解集即可.(2)不等式f(x)≤|x|(|a﹣1|+|a+1|)等价于≤|a﹣1|+|a+1|,利用绝对值不等式的几何意义求解左侧的最值,然后求解a的范围即可.【解答】解:(1)根据题意可得,当x<﹣1时,﹣x﹣1+2x﹣1≤x+2,解得﹣2<2,所以x<﹣1;…(1分)当﹣1≤x时,x+1+2x﹣1≤x+2,解得x≤1,所以﹣1;…(2分)当x时,x+1﹣2x+1≤x+2,解得x≥0,所以x;…(3分)综上,不等式f(x)≤x+2的解集为R…(5分)(2)不等式f(x)≤|x|(|a﹣1|+|a+1|)等价于≤|a﹣1|+|a+1|,…(6分)因为||=≤=3,…(8分)当且仅当时取等号,因为≤|a﹣1|+|a+1|,所以|a﹣1|+|a+1|≥3,解得a或a,故实数a的取值范围为(﹣∞,﹣]∪[,+∞)…(10分)【点评】本题考查不等式恒成立,绝对值不等式的解法,考查转化思想以及分类讨论思想的应用.20.【分析】(1)说明函数f(x)为奇函数,可得的值;(2)利用配方法求解集合B,再由集合间的关系得关于a的不等式求解.【解答】解:(1).由,得﹣1<x<1,∴函数f(x)的定义域为A=(﹣1,1).又,∴f(x)为奇函数,∴=0;(2)∵函数g(x)=﹣x2+2x+a=﹣(x﹣1)2+1+a在[0,3]上g min(x)=g(3)=a ﹣3,g max(x)=g(1)=a+1,∴B=[a﹣3,a+1].∵A∩B=∅,∴a﹣3≥1或a+1≤﹣1,解得a≤﹣2或a≥4.∴实数a的取值范围为(﹣∞,﹣2]∪[4,+∞).【点评】本题考查函数的定义域及值域的求法,考查集合间的关系的判定及应用,是中档题.21.【分析】(Ⅰ)根据向量的数量积和三角函数的化简,以及正弦函数的性质即可求出,(Ⅱ)根据余弦定理先求出B的范围,再求出B,即可求出答案.【解答】解:(Ⅰ)f(x)=•﹣=sinxcosx+sin2x﹣=sin2x﹣cos2x=sin (2x﹣),∵﹣1≤sin(2x﹣)≤1,∴f(x)的最大值为1,∵﹣+2kπ≤2x﹣≤+2kπ,k∈Z,∴﹣+kπ≤x≤+kπ,k∈Z,故函数f(x)的单调递增区间为[﹣+kπ,+kπ],k∈Z;(Ⅱ)∵b2=ac,∴cosB==≥=,∴0<B<∵f(B)=,∴sin(2B﹣)=,∴2B﹣=或2B﹣=,解得B=或B=(舍去),∴A+C=π﹣=,∴sin(A+C)=sinAcosC+cosAsinC=sin=把b2=ac,利用正弦定理化简得:sin2B=sinAsinC,∴sinAsinC=,∴+=+===2/【点评】本题考查了向量的数量积和三角函数的化简和求值,以及正弦定理和余弦定理,属于中档题.22.【分析】(1)设等差数列{a n}的公差为d(d≠0),由已知列关于首项与公差的方程组,得首项与公差,代入等差数列的通项公式得答案;(2)直接利用错误相减法求数列的前n项和S n.【解答】解:(1)设等差数列{a n}的公差为d(d≠0),由a3=7,且a1,a4,a13成等比数列,得,解得a1=3,d=2.∴a n=3+2(n﹣1)=2n+1;(2)∵,∴数列的前n项和S n=3•21+5•22+…+(2n+1)•2n,,∴=,∴S n=2﹣(1﹣2n)×2n+1.【点评】本题考查等差数列的通项公式与等比数列的性质,考查错位相减法求数列的前n项和,是中档题.23.【分析】(1)根据{a n}是各项均为正数的等差数列,依次令n=1,n=2,建立方程组即可求a1,公差d,可得通项公式;(2)利用裂项相消法求解数列{}的前n项和T n,即可证明;【解答】解:(1)由{a n}是各项均为正数的等差数列,且数列{}的前n 项和为,n∈N*当n=1时,可得=……①当n=2时,可得+=……②②﹣①得:∴a1×(a1+d)=6,……③(a1+d)(a1+2d)=12……④.由③④解得:.∴数列{a n}的通项公式为:a n=n+1;(2)由(1)可得,那么==.∴数列{}的前n项和T n=)===,n∈N*,∴T n.【点评】本题主要考查数列通项公式和前n项和的求解,利用裂项相消法是解决本题的关键.24.【分析】(1)根据数列的递推公式即可求出,(2)根据对数的运算性质和裂项求和,即可求出结果.【解答】解:(1)当n≥2时,a n=S n﹣S n﹣1=(23n+1﹣2)﹣(23n﹣2﹣2)=23n﹣2,当n=1时,a1=S1=23×1﹣2,符合上式∴a n=23n﹣2,(n∈N*).(2)由(1)得b n=log2a n=3n﹣2,∴==(﹣),∴=[(1﹣)+(﹣)+…+(﹣)]=(1﹣)=【点评】本题考查了数列的递推公式和裂项求和,考查了运算能力,属于中档题25.【分析】(1)设等差数列{a n}的公差为d≠0.S1+1,S3,S4成等差数列,且a1、a2,a5成等比数列,可得2S3=S1+1+S4,=a1a5,即a2+a3=1+a4,=a1(a1+4d),d≠0.解出即可得出.(2)由(1)可得:S n==n2,可得s4=42=16,s6=62=36.s4,s6,s n成等比数列,可得=S4•S n,362=16×n2,解出即可得出.【解答】解:(1)设等差数列{a n}的公差为d≠0.∵S1+1,S3,S4成等差数列,且a1、a2,a5成等比数列,∴2S3=S1+1+S4,=a1a5,即a2+a3=1+a4,=a1(a1+4d),d≠0.可得a1=1,d=2.∴a n=1+2(n﹣1)=2n﹣1.(2)由(1)可得:S n==n2,∴s4=42=16,s6=62=36.∵s4,s6,s n成等比数列,∴=S4•S n,∴362=16×n2,化为:36=4n,解得n=9.此等比数列的公比==.【点评】本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.26.【分析】(I)由得:a1=2a1﹣1,解得a1=S1=1,由S1+S2=2S2﹣4,解得a2.当n≥2时,S n=T n﹣T n﹣1,可得:S n=2S n﹣1+2n﹣1,S n+1=2S n+2n+1,相减即=2a n+2.变形为:a n+1+2=2(a n+2),又a2+2=2(a1+2),利用通项公式可得出a n+1即可得出.(Ⅱ)由,再利用错位相减法与求和公式即可得出.【解答】解:(I)由得:a1=2a1﹣1,解得a1=S1=1,由S1+S2=2S2﹣4,解得a2=4.当n≥2时,S n=T n﹣T n﹣1=,即S n=2S n﹣1+2n﹣1,①S n+1=2S n+2n+1②由②﹣①得a n=2a n+2.+1+2=2(a n+2),又a2+2=2(a1+2),∴a n+1所以数列{a n+2}是以a1+2=3为首项,2为公比的等比数列,∴,即.(Ⅱ)∵,∴﹣2(1+2+…+n)=3(1•20+2•21+…+n•2n﹣1﹣n2﹣n.记③,④,由③﹣④得=(1﹣n)•2n﹣1,∴.∴.【点评】本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、错位相减法,考查了推理能力与计算能力,属于中档题.27.【分析】(1)直接利用已知条件求出数列的通项公式.(2)利用裂项相消法求出数列的和,进一步利用放缩法求出参数的取值范围.【解答】解:(1)设等差数列{a n}的首项为a1,公差为d,则由S4﹣S2=7a1,S5=30,得,所以a n=2+(n﹣1)×2=2n,即a n=2n.(2)由(1)可得S n=n(n+1),所以…………8分.易知{T n}在n∈N*增,当n→+∞时,T n→1所以.【点评】本题考查的知识要点:数列的通项公式的求法及应用,利用裂项相消法求出数列的和及参数的取值范围.28.【分析】(Ⅰ)由a1=3,S3=39,知q2+q﹣12=0.故q=3,或q=﹣4,由此能求出,(Ⅱ)根据等差数列和等比数列的求和公式计算即可.【解答】解:(Ⅰ)设{a n}的公比为q,由a1=3,S3=39得,于是q2+q﹣12=0,解得q=3(q=﹣4不符合题意,舍去)故.(Ⅱ)由(Ⅰ)得,则,则…=.【点评】本题考查数列的通项及前n项和,考查等比数列的求和公式,属于中档题.29.【分析】(Ⅰ)根据数列的递推公式即可求出数列的通项公式,(Ⅱ)根据对数的运算性质,以及裂项求和,即可求出T n.【解答】解:(Ⅰ)a n=2+S n,(n∈N*),①+1当n=1时,a2=2+S1,即a2=4,当n≥2时,a n=2+S n﹣1,②,﹣a n=S n﹣S n﹣1=a n,由①﹣②可得a n+1=2a n,即a n+1∴a n=a2×2n﹣2=2n,n≥2,当n=1时,a1=21=2,∴a n=2n,(n∈N*).(Ⅱ)由(Ⅰ)得b n=log2(a n)2=2n,∴==(﹣),∴T n=(1﹣+﹣+…+﹣)=(1﹣)=.【点评】本题考查了数列的递推公式和裂项求和,考查了运算能力,属于中档题.30.【分析】(1)由n≥2时,a n=S n﹣S n﹣1.当n=1时,a1=S1,即可得出.(2)由b n=log2(a n﹣1)==n.==.利用裂项求和方法即可得出.【解答】解:(1)由n≥2时,a n=S n﹣S n﹣1=2n+1+n﹣2﹣(2n+n﹣1﹣2)=2n+1.当n=1时,a1=S1=3,综上可得:a n=2n+1.(2)由b n=log2(a n﹣1)==n.==.=+……+=1﹣=.【点评】本题考查了数列递推关系、对数运算性质、裂项求和方法,考查了推理能力与计算能力,属于中档题.31.【分析】(1)a1=1,又数列{}(n∈N*)是公差为1的等差数列.可得=2+(n﹣1),即可得出a n.(2)由a n==2.利用“裂项求和”即可得出.【解答】解:(1)∵a1=1,又数列{}(n∈N*)是公差为1的等差数列.∴=2+(n﹣1)=n+1,∴a n=.(2)∵a n==2.∴数列{a n}的前n项和S n=2+…+=2=.【点评】本题考查了等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.32.【分析】(1)直接利用已知条件对关系式进行变换,把函数的关系式变形成正弦函数,进一步求出数列的通项公式.(2)利用数列的通项公式,进一步利用裂项相消法求出数列的和.【解答】解:(1)函数f(x)=2sin(x﹣)+cosx,=,=sinx.根据正弦函数的性质,当x=k(k∈Z)时,函数取得极值点,又x>0,所以数列{a n}是以为首项,π为公差的等差数列,则数列的通项公式为:=.(2)由(1)得出,=,所以:,=,=.【点评】本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用.33.【分析】(1)求导,由f′(e)=0,求得b=0,根据函数单调性与导数的关系,即可求得a的取值范围;(2)证法1:构造函数,求导,根据函数的单调性,求得g(x)最大值,由g (x)max<0,即可求得xf(x)+2<0.证法2:将原式化简xf(x)+2=lnx﹣(x﹣1)+[(x+1)﹣e x],根据经典不等式,即可求得xf(x)+2<0.【解答】解:(1)f(x)=,(x>0),求导f′(x)=,由f′(e)=0,则b=0,则f′(x)=,当a>0时,f′(x)在(0,e)内大于0,在(e,+∞)内小于0,∴f(x)在(0,e)内为增函数,在(e,+∞)为减函数,∴f(x)有极大值无极小值;当a<0时,f(x)在(0,e)为减函数,在(e,+∞)为增函数,∴f(x)有极小值无极大值;∴实数a的取值范围(﹣∞,0);(2)证明:证法1:当a=b=1时,设g(x)=xf(x)+2=lnx﹣e x+2,g′(x)=﹣e x,在(0,+∞)为减函数,由g′(1)=1﹣e<0,g′()=2﹣>0,∴存在实数x0∈(,1)使得g′(x0)=﹣=0,∴g(x)在区间(0,x0)内为增函数,在(x0,+∞)内为减函数,由g′(x0)=﹣=0,则x0=﹣lnx0,g(x)max=g(x0)=lnx0﹣+2=﹣x0﹣+2=﹣(x0+)+2,由x0∈(,1),﹣(x0+)<﹣2,∴g(x)max<0,∴xf(x)+2<0.证法2:当a=b=1时,设g(x)=xf(x)+2=lnx﹣e x+2=lnx﹣(x﹣1)+[(x+1)﹣e x],因为曲线y=lnx与直线y=x﹣1相切于点(1,0);直线y=x+1与曲线y=e x相切于点(0,1),……………………(8分)lnx≤x﹣1,x+1≤e x且“=”不同时成立,故x>1时,lnx﹣(x﹣1)+[(x+1)﹣e x]<0,即xf(x)+2<0.………………………………………(12分)【点评】本题考查导数与函数单调性及极值的判断,考查利用导数求函数的最值,经典不等式的应用及几何关系,考查转化思想,分类讨论思想,属于中档题.34.【分析】(1),n≥2时,a n=S n﹣S n﹣1.利用等比数列的通项公式即可得出.由得b1=1,由a2(b2+2)=1得,解得b2=2,可得公差,利用等差数列的通项公式即可得出.(2)a n b n=,利用错位相减法即可得出.【解答】解:(1),n≥2时,,适合,∴,由得b1=1,由a2(b2+2)=1得,∴b2=2,∴d=1,∴b n=1+(n﹣1)•1=n.(2)a n b n=,由,得,相减,得,∴T n=2﹣.【点评】本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、错位相减法,考查了推理能力与计算能力,属于中档题.35.【分析】(I)等比数列{a n}的公比设为q,若a1=2b1=t,运用等比数列和等差数列的通项公式,解方程可得首项和公比,即可得到所求通项;(Ⅱ)化简c n,运用裂项相消求和和等比数列的求和公式,计算即可得到所求和.【解答】解:(I)等比数列{a n}的公比设为q,前n项和为S n,数列是公差为d=1的等差数列,即有=t+n﹣1,即b n=n(t+n﹣1),若a1=2b1=t,a4﹣a2=12,S4+2S2=3S3,可得tq3﹣tq=12,S4﹣S3=2(S3﹣S2),即为a4=2a3,即q==2,解得t=2,可得a n=2n;b n=n2;(2)c n=,即为c n=,T2n=(c1+c3+…+c2n﹣1)+(c2+c4+…+c2n)=[++…+]+(++…+)=(1﹣+﹣+…+﹣)+=﹣•+(1﹣)=﹣•﹣•.【点评】本题考查等差数列、等比数列的通项公式和求和公式的运用,考查数列的求和方法:裂项相消求和和分组求和,考查化简变形能力,属于中档题.36.【分析】(I)设等比数列{a n}的公比为q(q>0),由题意得,解得即可得出.(II)由(I)得,利用求和公式可得S n,利用裂项求和方法可得T n,再利用单调性即可得出.【解答】解:(I)设等比数列{a n}的公比为q(q>0),由题意,得…(2分)解得…(3分)所以…(4分)(II)由(I)得,…(5分).…(6分)∴,…(8分)∴,…(10分)若恒成立,则恒成立,则,所以…(12分)【点评】本题考查了等差数列与等比数列的通项公式与求和公式及其性质、裂项求和方法、单调性,考查了推理能力与计算能力,属于中档题.37.=【分析】(I)当n=1时,有,解得a1.当n≥2时,有S n﹣1(a n﹣1),可得,利用等比数列的通项公﹣1式即可得出.(II)由(I)有,则,利用裂项求和方法可得T n,即可证明.【解答】(I)解:当n=1时,有,解得a1=4.=(a n﹣1﹣1),当n≥2时,有S n﹣1则,整理得:a n=4a n﹣1,∴数列{a n}是以q=4为公比,以4为首项的等比数列.∴即数列{a n}的通项公式为:.(II)证明:由(I)有,则,∴T n=+……+=,故得证.【点评】本题考查了数列递推关系、等比数列的通项公式、裂项求和方法、数列的单调性,考查了推理能力与计算能力,属于中档题.38.【分析】(1)根据等差数列的求和公式和等差数列的性质即可求出,(2)根据错位相减法即可求出.【解答】解:(1)由,得a4=7∵a3=6,∴d=1,∴a1=4,∴a n=n+3(2)=n•3n,∴T n=1×31+2×32+3×33+…+n×3n,∴3T n=1×32+2×33+3×34+…+n×3n+1,∴﹣2T n=3+32+33+34+…+3n﹣n×3n+1=﹣n×3n+1,∴T n=【点评】本题考查了等差数列的求和公式和等差数列的性质以及错位相减法,属于中档题39.【分析】(1)a n2+a n=a n+12﹣a n+1可得a n+1﹣a n=1,即数列{a n}是以1为首项,以1为公差的等差数列,即可求出a n=n,再根据S n=n2+n,即可求出b n=2n,(2)由==(﹣),根据裂项求和即可求出【解答】解:(1)由a n2+a n=a n+12﹣a n+1,+a n=a n+12﹣a n2=(a n+1+a n)(a n+1﹣a n),∴a n+1∵a n>0,﹣a n=1,∴a n+1∴数列{a n}是以1为首项,以1为公差的等差数列,∴a n=1+n﹣1=n,∴S n=n2+a n=n2+n,①当n=1时,b1=S1=2,当n≥2时,S n=(n﹣1)2+n﹣1,②,﹣1由①﹣②可得b n=2n,当n=1时,也成立,∴b n=2n,(2)==(﹣),∴T n=(1﹣++…+﹣)=(1﹣)=【点评】本题考查了数列的递推公式和裂项求和,考查了运算能力,属于中档题40.【分析】(Ⅰ)S n=2﹣2a n+1,a1=1,当n=1时,S1=2﹣2a2,得a2.当n≥2时,S n =2﹣2a n,当n≥2时,a n=2a n﹣2a n+1,即,利用等比数列的通项公式﹣1即可得出.(Ⅱ)由(Ⅰ)知,,,对n分类讨论即可得出.【解答】解:(Ⅰ)∵S n=2﹣2a n+1,a1=1,∴当n=1时,S1=2﹣2a2,得;=2﹣2a n,当n≥2时,S n﹣1∴当n≥2时,a n=2a n﹣2a n+1,即,又,∴{a n}是以a1=1为首项,为公比的等比数列.∴数列{a n}的通项公式为.(Ⅱ)由(Ⅰ)知,,,当n为偶数时,T n=(﹣0+1)+(﹣2+3)+……+[﹣(n﹣2)+n﹣1]=;当n为奇数时,,∴.【点评】本题考查了数列递推关系、等比数列的通项公式、分组求和、分类讨论方法,考查了推理能力与计算能力,属于中档题.。
2018年高考理科数学专题题库

2018年高考数学冲刺培优专题训练专题1 集合与常用逻辑用语、复数与算法第1讲 集合与常用逻辑用语(A)卷一、选择题(每题5分,共70分)1.(2015·黑龙江省哈尔滨市第三中学高三第三次模拟考试数学(理)试题·2)命题“R ∈∃0x ,030≤x ”的否定是( )A .R ∈∀x ,03≤xB .R ∈∃0x ,030≥xC .R ∈∃0x ,030>xD .R ∈∀x ,03>x2.(2015·山东省济宁市兖州第一中学高三数学考试·1)若{}{}2|22,|log (1)M x x N x y x =-≤≤==-,则M N =( )A .{}|20x x -≤<B .{}|10x x -<<C .{}2,0-D . {}|12x x <≤ 3.(2015济宁市曲阜市第一中学高三校模拟考试·1)集合,,,则等于( ) A . B . C . D .4. (2015·青岛市高三自主诊断试题·2)已知集合2{|lg(2)}M x y x x ==-,22{|1}N x x y =+=,则M N =( )A .[1,2)-B .(0,1)C .(0,1]D .∅5.(2015·山东省潍坊市高三第二次模拟考试·3) 已知命题44,0:≥+>∀x x x p ;0x 命题212),,0(:00=+∞∈∃x x q ,则下列判断正确的是( ) A .p 是假命题 B .q 是真命题 C .)(q p ⌝∧是真命题D .q p ∧⌝)(是真命题6.(2015·开封市高三数学(理)冲刺模拟考试·3)下列命题中为真命题的是( )A .若x≠0,则x+≥2B .命题:若x 2=1,则x=1或x=﹣1的逆否命题为:若x≠1且x≠﹣1,则x 2≠1C .“a=1”是“直线x ﹣ay=0与直线x+ay=0互相垂直”的充要条件D .若命题p :∃x ∈R ,x 2﹣x+1<0,则¬p :∀x ∈R ,x 2﹣x+1>07.(2015·山东省潍坊市高三第二次模拟考试·1) 设全集R U =,集合}1|||{≤=x x A ,}1log |{2≤=x x B ,则B A U 等于( ) A .]1,0( B .]1,1[-C .]2,1(D .]2,1[)1,( --∞ 8.(2015·陕西省咸阳市高考模拟考试(三)·6)9.(2015·黑龙江省哈尔滨市第三中学高三第三次模拟考试数学(理)试题·1)已知全集R =U ,集合}02|{2>-=x x x A ,)}1lg(|{-==x y x B ,则=B A C U )(( )A .2|{>x x 或}0<xB .}21|{<<x xC .}21|{≤<x xD .}21|{≤≤x x10. (2015·海淀区高三年级第二学期期末练习·4)已知命题p ,q ,那么“p q ∧为真命题”是“p q ∨为真命题”的( )(A )充分不必要条件(B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件11.(2015.菏泽市高三第二次模拟考试数学(理)试题·3)设x ,y 是两个实数,命题“x ,y 中至少有一个数大于1”成立的充分不必要条件是( )A .2x y +=B .2x y +>C .222x y +>D .1xy >12.(2015·赣州市高三适用性考试·1)13.(2015·山东省潍坊市第一中学高三过程性检测·1)设全集(){}{}(),ln 1,11,U U R A x y x B x x C A B ===-=-<⋂=则( )A.()2,1-B. (]2,1-C. [)1,2D. ()1,214.(2015·北京市东城区综合练习二·5)已知p ,q 是简单命题,那么“p q ∧是真命题”是“p ⌝是真命题”的( )(A 充分而不必要条件(B 必要而不充分条件(C 充分必要条件(D )既不充分也不必要条件二、非选择题(30分)15. (2015·徐州、连云港、宿迁三市高三第三次模拟·2)已知集合},4,2{],3,1(=-=B A 则=B A .16.(2015.南通市高三第三次调研测试·1)设集合A={3,m},B={3m ,3},且A=B ,则实数m 的值是 .17(2015·苏锡常镇四市高三数学调研(二模)·1)已知集合{}{}{}1,1,3,2,21,1a A B A B =-=-=,则实数a 的值为18.(2015·启东中学高三第二学期初调研测试·2)由命题“∃x ∈R ,x 2+2x +m ≤0”是假命 题,求得实数m 的取值范围是(a ,+∞),则实数a = .19.(2015·日照市高三校际联合5月检测·5) ①.若“p 且q ”为假,则p ,q 至少有一个是假命题②.命题“2,10x R x x ∃∈--<”的否定是“2,10x R x x ∀∈--≥”③.“2πϕ=”是“()sin 2y x ϕ=+为偶函数”的充要条件④.当0α<时,幂函数()0,y x α=+∞在上单调递减 。
2018高考数学冲刺试卷(江苏卷20)(每题均有详细解答)

2018年江苏高考数学冲刺猜题卷命题人: 王建宏本试卷分为第I 卷(必做题)和第II 卷(附加题)两部分.选修测试历史的考生仅需做第I 卷,共160分,考试用时120分钟.选修测试物理的考生需做第I 卷和第II 卷,共200分,考试用时150分钟.第I 卷(必做题 共160分)一、填空题:本大题共14小题,每小题5分,共70分.将答案填在题中的横线上.1.复数21(215)5z a a i a =++-+为实数,则实数a = . 解析:3 ∵21(215)5z a a i a =++-+为实数, ∴22150a a +-=, 解之得5a =-或3a =. ∵5a ≠-, ∴3a =.2.直线1:2(1)l y k x -=-和直线2l 关于直线1y x =+对称,则直线2l 恒过定点 .” 解析:(1,1) ∵直线1:2(1)l y k x -=-过定点(0,2), 而点(0,2)关于直线1y x =+对称的点坐标为(1,1), ∴直线2l 恒过定点(1,1) .3.右图是一个空间几何体的三视图,根据图中尺寸(单位:cm ), 可知几何体的表面积是 2cm解析:18+ 由三视图可得,该几何是一个底面边长为2高为3的正三棱柱,其表面积2232322184S cm =⨯⨯+⨯=+. 4.如图是容量为100的样本的频率分布直方图,则样本 数据在[6,10)内的频率和频数分别是 . 解析:0.32,32 在[6,10)内频率为0.08×4=0.32,频数为0.32×100=32.5.右面框图表示的程序所输出的结果是 .解析:1320 1211101320s =⨯⨯=.6.函数y =A sin(ωx +φ)(ω>0,| φ|≤2π)的部分图象如图, 则函数的一个表达式为 . 解析f (x )=2sin (4πx +ϕ). 由函数图象可知A =2,2T =7-3=4,即T =8,∴ω=T π2=82π= 4π. ∴f (x )=2sin (4πx +ϕ).∵(3,0)为“五点法”作图的第三个点. ∴4π×3+ϕ=π,即ϕ=4π. ∴f (x )=2sin (4πx +4π).7.已知y x ,的取值如下表所示:从散点图分析,y 与x 线性相关,且ˆ0.6yx a =+,则a = . 解析:-0.2 计算4y =,7x =,由公式a y bx =-,又0.6b =,从而0.2a =-, 8.在平面直角坐标系中,O 为坐标原点,已知(3,1),(1,3)A B -,若点C 满足||||CA CB CA CB +=- ,则C 点的轨迹方程是 . 解析:22(1)(2)5x y -+-= 解析:由||||CA CB CA CB +=-知CA CB ⊥ ,所以C 点的轨迹是以A 、B 为直径的两个端点的圆,圆心坐标为AB 的中点(1,2)以C 点的轨迹方程是22(1)(2)5x y -+-=.9.要称量一根既长又重且粗细不一样的水泥电线杆的重量G ,现采用如下“二次”称量法:即先在一端称得电线杆的重量为1G ,然后在另一端称得电线杆的重量为2G , 则G 12G G + (填:“>”或“<”或“≥”或“≤”或“=”).解析:= 设电线杆的重心到一端距离为a ,到另一端距离为b ,电线杆长为l ,则a +b =l . ∵12,G l Ga G l Gb ==, ∴12()()G G l G a b +=+, ∴12G G G =+. 10.若a 是b 21+与b 21-的等比中项,则ba ab22+的最大值为 .解析:42 ∵22(12)(12)14a b b b =+-=-,∴22144||a b ab =+≥ (||2||a b =时取等号). 此时有1||4ab ≤.∴2||21224||||ab a b b a ===++ .(||2||a b =时取等号). 11.下列关于函数x e x x x f )2()(2-=,下列判断中:①()0f x >的解集是{|02}x x <<. ②)2(-f 是极小值,)2(f 是极大值. ③)(x f 没有最小值,也没有最大值. 其中判断正确的是 .解析:①② 由2()(2)0x f x x x e =->可得02x <<,故①正确;又2'()(2)x f x x e =-,令2'()(2)0x f x x e =-=可得,x =,且当x <或x >时,'()0f x <;当x <,'()0f x >,故)2(-f 是极小值,)2(f 是极大值,即②正确.根据图像的特点易知③不正确.12.设21,F F 为椭圆1422=+y x 的两个焦点,P 在椭圆上,当21PF F ∆面积为1时,则12PF PF ⋅=.解析:0 设12,PF m PF n ==,则24m n a +==,22222124()242cos 122m n c m n mn c F PF mn mn mn+-+--∠===- ,∴1221cos mn F PF =+∠, 12F PF S ∆=121212sin 1sin 121cos F PF mn F PF F PF ∠∠==+∠.解之得1212sin 1,cos 0F PF F PF ∠=∠=, ∴12PF PF ⋅=0.13.若定义在区间D 上的函数f (x )对于D 上任意n 个值x 1、x 2、…x n 总满足)()]()()([12121nx x x f x f x f x f n n n ++≤+++,则f (x )称为D 上的凸函数,现已知)2,0(cos )(π在x x f =上凸函数,则锐角△ABC 中C B A cos cos cos ++的最大值为 . 解析:32由题意,因为)2,0(cos )(π在x x f =上凸函数,所以C B A cos cos cos ++33cos()3cos 332A B C π++≤==. 14.已知:()1xf x x=-,设1()()f x f x =,*11()[()](1,)n n n f x f f x n n N --=>∈,则3()f x 的表达式为 ,猜想()n f x *()n N ∈的表达式为 .解析:12x x-, 112n x x -- (n N *∈) 由1()()f x f x =,得 2111()[()]1211xxx x f f x x x x f -===---, 322212()[()]212112xx x x f f x x x xf -===---,……, 由此猜想1()12n n x x x f -=-(n N *∈) 二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)小明、小华用4张扑克牌(分别是黑桃2、黑桃4,黑桃5、梅花5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,小明先抽,小华后抽,抽出的牌不放回,各抽一张。
2018年高考数学三轮冲刺专题解析几何练习题理

解析几何1.圆心在直线4y x =-,且与直线10x y +-=相切于点()32P -,的圆的标准方程为__________. 2.若双曲线2212516x y -= 的左、右焦点分别为12,F F ,点P 在双曲线上,且13PF =,则2PF 等于__________. 3.已知双曲线S与椭圆221934x y +=的焦点相同,如果34y x =是双曲线S的一条渐近线,那么双曲线S的方程为_______________.4.已知抛物线22,,y x A B =是抛物线上的两点,线段AB 的垂直平分线与x 轴相交于点()00P x ,则0x 的取值范围是__________.(用区间表示)52的直线l 与椭圆22221x y a b +=(0a b >>)交于不同的两点,且这两个交点在x 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( ) 3 B. 122136.已知F 为抛物线2y x =的焦点,点,A B 在该抛物线上且位于x 轴的两侧,而且·6OAOB =(O 为坐标原点),若ABO ∆与AFO ∆的面积分别为1S 和2S ,则124S S +最小值是 73 B. 6 C. 132D. 437.已知圆22:20M x y ay +-=(0a >)截直线0x y +=所得弦长是22a 的值为2 B. 26 D. 38.已知点M 是抛物线2:2(0)C y px p =>上一点, F 为C 的焦点, MF 的中点坐标是()2,2,则p 的值为( ) A. 1 B. 2 C. 3 D. 49.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线为2y =,则该双曲线的离心率等于 6236 10.“直线1y kx =+与圆()2221x y -+=相切”是“43k =-”的( ) A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件11.设m R ∈,则“0m = ”是“直线()()1:1110l m x m y ++--=与直线()()2:12140l m x m y -+++=垂直”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件12.已知双曲线C : 2219x y a -= (a>0)与双曲线221412x y -=有相同的离心率,则实数a 的值为( ) A. 1 B. 2 C. 3 D. 413.已知双曲线22221x y a b-=(0,0a b >>)的一条渐近线被圆22650x y x +-+=截得的弦长为2,则该双曲线的离心率为A. 2356 14.已知双曲线22221(00)x y a b a b-=>>,的左右焦点分别为12,F F ,以2OF 为直径作圆C ,再以1CF 为直径作圆E ,两圆的交点恰好在已知的双曲线上,则该双曲线的离心率为( ) 26+423-423-326+ 15.设双曲线22221(00)x y a b a b-=>>,的左、右焦点分别为F 1、F 2,离心率为e ,过F 2的直线与双曲线的右支交于A 、B 两点,若△F 1AB 是以A 为直角顶点的等腰直角三角形,则2e =( )A. 322+B. 522-122+422-16.已知1F , 2F 是椭圆和双曲线的公共焦点, p 是它们的一个公共点,且123F PF π∠=,设椭圆和双曲线的离心率分别为1e , 2e ,则1e , 2e 的关系为( )A. 1213e e =B. 2212143e e +=C. 2211134e e += D. 221134e e += 17. 设直线l 的方程为()25x m y =++,该直线交抛物线2:4C y x =于,P Q 两个不同的点.(1)若点()5,2A -为线段PQ 的中点,求直线l 的方程;(2)证明:以线段PQ 为直径的圆M 恒过点()1,2B .18.已知O 为坐标原点, ()11,M x y , ()22,N x y 是椭圆22193x y +=上的点,且121230x x y y +=,设动点P 满足3OP OM ON =+.(Ⅰ)求动点P 的轨迹C 的方程;(Ⅱ)若直线():0l y x m m =+≠与曲线C 交于,A B 两点,求三角形OAB 面积的最大值.19.已知椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ,上顶点为M ,若直线1MF 的斜率为1,且与椭圆的另一个交点为2,N F MN ∆的周长为42(1)求椭圆的标准方程;(2)过点1F 的直线l (直线l 的斜率不为1)与椭圆交于,P Q 两点,点P 在点Q 的上方,若1123F NQ F MP S S ∆∆= ,求直线l 的斜率. 20.设椭圆22122:1(0)x y C a b a b +=>>的左焦点为F ,右顶点为A 22,已知A 是抛物线22:2(0)C y px p =>的焦点.(1)求椭圆1C 的方程和抛物线2C 的方程;(2)若抛物线2C 的准线l 上两点,P Q 关于x 轴对称,直线AP 与椭圆相交于点B (B 异于点A ),直线BQ 与x 轴相交于点D ,若APD ∆22AP 的方程.21.已知椭圆的中心为坐标原点O ,椭圆短轴长为2,动点()2M t ,(0t >)在椭圆的准线上. (1)求椭圆的标准方程;(2)求以OM 为直径且被直线3450x y --=截得的弦长为2的圆的方程;(3)设F 是椭圆的右焦点,过点F 作OM 的垂线与以OM 为直径的圆交于点N ,求证:线段ON 的长为定值,并求出这个定值.22.已知椭圆C : 22221x y a b += (a>b>0)过点(1, 32),且离心率e =12. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线l :y =kx +m 与椭圆C 相交于A ,B 两点(A ,B 不是左右顶点),椭圆的右顶点为D ,且满足DA ·DB =0,试判断直线l 是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.。
2018高考数学冲刺试卷(江苏卷18)(每题均有详细解答)

HHH H H HH HHHH HC 全国著名重点中学领航高考冲刺试卷数 学(江苏卷)18命题:王建宏本试卷分为第I 卷(填空题)、第II 卷(解答题)和第Ⅲ卷(附加题)三部分,文科考生只要求...做第I 卷、第II 卷,第Ⅲ卷...不做..,满分160分,考试时间120分钟;理科考生第I 卷、第II 卷和第Ⅲ卷都必须...做.,满分160+40分,考试时间120+30分钟. 第I 卷(填空题 共70分)一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填空在答题..卡相应位置上....... 1. 已知集合A ={x ||x |≤2,x ∈R },B ={x |x ≥a }且A ⊆B ,则实数a 的取值范围是 ▲ .2.如果复数()()21m i mi ++是实数,则实数m = ▲ .3.设a ≠b ,若关于x 的方程x 2-x+a=0和x 2-x+b=0的四个根可以组成首项为41的等差数列,则a+b 的值是 ▲ .4.已知y x ,的取值如下表所示:x0 1 3 4 y2.24.34.86.7从散点图分析,y 与x 线性相关,且ˆ0.95yx a =+,则a = ▲ . 5. 若191x yx y R +=∈+(),,则x y +的最小值是 ▲ . 6.一个几何体的三视图如图所示,其中,主视图中△ABC 是边长为2的正三角形,俯视图为正六边形,那么该几何体的体积为 ▲ .左视图主视图俯视图CBA7.下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式...是 ▲ .8.已知圆221:(1)1C x y ++=,圆2C 与圆1C 外切,且与直线3x =切于点(3,1),则圆2C 的方程 为 ▲ .9. 已知点A (3,1),B(0,0),C (3,0).设∠BAC 的平分线AE 与BC 相交于E ,那么有λ= ,其中λ等于 ▲ . 10.若cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭cos sin αα+的值为 ▲ .11.读程序甲: i=1 乙:S=0S=0 For I From 1000 to 1 step 1 While i≤1000 S=S+i S=S+i End For i=i+l Print S End While End Print SEnd对甲、乙两程序和输出结果判断是 ▲ .12.若动点(,)P x y 在曲线2221(0)4x y b b+=>上变化,则22x y +的最大值为 ▲ .13.我国男足运动员转会至海外俱乐部常会成为体育媒体关注的热点新闻。
2018年高考数学三轮冲刺点对点试卷集合平面向量与复数

集合、平面向量与复数1.已知集合{}|31,A x x n n Z ==+∈, {}|44B x x =-≤≤,则集合A B ⋂=A. {}4,1,1,4--B. {}2,1,4-C. {}1,4D. {}4,1,2--【答案】B2.已知全集U Z =,集合{}220,M x x x x Z =--<∈, {}1,0,1,2N =-,则()U C M N ⋂=( )A. {}1,2-B. {}1,0-C. {}0,1D. {}1,2 【答案】A 3.【设集合()22,| 1 416x y A x y ⎧⎫=+=⎨⎬⎩⎭, (){},|3 x B x y y ==,则A B ⋂的子集的个数是:( ) A. 4 B. 3 C. 2 D. 1【答案】A4.已知集合2{|230}A x x x =+-=, {}1,1B =-,则A B ⋃=( ) A. {}1 B. {}1,1,3- C. {}3,1,1-- D. {}3,1,1,3--【答案】C5.已知集合2{|20}A x x x =--≥,则R C A =( )A. ()1,2-B. []1,2-C. ()2,1-D. []2,1-【答案】A6.已知,m n R ∈,集合{}72,log A m =,集合{},B m n =,若{}1A B ⋂=,则m n +=( )A. 1B. 2C. 4D. 8【答案】D7.已知(){}2log 31A x y x ==-, {}224B y x y =+=,则()R C A B ⋂=( )A. 12,3⎡⎤-⎢⎥⎣⎦B. 12,3⎡⎫-⎪⎢⎣⎭C. 1,23⎛⎤ ⎥⎝⎦D. 1,23⎛⎫ ⎪⎝⎭【答案】A8.已知集合(){}{}2A |log 31,|02x R x B x R x =∈-≤=∈≤≤,则A B ⋃= ( )A. []0,3B. []1,2C. )[0 ,3D. []1,3【答案】C9.若复数2i z i-=-,则复数z 所对应的点在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】A10.复数2i 12i =+( ) A. 42i 55+ B. 42i 55- C. 42i 55-+ D. 42i 55-- 【答案】A11.复数2i 1iz -=(i 是虚数单位)在复平面内对应的点在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】A12.已知复数()12i i a bi +=+, a R ∈, b R ∈, a b +=( )A. 3-B. 1-C. 1D. 3【答案】B13.欧拉公式cos sin ix e x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数集,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位.特别是当x π=时, 10i e π+=被认为是数学上最优美的公式,数学家们评价它是“上帝创造的公式”.根据欧拉公式可知, 4i e 表示的复数在复平面中位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】C14.已知a 是实数, 1a i i +-是实数,则7cos 3a π的值为( ) A. 12 B. 12- C. 0 D. 32 【答案】A15.已知复数z 满足()1+243i z i =+,则z 的虚部是( )A. -1B. 1C. -2D. 2【答案】B16.已知i 为虚数单位,复数322i z i+=-,则以下为真命题的是( ) A. z 的共轭复数为7455i - B. z 的虚部为85 C. 3z = D. z 在复平面内对应的点在第一象限17.如图,已知平行四边形ABCD 中, 2BC =, 45BAD ∠=︒, E 为线段BC 的中点, BF CD ⊥,则AE BF ⋅=( )A. 222 D. 1【答案】D18.已知12,e e 为单位向量,且1e 与122e e +垂直,则12,e e 的夹角为( )A. 30B. 60C. 120D. 150【答案】C19.已知a = πsin ,24b = πcos 24,且、a b 的夹角为π12,则⋅=a b A. 116 B. 18314【答案】B20.在平面直角坐标系xOy 中,已知点)3,0A , ()1,2B ,动点P 满足OP = OA OB λμ+,其中][,0,1,1,2λμλμ⎡⎤∈+∈⎣⎦,则所有点P 构成的图形面积为( )A. 1B. 2C. 3D. 2321.已知菱形ABCD 的边长为2,,点E 、F 分别在边,BC CD 上, BE BC λ=, DF DC μ=,若522λμ+=, 则AE AF ⋅的最小值___________. 【答案】3 22.已知向量a , b 满足5b =, 253a b +=, 52a b -=,则a =__________.56。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018高考数学冲刺单选试题精选50道(代数部分)1. ( 2分) 已知x∈R且x≠0,则函数f(x)=+是[ ]A.偶函数B.奇函数C.既是奇函数, 又是偶函数D.既不是奇函数, 又不是偶函数2. ( 2分)从{0, 1 , 2, 3 , 4 , 5 }中取出3个不同元素作为方程ax+by+c =0的系数, 可表示出的不同直线条数为[ ] A.C63 B.P63C.P63-6D.C63-63. ( 2分) 已知数列{a n}的通项公式a n=11-2n, 设T n=|a1|+|a2|+…+|a n│,则T10的值是[ ] A. 100 B. 50 C. 25 D. 204. ( 2分)设m·n<0,m+n=1 将(m+n)9按m的降幂排列, 其第二项不大于第三项, 则m的取值范围是[ ]A.(-∞,0.2)B.(0.8,+∞)C.(-∞,0.8)D.(1,+∞)5. ( 2分)设θ是第一象限的角, 且满足│sin│=-sin, 则是[ ]A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角6. ( 2分) 设M={x│x2-4x+3<0 }, N={x│lgx+lg(x-1)>lg2 }则M∩N是[ ]A. {x│x>3 }B. {x│1<x<2 }C. {x│2<x<3 }D. {x│1<x<3 }7. ( 2分)若sin=,cos=- , 则θ角的终边所在象限是[ ]A.第一象限B.第三象限C.第四象限D.第三或第四象限8. ( 2分) 设cosθ+cos2θ=1则sin2θ+sin6θ+sin8θ的值为[ ] A.1 B.-1 C.2 D.-29. ( 2分) 设t=i, n∈N,则C n0-C n1t(t-1)+C n2t2(t-1)2+…+(-1)r C n r t r(t-1)r+…+(-1)n C n n t n(t-1)n=[ ] A. 2n+1 B. 2n-1 C. 2n D. 22n10. ( 2分)化tg3θ-tg2θ-tgθ为积的形式应为[ ] A.tg3θtg2θtgθ B.tg3θtg2θC.tg2θtgθD.tgθtg3θ11. ( 2分)那么M、N 间的关系有[ ] A. M=N B. M NC. M ND. M N12. ( 2分)求sin69°-sin3°+sin39°-sin33°的值为[ ] A. B.C. D.013. ( 2分)使函数y=sin(2x+ψ)+cos(2x+ψ)为偶函数,且在[0,]上是减函数的ψ的一个值是[ ]14. ( 2分)使∈R的最小自然数n为[ ]A.3B.4C.5D.615. ( 2分) 小于50000且含有奇数个数码“5”的五位数共有( )个.[ ] A.2952 B.11808 C.16160 D.2656816. ( 2分) 若函数f(x+1)的定义域是(-∞,- )∪(,+∞),则函数f(x)的定义域是[ ]A.(-∞,-)B.(- ,+∞)C.(-∞,- )∪(,+∞)D.(-∞,- ]∪[,+∞)17. ( 2分) 则s K+1为[ ]18. ( 2分)若点(1, 2)既在函数f(x)=的图象上, 又在它的反函数的图象上, 则实数a、b的值依次是[ ] A.-3, 7 B.-3, -7 C.3, 7 D.3, -719. ( 2分)若函数y=f(x)的图象如图所示, 则它的反函数的解析式为[ ]20. ( 2分) 已知-b<a<0, 和四个不等式: ①>; ②a2>b2; ③>-; ④│a│>│b│,则其中正确的个数是[ ] A.0个 B.1个 C.2个 D.3个21. ( 2分) 函数y=8sec2x+18cos2x的极小值是[ ] A.24 B.23 C.22 D.2122. ( 2分)[ ]23. ( 2分)函数y=cos2x+3sinx的值域是[ ] A.[-4,4]24. ( 2分)[ ] A.0 B.±10 C.10 D.-1025. ( 2分) 方程lgx·lnx=2lgx的解集是[ ] A. {1} B. {e2} C. {1, e2} D. {0}26. ( 2分) 已知△ABC中, 三个内角A、B、C所对的边为a、b、c, 则下列各结论中不正确的一个是[ ] A. 当B=45°,b=2, c=2时, 三角形有一解;B. 当B=45°,b=2, c=2时, 三角形有一解;C. 当B=45°,b=2, c=3时, 三角形无解;D. 当B=45°,b=3, c=4时, 三角形无解.27. ( 2分)若x=2 则(1+x)15的展开式中第_____项最大.[ ] A.10 B.11 C.12 D.1328. ( 2分) 复数z=(sin160°-icos340°)-1的辐角主值是[ ] A.70° B.110° C.20° D.340°29. ( 2分)arccos(-x)>arccosx的充要条件是[ ] A.x∈(0, 1] B.x∈[-1, 0]C.x∈[0, 1]D.x∈[0, ]30. ( 2分) 设│x│<1, 则ctg2(arccosx)的值为[ ]31. ( 3分)函数y=+的定义域是[ ]A.[,1)∪(1,+∞)B.[,)∪(1,+∞)C.[,)∪(,1)∪(1,+∞)D.(1,+∞)32. ( 3分)函数是[ ] A.周期为的偶函数B.周期为的奇函数D.周期为π的奇函数C.周期为的偶函数33. ( 3分) 已知定义域为R的偶函数y=f(x)的一个单调增区间是(2,6), 则函数y=f(2-x)的[ ]A. 对称轴为x=-2, 且一个单调减区间是(4,8)B. 对称轴为x=-2, 且一个单调减区间是(0,4)C. 对称轴为x=2, 且一个单调增区间是(4,8)D. 对称轴为x=2, 且一个单调增区间是(0,4)34. ( 3分) 用1, 2, 3, 4四个数字, 组成个位数字是1, 且恰有三个相同数字的四位数, 一共可以组成[ ]A. 18个B. 15个C. 12个D. 9个35. ( 3分) 函数y=cos(sinx+2.2)的值域是[ ] A.[-1,1] B.[-1,cos1.2]C.[cos1.2,cos3.2]D.[cos3.2,cos1.2]36. ( 3分) 当x>0时, 函数y=x2+3x+有[ ] A.最小值27 B.最大值27C.最小值81D.最大值8137. ( 3分) 设x=a时, 二次函数f(x)有最大值5, 又二次函数g(x)的最小值为-2, 且a>0,f(x)+g(x)=x2+16x+13, g(a)=25, 则g(x)的表达式为g(x)=[ ]A. 3x2-12x+10B. 3x2+12x-10C. 3x2+12x+10D. 3x2-12x-1038. ( 3分) 不等式+>0的解是[ ] A. x>- B. x<-C. x>-D. x<-39. ( 3分) 已知α、β是锐角, tgα=, sinβ=, 求α+2β的值为[ ]40. ( 3分)已知函数y=在区间(-||,0)上是减函数,那么它的增区间是[ ]41. ( 3分)已知函数:(1)y=x+(x≠0);(2)y=cosx+(0<x<);(4)y=(1+ctgx)(+2tgx)(0<x<)其中最小值为4的函数有[ ] A. 0个 B. 1个 C. 2个 D. 3个42. ( 3分)数列{x n}满足x n sinθ+x n+1cosθ=1(n=1, 2, 3……)且x1=a, x2=b, a≠b,且数列{x n}有极限, 则θ的范围是[ ]43. ( 3分) 从1到10n-1的所有自然数中,仅含一个数字0的自然数的个数是[ ]44. ( 3分)[ ]45. ( 3分)已知: a>0, a2+b2=1, 则a的最大值是[ ]46. ( 3分) 设a>b>0, x=-, y=-.则x, y的大小关系是[ ] A.x>y B.x<y C.x≥y D.x≤y47. ( 3分) 在△ABC中,条件甲:A=90°条件乙sinC=cosA+cosB则[ ]A.甲是乙的充分条件B.甲是乙的必要条件C.甲是乙的充要条件D.甲既不是乙的充分条件, 也不是乙的必要条件.48. ( 3分)已知0<α<π,x=2sin2α,y=ctg,那么x、y的大小关系是[ ] A. x>y B.x<y C.x≥y D.x≤y49. ( 3分) 在△ABC中, 若sinC=cosA+cosB, 则三角形为[ ]A.直角三角形但不是等腰三角形.B.等腰三角形但不是直角三角形.C.等腰直角三角形.D.等腰三角形或直角三角形.50. ( 3分) 已知对任意实数x,y有f(xy)=f(x)f(y),f(1)≠0,则函数f(x)[ ]A.必是奇函数B.必是偶函数C.可以是奇函数,也可以是偶函数D.不能判断奇偶性参考答案1. ( 2分) B2. ( 2分) C3. ( 2分) B4. ( 2分) D6. ( 2分) C7. ( 2分) C8. ( 2分) A9. ( 2分) C10. ( 2分) A11. ( 2分) B12. ( 2分) C13. ( 2分) B14. ( 2分) A15. ( 2分) B16. ( 2分) C17. ( 2分) C18. ( 2分) A19. ( 2分) A20. ( 2分) A21. ( 2分) A22. ( 2分) C23. ( 2分) C24. ( 2分) D25. ( 2分) C26. ( 2分) D27. ( 2分) B28. ( 2分) A30. ( 2分) B31. ( 3分) C32. ( 3分) A33. ( 3分) C34. ( 3分) C35. ( 3分) B36. ( 3分) A37. ( 3分) C38. ( 3分) A39. ( 3分) B40. ( 3分) A41. ( 3分) A42. ( 3分) C43. ( 3分) A44. ( 3分) B45. ( 3分) A46. ( 3分) B47. ( 3分) A48. ( 3分) D49. ( 3分) C50. ( 3分) C。
