三角形“四心”定义与性质之欧阳光明创编
三角形“四心”的向量表示之欧阳地创编

三角形“四心”的向量表示我们都知道,在三角形中,因为有三条边和三个内角,所以有很多的性质。
在三角形众多的“心”中,有几个是学生应该掌握的,主要是四个心:重心,内心,外心,垂心。
不仅要理解其定义、性质,还需了解和分析其向量的表示形式。
由于向量是一种研究几何图形的另一种工具,所以我们有必要对它们进行整理和归纳,让同行借鉴。
一.各心的定义。
1.重心:三角形三条边的中线的交点。
其性质一是连接重心和顶点,延长后必交于对应边的中点。
其性质二是重心把中线长分成2:1。
2.垂心:三角形三边的高线的交点。
其性质为垂心与顶点的连线必与对应的边垂直。
3.外心:三角形三边的中垂线的交点,即三角形的外接圆的圆心。
其性质是外心到三顶点等距离。
4.内心:三角形三内角平分线的交点,即三角形的内切圆的圆心。
其性质是内心到三边等距离。
二.各心的向量表示。
在三角形ABC中,点O为平面内一点,若满足:1.=++,则点O 为三角形的重心。
分析:由+=-,以OC OB ,为邻边作一平行四边形OBEC ,点D 为BC 中点,如图,由向量的平行四边形法则, 有+=,交BC 于D ,从而有-===2故O 为重心。
2==,则点O 为三角形的外心。
3.OA OC OC OB OB OA ⋅=⋅=⋅,+=+=+,则点O 为三角形的垂心。
分析:由⋅=⋅=⋅有三个等式,其中一个如OC OB OB OA ⋅=⋅,则有0)(=-,有0=⋅CA OB ,故AC OB ⊥。
同理可证,点O 为三角形的垂心。
而在三角形ABC 中,记OA a =,OB b =,OC c =,则由2222BO AC CO AB +=+2222)()(b c a c b a +-=+-,展开为⋅=⋅22,则0)(=⋅-b c a 故OB AC ⊥,同理可证OA BC ⊥,从而点O 为三角形的垂心。
4=++,则点O 为三角形的内心。
分析:若点O 为三角形ABC 的内心。
如图,延长AO ,过点C 作BO CE //,由于CDE BDO ∆∆与相似,有DB CD OB CE =,由AD 为角A 的平分线,有ABAC DB CD =,从而有AB AC OB CE =,,OB AB AC CE ⋅=故ABAC ⋅= 同理可得,BC BD OE OD =,BC BDOD OE ⋅=,而BO 为角B 的内角平分线,ABOA BD OD =, 有OA AB BC BC AB OA OE ⋅=⋅=,故ABBC ⋅= 而CE OC OE +=,所以OB ABAC OC AO AB BC ⋅+=⋅, OB AC OC AB OA BC ⋅+⋅=⋅-,=++ 三.动点的轨迹过三角形心的问题:设点P 为三角形ABC 所在平面内的一个定点,点Q 为平面内的一个动点,若满足:1.)(++=λ,(其中R ∈≠λλ,0),则动点Q 一定过ABC ∆的重心。
三角形各种心的性质归纳之欧阳音创编

三角形各种心的性质研究一、基础知识三角形的心是指重心、外心、垂心、旁心和界心.三角形的心是三角形的重要几何点.在数学竞赛中,有关三角形的心的几何问题是竞赛的热点问题,因此,我们对三角形的心的几何性质做概括归纳,对有关的证明方法和解题技巧做深入探讨.1.重心:设G 是ABC ∆的重心,AG 的延长线交BC 于D ,则,DC BD =)1(, ( 2)3:2:=AD AG ;(3)4222222BC AC AB AD -+=,(4)3ABCGBC S S ∆∆=. 2.外心:设⊙O (R )是ABC ∆的外接圆,BC OD ⊥于D交⊙O 于E ,则(1)R OC OB OA ===;(2)A BOC ∠=∠2或)180(20A ∠-; (3)DC BD =⌒BE =⌒EC ;(4)C B A R RabcS ABCsin sin sin 24==∆(正弦定理) 3.内心:设ABC ∆的内心圆⊙I ()r 切边AB 于P ,AI 的延长线交外接圆于D ,则 (1)A BIC ∠+︒=∠2190;(2)a cb a ac b A r AP -++=-+=∠=)(21221cot ;(3)DC DI DB ==;(4)2)(c b a r S ABC ++=∆;4.垂心:设H G O ,,分别是ABC ∆的外心,重心,垂心,BC OD ⊥于D ,AH 的延长线交外接圆于1H ,则,(1)OD AH 2=;(2)H 与1H 关于BC 成轴对称;(3)⊙=BCH ⊙ABC ;(4),,,H G O 三点共线,且2:1:=GH OG ;5.旁心:设ABC ∆在A ∠内的旁切圆⊙1I ()1r 与AB 的延长线切于1P ,则,(1)A C BI ∠-=∠219001;(2)2211c b a A ctg r AP ++=∠=;(3)21c b a BP -+=;(4)21CB AI ∠=∠;(5)2)(1a c b r S ABC -+=∆6.三角形中内切圆、旁切圆和外圆半径的几个关系 在△ABC 中,内切圆⊙O 分别与三边相切于点K M ,L ,BC 边上的帝切圆⊙a O 与BC 边切于点H ,且分别与AB 边和AC 这的延长线相切于点Q 、点P .设三边BC 、CA 、AB 分别为c b a ,,,C B A ∠∠∠,,分别为γβα,,,)(21c b a p ++=,内切圆半径为r ,旁切圆半径分别为c b a r r r ,,,外接圆半径为R ,三角形面积为∆S ,则有如下关系式:(1)p AP =,a p AK -=,c b LH -=;(2)ap rpr a-=;(3)直角三角形斜边上的旁切圆的半径等于三角形周长的一半;(4)))((1c p b p rr a --=;(5)c b a r r r r 1111--=;(6)2tan2tanγβ⋅=rr a7.界心如果三角形一边上的一点和这边对的顶点把三角形的周界分割为两条等长的折线,那么就称这一点为三角形的周界中点.其中三角形的周界是指由M三角形的三边所组成的围.由于三角形的任意两边之和大于第三边,可知三角形任一边上的周界中点必介于这边两端点之间.三角形的顶点与其对边的周界中点的连线,叫三角形的周界中线(有时也称周界中线所在直线为三角形的周界中线).三角形的周界中线交于一点.定义:称三角形的周界中线的交点为三角形的界心.二、例题分析例1.设△ABC的外接圆O的半径为R,内心为I,A∠B,C∠,A<∠60︒=∠的外角平分线交圆O于E,证明:(1)AEIO=;(2)R<+2++<.IOIC1(IAR)3【证明】(1)延长BI交外接圆于M,连结Am,,OA,OM易知︒B∠60AOM,故△AOM为正三角形,==∠∴CM=.易证MAI=AMOM=OA=∠,MIA∠∴MIMA=.同理,MIMC=,即CA,,在以M为圆心,R为,OI半径的圆上,设AI的延长线交⌒BC于F,则AF、AE分别为A∠的内、外角平分线,︒EAF,即EF为⊙O的直径,=∠90∴AOE OFI OAI ∠=∠=∠21.又在⊙M 中,OMI OAI ∠=∠21,∴OMI AOE ∠=∠,但⊙M 与⊙O 为等圆,故OI AE =.(2)连接FC ,同上易证FC IF =,又︒=∠=∠60ABC IFC ,∴△IFC 为等边三角形,IF IC =∵)60(21)(212121︒-∠=∠-∠=∠=∠=∠C AMO AMI OMI AOE AFE ,记AFE ∠为θ∴AFAE AF IA AE IC IA IO +=++=++)cos (sin 2cos 2sin 2θθθθ+=+=R R R由C A ∠<∠知,︒<∠<︒12060C ,从而有︒<∠<︒602130C ,即︒<︒+∠<︒75152145C∴︒<++<︒75sin 2245sin 22R IC IA IO R ,又46275sin +=︒,故R IC IA IO R )31(2+<++<.例2.锐角△ABC 的外心为O ,线段BC OA ,的中点分别为M 、N .,OMN ABC ∠=∠4OMN ACB ∠=∠6.求OMN ∠.【解】设θ=∠OMN ,则θ4=∠ABC ,θ6=∠ACB ,θ10180)(180-︒=∠+∠-︒=∠ACB ABC BAC又θ1018021-︒=∠=∠=∠BAC BOC NOC ;θ82=∠=∠=∠ABC AOC MOC从而θθθ2180)10180(8-︒=-︒+=∠MON即OMN ∆为等腰三角形,OC OA OM ON 2121===∵︒=∠90ONC ,∴︒=∠60NOC ,又∵θ10180-︒=∠NOC ,∴︒==∠12θOMN例3.如图I O ,分别为△ABC 的外心和内心,AD 是BC边上的高。
三角形的、外心、内心、重心、垂心、和旁心(五心定理)之欧阳学文创编之欧阳家百创编
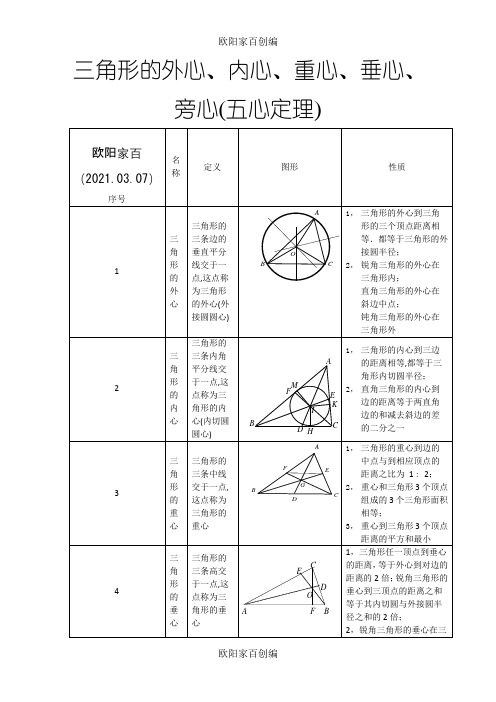
三角形的旁心
三角形的一条内角平分线与另两个外角平分线交于一点,称为三角形的旁心(旁切圆圆心)
1,每个三角形都有三个旁心;
2,旁心到三边的距离相等
附:三角形的中心:只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
三角形的外心、内心、重心、垂心、旁心(五心定理)
欧阳家百(2021.03.07)
序号
名称
定义
图形
性质
1
三角形的外心
三角形的三条边的垂直平分线交于一点,这点称为三角形的外心(外接圆圆心)
1,三角形的外心到三角形的三个顶点距离相等.都等于三角形的外接圆半径;
2,锐角三角形的外心在三角形内;
直角三角形的外心在斜边中点;
2,重心和三角形3个顶点组成的3个三角形面积相等;
3,重心到三角形3个顶点距离的平方和最小
4
三角形的垂心
三角形的三条高交于一点,这点称为三角形的垂心
1,三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍;锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍;
2,锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外;
钝角三角形的外心在三内角平分线交于一点,这点称为三角形的内心(内切圆圆心)
1,三角形的内心到三边的距离相等,都等于三角形内切圆半径;
2,直角三角形的内心到边的距离等于两直角边的和减去斜边的差的二分之一
3
三角形的重心
三角形的三条中线交于一点,这点称为三角形的重心
1,三角形的重心到边的中点与到相应顶点的距离之比为1∶ 2;
三角形“四心”定义与性质

三角形“四心”定义与性质-CAL-FENGHAI.-(YICAI)-Company One1三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心 定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;(2))(31++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
三角形“四心”定义与性质

三角形“四心”定义与性质之巴公井开创作所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 暗示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 暗示,它具有如下性质: 性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 暗示。
性 质:1.顶点与垂心连线必垂直对边, 即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 暗示。
性 质:G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=.4.向量性质:(1)0=++GC GB GA ;(2))(31PC PB PA PG ++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
三角形“四心”定义与性质

三角形“四心”定义与性质三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
〖半径〗2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.〖定义〗 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
〖圆周角与圆心角〗 4.向量形式:若点O 为ABC ∆所在的平面内一点,满足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(=0,则点O 为ABC ∆的外心。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
〖半径、定义〗2.三角形的面积=⨯21三角形的周长⨯内切圆的半径.〖三角形拆分〗 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
〖三角形全等〗 4.,2190A BIC ∠+=∠B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
4.向量形式:(1)若点I 为ABC ∆所在的平面内一点,并且满足=⋅+⋅+⋅c b a (其中c b a ,,为三角形的三边),则点I 为△ABC 的内心。
(2)设()+∞∈,0λ,则向量(+=λ,则动点P 的轨迹过ABC ∆的内心。
证4①:∠三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
(完整版)三角形“四心”定义与性质(可编辑修改word版)
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
∆ABC 的重心一般用字母O 表示。
性质:1.外心到三顶点等距,即OA =OB =OC 。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即OD ⊥BC, OE ⊥AC, OF ⊥AB .3. ∠A = 1∠BOC, ∠B =21∠AOC, ∠C =21∠AOB 。
2二、三角形的内心定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
∆ABC 的内心一般用字母I 表示,它具有如下性质:性质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
12.三角形的面积=⨯三角形的周长⨯内切圆的半径.23.AE =AF ,BF =BD, C D =CE ;AE +BF +CD =三角形的周长的一半。
4. ∠BIC = 90 +1∠A, ∠CIA = 90 +1∠B ,∠AIB = 90 +1∠C 。
2 2 2三、三角形的垂心定义:三角形三条高的交点叫重心。
∆ABC 的重心一般用字母H 表示。
性质:1.顶点与垂心连线必垂直对边,即AH ⊥BC, BH ⊥AC, CH ⊥AB 。
2.△ABH 的垂心为C ,△ BHC 的垂心为A ,△ ACH 的垂心为B 。
+ = + = + 四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
∆ABC 的重心一般用字母G 表示。
性 质:1. 顶点与重心G 的连线必平分对边。
2. 重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2 倍。
即GA = 2GD , GB = 2GE , GC = 2GF3. 重心的坐标是三顶点坐标的平均值. 即 x G =x A + x B + x C , y 3 G = y A + y B + y C . 34. 向量性质:(1) GA + GB + GC = 0 ;1 (2) = (PA + PB + PC ) ,5. 3 S ∆BGC = S ∆CGA = S ∆AGB = 1 S 3∆ABC 。
三角形“四心”定义与性质
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC 的重心一般用字母O 表示。
性质:1. 外心到三顶点等距,即OA OB OC 。
2. 外心与三角形边的中点的连线垂直于三角形的这一边,即OD BC ,OE AC ,OF AB .1 1 13. A BOC B AOC C AOB, ,2 2 2二、三角形的内心。
定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC 的内心一般用字母I 表示,它具有如下性质:性质:1. 内心到三角形三边等距,且顶点与内心的连线平分顶角。
2. 三角形的面积=12三角形的周长内切圆的半径.3. AE AF ,BF BD ,CD CE ;AE BF CD 三角形的周长的一半。
1 1 14. , 90 ,AIB C5.BIC 90 A CIA B 90 。
2 2 2三、三角形的垂心定义:三角形三条高的交点叫重心。
ABC 的重心一般用字母H 表示。
性质:1. 顶点与垂心连线必垂直对边,即AH BC ,BH AC ,CH AB。
2. △ABH 的垂心为 C ,△BHC 的垂心为 A ,△ACH 的垂心为 B 。
1四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
ABC 的重心一般用字母G 表示。
性质:4.顶点与重心G 的连线必平分对边。
5.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的 2 倍。
即GA 2GD , GB 2GE , GC 2GF6.重心的坐标是三顶点坐标的平均值.即x x x y y yA B C A B Cx , y .G G3 37.向量性质:(1)G A GB GC 0;1(2)( )PG PA PB PC ,38.S1BGC S S SCGA AGB3A BC。
五、三角形“四心”的向量形式:结论1:若点O 为ABC 所在的平面内一点,满足OA OB OB OC OC OA,则点O 为ABC 的垂心。
三角形外心内心重心垂心与向量性质
三角形外心内心重心垂心与向量性质第一篇:三角形外心内心重心垂心与向量性质三角形的“四心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
∆ABC的重心一般用字母O表示。
性质:1.外心到三顶点等距,即OA=OB=OC。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即OD⊥BC,OE⊥AC,OF⊥AB.3.向量性质:若点O为∆ABC所在的平面内一点,满足(OA+OB)⋅BA=(OB+OC)⋅CB=(OC+OA)⋅AC,则点O为∆ABC 的外心。
二、三角形的内心定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
∆ABC的内心一般用字母I表示,它具有如下性质:性质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=1⨯三角形的周长⨯内切圆的半径.23.向量性质:设λ∈(0,+∞),则向量AP=λ(点P的轨迹过∆ABC的内心。
AB|AB||AC|+AC),则动三、三角形的垂心定义:三角形三条高的交点叫重心。
∆ABC的重心一般用字母H表示。
性质:1.顶点与垂心连线必垂直对边,即AH⊥BC,BH⊥AC,CH⊥AB。
2.向量性质:结论1:若点O为∆ABC所在的平面内一点,满足OA⋅OB=OB⋅OC=OC⋅OA,则点O为∆ABC的垂心。
结论2:若点O为△ABC所在的平面内一点,满足OA+BC=OB+CA=OC+AB,则点O为∆ABC的垂心。
222222四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
∆ABC的重心一般用字母G表示。
性质:1.顶点与重心G的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GA=2GD,GB=2GE,GC=2GF 3.重心的坐标是三顶点坐标的平均值.即xG=xA+xB+xCy+yB+yC,yG=A.334.向量性质:(1)GA+GB+GC=0;(2)PG=1(PA+PB+PC)。
三角形的四心定义
∙三角形的四心定义:1、内心:三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
2、外心:是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
3、中心:三角形只有五种心重心、垂心、内心、外心、旁心,当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心。
4、重心:重心是三角形三边中线的交点。
∙三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心;2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合;3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合。
在△ABC中4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA6.S△ABC=abc/4R三角形的内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△=[(a+b+c)r]/2 (r是内切圆半径)三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3. 垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO?OD=BO?OE=CO?OF5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形“四心”定义与性质
欧阳光明(2021.03.07)
所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心
定 义:三角形三条中垂线的交点叫外心,
即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:
1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一
边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心
定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质: 性 质:
1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径.
3.CE CD BD BF AF AE ===,,;
=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心
定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:
1.顶点与垂心连线必垂直对边,
即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的
垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:
定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:
1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===
3.重心的坐标是三顶点坐标的平均值.
即3,3C B A
G C B A G y y y y x x x x ++=++=.
4.向量性质:(1)0=++GC GB GA ;
(2))(31PC PB PA PG ++=,
5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
五、三角形“四心”的向量形式:
结论1:若点O 为ABC ∆所在的平面内一点,满足⋅=⋅=⋅,
则点O 为ABC ∆的垂心。
结论2:若点O 为△ABC 所在的平面内一点,满足2
22222+=+=+, 则点O 为ABC ∆的垂心。
结论3:若点G 满足0=++GC GB GA ,则点G 为ABC ∆的重心。
结论4:若点G 为ABC ∆所在的平面内一点,满足
)(31++=,
则点G 为ABC ∆的重心。
结论5:若点I 为ABC ∆所在的平面内一点,并且满足
=⋅+⋅+⋅c b a
(其中c b a ,,为三角形的三边),则点I 为△ABC 的内心。
结论6:若点O 为ABC ∆所在的平面内一点,满足
⋅+=⋅+=⋅+)()()(,则点O 为ABC ∆的外心。
结论7:设()+∞∈,0λ,则向量
||||(AC AB AP +=λ,则动点P 的轨迹过
ABC ∆的内心。
