信号与系统 matlab答案
信号与系统matlab实验及答案
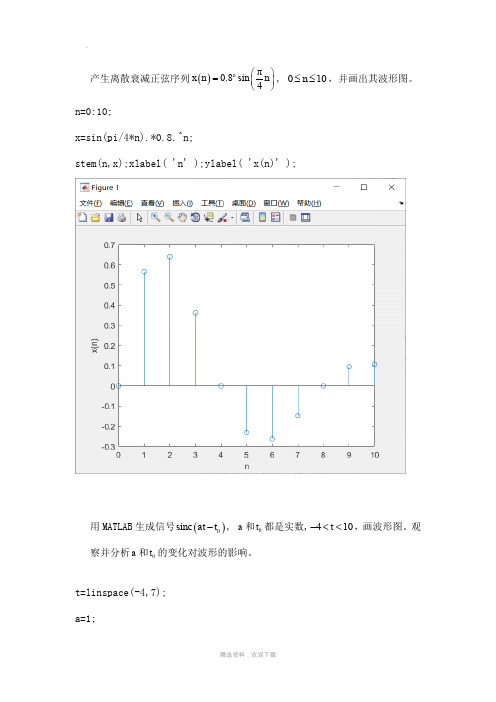
产生离散衰减正弦序列()π0.8sin 4n x n n ⎛⎫= ⎪⎝⎭, 010n ≤≤，并画出其波形图。
n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<，画波形图。
观察并分析a 和0t 的变化对波形的影响。
t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a 越大最大值越小，t0越大图像对称轴越往右移某频率为f 的正弦波可表示为()()cos 2πa x t ft =，对其进行等间隔抽样，得到的离散样值序列可表示为()()a t nT x n x t ==，其中T 称为抽样间隔，代表相邻样值间的时间间隔，1s f T=表示抽样频率，即单位时间内抽取样值的个数。
抽样频率取40 Hz s f =，信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。
请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图，并观察和对比分析样值序列的变化。
可能用到的函数为plot, stem, hold on 。
fs = 40;t = 0 : 1/fs : 1 ;% ƵÂÊ·Ö±ðΪ5Hz,10Hz,20Hz,30Hz f1=5;xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ;plot(t, xa) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('t(s)') ;ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ; subplot(1, 2, 2) ;stem(t, xa, '.') ;line([0, max(t)], [0, 0]) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('n') ;ylabel('X(n)') ;频率越高，图像更加密集。
matlab软件仿真实验（信号与系统）（1）
matlab软件仿真实验（信号与系统）（1）《信号与系统实验报告》学院：信息科学与⼯程学院专业：物联⽹⼯程姓名：学号：⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的：学习MATLAB的基本⽤法，了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
⼆、实验内容：例⼀已知x的取值范围，画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围，x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围，⽤subplot函数绘图。
参考程序：x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号：指数信号Ae at在MATLAB中可⽤exp函数表⽰，其调⽤形式为：y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序：A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号：正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰，其调⽤形式为：A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1，w0=2π，?=π/6) 参考程序：A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数：抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰，其定义为：sinc(t)=sin(πt)/( πt)其调⽤形式为：y=sinc(t)参考程序：t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号：在MATLAB中⽤rectpuls函数来表⽰，其调⽤形式为：y=rectpuls(t,width),⽤以产⽣⼀个幅值为1，宽度为width,相对于t=0点左右对称的矩形波信号，该函数的横坐标范围由向量t决定，是以t=0为中⼼向左右各展开width/2的范围，width的默认值为1。
信号与系统_MATLAB_实验_课后习题答案
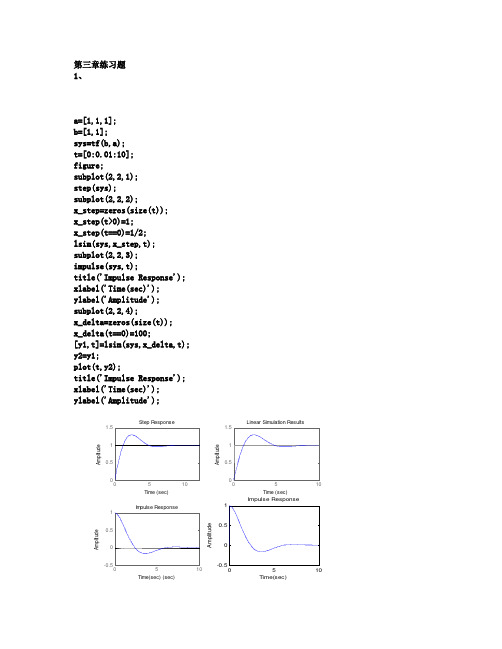
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下：function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下：t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下：function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下：function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同（b）Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数：Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统：Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统：Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
长江大学信号与系统matlab实验答案
实验1 信号变换与系统非时变性质的波形绘制●用MA TLAB画出习题1-8的波形。
●用MA TLAB画出习题1-10的波形。
Eg 1.8代码如下：function [y]=zdyt(t) %定义函数zdyty=-2/3*(t-3).*(heaviside(-t+3)-heaviside(-t));endt0=-10;t1=4;dt=0.02;t=t0:dt:t1;f=zdyt(t);y=zdyt(t+3);x=zdyt(2*t-2);g=zdyt(2-2*t);h=zdyt(-0.5*t-1);fe=0.5*(zdyt(t)+zdyt(-t));fo=0.5*(zdyt(t)-zdyt(-t));subplot(7,1,1),plot(t,f);title('信号波形的变化')ylabel('f(t)')grid;line([t0 t1],[0 0]);subplot(7,1,2),plot(t,y);ylabel('y(t)')grid;line([t0 t1],[0 0]);subplot(7,1,3),plot(t,x);ylabel('x(t)')grid;line([t0 t1],[0 0]);subplot(7,1,4),plot(t,g);ylabel('g(t)')grid;line([t0 t1],[0 0]);subplot(7,1,5),plot(t,h);ylabel('h(t)')grid;line([t0 t1],[0 0]);subplot(7,1,6),plot(t,fe);ylabel('fe(t)')grid;line([t0 t1],[0 0]);subplot(7,1,7),plot(t,fo);ylabel('fo(t)')grid;line([t0 t1],[0 0]);xlabel('Time(sec)')结果：Eg1.10代码如下：function [u]=f(t) %定义函数f(t) u= heaviside(t)-heaviside(t-2); endfunction [u] =y(t) %定义函数y(t)u=2*(t.*heaviside(t)-2*(t-1).*heaviside(t-1)+(t-2).*heaviside(t-2)); endt0=-2;t1=5;dt=0.01; t=t0:dt:t1; f1=f(t); y1=y(t); f2=f(t)-f(t-2); y2=y(t)-y(t-2); f3=f(t)-f(t+1); y3=y(t)-y(t+1);subplot(3,2,1),plot(t,f1); title('激励——响应波形图') ylabel('f1(t)')grid;line([t0 t1],[0 0]);-10-8-6-4-2024012信号波形的变化f (t)-10-8-6-4-2024012y (t)-10-8-6-4-2024012x (t)-10-8-6-4-2024012g (t)-10-8-6-4-2024012h (t)-10-8-6-4-202400.51f e (t)-10-8-6-4-2024-101f o (t)Time(sec)subplot(3,2,2),plot(t,y1); ylabel('y1(t)')grid;line([t0 t1],[0 0]); subplot(3,2,3),plot(t,f2); ylabel('f2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,4),plot(t,y2); ylabel('y2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,5),plot(t,f3); ylabel('f3(t)')grid;line([t0 t1],[0 0]); subplot(3,2,6),plot(t,y3); ylabel('y3(t)')grid;line([t0 t1],[0 0]); xlabel('Time(sec)')结果：实验2 微分方程的符号计算和波形绘制上机内容用MA TLAB 计算习题2-1，并画出系统响应的波形。
信号与系统第六章习题答案
第六章 离散系统的Ｚ域分析 ６．１学习重点 1、离散信号z 域分析法—ｚ变换，深刻理解其定义、收敛域以及基本性质；会根据ｚ变换的定义以及性质求常用序列的ｚ变换；理解ｚ变换与拉普拉斯变换的关系。
2、熟练应用幂级数展开法、部分分式法及留数法，求z 反变换。
3、离散系统z 域分析法，求解零输入响应、零状态响应以及全响应。
4、z 域系统函数()z H 及其应用。
5、离散系统的稳定性。
6、离散时间系统的z 域模拟图。
7、用MATLAB 进行离散系统的Z 域分析。
６．２ 教材习题同步解析 6.1 求下列序列的z 变换，并说明其收敛域。
（1）n 31，0≥n （2）n−−31，0≥n（3）nn−+ 3121，0≥n （4）4cos πn ，0≥n（5）+42sin ππn ，0≥n 【知识点窍】本题考察z 变换的定义式 【逻辑推理】对于有始序列离散信号[]n f 其z 变换的定义式为()[]∑∞=−=0n nzn f z F解：（1）该序列可看作[]n nε31()[][]∑∑∞=−∞=− == =010313131n n n nn n z z n n Z z F εε对该级数，当1311<−z ，即31>z 时，级数收敛，并有 ()13331111−=−=−z zz z F其收敛域为z 平面上半经31=z 的圆外区域 （2）该序列可看作[]()[]n n nnεε331−=−−()()[][]()[]()∑∑∞=−∞=−−=−=−=010333n nn nnnzzn n Z z F εε对该级数，当131<−−z ，即3>z 时，级数收敛，并有()()33111+=−−=−z zz z F 其收敛域为z 平面上半经3=z 的圆外区域（3）该序列可看作[][]n n nn n n εε+ = + −3213121()[][]()∑∑∑∞=−∞=−∞=−+ =+ = + =01010*********n nn n n nn n n n z z z n n Z z F εε对该级数，当1211<−z 且131<−z ，即3>z 时，级数收敛，并有 ()3122311211111−+−=−+−=−−z zz z z zz F 其收敛域为z 平面上半经3=z 的圆外区域（4）该序列可看作[]n n επ4cos()[]∑∑∑∑∞=−−∞=−−∞=−∞=−+=+== =0140140440*******cos 4cos n nj n nj nn j j n n z e z e z e e z n n n Z z F πππππεπ对该级数，当114<−ze j π且114<−−zejπ，即1>z 时，级数收敛，并有()122214cos 24cos 21112111212222441414+−−=+−−=−+−=−×+−×=−−−−z z zz z z z z e z z e z z z eze z F j j j j ππππππ其收敛域为z 平面上半经1=z 的圆外区域 （5）该序列可看作[][][]n n n n n n n n εππεππππεππ+=+= +2cos 2sin 222sin 4cos 2cos 4sin 42sin()[]()122212212212cos 22cos 2212cos 22sin 222cos 222sin 222cos 2sin 222222222200++=+++=+−−++−=+=+=∑∑∞=−∞=−z z z z z z z z z z z z z z z n z n n n n Z z F n nn n ππππππεππ 其收敛域为z 平面上半经1=z 的圆外区域 6.2 已知[]1↔n δ，[]a z z n a n −↔ε，[]()21−↔z z n n ε， 试利用z 变换的性质求下列序列的z 变换。
信号与系统 matlab答案
M2-3(1) function yt=x(t)yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); (2)function yt=x (t)yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5);t=0:0.001:6;subplot(3,1,1)plot(t,x2_3(t))title('x(t)')axis([0,6,-2,3])subplot(3,1,2)plot(t,x2_3(0.5*t))title('x(0.5t)')axis([0,11,-2,3])subplot(3,1,3)plot(t,x2_3(2-0.5*t))title('x(2-0.5t)')axis([-6,5,-2,3])图像为：M2-5(3) function y=un(k)y=(k>=0)untiled3.mk=[-2:10]xk=10*(0.5).^k.*un(k); stem(k,xk)title('x[k]')axis([-3,12,0,11])M2-5(6) k=[-10:10]xk=5*(0.8).^k.*cos((0.9)*pi*k) stem(k,xk)title('x[k]')grid onM2-7A=1;t=-5:0.001:5;w0=6*pi;xt=A*cos(w0*t);plot(t,xt)hold onA=1;k=-5:5;w0=6*pi;xk=A*cos(w0*0.1*k);stem(k,xk)axis([-5.5,5.5,-1.2,1.2])title('x1=cos(6*pi*t)&x1[k]')A=1;t=-5:0.001:5;w0=14*pi;xt=A*cos(w0*t);plot(t,xt)hold onA=1;k=-5:5;w0=14*pi;xk=A*cos(w0*0.1*k);stem(k,xk)axis([-5.5,5.5,-1.2,1.2])title('x2=cos(14*pi*t)&x2[k]')A=1;t=-5:0.1:5;w0=26*pi;xt=A*cos(w0*t);plot(t,xt)hold onA=1;k=-5:5;w0=26*pi;xk=A*cos(w0*0.1*k);stem(k,xk)axis([-5.5,5.5,-1.2,1.2])title('x1=cos(26*pi*t)&x1[k]')M2-9(1)k=-4:7;xk=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1];stem(k,xk,'file')(2) k=-12:21;x=[-3,0,0,-2,0,0,3,0,0,1,0,0,-2,0,0,-3,0,0,-4,0,0,2,0,0,-1,0,0,4,0,0,1,0,0,-1]; subplot(2,1,1)stem(k,x,'file')title('3倍内插')t=-1:2;y=[-2,-2,2,1];subplot(2,1,2)stem(t,y,'file')title('3倍抽取')axis([-3,4,-4,4])(3) k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; subplot(2,1,1)stem(k+2,x,'file')title('x[k+2]')subplot(2,1,2)stem(k-4,x,'file')title('x[k-4]')(4) k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1];stem(-fliplr(k),fliplr(x),'file')title('x[-k]')M4-1（1）对于周期矩形信号的傅里叶级数cn =-1/2j*sin(n/2*pi)*sinc(n/2) n=-15:15;X=-j*1/2*sin(n/2*pi).*sinc(n/2);subplot(2,1,1);stem(n,abs(X),'file');title('幅度谱')xlabel('nw');subplot(2,1,2);stem(n,angle(X),'file'); title('相位谱')（2）对于三角波信号的频谱是：Cn=-4n2π2+2nπsin nπ2+4n2π2cos nπ2n=-15:15;X=sinc(n)-0.5*((sinc(n/2)).^2); subplot(2,1,1);stem(n,abs(X),'file');title('幅度谱')xlabel('nw');subplot(2,1,2);stem(n,angle(X),'file');title('相位谱')M4-4(1) tau=0.5;T=100;N=T/tau;t=[0:tau:(T-tau)];x=(t>=0 & t<=2).*1;X=fftshift(tau*fft(x));w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau)); plot(w,X)grid on(4)tau=0.1;T=50;N=T/tau;t=[0:tau:(T-tau)];x=(t>=0).*exp(-t);X=fftshift(tau*fft(x));X=abs(X);w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau)); plot(w,X)grid on。
信号与系统实验__matlab
信号与系统部分01.分别用MATLAB 表示并绘出下列连续时间信号的波形：2()(2)()t f t e u t -=-02.分别用MATLAB 表示并绘出下列连续时间信号的波形：[]()cos()()(4)2tf t u t u t π=--03.分别用MATLAB 表示并绘出下列离散时间信号的波形：()12()()kf k u k =-04.分别用MATLAB 表示并绘出下列离散时间信号的波形：[]()()(8)f t k u k u k =--05.已知信号f (t)的波形如下图所示，试用MATLAB 绘出满足下列要求的信号波形。
()f t -06.已知信号f (t)的波形如下图所示，试用MATLAB 绘出满足下列要求的信号波形。
()f ata ＝0.507.已知信号f (t)的波形如下图所示，试用MATLAB 绘出满足下列要求的信号波形。
()f at ，a ＝208.已知信号f (t)的波形如下图所示，试用MATLAB 绘出满足下列要求的信号波形。
(0.51)f t +09.已知两信号1()(1)()f t u t u t =+-，2()()(1)f t u t u t =--，求卷积积分12()()()g t f t f t =*。
10.已知两信号1()()f t tu t =，20()()0t tt te u t f t t e-≥⎧=⎨<⎩，求卷积积分12()()()g t f t f t =*。
11.已知{}{}12()1,1,1,2,()1,2,3,4,5f k f k ==，求两序列的卷积和。
12.已知描述系统的微分方程如下，试用理论分析并计算系统的单位冲激响应h(t)，并用MATLAB 绘出系统单位冲激响应的波形，验证结果是否相同。
''()4'()4()'()3()y t y t y t f t f t ++=+13.已知描述系统的微分方程如下，试用解析方法求系统的单位冲激响应h(t)，并用MATLAB 绘出系统单位冲激响应的波形，验证结果是否相同。
信号与系统matlab实验习题3 绘制典型信号及其频谱图
绘制典型信号及其频谱图答案在下面四个常用信号及其傅里叶变换式如表1所示。
(1)绘制单边指数信号及其频谱图的MATLAB程序如下：close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;max_logF=max(abs(F));plot(w,20*log10(abs(F)/max_logF));xlabel('\omega');ylabel('|F(\omega)| indB');figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');请更改参数，调试此程序，绘制单边指数信号的波形图和频谱图。
观察参数a 对信号波形及其频谱的影响。
注：题目中阴影部分是幅频特性的对数表示形式，单位是(dB)，请查阅相关资料，了解这种表示方法的意义及其典型数值对应的线性增益大小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图，观察并对比各信号的频带宽度和旁瓣的大小。
(3)更改参数，调试程序，绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
答案附上程序代码：close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|';E=1，a=1,波形图 频谱图更改参数E=2，a=1;更改参数a ，对信号波形及其频谱的影响。
(完整版)信号与系统Matlab实验作业
实验一 典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示（单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号）1）画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
function y=u(t) y=t>=0;t=-3:0.01:3;f='exp(t)*(u(6-3*t)-u(-6-3*t))';ezplot(f,t);grid on;2）画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)';f2='exp(0.4*t)*sin(8*t)';figure(1)ezplot(f1,t);grid on;figure(2)ezplot(f2,t);grid on;t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on;t=0:0.01:10;f='(sign(t-3)+1)/2'; ezplot(f,t);grid on;5）单位冲击信号可看作是宽度为∆，幅度为1/∆的矩形脉冲，即t=t 1处的冲击信号为11111 ()()0 t t t x t t t otherδ∆⎧<<+∆⎪=-=∆⎨⎪⎩画出0.2∆=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))';ezplot(f,t);grid on;axis([0 2 -1 6]);2、典型离散信号的表示（单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列）编写函数产生下列序列：1）单位脉冲序列，起点n0，终点n f，在n s处有一单位脉冲。
北京交通大学《信号与系统》 课后matlab作业
Matlab课后作业1.M2-1（1）Matlab程序：t=-5:0.01:5;x=(t>0)-(t>2);plot(t,x);axis([-5,5,-2,2]);仿真结果：（8）Matlab程序：t=-10:0.01:10;pi=3.14;x=sin(pi*t)./(pi*t).*cos(30*t);plot(t,x);仿真结果：M2-2Matlab程序：t=-2:0.001:2;x=(t>-1)-(t>0)+2*tripuls(t-0.5,1,0); plot(t,x);axis([-2,2,-2,2]);仿真结果：M3-3（1）function yt=f(t)yt=t.*(t>0)-t.*(t>=2)+2*(t>=2)-3*(t>3)+(t>5); （2）Matlab程序：t=-10:0.01:11;subplot(3,1,1);plot(t,f(t));title('x(t)');axis([-1,6,-2,3]);subplot(3,1,2);plot(t,f(0.5*t));axis([-1,11,-2,3]);title('x(0.5t)');subplot(3,1,3);plot(t,f(2-0.5*t));title('x(2-0.5t)');axis([-9,5,-2,3]);仿真结果：M2-9(1)Matlab程序：k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果：（2）Matlab程序：k=-12:21;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; N=length(x);y=zeros(1,3*N-2);y(1:3:end)=x;stem(k,y);仿真结果：Matlab程序：k=-1:3;x=[0,0,-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; x1=x(1:3:end);stem(k-1,x1);仿真结果：（3）Matlab程序：k=-6:5;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果：程序>> k=-2:9;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> stem(k,x);结果程序>> k=-4:7;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> xk=fliplr(x);>> k1=-fliplr(k);>> stem(k1,xk);结果M3-1（1）程序>> ts=0;te=5;dt=0.01; >> sys=tf([2 1],[1 3 2]); >> t=ts:dt:te;>> x=exp(-3*t).*(t>=0); >> y=lsim(sys,x,t);>> plot(t,y);>> xlabel('Time(sec)') >> ylabel('y(t)')结果（2）程序>> ts=0;te=5;dt=0.0001; >>sys=tf([2 1],[1 3 2]); >>t=sys:dt:te;>>x=exp(-3*t).*(t>=0); >>y=lsim(sys,x,t);>>plot(t,y);>>xlabel('Time(sec)') >>ylabel('y(t)')结果M3-4>> x=[0.85,0.53,0.21,0.67,0.84,0.12]; >> k1=-2:3;>> h=[0.68,0.37,0.83,0.52,0.71];>> k2=-1:3;>> y=conv(x,h);>> k=(k1(1)+k2(1)):(k1(end)+k2(end)); >> stem(k,y)结果M6-1(1)>> num=[16 0 0];>> den=[1 5.6569 816 2262.7 160000]; >> [r,p,k]=residue(num,den)得r =0.0992 - 1.5147i0.0992 + 1.5147i-0.0992 + 1.3137i-0.0992 - 1.3137ip =-1.5145 +21.4145i-1.5145 -21.4145i-1.3140 +18.5860i-1.3140 -18.5860ik =[]所以可得 X(s)=j s j j s j j s j 5860.183140.13137.10992.05860.183140.13137.10992.04145.215145.15147.10992.021.4145j -1.5145s j 5147.1-0992.0++--+-++-++++++x(t)=3.0108e-1.5145tcos(21.4145t-1.5054)u(t)+2.635e-1.314tcos(18.586t+1.6462)u(t ) (2)X(s)=)2552^)(5(2^+++s s s s解:>> num=[1 0 0 0];den=conv([1 5],[1 5 25]);[r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r))得r =-5.0000 + 0.0000i-2.5000 - 1.4434i-2.5000 + 1.4434ip =-5.0000 + 0.0000i-2.5000 + 4.3301i-2.5000 - 4.3301ik =1angle =3.1416-2.61802.6180mag =5.00002.88682.8868所以X(s)=3301.45.24434.15.23301.45.24434.15.25s 5.0-1j s j j s j +++-+-+--+++x(t)=δ(t)+5e-5tu(t)+5.7736e-2.5tcos(4.3301t-2.618)u(t)M6-2程序>> t=0:0.1:10;>> y1=(2.5*exp(-t)-1.5*exp(-3*t)).*(t>=0);>> y2=((1/3)+2*exp(-t)-(5/6)*exp(-3*t)).*(t>=0);>> y=((1/3)+(9/2)*exp(-t)-(7/3)*exp(-3*t)).*(t>=0);>> plot(t,y1,'r-',t,y2,'g--',t,y,'b-')>> xlabel('Time');>> legend('零输入响应','零状态响应','完全响应')结果M6-5>> num=[1 2];>> den=[1 2 2 1];>> sys=tf(num,den);>> pzmap(sys)>> num=[1 2];den=[1 2 2 1];[r,p,k]=residue(num,den) [angle,mag]=cart2pol(real(r),imag(r))1.0000 + 0.0000i-0.5000 - 0.8660i-0.5000 + 0.8660ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660ik =[]angle =-2.09442.0944mag =1.00001.00001.0000所以H(s)=866.05.0866.05.0866.05.0866.05.01s 1j s j j s j +++-+-+--++系统冲激响应h(t)=e-tu(t)+2e-0.5tcos(0.866t-2.0944)u(t)>> num=[1 2];>> den=conv([1 0],[1 2 2 1]);>> [r,p,k]=residue(num,den)r =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i2.0000 + 0.0000ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i0.0000 + 0.0000ik =[][angle,mag]=cart2pol(real(r),imag(r))angle =3.14162.0944-2.0944mag =1.00001.00001.00002.0000所以Y(s)=s j s j j s j 2866.05.0866.05.0866.05.0866.05.0-1s 1-+++--+-++++ 系统阶跃响应y(t)=e-tu(t)+2e-0.5tcos(0.866t+2.0944)u(t)因为系统的冲激响应h(t)=e-tu(t)-1.00001e-0.5tcos(0.866t)u(t)+1.73205e-0.5tsin(0.866t)u(t) 所以系统的频率响应H(j ω)=5.0)866.0(866.05.0)866.0(866.05.0)866.0(5.05.0)886.0(5.01j 1j j j j ++--+--++-+++++ωωωωω。
信号与系统matlab作业2：对任意两段声音的卷积
题目：录两段不同的声音（语音、音乐、噪声均可），时间自己设定，然后再将这两段声音卷积。
要求：分别播放出每段声音（自己听）、分别显示每段声音的波形，从声音和波形两方面理解卷积的作用。
解：先用MATLAB录制两段不同的声音（即附件里的shengyin1,shengyin2）,其音频时间均为5秒，采样频率为40000Hz。
然后再用MATLAB画出两段声音及卷积后声音的波形图（如图【1】），并保存下两段卷积后的声音（即附件里的juanjishengyin）。
图【1】图【1】的MATALB程序：clc,clear[Y1,fs1]=audioread('shengyin1.wav');%获取音频1文件，并返回采样数据到向量y 中，fs表示采样频率[Y2,fs2]=audioread('shengyin2.wav');%获取音频1文件，并返回采样数据到向量y 中，fs表示采样频率ft1 = Y1(:,1);sigLength1 = length(ft1); %获取声音长度t1=(0:sigLength1-1)/fs1; %求出音频1对应的时间坐标subplot(3,1,1);plot(t1,ft1);%画出音频1的波形图title('音频1的波形图');xlabel('时间(s)');ylabel('振幅');grid;ft2 = Y2(:,1);sigLength2 = length(ft2); %获取声音长度t2=(0:sigLength2-1)/fs2; %求出音频2对应的时间坐标subplot(3,1,2);plot(t2, ft2);%画出音频2的波形图title('音频2的波形图');xlabel('时间(s)');ylabel('振幅');grid;ft=conv(ft1,ft2); %将两段音频进行卷积sigLength = length(ft); %获取声音长度t=(0:sigLength-1)/fs1;subplot(3,1,3);plot(t,ft);%画出卷积后的波形图title('音频1和音频2卷积后的波形图');xlabel('时间(s)');ylabel('振幅');grid;wavwrite(ft,40000,16,'juanjishengyin');%保存卷积后的声音总结：通过这次MATALB作业，观察三个不同的波形图（如图【1】）可知，卷积的作用就是一个信号函数在另一个信号函数上的加权叠加，通俗的说，它就是在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。
信号与系统matlab实验与答案
产生离散衰减正弦序列xn 0.8nsin πn, 0 n 10，并画出其波形图。
4n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB生成信号sincat t0,a和t0都是实数,4 t 10，画波形图。
观察并分析a和t0的变化对波形的影响。
t=linspace(-4,7);a=1;t0=2;y=sinc(a*t-t0);plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a越大最大值越小，t0越大图像对称轴越往右移某频率为f的正弦波可表示为x a t cos2π，对其进行等间隔抽样，得到ft的离散样值序列可表示为xnx a t ，其中T称为抽样间隔，代表相邻tnT样值间的时间间隔，f s1表示抽样频率，即单位时间内抽取样值的个数。
T抽样频率取f s40Hz，信号频率f分别取5Hz,10Hz,20Hz和30Hz。
请在同一张图中同时画出连续信号x a t t和序列xn nT的波形图，并观察和对比分析样值序列的变化。
可能用到的函数为plot,stem,holdon。
fs=40;t=0:1/fs:1;%?μ?ê·?±e?a5Hz,10Hz,20Hz,30Hzf1=5;xa=cos(2*pi*f1*t);subplot(1,2,1);plot(t,xa);axis([0,max(t),min(xa),max(xa)]);xlabel( 't(s)' );ylabel('Xa(t)');line([0,max(t)],[0,0]);subplot(1,2,2);stem(t,xa, '.' );line([0,max(t)],[0,0]);axis([0,max(t),min(xa),max(xa)]);xlabel( 'n' );ylabel( 'X(n)' );频率越高，图像更加密集。
《信号与系统》MATLAB仿真实验讲义
《信号与系统》MATLAB仿真实验讲义（第二版）肖尚辉编写宜宾学院电信系电子信息教研室《信号与系统》课程2004年3月 宜宾使用对象：电子专业02级3/4班（本科）实验一 产生信号波形的仿真实验一、实验目的：熟悉MATLAB软件的使用，并学会信号的表示和以及用MATLAB来产生信号并实现信号的可视化。
二、实验时数：3学时+3学时（即两次实验内容）三、实验内容：信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。
对信号进行时域分析，首先需要将信号随时间变化的规律用二维曲线表示出来。
对于简单信号可以通过手工绘制其波形，但对于复杂的信号，手工绘制信号波形显得十分困难，且难以绘制精确的曲线。
在MATLAB中通常用三种方法来产生并表示信号，即（1）用MATLAB软件的funtool符合计算方法（图示化函数计算器）来产生并表示信号；（2）用MATLAB软件的信号处理工具箱（Signal Processing Toolbox）来产生并表示信号；（3）用MATLAB软件的仿真工具箱Simulink中的信号源模块。
（一） 用MATLAB软件的funtool符合计算方法（图示化函数计算器）来产生并表示信号在MATLAB环境下输入指令funtool，则回产生三个视窗。
即figure No.1：可轮流激活，显示figure No.3的计算结果。
figure No.2：可轮流激活，显示figure No.3的计算结果。
figure No.3：函数运算器，其功能有：f，g可输入函数表达式；x是自变量，在缺省时在[－2pi，2pi]的范围内；自由参数是a；在分别输入完毕后，按下面四排的任一运算操作键，则可在figure No.1或figure No.2产生相应的波形。
学生实验内容：产生以下信号波形3sin(x)、5exp(-x)、sin(x)/x、1－2abs(x)/a、sqrt(a*x)（二） 用MATLAB软件的信号处理工具箱（Signal Processing Toolbox）来产生并表示信号一种是用向量来表示信号，另一种则是用符合运算的方法来表示信号。
matlab与信号系统实验题库（1）
matlab与信号系统实验题库（1）1．设，试⽤MATLAB画出该系统的幅频特性和相频特性。
w=0:0.025:15;b=[1];a=[0.08,0.4,1];H=freqs(b,a,w);subplot(2,1,1);plot(w,abs(H));grid;title('H(jw)的幅频特性');subplot(2,1,2);plot(w,angle (H));grid;title('H(jw)的相频特性');2. 绘制出y（t)=ε（t-1)- ε（t-4)的幅频特性曲线。
syms t wGt=sym('heaviside(t-1)-heaviside(t-4)');Fw=fourier(Gt,t,w);FFw=maple('convert',Fw,'piecewise');FFP=abs(FFw);ezplot(FFP,[-10*pi 10*pi]);grid;axis([-10*pi 10*pi 0 3.5])3.若某连续系统的输⼊为e(t)，输出为r(t)，系统的微分⽅程为：,y’(0_)=5,y(0_)=0;,求全响应。
a=[1 5 6];b=[0 3 2];%定义a，b[A B C D]=tf2ss(b,a);%定义A,B,C,,D的返回值t=0:0.01:5;%定义时间范围f=exp(-2*t); %定义函数X0=[5,0];%系统状态变量X=[x1,x2,…..xn]'在t=0时刻的初值。
xlabel('t');%定义横标题title('全响应y(t)');%定义总横标题grid on;%⽹格4.求的拉⽒变换式，并⽤MATLAB绘制拉⽒变换在s平⾯的三维曲⾯图。
syms t s %定义符号变量ft=sym('2*exp(-t)*Heaviside(t)+5*exp(-3*t)*Heaviside(t)'); %定义时间函数f(t)的表达式Fs=laplace(ft) %求f(t)的拉⽒变换式F(s)FFss=abs(Fs); %求出F(s)的模ezmesh(FFss); %画出拉⽒变换的⽹格曲⾯图ezsurf(FFss); %画出带阴影效果的三维曲⾯图colormap(hsv); %设置图形中多条曲线的颜⾊顺序5.求的拉⽒变换式，并⽤MATLAB绘制拉⽒变换在s平⾯的三维曲⾯图。
信号与系统基础-应用WEB和MATLAB第三版英文影印版课后练习题含答案
信号与系统基础-应用WEB和MATLAB第三版英文影印版课后练习题含答案简介《信号与系统基础-应用WEB和MATLAB第三版》是一本介绍信号与系统基础理论及其在工程中应用的教材。
本书作者结合MATLAB软件及其工具箱来讲解教材，实现了理论和实践的结合。
为了深入学习信号与系统，本书配有大量课后习题，可有效帮助读者巩固和应用所学的理论知识。
本文为您提供该书的英文影印版课后习题答案，方便您学习和参考。
目录Chapter 11.1 信号的分类1. 什么是信号？信号是指在时间或空间上发生变化的物理量，包括声音、光、电等。
2. 信号的分类信号可根据其时间性质、频率性质、波形等特征进行分类。
其中，时间性质将信号分为连续时间信号和离散时间信号；频率性质将信号分为周期信号和非周期信号；波形将信号分为分段常值信号、线性信号、非线性信号等。
Chapter 22.1 系统的概念1. 什么是系统？系统是指由若干个元件组成的整体，它们相互作用，从而实现一定功能的。
在信号与系统中，系统可分为线性系统和非线性系统，以及时变系统和时不变系统等。
2. 系统的分类系统可根据其时变性质、线性性质、因果性质、稳定性质等特征进行分类。
其中，线性时不变系统(简称LTI系统)占据了信号与系统中相当重要的地位。
结论通过以上目录，我们可以发现，信号与系统是一门重要的学科，为电子与通信领域提供了核心知识。
而《信号与系统基础-应用WEB和MATLAB第三版》借助MATLAB软件实现理论与实践的结合，使得学习更加直观、丰富。
本文提供该书英文影印版的课后习题答案，希望能够对您的学习有所帮助。
信号与系统部分实验matlab代码-供参考
信号与系统第三版112学期部分实验代码目录实验一 常用信号的实现和时域变换部分实验答案 (1)实验二 LTI 时间系统的时域分析 (3)实验四 连续信号与系统的频域分析 (4)实验七 连续时间信号的采样与重构 (15)实验一 常用信号的实现和时域变换部分实验答案（1）⎪⎭⎫ ⎝⎛=-t e t f t 32sin )(1.0t=0:0.1:30; x=exp(-0.1*t).*sin(2/3*t);plot(t,x);axis([0 30 -1 1]); grid;xlabel('Time(sec)'); ylabel('f(t)'); …………………………………………………………………………………………… 对上面的f(t)进行抽样f(n)=f(t)|t=nT =x(nT)就可以得到抽样信号，将上述命令里的时间增量改为1s ，plot(t,x)命令改为 可以得到下图。
4．已知离散序列x(n)如图所示，试用Matlab 编程绘出以下的离散序列波形。
（1）x(-n+3)clc;close all;clear all;n=-3:2x=[3 3 3 3 2 1];[x1,n1]=xlpy(x,n,-3);[x2,n2]=xlfz(x1,n1);subplot(311)stem(n,x,'filled');axis([min(n)-1,max(n)+1,min(x)-0.5,max(x)+0.5]) subplot(312)stem(n1,x1,'filled');axis([min(n1)-1,max(n1)+1,min(x1)-0.5,max(x1)+0.5]) subplot(313)stem(n2,x2,'filled');axis([min(n2)-1,max(n2)+1,min(x2)-0.5,max(x2)+0.5])(2) x(n-3)x(n+2)clc;close all;clear all;n=-3:2x=[ 3 3 3 3 2 1 ];[x1,n1]=xlpy(x,n,3);[x2,n2]=xlpy(x,n,-2);nn=-5:5;x3=[0 0 0 0 0 x1];x4=[x2 zeros(1,5)];x=x3.*x4;subplot(311)stem(nn,x3,'filled');subplot(312)stem(nn,x4,'filled');subplot(313)stem(nn,x,'filled');实验二 LTI 时间系统的时域分析6.对于因果和稳定的LTI 系统，对于下列二阶微分方程确定其单位冲激响应是否是欠阻尼、过阻尼或临界阻尼，画出系统的h(t)和频率响应模的波特图。
信号与信号处理实验参考答案
信号与信号处理实验参考答案实验⼀熟悉MATLAB 环境2、（2）粗略描绘下列各函数的波形说明：MA TLAB 中有函数ttt c ππsin )(sin = ④ f(t)=sint/tt=-3*pi:0.01*pi:3*pi; t1=t/pi; y=sinc(t1); plot(t,y); hold onplot(t,0)⑤在⾃⼰的⼯作⽬录work 下创建Heaviside 函数的M ⽂件，该⽂件如下：function f=Heaviside(t)f=(t>0) %t>0时f 为1，否则f 为0在命令窗⼝输⼊如下语句，就能绘出u(t)的波形。
t=-1:0.01:3; f=Heaviside(t); plot(t,f) axis([-1 3 –0.2 1.2]) ⑥t=-1:0.01:2;g=Heaviside(t)-Heaviside(t-1); plot(t,g);axis([-1 2 -0.2 1.2]) hold on plot(t,0)4、分别⽤for 和while 循环结构编写程序，求出s=∑=632k k=1+2+22+23+…+262+263并考虑⼀种避免循环的简洁⽅法来进⾏求和。
程序如下： s=1; for k=1:63s=s+2^k;s运⾏结果是：s =1.8447e+019（2）s=1;k=1;while k<=63s=s+2^k;k=k+1;ends运⾏结果：s =1.8447e+019(3)k=0:63;s=sum(2.^k)实验⼆信号的卷积与系统的响应和阶跃响应1．n=0:20;hn=0.9.^n;xn=[0,0 ones(1,8),0,0];yn=conv(hn,xn);stem(yn)3. 利⽤MA TLAB绘制下列信号的卷积积分f1(t)*f2(t)的时域波形。
（1）f1(t)=2[u(t+1)-u(t-1)], f2(t)=u(t+2)-u(t-2)（2）f1(t)=tu(t), f2(t)=u(t)（3）f1(t)=u(t)-u(t-4), f2(t)=sin(лt)u(t);（4）f1(t)=e-2t u(t), f2(t)=e-t u(t)(1) 先编写实现连续信号卷积的通⽤函数sconv(),程序如下：function[f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t)%f:卷积积分f(t)对应的⾮零样值向量%k:f(t)的对应时间向量%f1:f1(t)⾮零样值向量%f2:f2(t)⾮零样值向量%k1:f1(t)的对应时间向量%k2:序列f2(t)的对应时间向量%p:取样时间间隔f=conv(f1,f2); %计算序列f1与f2的卷积ff=f*p;k0=k1(1)+k2(1); %计算序列f的⾮零样值的起点位置k3=length(f1)+length(f2)-2; %计算卷积和f的⾮零样值的宽度k=k0:p:((k3-(0-k0)/p)*p); %确定卷积和f⾮零样值的时间向量subplot(2,2,1)plot(k1,f1) %绘制f1(t)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) %将第三个⼦图的横坐标范围扩为原来的2.5倍title('f(t)=f1(t)*f2(t)') xlabel('t')ylabel('f(t)')p=0.01;k1=-1:p:1;f1=2*ones(1,length(k1));k2=-2:p:2;f2=ones(1,length(k2));[f,k]=sconv(f1,f2,k1,k2,p)（2）p=0.01;k1=0:p:10;k2=0:p:10;f2=ones(1,length(k2)); [f,k]=sconv(f1,f2,k1,k2,p)第（2）题图上实验⼆信号的卷积与系统的响应1．n=0:20;hn=0.9.^n;xn=stepseq(2,0,20)-stepseq(10,0,20);yn=conv(hn,xn);stem(yn)2．（1）p=0.01;k1=-2:p:2;f1=2*(u(k1+1)-u(k1-1));f2=u(k2+2)-u(k2-2);[f,k]=sconv(f1,f2,k1,k2,p)p=0.01;k1=-1:p:10;f1=k1.*u(k1);k2=k1;f2=u(k2);[f,k]=sconv(f1,f2,k1,k2,p)（3）p=0.01;k1=-4:p:10; f1=u(k1)-u(k1-4);k2=k1;f2=sin(pi*k2).*u(k2); [f,k]=sconv(f1,f2,k1,k2,p)5．已知描述某连续系统的微分⽅程为：y’’(t)+5y’(t)+8y(t)=3f’’(t)+2f(t)绘出系统的冲激响应波形，求出t=0.5s, 1s, 1.5s, 2s系统冲激响应的数值解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
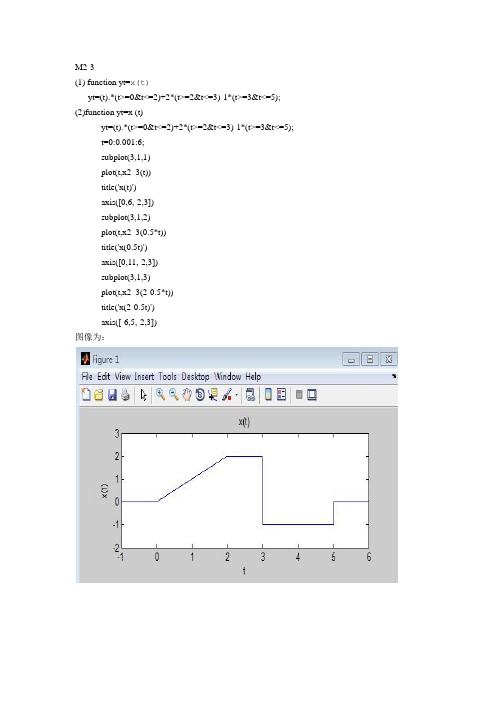
M2-3
(1) function yt=x(t)
yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5); (2)function yt=x (t)
yt=(t).*(t>=0&t<=2)+2*(t>=2&t<=3)-1*(t>=3&t<=5);
t=0:0.001:6;
subplot(3,1,1)
plot(t,x2_3(t))
title('x(t)')
axis([0,6,-2,3])
subplot(3,1,2)
plot(t,x2_3(0.5*t))
title('x(0.5t)')
axis([0,11,-2,3])
subplot(3,1,3)
plot(t,x2_3(2-0.5*t))
title('x(2-0.5t)')
axis([-6,5,-2,3])
图像为：
M2-5
(3) function y=un(k)
y=(k>=0)
untiled3.m
k=[-2:10]
xk=10*(0.5).^k.*un(k); stem(k,xk)
title('x[k]')
axis([-3,12,0,11])
M2-5
(6) k=[-10:10]
xk=5*(0.8).^k.*cos((0.9)*pi*k) stem(k,xk)
title('x[k]')
grid on
M2-7
A=1;
t=-5:0.001:5;
w0=6*pi;
xt=A*cos(w0*t);
plot(t,xt)
hold on
A=1;
k=-5:5;
w0=6*pi;
xk=A*cos(w0*0.1*k);
stem(k,xk)
axis([-5.5,5.5,-1.2,1.2])
title('x1=cos(6*pi*t)&x1[k]')
A=1;
t=-5:0.001:5;
w0=14*pi;
xt=A*cos(w0*t);
plot(t,xt)
hold on
A=1;
k=-5:5;
w0=14*pi;
xk=A*cos(w0*0.1*k);
stem(k,xk)
axis([-5.5,5.5,-1.2,1.2])
title('x2=cos(14*pi*t)&x2[k]')
A=1;
t=-5:0.1:5;
w0=26*pi;
xt=A*cos(w0*t);
plot(t,xt)
hold on
A=1;
k=-5:5;
w0=26*pi;
xk=A*cos(w0*0.1*k);
stem(k,xk)
axis([-5.5,5.5,-1.2,1.2])
title('x1=cos(26*pi*t)&x1[k]')
M2-9
(1)
k=-4:7;
xk=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1];
stem(k,xk,'file')
(2) k=-12:21;
x=[-3,0,0,-2,0,0,3,0,0,1,0,0,-2,0,0,-3,0,0,-4,0,0,2,0,0,-1,0,0,4,0,0,1,0,0,-1]; subplot(2,1,1)
stem(k,x,'file')
title('3倍内插')
t=-1:2;
y=[-2,-2,2,1];
subplot(2,1,2)
stem(t,y,'file')
title('3倍抽取')
axis([-3,4,-4,4])
(3) k=-4:7;
x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; subplot(2,1,1)
stem(k+2,x,'file')
title('x[k+2]')
subplot(2,1,2)
stem(k-4,x,'file')
title('x[k-4]')
(4) k=-4:7;
x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1];
stem(-fliplr(k),fliplr(x),'file')
title('x[-k]')
M4-1
（1）对于周期矩形信号的傅里叶级数cn =-1/2j*sin(n/2*pi)*sinc(n/2) n=-15:15;
X=-j*1/2*sin(n/2*pi).*sinc(n/2);
subplot(2,1,1);
stem(n,abs(X),'file');
title('幅度谱')
xlabel('nw');
subplot(2,1,2);
stem(n,angle(X),'file'); title('相位谱')
（2）对于三角波信号的频谱是：Cn=-4
n2π2+
2
nπ
sin nπ
2
+
4
n2π2
cos nπ
2
n=-15:15;
X=sinc(n)-0.5*((sinc(n/2)).^2); subplot(2,1,1);
stem(n,abs(X),'file');
title('幅度谱')
xlabel('nw');
subplot(2,1,2);
stem(n,angle(X),'file');
title('相位谱')
M4-4
(1) tau=0.5;T=100;N=T/tau;
t=[0:tau:(T-tau)];
x=(t>=0 & t<=2).*1;
X=fftshift(tau*fft(x));
w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau)); plot(w,X)
grid on
(4)
tau=0.1;T=50;N=T/tau;
t=[0:tau:(T-tau)];
x=(t>=0).*exp(-t);
X=fftshift(tau*fft(x));X=abs(X);
w=-(pi/tau)+(0:N-1)*(2*pi/(N*tau)); plot(w,X)
grid on。